图1 角度跟踪系统整体框图
马 越,李朝海
(电子科技大学电子工程学院,四川成都611731)
摘 要:飞机、导弹等高速运动载体与卫星系统实时通信过程中,载体的姿态变化,会影响通信质量。为使载体上的相控阵天线始终对准卫星方向,保持载体与卫星正常通信,提出了一种角度跟踪系统设计方案,对系统关键部分的功能进行说明;针对均匀对称的矩形阵列,在单脉冲测角理论和卡尔曼滤波算法的基础上进行研究和改进,提出了基于和差波束测角和自适应α-β滤波的角度跟踪算法,实现了对来波的角度测量与跟踪。通过仿真,对系统测角精度与跟踪精度进行说明,结合算法原理分析影响系统跟踪精度的因素。
关键词:相控阵天线;和差波束;α-β滤波;角度跟踪
运动载体卫星通信系统,即“动中通”,具有机动灵活、覆盖范围广、抗干扰能力突出等特点,在军事、民用领域上扮演着不可替代的角色。其系统设计的关键技术在于稳定准确的卫星跟踪能力。高精度的跟踪系统,能有效地隔离天线平台的运动,自身姿态的旋转以及平台周围位置环境对卫星通信的影响,使天线始终对准卫星,保证平台在高速运动中能够与卫星保持连续正常通信[1]。
卫星跟踪系统按功能主要分为天线波束控制、资源调度、信号搜索捕获、角度估计与跟踪等。角度估计与角度跟踪是整个系统的关键部分。常见的角度估计方法主要有直接比相法、子阵相关法[2-3]以及空间谱估计方法等。本文研究的和差波束测角方法,测角精度更高,并通过匹配滤波提高系统抗干扰能力。角度跟踪的经典方法是卡尔曼滤波[4]以及扩展卡尔曼滤波等。但其涉及增益矩阵的计算,运算量大,工程实现比较复杂。α-β滤波[5]能够克服这一问题,工程实现简单。本文在αβ滤波算法的基础上,提出自适应α-β滤波算法,根据方差的变化实时调整滤波器增益,提高算法的稳健性。
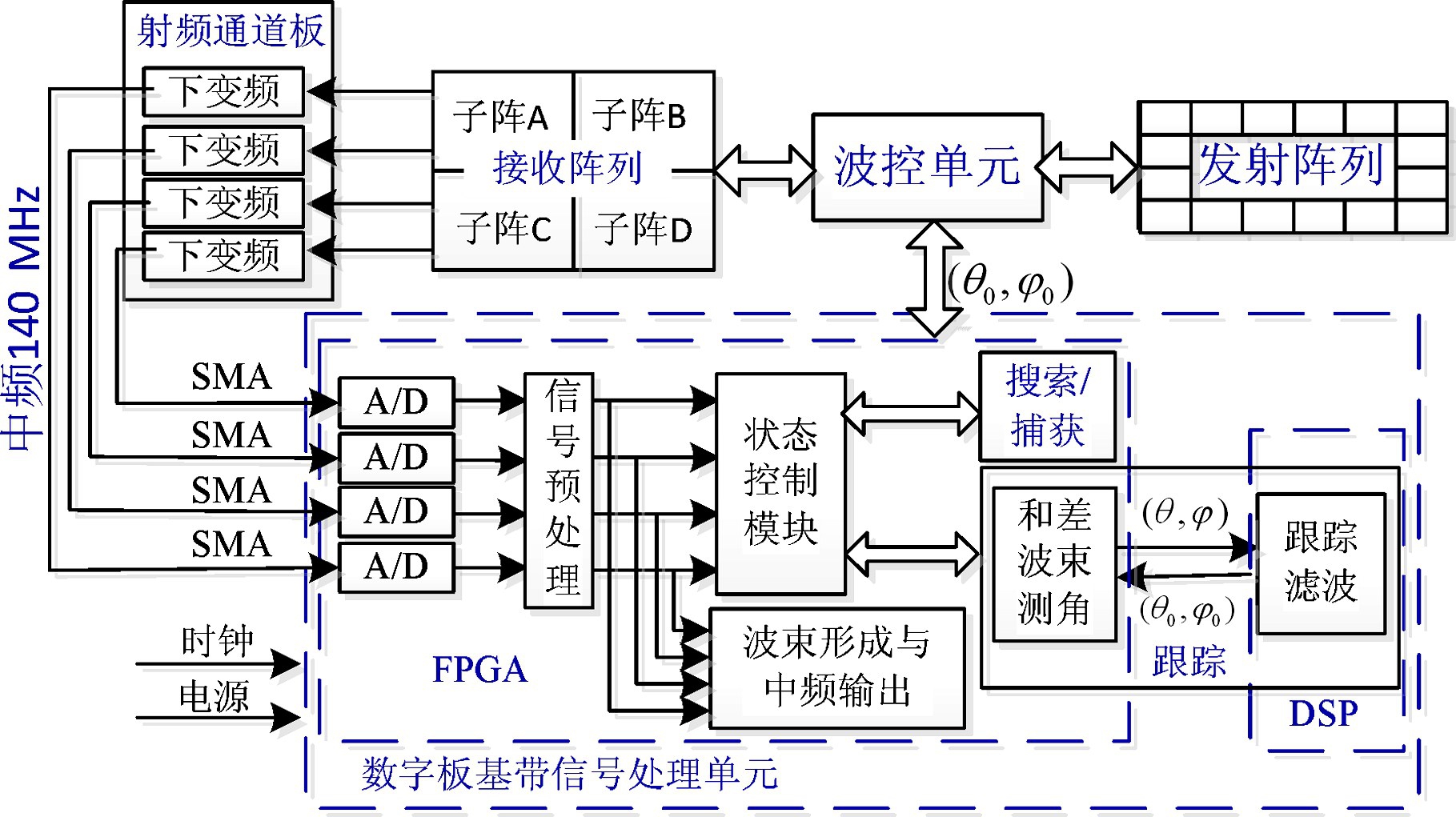
运动载体角度跟踪系统由波控单元、收发阵列、射频通路以及基带信号处理单元等部分组成。将接收阵列天线划分成4个子阵,每个子阵包含8×8个均匀分布的间距为半波长的阵元。各子阵输出的微弱信号经射频通路作放大以及模拟下变频处理,得到4路中频信号,通过SMA接口送入数字板。数字板基带信号处理单元通过4路ADC对各子阵输出信号进行采样,采样频率为100 MHz,得到基带数字信号。信号经过FIFO,数字下变频(DDC),通道幅相校正等预处理模块后,结合载体平台波控单元提供的系统初始引导信息,完成目标搜索/捕获,利用和差波束测角对卫星进行角度估计和跟踪滤波,把角度预测值传给运动载体波控单元,实时调整天线波束指向,从而保证阵列天线一直对准卫星来波方向。系统整体架构如图1所示。
图1 角度跟踪系统整体框图
在角度跟踪系统工作的开始阶段,载体波控单元提供的初始引导信息跟实际卫星方向存在一定偏差,若直接进入角度跟踪状态,系统角度测量和跟踪精度也会受到极大的影响。因此,需要先对来波方向进行搜索/捕获,成功捕获信号后转入跟踪状态。
搜索/捕获实现逻辑框图如图2所示。载体波控单元根据引导信息,给出初始天线波束指向。并根据系统搜索捕获状态下给出的波位调整信息,实时地对波束指向作出调整。对每一个波位,系统对四子阵输出信号A/D采样后,经预处理模块后对子阵间信号作互相关运算,若超过检测门限,则对其和波束进行解扩、解调等,确认是期望的协作通信信号,则捕获成功,系统转入角度跟踪状态;否则,捕获失败,反馈信息至波控单元,按照设定的波位编排方案调整波束指向,继续对来波方向进行搜索/捕获。
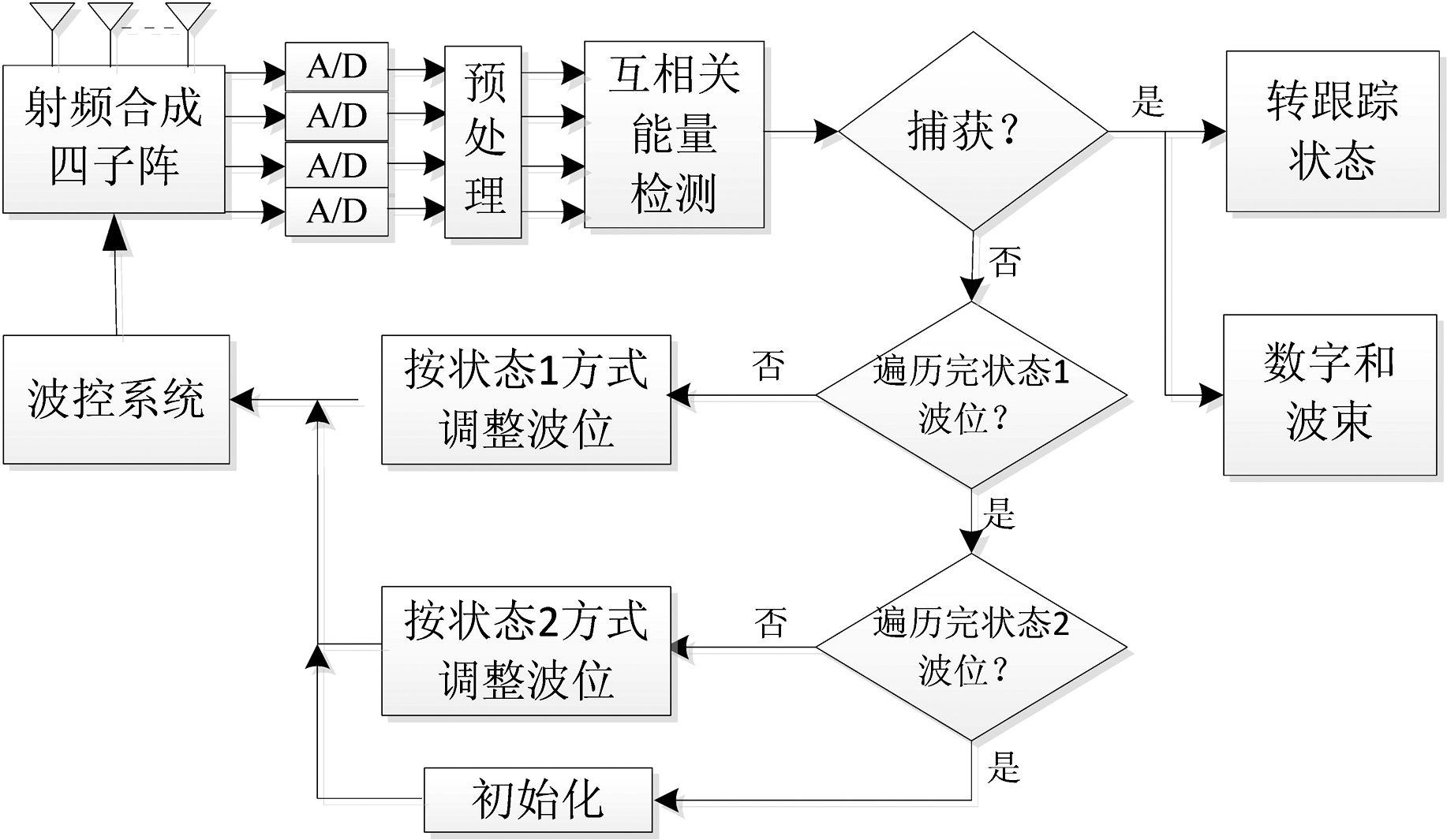
图2 搜索/捕获实现逻辑框图
系统波位顺序设定了两种状态[6],如图3所示。系统初始化获取引导信息,将引导信息中的指向作为初始波束指向的中心波位,按照状态1的顺序调整波束指向进行搜索。若遍历状态1中5个波位均未搜索/捕获信号,说明此时系统初始引导信息精度较差,则将状态1中的中心波位(波位1)按照状态2的顺序进行调整,在状态2中9个中心波位依次按照状态1方式形成5个搜索波位,进行搜索/捕获。若遍历状态2波位仍未捕获信号,则系统重新初始化,更新引导信息。
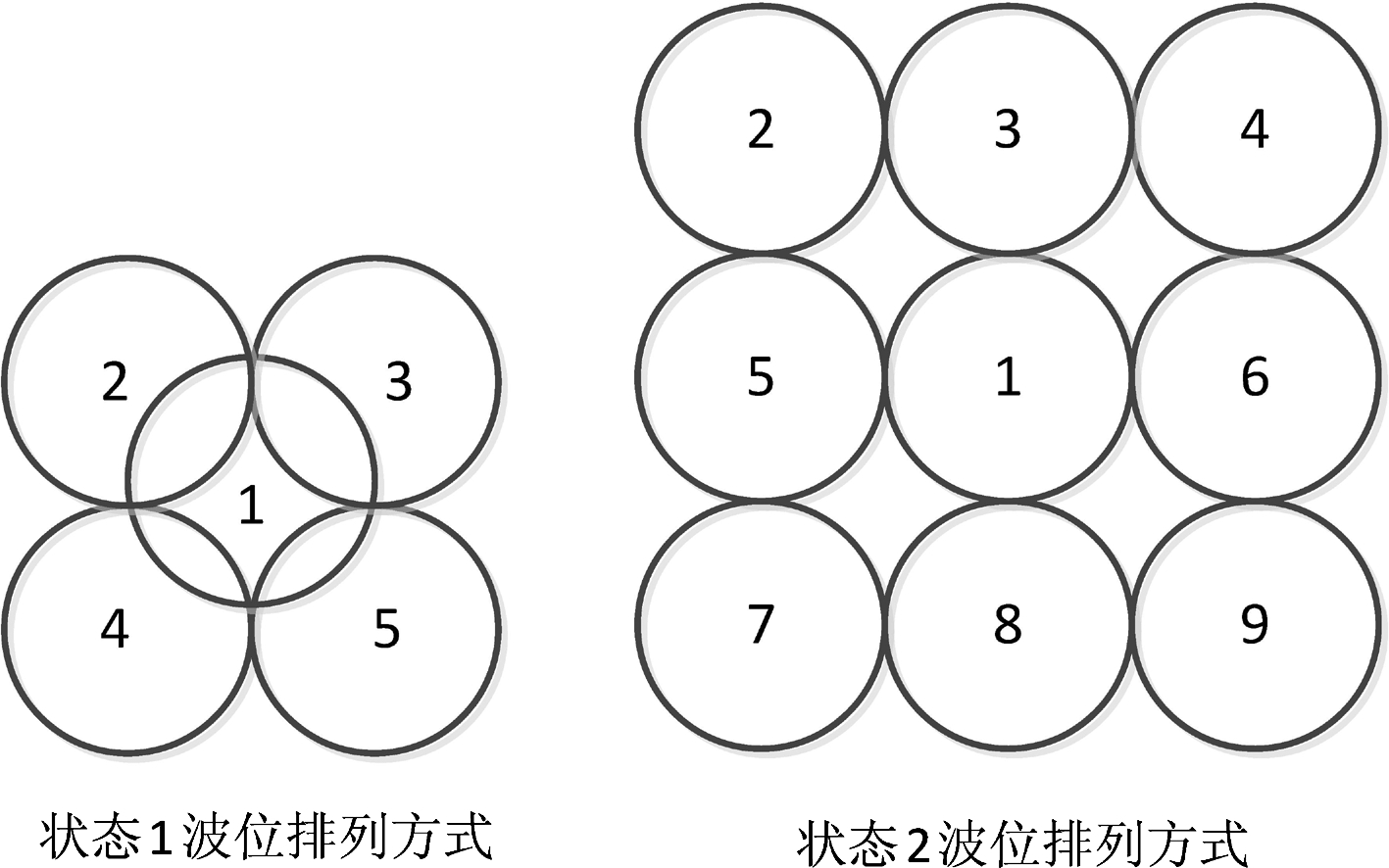
图3 波位编排两种状态
系统跟踪状态主要包括和差波束角度测量和自适应α-β滤波两部分。跟踪状态硬件实现逻辑框图如图4所示。
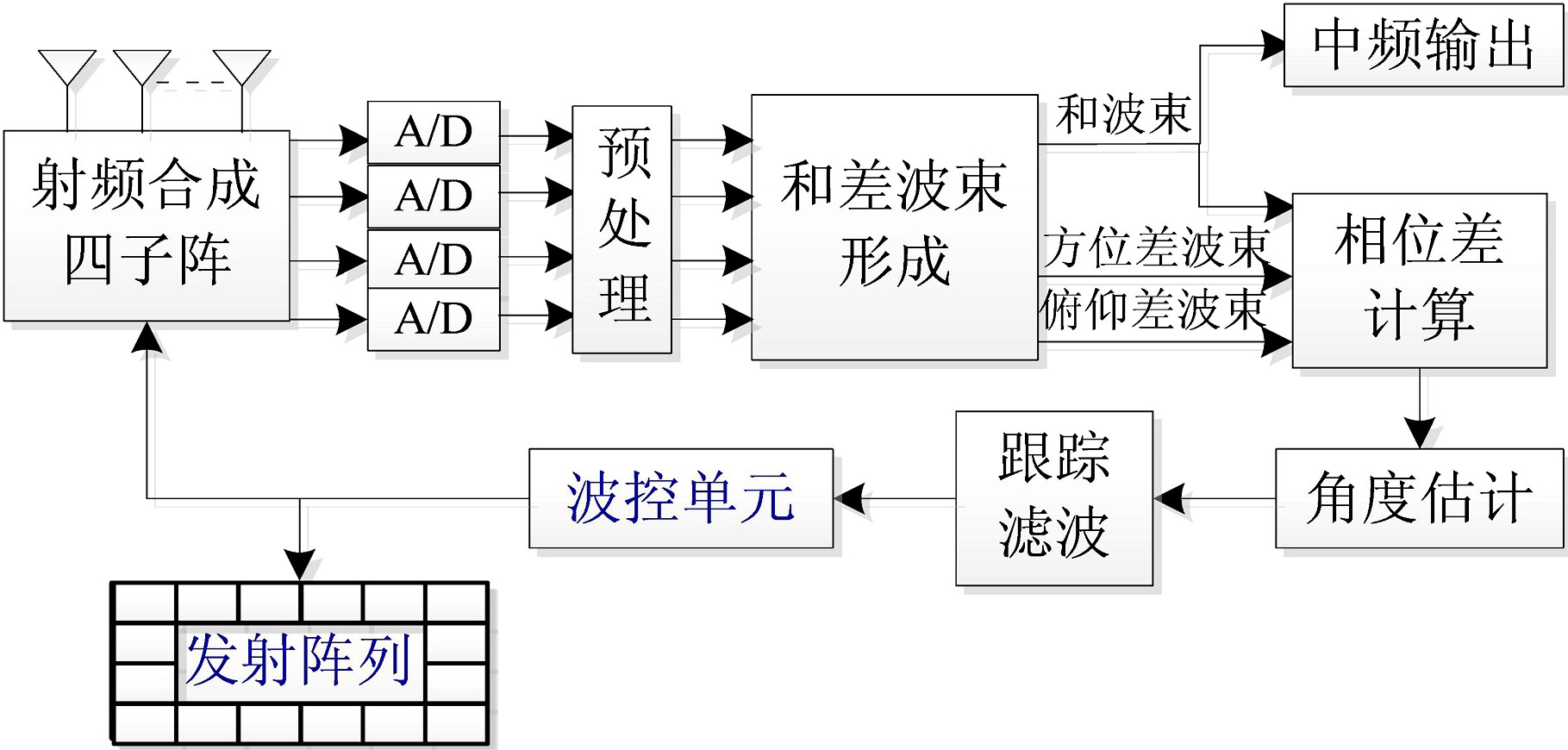
图4 跟踪状态实现逻辑框图
各子阵接收信号经数字板上A/D采样、数字下变频、低通滤波与抽取等,得到基带数字信号[7]。经过和差波束形成与匹配滤波,在提高信噪比的同时,保留子阵信号间的相位差信息。完成和差波束法角度测量,并将测量结果(φ,θ)实时地送入DSP中进行跟踪滤波,得到下一时刻来波方向的预测值(φ0,θ0),反馈到波控单元,用于调整阵列天线波束实时地对准卫星。
针对上节所述的系统角度跟踪状态中角度测量模块,本文提出一种基于和差波束测角的角度测量方法,主要包括和差波束形成、相位差计算和角度测量三部分。
均匀矩形面阵的几何结构以及阵列天线角度坐标定义如图5所示。相控阵雷达接收阵列位于xoy平面上,设阵元数为M×N,平行于x轴和y轴方向均匀分布的阵元且间距分别为dx和dy。记入射信号在xoy平面上的投影与x轴夹角为方位角φ,取值范围为-90°～90°;记入射信号与z轴夹角为俯仰角θ,取值范围为0°～90°。
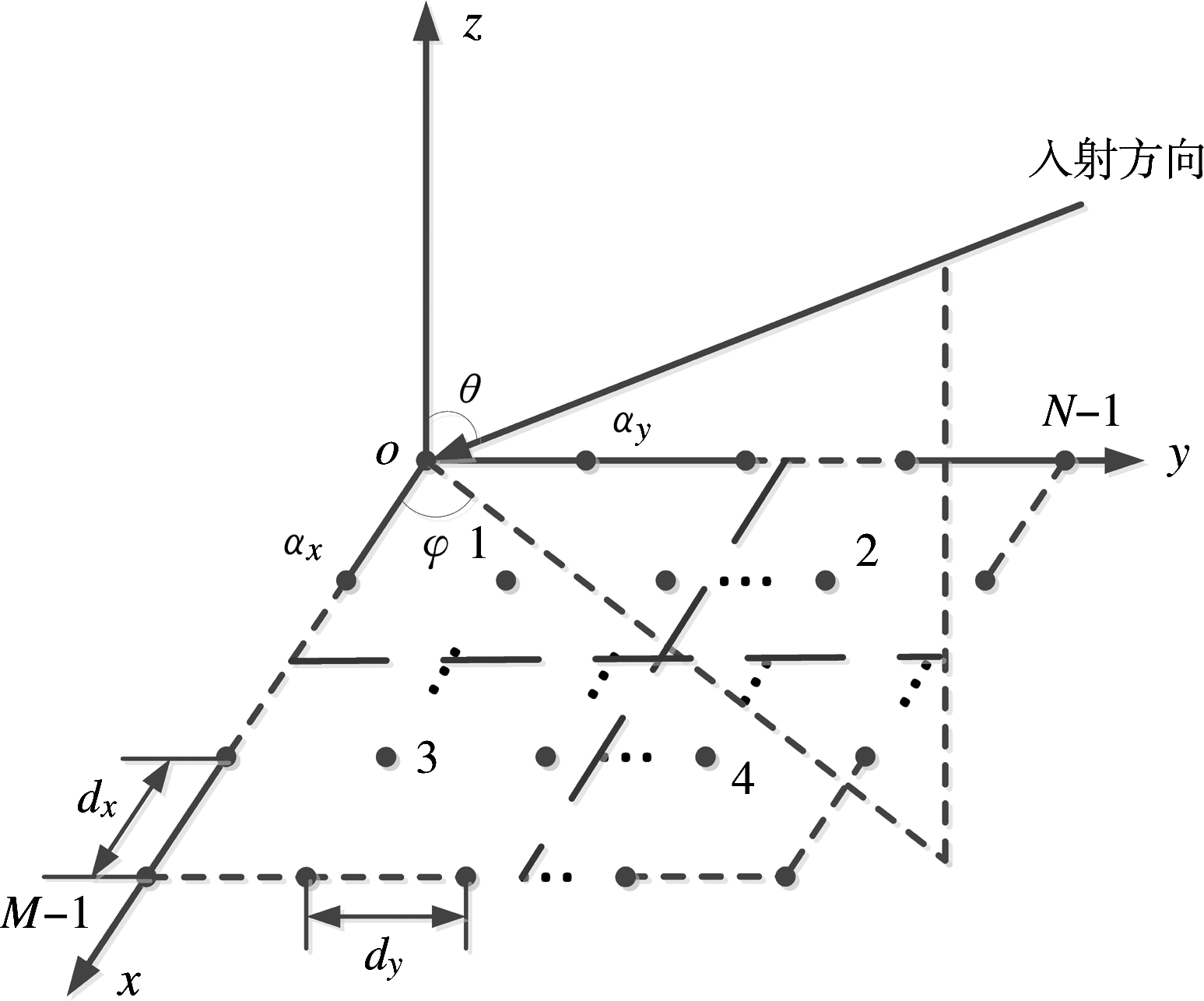
图5 均匀矩形面阵的几何结构
信号的方向向量为
以第1子阵为参考子阵,第2,3,4子阵的坐标分别是
若入射信号先到达第2,3,4子阵,根据相控阵空域滤波相关理论,可以得到第2,3,4子阵相对于参考子阵的相移分别为
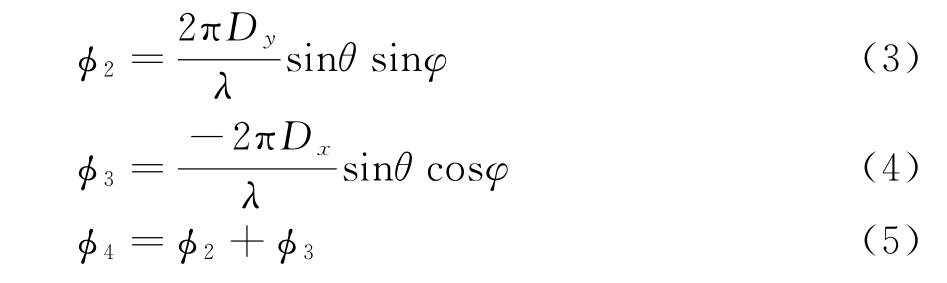
式中,Dx=Mdx/2,Dy=Ndy/2分别为x方向和y方向的子阵间距,M和N分别为x方向和y方向的阵元个数。
同理,记波束指向为(φ0,θ0),则第2,3,4子阵对应的相移量分别为
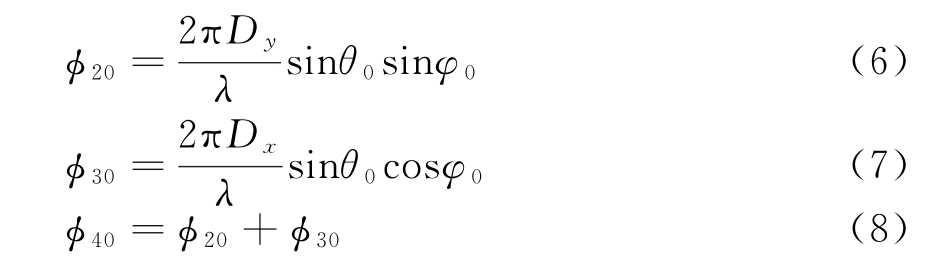
因此,移相之后,各个子阵信号之间的相位差分别为
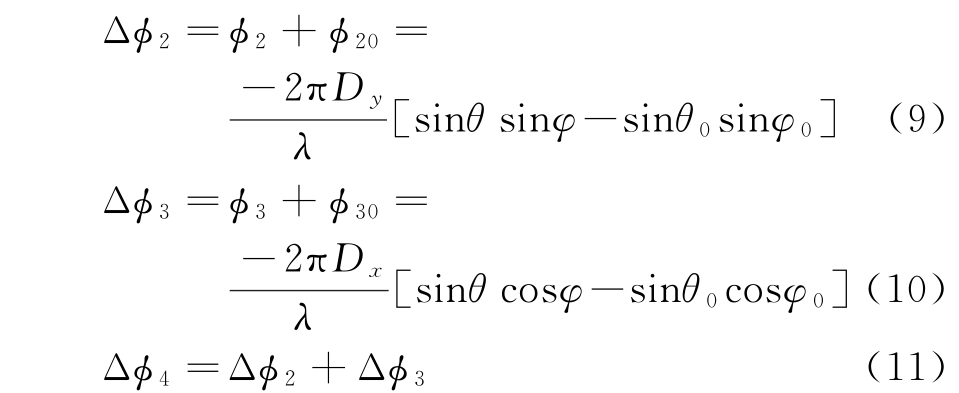
设子阵1的接收信号为
式中,v1(n)为子阵1输出噪声。则第2,3,4子阵接收信号为
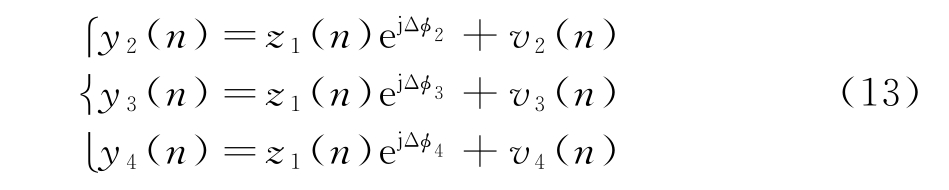
式中,v2(n),v3(n),v4(n)分别为第2,3,4子阵输出噪声。
对各子阵输出信号进行和差波束形成得到:和波束输出信号为
俯仰差波束输出信号为
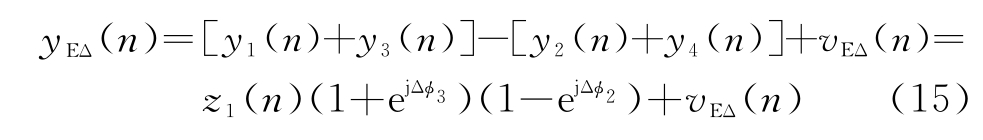
方位差波束输出信号为
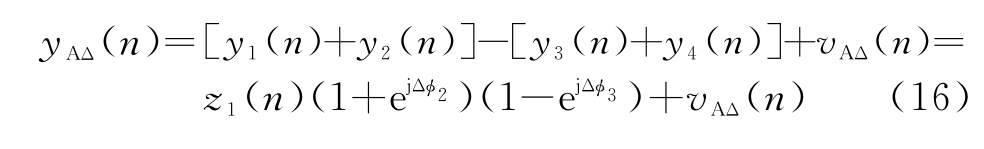
式中,vΣ(n),vEΔ(n),vAΔ(n)分别为和波束、俯仰差波束、方位差波束的输出噪声。
通过匹配滤波,提高和差波束信号信噪比的同时不改变原来的各子阵信号之间的相位关系,因此有效地提高角度测量的精度。匹配滤波后和波束通道输出信号为
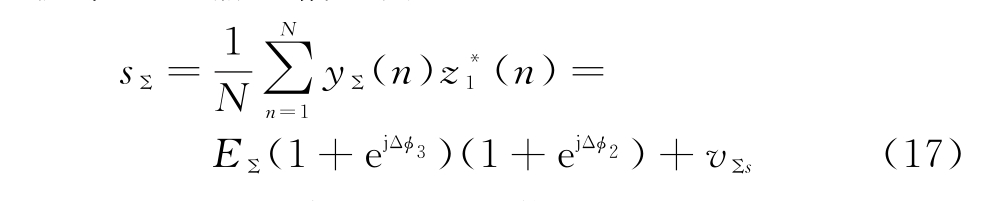
俯仰差波束通道输出信号为
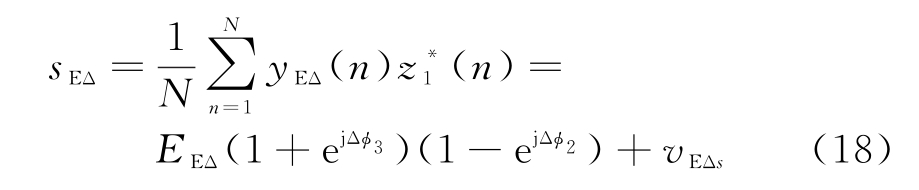
方位差波束通道输出信号为
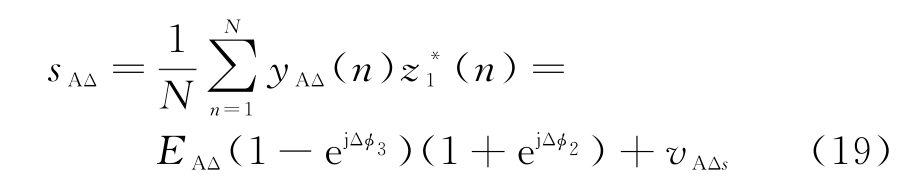
式中:N为信号采样点快拍数;EΣ,EEΔ,EAΔ分别为和波束信号、俯仰差波束信号和方位差波束信号的能量;vΣs,vEΔs,vAΔs分别为和波束信号、俯仰差波束信号和方位差波束信号的输出噪声幅度。
所以有
化简,提取出相位差Δϕ2,Δϕ3:
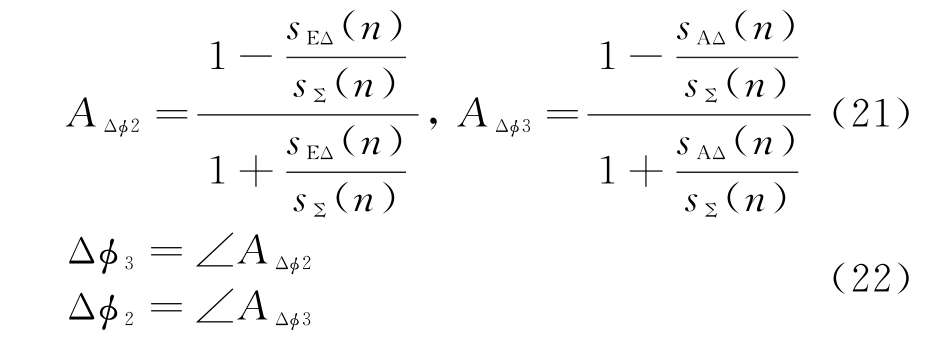
理论上,累积快拍数N足够大,角度测量的精度比较理想。
将2.1节的式(9)和式(10)进行化简可得
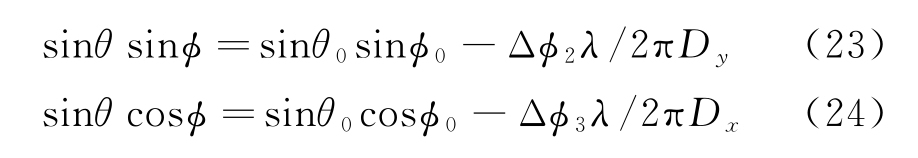
将2.2节得到的相位差Δϕ2,Δϕ3代入式(23)和式(24)中,求解出角度值(φ,θ)如下:
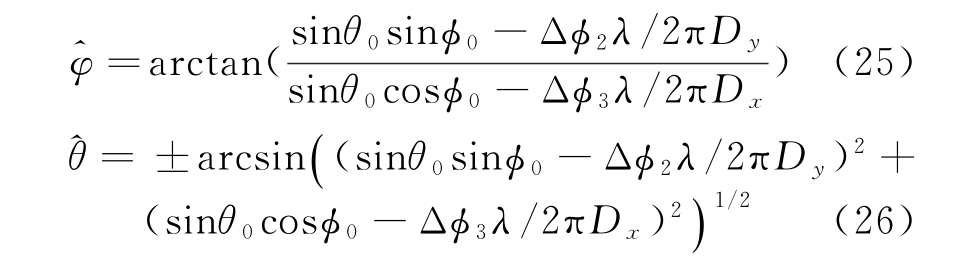
系统的跟踪过程是通过将和差波束测角得到的目标角度值(φ,θ)送给跟踪滤波器,通过跟踪滤波得到下一时刻来波方向的预测值(φ0,θ0),作为下一时刻角度测量的输入参数,完成一次闭环的自适应α-β跟踪滤波。
假设观测信息为目标角度测量值(φ,θ),通常用方向余弦作为状态向量。目标的方位角和俯仰角信息与方向余弦的对应关系如下:
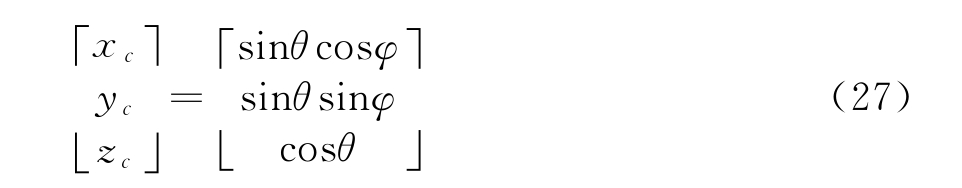
式中,xc,yc和zc分别为目标在惯性坐标系下3个方向的方向余弦。本文以目标在3个方向的方向余弦及其变化的速度为状态向量
其中的xc,yc和zc均可由(φ,θ)求得。
可由下式求得:
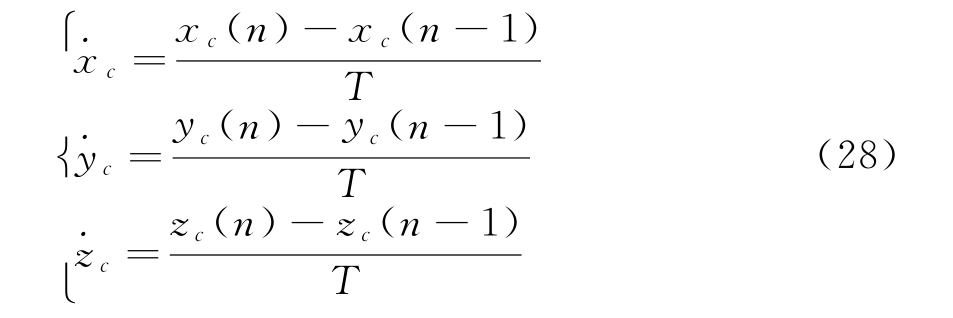
式中,T为跟踪滤波采样周期。
以一个通道的方向余弦估计为例进行说明,其余两通道类似。
假设目标运动状态方程为
式中,
为目标x方向的方向余弦、方向余弦变化速度构成的状态向量,
为状态转移矩阵,
为状态噪声输入矩阵,w(n)为该模型的过程噪声,服从零均值、方差为Q(n)的高斯分布。
观测方程为
式中,C(n)=[1 0]为观测矩阵,v(n)为测量噪声且服从零均值、方差为R(n)的高斯分布,它与过程噪声w(n)相互独立。
基于以上运动方程和观测方程,一次自适应α-β滤波的过程如下:
步骤1:状态一步预测
式中,
表示用观测量z(1),z(2),…,z(n-1)对信号x(n)进行的最小均方误差估计,下同。
步骤2:由观测信号计算新息过程
步骤3:计算卡尔曼增益K(n),具体计算过程由下文详细介绍。
步骤4:状态估计
步骤5:重复步骤1～4,进行递推滤波计算。
步骤3中,
由其中各个通道的增益根据相应的机动指数计算获得,定义目标机动指数为
式中,
分别为机动加速度和测量误差的方差。
α(n)和β(n)与r的关系为
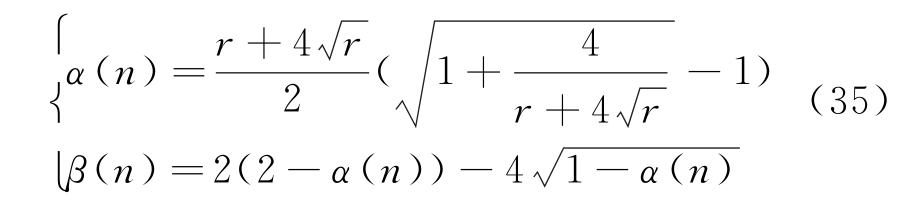
根据抽样统计知识以及目标机动的判定时间区间,可得到机动加速度的方差
的计算公式如下,其中V(n)是新息值,N可取3到5:
在建立起目标运动轨迹模型的基础上,对目标信号方向进行测量与跟踪,设子阵接收信号的信噪比为-8 d B,和差波束匹配滤波模块的累积快拍数为8 192,系统对其进行角度测量与跟踪的结果如图6和图7所示。
图中观测误差表示角度测量结果与真实轨迹的来波方向的偏差,跟踪误差表示系统跟踪滤波过程得到的下一时刻角度预测值与真实值之间的偏差。仿真结果表明,用和波束、俯仰差波束、方位差波束信号相比的方法进行角度测量,结合自适应α-β滤波进行角度跟踪,能有效地提高系统角度测量与跟踪精度。
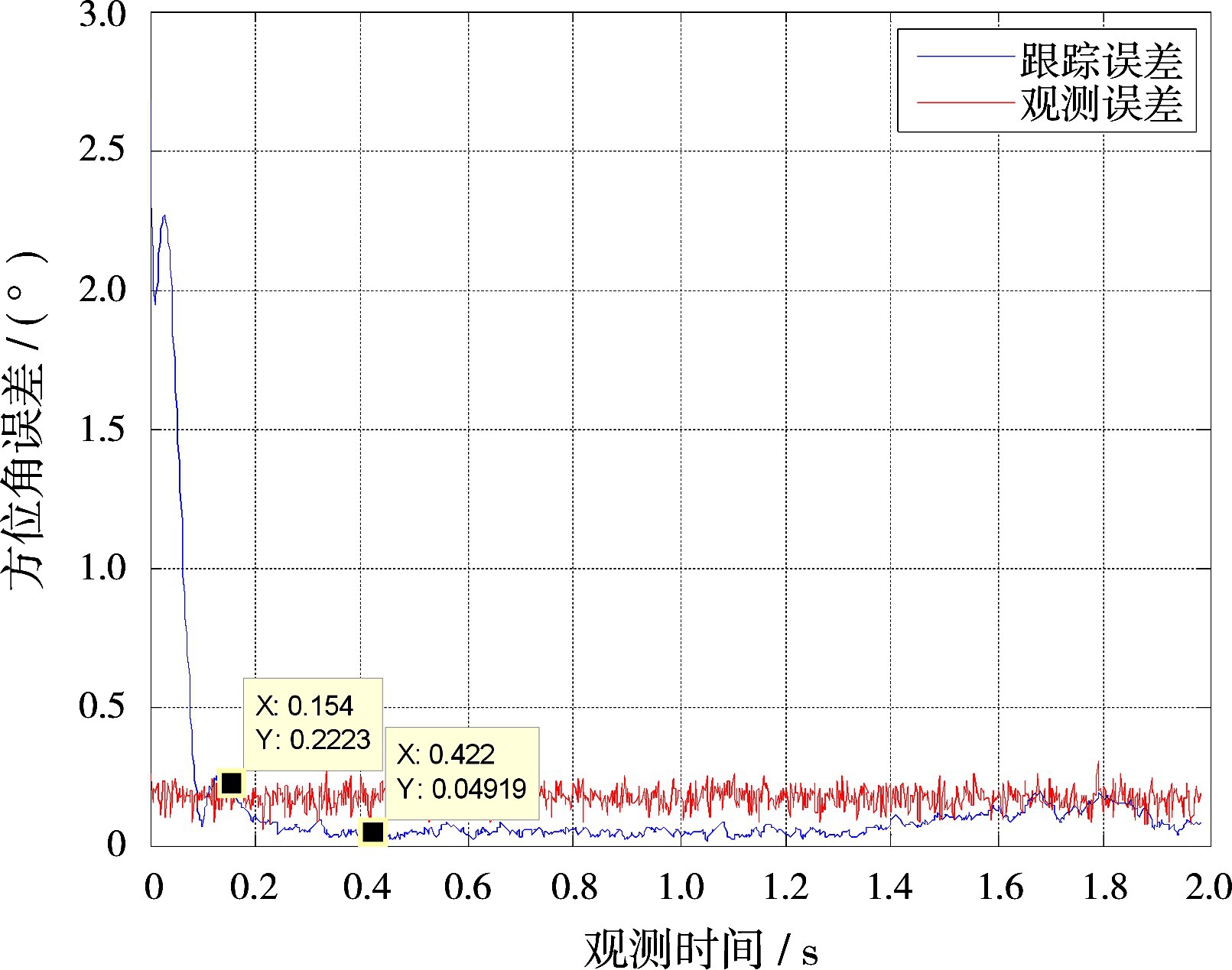
图6 方位角测量与跟踪误差
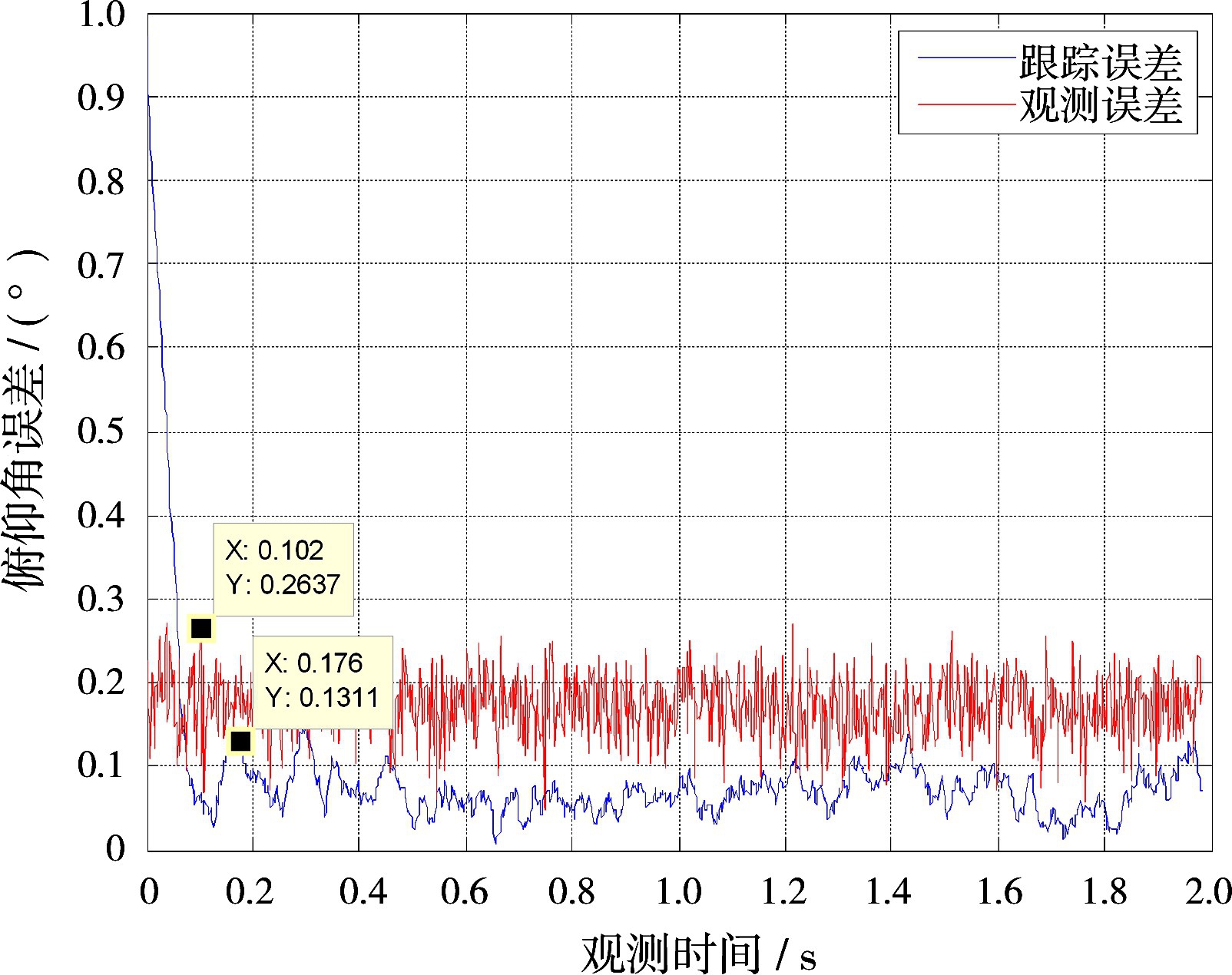
图7 俯仰角测量与跟踪误差
本文针对高速运动载体卫星实时通信的背景下,提出角度测量与跟踪系统的设计方案。结合阵列天线子阵划分的特点,在传统单脉冲测角理论的基础上,提出一种新的和差波束测角方法。并针对载体的运动特性,研究和发展了自适应α-β滤波算法,保证了系统角度测量跟踪的实时性和稳健性。综上,本文搭建的角度测量与跟踪的闭环系统,是实现高速运动载体卫星跟踪技术的关键,对工程实践具有一定的指导意义。
参考文献:
[1]赵来定.一种车载卫星通信跟踪技术[J].南京邮电大学学报(自然科学版),2014,34(5):80-86.
[2]姜义成,喻春曦.一种改善单脉冲雷达测角精度的新方法[J].雷达科学与技术,2009,7(5):380-383.
[3]杨雪亚,刘张林.子阵级和差波束形成及测角方法研究[J].中国电子科学研究院学报,2015,10(1):82-86.
[4]姜雯献,李朝海.相控阵跟踪系统测角与角度跟踪算法[J].雷达科学与技术,2015,13(2):190-194.
[5]张海成,杨江平,王晗中.大型跟踪测量雷达的卫星标定方法研究[J].雷达科学与技术,2014,12(5):470-472.
[6]LI Yang,LYU Huihui,PENG Sun,et al.Study on Search Performance of Subarray Multi-Channel Phased Array Radar Based on Multiple Received Beams[C]∥IET International Radar Conference 2013,Xi’an:IET,2013:1-6.
[7]吴越,严济鸿,何子述.基于FPGA的多通道高速数据采集系统[J].雷达科学与技术,2012,10(6):671-676.
Simulation Research of Angle Tracking Based on Angle Measurement of Sum and Difference Beams
MA Yue,LI Chaohai
(School of Electronic Engineering,University of Electronic Science and Technology of China,Chengdu611731,China)
Abstract:In the process of real-time communications between high-speed motion platforms such as aircraft,missiles and a repeater satellite,the postures of platforms change all the time,which affects the quality of communication seriously.For keeping communications with the satellite,the phased array antenna on them must aim at the direction of satellite all the time.The design of angle tracking system is given,and the key functions of the system are introduced.For the rectangular array with symmetrical and uniform characteristics,by studying and improving the traditional theory of monopulse angle measurement and Kalman filter,an angle tracking algorithm based on sum-difference angle measurement and adaptiveα-βfiltering is proposed.Through simulation,the angle measurement and tracking precision is given,and the factors affecting the system tracking precision is analysed.
Key words:phased array antenna;sum and difference beams;α-βfiltering;angle tracking
中图分类号:TN953+.5;TN958.92
文献标志码:A
文章编号:1672-2337(2017)01-0068-05
DOI:10.3969/j.issn.1672-2337.2017.01.012
收稿日期:2016-07-14;
修回日期:2016-08-23
作者简介:
马越男,1991年生,山东烟台人,硕士研究生,主要研究方向为雷达信号处理。E-mail:woshimyue@163.com
李朝海男,1972年生,四川南充人,电子科技大学电子工程学院教授级高级工程师,主要研究方向为高速实时信号处理、雷达系统及信号处理。