图1 雷达抗干扰性能评估方法
陈文东1,2,汤 斌2
(1.中国航天科工集团第二研究院,北京100854;2.北京遥感设备研究所,北京100854)
摘 要:根据现有的雷达抗干扰性能评估方法存在的问题,提出了一种基于高维量测特征空间几何分析的雷达抗干扰性能评估方法。该方法将抗干扰试验中雷达得到的量测数据映射到高维量测特征空间中,利用量测数据的多元密度分布的几何特征定义量测误差影响因子(MEIF)、量测稳定性影响因子(MSIF)和干扰影响因子(JIF),定量分析干扰对雷达的影响以及雷达的综合抗干扰性能。计算机仿真表明,新的评估指标可以准确反映雷达的抗干扰性能,实验结果与理论分析相符。
关键词:复杂电磁环境;雷达;抗干扰;性能评估
现代战场上,雷达通常需要在复杂电磁环境中工作,在面对各式各样干扰的情况下,同样需要具备精确可靠探测的能力,即抗干扰能力[1]。如何对雷达的抗干扰性能进行综合的、定量的、有针对性的描述成为抗干扰研究中一个复杂而且极其重要的问题。近年来,研究人员在雷达抗干扰效果以及性能评估方面做了大量工作[2-4],并且针对不同体制雷达、不同干扰类型提出了一系列方法和指标,但是至今并未形成一个统一的评估方法和度量标准。
雷达抗干扰性能评估的意义在于科学地描述雷达在电磁环境中的工作能力,发现雷达在对抗各种干扰时的薄弱环节,有针对性地提升雷达的综合抗干扰能力。因此,一个科学、有效的雷达抗干扰性能评估方法,必须能够综合分析干扰对雷达影响效果的同时,发现雷达抗干扰能力的瓶颈,以及针对不同的抗干扰方法、不同的干扰方式,给出相应的抗干扰性能分析,为雷达的抗干扰能力建设提供强有力的数据支撑和理论依据。
本文从雷达抗干扰能力建设的实际需求出发,提出了一种基于高维量测特征空间的统计建模方法,利用多元密度函数分析干扰效果以及雷达的综合抗干扰能力,同时兼具了单项抗干扰性能分析,考虑了不同抗干扰手段、不同干扰方式的性能评估问题。
评估雷达抗干扰性能的指标一般都遵循如下三个准则[5]:
功率准则:通过干扰前后功率变化描述抗干扰能力,比如抗干扰改善因子(EIF)[6]等。一般适用于压制式干扰下的抗干扰性能评估。
概率准则:通过干扰成功概率或者雷达识别干扰成功概率来描述抗干扰能力。
信息准则:通过干扰前后雷达信息的损失程度描述雷达的抗干扰能力。
雷达抗干扰性能评估方案[7]包括:
试验法:通过试验获取的实际雷达数据的分析,对雷达的抗干扰能力进行评估。
仿真法:通过半实物仿真实验,或者全数字仿真实验,模拟真实电子对抗环境,对雷达的抗干扰能力进行评估。
数学解析法:通过分析雷达和干扰机的性能指标之间的关系,建立评估数学模型对雷达系统的抗干扰性能进行评估。
1)试验法与解析计算法融合的问题
试验法的优点在于数据来源可靠,但考虑到成本问题,数据量有限。而数学解析法则没有成本的限制,但是其数据来源于雷达和干扰机的性能指标,实时性较差。现有的方法很少能够实现两者优势的共享与劣势的互补。
2)综合能力评估和单项性能分析的问题
一般的抗干扰性能评估指标都是有针对性的评估指标,不能对综合能力与单项性能统一进行评估,从而很难直接反映出雷达抗干扰能力的薄弱环节,不利于抗干扰能力的建设和提升。
3)单项干扰与复合干扰统一评估的问题
在实战中,不同类型雷达面临的干扰不同,并且干扰的部署灵活可控,可以采用单一干扰,也可以采用复合干扰。一般评估指标的最大问题在于评价依据与干扰方式相关,缺少综合评估的方法和指标。
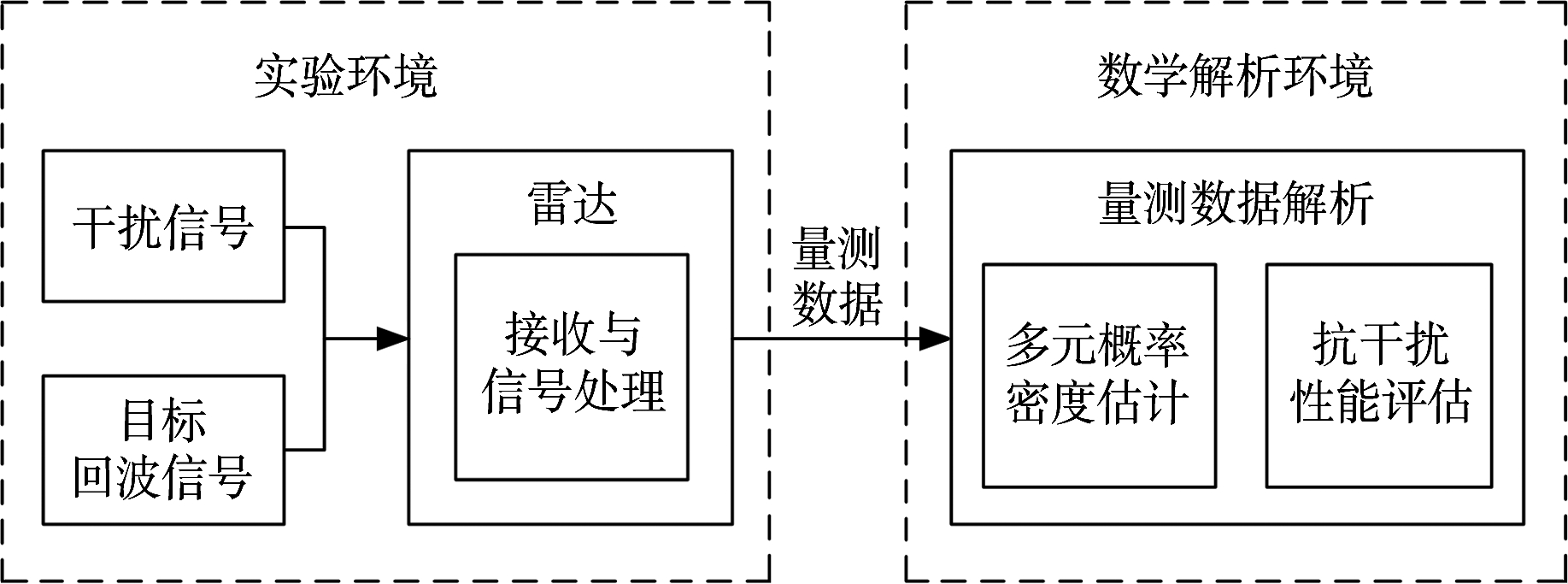
本文针对抗干扰评估面临的四个问题,提出了一种新的评估理论,具体方法如图1所示。

图1 雷达抗干扰性能评估方法
首先,在实验环境中,干扰信号经过雷达接收处理之后,输出为量测数据。利用量测数据作为性能评估模型的输入,可以屏蔽单项干扰与复合干扰对于评估指标的影响。其次,该方法结合试验法与数学解析法,通过对量测数据多元概率分布的统计分析(如图2所示),可以利用有限样本数据分析总体性能,并且通过向具体量测特征轴上的映射,可以对雷达单项量测数据进行分析,找出性能瓶颈。在实际应用中,量测数据一般符合正态分布模型,尤其是当样本数据充足的时候,根据中心极限定理,可以利用正态模型进行分析。但是在某些干扰环境中,很难用数学解析方法确定量测数据在特征空间中满足的概率分布。因此,对于输入的量测数据,首先需要检验其正态性。对于非正态数据,可以通过正态转换方法对数据进行预处理,对于经过正态转换之后依然不满足正态分布的数据,可以通过概率密度估计的方法进行建模。
1)量测数据与真实目标特性
定义试验获取的N组雷达量测数据Xm为
式中,量测向量xi=(x1i,x2i,…,xMi)T,i=1,2,…,N。且各量测向量之间满足独立同分布假设,定义xi的期望和协方差矩阵为μm和Σm,即
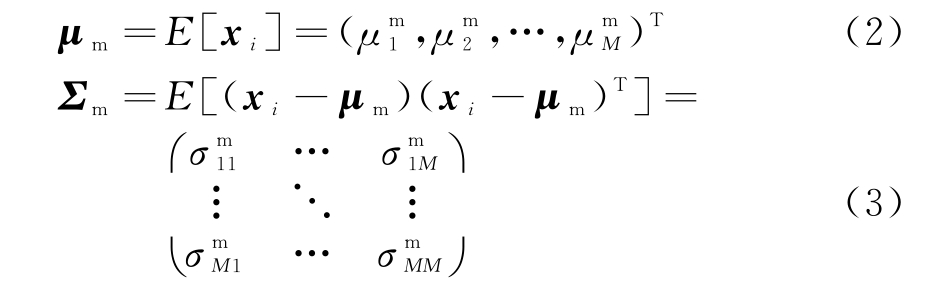
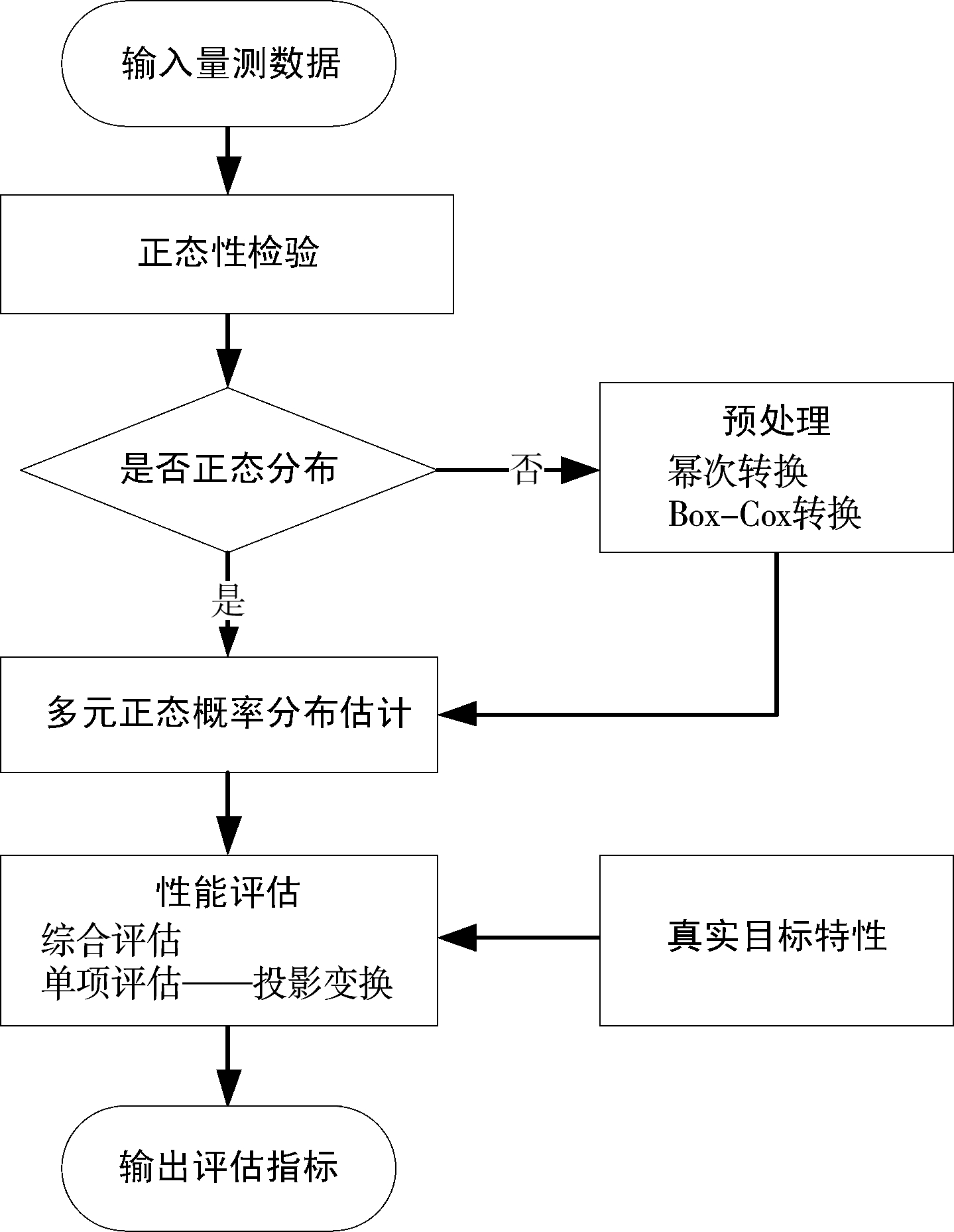
图2 量测数据解析流程
式中![]()
定义真实目标信息为x=(x1,x2,…,xM)T,且x的期望和协方差矩阵为μ和Σ,即
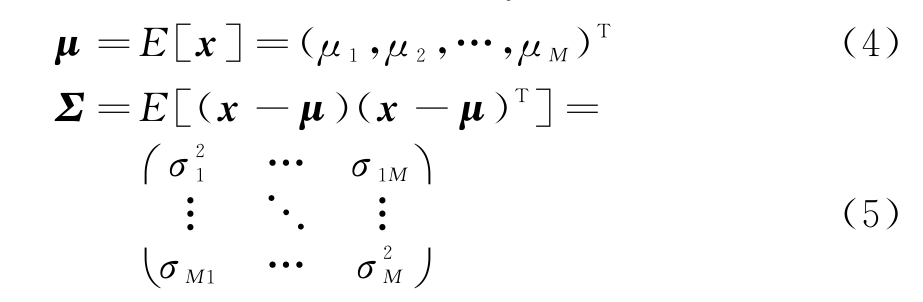
要求Σ和Σm为正定矩阵,当各量测量之间不相关时,Σ和Σm为对角阵。
2)多元正态性检验与数据预处理
由于雷达的量测向量的统计特性为多元分布函数,因此需要选择多元正态性检验方法对数据进行检验。常用的多元正态性检验方法包括卡方图检验法和主成分检验法[8]。卡方图检验法相对简单,但是精度较低,而且在小数据情况下检验性能较差。主成分检验法步骤如下:
步骤1 对于量测数据{Xm}M×N,根据式(6)、式(7)计算均值![]() 和协方差矩阵
和协方差矩阵![]()

步骤2 对![]() 作特征值分解,使得
作特征值分解,使得
式中,Λ=diag(λ1,λ2,…,λM),且λi>0,i=1,2,…,M;Φ=(a1,a2,…,aM)为单位正交矩阵。
步骤3 令
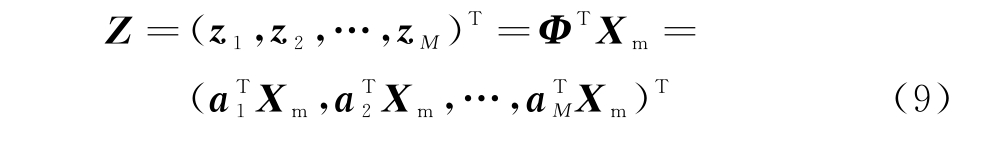
式中,![]() 为Xm的第i个主成分。
为Xm的第i个主成分。
步骤4 依次对各个主成分分量作一元正态性检验[9]。当且仅当所有![]() 均满足正态性检验时,认为量测数据符合多元正态分布。对于不满足正态性检验的分量,需要进行正态转换预处理。一般的转换方法有幂次转换、Box-Cox转换[10]和Johnson转换[11]等,可以在一定程度上将非正态分布数据转换为近似正态分布的数据。
均满足正态性检验时,认为量测数据符合多元正态分布。对于不满足正态性检验的分量,需要进行正态转换预处理。一般的转换方法有幂次转换、Box-Cox转换[10]和Johnson转换[11]等,可以在一定程度上将非正态分布数据转换为近似正态分布的数据。
3)多元正态分布建模
正态性检验之后经过正态转换的数据,可以通过正态或高斯密度函数进行建模。M元正态密度的形式如下:
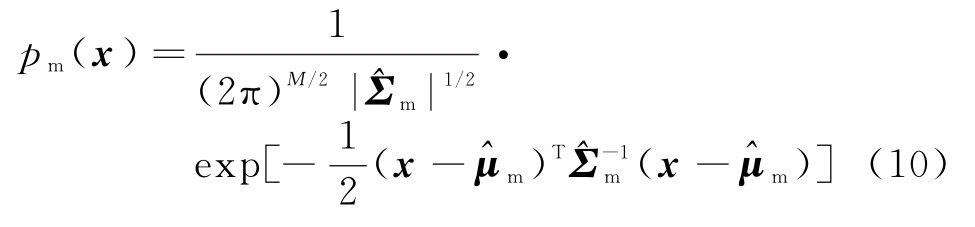
式中,![]() 在正态性检验的步骤1中已经求出。对于概率密度p(x)的估计,可以记为pm(x)~
在正态性检验的步骤1中已经求出。对于概率密度p(x)的估计,可以记为pm(x)~![]()
同理,对于真实目标特性的建模如下:
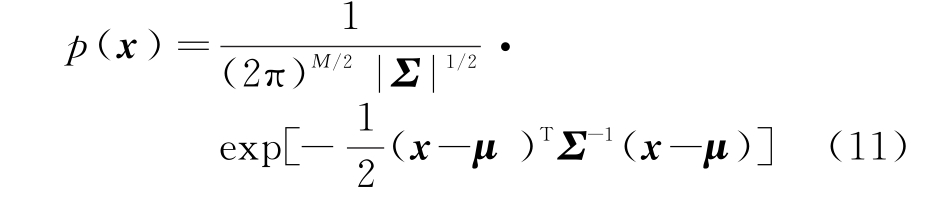
式中,μ由目标静态位置决定,Σ由雷达性能决定,|Σ|为矩阵Σ的行列式,Σ-1为矩阵Σ的逆矩阵,记p(x)~N(μ,Σ)。
4)性能评估指标
定义量测误差影响因子(Measurement Error Impact Factor,MEIF):
式中,![]() 称为向量μ到
称为向量μ到![]() 的平方Mahalanobis距离(或称为马氏距离),如图3所示。干扰对于雷达的影响最终体现在量测量上,从定义可以看出,真实目标量测特性距离实际量测量越大,表明干扰对于雷达的影响越大。因此,MEIF体现了干扰对雷达量测偏差的影响程度。
的平方Mahalanobis距离(或称为马氏距离),如图3所示。干扰对于雷达的影响最终体现在量测量上,从定义可以看出,真实目标量测特性距离实际量测量越大,表明干扰对于雷达的影响越大。因此,MEIF体现了干扰对雷达量测偏差的影响程度。
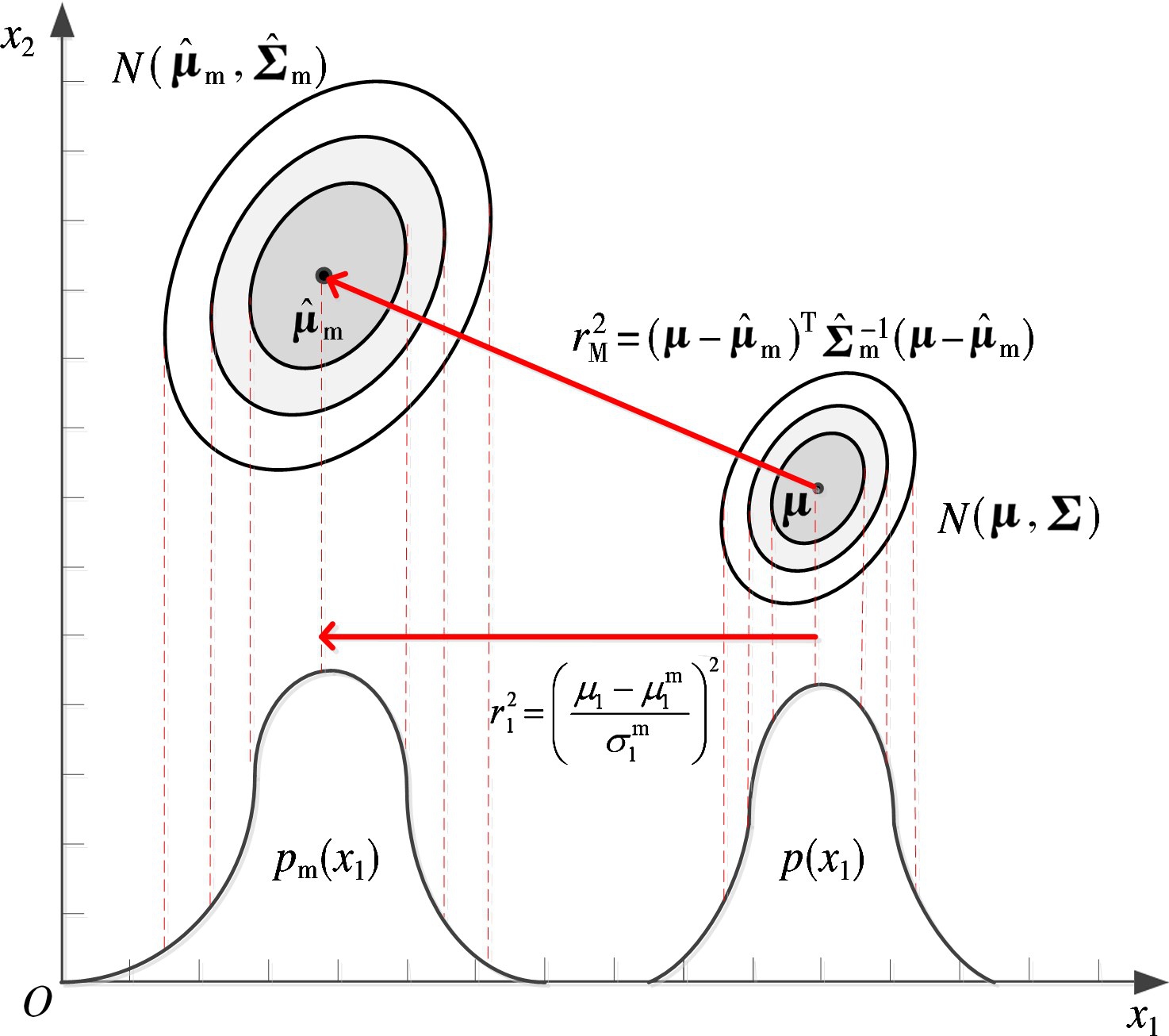
图3 多元正态分布和一元投影变换
定义量测稳定性影响因子(Measurement Stability Impact Factor,MSIF):
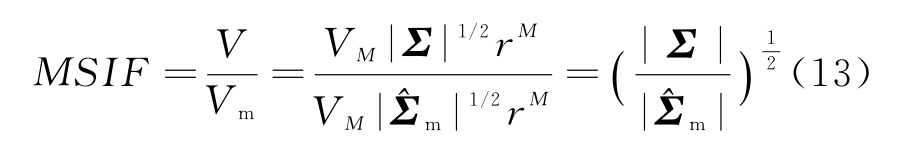
式中,V表示距离μ为r的超椭球体积,Vm表示距离![]() 为r的超椭球体积,VM为单位超椭球体积。量测特征空间中超椭球体积大小Vm决定了量测数据的离散程度,而V代表了无干扰时雷达量测量的离散程度。因此,MSIF体现了干扰对雷达量测稳定性的影响程度。
为r的超椭球体积,VM为单位超椭球体积。量测特征空间中超椭球体积大小Vm决定了量测数据的离散程度,而V代表了无干扰时雷达量测量的离散程度。因此,MSIF体现了干扰对雷达量测稳定性的影响程度。
定义干扰影响因子(Jamming Impact Factor,JIF):
从定义可以看出,干扰影响因子(JIF)综合体现了干扰对量测误差和量测稳定性的影响,因此可以体现出雷达的综合抗干扰性能。
定义投影向量ei为
式中,除了第i个元素为1外,其余元素均为0。
那么,令
显然,![]()
![]() 分别表示多元密度函数pm(x)和p(x)在xi方向的一元投影分布函数,如图3所示。通过pm(xi)和p(xi)可以分析干扰对于雷达某一个量测特征的影响。
分别表示多元密度函数pm(x)和p(x)在xi方向的一元投影分布函数,如图3所示。通过pm(xi)和p(xi)可以分析干扰对于雷达某一个量测特征的影响。
定义为真实目标特征中心到实际量测数据中心在方向xi上投影的马氏距离。那么,MEIF,MSIF和JIF在xi方向上定义如下:
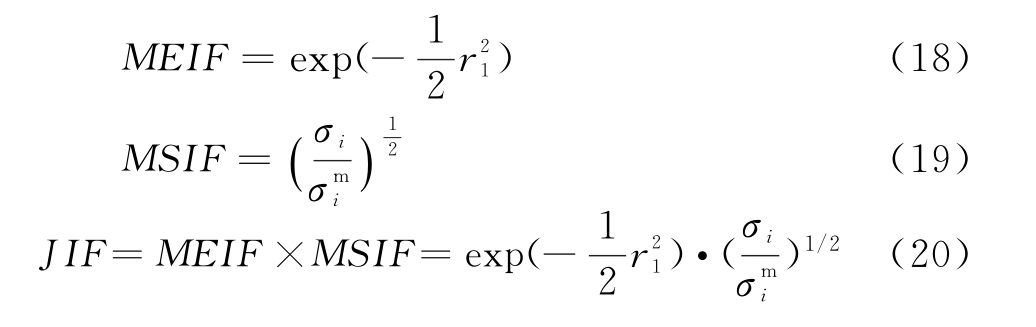
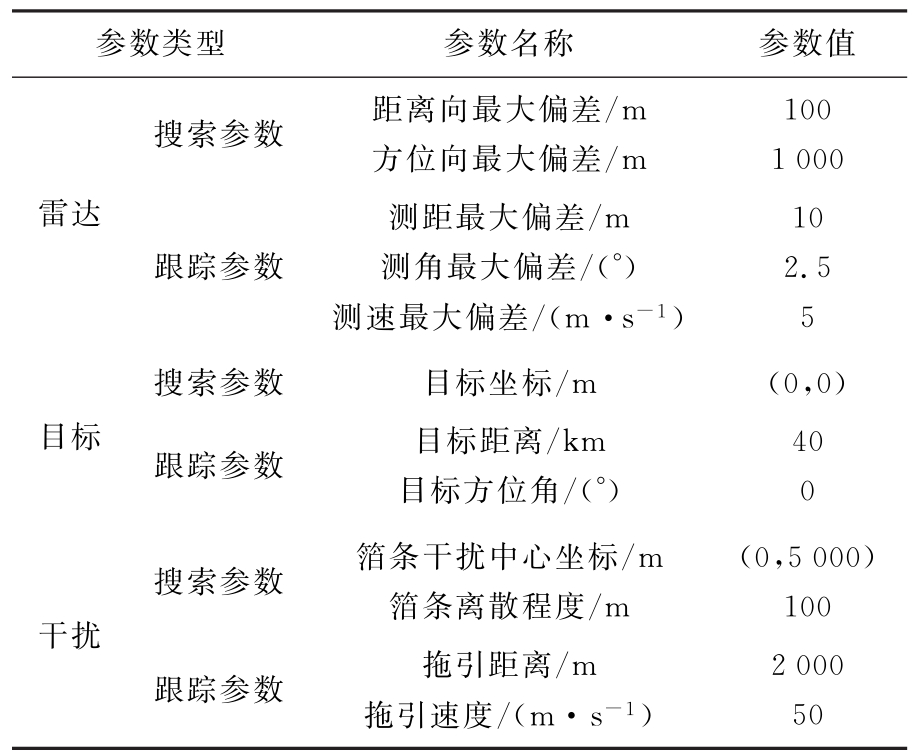
MEIF,MSIF和JIF不仅可以用于定量验证抗干扰方法的实际效果,还可以评价复杂电磁环境中干扰对于雷达量测性能的影响。在仿真中,首先针对搜索雷达,分析了无源冲淡箔条干扰对于雷达搜索目标的影响。然后对于跟踪雷达常见的距离-速度联合拖引干扰,验证了雷达采用抗干扰手段之后的效果。雷达参数、目标参数与干扰参数的设置详见表1。
表1 仿真参数设定
搜索雷达以发现与定位目标为主要目的,其量测值为搜索坐标系下目标坐标,包括距离向坐标和方位向坐标。在箔条干扰环境中,量测数据及其分布如图4所示。从量测数据仿真结果可以看出:雷达受到干扰,将目标锁定为干扰中心点附近。且量测数据经过Anderson-Darling正态分布检验后,均判定为正态分布。量测特征空间正态分布估计情况如图5所示。
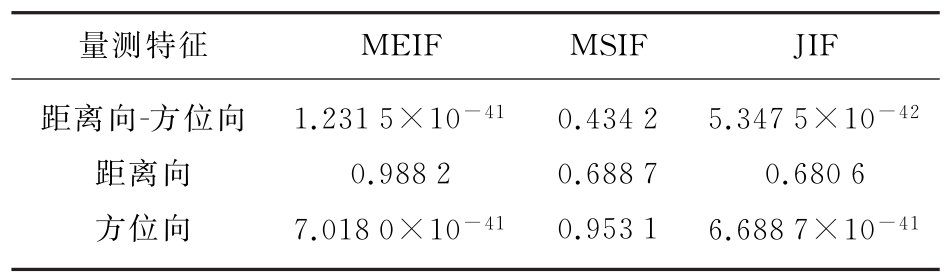
干扰对雷达量测性能的影响评估详见表2。在这种情况下,MEIF与JIF接近于0,可见在这种场景下无源冲淡箔条干扰会对搜索类雷达产生较大的影响。
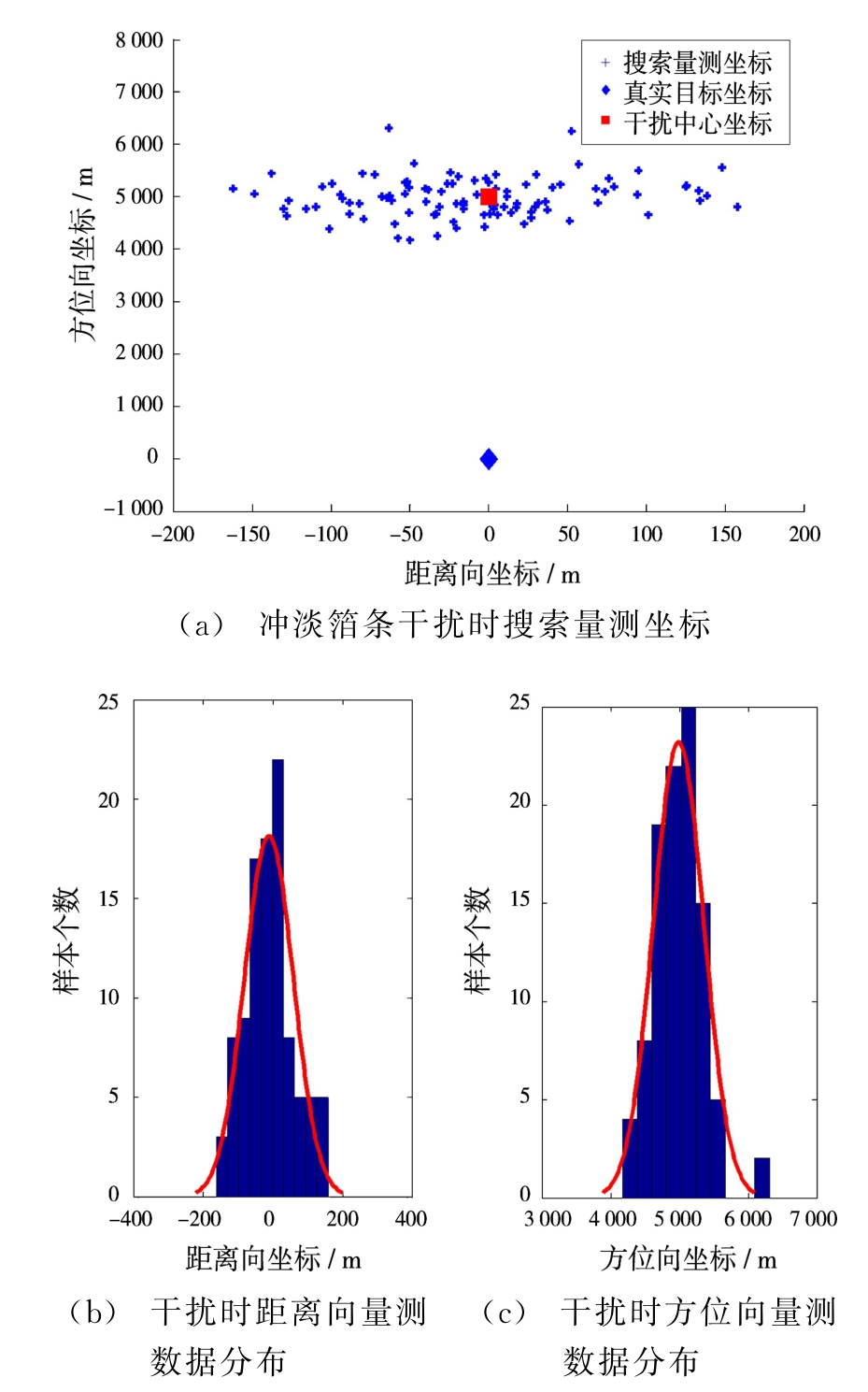
图4 有干扰时搜索量测数据及其分布情况
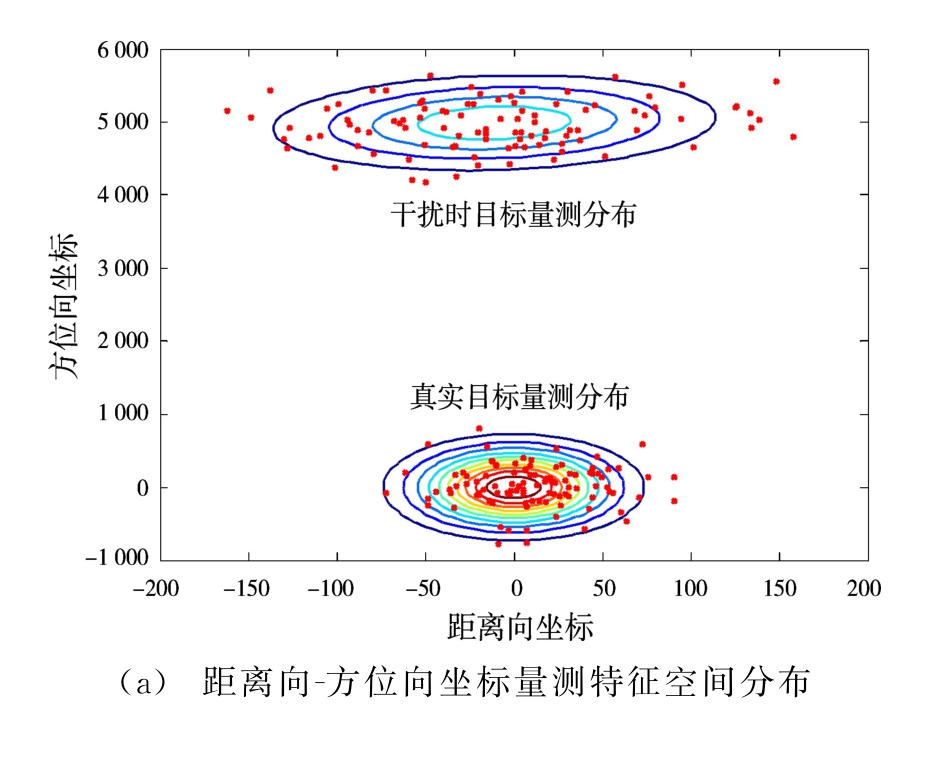
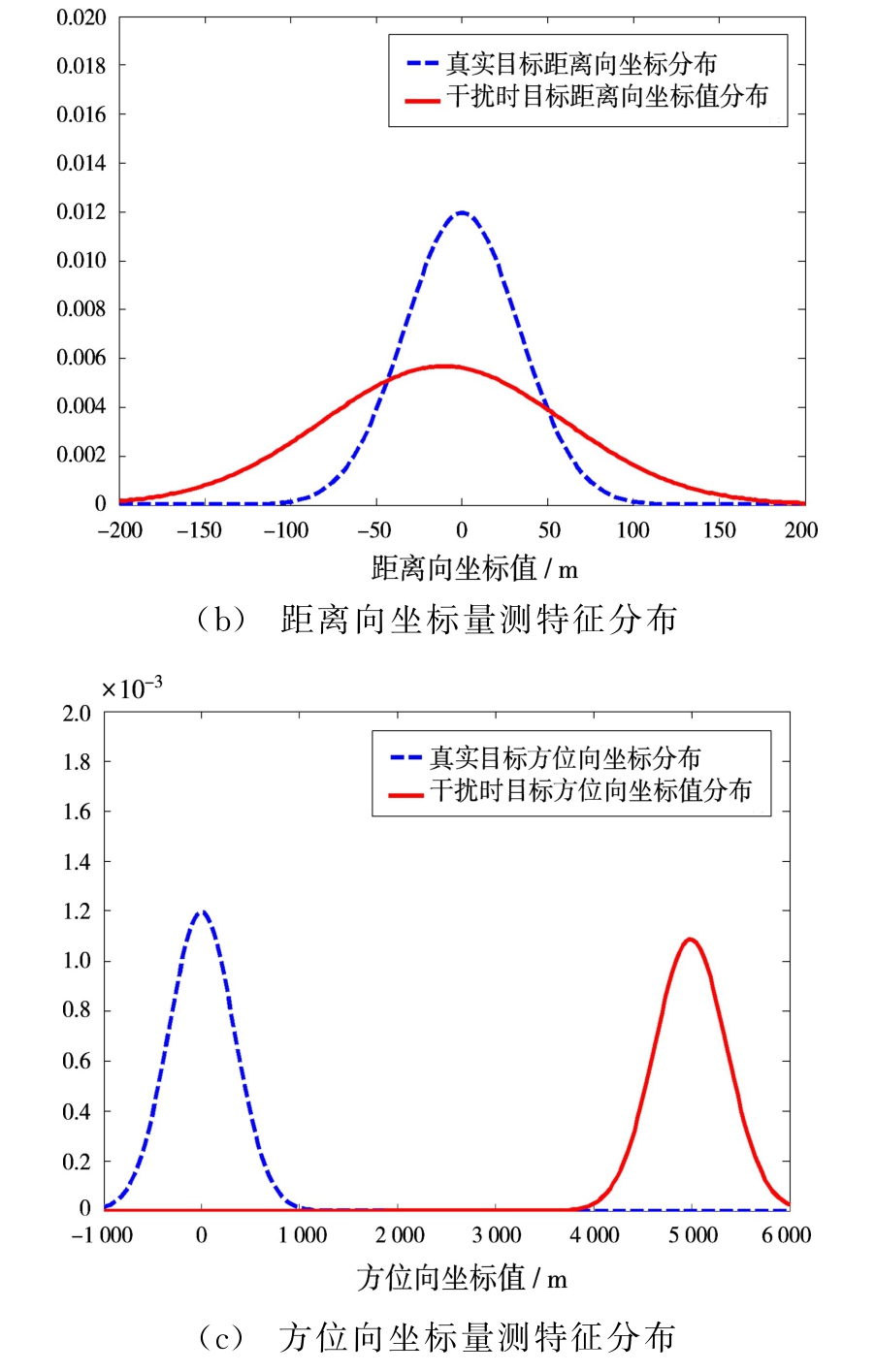
图5 量测特征空间正态分布估计情况
表2 干扰对雷达量测性能的影响评估
以距离-速度联合拖引干扰为例,对跟踪雷达采用抗干扰方法前后的抗干扰性能进行仿真。量测数据包括距离、方位角和目标速度。
场景1:雷达无抗干扰方法,受到距离-速度联合拖引干扰影响。
场景2:雷达通过增加速度门限,对抗距离-速度联合拖引干扰。
场景1时,量测数据及其分布如图6所示。
从量测数据仿真结果可以看出:雷达在距离上被拖引;距离分布为均匀分布并且无法通过预处理转变为正态数据。因此将量测分布向方位角速度联合特征空间进行映射,映射后量测特征空间正态分布估计情况如图7(a)所示。然后将量测分布分别投影到方位角和速度量测轴上,分布情况如图7(b)、(c)所示。从图中可以看出,距离 速度联合拖引干扰对于雷达的影响主要体现在速度量测值上。因此,可以通过在速度域上加门限的手段,限制距离-速度联合拖引干扰。
场景2时,增加速度门限,量测数据及其分布如图8所示。从量测数据仿真结果可以看出:加入速度门限之后,雷达在距离上没有受到拖引干扰影响。特征空间正态分布估计情况如图9所示。
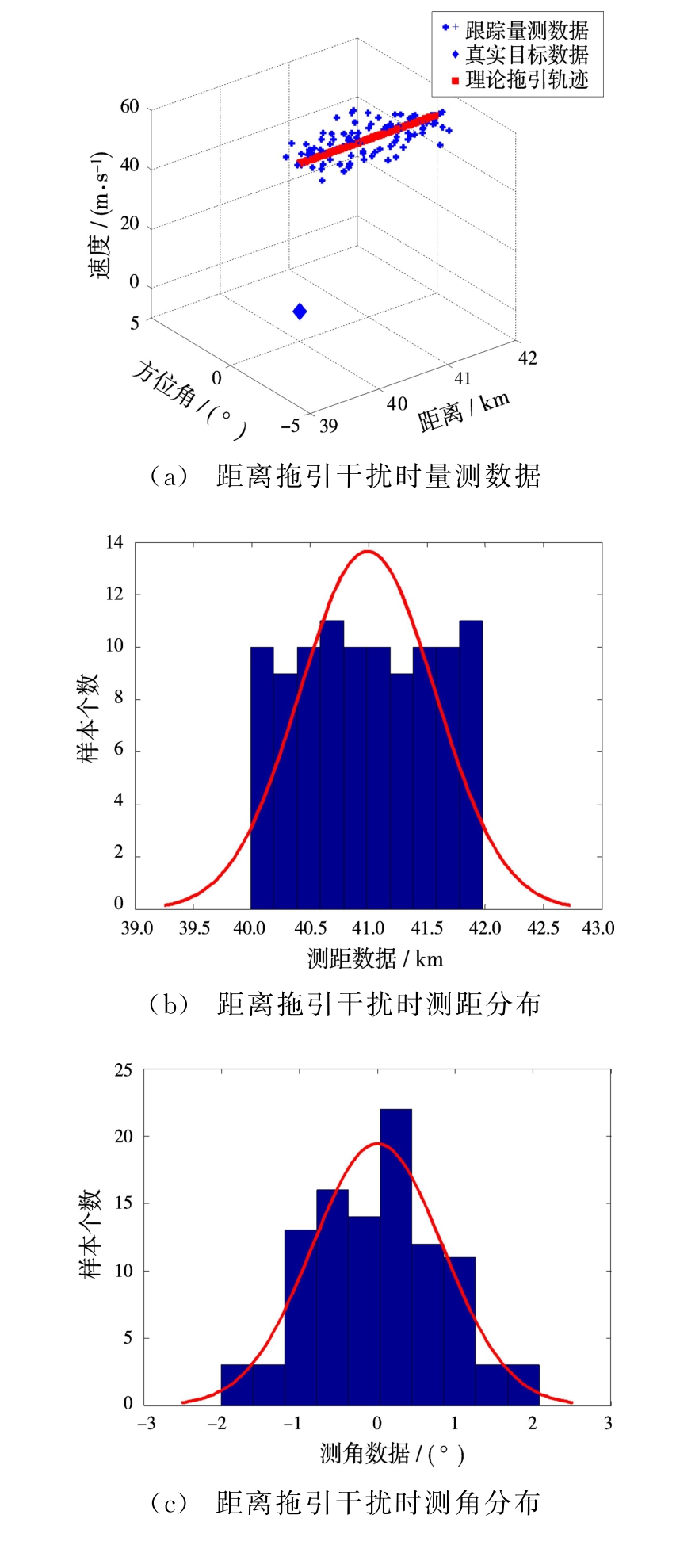
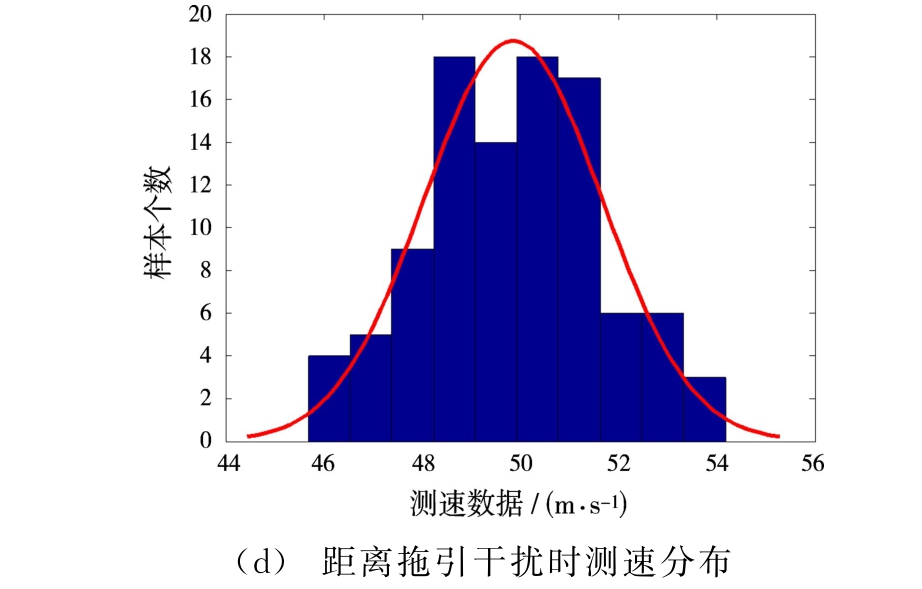
图6 距离拖引干扰时跟踪量测数据及其分布情况
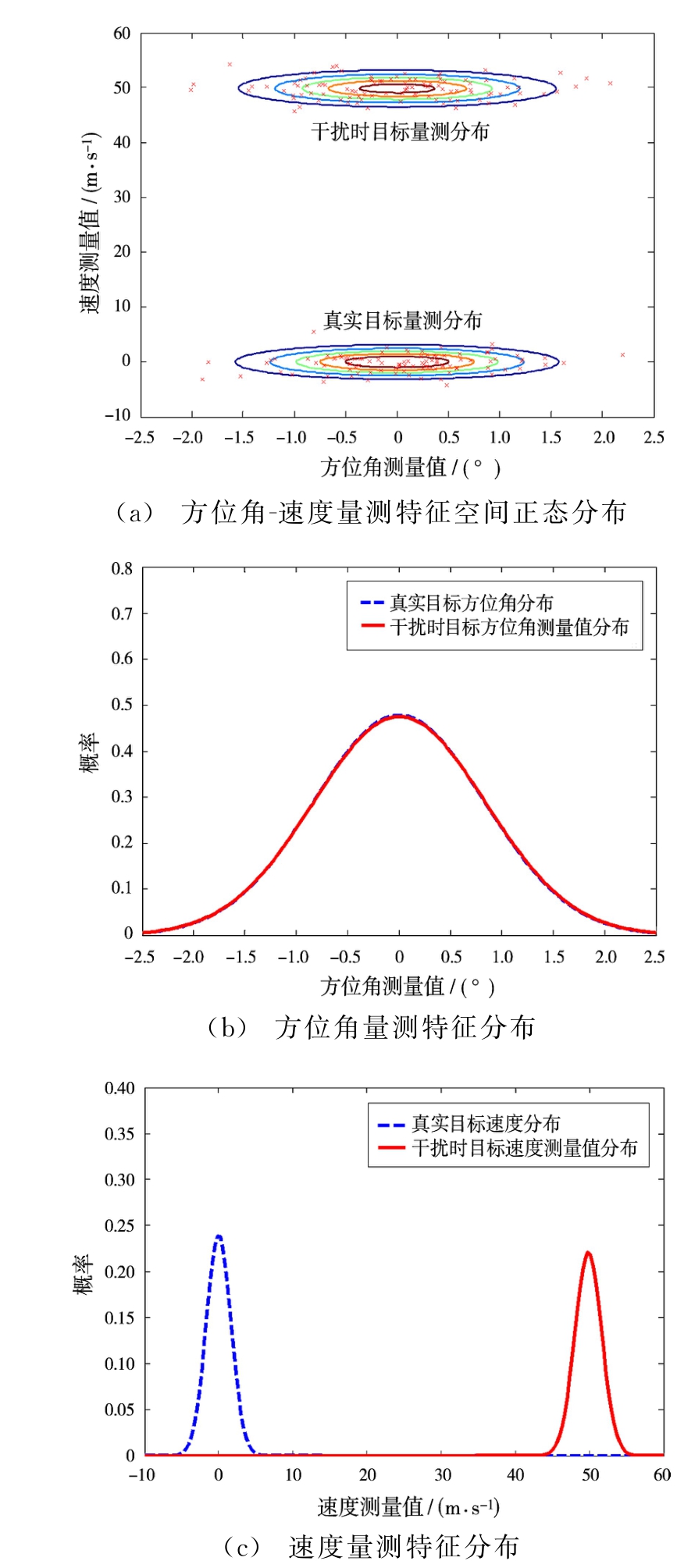
图7 量测特征空间正态分布估计情况

图8 增加对抗方法后量测数据及其分布情况
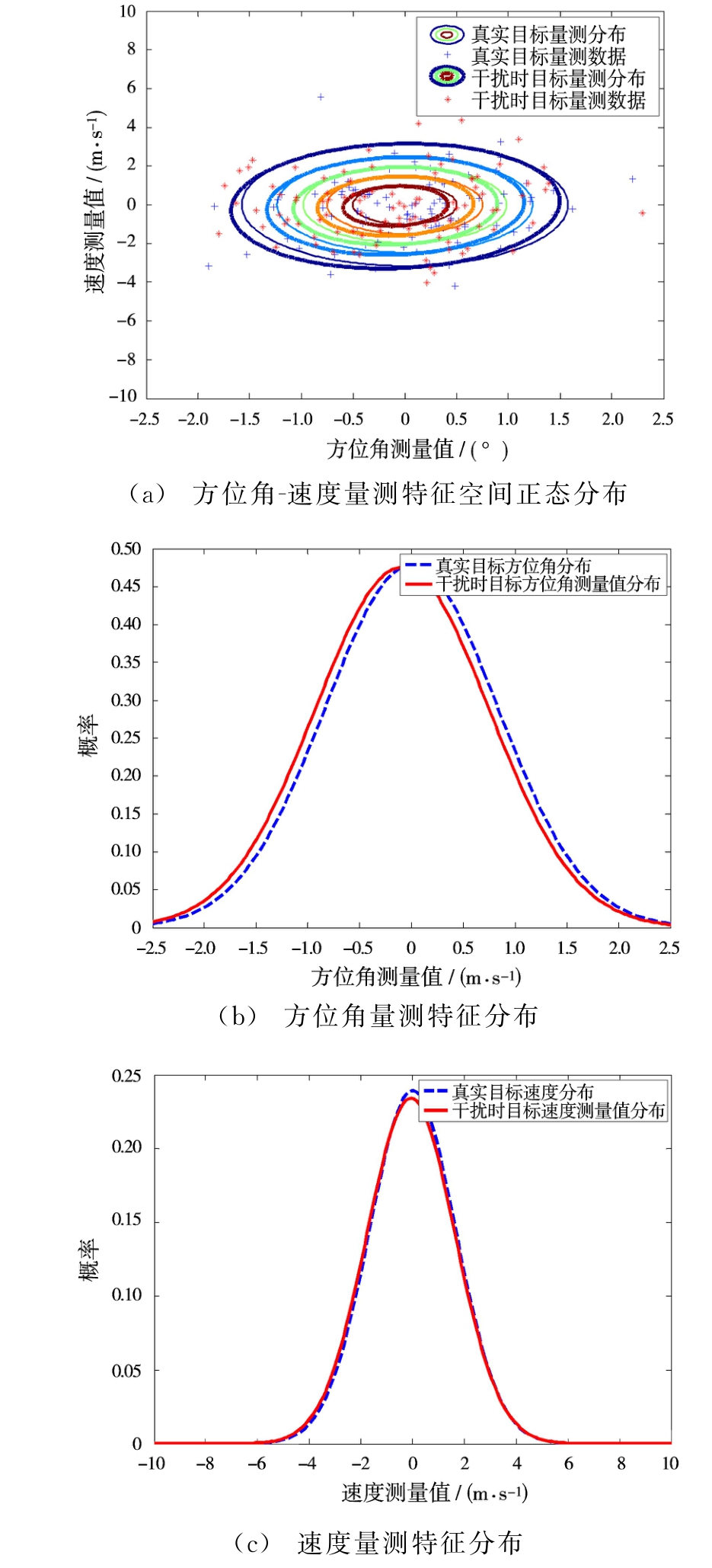
图9 量测特征空间正态分布估计情况
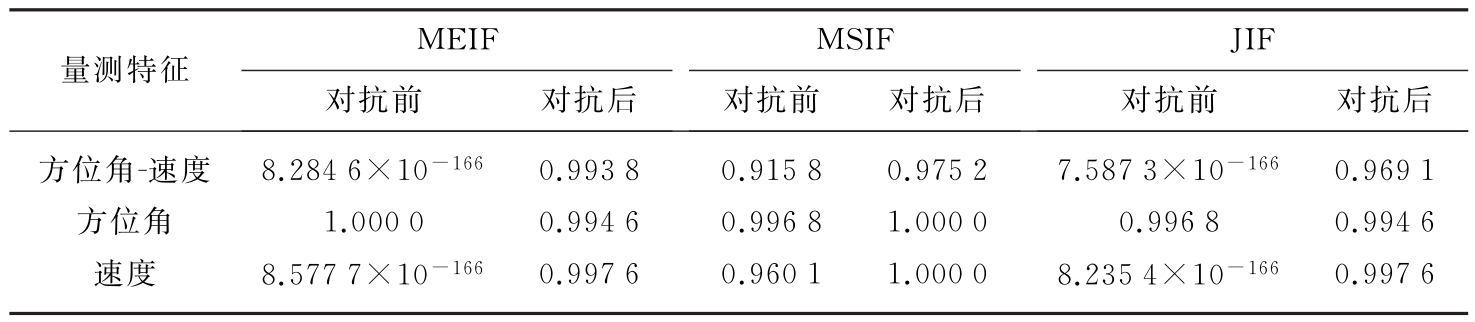
雷达抗干扰方法效能评估结果详见表3。从表3可以看出,增加速度门限后,MEIF与JIF显著提升,说明雷达对于距离-速度联合拖引干扰的抵抗能力显著增强。
本文针对一般抗干扰性能评估理论中存在的问题,提出了一种基于高维量测特征空间统计模型分析的雷达在复杂电磁环境下的抗干扰性能定量评估方法。该方法将试验数据映射到高维量测特征空间中,通过统计理论分析量测值与真实目标特性的差异,提出了MEIF、MSIF和JIF三种指标,既可以描述干扰对于雷达的影响,也可以反映雷达的抗干扰能力,并且对于单一干扰、复合干扰不敏感,对复杂电磁干扰环境具有良好的适用性。通过仿真,可以看出该方法理论可行,对雷达的抗干扰能力建设具有指导性意义。
表3 雷达抗干扰方法效能评估
参考文献:
[1]李浩,邱超凡,赵小亮.雷达抗干扰效能的多层次模糊评估方法[J].雷达科学与技术,2012,10(2):143-149,155.
[2]徐沙,张洁.一种基于层次分析法的雷达抗干扰效能评估方法[J].航天电子对抗,2016,32(3):13-15.
[3]刘松涛,姜宁,刘振兴.舰载电子对抗干扰效果在线评估方法[J].电子信息对抗技术,2016,31(4):63-67.
[4]周振宇,贺志毅,刘建欣.末制导雷达抗干扰性能评估系统工程实现[J].现代防御技术,2011,39(2):138-141.
[5]刘江波,舒敬环.复杂电磁环境下的雷达抗干扰效能评估指标体系构建[J].信息化研究,2015,41(5):1-5.
[6]李亚南,韩壮志.雷达抗干扰性能评价指标体系及发展趋势[J].火力与指挥控制,2015,40(4):1-5.
[7]聂红霞.雷达抗干扰效能评估方法探讨[J].舰船电子工程,2013,33(4):75-77.
[8]朱宁,赵肖肖,唐庆华.多元正态性检验三种方法的比较及SAS程序设计[J].苏州大学学报(自然科学版),2012,28(3):20-25.
[9]梁小筠.我国正在制定“正态性检验”的新标准[J].应用概率统计,2002,18(3):269-276.
[10]BOX G E P,COX D R.An Analysis of Transformations[J].Journal of the Royal Statistical Society,1964,26(2):211-252.
[11]李长江,邓文平,曹元元,等.基于Box-Cox变换与Johnson变换非正态过程能力分析[J].齐齐哈尔大学学报(自然科学版),2015,31(1):66-70.
A Radar ECCM Performance Evaluation Method in Complex Electromagnetic Environment
CHEN Wendong1,2,TANG Bin2
(1.The Second Academy of China Aerospace Science and Industry Corporation,Beijing100854,China;2.Beijing Institute of Remote Sensing Equipment,Beijing100854,China)
Abstract:According to the problems in radar ECCM performance evaluation,a statistic method based on geometry analysis in high-dimensional measurement feature space is proposed.The method projects the measurement information into the high-dimensional measurement space and utilizes geometry feature of the multivariate density distribution to define the measurement error impact factor(MEIF),the measurement stability impact factor(MSIF)and the jamming impact factor(JIF)to evaluate the ECM effect as well as the comprehensive ECCM performance.It is proved by computer simulation that the method is able to describe the radar ECCM performance exactly and the results are consistent with theoretic analysis.
Key words:complex electromagnetic environment;radar;electronic counter-countermeasures(ECCM);performance evaluation
中图分类号:TN973.3
文献标志码:A
文章编号:1672-2337(2017)01-0073-08
DOI:10.3969/j.issn.1672-2337.2017.01.013
收稿日期:2016-06-05;
修回日期:2016-09-01
作者简介:

陈文东男,1987年出生于山西永济,在读博士研究生,主要研究方向为雷达总体设计与雷达电子反对抗技术。E-mail;chen_eecs@sina.com
汤斌男,1977年出生,高级工程师,主要研究方向为雷达总体设计与雷达电子反对抗技术。