图1 定期维修策略的装备工作示意图
武高卫,江 峰,杨江平,王永攀
(空军预警学院,湖北武汉430019)
摘 要:针对定期维修策略下的k/N系统维修渠道的配置问题,建立了多类故障单元批量定期送修的维修渠道优化模型。首先,给出了定期维修策略下的k/N系统工作流程和故障单元维修流程;然后,根据故障单元批量定期送修的特点,提出了Dξ/M/c排队模型,并对关键输入参数进行了修正与计算,对排队系统的稳态概率进行了求解;接着,建立了多类故障单元同时送修的维修渠道优化模型,通过将多类顾客源多服务台排队系统转化为单类顾客源多服务台排队系统,对优化模型进行了求解;最后,通过算例仿真与分析,对模型进行了验证。结果表明,该模型能够为k/N系统维修渠道数量的确定提供理论依据,对部队维修资源的合理配置具有一定的指导意义。
关键词:k/N系统;定期维修;维修渠道;排队系统
维修渠道属于装备维修保障资源的范畴,通常由一组配套的维修资源组成,如维修设备设施、维修人员以及技术资料等,其配置水平直接影响着故障单元的维修进度进而影响整个武器装备的作战效能发挥[1]。因此,开展维修渠道的优化配置研究,意义重大。
为了满足高可用度和高可靠性的要求,许多大型复杂装备如舰船、相控阵雷达等越来越多地使用k/N结构系统[2]。考虑到k/N系统的冗余性设计,即当少数单元出现故障时不必立即维修,这类装备又有其独特的维修保障特点。然而,在维修渠道的配置方法上,当前部队的普遍做法是采用GJB 5967—2007《保障设备规划与研制要求》[3]中的类比法或估算法对维修渠道的配置数量进行确定,从部队的实际状况来看,该方法暴露出以下问题,造成维修渠道配置数量不合理:①没有考虑故障单元批量送修的影响;②没有考虑多类故障单元同时送修的影响。
针对上述问题,许多专家学者展开了深入的研究。文献[4-5]通过在装备研制阶段分析保障活动,对保障资源的配置效率进行了研究,但是没有考虑故障单元的规律分布,并不适用于长期运行的有故障规律的装备的保障问题;文献[6-9]根据部件失效规律特点,建立了基于M/M/c排队论的维修设备优化配置模型,在一定程度上解决了故障单元单件送修策略下的维修设备的配置问题;在故障单元批量送修的问题上,文献[10]根据保障设备数量与每批次故障产品数量的大小关系,单纯的通过对保障设备和故障单元进行分组,将问题转化为单服务台排队系统,虽然能够解决批量送修的问题,但是误差较大;文献[11-12]通过建立Mξ/M/c/∞排队模型,解决了故障单元成批到达、每批到达数随机、批与批之间的到达时间间隔服从指数分布的维修排队问题,为解决故障单元批量送修提供了较好的思路和方法,但是没有考虑多种故障单元同时送修的影响;在多类故障单元同时送修的问题上,文献[13-15]基于METRIC模型,分析了多类故障单元同时送修的情况下有限维修渠道对备件供应的影响,但其前提是(S,S-1)库存策略,而非批量送修策略。
结合部队定期维修作业体制,针对k/N系统故障单元批量定期送修的特点,考虑到多类故障单元同时送修的问题,本文依次建立了Dξ/M/c排队模型和维修渠道优化模型,对定期维修策略下多类故障单元批量定期送修的维修渠道配置问题进行了研究。
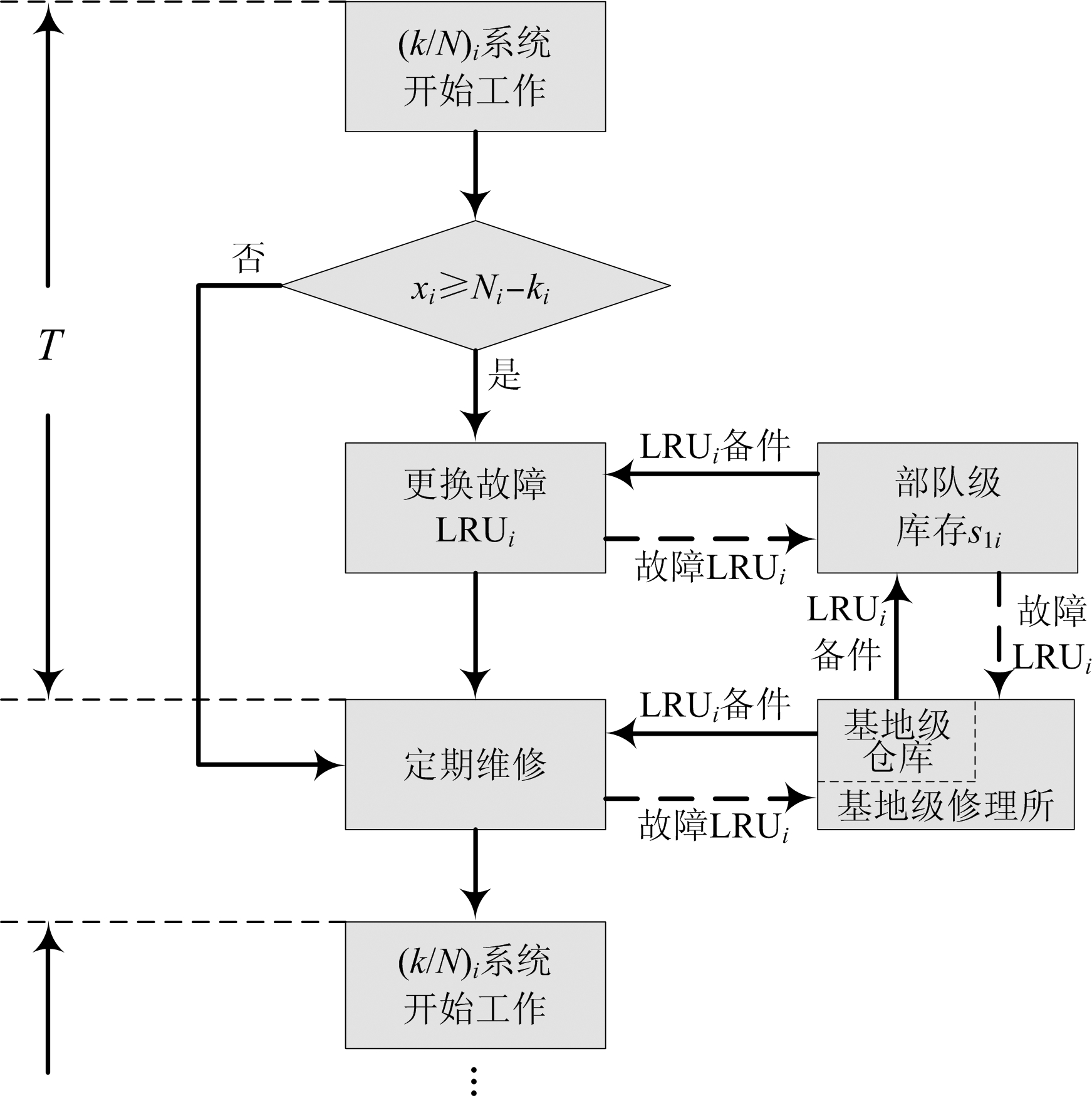
设某大型复杂装备由l种现场可更换单元(Line Replaceable Unit,LRU)组成,LRUi包含Ni个故障间隔时间服从参数为λi的指数分布,且相互独立的单元,当至少有ki个单元正常工作时装备才能正常运行,即该装备由l个k/N系统组成。该装备采用两级维修作业体系(部队级和基地级)和定期维修策略,维修周期为T。定期维修策略的装备工作示意图如图1所示,系统开始正常工作后,若在定期维修周期T内LRUi故障件数xi<Ni-ki,则(k/N)i系统正常工作;若xi≥Ni-ki,则(k/N)i系统失效,立即从部队级库存中领取LRUi备件对(k/N)i系统进行换件维修,修复完成后装备继续运行。当运行到定期维修周期T时,对所有故障LRUi进行换件维修,系统恢复完好,进入下一个定期维修周期,同时将故障LRUi进行送修。

图1 定期维修策略的装备工作示意图
考虑到k/N系统的冗余性设计,对其进行维修时需要采用批量换件维修方式,所以传统的(S,S-1)库存策略以及与之对应的单件送修方式不再适用。本文采取(T,S)库存策略和批量送修方式。
根据实际维修保障特点,建立模型需作如下关键性假设:
1)部队级只对LRU进行换件维修,换件维修时间忽略,基地级修理所对故障LRU进行修复性维修;
2)维修渠道为通用维修渠道,可以对该装备所有种类的故障LRU进行修理;
3)维修渠道是完好不坏的,可以连续作业,不会出现故障而影响维修作业;
4)所有的故障LRU没有优先等级,按照FCFS规则接受维修服务。
每次定期维修后,需将故障LRUi送往基地级修理所进行维修。设故障LRUi批量定期送修,每批次送修的故障LRUi数为随机变量ξi,批与批之间的到达间隔为维修周期T。修理所内有c组并行的维修渠道,每个维修渠道对故障LRUi的维修时间t服从参数为μi的指数分布;排队系统只有一个队列,等待位置无限,送修过程与维修过程相互独立。当ξi>c时,c个故障LRUi直接进入维修作业,ξi-c个故障LRUi等待维修;当某个维修设备完成对故障LRUi的维修时,维修队列中的故障LRUi依次进入维修设备接受服务,直到该批所有故障LRUi维修完毕。则定义该维修过程为Dξ/M/c排队过程。故障LRUi维修流程如图2所示。
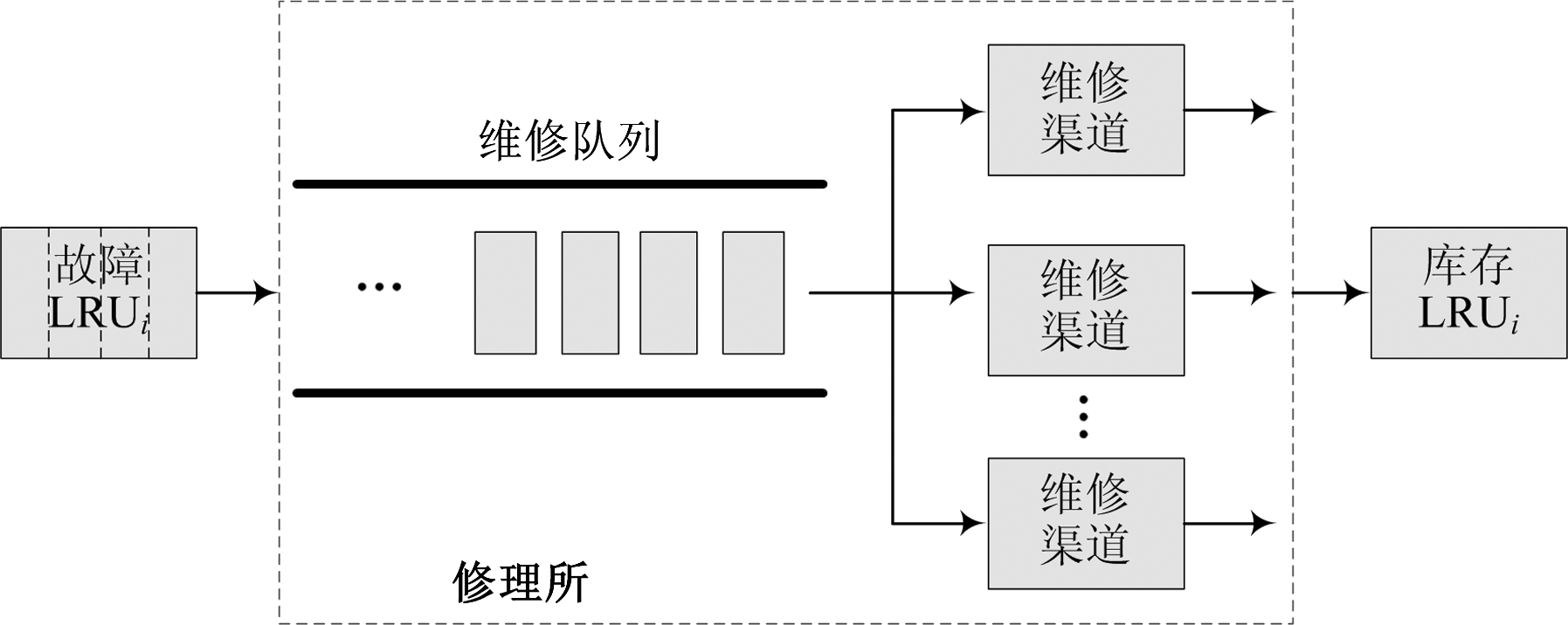
图2 故障LRUi维修流程
设LRUi的故障率服从参数为λi的指数分布,由指数分布规律得,每个LRUi的故障密度函数为
则每个LRUi的可靠度函数为
(k/N)i系统的正常工作时间期望[16]为
当采用单件维修方式时,文献[17]对k/N系统在时间T内的故障数ξi的概率分布进行了计算:
上式得出的前提是每个故障单元能够得到及时修复。然而采用定期批量维修方式时,只有当系统工作时间达到维修周期T或故障单元数达到mi=Ni-ki时,才进行维修。因此本文对k/N系统在时间T内的故障数ξi的概率分布进行修正如下:
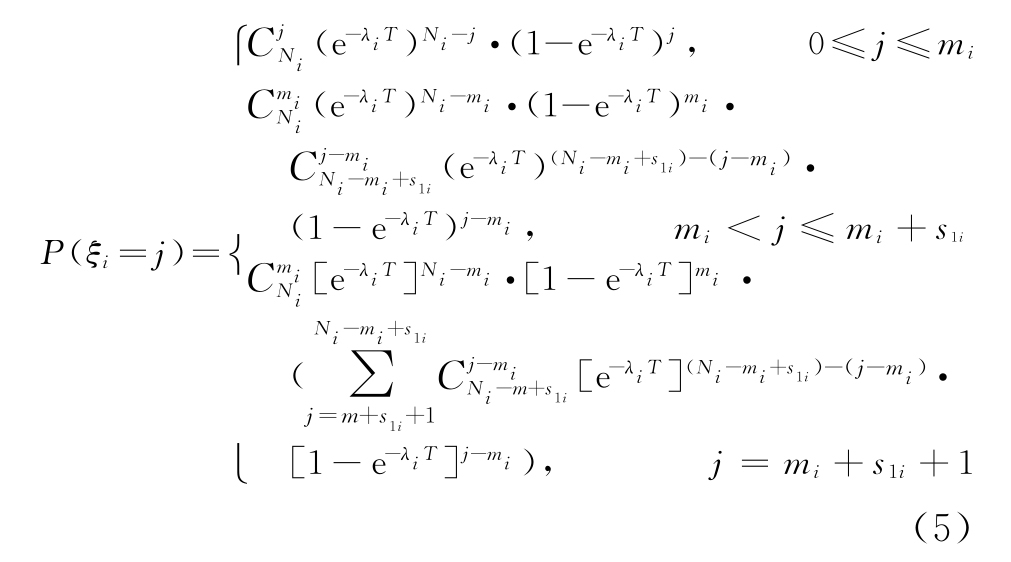
记![]() ,式(5)化简为
,式(5)化简为
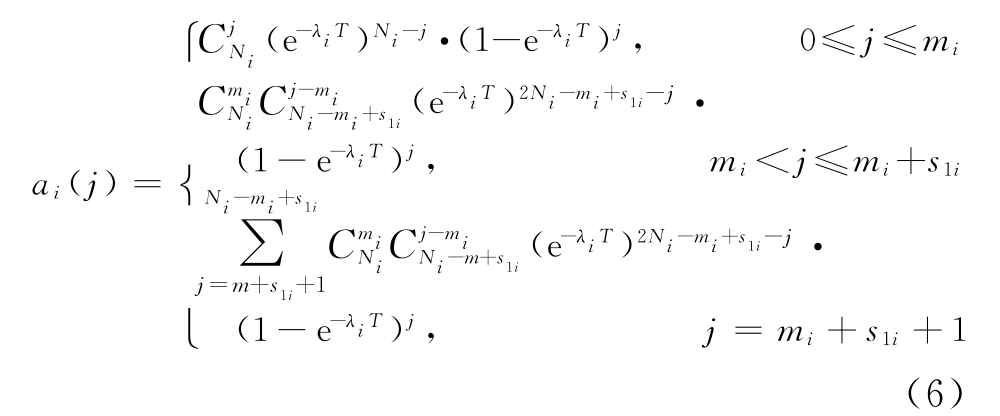
服务强度ρ描述了维修设备的繁忙程度,ρ越大,维修设备越繁忙。当ρ<1时,排队系统能够达到平衡状态,存在稳态分布;当ρ≥1时,排队系统不能达到平衡状态,即该系统不能构成概率分布。Dξ/M/c排队系统的服务强度表达式为

式中![]() 表示每批次故障LRUi的到达率。
表示每批次故障LRUi的到达率。
设Ni(t)表示时刻t排队系统内故障LRUi数,包括正在进行维修的故障LRUi,即Ni(t)表示时刻t排队系统的队长,{Ni(t),t≥0}的状态空间为{0,1,2,3,…}。设pij(t)=P{Ni(t)=j}为Ni(t)的瞬时分布,由于排队系统的概率随机性,求解其瞬时分布是不精确且没有意义的,因此通常求当排队系统达到平稳状态后的稳态分布![]() 下面讨论ρi<1条件下Ni(t)的稳态分布pij。
下面讨论ρi<1条件下Ni(t)的稳态分布pij。
由2.1节的排队过程,可得出队长Ni(t)的状态转移图,如图3所示。
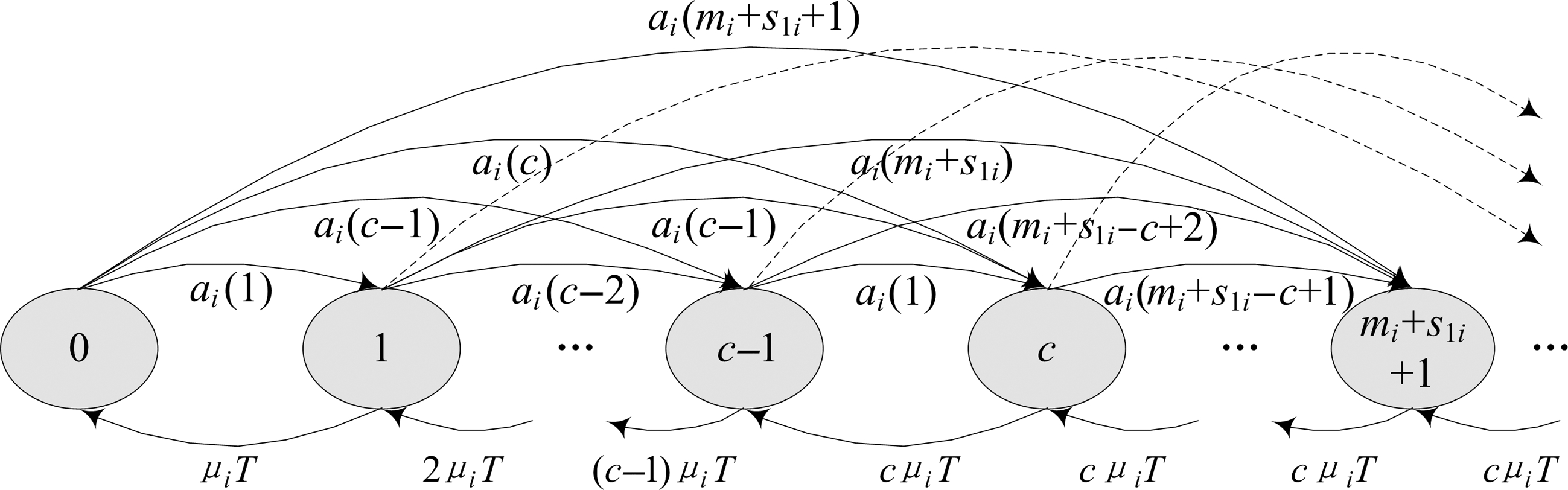
图3 队长Ni(t)的状态转移图
根据状态转移图,可列出平衡条件下的K氏代数方程:
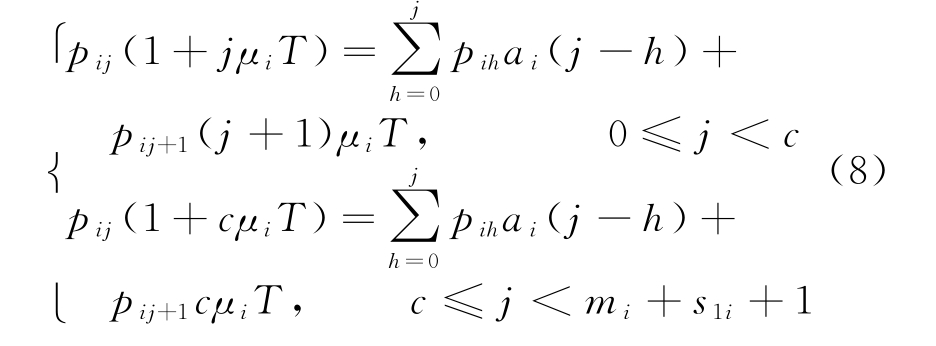
文献[18]对MX/G/1/∞排队系统的稳态概率求解方法进行了推导和证明,本文运用其思想和方法,推导出Dξ/M/c排队系统的稳态概率如下:
1)当ρi≥1时,pij=0;
2)当ρi<1时,pij存在且构成概率分布,进一步有递推式:
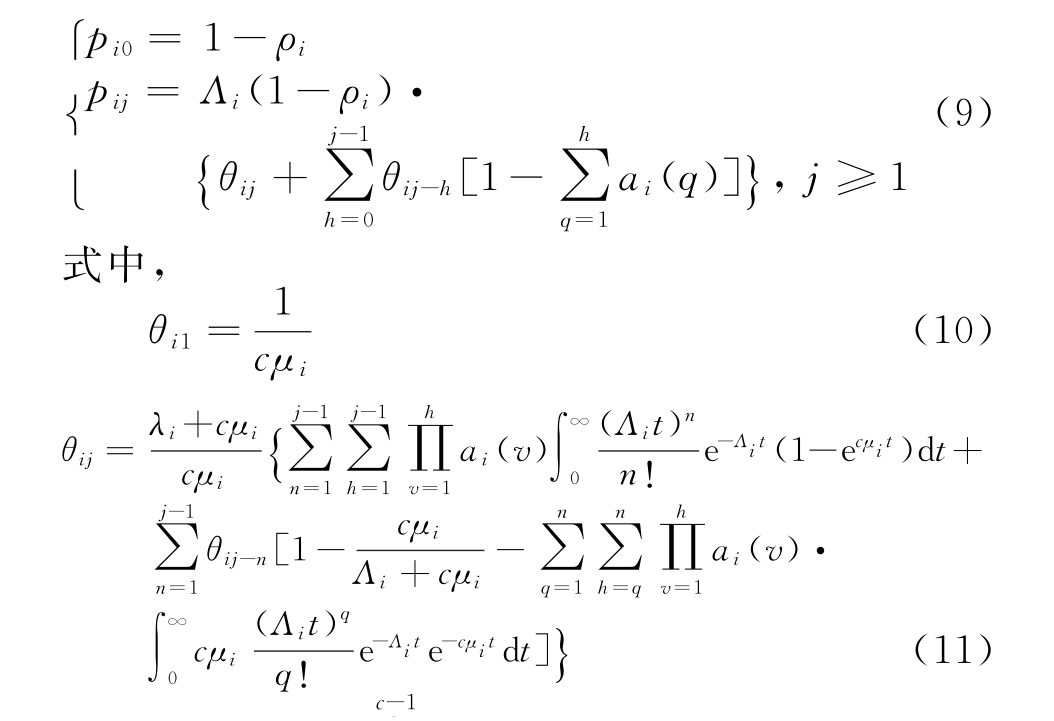
记![]() ,求得稳态下的平均队长Li为
,求得稳态下的平均队长Li为
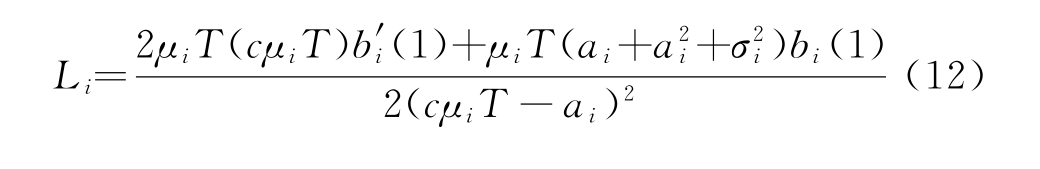
基地级修理所的通用维修渠道能够对多种不同类型的故障LRUi进行维修,因此维修系统可以看作一个多类顾客源多服务台排队系统。设某维修渠道能够对l种故障LRU进行维修,对故障LRUi的维修率为μi,由于不同种类LRU相互独立,互不影响,为了便于分析,通常将多类顾客多服务台排队系统转化为单类顾客多服务台排队系统。
1)平均到达率Λ
装备采用定期维修策略时,到达维修周期T后对所有(k/N)i系统进行维修,则进入维修渠道的各种故障LRUi的平均到达率为
2)每批次平均故障数概率分布P(ξ)
式中,ji表示LRUi的故障数,且![]()
3)平均服务强度ρ
4)平均维修率μ
由服务强度的定义得

式中,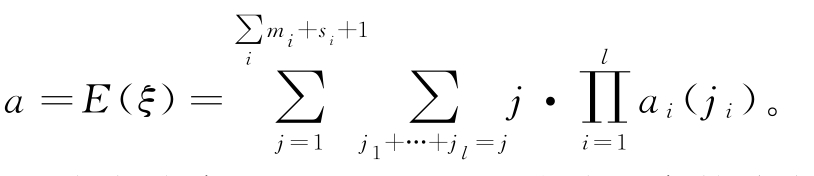
考虑多类故障LRUi的排队系统输入参数确定之后,便可求解出排队系统的平均稳态队长pj。
在对维修渠道进行优化配置时,维修渠道满足率是比较常用的约束指标。维修渠道满足率是指当故障LRU到达修理所时不用等待,能够马上开始维修作业的概率。可见,维修渠道满足率从装备维修保障的角度考虑,反映了维修渠道的配置数量对于维修活动及时开始的影响程度。根据维修渠道满足率的定义,在本文的排队模型中,维修渠道满足率P可以表示为排队模型的稳态队长不大于维修渠道的数量的概率,即
费用是配置维修资源时必须考虑的因素。假设每组维修渠道的配置费用为r万元,则以维修渠道配置费用C为优化目标,以维修渠道满足率为约束条件建立维修渠道优化模型:
式中,P0为最低可接受的维修渠道满足率。
某相控阵雷达天线阵面主要由两种LRU组成:T/R组件和发射电源,其基本数据见表1,假设每组维修渠道配置费用r=50万元,最低可接受的维修渠道满足率P0=0.95。
表1 天线阵面LRU基本数据

维修渠道满足率P与维修渠道数量c、定期维修周期T,以及每批次送修数量ξ有关,当天线阵面的LRU参数确定时,ξ还与部队级备件库存数量s1有关。图4以T/R组件为例,分别给出了控制变量条件下维修渠道满足率P随维修渠道数量c、定期维修周期T,以及T/R组件的部队级备件库存数量s1的变化情况。
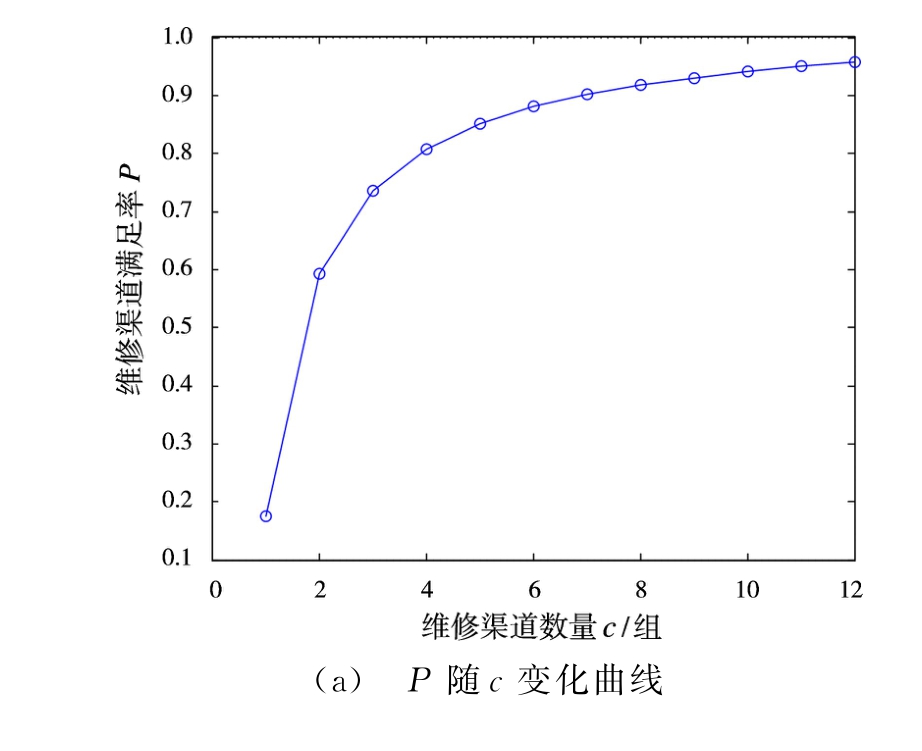
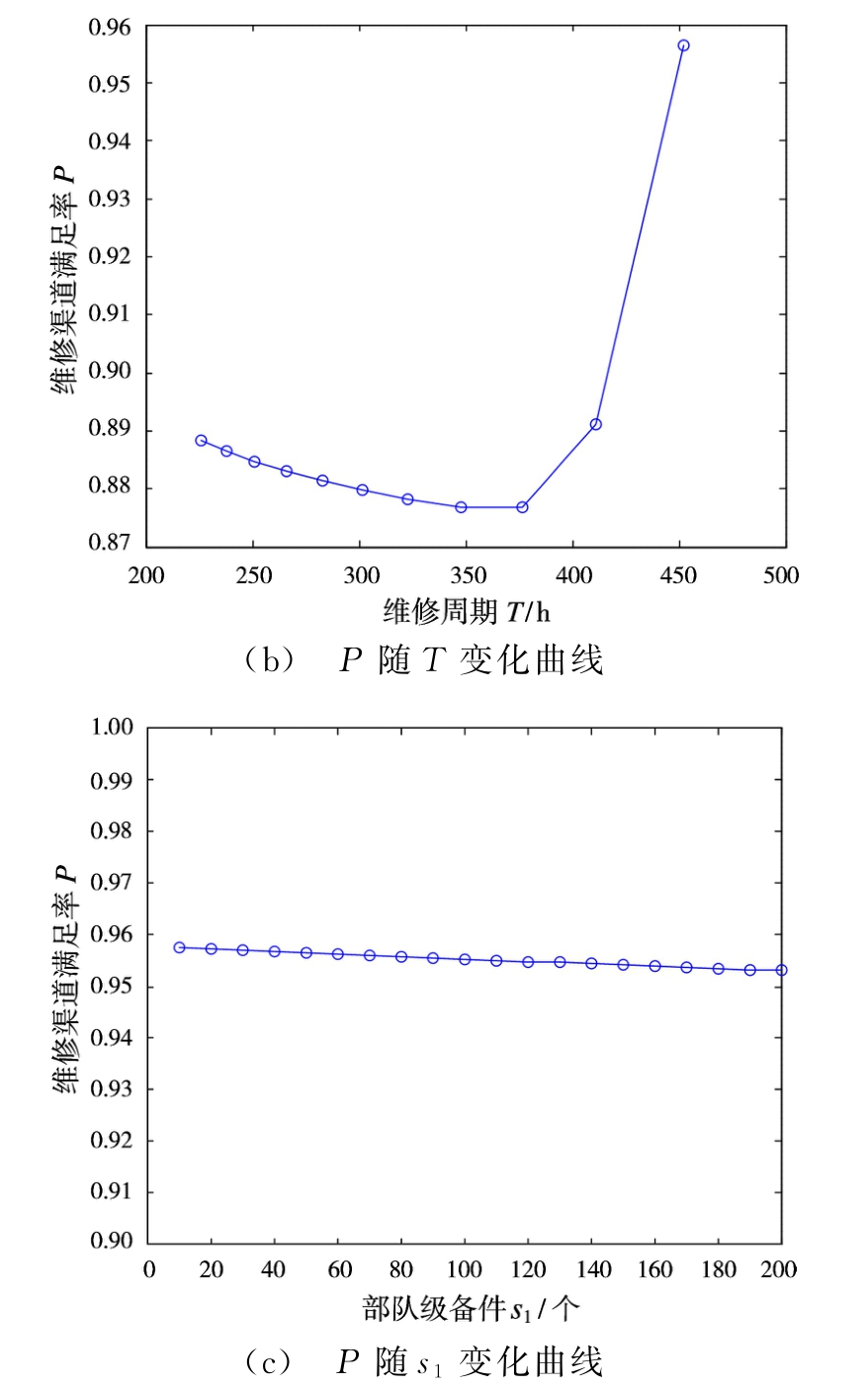
图4 维修渠道满足率变化曲线
从图中可以看出,维修渠道数量c是影响维修渠道满足率P的关键因素,且P是c的单调递增凸函数。维修周期T对维修渠道满足率P的影响比较复杂,随着T的增加,在每批次送修数量增大的同时,维修渠道能够维修的故障单元的数量也在增大,因此变化规律不是单调曲线。由于T的确定不仅与维修渠道满足率有关,还与系统使用可用度、备件数量以及维修规划等因素有关,本文中不作讨论,取值T=E(T0)。部队级备件数量s1对维修渠道满足率P的影响则几乎可以忽略不计。
选取T1=E(T0)1=452.054 0 h,s11=50个,计算得出T/R组件每批次送修数量期望a1=93.111 2个;当c=12组时,维修渠道满足率P1=0.956 5,维修渠道的稳态队长L1=5.481 6个,维修渠道配置费用C1=600万元。
同理对发射电源进行计算,选取T2=E(T0)2=467.809 0 h,s12=10个,计算得出发射电源每批次送修数量期望a2=53.711 7个;当c=8组时,维修渠道满足率P2=0.954 2,维修渠道的稳态队长L2=3.397 9个,配置总费用C2=400万元。
综合考虑两种LRU的送修情况,选取T=450 h,s11=50个,s12=10个,计算得出每批次平均送修数量期望a=98.029 7个,维修渠道的平均维修率μ=0.130 4;当c=1时,ρ=1.600 1>1,不能构成稳态,当c≥2时,ρ<1。图5给出了两种LRU综合考虑与单独考虑两种情况的维修渠道满足率随总费用的变化曲线。
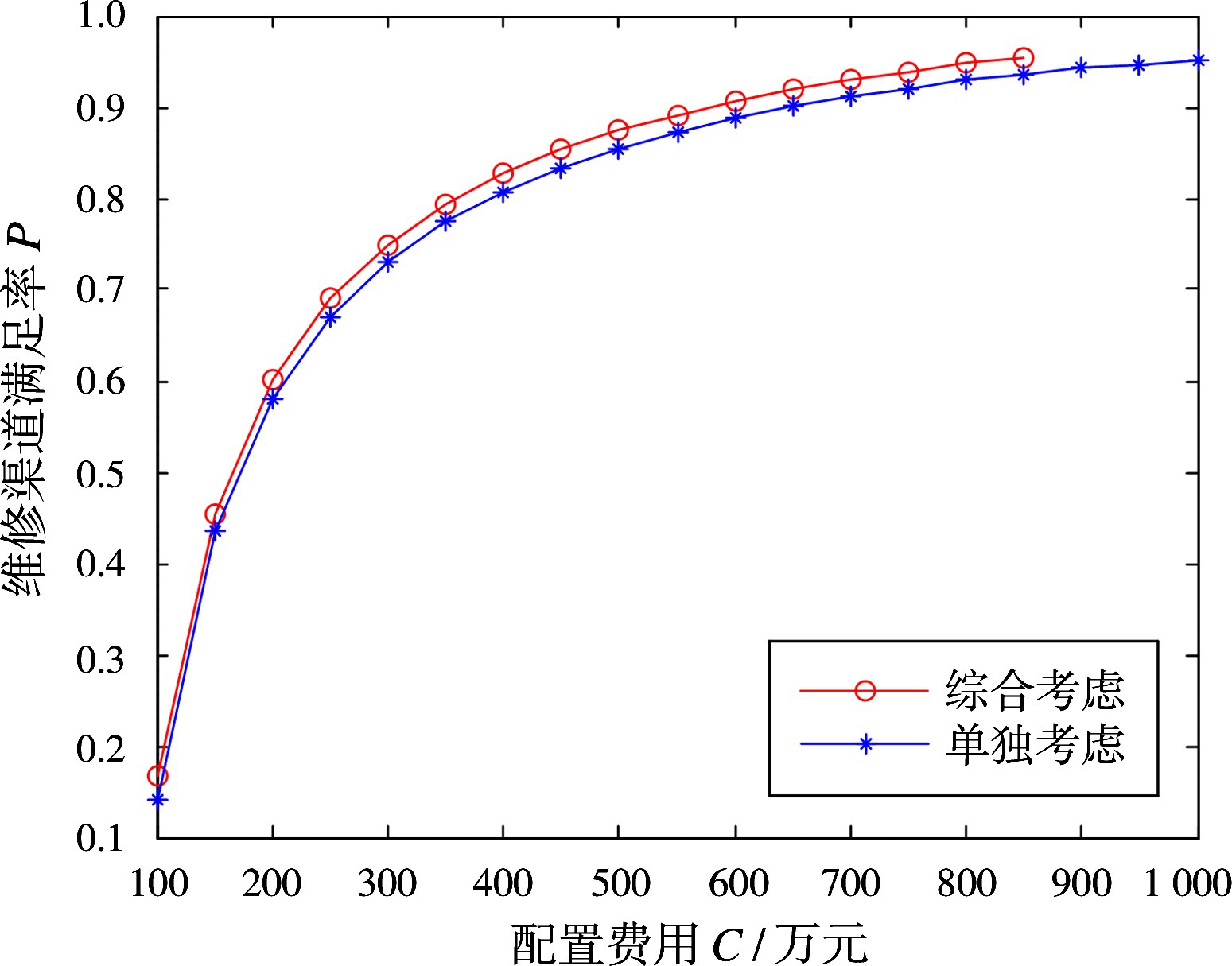
图5 两种方法的维修渠道满足率对比图
最后计算得出所需维修渠道数量c=17组时,维修渠道满足率P=0.955 0,维修渠道的稳态队长L=13.271 8个,配置总费用C=850万元。比较可得,综合考虑两种LRU送修所需的维修渠道配置费用比单独考虑时的费用降低了15%。
本文从k/N系统的维修实际入手,根据故障单元批量定期送修的特点,建立了多类故障单元批量定期送修的维修渠道优化模型,通过对关键输入参数和排队系统的稳态概率进行修正与计算,并将多类顾客源多服务台排队系统转化为单类顾客源多服务台排队系统,对优化模型进行了求解,为部队进行维修资源的合理配置提供了理论依据。另外,本文只将维修周期T对维修渠道配置的影响进行了简单的分析,其确定方法并没有进行讨论,还需进一步展开研究。
参考文献:
[1]甘茂治,康建设,高崎.军用装备维修工程学[M].北京:国防工业出版社,2005:339-341.
[2]DE SMIDT-DESTOMBES K S,VAN DER HEIJDEN M C,VAN HARTEN A.On the Availability of a k-out-of-N System Given Limited Spares and Repair Capacity Under a Condition Based Maintenance Strategy[J].Reliability Engineering and System Safety,2004,83(3):287-300.
[3]保障设备规划与研制要求:GJB5967-2007[S].北京:中国人民解放军总装备部,2007.
[4]LI D,LI G L,ZHAI J.Research on Missile Supportability Evaluation[M]∥CAO B Y,ZHANG C Y,LI T F.Fuzzy Information and Engineering,Berlin:Springer,2009:585-590.
[5]DOUGHERTY J J,HAZLETT R G.Maintenance Activities and Resources Simulation(MARS)Model[C]∥The Fourth Annual Conference on Applications of Simulation,New York:[s.n.],1970:106-110.
[6]KIM J-S,SHIN K-C,PARK S-K.An Optimal Algorithm for Repairable-Item Inventory Systems with Depot Spares[J].Journal of the Operational Research Society,2000,51(3):350-357.
[7]JUNG B-R,SUN B-G,KIM J-S,et al.Modeling Lateral Transshipments in Multi-Echelon Repairable-Item Inventory Systems with Finite Repair Channels[J].Computers&Operations Research,2003,30(9):1401-1417.
[8]MIRZAHOSSEINIAN H,PIPLANI R.A Study of Repairable Parts Inventory System Operating Under Performance-Based Contract[J].European Journal of Operational Research,2011,214(2):256-261.
[9]李韶亮,陈云翔,蔡忠义,等.基于排队论的内场维修设备数量确定方法[J].数学的实践与认识,2014,44(11):147-152.
[10]王乃超,康锐,王禹.基于产品维修策略的保障设备需求量计算模型研究[J].系统工程与电子技术,2009,31(5):1266-1269.
[11]丛国超,朱翼隽.批量到达的多服务台排队模型求解[J].成都信息工程学院学报,2007,22(1):98-100.
[12]张侦英,康锐,王乃超,等.典型情况下保障设备满足率计算模型[J].计算机集成制造系统,2010,16(10):2206-2210.
[13]SLEPTCHENKO A,VAN HEIJDEN M C,VAN HARTEN A.Effects of Finite Repair Capacity in Muli-Echelon,Multi-Indenture Service Part Supply System[J].International Journal of Production Economics,2002,79(3):209-230.
[14]徐立,李庆民,阮旻智.具备有限维修能力的舰船编队保障方案优化[J].系统工程与电子技术,2014,36(11):2226-2232.
[15]夏国清,陈红召,栾添添.有限维修渠道下两集维修供应系统性能评估模型[J].系统工程理论与实践,2015,35(4):1041-1047.
[16]卢雷,杨江平,左治方,等.大型相控阵雷达天线阵面事情维修优化模型[J].雷达科学与技术,2014,12(3):325-328.
[17]郭继周,赵朝先,郭波.面向多阶段任务的武器系统备件优化配置建模[J].数学的实践与认识,2009,39(12):64-70.
[18]CHAUDHRY M L,TEMPLETON J G C.FirstCourse in Bulk Queues[M].New York:Wiley,1983:87-94.
Optimization Model of Maintenance Channel for k/N System Based on Periodic Maintenance Policy
WU Gaowei,JIANG Feng,YANG Jiangping,WANG Yongpan
(Air Force Early Warning Academy,Wuhan430019,China)
Abstract:Aiming at the configuration problem of maintenance channel fork/Nsystem based on periodic maintenance policy,an optimization model is established for maintenance channel considering the batched periodic delivery of multi-class failed units.Firstly,thek/Nsystem operation process and the failed units maintenance flow are given.Secondly,theDξ/M/cqueuing model is proposed according to the feature of the batched periodic delivery of the failed units,the key parameters are calculated and modified,and the steadystate probability of the queuing system is calculated.Then,the optimization model is developed for maintenance channel considering multi-class failed units delivery simultaneously,and the model is solved through converting the multi-class-source-multi-server queuing system into the single-class-source-multi-server queuing system.Finally,simulation and analysis of an example are conducted to verify the proposed model.The results show that the model can solve the maintenance channel allocation problem well and may improve the allocation of maintenance resources.
Key words:k/Nsystem;periodic maintenance policy;maintenance channel;queuing system
中图分类号:TN956;N945.12
文献标志码:A
文章编号:1672-2337(2017)01-0089-06
DOI:10.3969/j.issn.1672-2337.2017.01.016
收稿日期:2016-04-29;
修回日期:2016-08-22
基金项目:国家部委资助项目(No.KJ2014023200B11145);博士研究生专项课题(No.2014JY546)
作者简介:

武高卫男,1991年生于河北邢台,硕士研究生,主要研究方向为预警装备综合保障技术。E-mail:13098886064@163.com