高梓植,李志强
(军械工程学院,河北石家庄050003)
摘 要:多频段子脉冲信号合成距离像,可以降低系统的瞬时带宽以及信号的采样率要求,并且提高距离分辨率。在原有基于合成带宽技术的融合子带基础上,采用高斯插值对融合后信号进行均匀化处理,获得了更高分辨率的距离像。在运算速度上将高斯插值与辛格插值进行比较,最终得出高斯插值模型在运算速度上优于辛格插值模型。仿真实验表明,此方法不仅能够解决不同参数的子脉冲合成问题,还能有效地改善距离分辨率,并且对比辛格插值还能减少运算时间。
关键词:合成带宽;距离分辨率;非均匀采样;高斯插值
随着现代战争对雷达目标探测精度的进一步要求,对雷达在距离分辨率上的要求也越来越高,现代雷达一般通过发射大时宽带宽积的LFM信号来解决雷达存在的雷达探测距离与距离分辨率之间的矛盾[1],而距离分辨率受限于带宽的影响,增加带宽意味着要增大雷达数据处理能力,从而增大了雷达自身成本,近年来发展了一种合成带宽雷达体制,其实质是由两个或者多个线性调频脉冲信号来获得更高的带宽。通过此类方法既能降低信号瞬时带宽,也能够降低信号的采样率要求。
合成带宽技术有时域和频域两种方法[2-3],文献[3]提出先经过解线性调频技术去斜,然后利用时移来实现合成带宽处理,这种方法对脉冲信号参数有很高的要求,需要步进线性调频信号模型才能使用这种方法,而更一般的情况下,采样率和带宽不同,频段可以重叠和分隔,文献[4]提出了非均匀化模型来解决这一类问题,并通过辛格(Sinc)插值方法实现信号的均匀化重建,并最终获得了高分辨距离像。非均匀采样是相对于均匀采样提出的一种采样方法,理想均匀采样的采样时间间隔是完全相等,而非均匀采样的采样时间间隔是不确定的[5]。
针对原有的信号均匀化模型,本文提出了采用高斯插值方法进行信号的均匀化重建,在频段重叠或分隔等情况下,最终获取高分辨距离像。
假设雷达发射线性调频信号,考虑两个子脉冲情况,多脉冲情况以此类推,两个子脉冲信号模型分别为
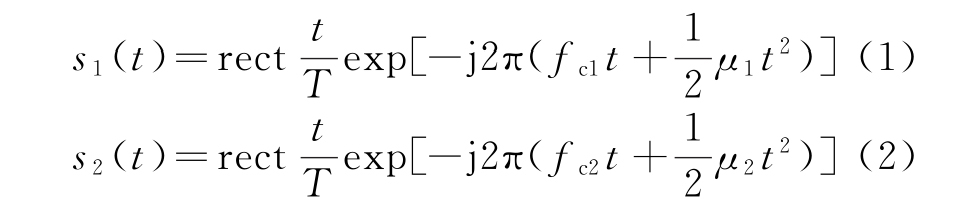
式中,T为脉宽,fc为载频,μ为调频率,t为快时间。
设散射点到雷达的距离为R,则
,那么该散射点的回波模型可分别表示为
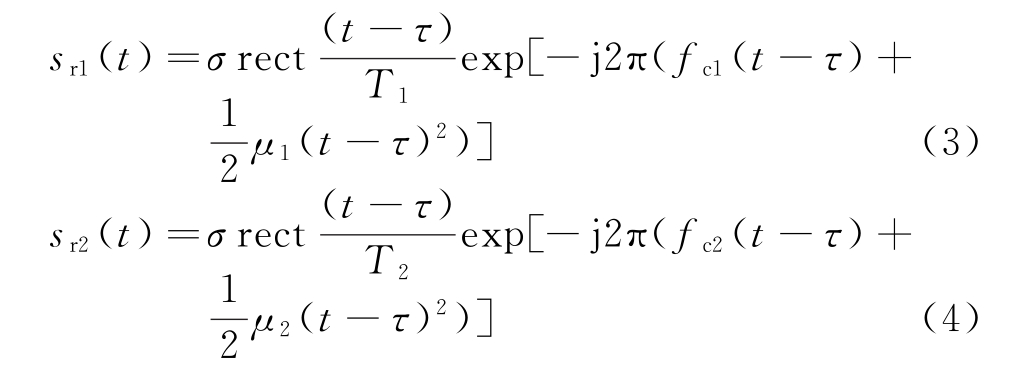
式中,σ为该散射点的RCS。为了简化运算,所有的散射点具有相同的σ。对式(3)采用参考位置为0的回波,对回波作去斜处理得
将去斜信号换作频域表示法,令f1=fc1+μ1t得
同理,
式中,f2=fc2+μ2t。
考虑最简单的情况,若B1=B2,前面又有脉宽相同,则可以得到μ1=μ2,对于这类问题,可以利用时移或者频移的方法对两个子脉冲完成合成带宽处理[3]。若B1≠B2,则不能直接将频带进行拼接,需要作平移或者频带剪裁。若距离向采样率不同,也不能直接作FFT变换,还需要进行插值处理。
对于一个N点的数据
FFT的表达式为
式中,
,M表示FFT点数,fj表示N点各点的值,
,其中n=1,…,N。
由于子带拼接所带来的信号非均匀问题,直接对拼接数据作FFT就会使得xj不是一个均匀采样,造成频谱失真。文献[4]已经通过非均匀采样模型说明了对脉宽不同,带宽不同的子带进行均匀采样的必要性,在频域角度说明了将两个子脉冲直接拼接所带来的非均匀性问题。要想解决非均匀性问题,就必须对已知数据进行均匀化处理。
本文采用高斯插值方法来对信号进行均匀化处理,构造以2π为周期的高斯函数
定义fτ(x)为f(x)与gτ(x)的卷积,其表达式为
由卷积的性质可知,fτ是以2π为周期的函数,其实质就是将原来非均匀的数据进行高斯化,使其分布在xj附近的一段频带上,通过这种手段就可以使原来非均匀的xj通过一个重建的均匀的高斯模型来表示,实现信号的均匀化处理。而τ则决定了高斯函数的下降速度。τ值越大,下降速度越慢,有效的延伸值越多,τ值越小,下降速度越快,有效的延伸值越少。通常在高斯插值时,取双向各6位延伸值为单精度表示,取双向各12位延伸值为双精度表示。由fτ(x)可知,其FFT表达式为
对于一个过采样的标准FFT变换来说,
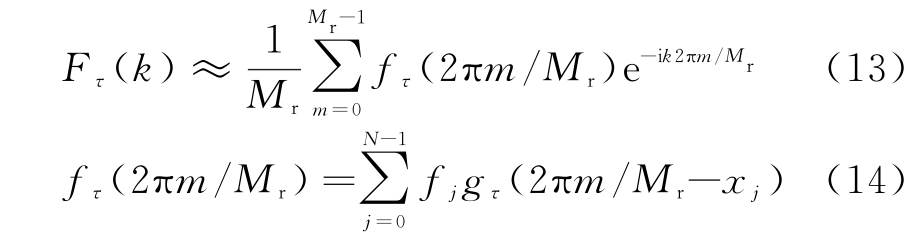
式中,Mr表示过采样点数。
由于gτ的FFT变换Gτ(k)=2τe-k2τ,所以
也就是说只要知道Fτ(k),也就可以通过上述算式求得F(k)。
由上述分析可知,求得F(k)的核心就是求得fτ(2πm/Mr)。根据式(10),(14)可知
考虑仅只有一个高斯核作用的情况下,令h=0,对式(15)进行计算得
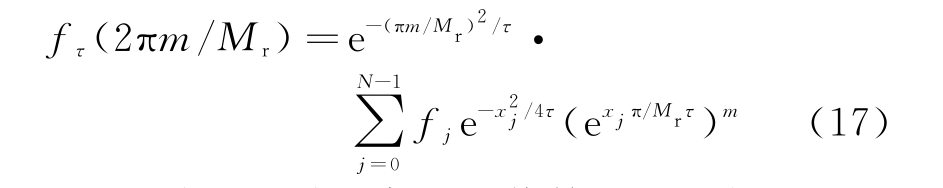
由上述推导可知,高斯插值算法过程如下:
1)令β=2πm/Mr表示距离xj最近的均匀采样点,Msp表示从β开始的双向延伸点个数,Msp=6为单精度,Msp=12为双精度。
2)设E1=e-(xj-β)2/4τ,E2=e(xj-β)π/Mrτ,考虑延伸量的影响:
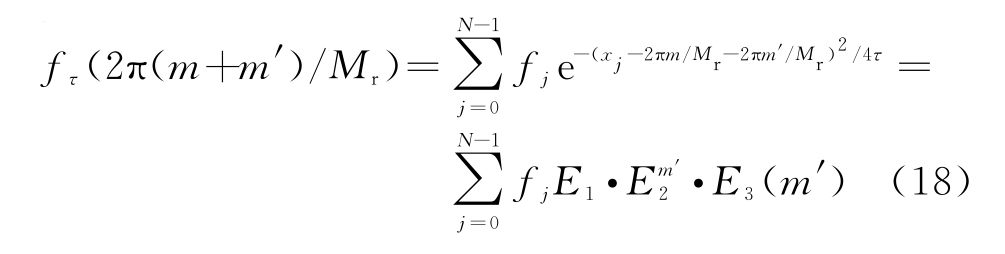
式中,E3(m′)=e-(πm′/Mr)2/τ,-Msp≤m′≤Msp。
3)将所求得的fτ进行FFT变换得到Fτ(k),最终由式(15)得F(k)。
由理论分析可知,距离分辨率只与带宽B有关,理论上的最大值为
,在实际情况中,由于非均匀插值所带来的误差影响,分辨能力要稍微比理论值差一点。由于距离分辨率只与带宽有关,所以说在选择子带时应该注意尽量不要让两个子带重叠,也不要使两个子带频率间隔太大,避免高斯插值引起的信息损失。
假设距离维上存在3个点目标,其位置分别为2 500,2 500.4,2 504。设第一个子脉冲的载频为10 GHz,带宽为320 MHz,脉宽为0.33μs,采样点数为1 024点;第二个子脉冲的载频为10.3 GHz,带宽为300 MHz,脉宽为0.33μs,采样点数为512点。通过上述假设,子载频之间的频率间隔为300 MHz,且子脉冲之间有一定的重叠,调频率、带宽、采样率也都不同。
通过理论分析,子带1带宽为310 MHz,其理论上的最大距离分辨能力为0.48 m,子带2的带宽为300 MHz,其理论上的最大距离分辨能力为0.5 m,显然都无法分辨2 500与2 500.4这两个点目标的位置,而在合成后的带宽约为610 MHz,其理论上的最大距离分辨能力为0.25 m,是可以分辨出2 500与2 500.4这两个点目标的。仿真结果如图1～4所示。
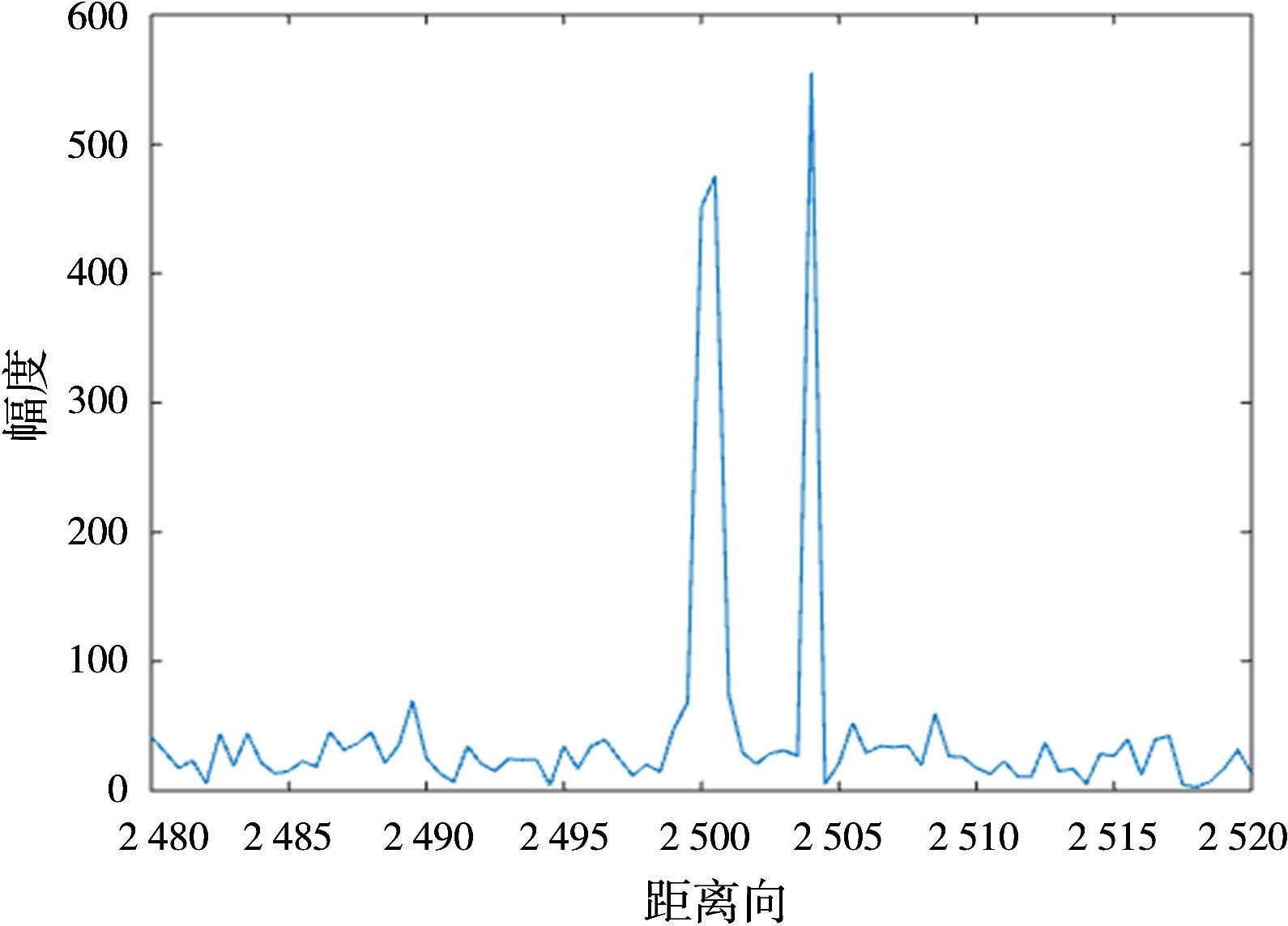
图1 子脉冲1距离像
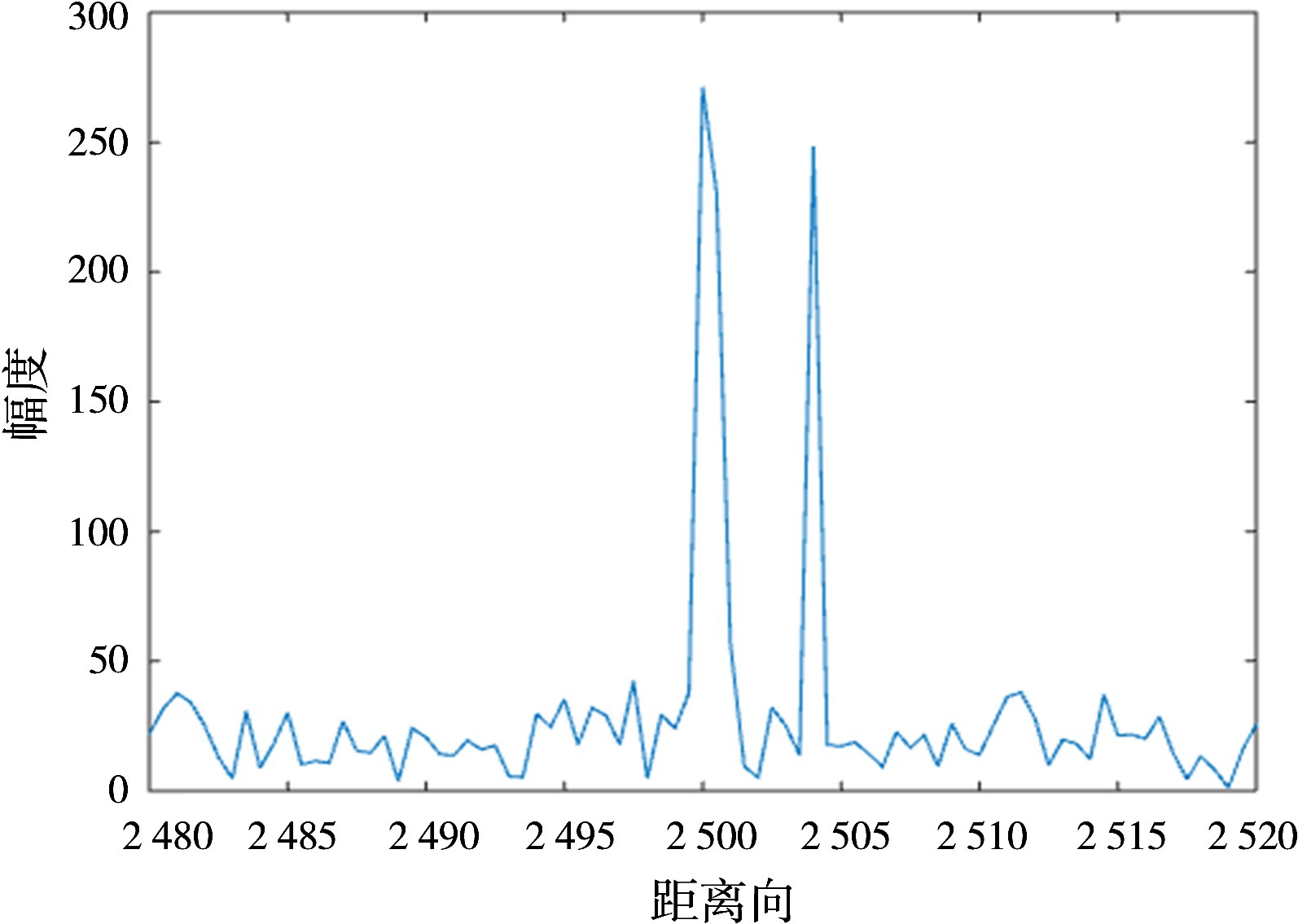
图2 子脉冲2距离像
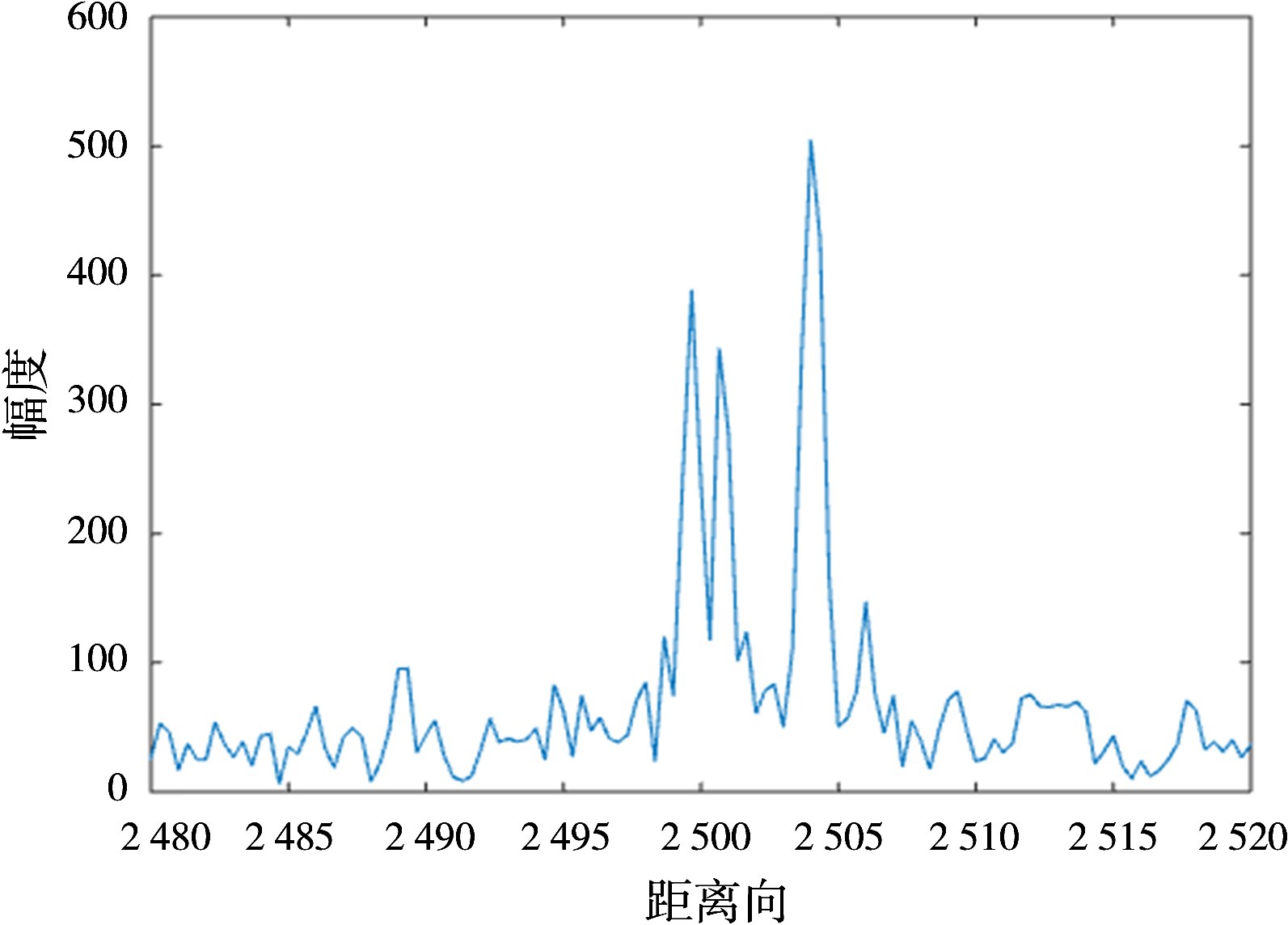
图3 合成脉冲经过Sinc插值距离像
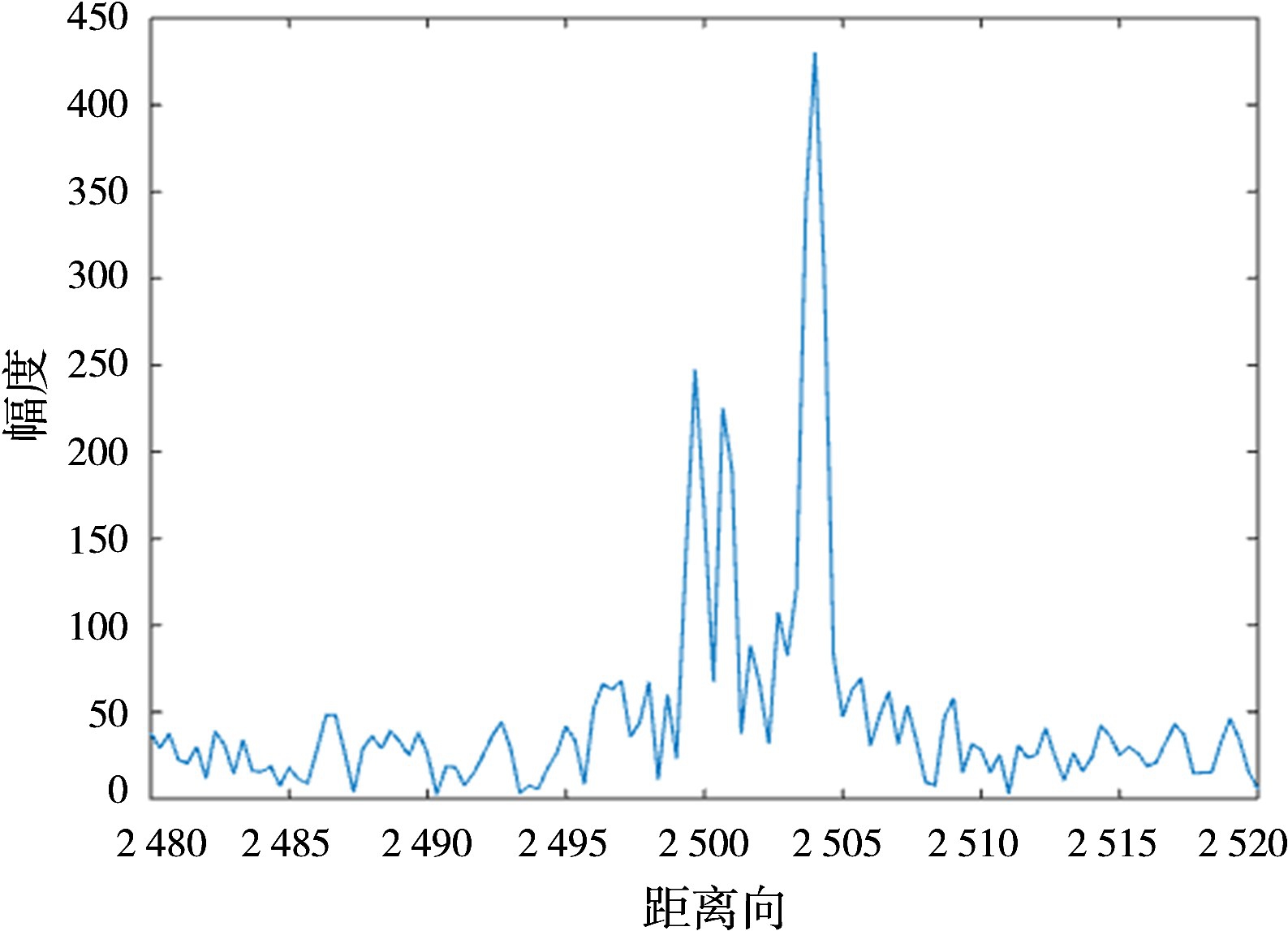
图4 合成脉冲经过高斯插值距离像
图1～4分别表示子脉冲1、子脉冲2、合成脉冲经过Sinc插值和合成脉冲经过高斯插值后的距离像。子脉冲1与子脉冲2能够分辨出相距4 m的点目标信号,但是无法分辨出相距0.4 m的点目标信号,而经过子带融合及均匀化处理之后,合成带宽信号能够分辨出相距为0.4 m的点目标信号,从仿真上对理论算法进行了验证。
表1表示Sinc插值与高斯插值各自所需要的时间。对于Sinc插值来说,由于Sinc函数自身的性质,文献[3]所用的是全数据的Sinc插值,对于N点数据,插值后点数为M点,其运算量为N×M,而对于高斯插值来说,由于高斯函数的性质,其分布决定于τ值,所以说根据插值间隔,只要选取适当的τ值,就可以保证高斯函数在-Msp≤m′≤Msp的范围内占主导作用。这样就大大地减少了运算量,其插值运算量为2×Msp×N。可见,在运算量方面,高斯插值要优于Sinc插值。在仿真中,也验证了这一点。
表1 Sinc插值与高斯插值所需时间
本文通过高斯插值算法来实现对合成子带信号的均匀化重建,和原有Sinc插值比较,能够在不降低其距离分辨能力的同时,大大地减少运算时间,更加有利于信号的实时处理。本文研究了多频段子脉冲融合思想,提出了利用高斯插值来处理各个子脉冲之间的均匀重建问题。最后,针对数据对高斯插值与Sinc插值的结果进行了比较,用Matlab仿真实验验证了本文方法能够在提高距离分辨率的同时比Sinc插值用时更短,实时性更强。
参考文献:
[1]李少东,裴文炯,杨军.基于CS的LFM信号脉冲压缩实现算法研究[J].雷达科学与技术,2013,11(3):295-301.LI Shaodong,PEI Wenjiong,YANG Jun.Pulse Compression Implementation of LFM Signal via CS[J].Radar Science and Technology,2013,11(3):295-301.(in Chinese)
[2]LORD R T,INGGS M R.High Resolution SAR Processing Using Stepped-Frequencies[C]∥International Geoscience and Remote Sensing Symposium,[S.l.]:[s.n.],1997:490-492.
[3]白霞,毛士艺,袁运能.时域合成带宽方法:一种0.1米分辨率SAR技术[J].电子学报,2006,34(3):472-477.
[4]彭岁阳,卢大威,张军,等.基于合成带宽技术提高距离分辨率的新方法[J].系统工程与电子技术,2010,32(2):235-238.
[5]李杰,赵红东,苏周.非均匀采样的频谱研究[J].电子设计工程,2013,21(4):33-35.
An Improved Method for Increasing Range Resolution Based on Synthesized Bandwidth Technique
GAO Zizhi,LI Zhiqiang
(Ordnance Engineering College,Shijiazhuang050003,China)
Abstract:Synthesizing range profile by multi-band sub-pulse signal can reduce the instantaneous bandwidth of the system as well as the sampling rate requirement of the signal.On the basis of the original fusion sub-bandwidth using synthetic bandwidth technology,this paper adopts Gaussian interpolation to reconstruct the signal,which can obtain a higher resolution range image.Compared the Gaussian interpolation with the Sinc interpolation in the speed of operation,it is concluded that the Gaussian interpolation model is superior to the Sinc interpolation model in the computation speed.Simulation results show that this method can not only solve the problem of sub-pulse synthesis with different parameters,but also can effectively improve the range resolution,and even reduce the computation time compared with Sinc interpolation.
Key words:synthesized bandwidth;range resolution;non-uniform sampling;Gaussian interpolation
中图分类号:TN958
文献标志码:A
文章编号:1672-2337(2017)01-0095-04
DOI:10.3969/j.issn.1672-2337.2017.01.017
收稿日期:2016-03-22;
修回日期:2016-10-25
作者简介:
高梓植男,1992年12月出生,四川江安县人,硕士研究生,主要研究方向为信息与信号处理。E-mail:121500045@qq.com
李志强男,1965年7月出生,北京人,硕士生导师,主要研究方向为信息与信号处理。