魏 鹏,刘洛琨,菅春晓
(信息工程大学信息系统工程学院,河南郑州450002)
摘 要:针对相控阵天线网络相差,提出了一种中场校准新方法,建立了中场校准模型,分析了中场校准方法的基本原理。该方法对辅助天线位置进行估计,求出接近原阵面相位曲面的拟合曲面,得到阵面相位误差分布,通过相位补偿达到校准的目的。仿真结果表明,校准后的天线方向图第一级副瓣电平降低了3 dB左右,第三、四级副瓣电平降低了5 dB,归一化副瓣电平平均下降了2.5 dB左右;校准后的方向图较为接近标准方向图。该中场校准方法操作简便,具有很高的工程价值。
关键词:中场校准;相控阵天线;相位误差;方向图;副瓣
相控阵雷达能在设定的空域,根据战术需要,灵活地改变波束形状及指向,对多达数百批目标实施无惯性搜索、跟踪、编码、识别和分类,在众多领域广泛应用。相控阵雷达以拥有相控阵天线而得名。相控阵天线能够迅速改变波束指向,形成特种方向图,并且一部相控阵天线可以完成多部其他品种天线才能完成的任务,是相控阵雷达的核心部件。要使相控阵天线的这些功能付诸实现,在其研制和实验过程以及在使用过程必须进行大量的工作。这些工作包括对相控阵天线各通道幅、相的检测与调整,阵内故障或失效单元的排除以及测定相控阵天线及其所属系统在各种工作状态下的相对应的发射或接收方向图,其中幅相校准是一项十分关键的工作,这直接关系到相控阵天线能否正常工作。
相控阵天线出厂验收前一般都会经过幅相校准,但是在多变的环境中,即使在出厂前进行过阵面的校准,在运送到目的地使用一段时间后,由于环境的改变及器件老化等因素会产生相位误差,进而导致副瓣电平升高、指向偏离[1-2],因此需要定期对其进行校准,以保证雷达工作在良好状态。近场法需要近场测试设备在微波暗室中进行操作,十分不便,因此考虑中场校准方法。学者施长海等对有源相控阵中场测量中的空间误差进行了研究[3],但并未给出具体的校准方案。国内学者郑雪飞对中场校准研究和发展[4],得出了两点法和三点法,但该方法对位置精确度要求较高,需要多个辅助天线,并且校准过程中需要移动辅助天线,较为繁琐,校准精度也不够高。
本文提出的方法解决的是在校准辅助天线确切位置未知的前提下,相控阵天线阵面单元存在网络相差应如何校准的问题。阵面存在网络相差时,辅助天线到各个阵面单元的相位形成的相位曲面发生畸变。该方法通过估计辅助天线位置,进一步得到阵面误差分布,通过相位补偿实现校准。文中推导了校准的原理,并通过对12×20平面阵仿真,给出了阵面相差的校准情况。仿真结果表明:该方法能够明显抑制副瓣电平,提高天线指向精度,对相控阵天线阵面相差的校准具有很好的工程指导意义。
均匀线阵的远场阵列因子[5]为
式中,I(i),φ(i)分别为第i个天线单元激励电流的峰值和相位,![]() 为相邻两天线单元间的波程差引起的相位差。当阵元存在相位误差时,其在远场产生的方向图可表示为
为相邻两天线单元间的波程差引起的相位差。当阵元存在相位误差时,其在远场产生的方向图可表示为
式中,δi为第i个天线单元的电流相位误差。由式(2)可知,阵元相位误差直接影响相控阵天线远场方向图,必须采取措施校准阵元相差,使天线处于良好的工作状态。
阵元相位误差[6]主要分两种:量化相差和网络相差。
量化相差主要是由于移相器本身的移相特性造成的。现在普遍使用的数字移相器位数一般不超过6位,位数过多会引起较大的插入损耗。由于移相器移相位数的限制,移相器无法实现连续移相,只能按其最小相移量Δ=2π/2k的整数倍进行量化,使得实际值与理想值之间存在一定的偏差,即量化相差。这是一种原理性的误差,它对波形的影响程度与采用的馈相算法有关,采用随机馈相算法和虚位技术可以有效降低量化误差的影响[7]。
网络相差是由阵列上的非理想元件和信号分配网络造成的随机和空间上相关的误差,该类误差大小与元件参数、电路的传输线长度以及环境有关,是随机变化的。但是,如果元件确定且工作环境稳定,则可认为它是一个定值[8]。
对于由馈相网络产生的相位误差,可采用多种方法来克服,如固定补偿值法和中场校准方法等。固定补偿值法是在天线的标准工作环境下,通过实际测量获得一组补偿值,然后在馈相时将这组值对应加到理想值上。该方法工作量较大,而且不够灵活,通常不单独使用。中场校准方法较为灵活,实用性强。本文提出的中场相差校准方法仅需一个辅助天线,并且精确位置未知,不需要移动,十分方便快捷。
设阵面天线所在平面为XY面,阵面顶点为坐标原点,与原点相连的长边作为X轴,宽边作为Y轴,垂直于阵面且过原点的直线作为Z轴,阵面大小为M×N,长边单元间间隔为dx,宽边为dy,辅助天线位于空间某点A,假设其坐标为P0(a0,b0,c0)(实际位置未知,但必须保证辅助天线位于中场范围内),如图1所示。
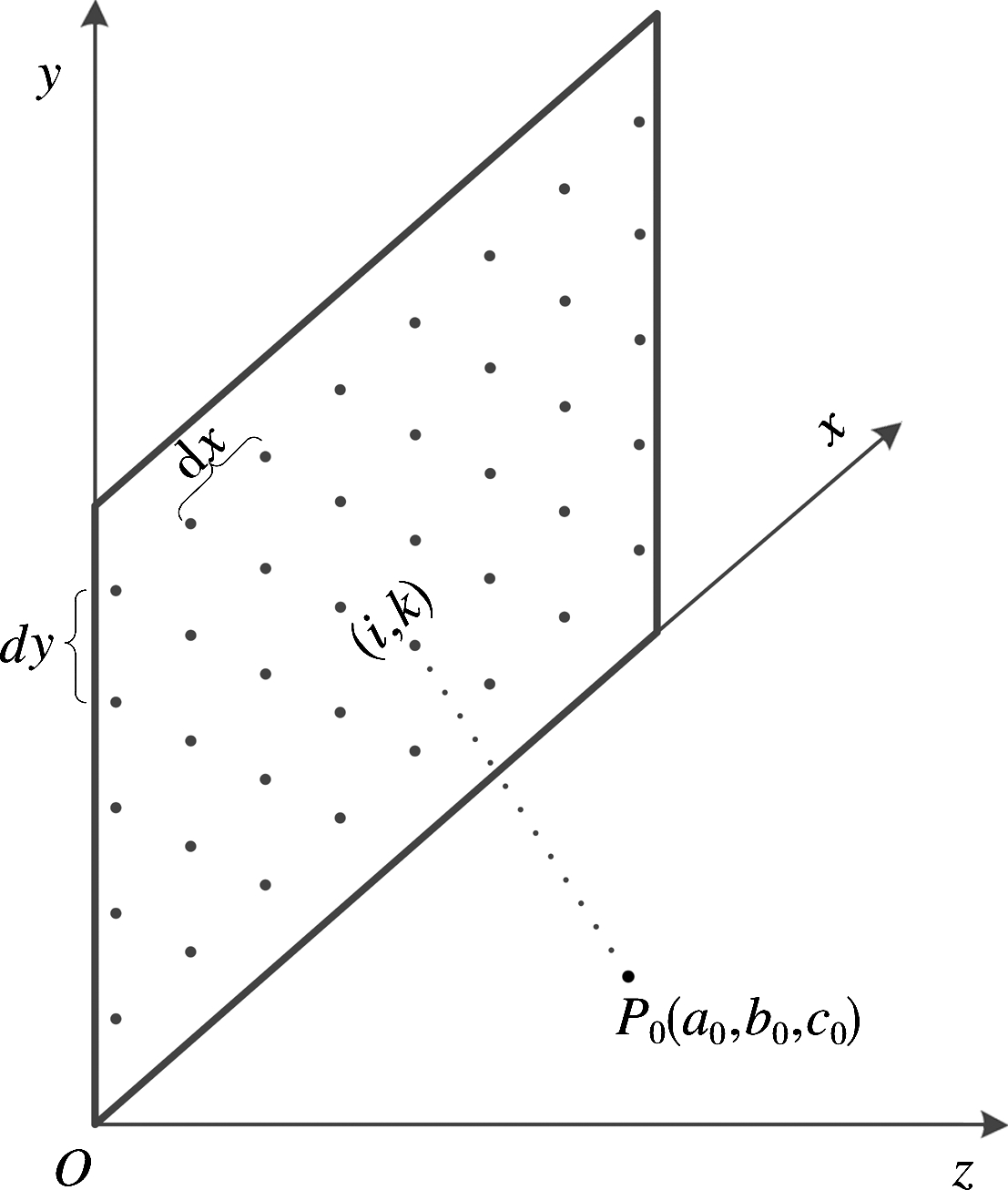
图1 中场校准模型
则阵面单元天线(i,k)与辅助天线的距离为
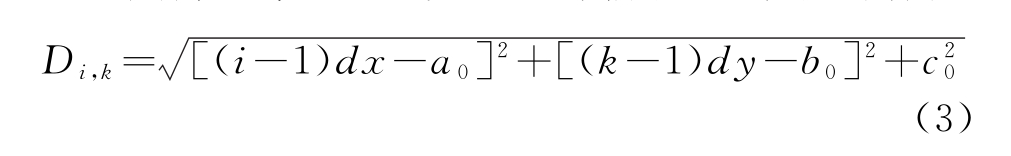
式中,i=1,2,…,M,k=1,2,…,N。为计算方便,设辅助天线处相位为零,则单元天线(i,k)的相位为
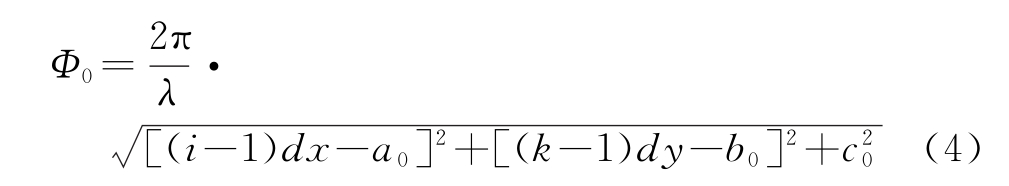
设阵面相位误差分布为Δ,则实际接收到的单元天线的相位为
为对Φ1进行修正,用一个与Φ1格式类似的式子作为优化函数,设为
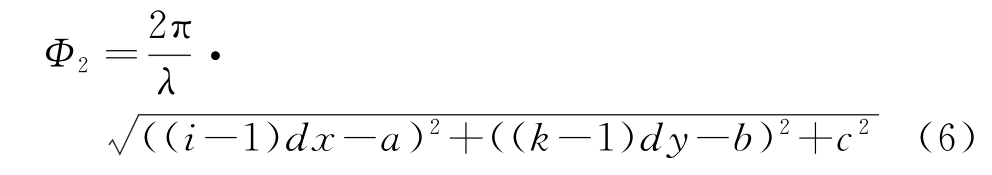
式中,(a,b,c)代表待估计的辅助天线位置所对应的坐标点。

采用最小二乘法进行估计,为便于计算,将Φ1和Φ2作一定的变换,令矩阵I和K都是M×N的矩阵,内部元素代表着阵列单元的序号,将矩阵I和K按列展开为行向量:
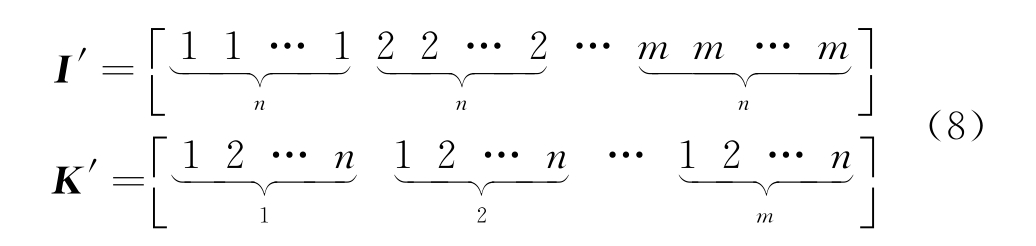
则I′和K′均为1×(M×N)的矩阵,也就有
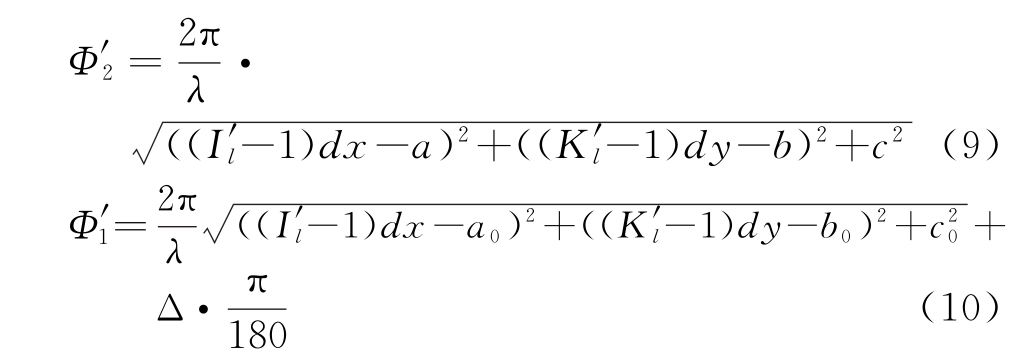
式中,i=1,2,…,(M×N)。将Φ′1和Φ′2作最小二乘拟合[9],即能得到目标函数:

当目标函数ε取到最小值时即为最优解,将求得的最优辅助天线坐标代入下式:
求出拟合后的阵面相位误差Δ′。然后根据理想平面阵远场方向图函数有

式中,aik为单元天线的泰勒幅度权值,且
θ和ϕ分别为方位角和俯仰角。令
则带有相位误差的平面阵远场方向图函数为
校准后的方向图函数为
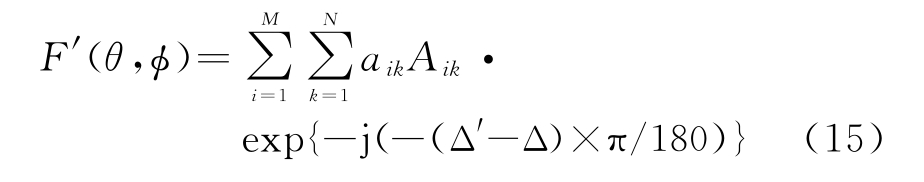
校准操作流程如图2所示。首先用全站仪标定各阵元坐标。然后将辅助天线置于中场范围内(确切位置未知),通过波束控制系统配置移相器,使整个阵面的移相器处于相同的移相状态。辅助天线发射信号,波控机控制通道接通,接收机记录下各个通道的幅相信息,提取出相位信息,即为带有相位误差的阵面相位分布Φ1(每次通道接通时,用时钟来控制辅助天线的初始相位保持一致);设需要拟合的辅助天线位置为(a,b,c),根据式(6)写出Φ2。通过式(7)、(8)将Φ1,Φ2变形成Φ′1,Φ′2,用最小二乘法求出ε最小值,得出估计的校准源位置,根据式(12)求得阵面相位误差分布Δ′。根据得到的阵面相位误差分布对各个通道进行补偿从而实现阵面校准。
用Matlab对校准过程进行了建模仿真。因为相控阵天线在出厂前已经经过了校准,波控机未给移相器移相指令时,可近似认为阵面相位已较为平整,使用一段时间后,由于环境等因素的影响会产生相位误差,可近似看作服从正态分布。在仿真中进行如下设定:均值为0,方差为50的服从正态分布的随机数来模拟信号经过馈相网络所产生的相位误差;阵列为12×20的平面阵;俯仰角为0°,方位角分别为-45°,0°和45°。仿真结果如图3所示。
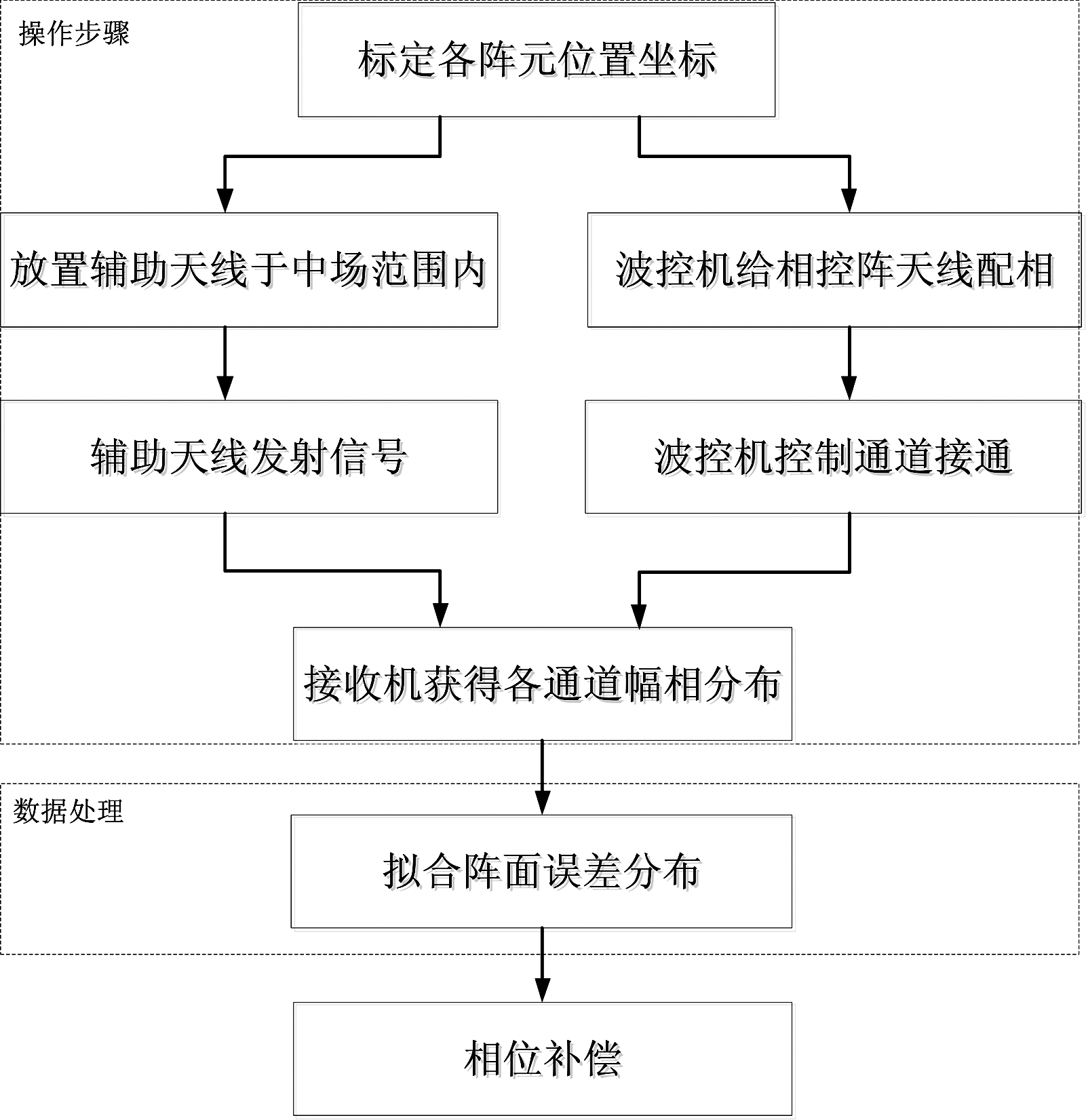
图2 方法流程图
图中细线代表无误差的标准方向图,星字线代表有相位误差的方向图,圆圈线代表经过拟合校准后的方向图,由仿真结果可知:经过拟合校准之后的方向图与标准方向图契合度较好;通过比较可以看出,校准后的天线副瓣电平得到了有效抑制,第一级副瓣电平降低了3 d B左右,第三、四级副瓣电平降低了5 d B,平均副瓣电平下降了约2.5 dB,方向图改善明显。这些都是由于通过相位校准获得了馈相网络的有效相位补偿值,使得天线各阵元间馈入的电流相位差接近于理想值。
在实际应用中,辅助天线的相位方向图会对中场校准产生一定的影响,选取小口径的辅助天线以及将辅助天线放置于中场偏远位置可以减少辅助天线相位方向图对校准过程的影响。
馈相网络造成的相位误差是相控阵天线相位误差的主要来源之一,它会引起波束寄生副瓣并提高副瓣电平,较大地影响相控阵天线的性能。本文提出的中场校准方法能够有效抑制相控阵天线的网络相差,仿真结果表明:经过网络相差校准,归一化平均副瓣电平降低2.5 dB左右,相控阵天线的方向图得到优化。该方法简便易行,具有很高的工程价值。

图3 方位角分别为-45°,0°,45°的标准方向图及校准前后的方向图
参考文献:
[1]熊哲,刘正权,韩轶凡.随机误差对相控阵天线的副瓣影响分析[J].计算机与数字工程,2013,41(4):535-537.
[2]董鹏曙,金加根,谢幼才,等.天线副瓣对雷达探测的影响研究[J].雷达科学与技术,2014,12(1):112-115.
[3]施长海,章传芳,陈振中,等.有源相控阵中场测量中的空间误差研究[J].航空电子技术,2008,39(1):28-32.
[4]郑雪飞.相控阵天线中场校正技术及其工程应用研究[D].南京:南京理工大学,2005.
[5]张光义,赵玉洁.相控阵雷达技术[M].北京:电子工业出版社,2006.
[6]束咸荣,何炳发,高铁.相控阵雷达天线[M].北京:国防工业出版社,2007.
[7]张祖伦.相控阵雷达中相位误差分析及补偿方法[J].雷达科学与技术,2010,8(2):95-100.
[8]唐山东,张斌,吴德伟.一种基于曲线拟合的相控阵天线相位校准方法[J].弹箭与制导学报,2008,28(2):303-306.
[9]李二涛,张国煊,曾虹.基于最小二乘的曲面拟合算法研究[J].杭州电子科技大学学报,2009,29(2):48-51.
A Novel Mid-Field Phase Calibration Method for Phased-Array Antenna
WEI Peng,LIU Luokun,JIAN Chunxiao
(Institute of Information System Engineering,Information Engineering University,Zhengzhou450002,China)
Abstract:In order to calibrate phased-array antenna network’s phase error,a novel mid-field calibration method is proposed.It is modeled and its theory is analyzed.Through estimating the position of the auxiliary antenna,a fitting surface which is close to the original one is obtained,and then the phase error is figured out.The calibration is achieved by phase compensation.Simulation shows that the first sidelobe level reduces by about 3 dB;the 3th and 4th sidelobe levels reduce by 5 dB;the normalized sidelobe level reduces by about 2.5 dB on average after calibration.The pattern after calibration is close to the standard one.This method is easy to operate and it is of great engineering value.
Key words:mid-field calibration;phased-array antenna;phase error;pattern;sidelobe
中图分类号:TN820.1;TN821+.8
文献标志码:A
文章编号:1672-2337(2017)01-0099-04
DOI:10.3969/j.issn.1672-2337.2017.01.018
收稿日期:2016-06-27;
修回日期:2016-09-30
基金项目:国家自然科学基金(No.61271253)
作者简介:

魏鹏男,1990年出生于山东济南,信息工程大学信息系统工程学院研究生,主要研究方向为相控阵天线接收技术、雷达信号处理。E-mail:592653736@qq.com

刘洛琨男,1963年出生于河南洛阳,信息工程大学信息系统工程学院博士生导师,主要研究方向为超宽带通信技术、微波射频电路、相控阵雷达技术、阵列信号处理。

菅春晓男,1983年出生于河南商丘,信息工程大学信息系统工程学院讲师,主要研究方向为微带天线、阵列信号处理、电磁兼容。