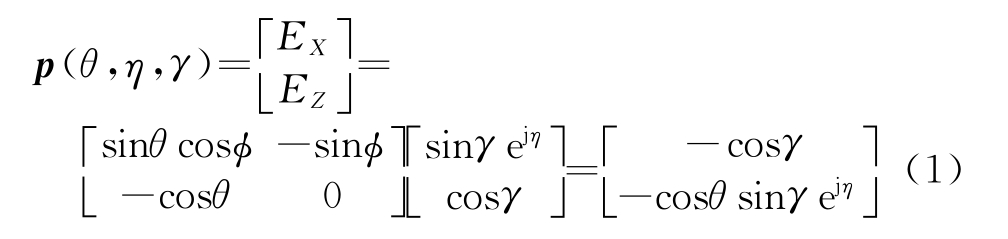
郑轶松1,2,陈伯孝1,2
(1.西安电子科技大学雷达信号处理国家重点实验室,陕西西安710071;2.西安电子科技大学信息感知技术协同创新中心,陕西西安710071)
摘 要:电磁矢量阵列由于利用了信号的极化信息,能显著提高阵列的环境感知性能。建立双正交电磁矢量阵列低仰角测高多径模型,提出利用极化平滑与空间平滑结合的预处理方法对直达波和多径进行解相干,同时利用极化和空域信息提高低仰角角度估计性能;并推导低仰角多径模型下双正交电磁矢量阵列的Cramer-Rao界,分析极化参数对测角性能的影响。仿真实验结果表明,低角情形下电磁矢量阵列相较于标量阵列测角性能更优;所提的极化空间平滑算法由于结合了极化平滑和空间平滑的优点,较现有方法解相干效果更好,精度更高,特别适用于直达波和多径极化状态差异较小的低仰角情形。
关键词:双正交电磁矢量阵列;低仰角角度估计;Cramer-Rao界;多径
常规的标量天线仅能获取电磁波的幅度信息,无法感知完备的电磁场矢量,而电磁矢量传感器则可感知多个(2～6个)电磁场分量,提供极化信息,且能显著地改善空域信息的感知性能。针对空域间隔较小甚至相同的信号源,可通过极化信息的不同对其进行区分和辨别。低仰角角度估计问题[1-6]可等效看作两间隔很小的相干源的分辨、测量问题。因阵列孔径的限制,常规的标量阵列往往无法提供足够的空域分辨率对低仰角目标与其多径进行区分,而电磁矢量阵列[7-9]可利用极化信息改善低仰角目标测角性能,为解决低仰角测高问题提供了一种新的思路。实际中一般假设回波包含直达波和多径两个相干信号,只需双正交电磁矢量阵列即可进行解相干,且具有设计方便的特点。文献[7]提出极化平滑的预处理方法来消除直达波与多径的时域相干性。文献[8]通过比较分析多种电磁矢量阵列与标量阵列的性能,展现了电磁矢量阵列在低仰角目标被动定位中的优势。文献[9]针对米波雷达极化敏感阵列提出一种基于极化平滑的低仰角测高方法,并通过条件数分析其去相关性能。以上文献中所提算法均假设目标在极化域可区分,若目标极化参数相近,算法性能将下降甚至失效。低角情形下,直达波和多径的极化差异来自于地面反射系数的不同,而仰角越低,其地面反射系数越接近,极化参数差异会减小,现有算法性能将下降。因此本文利用双正交电磁式矢量阵列,提出通过空间平滑和极化平滑结合的预处理方法以达到更稳定的测角效果,并通过推导低仰角情形下波达方向估计的Cramer-Rao界(CRB),分析双正交电磁矢量阵列在低角情形下的测角性能下界。
考虑双正交电磁矢量阵列如图1所示,双正交偶极子沿Z轴排列,指向分别与X轴和Z轴平行,阵元数为M,阵元间距d为半波长。图1中θ为目标俯仰角,ϕ为目标方位角,η∈[-π,π]为极化相位差,γ∈[0,π/2]为极化辅助角。考虑方位角ϕ=π/2,即目标位于YOZ平面内入射的情形,对于双正交电磁矢量阵列,其电磁场矢量为
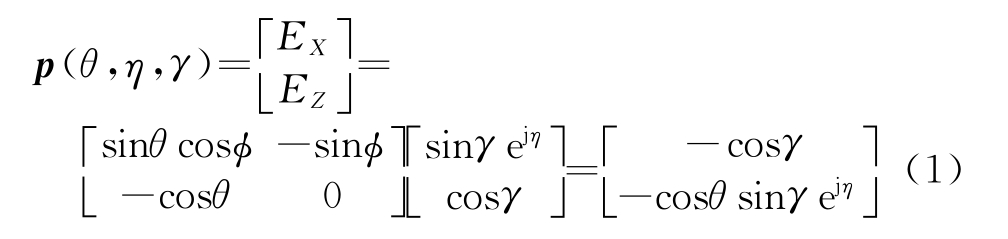
t时刻双正交电磁矢量阵列接收的信号为
式中,
(M-1)/2]T)为空域导向矢量,上标(T)为矩阵转置,K为目标个数,t=1,2,…,T,T为快拍数,⊗为Kronecker积,s(t)为信号复包络,n(t)为高斯白噪声。
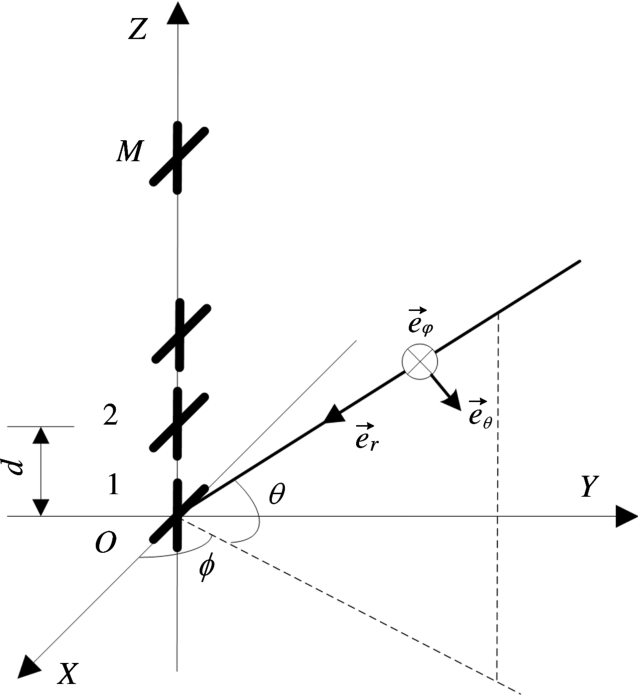
图1 双正交电磁矢量阵列示意图
考虑平坦地面镜面反射,低仰角单目标的情形,此时有直达波和多径两个强相干目标,K=2,令下标k=1为直达波,下标k=2为多径。由于垂直极化和水平极化的地面反射系数不同[8],多径的极化状态相对于直达波发生变化:
其中EH和EV分别为多径的水平和垂直极化电场分量,ρH和ρV分别为水平极化和垂直极化的反射系数。由于水平极化和垂直极化的地貌反射系数不同,则直达波与多径的极化状态也不同,这使得从极化域对二者进行区分成为可能。
定义b(θ,η,γ)=a(θ)⊗p(θ,η,γ)为极化空域联合导向矢量,垂直极化和水平极化电磁波地面反射系数的不同将导致直达波和多径的极化辅助角和极化相位差发生变化。在低仰角单目标情形下,t时刻接收信号为
式中,ΔR≈2hrsinθ1为直达波与多径的波程差,hr为雷达参考阵元与反射面的高度。定义合成导向矢量
表征直达波与多径路程差导致的多径相位差,其中
分别为ε的实部和虚部。低仰角跟踪时,直达波与多径波程差的变化会导致ε2相位的变化,因此下文也将讨论多径相位差对Cramer-Rao界和测角性能的影响。t时刻阵列接收信号和协方差矩阵分别为
式中,上标(H)为矩阵共轭转置
分别为信号功率和噪声功率,I为单位阵。
电磁矢量阵列对相干源的处理一般采用极化平滑[7]和空间平滑[10]两种解相干的预处理方法。空间平滑方法是应用最为广泛的一种解相干算法。极化平滑法无孔径损失,实现简单,但极化平滑法仅能在相干源极化状态差异较大时有较好的解相干性能。低仰角情形下,直达波与多径的极化状态差异本质是由水平和垂直极化反射系数差异引起,而仰角越低,垂直反射系数和水平反射系数的差异将越小,因此仅利用极化平滑不能完全满足电磁矢量阵列的解相干需求。在本文中利用极化平滑和空间平滑预处理结合的方法对低仰角目标进行解相干处理,即先对信号进行极化平滑在极化域解相干,再进行空间平滑处理。极化空间平滑预处理方法既利用了直达波和多径的极化信息,同时通过空间平滑预处理避免了极化平滑在极化差异小时测角性能的下降,能在直达波和多径极化状态差异未知情况下达到更好的测角效果,更适合在低角情形下的角度估计。
近年来众多学者提出了诸多空间平滑预处理及其改进方法,其原理与步骤参见文献[10-12],在此不再赘述。本文采用经典的前后向空间平滑,其余众多空间平滑及其改进算法皆可直接应用于极化空间平滑预处理方法中。下面介绍极化平滑预处理方法。阵列如图1所示,考虑式(3)所示低仰角情形(假设直达波和多径两个相干信号入射至阵列),t时刻指向与X轴和Z轴平行的电偶极子阵列接收信号分别为
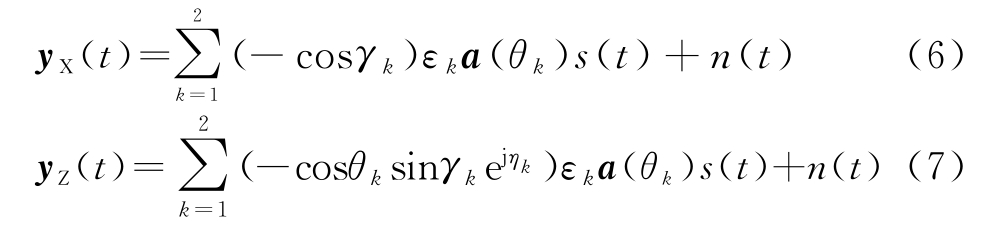
相应的协方差矩阵为
式中 ,
易知rank(RX)=rank(RZ)=1,由于协方差矩阵欠秩,无法直接使用超分辨方法(如M USIC方法)进行测角,而极化平滑预处理方法通过对二者进行平均得到平均协方差矩阵Ravr:
易知,当直达波与多径二者极化状态(极化相位差η和极化辅助角γ)不同时,平均协方差矩阵的秩恢复为2,即
完成解相干处理后,可对平均协方差矩阵Ravr直接应用MUSIC等超分辨方法进行测角。值得注意的是,由于双正交电磁矢量传感器仅利用了双正交电偶极子的信息,极化平滑法解相干的信源个数仅为2。若利用六维电磁矢量传感器获取入射电磁场所有的六维信息,最大可解相干的信源个数为6。由于实际中同一距离单元的回波一般仅包含直达波和多径两个相干信号,只需双正交电磁矢量阵列即可满足需求。
通过极化空间平滑预处理解相干后,可直接利用多重信号分类(MUSIC)等超分辨算法进行测角,在完成低仰角目标俯仰角测量后,进而利用已知的目标距离可计算得到目标高度。下文对双正交电磁矢量阵列的Cramer-Rao界进行分析,分析各极化参数对Cramer-Rao界的影响,继而通过仿真实验表明所提极化空间平滑预处理的有效性。
由文献[13]可知,噪声功率是否已知不会对Cramer-Rao界产生影响,因此为方便计算,本文假设噪声功率已知。未知参数为
Fisher信息矩阵(Fisher Information Matrix,FIM)的第(i,j)个元素可通过下式计算[14]:
式中
根据协方差矩阵对未知参数求偏导形式的不同,可将未知参数分为两类分别求解其Fisher信息矩阵。
由式(5)可得协方差矩阵对未知参数ui∈
的偏导:
定义
,为合成导向矢量对未知参数的偏导,将式(12)代入式(11)可得
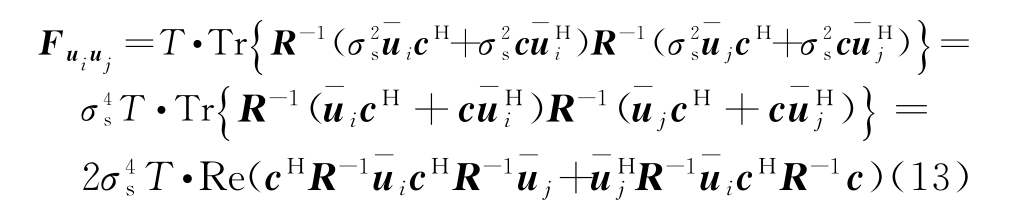
下面求合成导向矢量c对未知参数{θ,η,γ,
的偏导:
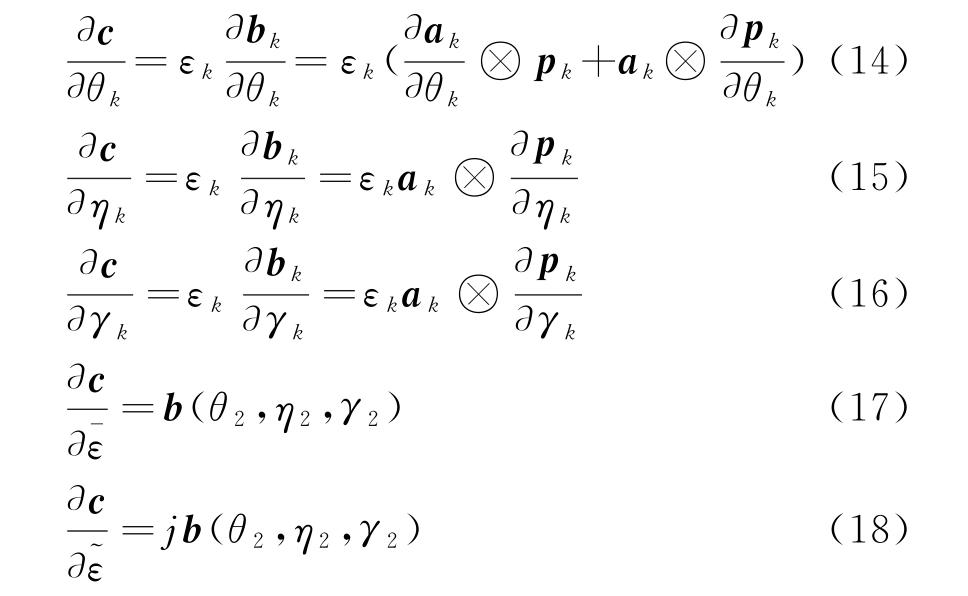
式中
由式(19)～(22)计算可得
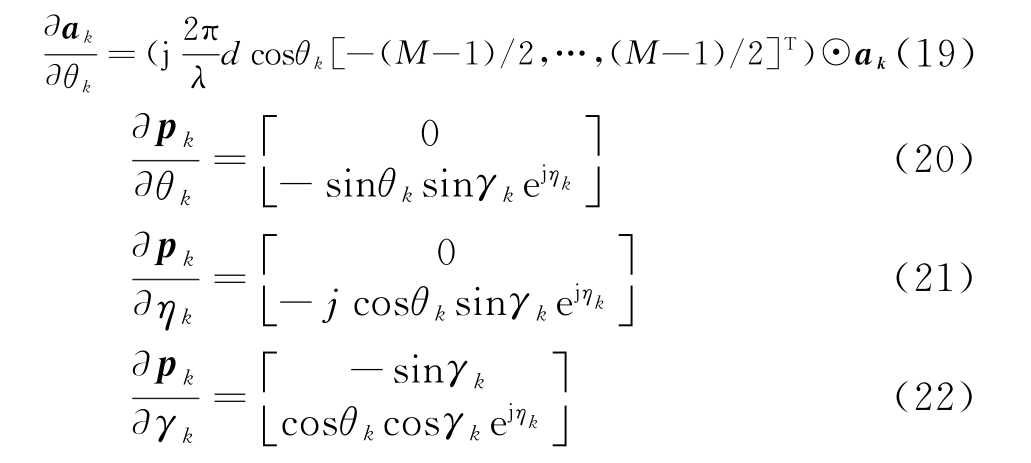
式中,
表示Hadamard积。
定义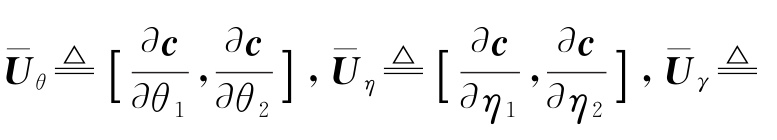
根 据
维 数,C为c对应的矩阵形式,可将式(13)简化为
式 中
由式(5)可得协方差矩阵对信号功率
的偏导
将其代入式(11)可得
式 中
至此,Fisher信息矩阵全部元素可由式(23)～(26)得到,由下式可得相应未知参数的Cramer-Rao界:
式中
表示所有未知参数。
仿真1 Cramer-Rao界与极化参数的关系
考虑20阵元的双正交电磁矢量阵列,单元信噪比为10 dB,快拍数为10,直达波与多径入射角度分别为2°和-2°。首先仿真查看极化参数对双正交电磁矢量阵列DOA估计Cramer-Rao界的影响。假设直达波与多径相位差为0,即ε2=1,直达波的极化辅助角和极化相位差均为0°,多径的极化辅助角变化范围为[0,π/2],极化相位差变化范围为η∈[-π,π),直达波DOA估计Cramer-Rao界如图2所示。可见多径极化相位差对Cramer-Rao界的影响较小,而直达波与多径的极化辅助角相差越大,Cramer-Rao界越低,能获得更好的测角结果,因此下文均假设直达波与多径极化相位差相同,重点考察二者极化辅助角的不同对直达波DOA估计性能的影响。
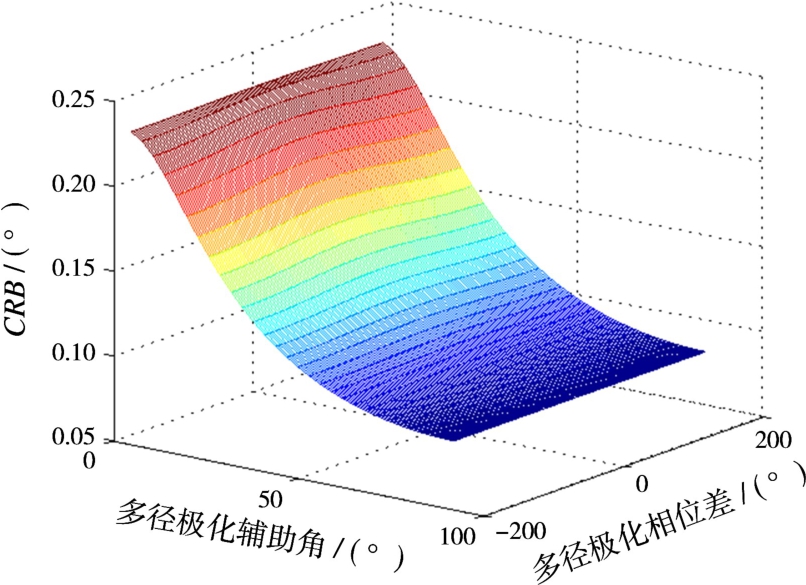
图2 极化参数对Cramer-Rao界的影响
仿真2 DOA估计性能与信噪比的关系
考虑20阵元的双正交电磁矢量阵列,快拍数为10,直达波与多径入射角度分别为2°和-2°,极化相位差相同,均为0°,极化辅助角分别为10°和35°,ε2的相位为0°,即ε2=1,设计仿真实验考察信噪比对直达波测角性能的影响,结果如图3所示。其中,指向与X轴平行的电偶极子阵列组成标量阵列,其Cramer-Rao界表示为标量CRB,空间平滑表示对标量阵列采用SSMUSIC算法进行测角的结果,极化平滑和极化空间平滑均表示电磁矢量阵列的测角结果,空间平滑均采用三阶前后向空间平滑。由图3可见,双正交电磁矢量阵列的Cramer-Rao界明显低于标量阵列,验证了电磁矢量阵列的优越性。而所提极化空间平滑算法性能优于极化平滑和空间平滑算法,具有信噪比门限低、测角均方根误差小的优点,即使在高信噪比时本文算法精度也较其余两种算法更高。
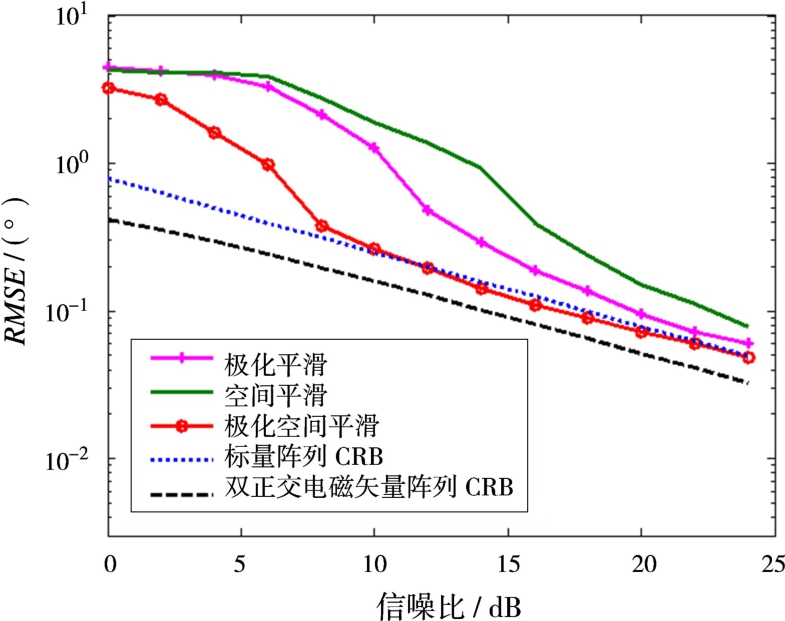
图3 信噪比对DOA估计性能的影响
仿真3 DOA估计性能与多径相位差的关系
考虑20阵元的双正交电磁矢量阵列,单元信噪比10 dB,快拍数10,直达波与多径入射角度分别为2°和-2°,极化相位差相同,均为0°,极化辅助角分别为10°和65°。由于ε2=exp(-j2πΔR/λ)的相位会随着目标仰角的变化而变化,因此设计仿真实验考察ε2的相位对直达波测角性能的影响,仿真中采用的测角算法与仿真2相同,结果如图4所示。由图4(a)可见,多径相位差的变化会导致Cramer-Rao界和测角性能的波动,多径相位差为0°,180°和-180°处Cramer-Rao界和算法性能较差,这是中心对称标量阵列和中心对称极化敏感阵列的固有特征。尽管Cramer-Rao界会随着多径相位差的变化而波动,由于双正交电磁矢量阵列利用了极化信息,其Cramer-Rao界明显低于标量阵列的Cramer-Rao界。而标量阵列的空间平滑算法性能明显较电磁矢量阵列的极化平滑和极化空间平滑方法性能差,验证了电磁矢量阵列的优越性。本文所提的极化空间平滑算法相较于极化平滑算法更接近Cramer-Rao界,但是值得注意的是,由于空间平滑的孔径损失,在ε2相位大于130°或小于-130°时极化平滑性能略好于极化空间平滑算法。
进一步考察直达波与多径极化辅助角相差较小的情况,直达波与多径的极化辅助角分别为10°,35°,其余参数不变,实验结果如图4(b)所示。极化辅助角相近时,仅依靠极化域信息难以对直达波和多径进行解相干,极化平滑算法几乎不能精确测角,解相干性能甚至差于空间平滑算法。多径相位为0°时,极化平滑和空间平滑均无法正确测角,而本文所提的极化空间平滑算法由于同时利用了极化域和空间域信息,可得到较好的测角结果,性能逼近Cramer-Rao界。实验结果表明,在直达波与多径极化差异较小时本文算法也具有优异的测角性能。
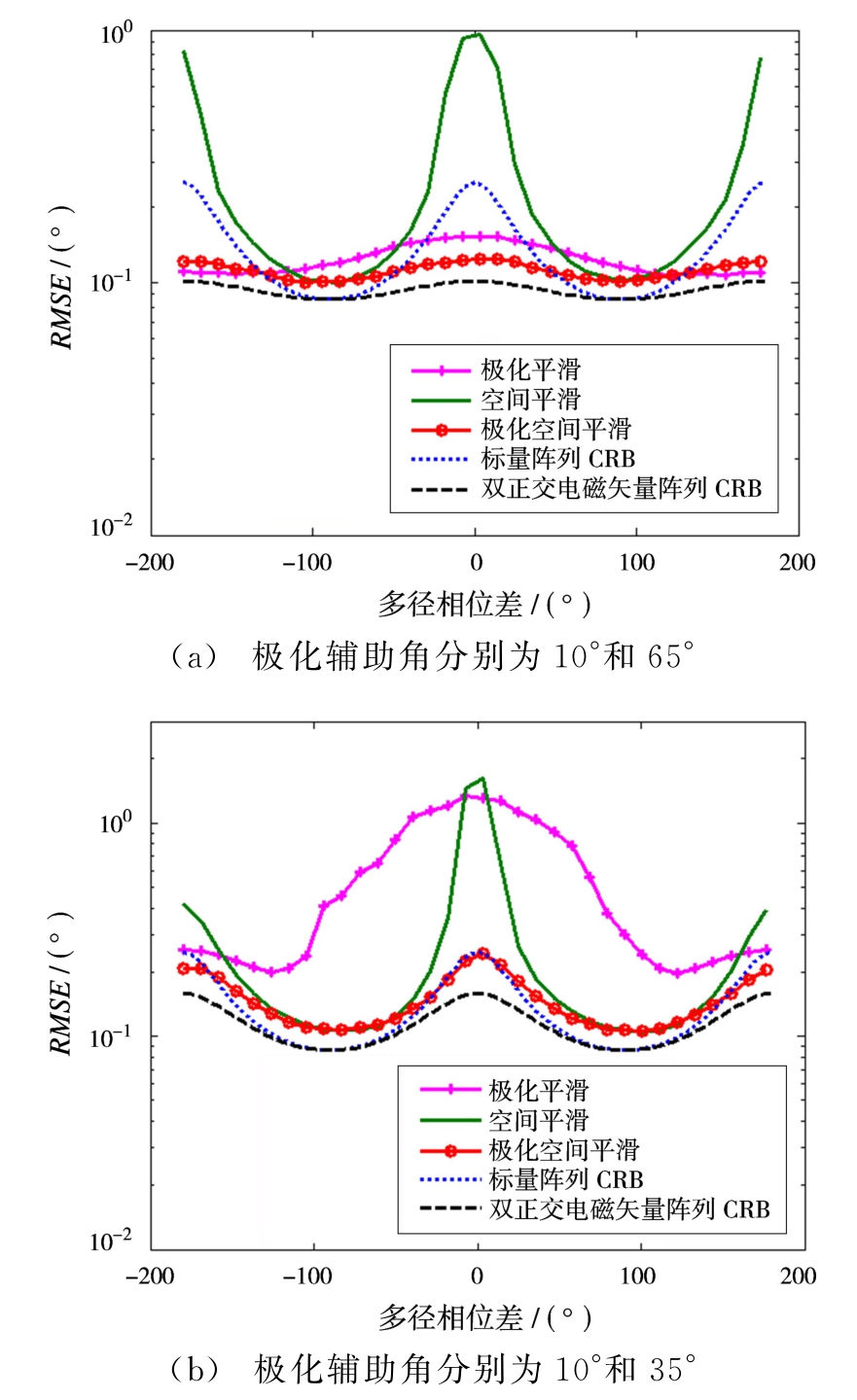
图4 多径相位差对DOA估计性能的影响
本文建立双正交电磁矢量阵列多径模型,利用极化空间平滑预处理进行解相干,提出一种双正交电磁矢量阵列的低仰角角度估计方法,并推导低仰角情形下的Cramer-Rao界,对测角算法的性能下界进行分析。通过理论分析和计算机仿真,本文得到的结论如下:
1)直达波与多径的极化差异会影响Cramer-Rao界和算法测角性能,其中极化相位差对Cramer-Rao界影响较小,而直达波与多径的极化辅助角相差越大,Cramer-Rao界越低。
2)与标量阵列类似,低角情形下直达波与多径的相位差会影响Cramer-Rao界和算法测角性能,而电磁矢量阵列的Cramer-Rao界明显低于标量阵列,体现了电磁矢量阵列在低角估计中的潜力和优越性。
3)仰角越低,直达波与多径的极化差异越小,仅利用极化平滑算法无法达到令人满意的解相干性能。本文所提的极化空间平滑预处理方法由于联合空域和极化域进行解相干处理,其测角性能逼近Cramer-Rao界,在直达波和多径极化差异较小时也有高精度测角性能,解决了现有极化平滑算法在低仰角情形下解相干性能差的难题。
参考文献:
[1]LO T,LITVA J.Use of a Highly Deterministic Multipath Signal Model in Low-Angle Tracking[J].IEE Proceedings F,Radar and Signal Processing,1991,138(2):163-171.
[2]CHEN Baixiao,ZHAO Guanghui,ZHANG Shouhong.Altitude Measurement Based on Beam Split and Frequency Diversity in VHF Radar[J].IEEE Trans on Aerospace and Electronic Systems,2010,46(1):3-13.
[3]宋秀芬,朱伟,谢腾飞,等.复杂阵地米波雷达低仰角测高算法研究[J].雷达科学与技术,2014,12(2):156-160.SONG Xiufen,ZHU Wei,XIE Tengfei,et al.Study on Low-Angle Height-Finding,Algorithm of VHF Radar in Complex Terrain[J].Radar Science and Technology,2014,12(2):156-160.(in Chinese)
[4]郑轶松,陈伯孝.米波雷达低仰角目标多径模型及其反演方法研究[J].电子与信息学报,2016,38(6):1468-1474.
[5]PARK D,YANG E,AHN S,et al.Adaptive Beamforming for Low-Angle Target Tracking Under Multipath Interference[J].IEEE Trans on Aerospace and Electronic Systems,2014,50(4):2564-2577.
[6]ZHENG Yisong,CHEN Baixiao.Altitude Measurement of Low-Angle Target in Complex Terrain for Very High-Frequency Radar[J].IET Radar,Sonar and Navigation,2015,9(8):967-973.
[7]RAHAMIM D,TABRIKIAN J,SHAVIT R.Source Localization Using Vector Sensor Array in a Multipath Environment[J].IEEE Trans on Signal Processing,2004,52(11):3096-3103.
[8]HURTADO M,NEHORAI A.Performance Analysis of Passive Low-Grazing-Angle Source Localization in Maritime Environments[J].IEEE Trans on Aerospace and Electronic Systems,2007,43(2):780-789.
[9]XU Zhenhai,WU Jiani,XIONG Ziyuan,et al.Low-Angle Tracking Algorithm Using Polarization Sensitive Array for Very-High Frequency Radar[J].IET Radar,Sonar and Navigation,2014,8(9):1035-1041.
[10]SHAN T,WAX M,KAILATH T.On Spatial Smoothing for Direction-of-Arrival Estimation of Coherent Signals[J].IEEE Trans on Acoustics,Speech and Signal Processing,1985,33(4):806-811.
[11]刘芳,李会勇,张俊波.基于四元数的改进空间平滑解相干算法[J].雷达科学与技术,2014,12(4):432-436,445.LIU Fang,LI Huiyong,ZHANG Junbo.An Improved Spatial Smoothing Algorithm Based on Quaternion[J].Radar Science and Technology,2014,12(4):432-436,445.(in Chinese)
[12]吴向东,马仑,梁中华.一种改进的加权空间平滑算法[J].数据采集与处理,2015,30(4):824-829.
[13]WEISS A J,FRIEDLANDER B.On the Cramer-Rao Bound for Direction Finding of Correlated Signals[J].IEEE Trans on Signal Processing,1993,41(1):495-499.
[14]TREES H L.Optimum Array Processing(Part IV):Detection,Estimation,and Modulation Theory[M].New York:Wiley,2002:927.
Study on Direction of Arrival Estimation Method of Low Angle Targets for Double Orthogonally Oriented Electromagnetic Vector-Sensor Array
ZHENG Yisong1,2,CHEN Baixiao1,2
(1.National Key Lab of Radar Signal Processing,Xidian University,Xi’an710071,China;2.Collaborative Innovation Center of Information Sensing and Understanding at Xidian University,Xi'an710071,China)
Abstract:The electromagnetic vector-sensor array could significantly enhance the performance of environment sensing by utilizing the polarization information.In this paper,the multipath model of low angle target for double orthogonally oriented electromagnetic vector-sensor array is proposed.Moreover,to improve the performance of the estimation of the direction of arrival(DOA)for low angle targets with polarization and spatial information simultaneously,polarization smoothing and spatial smoothing are combined to decorrelate the direct signal and multipath signal.Furthermore,the Cramer-Rao bound of double orthogonally oriented electromagnetic vector-sensor array for low angle tracking is derived to analysis the influence of the polarization parameter for the performance of the estimation of directional of arrival.Simulations indicate that electromagnetic vector-sensor array considering the polarization information has advantages over the scalar array on the performance of DOA estimation.Because the proposed polarization-spatial smoothing algorithm takes advantages of polarization smoothing and spatial smoothing simultaneity,it outperforms the methods the state of the art,especially in the low-angle scenario that the direct signal and the multipath signal have little difference in polarization domain.
Key words:double orthogonally oriented electromagnetic vector-sensor array;DOA estimation for low angle target;Cramer-Rao bound;multipath
中图分类号:TN958;TN957
文献标志码:A
文章编号:1672-2337(2017)02-0131-06
DOI:10.3969/j.issn.1672-2337.2017.02.004
收稿日期:2016-09-12;
修回日期:2016-11-02
基金项目:国家自然科学基金(No.61571344);上海航天科技创新基金(No.SAST2015071,SAST2015064)
作者简介:
郑轶松男,1990年生,安徽宿松人,西安电子科技大学博士研究生,主要研究方向为阵列信号处理、米波雷达低仰角测高方法。
E-mail:zhengys90@163.com
陈伯孝男,1966年生,安徽宿松人,西安电子科技大学教授、博士生导师,主要研究方向为新体制雷达系统设计及其实现、雷达信号处理、目标精确制导与跟踪。