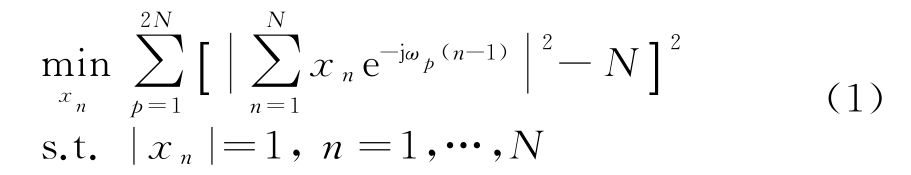
宋阳春1,唐旭艳2,冯 翔1,赵宜楠1
(1.哈尔滨工业大学(威海)信息与电气工程学院,山东威海264209;2.上海机电工程研究所,上海200233)
摘 要:为满足雷达复杂工作场景任务需求,提出一种基于主优化(MM)算法的低相关旁瓣、稀疏频谱波形设计方法;该方法首先建立最小化积分旁瓣电平准则下的恒模发射信号模型,并考虑工作频段拥塞情况下波形稀疏频谱特性,进而建立低相关旁瓣和稀疏频谱任务需求下的主优化(MM)目标函数表达式,最后利用主优化(MM)思想构造最小化积分旁瓣电平或稀疏频谱的算法框架。仿真结果表明,该算法能够有效降低积分旁瓣电平,并能够在干扰频段形成频带陷波,且在码长较长时仍具有较佳效果。
关键词:稀疏频谱;恒模波形;低相关旁瓣;主优化(MM)算法
传统雷达发射波形模式单一,难以灵活满足目标检测、跟踪等任务需求[1]。为能够适应多变的电磁环境进而提升整体性能,认知概念应运而生[2-3];认知雷达通过不断获取环境相关知识,提高系统各方面的能力[4-5];而对于认知雷达发射端而言,其自适应性体现在波形的设计上。
为解决波形高自相关旁瓣问题,文献[6]设计混沌波形并利用序列随机性降低旁瓣峰值,但混沌波形生成缺乏统一标准,难以应用工程实践;文献[7]基于小波包构造旁瓣抑制波形,但小波方法耗时较大使得难以在线设计;文献[8]在LFM波形基础上提出一种约束自相关旁瓣的非线性调频波形;文献[9]通过设计波形协方差矩阵得到具有低相关旁瓣和高信干噪比的波形。但这些方法对于大长度序列可能耗时较长。文献[10]针对雷达在复杂电磁环境下隐蔽工作的情况设计谱约束下的优化波形;文献[11]利用循环迭代算法设计稀疏频谱波形;文献[12]提出交替投影算法设计低距离旁瓣与稀疏频谱的恒模波形。但这些方法对于恒模约束导致的非凸问题往往陷入局部区域难以收敛。文献[13]在峰均功率比约束下设计频带陷波优化的低距离旁瓣波形,但算法数值稳定性较弱,在波形序列较长时难以保持良好效果。
本文针对认知雷达基于已有先验信息的优化波形设计问题,建立满足最小化积分旁瓣电平准则的恒模发射信号模型,同时考虑干扰频带场景,建立低相关旁瓣和稀疏频谱的联合优化模型;分别构造最小化积分旁瓣电平的主优化算法(MISL)和加权谱-MISL算法,得到低相关旁瓣稀疏频谱恒模波形。仿真结果表明,MISL算法可有效降低构造波形序列的积分旁瓣电平,加权谱-MISL算法能够在受干扰区间形成明显频带陷波;波形序列码长较长时,算法仍保持理想效果。
设波形序列为x=[x1,…,xN]T,其中N代表码长。由文献[14]知,恒模约束下,按最小化积分旁瓣电平准则构造优化表达式为
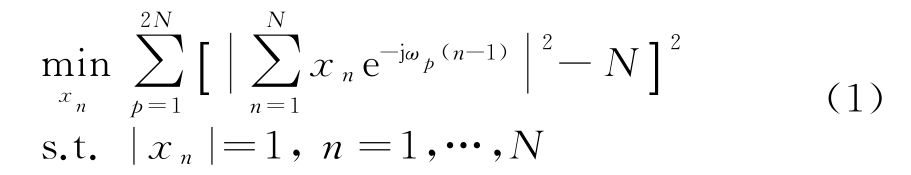
式中
为离散傅里叶采样(DFT)频率。进一步向量化式(1)中的目标函数,定义 DFT 矢 量ap=[1,ejωp,…,
展开目标函数中的完全平方形式,式(1)中优化表达式可以转化为
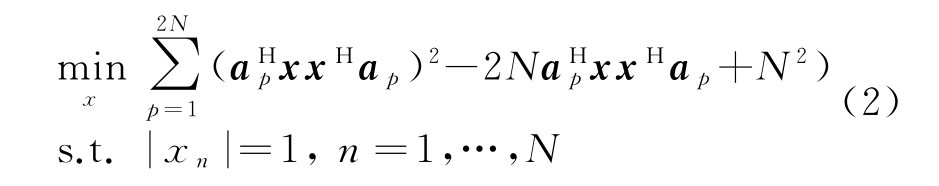
式中,(·)H表示取共轭转置。根据Parseval定理:
可得目标函数后两项仅与码长有关,码长固定时可视为常数,按最小ISL准则的恒模波形优化表达式可简化为
认知雷达能够随外部环境变化自适应调整发射波形,当工作频段内子频段被占用或受同频干扰时,认知雷达应在受干扰的区间形成频带陷波(稀疏频谱)以抑制场景中的干扰。设存在干扰的频段个数为Ns,其中第k个凹口的频带范围为[fk1,fk2],权重系数为wk,Δ为采样间隔。针对抑制特定频段电磁干扰的波形设计目标函数可表示为
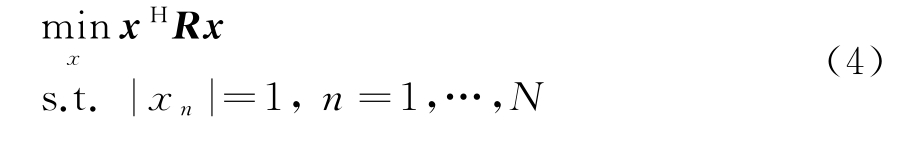
式中,R为N×N的矩阵,第(p,q)个元素为
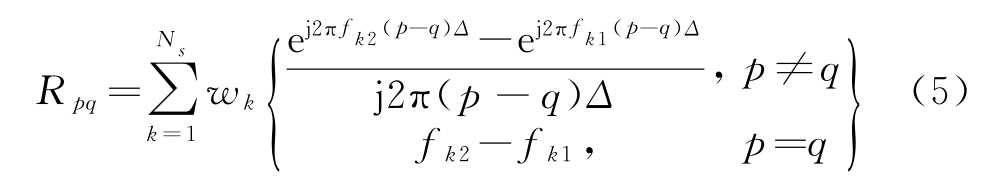
为获得较强的抗干扰能力,设计同时具备低相关旁瓣和稀疏频谱的恒模波形,引入权值λ∈(0,1)联合相关旁瓣和稀疏频谱要求,构造联合优化目标函数[15]为
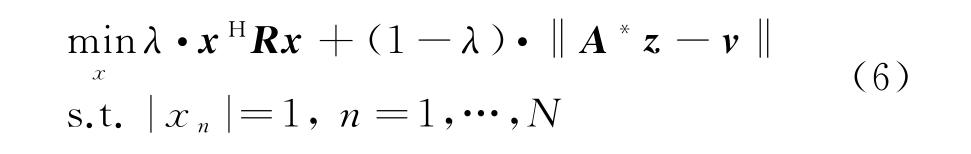
式中,
定义
A∗v,式(6)转化为
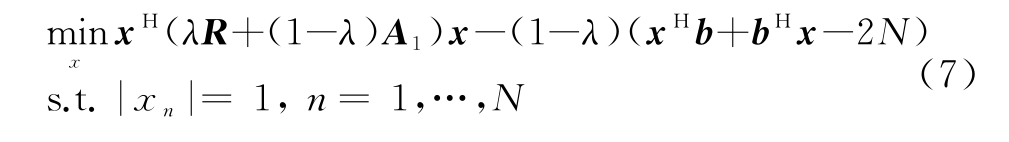
综上,针对认知雷达的典型波形设计场景,本节构造了最小化积分旁瓣电平准则下恒模发射信号模型,并在此基础上构造了低相关旁瓣和稀疏频谱的优化表达式。由于式(3)中目标函数对于x为四次,式(7)中目标函数对于x为二次,恒模约束条件为非凸函数,难以通过凸优化得到解析解。下文利用主优化(M M)算法对优化问题进行求解,通过寻找优化函数将原问题简化,设计用于积分旁瓣电平的主优化算法(MISL)以及加权谱-MISL算法。
主优化(MM)算法针对优化问题难以直接解决的情况,构造凸函数集,将难以直接求解的非凸问题转化为易于求解的凸优化问题。对于当前迭代点x(k),构造凸优化函数c(x,x(k)),使其满足
进而寻找x(k+1)使得c(x(k+1),x(k))最小。
主优化(MM)算法核心在于将原目标函数转化为光滑凸函数,通过最小化f(x)可行点x(k)处的优化函数c(x,x(k)),降低原问题的求解难度。由x(k+1)的选取方法和式(8)中的关系式可知f(x(k+1))≤f(x(k)),此递减趋势使得M M算法具有显著的数值稳定性。
针对第2节中“认知雷达最小化积分旁瓣电平的恒模波形设计”,为构造式(3)中按最小ISL准则的恒模波形优化表达式的主优化(MM)算法,需将原问题中的目标函数转换为光滑凸函数,定义
式(3)可进一步写为
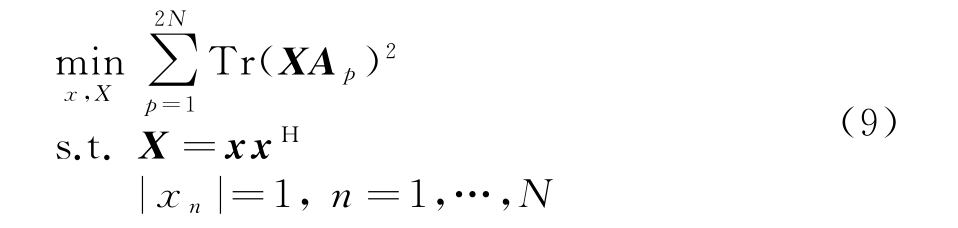
式中,Tr(·)代表取矩阵的迹,可得Tr(XAp)=vec(X)Hvec(Ap),式(9)可以写为
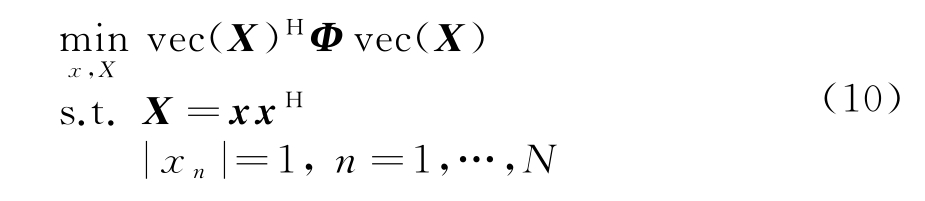
式中
为矩阵的拉直算子。设λmax(·)代表矩阵最大特征值,由矩阵Φ的最大特征值构成对角阵L,即L=λmax(Φ)I。由定义可知,Φ,L均为n×n维的埃尔米特矩阵,且有L≻Φ。对于二次函数xHΦx的任一可行点x0∈ℂn,存在
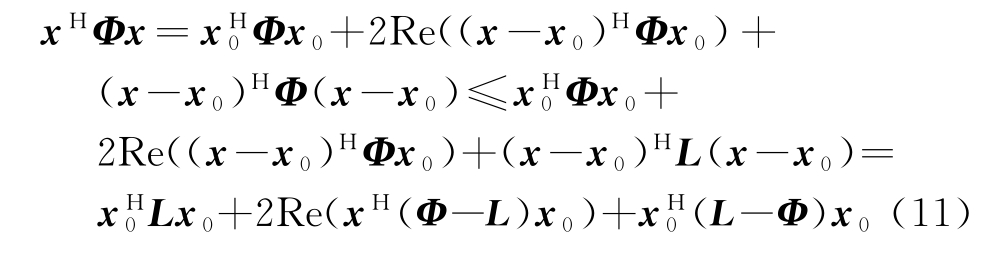
式中,Re(·)代表取实部。令式(11)中的x=vec(X),可得到式(11)中目标函数在X(k)的优化函数为
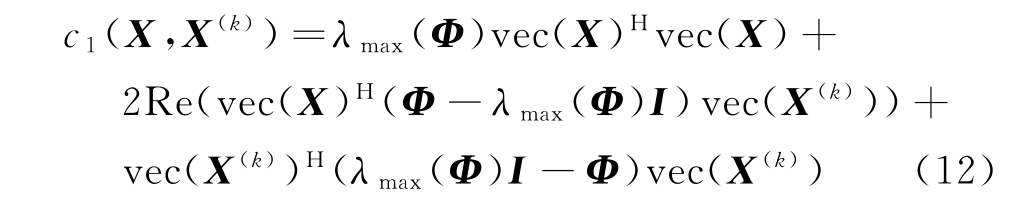
由列向量的性质可得vec(X)Hvec(X)=(xHx)2=N2,忽略常数部分对最小值点取值的影响,利用式(12)中优化函数替代原问题中的目标函数,关于X的优化问题可以表示为
将上式转化为关于x的优化表达式,进一步写为
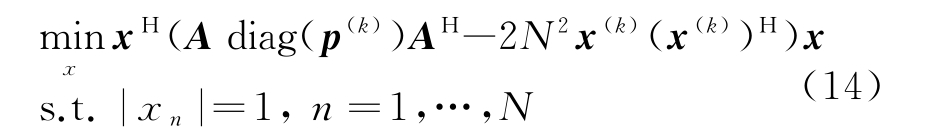
式中
表示由向量变量形成的对角矩阵。上式中目标函数对x而言是二次的,因此式(14)为恒模二次规划问题,通常情况下为NP-hard,难以直接求解。为进一步寻找易于直接求解的优化函数,设
1,…,2N},可得式(14)中目标函数的一个上界,构造得到原函数在x(k)的优化函数如下:
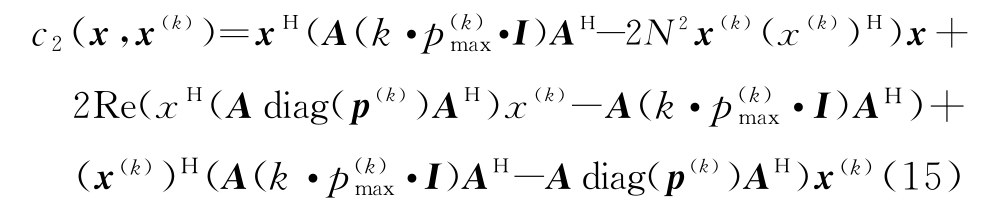
定义
由于AAH=2N I,忽略常数部分对最小值点的影响,用式(15)中优化函数替代原问题中的目标函数,关于x的优化问题可以表示为
为便于求解,定义
式(16)中的优化问题可以被重新写为
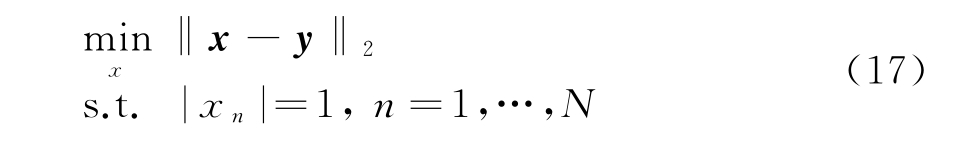
通过以上基于主优化(M M)算法的推导过程,得到最小ISL准则的恒模波形的优化表达式如式(17),可得闭式解为
上述过程通过寻找原目标函数关于X的优化函数,进一步得到关于x的优化问题,保持了主优化(MM)算法的单调性,得到最小化积分旁瓣电平的主优化算法(MISL)步骤如下:
算法1 最小化积分旁瓣电平的主优化算法(MISL)
1)迭代初始化:设置迭代计数器k=0,初始波形序列
2)基于当前时刻迭代优化解x(k),计算以下表达式:
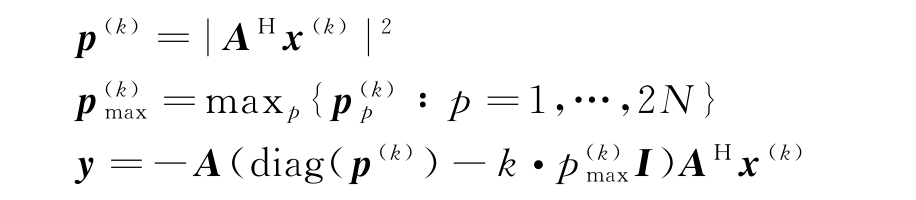
3)求取更新迭代解:令k=k+1,利用
计算更新迭代解;
4)收敛判别:根据所定义收敛误差σ,如果
则跳出迭代;
5)重复步骤2)～4),直到满足收敛条件。
针对“认知雷达抑制特定频段电磁干扰及最小化积分旁瓣电平的恒模波形设计”,可以采用与上文相似的方式,利用主优化(MM)算法进行求解。为寻找式(7)中目标函数的优化函数,定义Rr=λR+(1-λ)A1,矩阵Rr最大特征值λmax(Rr),则有λmax(Rr)·I≻Rr,可以得到关系式如下:
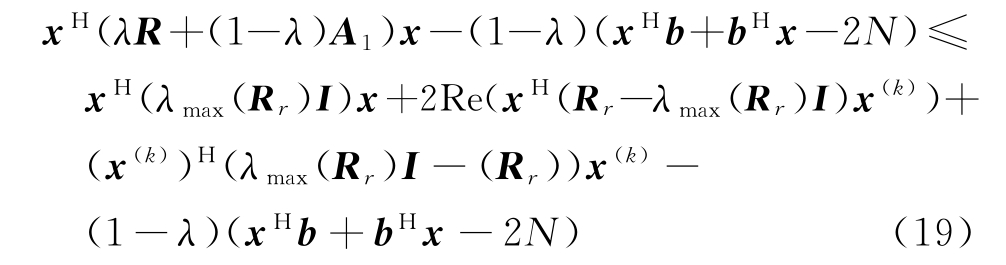
上式中第一项、第三项均为常数,忽略常数项对最小值点的影响,优化函数可近似等价为
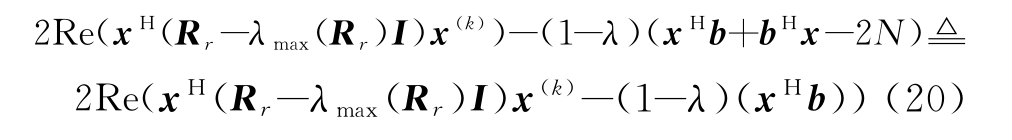
令
将Rr=λR+(1-λ)A1和
代入式(20),优化函数转化为
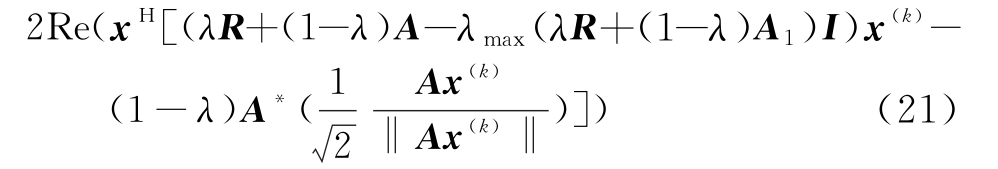
为便于求解,进行如下定义:
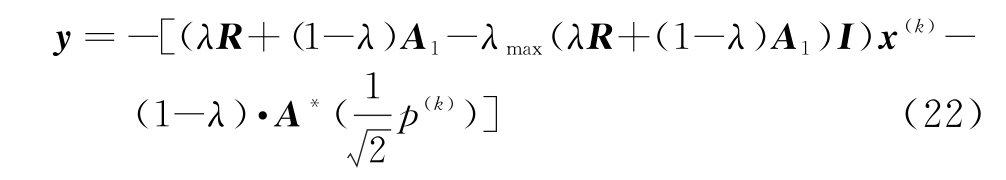
经过以上定义,优化问题最终形式为
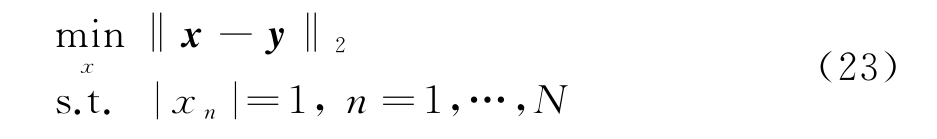
可得到与式(18)具有相似形式的闭式解为
通过上述推导,设计得到基于主优化(MM)的低相关旁瓣稀疏频谱恒模波形,加权谱-MISL算法过程如下:
算法2 加权谱-MISL算法
1)迭代初始化:设置迭代计数器k=0,初始波形序列
2)基于当前时刻迭代优化解x(k),计算以下表达式:
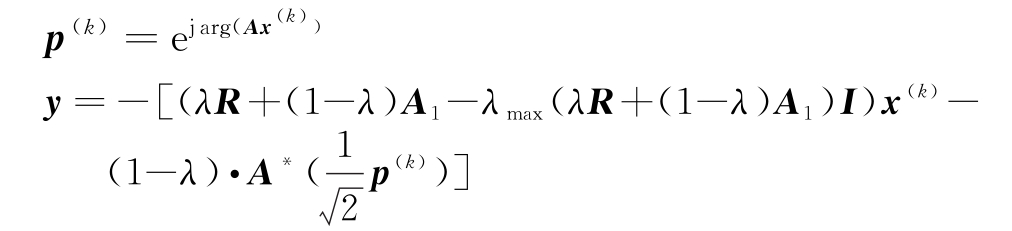
3)求取更新迭代解:令k=k+1,利用
计算更新迭代解;
4)收敛判别:根据所定义收敛误差σ,如果
则跳出迭代;
5)重复步骤2)～4),直到满足收敛条件。
设定仿真波形序列码长N=3 000,使用本文MISL算法得到发射波形序列,设置收敛误差σ=1×10-8时的波形相关水平,如图1(a)所示;使用文献[14]中算法得到波形相关水平,如图1(b)所示;使用蒙特卡罗法进行100次试验后取统计平均,算法性能比较如表1所示。
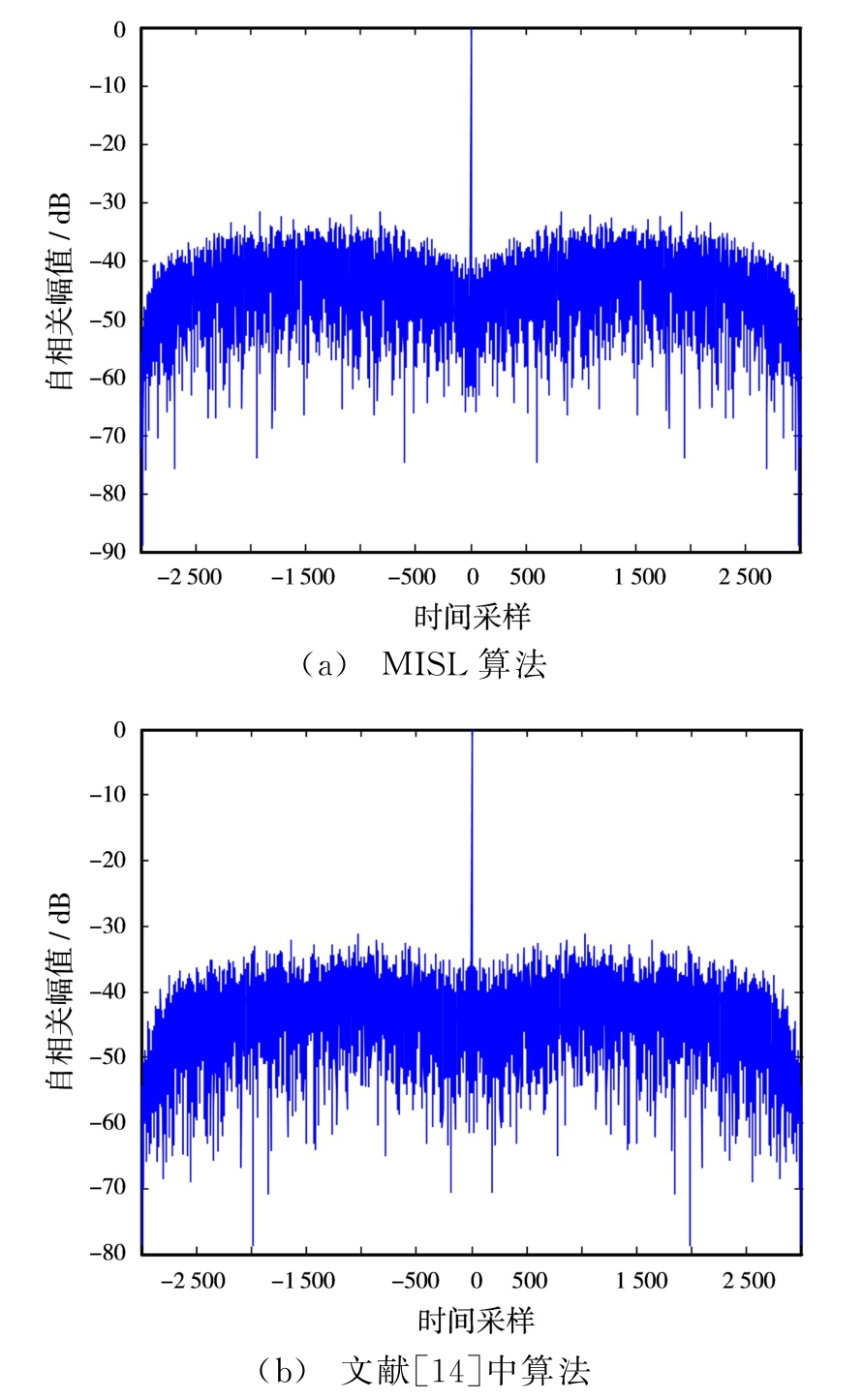
图1 波形序列自相关函数
表1 MISL与文献[14]中算法性能比较
由图1可以看出,使用本文MISL算法构造得到发射波形序列的积分旁瓣电平受到了明显抑制,MISL算法针对波形序列码长较长时,能够保持稳定效果。由表1可以看出,本文MISL算法可以得到更低的自相关旁瓣,且运行时间明显缩短。
设定仿真波形序列码长N=3 000,假定干扰位于[200,300]k Hz的波段中,其通带处于[0,1 000]k Hz中剩余部分。使用加权谱-MISL算法序列构造得到发射波形序列的自相关函数,如图2(a)所示,功率谱密度如图2(b)所示;使用SCAN算法[16]序列构造得到发射波形序列的自相关函数,如图3(a)所示,功率谱密度如图3(b)所示。使用蒙特卡罗法进行100次试验后,算法性能比较如表2所示。
从图2(a)可以看出,使用加权谱-MISL算法构造得到的波形序列在单一干扰波段下积分旁瓣电平受到了明显抑制。从图2(b)可以看出,功率谱在受干扰区间能够形成明显频带陷波。由表2可以看出,加权谱-MISL算法可以在干扰频段形成更低的陷波深度,且运行时间缩短近三分之二。
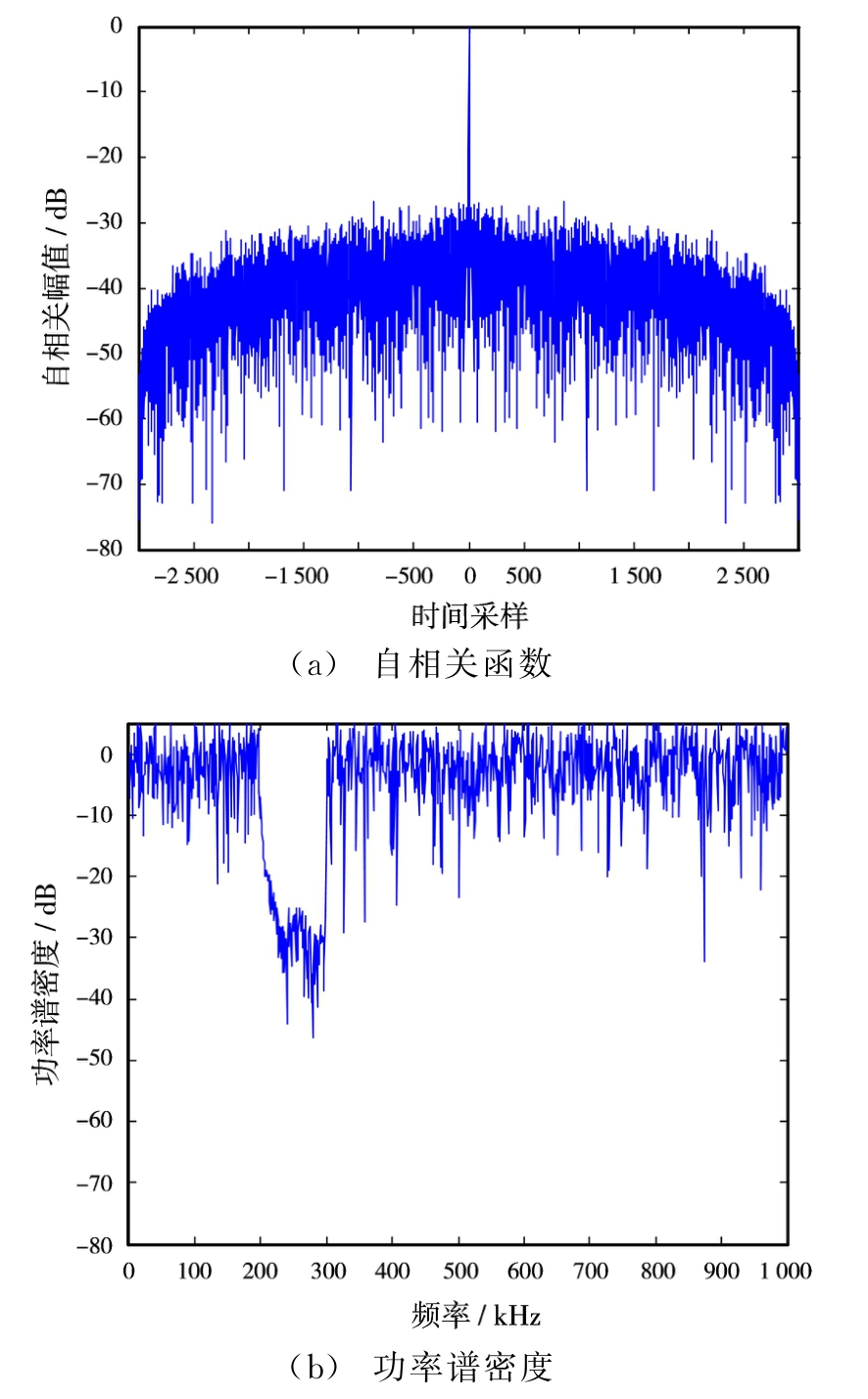
图2 单一干扰波段下加权谱-MISL算法波形序列
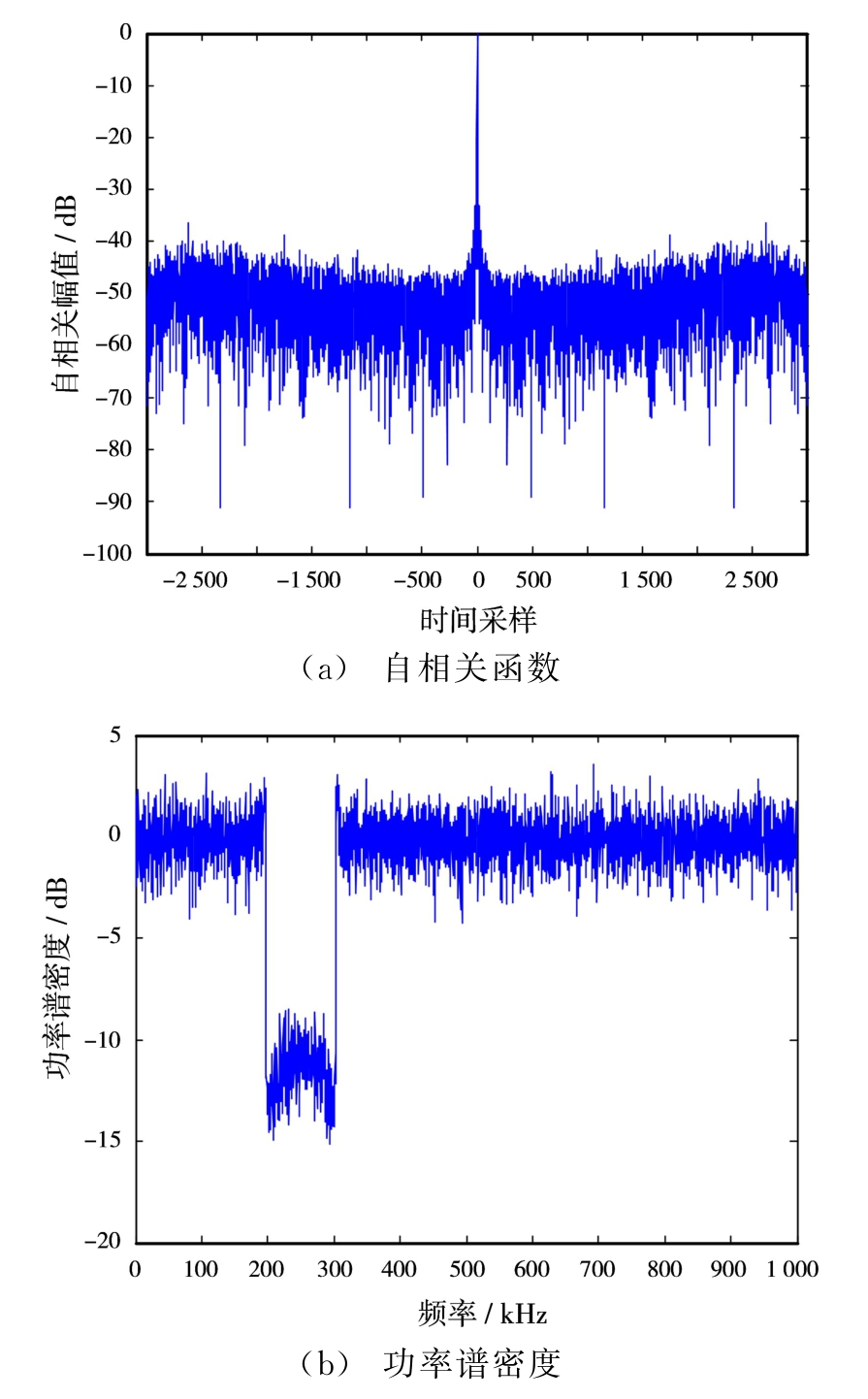
图3 单一干扰波段下SCAN算法波形序列
表2 单一干扰波段下加权谱-MISL与SCAN算法性能比较
进一步针对多干扰波段情况下加权谱-MISL算法的性能进行研究,假定干扰位于[150,200]∪[500,550]∪[850,900]k Hz的波段中,其通带处于[0,1 000]k Hz中剩余部分。使用加权谱-MISL算法序列构造得到发射波形序列的自相关函数,如图4(a)所示,功率谱密度如图4(b)所示。使用SCAN算法序列构造得到发射波形序列的自相关函数,如图5(a)所示,功率谱密度如图5(b)所示。使用蒙特卡罗法进行100次试验后取统计平均,算法性能比较如表3所示。
从图4(a)可以看出,使用加权谱-MISL算法构造得到的波形序列在多干扰波段下积分旁瓣电平仍然保持在较低水平。从图4(b)可以看出,功率谱在各干扰区间均能够形成明显频带陷波。由表3可以看出,加权谱-MISL算法可以在多干扰频段下,保持陷波深度低于SCAN算法,且运行时间大大缩短。
以上仿真结果表明,MISL算法可有效降低构造波形序列的积分旁瓣电平,加权谱-MISL算法能够在降低构造波形序列的积分旁瓣电平的同时,在受干扰区间形成明显频带陷波。算法在仿真效果和收敛速度上,均优于文献[14]中算法和SCAN算法。
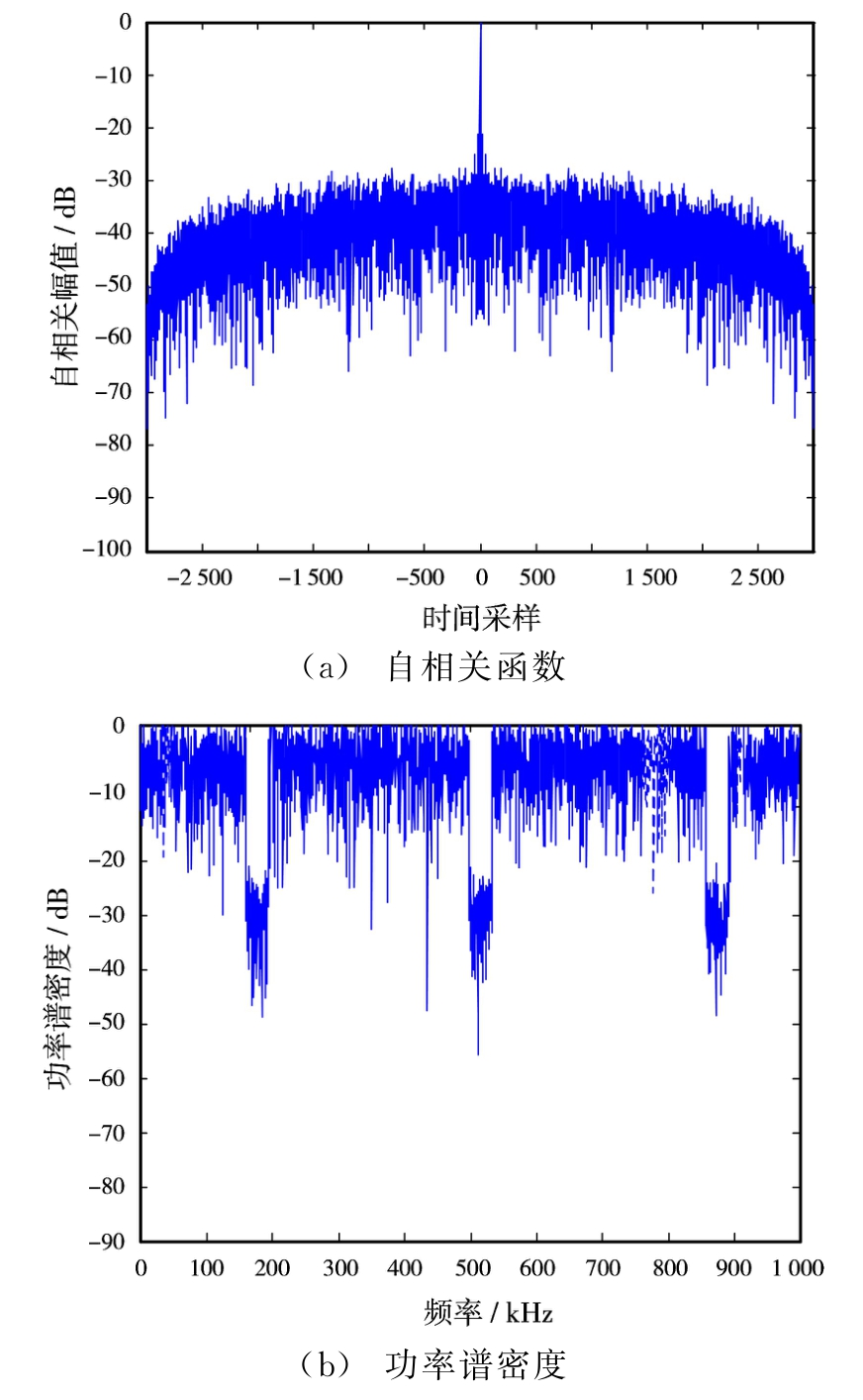
图4 多干扰波段下加权谱-MISL算法波形序列
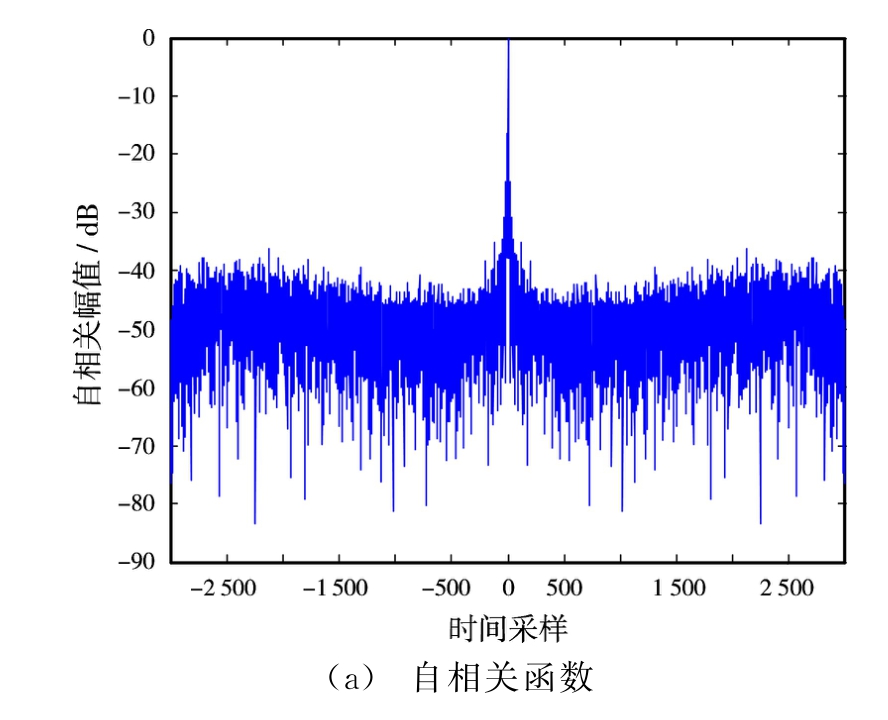
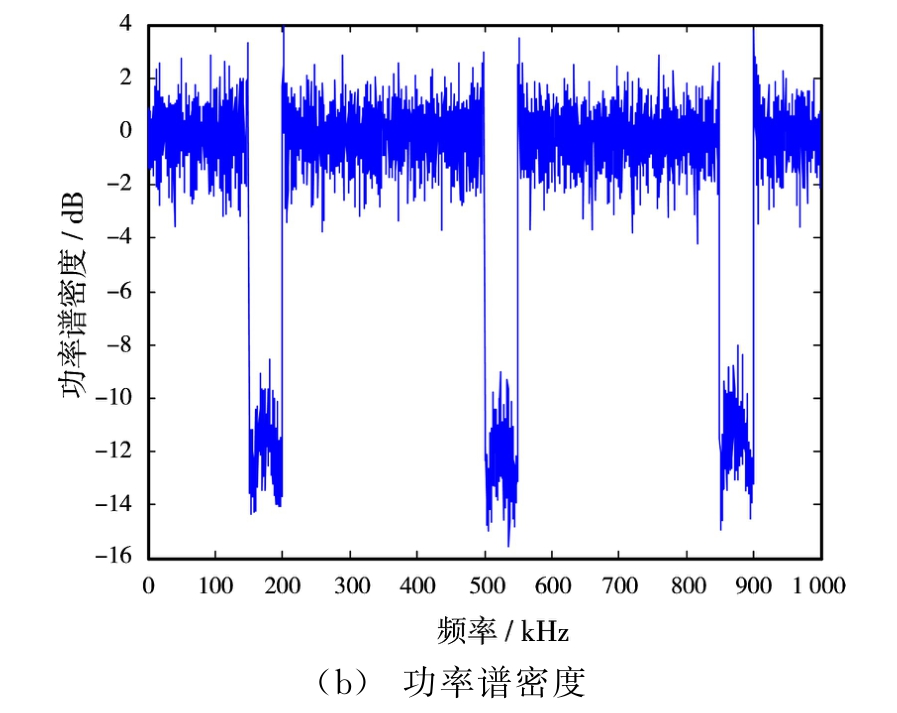
图5 多干扰波段下SCAN算法波形序列
表3 多干扰波段下加权谱-MISL与SCAN算法性能比较
本文针对雷达的优化波形设计问题,提出基于主优化(MM)算法的低相关旁瓣稀疏频谱恒模波形设计方法。建立最小化积分旁瓣电平准则下的恒模发射信号模型;对于环境中存在干扰频带的情况,建立低相关旁瓣和稀疏频谱的恒模优化表达式。构造最小化积分旁瓣电平的主优化算法(MISL)和加权谱-MISL算法。仿真结果表明,MISL算法可有效降低构造波形序列的积分旁瓣电平,加权谱-MISL算法能够在降低积分旁瓣电平的同时,在受干扰区间形成频带陷波,针对码长较长的情况能够保持算法稳定性。
参考文献:
[1]闫东,张朝霞,赵岩,等.基于信号杂波噪声比的认知雷达扩展目标探测波形设计[J].计算机应用,2015,35(7):2105-2108.
[2]代泽洋,王贺,刘宝泉,等.认知雷达中协作频谱感知技术研究[J].雷达科学与技术,2015,13(1):17-20.DAI Zeyang,WANG He,LIU Baoquan,et al.Study on Cooperative Spectrum Sensing in Cognitive Radar[J].Radar Science and Technology,2015,13(1):17-20.(in Chinese)
[3]BELL K L,BAKER C J,SMITH G E,et al.Cognitive Radar Framework for Target Detection and Tracking[J].IEEE Journal of Selected Topics in Signal Processing,2015,9(8):1427-1439.
[4]TURLAPATY A,JIN Y.Bayesian Sequential Parameter Estimation by Cognitive Radar with Multiantenna Arrays[J].IEEE Trans on Signal Processing,2015,63(4):974-987.
[5]鞠默然,李新波,石要武.基于信噪杂比最大能量分配认知雷达波形设计[J].吉林大学学报(信息科学版),2015,33(3):230-234.
[6]SHEN D,ZHANG L,LIU X,et al.Reducing the Waveform Auto-Correlation Sidelobes and Cross-Correlation of MIMO Radar by Using Chaotic Sequences[J].Journal of Xidian University,2012,39(5):42-46.
[7]CAO S,ZHENG Y F,EWING R L.Wavelet-Based Waveform for Effective Sidelobe Suppression in Radar Signal[J].IEEE Trans on Aerospace and Electronic Systems,2014,50(1):265-284.
[8]THOMAS D,KAMALANATHAN C,VALARMATHY D S.Sidelobe Deduction by Piecewise Nonlinear Frequency Modulation Waveform[J].International Journal of Innovative Research in Science,Engineering and Technology,2013,2(3):795-801.
[9]AHMED S,ALOUINI M S.MIMO-Radar Waveform Covariance Matrix for High SINR and Low Side-Lobe Levels[J].IEEE Trans on Signal Processing,2014,62(8):2056-2065.
[10]AUBRY A,DE MAIO A,PIEZZO M,et al.Radar Waveform Design in a Spectrally Crowded Environment via Nonconvex Quadratic Optimization[J].IEEE Trans on Aerospace and Electronic Systems,2014,50(2):1138-1152.
[11]周宇,张林让,赵珊珊.组网雷达低自相关旁瓣和互相关干扰的稀疏频谱波形设计方法[J].电子与信息学报,2014,36(6):1394-1399.
[12]ZHAO Y N,ZHANG T,LI F C,et al.Optimal Waveform Design for MIMO Radar via Alternating Projection[J].Journal of Electronics&Information Technology,2014,36(6):1368-1373.
[13]申东,张林让,周宇,等.频带陷波优化的低距离旁瓣波形设计方法[J].北京理工大学学报,2015,35(3):321-325.
[14]SONG J,BABU P,PALOMAR D P.Optimization Methods for Designing Sequences with Low Autocorrelation Sidelobes[J].IEEE Trans on Signal Processing,2014,63(15):3998-4009.
[15]WANG G,LU Y.Designing Single/Multiple Sparse Frequency Waveforms with Sidelobe Constraint[J].IET Radar,Sonar and Navigation,2011,5(1):32-38.
[16]HE H,STOICA P,LI J.Waveform Design with Stopband and Correlation Constraints for Cognitive Radar[C]∥2nd International Workshop on Cognitive Information Processing,Elba:IEEE,2010:344-349.
Radar Waveform Design Based on Majorization-Minimization Algorithm
SONG Yangchun1,TANG Xuyan2,FENG Xiang1,ZHAO Yinan1
(1.School of Information and Electrical Engineering,Harbin Institute of Technology at Weihai,Weihai264209,China;2.Shanghai Electro-Mechanical Engineering Institute,Shanghai200233,China)
Abstract:To tackle the sophisticated radar scene,a novel method based on majorization-minimization mechanism is presented to design waveforms with low correlation sidelobes and sparse spectrum.Firstly,the unimodular waveform,in the case of minimizing the integrated sidelobe level as well as suppressing the congested spectrum,is formulated.Next,the objective function incorporating the idea of majorization-minimization is derived,and then,the MISL algorithm and the weighted spectral-MISL algorithm are proposed.Simulations demonstrate that these algorithms can obtain low integrated sidelobe level and sparse spectrum in the suppressed bands,which also performed for long waveforms.
Key words:sparse spectrum;unimodular waveform;low correlation sidelobe;majorization-minimization(MM)algorithm
中图分类号:TN958.5
文献标志码:A
文章编号:1672-2337(2017)02-0159-07
DOI:10.3969/j.issn.1672-2337.2017.02.009
收稿日期:2016-08-15;
修回日期:2016-11-04
基金项目:国家自然科学基金(No.61371181)
作者简介:
宋阳春女,1993年出生于山东德州,哈尔滨工业大学(威海)硕士研究生,主要研究方向为认知雷达与雷达信号处理。
唐旭艳女,1979年出生于湖南衡山,上海机电工程研究所高级工程师,主要研究方向为发射系统总体设计。
冯 翔男,1988年出生于山东潍坊,哈尔滨工业大学博士研究生,主要研究方向为认知雷达与雷达信号处理。
E-mail:fengxiang230316@163.com
赵宜楠男,1977年出生于黑龙江哈尔滨,哈尔滨工业大学(威海)信息与电气工程学院教授、博士生导师,主要研究方向为雷达信号处理。