个入射信号,本文中称有Q组相干源,即组内信号源相干,组间信号源独立。则M个阵元的阵列接收数据x(t)可以表示为李 帅,陈 辉
(空军预警学院,湖北武汉430019)
摘 要:针对冲击噪声背景下相干信号源的波达方向(Direction of Arrival,DOA)估计问题,提出一种基于时延分数低阶矩的分组解相干算法——FLOM-TDD(Fractional Lower Order Moment Time Delay Decorrelation)。首先基于两个时延不同的分数低阶矩矩阵,利用DOA矩阵方法得到每组相干源的广义导向矢量;然后根据多径衰减的特征,对每组相干源进行时域解相干,得到相干源的波达方向估计。该方法适用于冲击噪声背景下的波达方向估计而且可以估计大于阵元数目的相干源,计算机仿真分析验证了算法的性能优势。
关键词:波达方向估计;冲击噪声;相干源
波达方向(Direction of Arrival,DOA)估计在军事和民用领域有着广泛的应用,如雷达、声纳、射电天文望远镜和地震预测等都需要精确的波达方向估计。经典的子空间类算法包括多重信号分类(Multiple Signal Classification,MUSIC)算法、旋转不变子空间(Estimation of Signal Parameters via Rotational Invariance Techniques)等,具有较高的估计精度,这些算法都以高斯噪声为背景,利用二阶统计量或者高阶统计量进行计算。然而实际环境中的噪声并不都是高斯分布的,比如大气噪声、无线信道噪声、海杂波和地杂波等,这些噪声相对高斯噪声有明显的脉冲特性,研究发现这类噪声模型更适合用SαS(SymmetricαStable)分布来表示[1-3]。不过SαS分布不存在二阶或者二阶以上的矩,所以传统的基于二阶统计量或者高阶统计量的方法失效[4]。针对SαS分布噪声模型下的DOA估计,文献[5]基于阵列接收数据定义了共变矩阵,利用共变矩阵和子空间正交的原理提出了一种ROC-MUSIC(Robust Covariation-Based MUSIC)算法,可以实现信号源的波达方向估计,不过ROC-MUSIC算法假设信号和噪声都服从SαS分布,这与实际情况不符,因为实际中信号的能量通常是有限的。FLOM-MUSIC(Fractional Lower Order Moment MUSIC)算法[6-7]则将信号从SαS分布推广到圆信号(Circular Signals),进一步拓展了应用范围。文献[8-9]是一类从接收数据幅值角度提出的方法,其中文献[8]利用无穷范数归一化的方法,对接收数据的幅值进行归一化处理,文献[9]则是通过估计幅值上限,对接收数据去冲击预处理来削弱数据中的冲击成分。
以上算法都假设信号是非相干的,当信号相干时,由于共变矩阵或者低阶矩矩阵秩的损失,会导致后续的子空间类算法失效,无法估计出信号的波达方向。针对这一问题,文献[10]提出了ROC-SS算法和FLOM-SS算法,将前后向平滑方法与ROC-MUSIC算法和FLOM-MUSIC算法结合起来,通过构建前后向平滑共变矩阵和前后向平滑低阶矩矩阵,再利用子空间类算法实现了对相干源的波达方向估计。文献[11]基于重构的分数低阶矩阵,提出了重构分数低阶协方差矩阵子空间拟合测向算法,利用差分粒子群方法进行多维搜索求出最优解。文献[12]提出了基于虚拟空间平滑共变系数矩阵的DOA估计方法,构建的新的共变系数矩阵维数等于阵元数,避免了阵列孔径的损失,适用于具有实值特性的信号。文献[13]讨论了波束变换后ROC-SS算法和FLOM-SS算法的应用。文献[14]则是将无穷范数归一化与空间平滑结合起来。
本文提出了基于时延分数低阶矩的分组解相干算法——FLOM-TDD(Fractional Lower Order Moment Time Delay Decorrelation)。首先结合分数低阶矩方法,构建两个不同时延的分数低阶矩矩阵,利用波达方向矩阵法得到广义导向矢量;然后根据典型移动通信环境中多径的衰减系数特征,进行时域平滑,从而可以分组估计出所有相干源的波达方向,实现了冲击噪声背景下的解相干。
对于一M元均匀线阵,假设有Q个独立信号源,其中第i个信号源有Pi条多径,即总共有个入射信号,本文中称有Q组相干源,即组内信号源相干,组间信号源独立。则M个阵元的阵列接收数据x(t)可以表示为
式中:a(θ)=[1,ejϕ,…,ej(M-1)ϕ]表示理想的导向矢量
表示信号到达相邻阵元的相位差,d表示阵元间距,λ表示信号的波长,θji表示第i组信号源第j条多径的波达方向;zji表示第i组信号源第j条多径的衰减系数,
表示第i组相干源在阵列上所形成的M×1维广义导向矢量,它包含着该组相干源所有信号的波达方向信息和衰减系数信息;si(t)表示第i组信号源直达径的复包络,n(t)表示M×1维噪声矢量,这里假设各阵元的噪声独立且同服从SαS分布。
式(1)可以写成矩阵形式:
式中,B=[b1,b2,…,bQ]为广义导向矢量组成的M×Q维矩阵,s(t)=[s1(t),s2(t),…,sQ(t)]T为Q组相干源的Q×1维信号矢量。
α稳定分布是唯一一种满足广义中心极限定理的分布,研究表明,α稳定分布能够非常好地与实际情景中的噪声数据吻合。由于α稳定分布没有闭式的概率密度分布函数,通常用特征函数来表示:
式中
α为特征指数,表征分布的非高斯性,α越小,非高斯性越强,冲击特性越明显;β为对称参数,表征分布的斜度,β=0时为对称分布,此时α分布称为对称α稳定(SαS)分布,β＞0时为右偏斜分布,β＜0时为左偏斜分布;参数σ为分散系数,类似于高斯分布中的方差,表征分布样本相对于均值的分散程度;参数μ为位置参数,表征分布中值(0＜α≤1)或者均值(1＜α≤2),当σ=1,μ=0时,α分布称为标准α分布。
图1是标准SαS分布在α取不同值时产生的样本序列,可以看出,当0＜α＜2随着α的增大,样本的冲击特性逐渐减弱;实际上,当α=2时,SαS分布就成为高斯分布,也就是说高斯分布是SαS分布的一个特例。
图1 不同α时的冲击噪声样本
SαS分布的随机变量不存在二阶矩,这导致常规的基于协方差矩阵的算法失效,不过,可以利用分数低阶矩矩阵进行计算,文献[5]提出了利用分数低阶矩进行DOA估计的方法,并比较了不同分数阶的估计性能,通过仿真证明了分数低阶矩在冲击噪声背景下的有效性。这里考虑对分数低阶矩进行延伸,将时延信息作为一个变量,从而拓展了可利用的信息量。
阵列接收数据分数低阶矩的定义如下:
式中,xi(t)和xk(t)分别表示第i个和第k个阵元的接收数据。很明显分数低阶矩与常规的二阶矩计算是不同的,为了得到接收数据分数低阶矩里所蕴含的信息,要对其进行一系列变换。
首先对信号、噪声之间的关系作如下假设:信号与噪声相互独立,不同阵元间的噪声相互独立,同一阵元不同时延的噪声之间相互独立。因此,可以得到以下分数低阶矩关系:
式中,ni(t)表示第i个阵元上的噪声,δ(·)表示Kronecker函数
为同一信号之间的分数低阶矩。
文献[5]中给出了阵列接收数据分数低阶矩的表示,但是没有考虑接收数据间存在时延时的情况,本文结合文献[5]中的结果,推导出了存在时延τ时阵列接收数据分数低阶矩的表示:
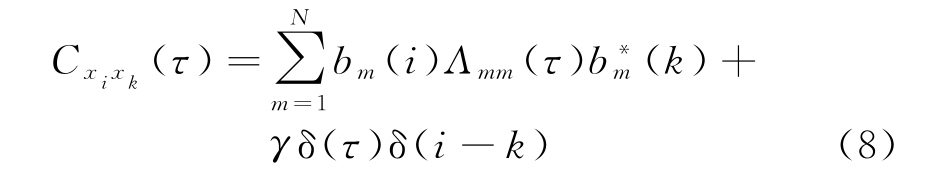
式中,
式中,bm(i)表示第m组相干源的广义导向矢量bm的第i个值,即第m组相干源到第i个阵元的相位差(相对于到第一个阵元)。
由式(8)可以得到阵列接收数据分数低阶矩矩阵的表示:
式 中,Λ(τ)=diag([Λ11(τ),Λ22(τ),…,ΛQQ(τ)])可以看作是信号分数低阶矩矩阵,γ可以看作是噪声的分数低阶矩“功率”,I是M×M维的单位矩阵。
上节中推导出了时延下接收数据的分数低阶矩,其中,分数低阶矩的方法解决了SαS分布没有二阶矩的问题,而时延的考虑则进一步扩展到了时间维,增加了可利用的信息[14-15],后面的求解过程可以看到这种方法的优势,就是利用时间维度的拓展替代了传统方法对于阵列结构平移不变性的要求。
观察式(11)可以看出,利用分数低阶矩得到的接收数据矩阵类似于高斯噪声下的数据协方差矩阵,从而可以将传统的基于数据协方差矩阵的方法应用到分数低阶矩矩阵上。由式(11)可以得到不同时延τ1,τ2≠0的接收数据的分数低阶矩矩阵:
式中,
另外Cx(τ1)特征分解可得
根据DOA矩阵方法[16]的思想,可以构建如下矩阵:
式中
的伪逆。
由文献[16]的结论可知,CB=Bφ,即对C特征分解所得的特征矢量为广义导向矢量bi。相比传统的DOA矩阵方法,该方法适用于任意结构的阵列,不再要求阵列结构必须具有平移不变性。这正是研究具有时延信息的分数低阶矩矩阵的意义所在,通过增加时域信息减少了对阵列结构的要求。
在得到每组相干源所形成的广义导向矢量后,需要提取出组内各个信号源的波达方向信息。广义特征矢量bi可以表示如下:
式 中,Ai=[a(θ1i),a(θ2i),… ,a(θPii)],zi=[z1i,z2i,…,zPii]T。
从式(16)可以看出,广义导向矢量由信号源的波达方向信息,以及各信号源的多径衰落系数两部分组成,考虑典型的移动通信环境,多径衰落系数是快变化的,这是由于信号波长较短引起的,比如信号载频为1 GHz时,信号波长只有30 cm,多径变化15 cm会导致信号相位改变180°,另外,多径衰落系数的相位可以看作是均匀分布的。而信号源的波达方向是慢变化的,因为目标与基站之间距离较远,在较短时间内,直达径和多径的波达方向不会发生较大变化[17]。基于以上分析,可以在这段时间里求得广义导向矢量的L个估计值,即
这里需要说明的是,为保证L个广义导向矢量属于同一组相干源,每次求解的广义导向矢量应该是对应同一大小次序的特征值的特征矢量。
式(17)中,可以将
看作接收数据,将
看作信号矢量,类似地可以得出相应的接收数据相关矩阵:
由于多径衰落系数的快变化特性及衰落系数相位的均匀分布,信号矢量
的秩等于组内相干源的数目,即为Pi。所以矩阵
可以作为已解相干的数据相关矩阵继续进行MUSIC等子空间分解类算法,求得组内相干源的波达方向。
仿真1
仿真采用8阵元均匀线阵,阵元间距为半波长,3组相干源,波达方向分别是{-30°,-20°,5°,20°},{40°,50°,70°},{-40°,-60°},假设多径衰减系数幅度和相位分别服从(0∶1)和(-π∶π)的均匀分布,各多径的衰减系数相互独立。噪声采用α=1.5,β=0,σ=1,μ=0的标准SαS分布,为表征信号和噪声的功率情况,定义广义信噪比(Generalized Signal-to-Noise Ratio,GSNR):
仿真中,GSNR=10 dB,快拍数为512,时延τ1=10,τ2=20。
从图2可以看出,通过求取每组相干源的广义导向矢量,实现了分组估计信号的空间谱。本文算法可以估计出所有10个信号源波达方向,大大提高了阵元利用效率,可以估计的信号源数目大于阵元数目。
图2 空间谱图
仿真2
仿真比较不同广义信噪比下本文算法与文献中的FLO M-SS算法的性能。本文算法采用12阵元均匀线阵,FLOM-SS算法采用18阵元均匀线阵,阵元间距都是半波长,信号源数目、波达方向、多径衰减系数、噪声分布、快拍数目同仿真1。本文算法采用时延为τ1=10,τ2=20,FLOM-SS算法子阵阵元数目为10。当估计角度与信号真实波达方向误差小于2°时视为估计成功,实验结果由200次独立重复实验得出,如图3所示。
图3 不同广义信噪比下的算法估计性能
从图3可以看出,本文算法在阵元数目(12)比FLOM-SS算法阵元数目(18)少时,仍然具有更好的估计性能。其中,本文算法的广义信噪比门限为10 dB左右,而FLOM-SS算法的信噪比门限大于25 d B;本文算法的估计偏差和均方误差都小于FLOM-SS算法,说明本文算法估计精度更高,以较小的阵元数得到了更好的估计性能。
仿真3
仿真比较不同快拍数下本文算法与文献中的FLOM-SS算法的性能。本文算法采用12阵元均匀线阵,FLOM-SS算法采用18阵元均匀线阵,阵元间距都是半波长,信号源数目及波达方向、多径衰减系数、噪声分布同仿真1,广义信噪比为20 dB。本文算法采用时延为τ1=10,τ2=20,FLOM-SS算法子阵阵元数目为10。当估计角度与信号真实波达方向误差小于2°时视为估计成功,实验结果由200次独立重复实验得出,如图4所示。
从图4可以看出,本文算法随着快拍数增加,估计的成功概率逐渐增加,估计偏差逐渐减小,而FLOM-SS算法在快拍数大于24后,成功概率和估计偏差没有明显改善,相对而言,在快拍数大于100时,本文算法的估计性能要好于FLOM-SS算法,快拍数小于100时,本文算法估计性能略差,但这是在本文算法阵元数目小于FLOM-SS算法时的情况。下面仿真比较两者在阵元数目都为18时的估计性能与快拍数的关系,这里只仿真快拍数在16～104的情况,因为由前面的仿真可知,当快拍数大于100时,本文算法即使阵元数目小于FLOM-SS算法的阵元数目,本文算法也有更好的估计性能。从图5可以看出,当阵元数目都是18时,两种算法的快拍数分界点是40左右,即当快拍数大于40时,本文算法估计性能更好,当快拍数小于40时,FLOM-SS算法性能更好。这是因为本文算法需要估计广义导向矢量,快拍数据不足会导致较大的估计误差,进而影响后续DOA估计的精度。
图4 不同快拍数下算法的估计性能
图5 不同快拍数下算法的估计性能
本文提出的FLOM-TDD算法适用于冲击噪声背景下的相干源波达方向估计。用SαS分布来表示冲击噪声,更好地反映了实际环境中的噪声情况,利用分数低阶矩解决冲击噪声没有二阶矩的问题;采用分组处理的方法,从而可以估计大于阵元数目的信号源数,阵元利用效率高,节省了元件成本;根据典型移动通信环境中多径衰减特征进行解相干,避免了传统空间平滑算法对阵列结构的要求及阵列孔径损失。不过,该方法在低快拍数时估计性能有待改进,这也是下一步的研究方向。
参考文献:
[1]HASSAN K,GAUTIER R,DAYOUB I,et al.Multiple-Antenna-Based Blind Spectrum Sensing in the Presence of Impulsive Noise[J].IEEE Trans on Vehicular Technology,2014,63(5):2248-2257.
[2]RAHMAN M M,MAJUMDER S P.Analytical Evaluation of BER Performance of a Power Line Communication System Using Symmetrical Alpha Stable(SαS)Impulsive Noise Model[C]∥18th International Conference on Computer and Information Technology,Dhaka:IEEE,2015:260-265.
[3]黄蕾.冲击噪声环境下的快速实值算法[J].雷达科学与技术,2010,8(2):146-150.
[4]CHEN Yunfei,CHEN Jiming.NovelSαSPDF Approximations and Their Applications in Wireless Signal Detection[J].IEEE Trans on Wireless Communications,2015,14(2):1080-1091.
[5]TSAKALIDES P,NIKIAS C L.The Robust Covariation Based MUSIC(ROC-MUSIC)Algorithm for Bearing Estimation in Impulsive Noise Environments[J].IEEE Trans on Signal Processing,1996,44(7):1623-1633.
[6]LIU T H,MENDEL J M.A Subspace-Based Direction Finding Algorithm Using Fractional Lower Order Statistics[J].IEEE Trans on Signal Processing,2001,49(8):1605-1613.
[7]吴华佳,赵晓鸥,邱天爽,等.脉冲噪声环境下基于分数低阶循环相关的MUSIC算法[J].电子与信息学报,2009,31(9):2269-2273.
[8]HE J,LIU Z,WONG K T.Snapshot-Instantaneous‖·‖∞Normalization Against Heavy-Tail Noise[J].IEEE Trans on Aerospace and Electronic Systems,2008,44(3):1221-1227.
[9]刁鸣,安春莲.冲击噪声背景下的DOA估计新方法[J].北京邮电大学学报,2013,36(5):99-104.
[10]李洪升,杨日杰,何友,等.冲击噪声背景下相干信源DOA估计方法研究[J].微波学报,2008,24(3):82-86.
[11]高洪元,刁鸣.重构分数低阶协方差的子空间拟合测向算法[J].电波科学学报,2009,24(4):729-734.
[12]姚林宏,高鹰,石宇,等.冲击噪声背景下的虚拟空间平滑算法[J].吉林大学学报(信息科学),2011,29(1):47-50.
[13]LI Hongsheng,HE You,YANG Rijie,et al.Beamspace Based DOA Estimation Methods of Coherent Sources in the Presence of Impultive Noise[C]∥8th International Conference on Signal Processing,Beijing:IEEE,2006:16-20.
[14]LIU Baobao,ZHANG Junying,XU Cong.DOA Estimation for Coherent Sources in Impulsive Noise Environments[J].Journal of Networks,2014,9(12):3237-3241.
[15]DU Ruiyan,WANG Jinkuan,LIU Fulai.Space-Time Matrix Method for Joint Frequency and 2-D DOA Estimation[C]∥First International Conference on Information Science and Engineering,Nanjing:IEEE,2009:671-674.
[16]任超,吴嗣亮,王菊,等.基于空时处理的稳健自适应波束形成算法[J].电子与信息学报,2009,31(6):1381-1385.
[17]殷勤业,邹理和,NEWCOMB R W.一种高分辨率二维信号参量估计方法:波达方向矩阵法[J].通信学报,1991,12(4):1-7.
[18]景小荣,隋伟伟,周围.基于四阶累积量和时间平滑的相干信号DOA估计[J].系统工程与电子技术,2012,34(4):789-794.
DOA Estimation of Coherent Sources in the Presence of Impulsive Noise
LI Shuai,CHEN Hui
(Air Force Early Warning Academy,Wuhan430019,China)
Abstract:A method called FLOM-TDD(Fractional Lower Order Moment Time Delay Decorrelation)is proposed to estimate the DOA(direction of arrival)of coherent sources in the presence of impulsive noise.Firstly,the generalized steering vector is obtained by DOA matrix method based on two fractional lower order moment matrices with different time delays.Secondly,the DOA of each group of coherent sources is estimated according to the multipath attenuation characteristics by temporal smoothing.This method performs well in the impulsive noise environment and can estimate the coherent sources with the number more than array sensors.Computer simulations prove the effectivity of the proposed method.
Key words:DOA estimation;impulsive noise;coherent sources
中图分类号:TN911.7
文献标志码:A
文章编号:1672-2337(2017)02-0178-07
DOI:10.3969/j.issn.1672-2337.2017.02.012
收稿日期:2016-07-18;
修回日期:2016-11-09
作者简介:
李 帅男,1991年出生,山东泰安人,硕士研究生,主要研究方向为空间谱估计。
E-mail:lishuaiwuhan@sina.com
陈 辉男,1974年出生,教授、博士生导师,主要研究方向为空间谱估计、阵列信号处理。