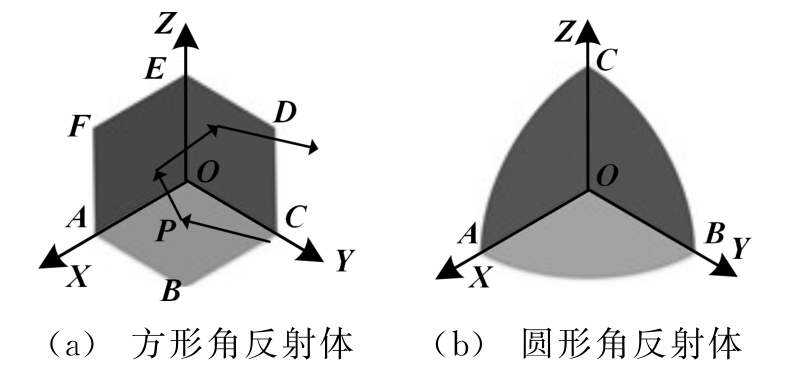
图1 方形和圆形三面角反射体
胡生亮,范学满,贺静波
(海军工程大学电子工程学院,湖北武汉430033)
摘 要:三面角反射体是一种重要的无源对抗器材,高效、准确、快速地预估其雷达散射截面积(Radar Cross Section,RCS)具有重要意义。以方形三面角反射体为例,推导了利用改进的几何光学/区域投影法(Geometrical Optics/Area Projection,GO/AP)进行RCS预估的一般流程;基于该流程对方形、圆形三面角反射体的单站RCS进行预估,将预估结果与RCS最大值的经验公式以及FEKO软件的仿真结果进行对比,表明改进的GO/AP法具有正确性、快速性和广泛适应性;针对异型三面角反射体,提出一种基于GO/AP算法利用Solid Works软件进行RCS快速预估的方法。
关键词:雷达散射截面积;改进几何光学/区域投影法;方形角反射体;圆形角反射体
雷达散射截面积(RCS)是表征军用目标的关键特性之一,是度量目标对雷达散射能力的一个重要物理量。三面角反射体在舰艇、飞机、导弹等军用目标上经常出现,是军用目标侧视方向的强散射源,特别是当各平板相互正交时,在一个很宽的观察角范围内能够呈现出很大的RCS。同时,三面角反射体也是一种重要的雷达无源对抗器材,美越战争中,越军曾使用由多个角反射体串联成的角反射体阵列模拟大桥的电磁散射特性,对清化大桥形成了有效的掩护。因此,高效、准确地分析角反射体的后向散射特性,是预估各类军用目标RCS的重要基础;同时,三面角反射体作为一类重要的强散射中心[1-2],研究其后向散射特性对光学区基于雷达成像的目标识别也有重要意义。
由于三面角反射体在实际应用中通常是电大目标或电极大目标,因此采用高频近似算法及相关专用软件进行RCS预估。文献[3-5]分别采用射线弹跳法(Shooting and Bouncing Rays,SBR)、高斯光束法(Gaussian Beams,GB)和复射线法(Complex Rays,CR),这三种方法对射线密度要求较高,计算量大;文献[6]利用物理光学法(Physical Optics,PO)进行RCS预估,需要分别计算1~3次的散射贡献,确定照亮区域的过程复杂;文献[7]多层快速多极法计算电磁散射,基于树形结构逐层聚合、逐层转移、逐层配置,效率有待进一步提高;文献[8]综合利用高阶矩量法和PO法,通过混合迭代避免了计算和存储耦合矩阵和互阻抗矩阵,但存储量、计算量有待进一步改善。专用软件方面,FEKO,XPATCH,GRECO,ADS电磁仿真软件也是RCS预估的有效手段[9-10]。上述RCS预估方法,能够给出角反射体RCS曲线结果,均没有给出RCS的完整表达式。另外,目前国内涉及雷达散射截面的相关书籍[11-12],都只给出了角反射体RCS最大值的经验公式和相关曲线,但未给出最大值公式的推导过程,更未给出不同观察角时RCS的完整表达式。笔者在文献[13]中针对三角形三面角反射体对GO/AP法进行了研究和改进,并建立起利用GO/AP法进行三角形角反射体RCS预估的一般流程,但该算法是否对各类三面角反射体都适应尚不可知。
为了验证改进的GO/AP法的有效性和广泛适应性,文章基于改进的GO/AP算法的基本思想,对方形角反射体在不同观察角时的RCS进行推导,并利用RCS最大值经验公式和FEKO仿真结果进行验证;随后借助Solid Works实现GO/AP算法,预估了圆形角反射体在随机选取的4个入射方向下的RCS,通过与经验公式和FEKO仿真结果对比进一步验证。
三角形角反射体、方形角反射体和圆形角反射体是三类较为常见的三面角反射体。笔者已在文献[13]中对三角形角反射体作了详细研究,故主要研究图1所示的方形角反射体和圆形角反射体,且以方形角反射体为例进行算法推导。

图1 方形和圆形三面角反射体
直角坐标系OXYZ由角反射体顶点O和三条交线OA,OC,OE构成。端点A,B,C,D,E,F决定角反射体的孔径大小,坐标分别为(L,0,0)、(L,L,0)、(0,L,0)、(0,L,L)、(0,0,L)、(L,0,L),其中L为垂直边长的长度。电磁波入射方向n=(l,m,n)=(cosα,cosβ,cosγ),其中,
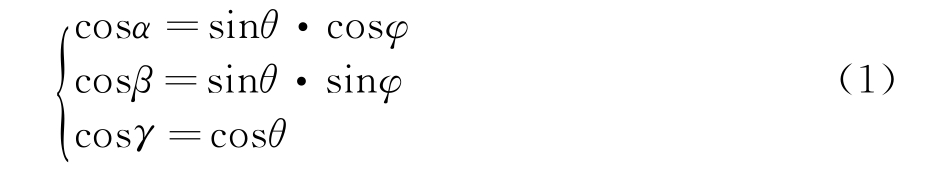
式中:θ为俯仰角,即入射方向与OZ轴夹角;φ为方位角,即入射方向在OXY平面上的投影与OX轴夹角。
GO法是波长为零的高频极限情形,这时散射现象可作为经典射线寻迹处理,遵循斯涅尔反射定律,GO法认为散射体上的“照亮点”与过该点和散射体相切的无限大平面对入射波的反射效果等效。只要目标尺寸大于波长的2~3倍,便可利用GO法分析。实际应用中,角反射体垂直边长通常为米/亚米级,对工作在厘米波段的雷达,显然符合GO法分析要求。
如图1所示,入射波在角反射体内可能发生0~3次反射,只有3次反射回波才会按原入射方向返回雷达接收机。在较大的角度范围内3次反射回波是角反射体RCS的最主要贡献,而0~2次反射回波在计算单站RCS时可忽略(边界入射方向1次或2次反射成为主要成分的情况将在2.2节中探讨)。入射波能否发生3次反射由入射点P和入射方向共同决定。对同一平面波而言,所有3次反射回波是等相位的,因此,用GO法预估RCS时,可以将角反射体等效为过顶点垂直于入射方向的某一特定大小的平面,该平面称为“等效孔径”,其面积记作Aeq。这样就可用波长l的平面波垂直入射平板时的RCS公式预估角反射体的RCS,即
因此,只需要确定“等效孔径”的形状并积分求得其面积Aeq,便可求得角反射体的RCS。Aeq可通过区域投影确定:将角反射体投影到过顶点O垂直于入射方向的平面上,所得投影称为“实孔径”;在投影面上,将“实孔径”绕顶点O旋转180°,得到“虚孔径”;实、虚孔径的重合区域即为“等效孔径”。利用Solid Works软件仿真了方位角φ=45°时,Aeq随俯仰角θ的变化情况,如图2所示(θ=45°见图4(d),此处不再重复列出),图中阴影区域为Aeq。可见Aeq为入射方向(θ和φ)的函数,随θ增大,Aeq呈现出平行四边形→六边形的变化过程。
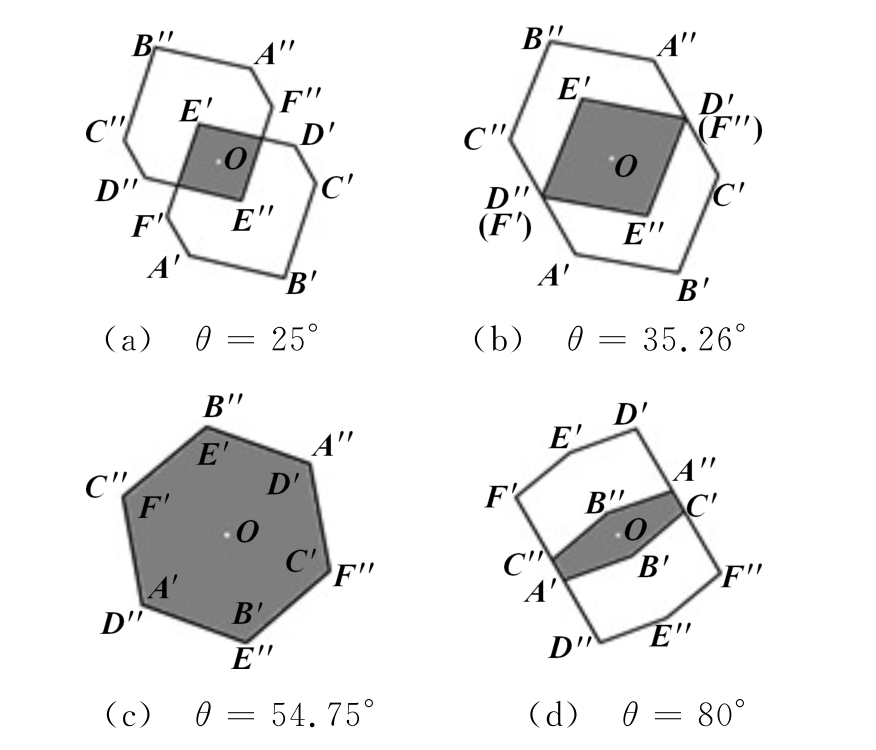
图2φ=45°时Aeq随θ的变化情况
由图2可知,只需要确定端点A,B,C,D,E,F的 投 影A′,B′,C′,D′,E′,F′,六 边 形A′B′C′D′E′F′即为“实孔径”,其关于顶点O的对称六边形A″B″C″D″E″F″即为“虚孔径”。仍以顶点O为原点,以OA′为OX′轴,入射方向的方向为OZ′轴,投影面内与OX′垂直满足右手螺旋法则的方向为OY′轴,建立坐标系OX′Y′Z′。为方便后续面积计算,将投影点A′~F′这六点的坐标从坐标系OXYZ变换到坐标系OX′Y′Z′,变换公式为
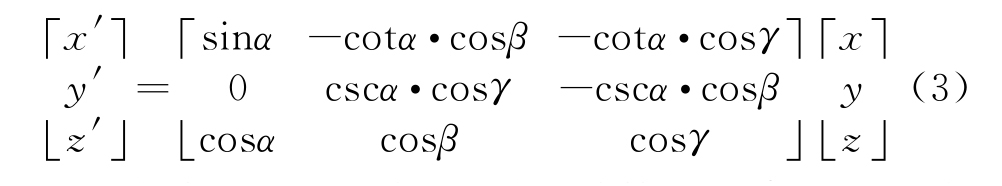
在求Aeq过程中,只需要计算x′,y′,因投影点的z′≡0。利用式(3)求得A′~F′和A″~F″在坐标系OX′Y′Z′下的坐标后,即可求得围成虚、实孔 径 的 12 条 边 界 线 (A′B′,B′C′,C′D′,D′E′,E′F′,F′A′,A″B″,B″C″,C″D″,D″E″,E″F″,F″A″)的方程:
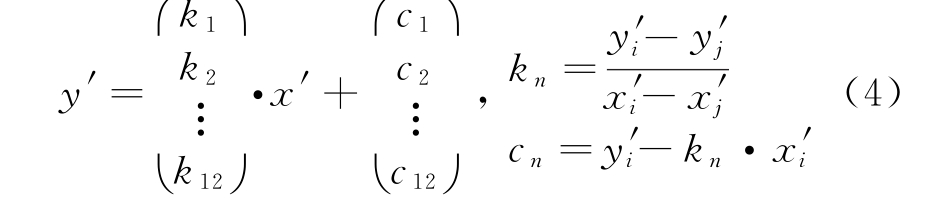
从而根据入射角度确定有效平面的顶点,这些顶点由虚、实孔径的顶点和虚、实孔径的边线交点组成。例如φ=45°,θ=25°时,等效平面由E′F′与D″E″的交点、E″F″与D′E′的交点、点E′、点E″这四个点确定。当确定顶点后利用MATLAB的polyarea函数辅助推导便可求得Aeq表达式,将Aeq代入式(2)即可求得RCS。
2.1节中推导GO/AP法的前提为3次反射是构成RCS的主要因素,试想θ=90°的这种极限情况,虚、实孔径的交集为0,显然此时传统的GO/AP法并不适应。分析发现对于方形角反射体GO/AP法约在1°≤θ≤89°∩1°≤φ≤89°入射方向角范围内与FEKO计算结果具有较好的一致性,因为GO/AP法是基于3次反射来计算有效反射面积Aeq,而在1°≤θ≤89°∩1°≤φ≤89°入射方向范围内,3次反射正是单站RCS的主要贡献,相比之下1次、2次反射分量可忽略不计;但在θ和φ接近0°和90°的边界入射方向处,几乎已经没有3次反射分量,相反1次或2次反射成为不可忽视的主要成分,此时RCS几乎在1°范围内由接近0跃升至一个上千甚至上万平方米的峰值(具体大小与角反射体的尺寸、入射波频率等因素有关),由于跃升曲线十分陡峭,用一条过峰值的直线来预估这1°范围内的RCS依然合理,因此问题的关键转化为分析求解边界入射方向时的峰值。
1)俯仰角θ=0°
此时入射波垂直照射底面(OABC),两个侧面不起作用,可以按正方形平板的RCS公式进行计算,即
式中,As为正方形面积,L为角反射体的垂直边长,λ为入射波长。
2)俯仰角θ=90°
此时入射波垂直OZ轴(OE边)入射到角反射体的两个侧面,此时底面(OABC)不起作用,三面角反射体等价于由两个正方形侧面构成的两面角反射体,其中射线传播路径图如图3所示。
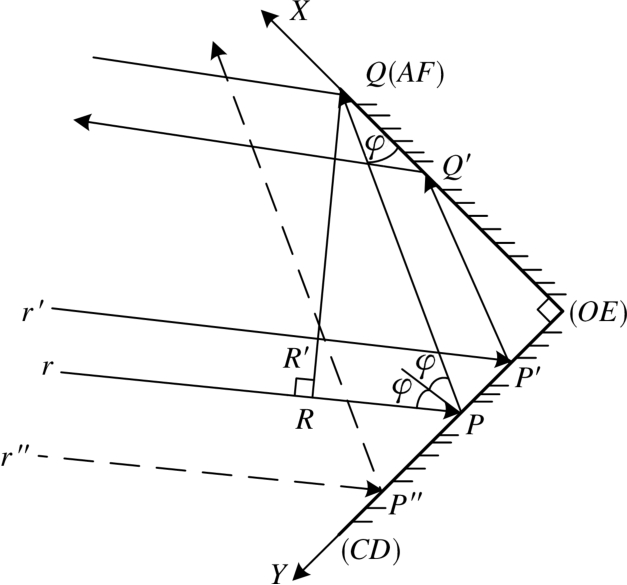
图3θ=90°时角反射体中的射线传播路径
平行线r,r′和r″代表入射平面波(与X轴夹角为φ),其中,r经P点反射后,又经位于角反射体AF边上的Q点擦边反射,按原方向返回。不难发现位于QR之间的入射波都将经历两次反射并按入射方向返回,且不难证明它们在角反射体内部的光程相等,即RPQ=R′P′Q′;该区域外的入射波如r″,只发生1次反射,将沿不同方向射出。因此,RQ即为两面角反射体的“等效孔径”的宽度,而OE为“等效孔径”的高度,因此,Aeq=RQ·OE。当0°<φ≤45°时,RQ=PQ·sin(2φ)=OQ·secφ·sin(2φ)=2L·sinφ,同理可得45°<φ<90°时,RQ=2L·cosφ。综上所述,θ=90°时RCS的计算公式为
式中,φ为入射波方位角。
3)方位角φ=0°或90°
与俯仰角θ=90°类似,φ=0°时,三面角反射体等价于以OC为公共边的两面角反射体;φ=90°时,三面角反射体等价于以OA为公共边的两面角反射体。此时,
式中,θ为入射波俯仰角。
综上所述,可分别求出θ和φ等于0°或90°时的峰值,利用过峰值的一条直线对边界入射方向的RCS进行预估,改进GO/AP算法对边界入射方向的不适应性。综合2.1和2.2两节即为完整的改进GO/AP算法。需要指出的是改进后的GO/AP算法也只在0°≤θ≤90°∩0°≤φ≤90°有效,其他方向的RCS值不存在多次反射贡献,可由平板的散射场直接给出[14]。
不失一般性,利用改进GO/AP算法对φ=45°∩0°≤θ≤90°和θ=45°∩0°≤φ≤90°两种情况进行推导,并将所得结果与方形角反射体的RCS最大值经验公式和FEKO仿真结果进行对比。
当φ=45°时,如图2所示“等效孔径”呈现出平行四边形→六边形的变化过程。可将“实孔径”顶点F′与“虚孔径”顶点D″重合作为Aeq从四边形向六边形过渡的临界条件,求得此时θ=![]() 将“等效孔径”面积Aeq取得最大值作为“等效孔径”由六边形E′F′D″E″F″D′向B″C″A′B′C′A″过渡的临界条件,求得此时
将“等效孔径”面积Aeq取得最大值作为“等效孔径”由六边形E′F′D″E″F″D′向B″C″A′B′C′A″过渡的临界条件,求得此时![]() 再考虑对边界入射方向的修正,将φ=45°时的入射方向划分为5个区域。按照改进GO/AP算法的思想推导得Aeq的最终表达式为
再考虑对边界入射方向的修正,将φ=45°时的入射方向划分为5个区域。按照改进GO/AP算法的思想推导得Aeq的最终表达式为
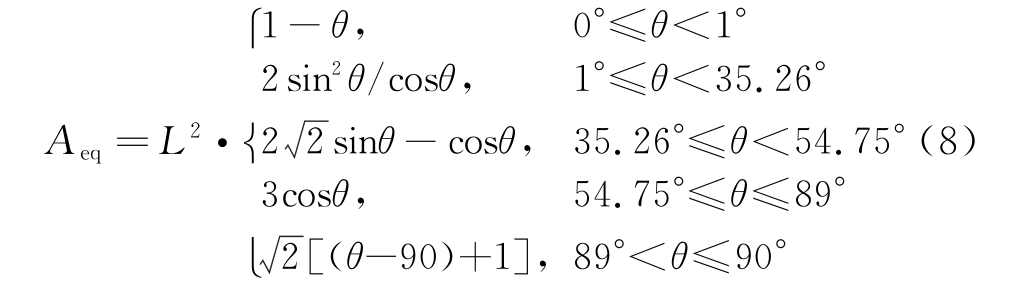
综合式(8)和式(2),即可得到方形角反射体在φ=45°∩0°≤θ≤90°条件下的RCS预估结果。
下面对所得结果进行验证。计算电磁波沿角反射体中心轴方向入射时的RCS,将θ=cos-1(1/![]() 代入式(8)和式(2),得角反射体RCS最大值的计算公式为
代入式(8)和式(2),得角反射体RCS最大值的计算公式为
式(9)与文献[12]中的RCS最大值的经验公式一致,说明GO/AP算法对RCS最大值的计算有效。同时也利用改进GO/AP算法解开了“方形角反射体RCS最大值经验公式从何得来”这一困惑。
选取FEKO 7.0电磁仿真软件中的几何光学/射线追踪(Geometrical Optics/Ray Launching,GO/RL)算法作为验证工具,仿真环境为Intel(R)Core(TM)i5-4590、4G内存,入射波频率f=10 GHz。对比FEKO和GO/AP算法的RCS预估结果,如图4所示。
由图4可知,改进后的GO/AP算法与FEKO的计算结果具有很好的一致性,在精度上能够满足RCS计算要求。
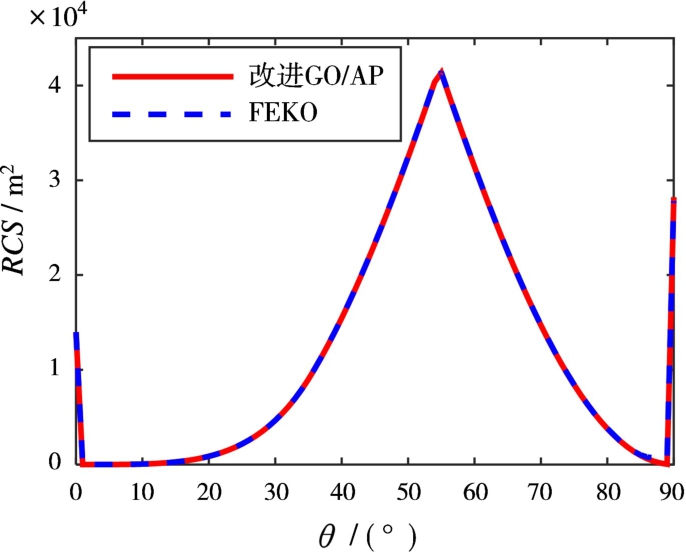
图4 改进GO/AP算法与FEKO预估结果对比(φ=45°)
当θ=45°时,根据对称性只需要分析0°≤φ≤45°即可。此时“等效孔径”随φ的变化规律如图5所示,Aeq由顶点E′,F′,E″,F″以及D″E″与A′F′的交点、D′E′与A″F″的交点共同决定,当φ=45°时,D″E″与A′F′的交点、D′E′与A″F″的交点分别为顶点D″、D′。
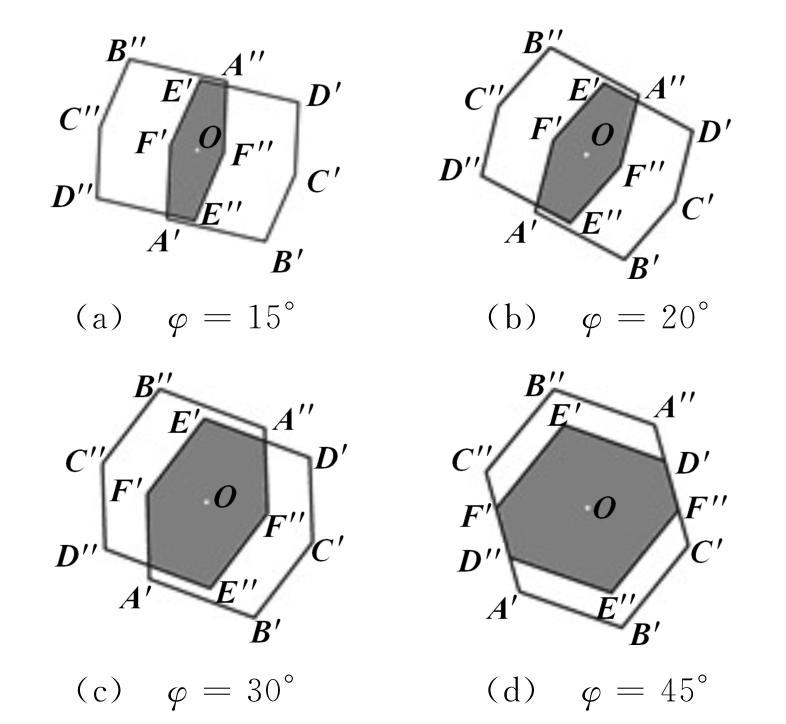
图5θ=45°时角反射体的Aeq随φ的变化情况
按照改进GO/AP算法的思路推导得俯仰角θ=45°时Aeq的表达式为
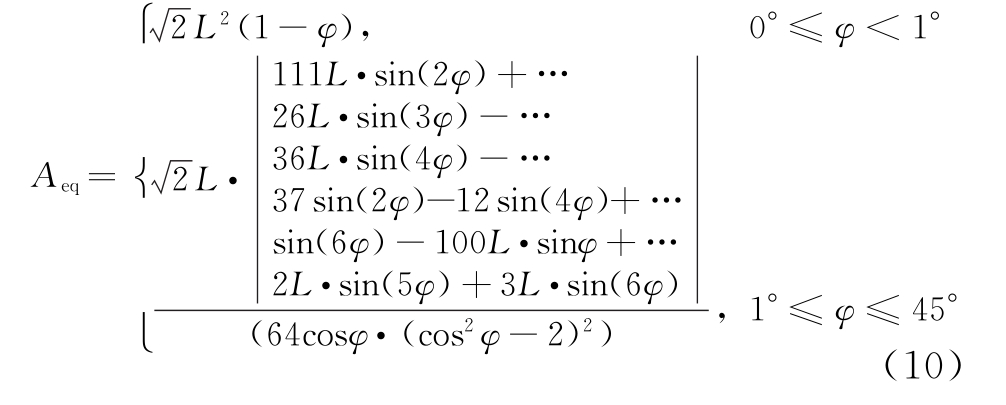
式中,|·|表示绝对值。45°<φ≤90°时Aeq的表达式只需将式(10)中的φ替换为90°-φ即可。综合式(10)和式(1)即可得到方形角反射体在θ=45°∩0°≤φ≤90°条件下的RCS预估结果。将其与FEKO仿真结果进行对比,如图6所示,可见改进后的GO/AP算法与FEKO的计算结果具有很好的一致性。
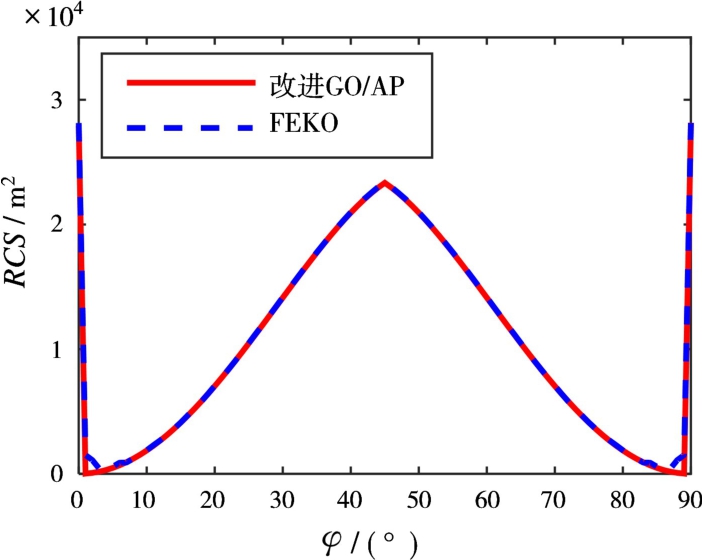
图6 改进GO/AP算法与FEKO预估结果对比(θ=45°)
利用改进GO/AP算法预估圆形角反射体的思路与第2节中方形角反射体类似,当φ=45°时,Aeq随θ的变化情况如图7所示。
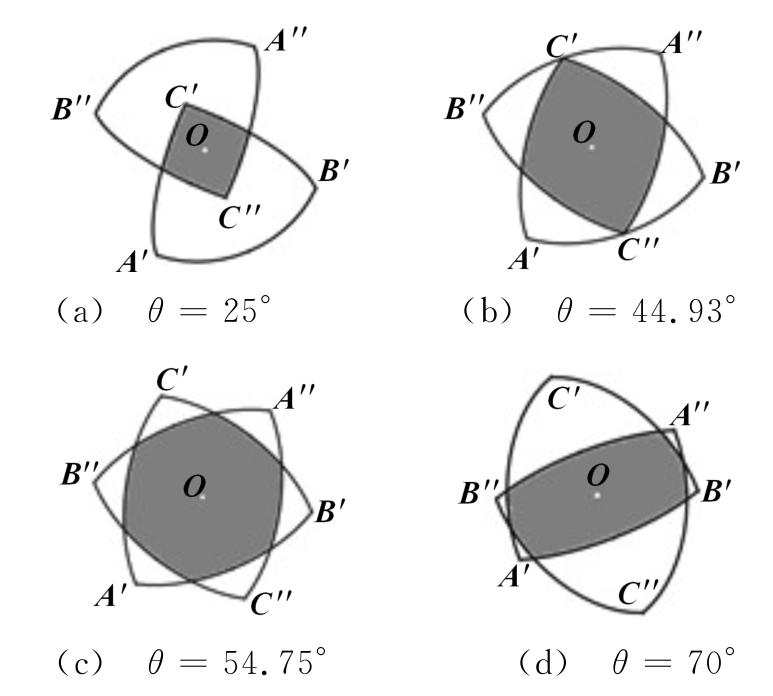
图7 圆形角反射体的Aeq随θ的变化情况
由图7可知,Aeq不再是规则的多边形,而是由投影曲线围成的不规则平面,从而导致Aeq面积求解相对复杂。此处不再推导圆形角反射体的完整公式,而是随机取4个入射方向进行验证,取角反射体的垂直边长L=1 m,入射波频率为10 GHz。方法是利用Solid Works的“测量”工具直接测得的Aeq大小,代入式(2)求得RCS,与最大值经验公式和FEKO仿真结果进行对比验证,结果如表1所示。
表1 GO/AP算法RCS预估结果验证 m2
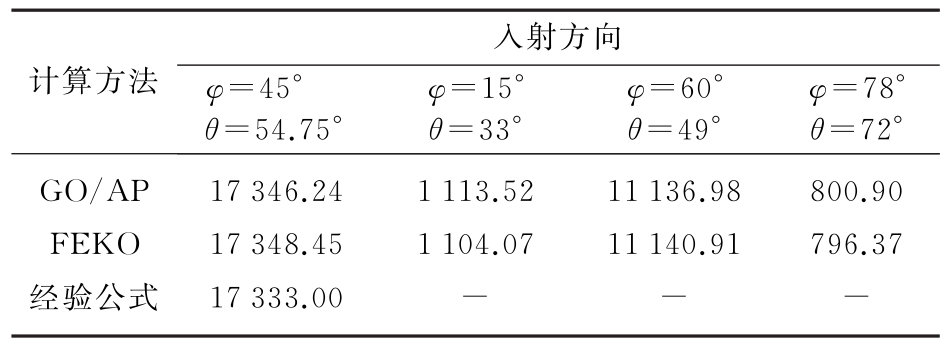
由表1可知,GO/AP算法同样适应圆形角反射体RCS预估,且对其他结构复杂的异型三面角反射体也可以通过Solid Works几何构图并测量Aeq大小的方法,方便快捷且较为准确地预估感兴趣入射方向的RCS。
以方形角反射体为例推导了利用GO/AP法进行RCS预估的基本流程,通过对边界入射方向的散射分析,利用过峰值的一条直线对GP/AP算法进行改进,提高了GO/AP算法对边界入射方向的适应性;通过将方形和圆形角反射体的改进GO/AP算法RCS预估结果与最大值经验公式以及FEKO仿真结果对比,验证了改进GO/AP算法的有效性,同时证明该算法对各类三面角反射体具有广泛适应性;最后,本文提出利用Solid-Works几何构图并测量Aeq大小直接计算某一入射方向RCS大小的方法,为结构复杂的异型三面角反射体RCS快速预估提供了新思路。
参考文献:
[1]刘勇,梁伟,王同权,等.基于OFDM信号的二维全极化信息提取[J].雷达科学与技术,2014,12(1):58-62.LIU Yong,LIANG Wei,WANG Tongquan,et al.Two-Dimensional Fully Polarimetric Information Extraction Based on OFDM Signal[J].Radar Science and Technology,2014,12(1):58-62.(in Chinese)
[2]段佳,邢孟道,张磊,等.联合属性散射中心的极化目标重构新方法[J].西安电子科技大学学报,2014,41(6):18-24.
[3]KEE C Y,WANG C F.Efficient Implementation of High-Frequency SBR-PO Method on GPU[J].IEEE Antennas and Wireless Propagation Letters,2013,12(2):941-944.
[4]MOTAMED M,RUNBORG O.A Wavefront-Based Gaussian Beam Method for Computing High Frequency Wave Propagation Problems[J].Computers&Mathematics with Applications,2015,69(9):949-963.
[5]谢军.复射线理论及其在电磁辐射和散射特性分析中的应用[D].南京:东南大学,2014.
[6]SHAN Xinjian,YIN Jingyuan,YU Danlin,et al.Analysis of Artificial Corner Reflector’s Radar Cross Section:a Physical Optics Perspective[J].Arabian Journal of Geosciences,2013,6(8):2755-2765.
[7]陈俊,曲长文,杨俭,等.基于并行MLFMA的SAR舰船目标RCS计算[J].雷达科学与技术,2013,11(4):368-374.CHEN Jun,QU Changwen,YANG Jian,et al.RCS Computation of Vessel Target in SAR Image Based on Parallel MLFMA[J].Radar Science and Technology,2013,11(4):368-374.(in Chinese)
[8]陈文锋.基于电磁场积分方程的快速混合算法的研究[D].西安:西安电子科技大学,2015.
[9]张晓玲,陈明领,廖可非,等.基于三维SAR成像的RCS近远场变换方法研究[J].电子与信息学报,2015,37(2):297-302.
[10]芦嘉,张春荣.高分配比不等分功率分配器的设计与仿真[J].雷达科学与技术,2013,11(2):223-226.LU Jia,ZHANG Chunrong.Design and Simulation of an Unequal Power Divider with High Dividing Ratio on Microstrip[J].Radar Science and Technology,2013,11(2):223-226.(in Chinese)
[11]赵国庆.雷达对抗原理[M].2版.西安:西安电子科技大学出版社,2012:207-208.
[12]庄钦文,袁乃昌,莫锦军,等.军用目标雷达散射截面预估与测量[M].北京:科学出版社,2007:16-18.
[13]范学满,胡生亮,贺静波.一种角反射体雷达散射截面积的高频预估算法[J].电波科学学报,2016,31(2):332-335,362.
[14]张浩斌,马凯学,郭陈江,等.任意多边形导体板的高频散射分析[J].电波科学学报,2003,18(1):53-56.
Evaluation of Radar Cross Section of Trihedral Corner Reflectors Based on Improved GO/AP Method
HU Shengliang,FAN Xueman,HE Jingbo
(Electronics Engineering College,Naval University of Engineering,Wuhan430033,China)
Abstract:The trihedral corner reflector is an important kind of passive countermeasure equipment,so it is quite significant to evaluate its radar cross section(RCS)efficiently and accurately.Taking the square trihedral corner reflector as an example,the general process of RCS estimation using GO/AP method is deduced,and the GO/AP method at boundary angles of incidence is improved.Then the RCS of square corner reflector and circular corner reflector are estimated by the improved GO/AP method.Comparison with FEKO simulation results as well as empirical formula of maximum value shows the validity and adaptability of the improved GO/AP method.Also,a fast RCS estimation method for all kinds of trihedral corner reflectors is proposed by combining the GO/AP method with the SolidWorks software.
Key words:radar cross section(RCS);improved GO/AP;square corner reflectors;circular corner reflectors
中图分类号:TN957.8+4;TN974
文献标志码:A
文章编号:1672-2337(2017)02-0185-06
DOI:10.3969/j.issn.1672-2337.2017.02.013
收稿日期:2016-05-16;
修回日期:2016-10-08
基金项目:国家自然科学基金(No.61401493);装备预研基金重点项目(No.9140A01010415JB11002)
作者简介:

胡生亮男,1974年出生,安徽池州人,海军工程大学电子工程学院教授、博士生导师,主要研究方向为无源对抗。

范学满男,1989年出生,山东青岛人,海军工程大学电子工程学院博士研究生,主要研究方向为精确制导与对抗。E-mail:oucfanxm@163.com

贺静波男,1979年出生,河北保定人,海军工程大学电子工程学院讲师,主要研究方向为随机微分理论及应用。