其中c为光速,f为工作频率。周辉林,刘猷文,王玉皞,陈良兵,张超群
(南昌大学信息工程学院,江西南昌330031)
摘 要:针对接收天线接收的目标散射体的散射强度取决于目标相对于收发天线的位置、目标电性能参数以及目标几何形状的问题,提出一种将不同位置的目标对齐到参考位置的目标对齐框架。该框架创新地从BP(Back Projection)算法与线性波恩近似(Born Approximation,BA)电磁场逆散射数学模型关系入手,结合修正Green函数设计,推导出目标特征受多个参数耦合约束的去相关数学模型。基于电磁场仿真数据,从定性和定量两个角度验证所提出的目标对齐框架的有效性。
关键词:穿墙雷达目标对齐;修正Green函数;后向投影成像;Born近似
穿墙雷达利用电磁波能穿透非金属材料的能力,实现墙后或封闭环境中目标的成像[1-2]。与其他室内环境感知系统相比,如计算机视觉系统、红外热成像仪、窄带微波与毫米波雷达,超宽带穿墙雷达(Ultra Wideband Through Wall Radar,UWB TWR)具有更高的带宽和时间分辨率,不受视觉条件、环境温度变化和天气变化等不利因素的影响,可提供更高的距离分辨率和定位精度图像,UWB TWR近年来在反恐、消防、城市巷战等领域获得极大的关注[3-4]。
目前基于穿墙雷达的室内环境感知与理解系统的研究热点集中在墙体反射信号的抑制、墙体参数(如介电常数和厚度)估计、成像方法、目标检测与跟踪、目标识别五大领域。Rosenbaum在文献[5]中提出一种与目标位置相关的室内静止目标识别方法,在穿墙雷达成像的基础上,提取高距离分辨率剖面(High Range Resolution Profile,HRRP)作为特征,并输入到分类器中实现室内目标分类,该方法的缺点在于待识别目标与训练是相同位置才能得到较高准确率。文献[6]提出一种基于自回归滑动平均滤波器的目标分类方法,克服了分类与目标位置相关的特性,但在处理更复杂室内场景时,该方法结果不稳定。这是由于穿墙雷达天线接收的目标散射强度取决于成像系统参数、墙体的厚度与介电常数、目标相对于收发天线的位置、目标电性能参数以及目标几何形状等几何和电性能参数[7],导致不同参数的组合可能会具有相似的目标散射信号。
针对此问题,Debes等在文献[8]中利用频域BP算法对室内静止目标成像,再利用图像分割实现感兴趣区域选择,并提取目标的统计参数和几何形状参数作特征,最后利用点扩展函数(Point Spread Function,PSF)补偿目标位置和成像系统参数变化的影响,实现了与目标位置无关的室内目标分类。该方法的不足在于未详细阐述如何利用PSF补偿目标位置和成像系统参数变化的影响。在Debes工作的基础上,Smith在文献[9]中提出了基于PSF和HRRP结合的与目标位置无关的强健室内静止目标识别方法。
以上方法的基本思路是利用PSF将不同位置的目标对齐到参考位置,从而解耦目标的散射强度与目标相对于收发天线位置的影响。这些方法存在不足之处,如只考虑到步进调频体制雷达的PSF解析表达式,不适用于脉冲体制穿墙雷达,且在表达式中没有考虑墙体可能对传播路径变化导致时延变化和对目标反射信号衰减效应的影响。本文提出一种更适用于表征室内电波传播机理的修正Green函数方法,创新地从BP与线性波恩近似(Born Approximation,BA)电磁场逆散射关系模型入手,推导穿墙雷达目标对齐框架。
图1为二维穿墙雷达成像模型示意图,雷达探测天线采用收发一体的陈列天线结构,天线沿x轴正方向以相同的间隔依次排列,天线的位置坐标为Rn=(xn,yn),n=1,2,…,N,N为阵列天线数,目标t位置矢量坐标为xt=(xt,yt),天线阵列距离前墙前表面为dy,O为坐标原点,x轴与y轴的正方向如图所示。区域Ⅰ和Ⅲ为自由空间,波数k1=2πf/c,区域Ⅱ 为介电常数εw,厚度为dw的墙体,波数其中c为光速,f为工作频率。
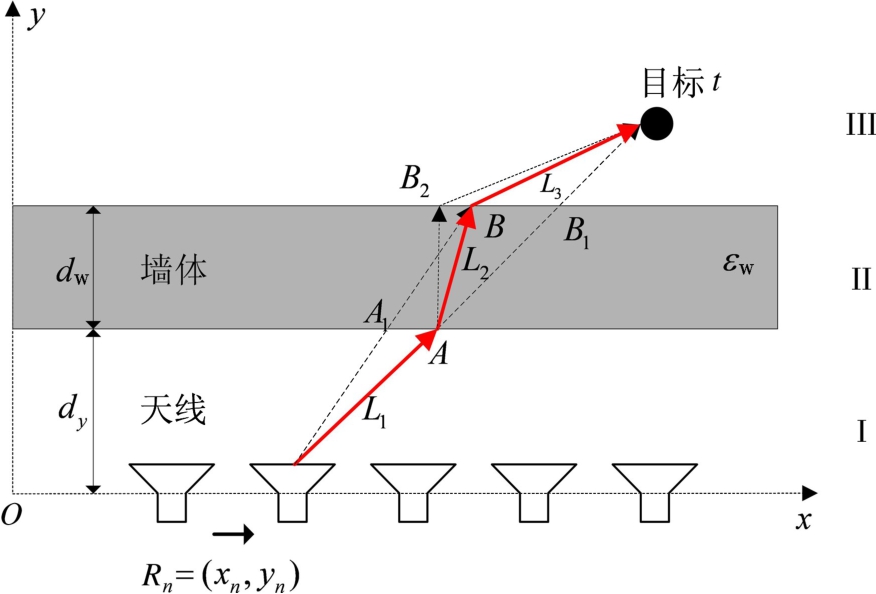
图1 二维穿墙雷达成像模型示意图
由于墙体的存在,使得发射天线发射的电磁波在到达目标之前,需要经过空气-墙体-空气三层介质,传统以Green函数表征穿墙雷达电波传播机理[10],如式(1)所示:
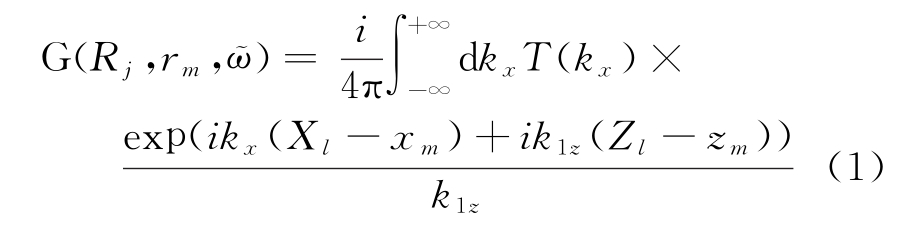
式中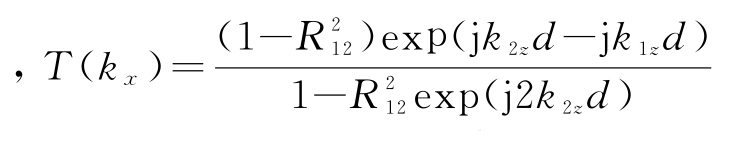
为三层介质的传输系数
为空气-墙体界面的反射系数
为电磁波在均匀墙体内部的波数
分别为波数k1,k2在Z方向的分量。
令Φ(kx)=kx(Xl-xm)+ik1z(Zl-zm),其计算过程中只考虑了墙体不存在情况下的视距传播路径,而没有考虑由于墙体的存在,导致的电磁波传播路径的变化,真实的传播路径如图1中箭头标注的Rn→A→B→t。因此,传统的基于Green函数的室内电波传播模型存在一定的误差。本文提出一种考虑非视距传播路径的修正Green函数计算模型:
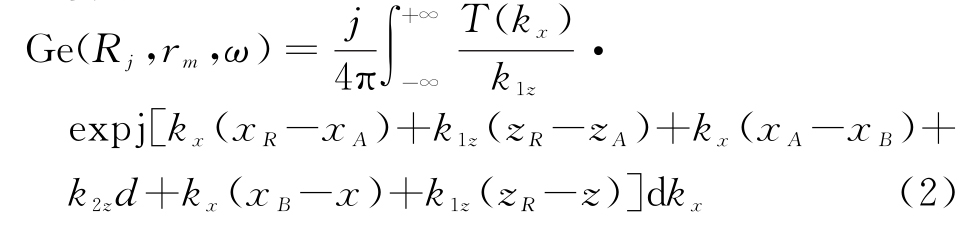
令
同时令相位函数Φ(kx)=kx(xR-x)+k1z(zR-z)+(k2z-k1z)d,则修正Green函数整理成
利用驻相法
对相位函数求一阶导数:
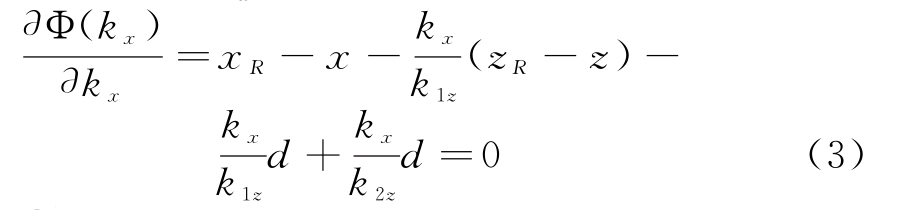
化简可得
由
其中θ为电磁波的入射角度,根据穿墙雷达的几何关系,整理可得
xA-xR+x-xB,将其代入式(4)中,可得驻相点为
对相位函数求二阶导数得到
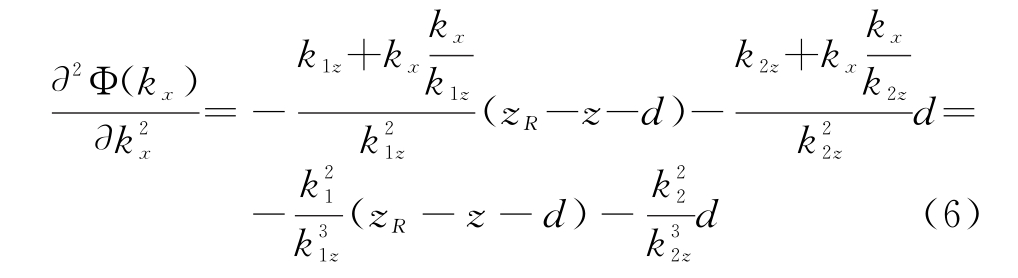
对相位函数Φ(kx)作kx=kx0处泰勒级数展开,并忽略其高阶项,则
由于函数F(kx)只在驻相点附近有值,其他位置的值为零,则修正后的穿墙雷达Green函数为
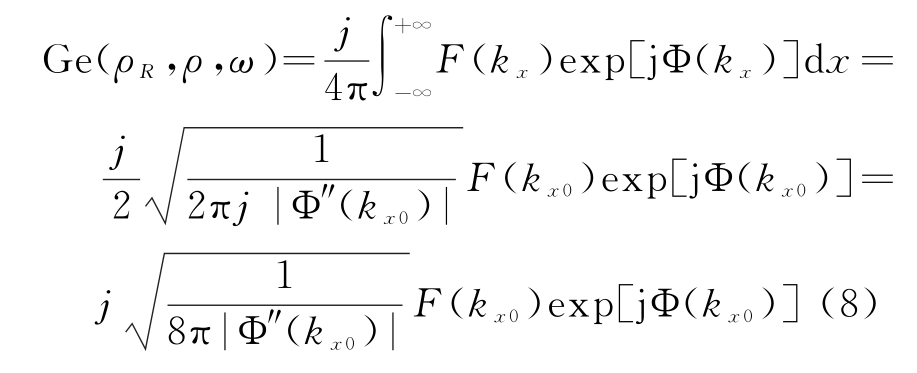
通过分析上述公式可知,修正Green函数数值计算的关键在于计算图1中的折射点A和B。而在考虑墙体影响的BP成像算法中也需要计算这两个折射点。
如图1所示,假设墙体前、后表面折射点分别为A=(xA,dy),B=(xB,yB),电磁波通过Rn→A→B→t这条真实的非视距传播路径所引入的双倍程时延为
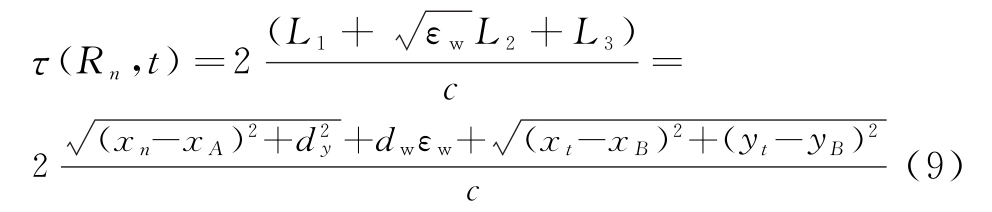
BP成像公式[11-12]为
式中,IBP(rm)为在网格rm位置上BP成像后的图像的像素值,Escat(Rj,tjm)为接收天线Rj接收到的时域散射场,j=1,…,N,其中N为接收源的数量,tjm=djm/c,c为自由空间中的光速(实验背景为自由空间),djm为在成像区域中第j个接收源与第m个网格之间的距离,那么tjm也即为在自由空间中从第j个接收源到第m个网格的电磁波所传播的时间。
本文利用快速近似计算方法与snell定理,计算L1+L2+L3的大小。如图1所示,假设墙体前、后表面折射点分别为A=(xA,dy),B=(xB,dy+dw),如果墙体相对介电常数无穷大,则电磁波从点A沿A→B2→t路径传播,此时的折射点为B2=(xA,dy+dw);如果墙体相对介电常数与自由空间的相同,则电磁波沿A→B1→t,其中B1=(xB1,dy+dw)为传播路径与墙体后表面的交点。而实际墙体的介电常数介于空气与无穷大之间,Rn→A→B→t为实际传播路径;因此结合三角形相似定律,对于Rn→A→B传播路径可以得到
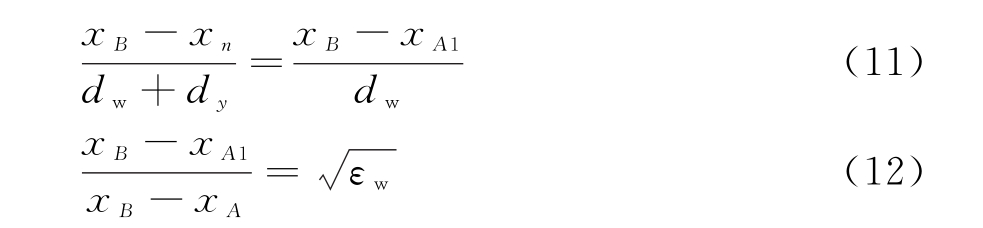
类似地,对于A→B→t传播路径有
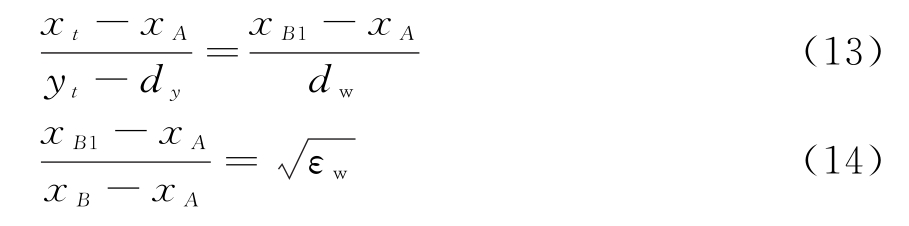
求解式(11)～(14)即可得到折射点A和B,进而得到L1+L2+L3(即图1中箭头标注的实线)。于是,可以得到传播时延τnt如下式:
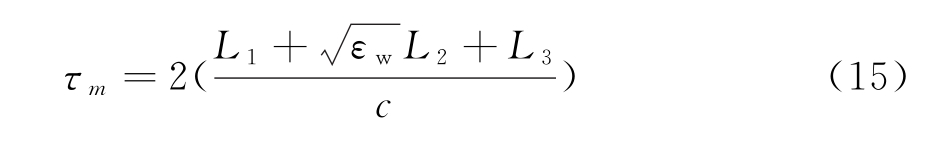
利用Green函数提供的关于雷达工作频带范围和目标与天线相对位置信息,补偿系统参数和相对位置敏感因素对系统的影响,可以实现目标位置的对齐过程。具体为结合Green函数和二维反卷积推导出目标对比度函数空间分布解析表达式,进而推导出目标对齐后的表达式,得到目标对齐后的图像。
由于Born近似[13-14],散射场Escat又可以表现为线性形式:
式中,G(Rj,r,ῶ)为背景媒介上的Green函数值,Rj为第j个接收天线,r为成像区域中的网格,
为由激励源Rt得到的入射场,本文选择脉冲超宽带穿墙雷达,
为雷达中心角频率,
为激励源的幅度
为发射信号的傅里叶变换。可以将成像区域D分成M个网格,任意一个网格rm的频域点反射系数为
其中
于是,目标对比度函数就可以表示为
式中,δ(r-rm)代表狄克拉函数。根据式(16)、式
可以表示为
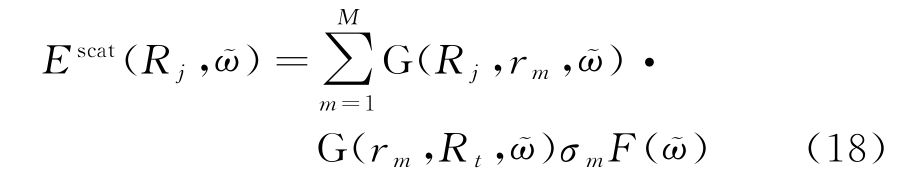
本文假设天线是收发一体的,由于对偶关系,那么Green函数
)以及
在数值上是相等的。结合式(5)～(8)和式(11)～(14)可数值计算修正后的Green函数。
将rm(xm,ym)表示成网格的位置,Rj(Xj,Yj)则表示第j个接收天线的位置。那么
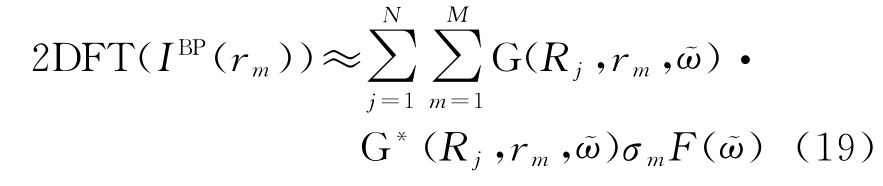
式中,2DFT[·]表示二维傅里叶变换,于是可以得到
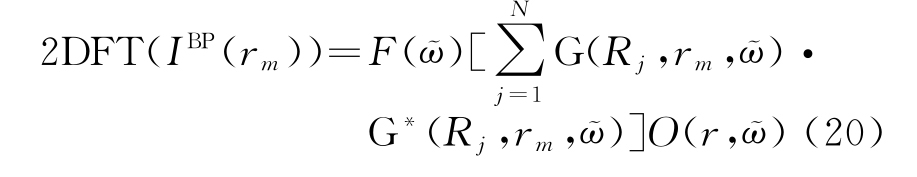
式中,位置rm上的目标的BP图像和Green函数分别为IBP(rm)和
对式(20)进行变换,可以推出目标对比度函数:
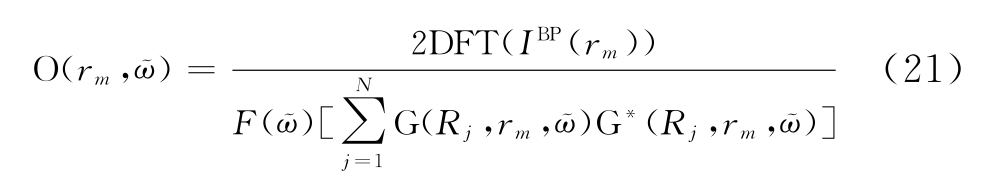
在同样的场景下目标移动到参考位置
此时新的Green函数为
根据式(21)可以得到移动到参考位置目标的BP图像的二维傅里叶变换:
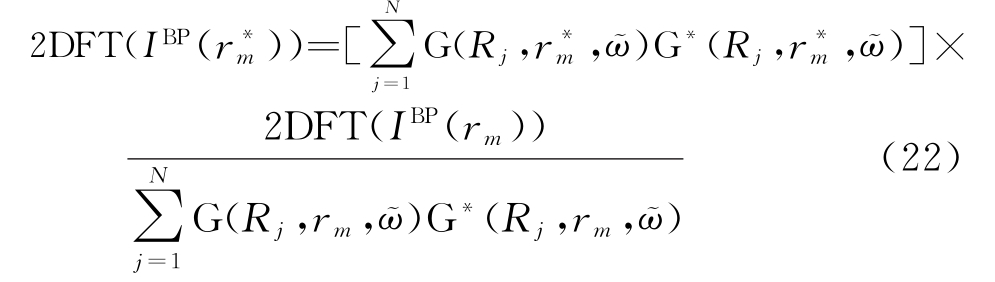
最后对式(22)进行傅里叶逆变换,可得目标在新位置的BP成像IBP(r∗m)。
本文运用gpr Max 2.0软件,仿真出了不同参数场景的穿墙雷达模型。再对成像进行BP成像处理。实验设置3层的媒介结构“自-空间-墙体 自由空间”,如图2所示,设置N根收发一体的雷达天线阵列激励源TR1,…,TRN,收发一体天线位置坐标为(X1,0)到(XN,0),步进(ΔX,0)。设置雷达发射信号为中心频率f=900 M Hz的Ricker波形,天线阵列与墙体距离l=0.15 m,墙体的厚度d=0.05 m,介电常数εr=6的均匀墙体,背景为自由空间。仿真场景中墙体的另一侧设置4个大小、形状以及介电常数等参数都完全相同的圆形目标,分别为目标1～目标4,它们的位置坐标分别为(2.0 m,3.0 m),(2.0 m,2.0 m),(2.0 m,1.0 m)和(1.0 m,1.0 m);设定目标2所在位置(x2,z2)=(2.0 m,2.0 m)为参考位置;目标的介电常数均为εt=25;目标半径均为r=0.06 m。
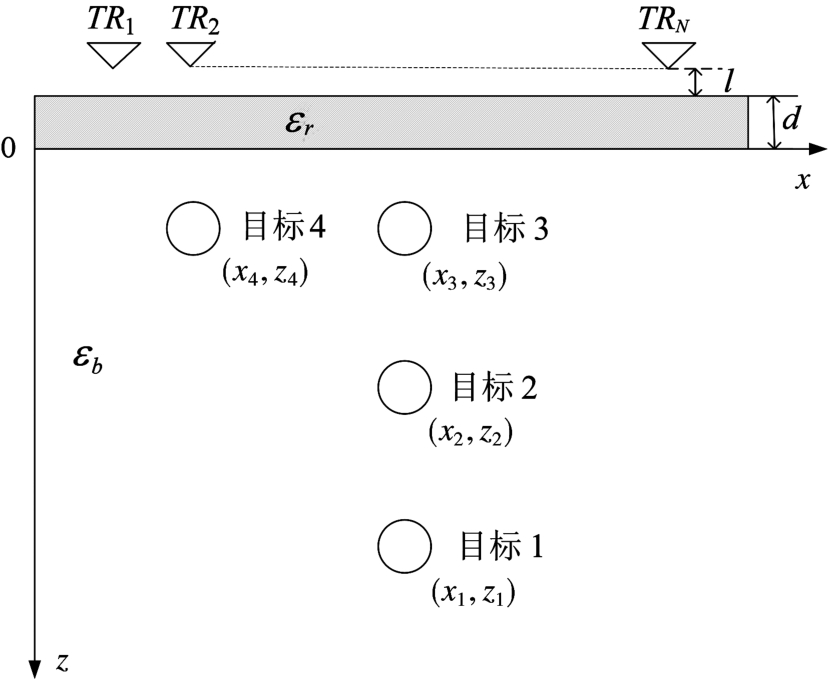
图2 场景图设置
为了验证本文所提出的目标对齐方法在距离向的对齐效果,首先在目标1和目标2位置放置相同大小、形状和电性能参数的目标,然后利用gpr Max仿真软件仿真穿墙雷达数据,并分别进行BP成像,其结果分别如图3(a)和图3(b)所示,然后利用本文所提出的目标对齐方法,将目标1对齐到目标2所在的参考位置,结果如图3(c)所示。
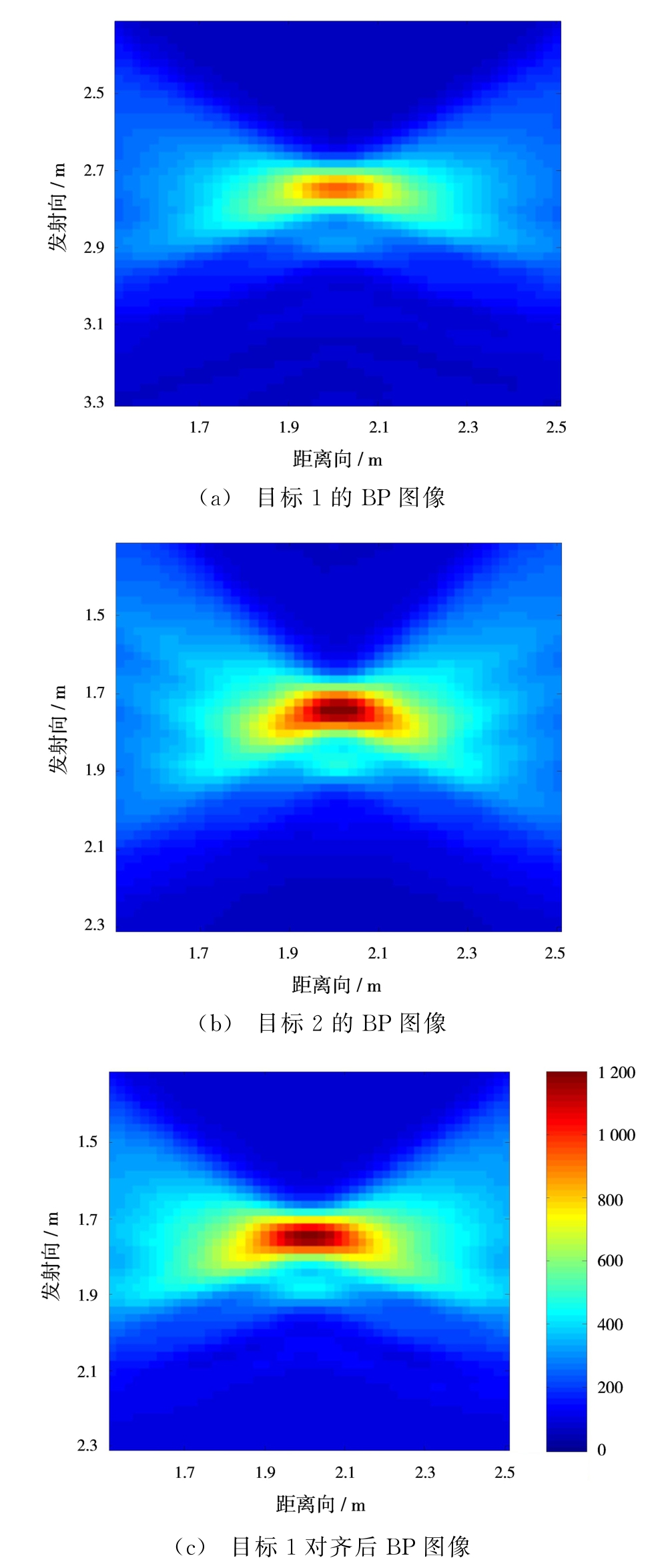
图3 目标1对齐前后成像效果
从图3(a)和图3(b)可以看出,目标1和目标2的BP成像由于目标与天线相对位置的不同而差别较大,但是通过对齐后,解耦了目标特征受目标与天线相对位置信息的影响,图3(b)和图3(c)非常相近,也即目标1的BP成像对齐到参考位置后与目标2的BP成像很相近,从定性的角度验证了本文所提出的目标对齐方法的有效性。
从距离向和方位向的HRRP定量验证本文所提出方法的有效性,图4(a)和图4(b)分别是穿过BP图像强度峰值的距离向和方位向。由图4可以看出,目标1的BP图像强度峰值的距离向和方位向经过对齐后与目标2很接近。在距离向上,对齐在参考位置的合成目标与真实目标2的最小均方误差(NMSE)为0.022;在方位向上,对齐在参考位置的合成目标与真实目标2的最小均方误差为0.069。
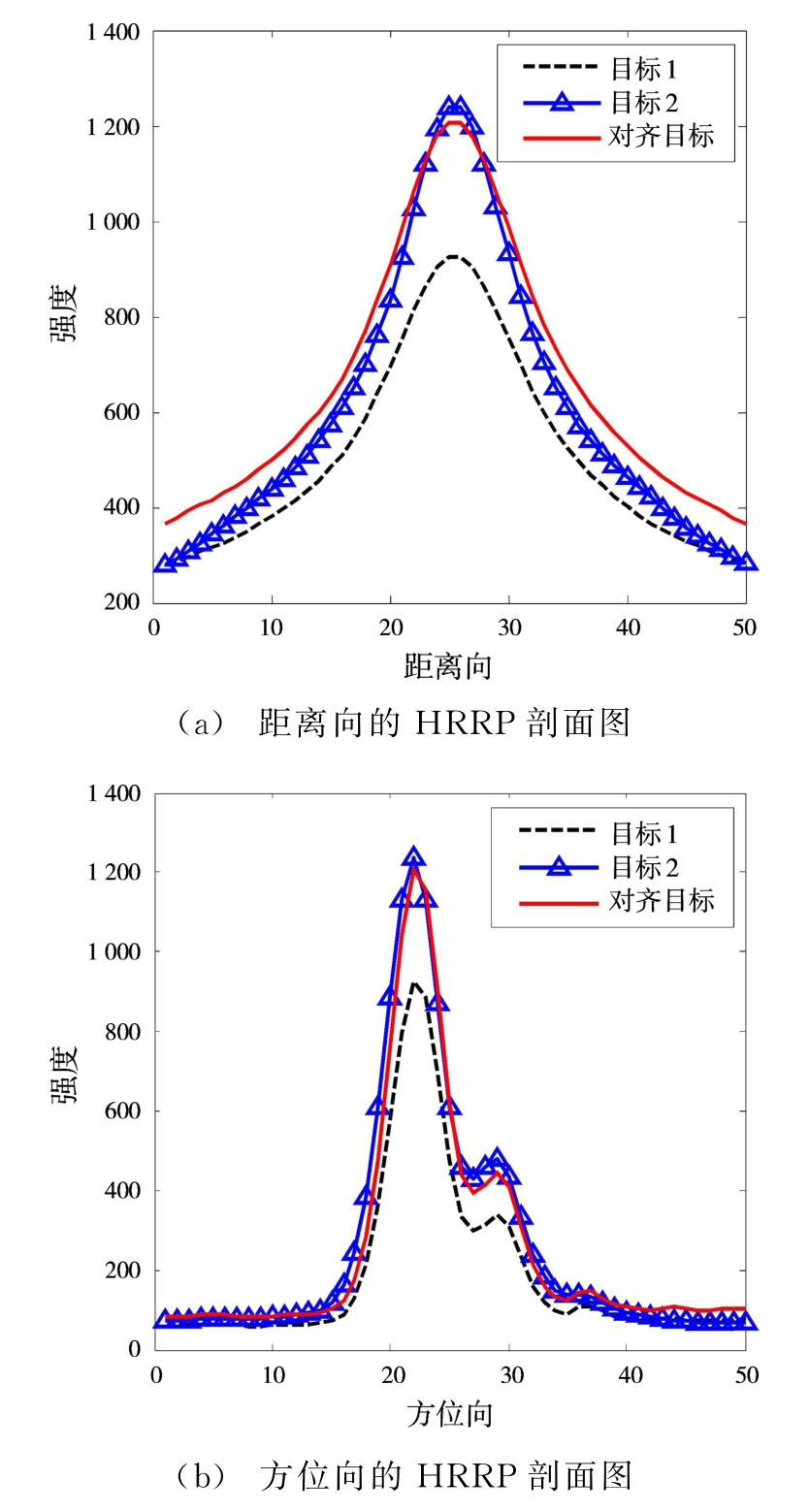
图4 距离向和方位向的HRRP剖面图
为验证本文所提出方法将任意位置目标对齐到参考位置的有效性,将位于(1.0 m,1.0 m)的目标4对齐到目标2的位置(2.0 m,2.0 m)。图5(a)和图5(b)分别为目标4和目标2的BP图像,图5(c)为将目标4对齐到目标2后的BP成像。目标4和目标2的BP图像由于目标与天线相对位置的不同而差别较大,但是通过对齐后,解耦了目标特征受目标与天线相对位置信息的影响,因而图5(b)和图5(c)非常相近,也即目标4的BP成像对齐到参考位置后与原本就在参考位置的目标2的BP成像很相近,从定性的角度验证了本文所提出的目标对齐方法的有效性。
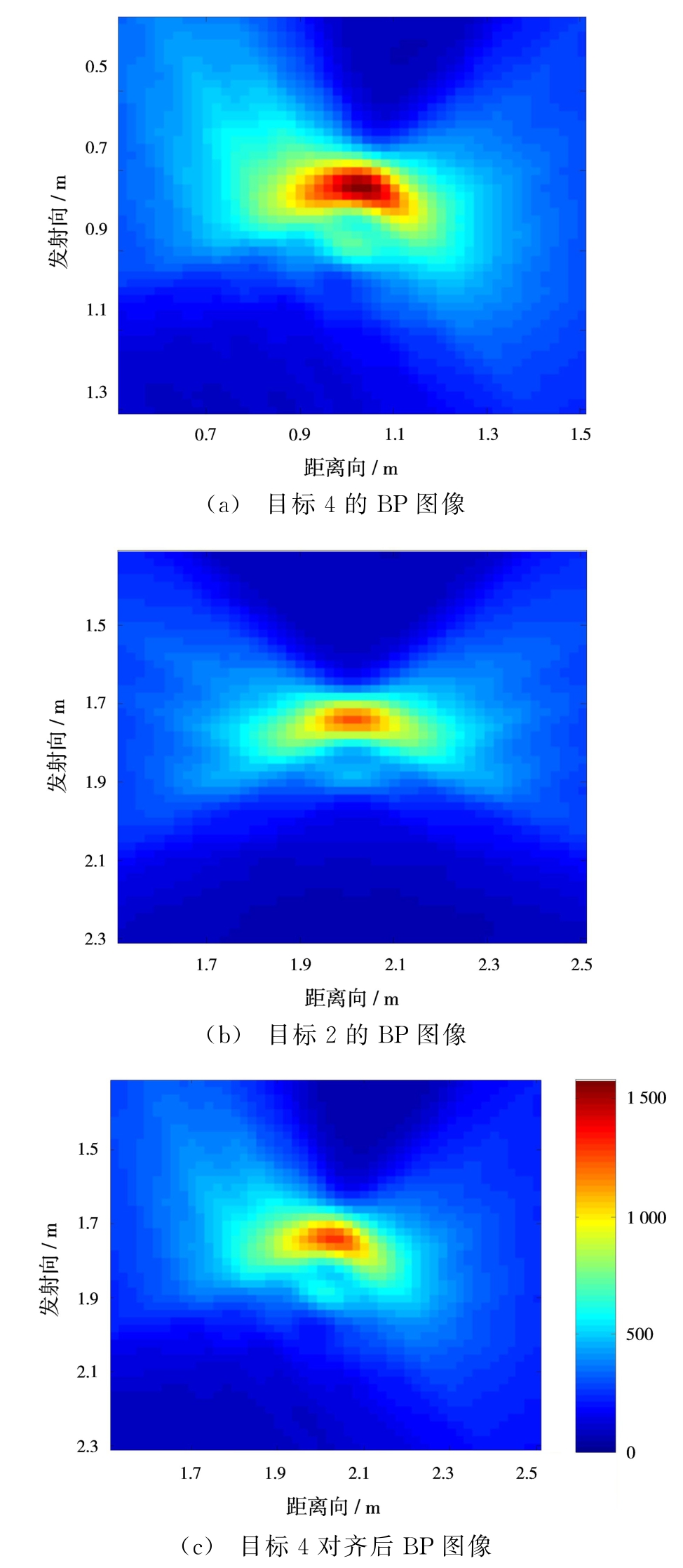
图5 目标4对齐前后成像效果
从距离向和方位向的HRRP定量验证本文所提出方法的有效性,图6(a)和图6(b)分别是穿过BP图像强度峰值的距离向和方位向。由图6可以看出,目标4的BP图像强度峰值的距离向和方位向经过对齐后与目标2很接近。在距离向上,对齐在参考位置的合成目标与真实目标2的最小均方误差为0.009;在方位向上,对齐在参考位置的合成目标与真实目标2的最小均方误差为0.698。
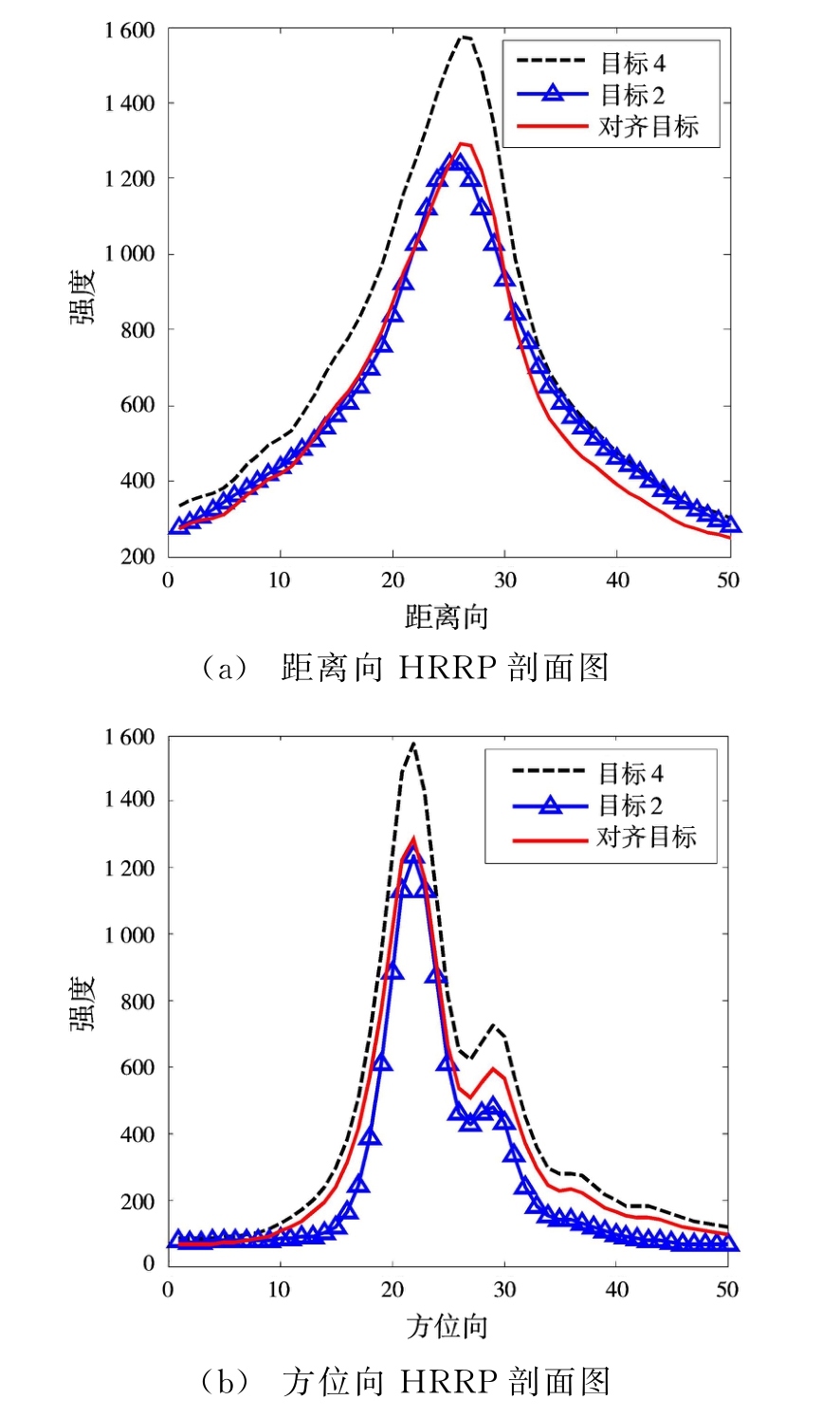
图6 距离向和方位向的HRRP剖面图
本文在考虑墙体对电磁波传播影响的基础上,结合驻相法和鞍点法,推导出适用于表征穿墙雷达电波传播模型的修正Green函数解析表达式。在此基础上,从BP与线性波恩近似(BA)电磁场逆散射关系模型的新角度入手,推导出目标特征受多个参数耦合约束的去相关数学模型,即穿墙雷达目标对齐框架。基于电磁场仿真数据,从定性和定量两个角度验证所提出的目标对齐框架的有效性,为后续与位置无关的强健室内目标分类方法研究打下坚实基础。
参考文献:
[1]SENG C H,BOUZERDOUM A,AMIN M G,et al.Two-Stage Fuzzy Fusion with Applications to Throughthe-Wall Radar Imaging[J].IEEE Geoscience and Remote Sensing Letters,2013,10(4):687-691.
[2]王宏,NARAYANAN R M,周正欧,等.基于改进EEMD的穿墙雷达动目标微多普勒特性分析[J].电子与信息学报,2010,32(6):1355-1360.
[3]谭覃燕,宋耀良.超宽带穿墙SAR对目标运动参数的估计和位置矫正[J].仪器仪表学报,2011,32(2):395-400.
[4]ZHANG Yu,XIA Tian.In-Wall Clutter Suppression Based on Low-Rank and Sparse Representation for Through-the-Wall Radar[J].IEEE Geoscience and Remote Sensing Letters,2016,13(5):671-675.
[5]ROSENBAUM Z,MOBASSERI B G.Interpretation of Through-the-Wall Radar Imagery by Probabilistic Volume Model Building[C]∥Proceedings of SPIE 6943,Orlando,Florida:SPIE,2008:1-10.
[6]MOBASSERI B G,SMITH G E,ESTEPHAN I.A Target Alignment Algorithm for Through-the-Wall Radar Imagery Classification[C]∥IEEE Radar Conference,Washington DC:IEEE,2010:756-761.
[7]KUO Y H,KIANG J F.An Iterative Approach to Improve Images of Multiple Targets and Targets with Layered or Continuous Profile[J].International Journal of Microwave Science and Technology,2015,2015(6):1-13.
[8]DEBES C,HAHN J,ZOUBIR A M,et al.Target Discrimination and Classification in Through-the-Wall Radar Imaging[J].IEEE Trans on Signal Processing,2011,59(10):4664-4676.
[9]SMITH G E,MOBASSERI B G.Robust Throughthe-Wall Radar Image Classification Using a Target-Model Alignment Procedure[J].IEEE Trans on Image Processing,2012,21(2):754-767.
[10]FALLAHPOUR M,ZOUGHI R.Fast 3-D Qualitative Method for Through-Wall Imaging and Structural Health Monitoring[J].IEEE Geoscience and Remote Sensing Letters,2015,12(12):2463-2467.
[11]程生见.超宽带探地雷达快速BP成像算法研究[D].桂林:桂林电子科技大学,2015.
[12]CHO Y S,JUNG H K,CHEON C,et al.Adaptive Back-Projection Algorithm Based on Climb Method for Microwave Imaging[J].IEEE Trans on Magnetics,2016,52(3):1-4.
[13]ANSELMI N,SALUCCI M,OLIVERI G,et al.Wavelet-Based Compressive Imaging of Sparse Targets[J].IEEE Trans on Antennas and Propagation,2015,63(11):4889-4900.
[14]GENNARELLI G,CATAPANO I,SOLDOVIERI F,et al.On the Achievable Imaging Performance in Full 3-D Linear Inverse Scattering[J].IEEE Trans on Antennas and Propagation,2015,63(3):1150-1155.
Through-Wall Radar Target Alignment Based on Modified Green Function
ZHOU Huilin,LIU Youwen,WANG Yuhao,CHEN Liangbing,ZHANG Chaoqun
(School of Information Engineering,Nanchang University,Nanchang330031,China)
Abstract:Usually in through-wall radar target imaging,the scattering intensity of target scatterers depends on multiple parameters,such as the relative position between targets and transmitting/receiving antennas,the electrical performance parameters and the geometry of targets.Aiming at such problem,this paper proposes a target alignment framework that aligns the targets at different positions to the reference position.Under the framework,starting from the relationship between BP(Back Projection)algorithm and linear Born approximation(BA)electromagnetic inverse scattering mathematical model and combining the modified Green function,a decorrelative mathematical model is derived that the target feature is constrained by the coupling of multiple parameters.Electromagnetic simulation data is used to validate the proposed target alignment framework in both qualitative and quantitative ways.
Key words:through-wall radar target alignment;modified Green function;back projection(BP)imaging;Born approximation
中图分类号:TN958.4
文献标志码:A
文章编号:1672-2337(2017)02-0208-07
DOI:10.3969/j.issn.1672-2337.2017.02.017
收稿日期:2016-09-04;
修回日期:2016-11-04
基金项目:国家自然科学基金(No.61561034,61261010,41505015);江西省自然科学基金(No.2015BAB207001);江西省科技支撑计划(No.20151BBE50090)
作者简介:
周辉林男,1979年出生,江西人,南昌大学电子信息工程系教授,主要研究方向为超宽带雷达成像、雷达信号处理、电磁逆散射成像。
E-mail:zhouhuilin@ncu.edu.cn
刘猷文男,1994年出生,江西人,在读硕士研究生,主要研究方向为超宽带雷达成像、电磁逆散射成像。
王玉皞男,1977年出生,湖北人,南昌大学电子信息工程系教授、博士生导师,主要研究方向为电波传播。
陈良兵男,1982年出生,湖北人,南昌大学电子信息工程系副教授,主要研究方向为微波遥感。
张超群男,1986年出生,江西人,博士,南昌大学电子信息工程系讲师,主要研究方向为天线理论与电波传播、电磁场理论。