0 引言
进入21世纪以来,航空技术发展迅速,空中目标的机动性越来越强,对机动目标的跟踪方法研究也成为了当前目标跟踪研究方向的一大热门。对雷达而言,目标机动具有不确定性和无先验性的特点[1],对于传统的单模型滤波器,一旦目标因为机动超出模型的跟踪范围,机动跟踪滤波会产生较大的误差[2]。交互式多模型(Interacting Multiple Model,IMM)算法[3]包含了多个不同模型的滤波器,利用Markov矩阵将滤波器之间的切换关系联系起来,取得了较好的效果。
实际应用中,IMM算法性能受到诸多因素影响。
一方面,Markov概率转移矩阵决定着IMM算法的交互程度,但是标准的IMM算法中,Markov概率转移矩阵是根据经验事先给出的固定值。针对这个问题,文献[4]提出了一种自适应的AMP-IMM算法,通过两模型误差压缩率的比值来实现Markov概率转移矩阵的自适应,但是这种算法仅仅在两模型的时候有效,难以满足实际多模型的需求;文献[5]针对文献[4]提出算法的短板,定义了一种新的误差压缩率,把文献[4]提出的算法推广到了3个及3个以上的模型中,但是算法实际应用中的稳定性不足;文献[6]提出了一种简单有效的利用量测数据在线估计模型转移概率的方法,但是该算法无法精准调整任意两种模型的切换概率,实际效果不够理想。
另一方面,滤波器模型的选择也影响着IMM算法的滤波结果。通常而言,在雷达跟踪系统中,状态方程和量测方程不可能在同一坐标系下都是线性方程[7],需要用到非线性的滤波算法。目前应用比较成熟的非线性滤波算法是无迹卡尔曼滤波(Unscented Kalman Filter,UKF)算法[8],在处理三维及三维以下的非线性系统时有较好的效果。在此基础上,Ienkaran提出了容积卡尔曼滤波(Cubature Kalman Filter,CKF)算法[9],相对于UKF算法,在三维以上的高维系统中,滤波效果更好,并且实现过程更简单,运算速度也更快,非常适合解决高维系统的滤波问题。
本文结合IMM算法和CKF算法提出了一种利用后验信息自适应修正Markov概率转移矩阵的IMM-CKF算法。
1 CKF算法
首先建立目标的状态方程和观测方程:
式中:Xk∈Rnx代表系统的状态量,Zk代表系统的观测量,f(·)和h(·)代表非线性函数;wk-1和vk分别代表过程噪声和观测噪声,它们都是零均值的高斯噪声,方差分别为Qk-1和Rk。
CKF算法的步骤如下:
第一步:状态预测
1)根据k时刻的状态估计值Xk和Pk生成容积点ξi,k:
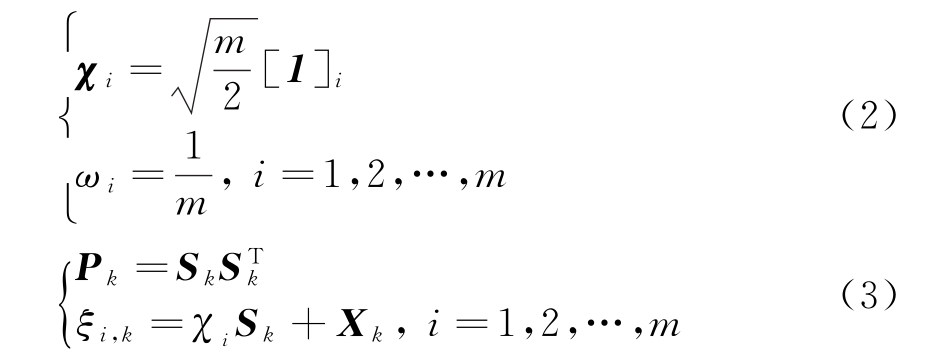
式中,m=2nx代表容积点个数,nx代表状态量的维数,其中[1]=[In×n,-In×n],I表示n维单位矩阵,[1]i为[1]的第i列向量。
2)计算容积点的传播
3)计算状态量的一步预测Xk+1|k和状态协方差的一步预测Pk+1|k
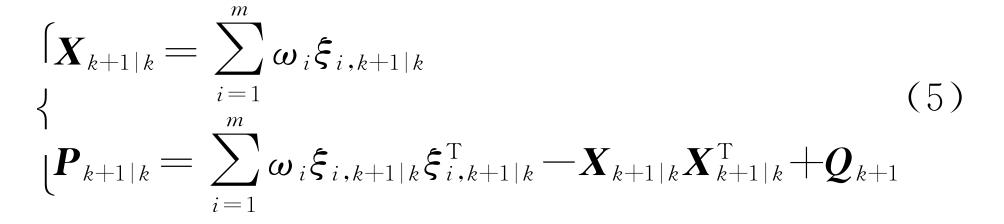
第二步:量测更新
1)根据一步预测值生成容积点ξi,k+1|k
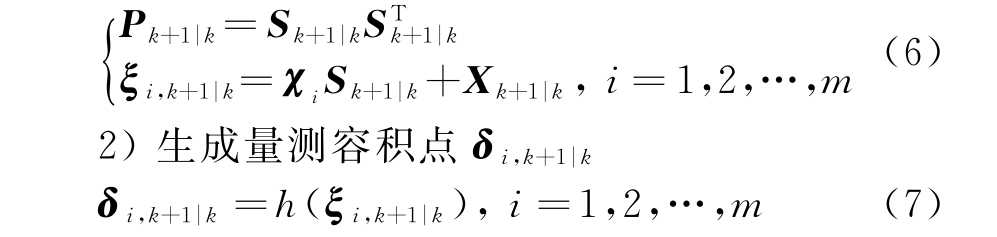
3)生成量测的一步预测和协方差的一步预测
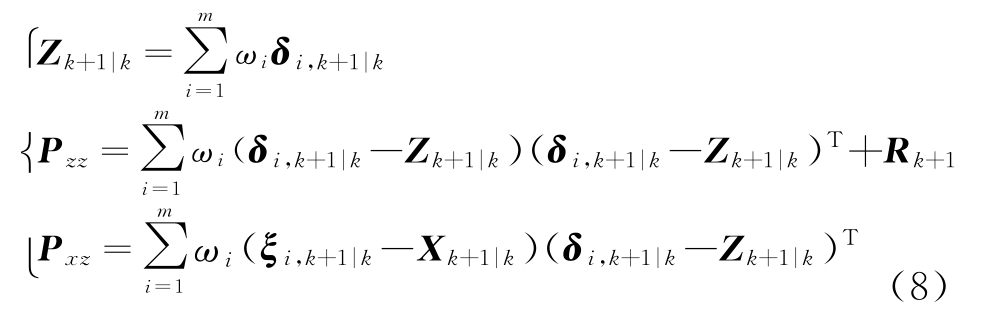
式中,Rk+1表示量测的噪声协方差,Pzz代表系统观测量的协方差,Pxz代表系统状态量和观测量的互协方差。
4)计算滤波增益
第三步:状态更新
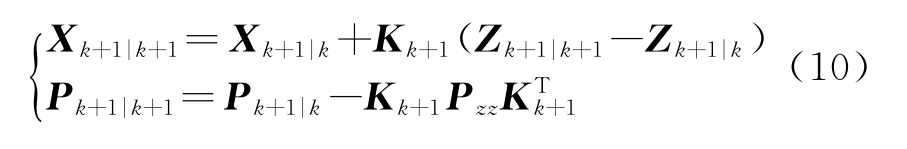
2 转移概率自适应的IMM-CKF算法
2.1 Markov概率转移矩阵自适应
IMM-CKF算法依旧存在着IMM算法固有的缺陷:Markov矩阵是固定不变的。而Markov矩阵控制着IMM-CKF算法中子模型之间的交互关系。在IM M-CKF算法中,由于多种子模型是并行工作的,如果子模型与目标的运动状态越匹配,那么其他模型转移到该子模型的概率就越大,该子模型在最终的滤波结果中占据的权值就越高。由于目标存在机动性,不同时刻的运动状态会发生较大的变化,模型之间的转移概率需要根据运动的情况进行调整,如果不能及时调整Markov矩阵中模型之间的转移概率大小,就会造成算法模型与目标实际运动情况的匹配度降低,运用不匹配模型进行滤波最终会降低算法的滤波精度。
针对上述问题,文献[6]提出了一种利用模型概率μi来调整PM的方法,它针对矩阵PM中同一列的所有元素都采用相同的变化率进行调整,但是目标在不同的运动状态,模型集M中每个子模型的匹配程度是不同的,因此,模型两两之间的切换速度的变化是不同的,即PM中每一个元素变化速度是不同的。综上所述,同一列元素的变化速度也就不一样,需要针对PM中的每一个元素设置单独的调整系数。在此基础上,本文提出了一种更加精细的调整算法。
假设IM M算法中包含有M个子模型,Markov概率转移矩阵为PM,PM中的元素Pij(i,j=1,2,…,M)表示模型i切换到模型j的概率。在IM M算法中,设定t-1时刻,模型i的概率表示为μi(t-1),模型i到模型j的混合转移概率为Uij:
式中,![]() 表示归一化常数,μi(t-1)为IMM算法中通过后验信息调整的模型概率。
表示归一化常数,μi(t-1)为IMM算法中通过后验信息调整的模型概率。
定义t-1时刻概率转移矩阵PM中元素Pij(t-1)的矩阵调整系数为
式中:i,j=1,2,…,M;α>0,α表示调整系数的强度参数。如果0<α<1,则减慢εij的调整速度;如果α>1,则加快εij的调整速度,本文默认值为α=1。如果Pij(t-1)-Uij(t-1)>0,那么εij>1,下一时刻需要提高Pij(t-1),此时模型j与目标的运动更匹配;如果Pij(t-1)-Uij(t-1)<0,那么εij<1,下一时刻需要减小Pij(t-1),此时模型j与目标的运动不匹配。这样可以通过每一个εij(t)单独调整PM中的每一个独立元素,更加精确地完成对目标不同运动模式的自适应调整。
设定调整后的Markov概率转移矩阵为P′M,则矩阵P′M中的元素为P′ij(t):
调整之后的Markov概率转移矩阵还需要进行归一化处理,使其满足Markov概率转移矩阵的两条要求:
1)Markov概率转移矩阵中的任意元素都不小于0;
2)Markov概率转移矩阵中任意一行的元素之和为1。
归一化之后的Markov转移概率为

式中, ,代表归一化常数。
,代表归一化常数。
经过上述处理步骤之后,Markov概率转移矩阵可以根据目标的运动情况进行自适应调整:对于匹配的子模型,提高其他模型转移到匹配子模型的概率,降低非匹配模型的转移概率。与此同时,在最终的输出结果中,匹配模型的权重也相应得到了提高,降低了非匹配模型与匹配模型在输出结果中的竞争带来的误差,提高了滤波的精度。
2.2 自适应IMM-CKF算法
自适应IM M-CKF算法的流程如图1所示。
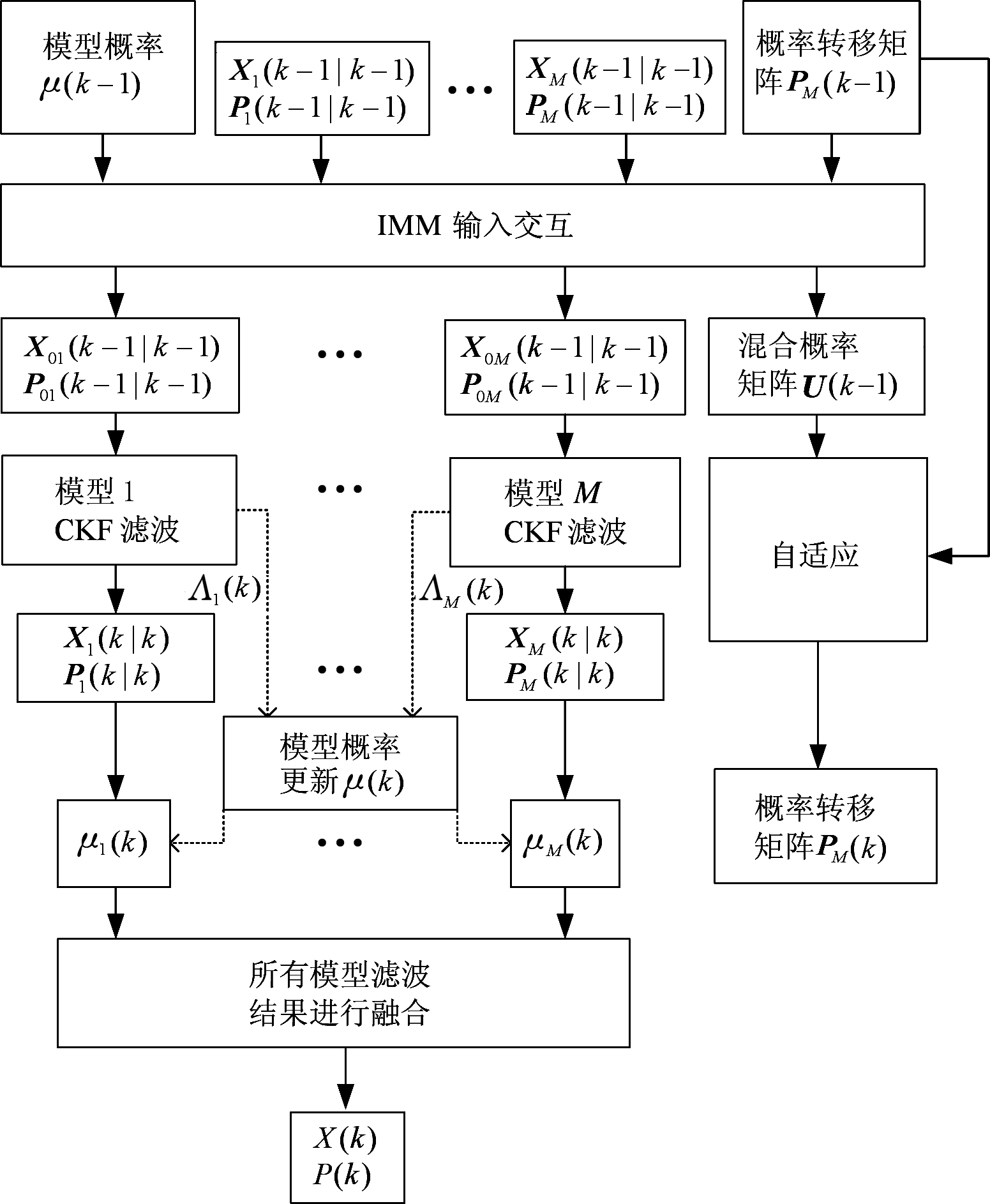
图1 自适应IM M-CKF算法的流程
假设跟踪的目标有M种可能的运动状态,设计的IMM模型集中包含M个滤波器模型。在k-1时刻,系统的最终的状态估计为X(k-1|k-1),模型j的状态估计为Xj(k-1|k-1),滤波协方差为Pj(k-1|k-1)。
第一步:模型j输入交互
将k-1时刻系统的状态估计与模型j的概率融合,得到模型j的混合状态估计,将混合估计作为当前滤波循环的初始状态:
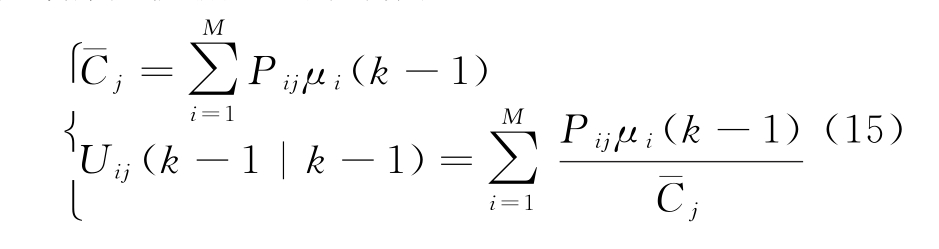
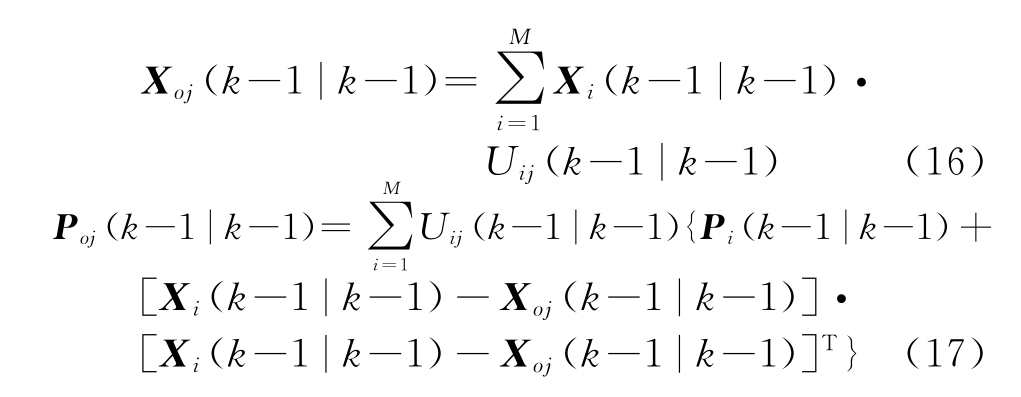
式中,![]() 为模型j的预测概率,Uij为模型i到模型j的混合转移概率,Xoj为模型j的混合状态估计,Poj为模型j的混合协方差估计。
为模型j的预测概率,Uij为模型i到模型j的混合转移概率,Xoj为模型j的混合状态估计,Poj为模型j的混合协方差估计。
第二步:模型j滤波开始
将第一步中生成的混合状态估计Xoj(k-1|k-1)和混合协方差估计Poj(k-1|k-1)作为模型j的输入,利用上一节给出的CKF算法进行滤波,模型j滤波输出的状态估计结果为Xj(k|k),协方差估计结果为Pj(k|k),并且得到残差为γj(k|k),残差的协方差为Pzz,j(k)。
第三步:模型j概率更新
模型j的似然函数为
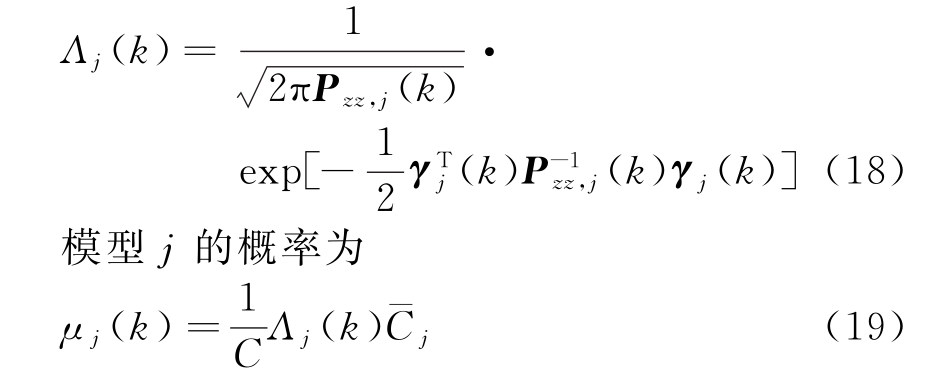
式中,![]() 为归一化常数。
为归一化常数。
第四步:所有滤波器输出结果融合
系统最终状态估计为
系统最终协方差估计为
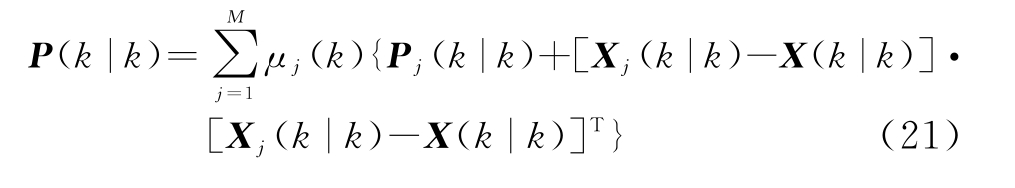
3 仿真分析
为了检验本文给出的Markov概率转移矩阵自适应IM M-CKF滤波算法的有效性,运用蒙特卡洛仿真实验来对算法的性能进行检验。
设定目标在二维平面运动,目标初始位置坐标为(2 000 m,2 000 m),雷达的初始位置为(-10 000 m,1 000 m),目标的初始速度为(0 m/s,100 m/s),初始协方差矩阵P0=diag(30,5,30,5),仿真的周期T=1 s,仿真时间为500 s,目标的运动轨迹为:在t=0~15 s目标进行匀速直线运动;在t=151~300 s,目标进行低速转弯运动,转弯角速度为-1.8°/s;在t=301~400 s,目标进行匀速直线运动;在t=401~450 s,目标进行高速转弯运动,转弯角速度为5.4°/s;在t=451~500 s,目标进行匀速直线运动。
算法的模型集包含3个子模型,分别为匀速模型、低速转弯模型和高速转弯模型。其中模型一的匀速运动采用CV模型建模,目标的运动状态方程[10]如下:
系统的过程噪声协方差Qcv=diag(0.01,0.01,0.01,0.01)。
模型二和模型三采用CT模型建模,目标的运动状态方程[10]如下:
对于低速转弯模型,w=-1.8°/s,对于高速转弯模型,w=5.4°/s。低速转弯模型的过程噪声协方差Qct1=diag(0.01,0.01,0.01,0.01),高速转弯模型的噪声协方差Qct2=diag(0.01,0.01,0.01,0.01)。
IMM算法中设定每个模型的初始模型概率值都为1/3,观测噪声方差R=diag(102,0.0062),模型的Markov概率转移矩阵为

仿真实验采用标准IMM-CKF算法以及本文提出的自适应IMM-CKF算法进行跟踪滤波,分别进行了100次蒙特卡洛仿真实验,通过位置和速度的均方根误差来比较算法的跟踪性能,算法仿真的结果如图2所示。
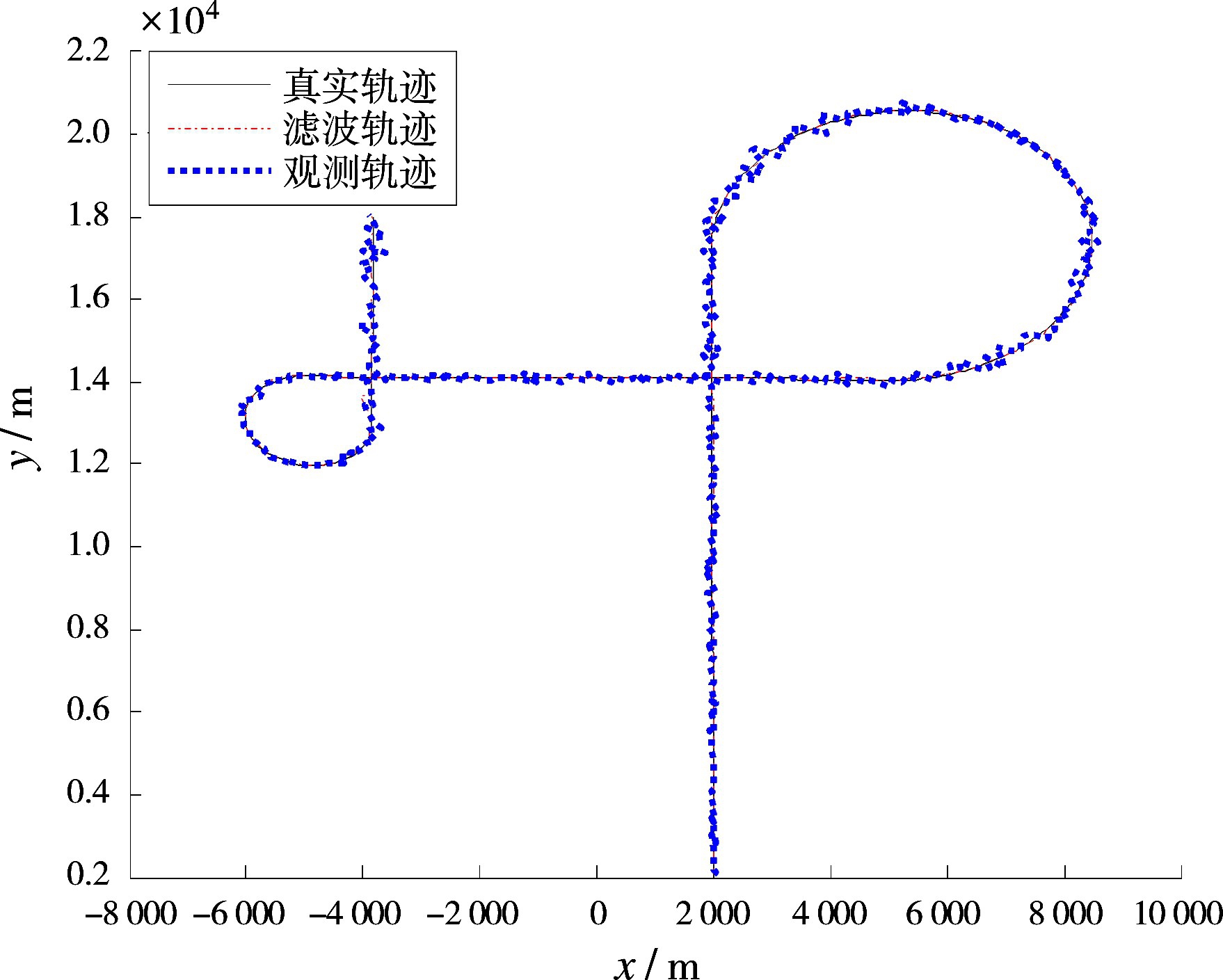
图2 跟踪滤波轨迹
3.1 模型概率对比分析
对比图3和图4,自适应IMM-CKF算法的滤波模型概率明显与运动状态的匹配程度更好。由于IMM算法的模型集包含多个子模型,因此在滤波的过程中模型之间存在竞争关系。以t=151~300 s慢速转弯阶段为例,在图3所示的标准IMM-CKF算法概率变化曲线中,慢速转弯的模型概率虽然达到了0.7左右,但是,其他几个不匹配模型的概率依然占到了0.3左右的概率,这会降低最终的融合结果精度;而在图4自适应的IMM-CKF算法概率变化曲线中,慢速转弯的模型概率基本趋近于1,其他不匹配模型的概率接近于0,自适应算法的模型概率与目标的运动状态匹配得更好。
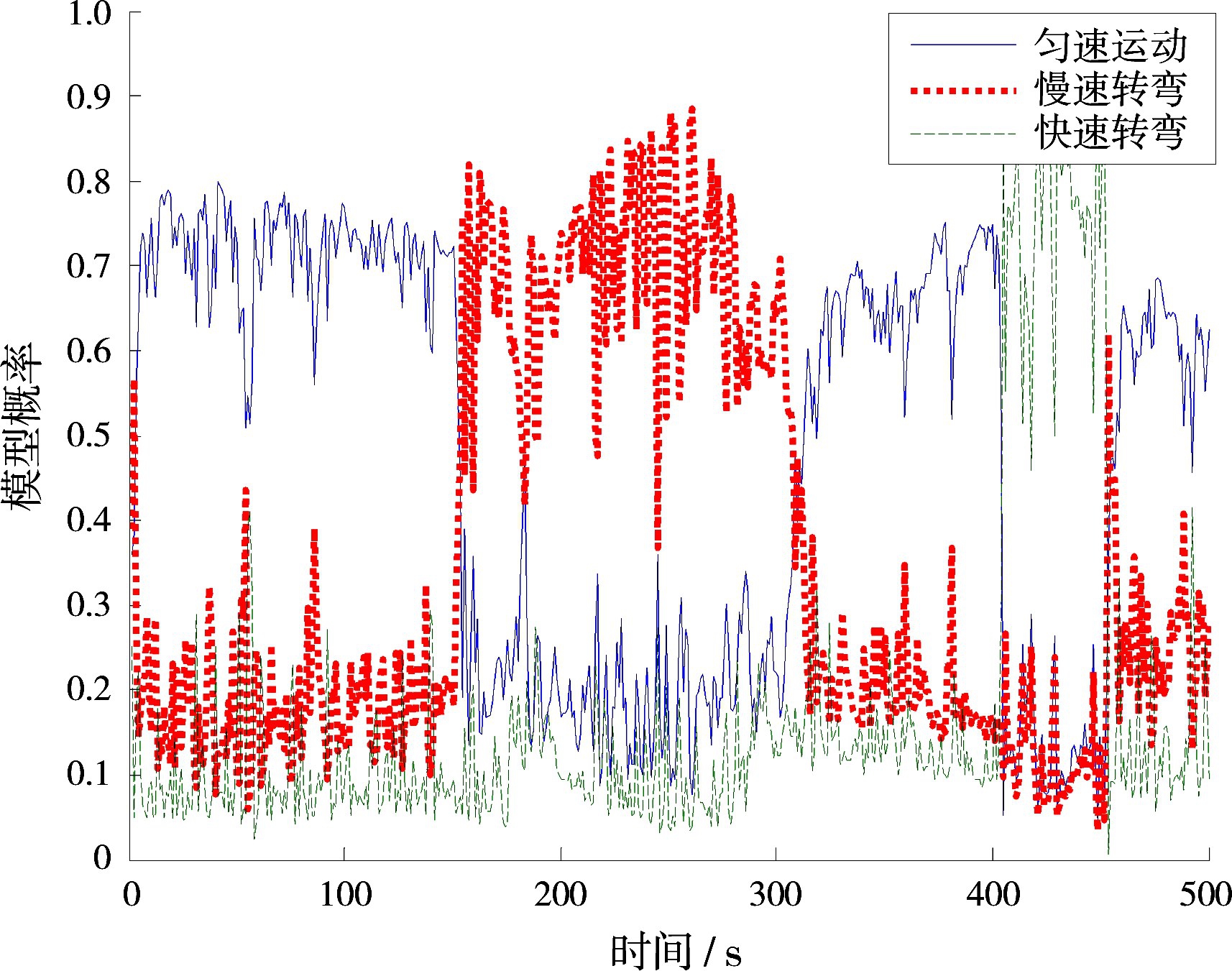
图3 IMM-CKF模型概率曲线
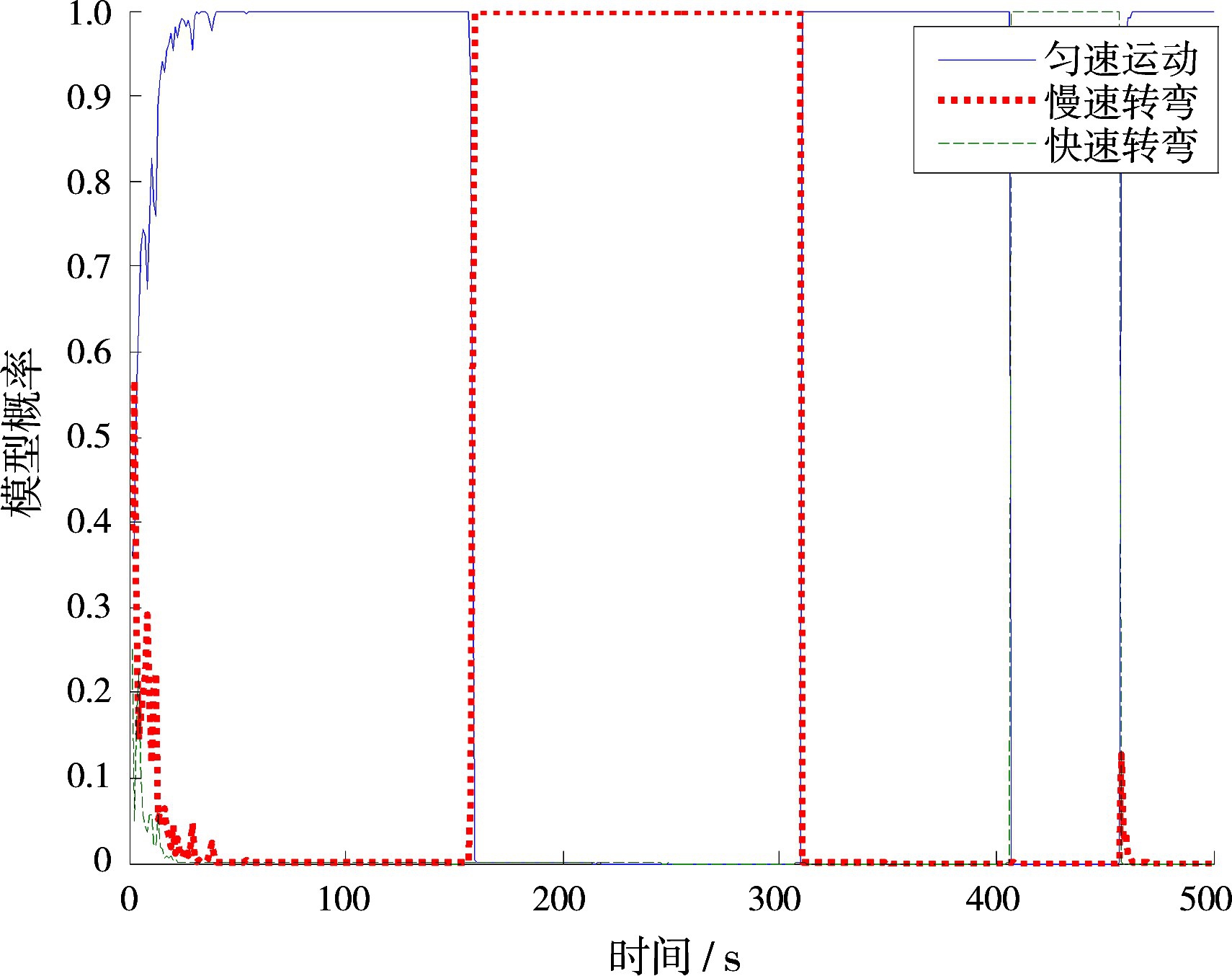
图4 自适应IMM-CKF滤波算法
3.2 跟踪性能对比分析
从仿真的结果可知:
1)模型误差更小。在图5中,在滤波开始阶段,位置均方根误差曲线在前期经过一段时间自适应调整之后,自适应IMM-CKF算法的误差曲线要低于标准IMM-CKF算法,这是因为自适应IMM-CKF算法引入了后验信息实时修正Markov概率转移矩阵,模型的匹配程度更好,在跟踪滤波效果上要优于标准IMM-CKF算法,这与前期的理论分析是一致的。但是由于IMM算法先天存在着模型切换时间滞后的问题,自适应算法没有明显改善这一缺点,在滞后的短暂几个时刻会引起较大的误差,这一点在图4和图5中也显示出来了。
2)模型之间的切换时间更短。对比图5和图6,在模型的切换时刻,即t=150,300,400和450 s,图5中自适应IMM-CKF算法可以迅速完成模型的切换,而图4中标准IMM-CKF算法需要一定的过渡时间才能完成模型的切换。
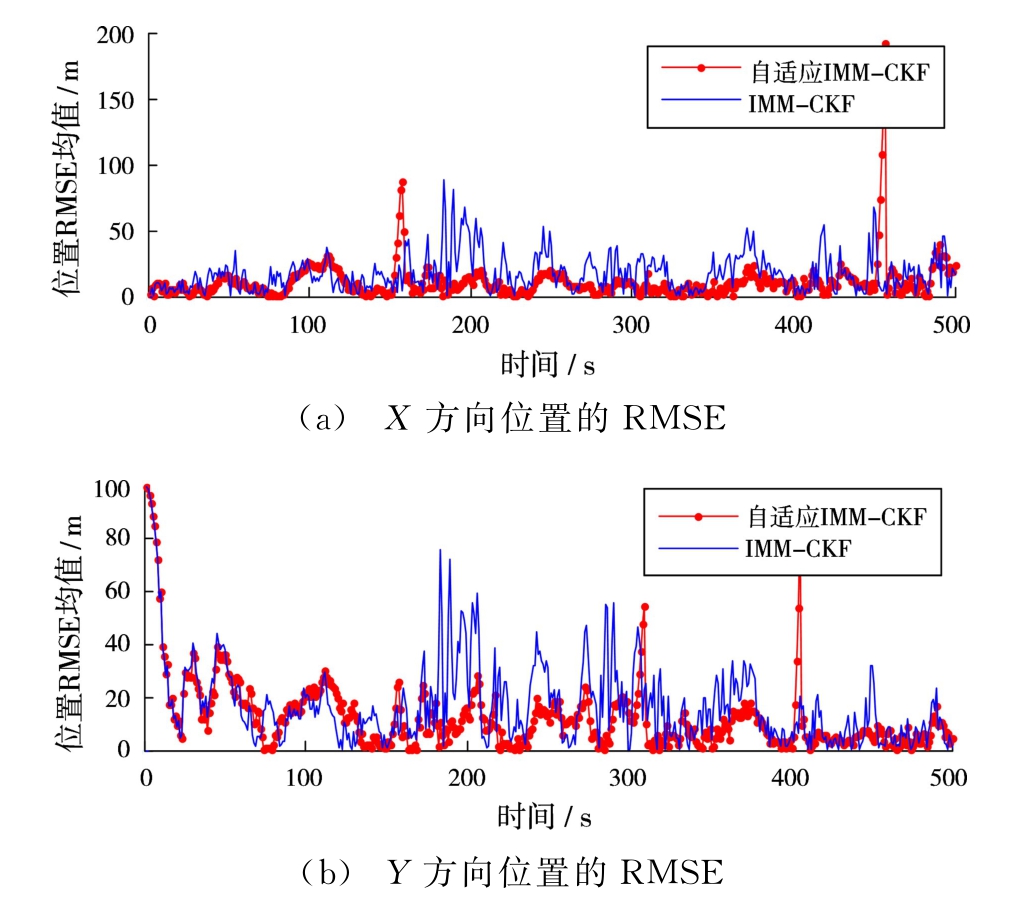
图5 位置的均方根误差
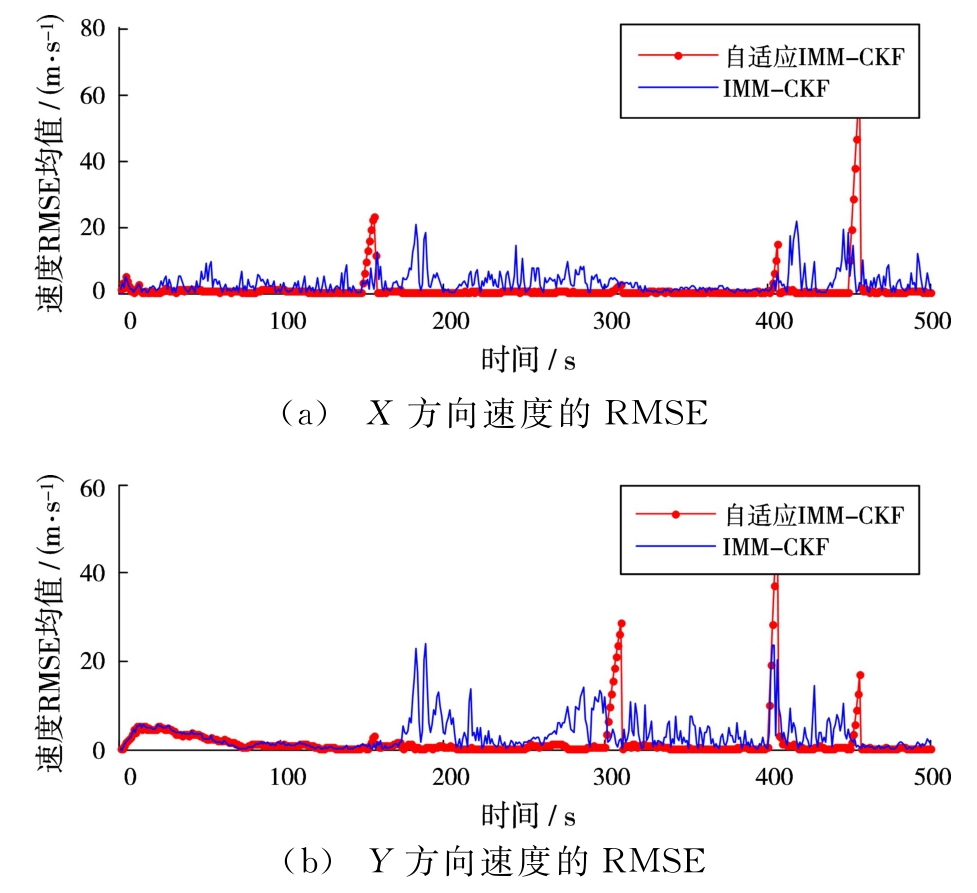
图6 速度的均方根误差
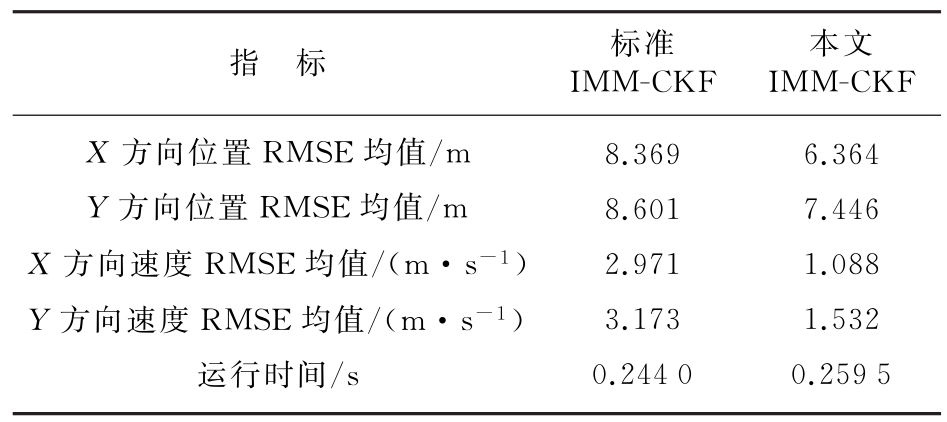
3)新算法的滤波性能更好。从表1的数据对比可以看出,新算法在X方向位置的RMSE均值比标准算法提高了23.96%,X方向速度的RMSE均值比标准算法提高了63.37%,而算法耗时仅仅增加了5.97%,新算法在性能上比标准算法提升明显。
表1 仿真结果性能对比
4 结束语
本文针对标准IMM算法中Markov概率转移矩阵固定不变的问题,通过Markov概率转移调整系数,引入后验信息对Markov概率转移矩阵进行实时调整,设计了一种自适应IMM-CKF算法,不仅提高了算法的跟踪滤波精度,并且算法具有更好的模型匹配度、更短的模型切换时间间隔。
参考文献:
[1]毛征,孟凡刚,孟灿,等.基于高机动目标跟踪的改进变结构IMM算法[J].北京工业大学学报,2015,41(3):353-360.
[2]陈宇威,朱晶星,杨海明,等.用于多策略机动目标跟踪的基于模糊理论的改进IMM算法[J].上海航天,2016,33(2):43-47.
[3]BLOM H A P,BAR-SHALOM Y.The Interacting Multiple Model Algorithm for Systems with Markovian Switching Coefficients[J].IEEE Trans on Automatic Control,1988,33(8):780-783.
[4]臧荣春,崔平远.马尔可夫参数自适应IFIMM算法研究[J].电子学报,2006,34(3):521-524.
[5]封晋文,黄长强,曹林平,等.马尔可夫矩阵修正IMM跟踪算法[J].系统工程与电子技术,2013,35(11):2269-2274.
[6]郭志,董春云,蔡远利,等.时变转移概率IMMSRCKF机动目标跟踪算法[J].系统工程与电子技术,2015,37(1):24-30.
[7]郭跃,刘新学,王才红.混合坐标系下跟踪自由段弹道导弹的IMM-UPF算法研究[J].弹道学报,2015,27(1):12-17.
[8]JULIER S J,UHLMANN J K.A New Extension of the Kalman Filter to Nonlinear Systems[C]∥Proceedings of the SPIE 3068,Signal Processing,Sensor Fusion,and Target Recognition VI,Orlando,FL:SPIE,1997:182-193.
[9]ARASARATNAM I,HAYKIN S.Cubature Kalman Filters[J].IEEE Trans on Automatic Control,2009,54(6):1254-1269.
[10]曹亚杰,李君龙,秦雷.临近空间目标交互式多模型跟踪定位算法研究[J].现代防御技术,2016,44(1):134-140.
