0 引言
在雷达信号检测过程中,海杂波的统计特性及其随时间和空间的变化对雷达信号检测算法的设计与性能评估具有重要的意义。海杂波的统计特性与电磁波入射余角、电磁波频率、海况等众多因素有关。通过对不同海况、不同风向条件下对海面起伏特性及规律的分析,海平面的起伏变化可划分为两个空间尺度的变化,分别由两种不同的物理机制造成,即海水的重力波和表面张力波,海杂波表现出明显的随机特性,即海杂波具有非高斯性、非平稳性和非均匀性[1]。海面形成的特定结构导致了海杂波的统计特性可以采用组合模型表示,即表示为两个不同相干长度的分量的乘积。海面大尺度结构分量对应海杂波的纹理分量,海面小尺度结构分量对应海杂波的散斑分量。因此,研究一种海杂波纹理分量的提取方法,利用X波段雷达对海杂波实测数据进行统计特性分析与仿真验证,对提高雷达目标检测具有较高的应用价值。
1 特性分析
海杂波的产生机理与海面运动特性有关,而海面的起伏规律受多种因素的影响,难以用简单的规律进行描述,对于海杂波的建模通常是基于观测信号的分析展开的[2],并同时观测海面的起伏规律,从而获得海面的起伏规律与海杂波统计特性之间联系。通过观察分析不同海况、不同风向条件下海面起伏特征,认为海平面的起伏可以划分为两个空间尺度的变化。这两个空间尺度的变化来自两种不同的物理机制:海水的重力波和表面张力波。表面张力波主要由风和海水的表面张力产生,其特性与气象条件密切相关。表面张力波通常具有较小的幅度,波长较短,数量级大约为2 cm以内[3]。实际上,在完全稳定的气象条件下,仍然可以观测到海水表面张力引起的海面连续的、随机的起伏运动,故这种张力波在海面上几乎处处存在,且具有一定的局部特性。此外,海面张力波不会携带过多的能量,但会散射电磁波。重力波则主要是由海水重力的累积产生的,其最初可能是由风、温差或其他气象条件触发。与张力波不同的是,重力波具有较大的幅度和波长,波长远大于2 cm。重力波的特性可以覆盖较大一片海域,具有较强的相关性,并携带大量的能量,对电磁波反射具有重要的影响。通过对重力波和张力波的不同物理特性的分析,容易确定海杂波也具有两个尺度上的随机特性。图1给出了海平面起伏示意图,小尺度表面张力波叠加在大尺度的重力波上,且重力波迎风面上叠加的表面张力波的幅度更大,还给出了海平面对电磁波散射效应,显然不规则的海面将电磁波散射到任意方向,并且海平面的某些位置可能会由于重力波的影响产生遮蔽效应[4]。
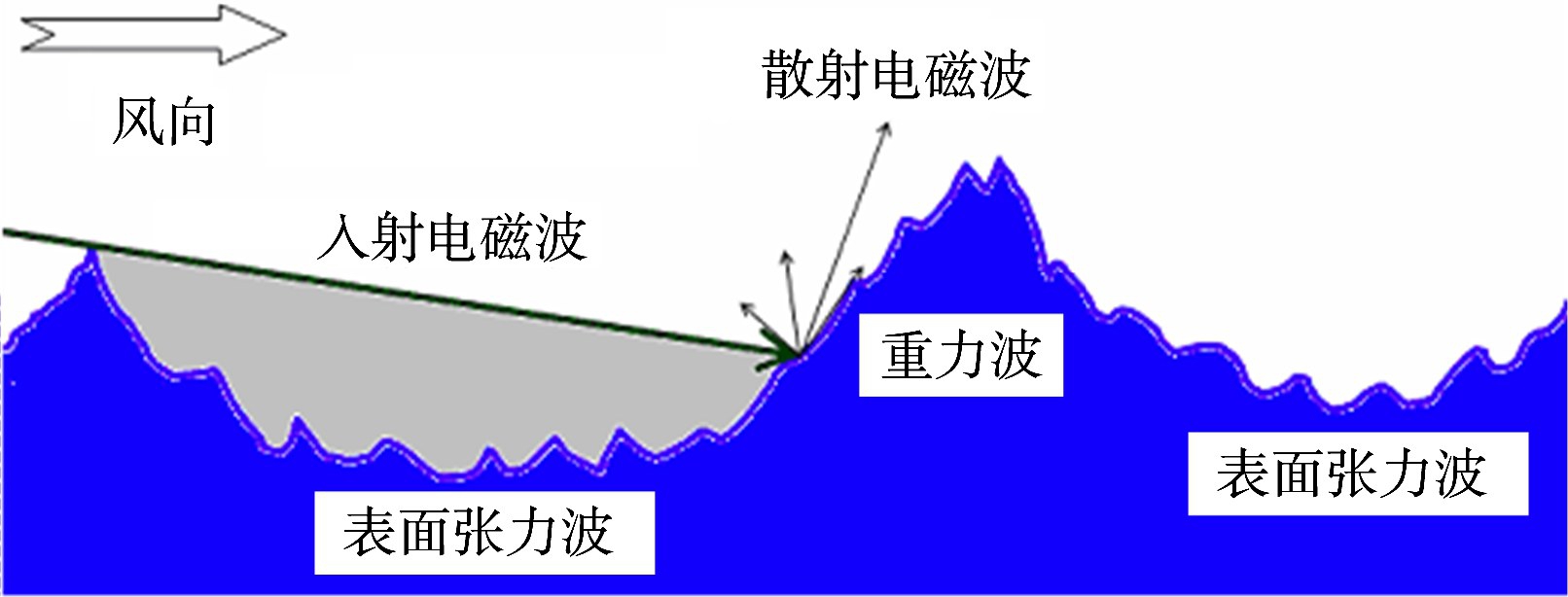
图1 海平面起伏示意图
海面的这种结构导致了海杂波的统计特性可以采用组合模型来表示,即表示为具有两个不同相干长度的分量的乘积。海面大尺度结构分量对应海杂波的纹理分量,海面小尺度结构分量对应海杂波的散斑分量。可以将散斑分量近似为高斯过程g(t),而纹理分量近似为非负的随机过程
那么海杂波可以用复合高斯过程c(t)=
来表示[5]。如果考虑到雷达信号处理过程是对回波以脉冲重复频率的采样,并假定在一个相干处理间隔内,纹理分量完全相关,即认为纹理分量在一个相干处理间隔内为一个随机变量,那么可以得到一个球不变随机矢量(SIRV)杂波模型:
相对于组合模型或复合高斯模型,SIRV杂波模型具有很多优点。最重要的就是SIRV的概率密度函数(Probability Distribution Function,PDF)完全由纹理分量的边缘PDF和高斯分布矢量的相关函数确定[6]。
2 算法提出
考虑到采用复合模型可以较好地拟合海杂波统计特性,那么进一步深入分析需要分别考虑复合模型中的纹理分量和散斑分量的统计特性。其中,纹理分量的统计特性表征了海杂波的非高斯性,而散斑分量的相关性直接与杂波功率谱有关[7]。因此,在对海杂波统计分析之前,必须考虑纹理分量的提取问题。
海杂波的纹理分量的提取本质上是利用了纹理分量和散斑分量具有不同的相干长度。文献[8]给出了计算海杂波纹理分量相干长度的算法,该算法是基于广义Kolmogorov-Smirnov检验,其过程需要统计独立的样本,检验门限需要利用Monte Carlo仿真得到,操作和计算比较复杂。而本文则给出了一种新的纹理分量提取算法,该算法能够自适应地搜索纹理分量的最佳相干长度,而无须进行统计假设检验。假定杂波纹理分量长度为L,那么长度为L的杂波序列可以近似为
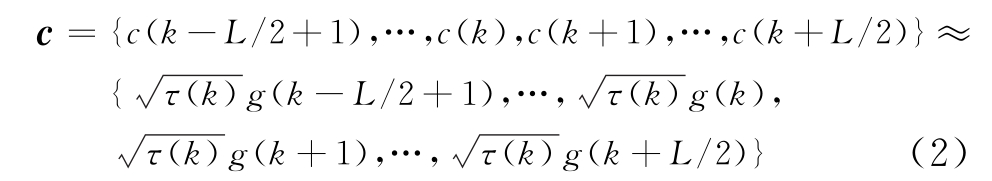
不失一般性,可以假定散斑分量为零均值单位方差的高斯分布过程,那么可以得到杂波序列中序号k的散斑分量估计值:
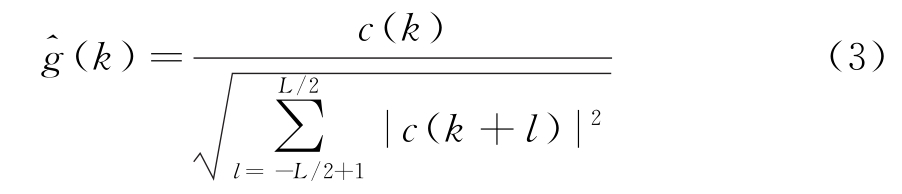
由此可以将散斑估计值与高斯分布的拟合程度作为评估纹理分量相干长度的估计指标:
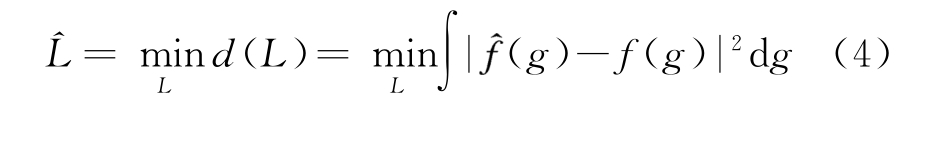
式中
为散斑分量估计值的经验PDF,而f(·)为高斯PDF,均值和方差来自散斑分量的估值。那么两个PDF的拟合程度显然和杂波纹理分量的相干长度估计值L有关[9]。当纹理分量相干长度估计值L接近真实值时,散斑分量接近高斯分布,这时d(L)达到最小值。而当纹理分量相干长度估计值L偏离真实值,无论是偏小还是偏大,d(L)值均会增大。因此从这个原理上分析,函数d(L)应该是一个下凸的、仅有一个最小值的函数。利用d(L)这种性质,在实际估计过程中,无需对所有可能的L值进行分析,可以采用简单的搜索算法得到函数d(L)最小值点对应的L的估值。
3 仿真分析
3.1 实测数据选取
以加拿大Mc Master大学的IPIX雷达在1998年获得的雷达海杂波实测数据为基础进行分析。该雷达工作频率为X波段,能够水平极化(H)和垂直极化(V)发射和接收,并具有发射多种宽度脉冲的能力,因此,利用该雷达杂波数据可以分析不同极化组合、不同距离分辨率条件下的杂波统计特性[10]。本文以Data1,Data2和Data3表示雷达分辨率为30 m,15 m和3 m的3种雷达杂波数据,数据包含34个距离分辨单元和60 000个脉冲回波数据,雷达入射余角为0.32°,每个数据具有4种极化组合形式:H H,HV,VH和VV,分别表示发射极化方式和接收极化方式。该杂波的具体参数参见文献[7]。文献[7]的研究结果表明,该雷达杂波数据在大多数情况下可以很好地拟合SIRV模型。本文利用纹理分量提取算法,可以实现复合高斯过程的纹理分量和散斑分量的分离,从而可以进一步分析纹理分量的PDF。
3.2 仿真结果分析
图2给出了3种分辨率杂波数据HH模式下的d(L)曲线,可以看出,d(L)近似为一条下凸的单个最小值的曲线,其最小值对应了纹理分量相干长度的最优估计值。需要指出的是,即便d(L)达到最小值,最小值的大小与数据的选择有关。对于高分辨率杂波Data3的数据,其d(L)最小值比其他的数据要大,这说明,该数据的散斑分量与高斯分布的拟合程度最差。文献[7]的结论也表明该数据与SIRV模型的拟合程度是最差的。
图2 HH模式下不同杂波数据d(L)
图3针对Data1的HH模式下的杂波,给出了纹理分量的提取效果,其基本上反映了杂波的短时平均功率的变化。
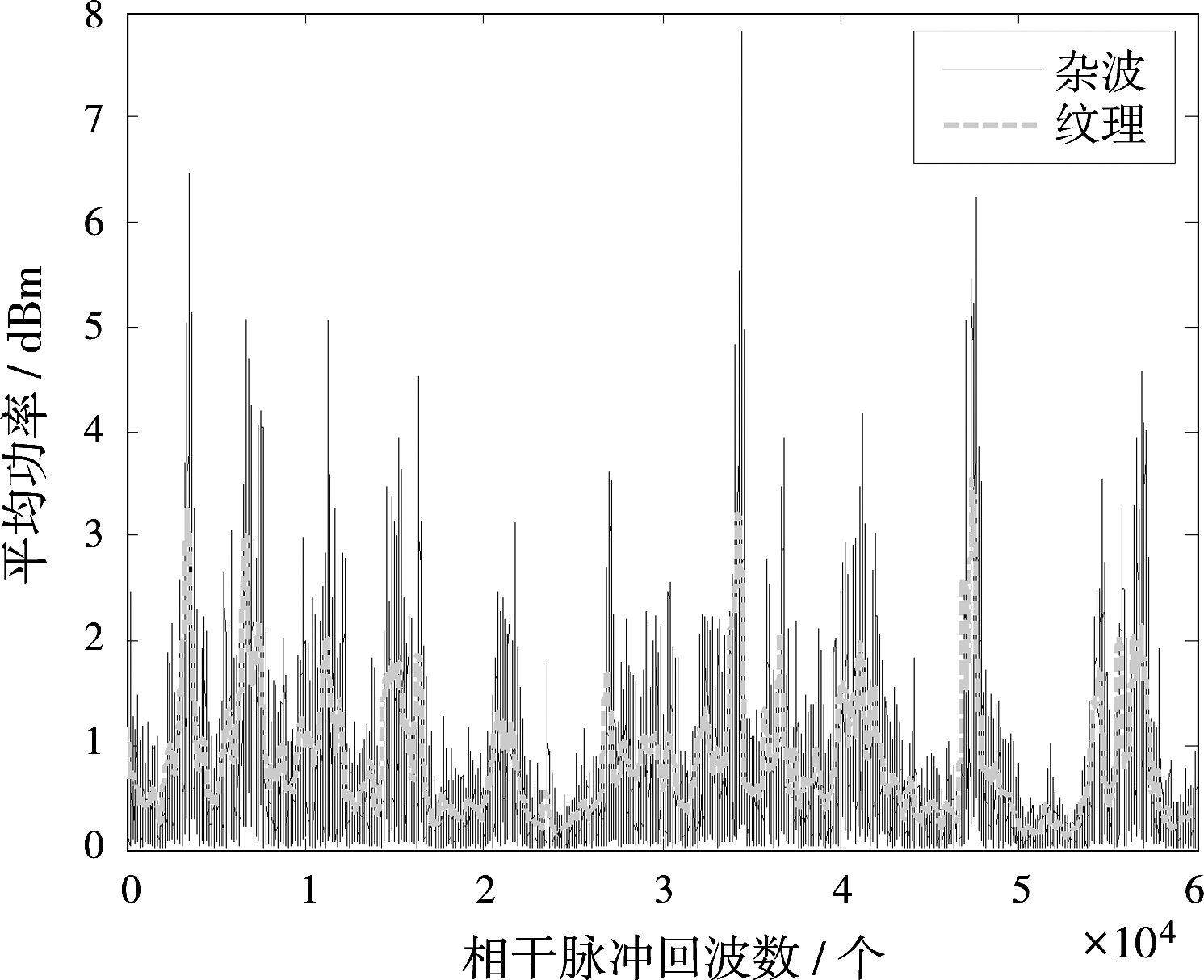
图3 Data1杂波数据HH模式下的纹理分量提取
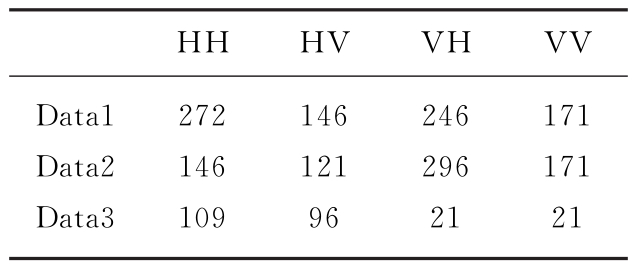
表1给出了距离单元编号为17的雷达杂波数据的纹理分量相干长度。可以发现,HH极化具有较长的纹理分量相干长度,而VV极化通常较小,这是由于海面对不同极化的散射机理不同导致的。其次,纹理分量相干长度随着分辨率的提高而减小。在雷达信号检测中,相干长度的估计具有重要的意义。当相干处理脉冲个数超过了纹理分量的相干长度,杂波的SIRV模型就不再成立,而退化为复合高斯模型,此时基于SIRV的信号检测理论中的很多假设就不再成立,即对于海杂波而言,通过提高相干累积脉冲个数,并不能保证检测性能的改善。
表1 雷达海杂波的相干长度
4 结束语
本文基于海面物理机制特性变化,通过对海杂波的产生机理与海面运动特性关联性分析,研究了海杂波具有两个尺度上的随机特性,其统计特性可采用复合高斯模型来表示,即两个不同相干长度的纹理分量和散斑分量的乘积。在此研究基础上,提出了一种新的纹理分量提取方法,基于此方法,可以有效分析实测海杂波数据纹理分量的去相关时间,完成海杂波的纹理分量与散斑分量的分离。进一步利用X波段雷达海杂波实测数据仿真分析了不同距离分辨率、不同极化组合条件下海杂波纹理分量的提取效果,对分析研究海杂波统计特性,提高雷达信号检测性能具有较好的应用价值。
参考文献:
[1]闫亮,孙培林,易磊,等.基于逆高斯分布的复合高斯海杂波建模研究[J].雷达学报,2013,2(4):461-465.
[2]WARD K D,TOUGH R J A,WATTS S.Sea Clutter:Scattering,the K Distribution and Radar Performance[M].Herts,UK:IET,2006.
[3]时艳玲.非平稳海杂波背景下子带开关相干检测器[J].电子学报,2014,42(10):1925-1930.
[4]TOTIR F,RADOI E,ANTON L,et al.Advanced Sea Clutter Models and Their Usefulness for Target Detection[J].MTA Review,2008,18(3):257-272.
[5]赵翠,江朝抒,马静,等.基于ZMNL的相关广义复合分布雷达海杂波仿真[J].现代雷达,2015,37(2):75-78.
[6]曹艳霞,李国君.基于K分布舰载雷达海杂波仿真方法研究[J].雷达科学与技术,2016,14(1):86-90.CAO Yanxia,LI Guojun.Study on Simulation Method of Ship-Borne Radar Sea Clutter Based on K Distribution[J].Radar Science and Technology,2016,14(1):86-90.(in Chinese)
[7]CONTE E,DE MAIO A,GALDI C.Statistical Analysis of Real Clutter at Different Range Resolutions[J].IEEE Trans on Aerospace and Electronic Systems,2004,40(3):903-918.
[8]CONTE E,BISCEGLIE M D,GALDI C,et al.A Procedure for Measuring the Coherence Length of the Sea Texture[J].IEEE Trans on Instrumentation and Measurement,1997,46(4):836-841.
[9]王佳宁,许小剑.一种小擦地角下空时相关的海杂波仿真模型[J].制导与引信,2014,35(4):7-13.
[10]李芾.基于实测海杂波数据的统计特性分析[D].西安:西安电子科技大学,2013.
