0 引言
随着飞行器机动特性的增强,机动目标跟踪问题普遍存在于各个军民领域。由于目标运动模型的不确定性,采用固定的系统状态方程无法描述机动目标的运动特性。交互多模型(Interacting Multiple Model,IMM)算法是一种解决运动模式未知情况下的机动目标跟踪的有效方法[1]。实际情况下,雷达量测是在极坐标或球坐标下测得,它与目标状态向量呈非线性关系,因此基于该信息的目标跟踪是一个非线性估计问题。针对这一问题,一般有两种方法。一类方法是在混合坐标系下的目标跟踪,主要包括扩展卡尔曼滤波器(Extended Kalman Filter,EKF)[2]和无迹卡尔曼滤波器(Unscented Kalman Filter,UKF)[3]等。另一类方法是量测转换卡尔曼滤波(Converted Measurement Kalman Filter,CMKF)[4]算法,即使用转换量测方法将极(球)坐标下的量测变换表示成直角坐标系下的量测,从而使目标跟踪成为一个线性估计问题。传统的转换量测的方法在转换量测时会产生偏差[4-5],已有不少学者对此问题提出了一些改进方法,如去偏量测转换(Debiased Converted Measurement,DCM)[4]和无偏量测转换(Unbiased Converted Measurement,UCM)[5]算法。DCM算法求得的转换量测的偏差和协方差矩阵会引入附加的误差,因而不够精确。UCM算法中转换量测误差的协方差矩阵在已获得的无偏转换量测值的基础上直接在量测值的条件下推导,存在兼容性的问题。文献[6]在文献[5]的基础上进行改进,改进的UCM(Modified Unbiased Converted Measurement,MUCM)算法克服了兼容性的问题。但是MUCM是在量测值的条件下推导转换量测误差的协方差矩阵,导致协方差矩阵和量测误差是相关的。这种相关性导致卡尔曼增益依赖于量测误差,进而状态估计是有偏的。因此,基于UCM提出了去相关无偏量测转换(Decorrelated Unbiased Converted Measurement,DUCM)[7]算法。该算法在计算转换量测误差的统计特性时,以直角坐标系下的位置预测值为条件获得转换量测误差的均值和协方差。消除了量测转换误差协方差与量测误差之间的相关性。
现有量测转换方法均与传统卡尔曼滤波结合,形成基于量测转换的卡尔曼目标跟踪方法。然而,实际情况下目标会呈现机动运行特性,本文将DUCM算法与交互多模型算法相结合,获得了基于去相关无偏量测转换的交互多模型算法(DUCM-IMM)。仿真结果表明,相对于基于扩展卡尔曼滤波的交互多模(EKF-IMM)算法和基于传统量测转换的交互多模(CONV-IMM)算法,本文方法具有更高的目标跟踪精度。
1 问题描述
在雷达目标跟踪中,系统的量测信息通常在极坐标或者球坐标系下获得。对于二维雷达,其量测信息包括目标径向距离rm以及方位角αm。在二维目标跟踪中,目标状态向量通常设为X=(x,vx,ax,y,vy,ay)T,其中x,y为目标在x和y方向的运动位置,vx,vy为目标在x和y方向的运动速度,ax,ay为目标在x和y方向的加速度。显然此时系统具有如下的非线性量测方程:
式中,
为相互独立的距离和方位角量测误差,假设为零均值的高斯量测噪声,其标准方差分别为σr和σα。
类似地,对于三维雷达,在上述模型基础上还能获得俯仰角的量测值θm。
基于上述量测方程,并充分考虑目标的机动特性,需要解决的问题是如何利用雷达极坐标或者球坐标下获得的非线性量测信息,采用有效的滤波方法获得机动目标状态向量的估计结果。
2 基于DUCM的交互多模型算法
为解决系统量测与目标状态向量之间的非线性特性,采取量测转换方法利用非线性量测获得转换后的线性量测信息,实现直角坐标系中的线性滤波。同时,考虑到机动目标的运动特性,将DUCM算法与IM M算法结合,估计机动目标的运动状态。
2.1 量测转换误差统计特性的计算
量测转换方法中,首先需要依据具体的量测转换方法计算量测转换误差的统计特性,其中包括均值和协方差两部分。在二维目标跟踪系统中,传统量测转换误差均值:
由式(2)可以看出,传统的量测转换值是有偏的。对转换量测进行无偏处理,可得到无偏量测值为
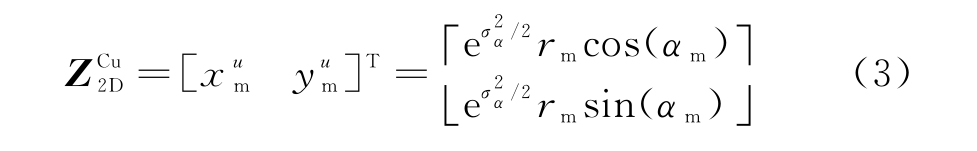
则无偏量测转换误差为
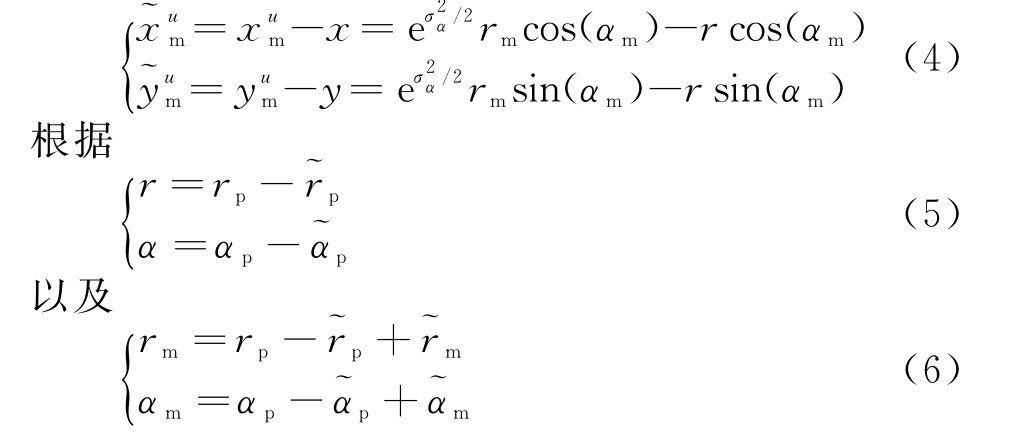
可以得到在位置预测值xp和yp及其位置误差协方差矩阵
条件下计算转换量测误差的均值
和协方差矩阵
的各个元素具体如下:
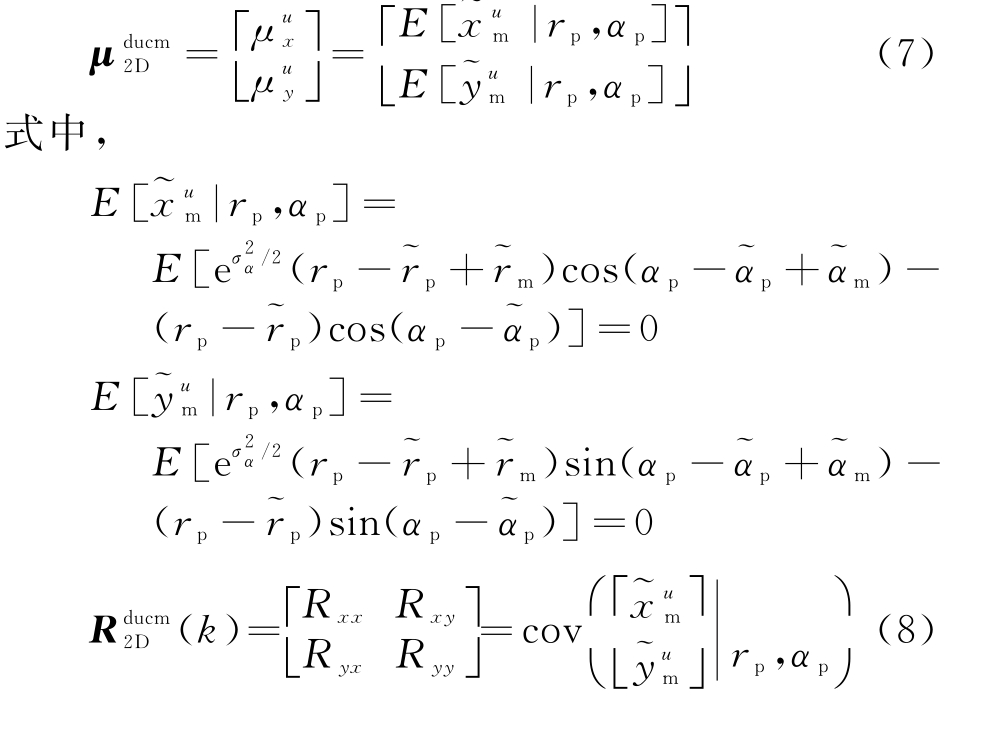
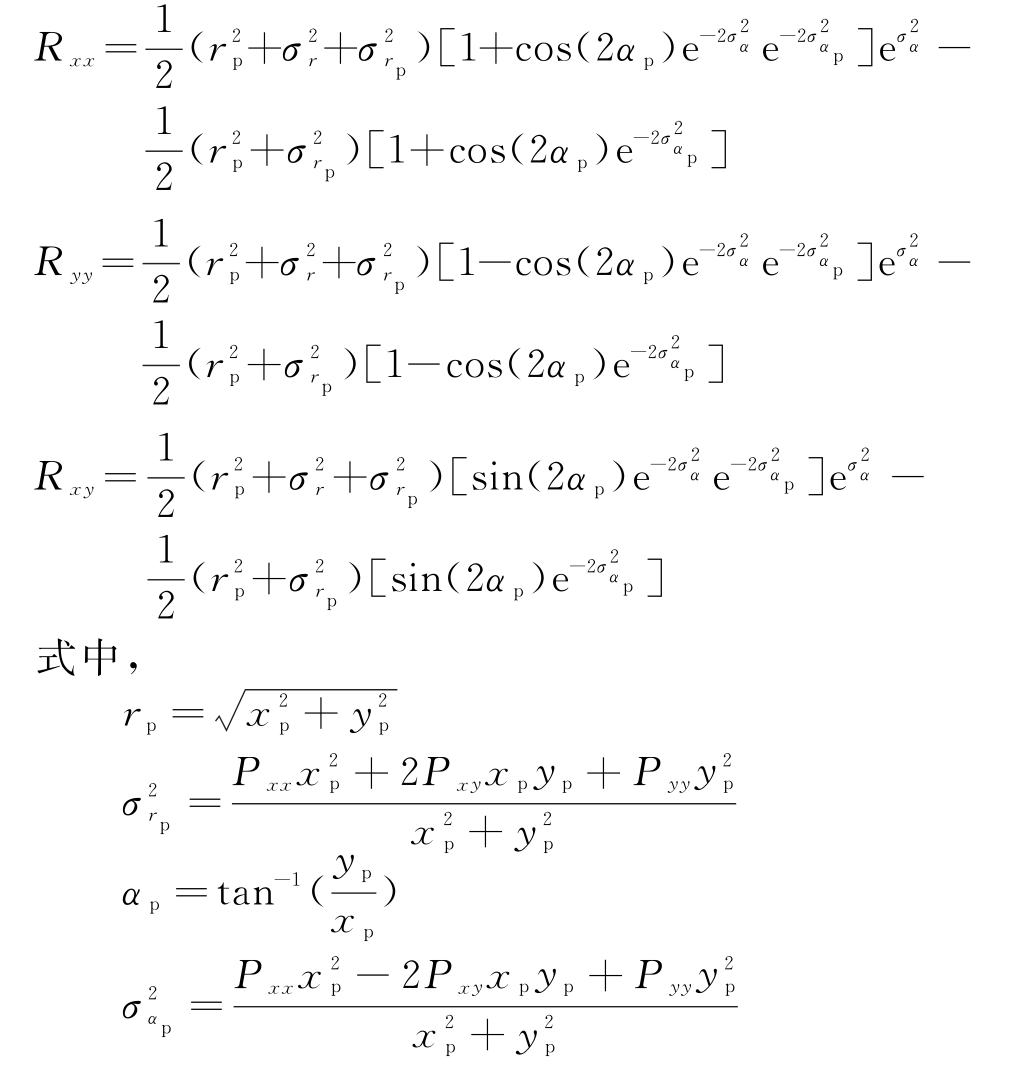
类似地,在三维目标跟踪系统中有无偏量测值
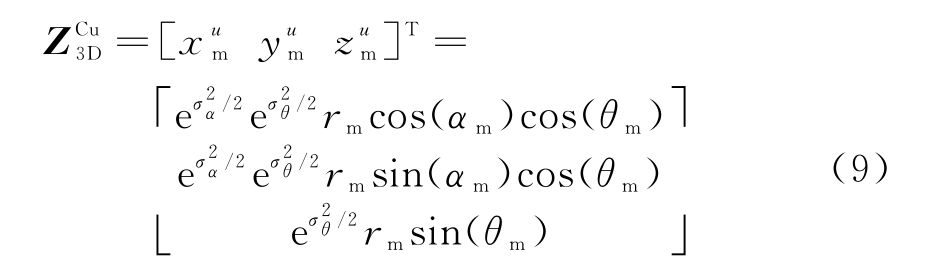
基于位置预测值xp,yp和zp及其误差协方差矩阵
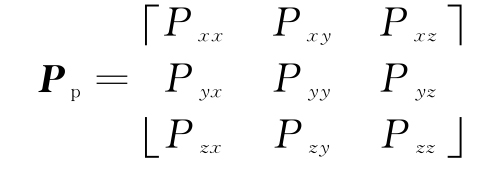
条件下计算转换量测误差的均值
和协方差矩阵
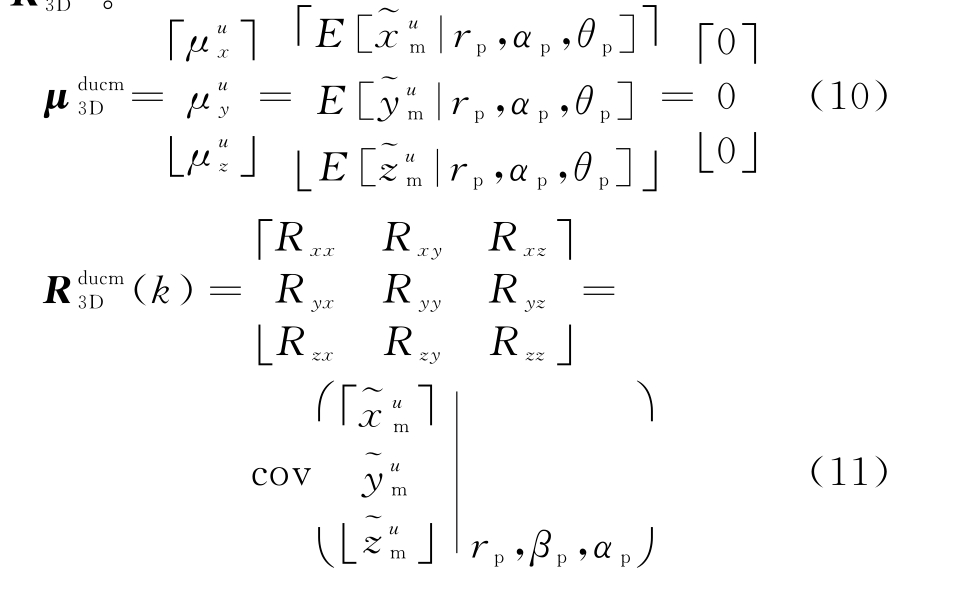
的各个元素具体如下:
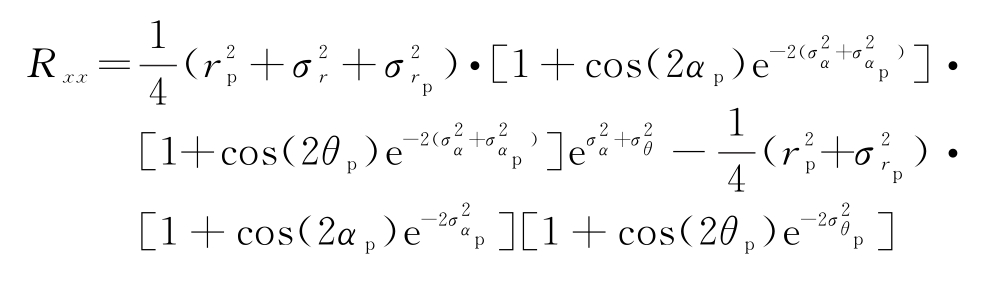
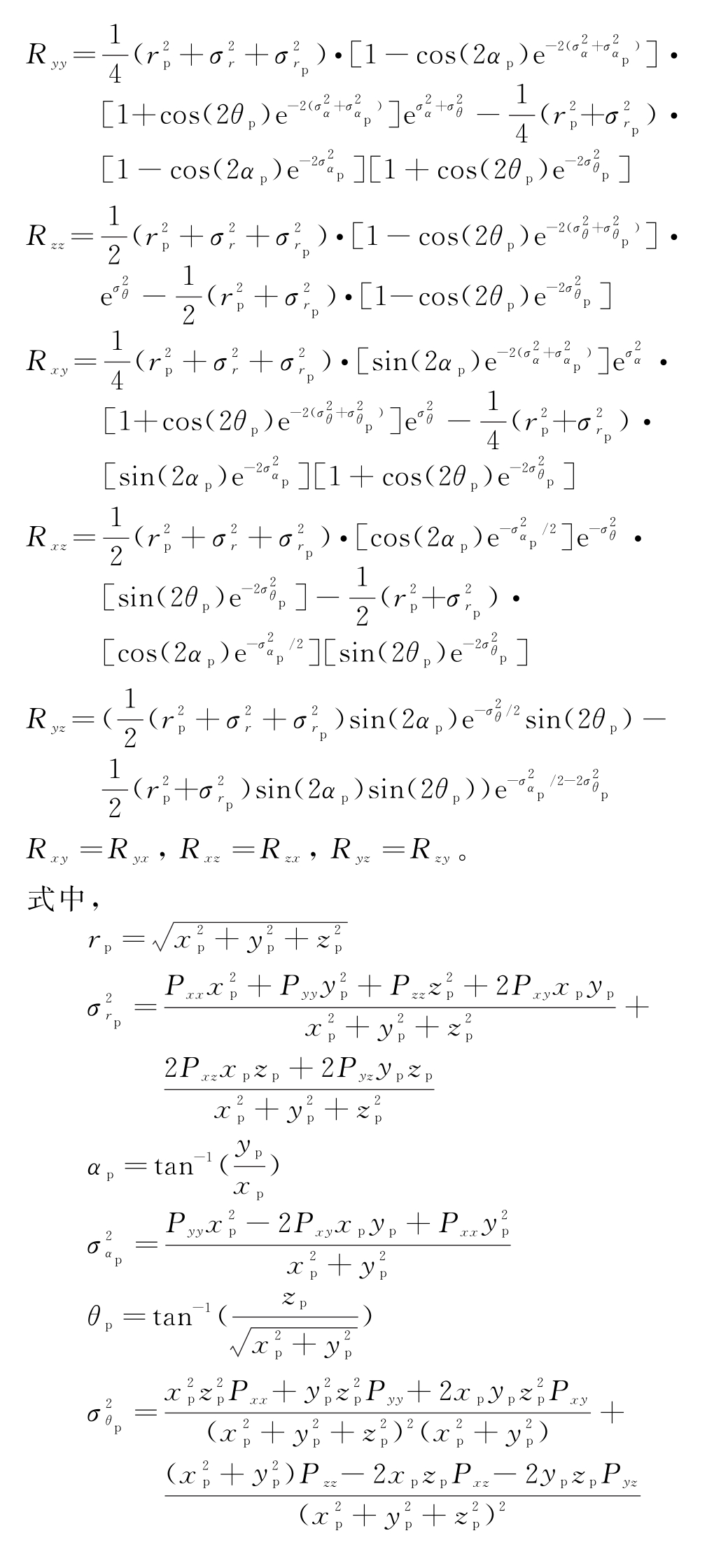
2.2 极/球坐标下基于DUCM的交互多模型算法
交互多模型算法是一种有效的机动目标跟踪算法,它包含一个交互作用器、多个滤波器、一个模型概率更新器和一个状态混合器。模型之间的转换规律遵循已知转换概率的马尔科夫过程。交互多模型的输入是上一时刻各个滤波器的状态估计输出值,其输出为各个滤波器输出状态的加权和,加权系数为更新后的模型概率。
假设交互多模算法设包含N个滤波器,即运动模型个数为N。目标的N个运动状态方程满足:X(k)=Fj(k-1)X(k-1)+Γj(k-1)wj(k-1)(12)式中,Fj,Γj和wj分别为模型j的运动状态方程、过程噪声输入矩阵和噪声向量,j=1,2,…,N。
基于式(12)所示的目标运动状态方程和非线性量测方程,可将量测转换方法与交互多模型算法相结合,获得基于DUCM的机动目标跟踪算法,具体步骤如下:
Step1:输入交互的估计
计算混合概率
式中,
为k-1时刻模型i的更新概率,πij为模型转换概率,Cj为归一化常数,有Cj=
Step2:每个滤波器输入的状态估计和误差自相关矩阵
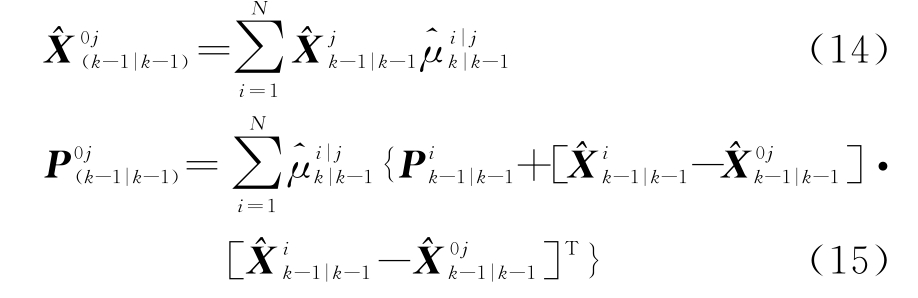
Step3:目标状态一步预测值
式中,二维坐标系下
Step5:计算无偏量测ZCu(k)
对于二维目标跟踪,采用式(3);对于三维目标跟踪,采用式(9)。
Step6:计算量测转换误差协方差矩阵
对于二维目标跟踪,采用式(8);对于三维目标跟踪,采用式(11)。
Step7:计算新息过程
Step8:计算新息过程自相关矩阵
Step11:模型j的目标状态估计和状态估计误差自相关矩阵
Step13:重复以上步骤,进行递推滤波算法,实现目标跟踪。
3 仿真
在二维目标跟踪场景中,假设雷达位于坐标原点。初始值的设置:初始位置(10 km,5 km),初始速度(-50 m/s,50 m/s)。目标在1～100 s内作匀速运动,100～130 s内作加速度为(5 m/s,5 m/s)的匀加速运动,130～200 s内作匀速运动。采样间隔为1 s,匀速过程噪声为0.01,匀加速过程噪声为0.05,雷达量测噪声为零均值的高斯白噪声。进行100次的蒙特卡洛仿真。
场景1:极坐标系下,传感器的距离量测误差为3 m,方位角的量测误差为1°。
场景2:极坐标系下,传感器的距离量测误差为10 m,方位角的量测误差为3°。
在三维目标跟踪场景下,假设雷达位于坐标原点。初始值的设置:初始位置(50 km,50 km,80 km),初始速度(-10 m/s,2 m/s,0)。1～70 s内作匀速运动,70～100 s作加速度为(1.5 m/s2,0,1.5 m/s2)的匀加速运动,100～150 s作匀速运动,150～180 s作加速度为(-1.5 m/s2,0,-1.5 m/s2)的匀加速运动,180～250 s作匀速运动。采样间隔为1 s,匀速过程噪声为0.01,匀加速过程噪声为0.02,雷达量测噪声为零均值的高斯白噪声。进行100次的蒙特卡洛仿真。
场景3:球坐标系下,传感器的距离量测误差为5 m,方位角的量测误差为1.5°,俯仰角的量测误差为1°。
场景4:球坐标系下,传感器的距离量测误差为15 m,方位角的量测误差为3°,俯仰角的量测误差为1°。
在上述4种场景下,分别采用DUCM-IMM算法实现目标跟踪,并同时采用基于传统量测转换的交互多模型方法(CONV-IMM)以及EKF-IMM算法,比较其跟踪性能。传统量测转换方法中:
其相应的转换量测误差协方差是
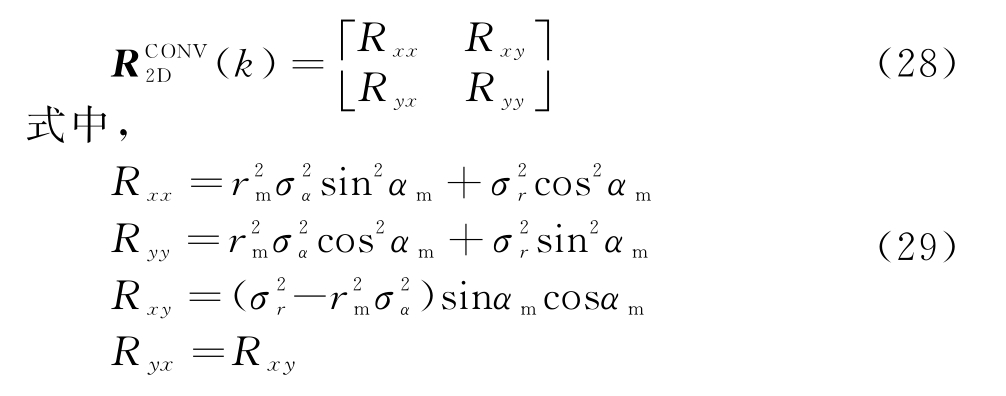
所有算法在仿真过程使用了相同的目标初始状态及其估计误差协方差矩阵。
图1和图2分别为本文提出的算法在极坐标系下2种场景与CONV-IMM算法的目标跟踪算法以及EKF-IMM算法对匀速目标的跟踪仿真结果对比图。图3和图4为球坐标系下的2种场景的仿真结果。
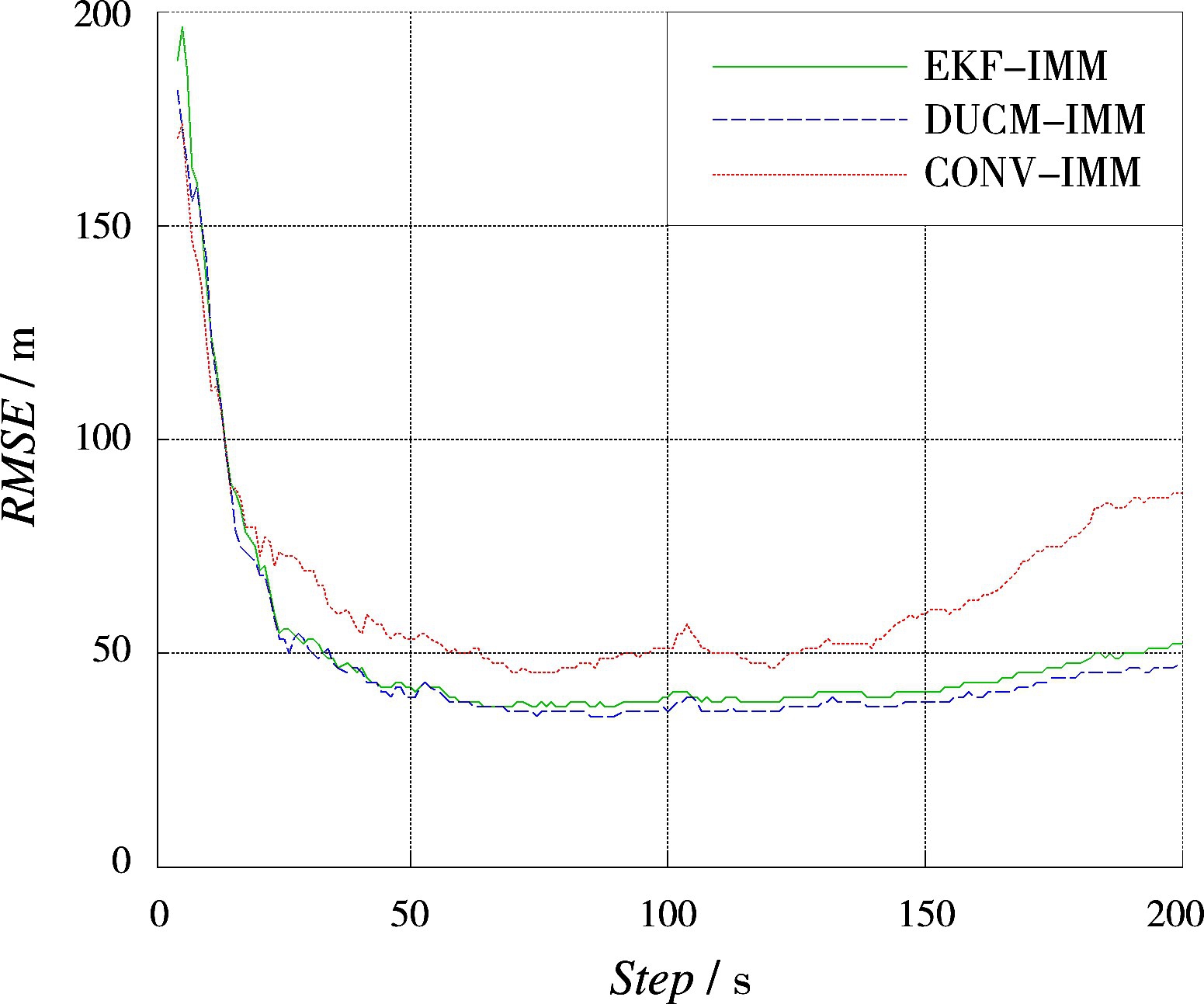
图1 场景1对应的RMSE曲线
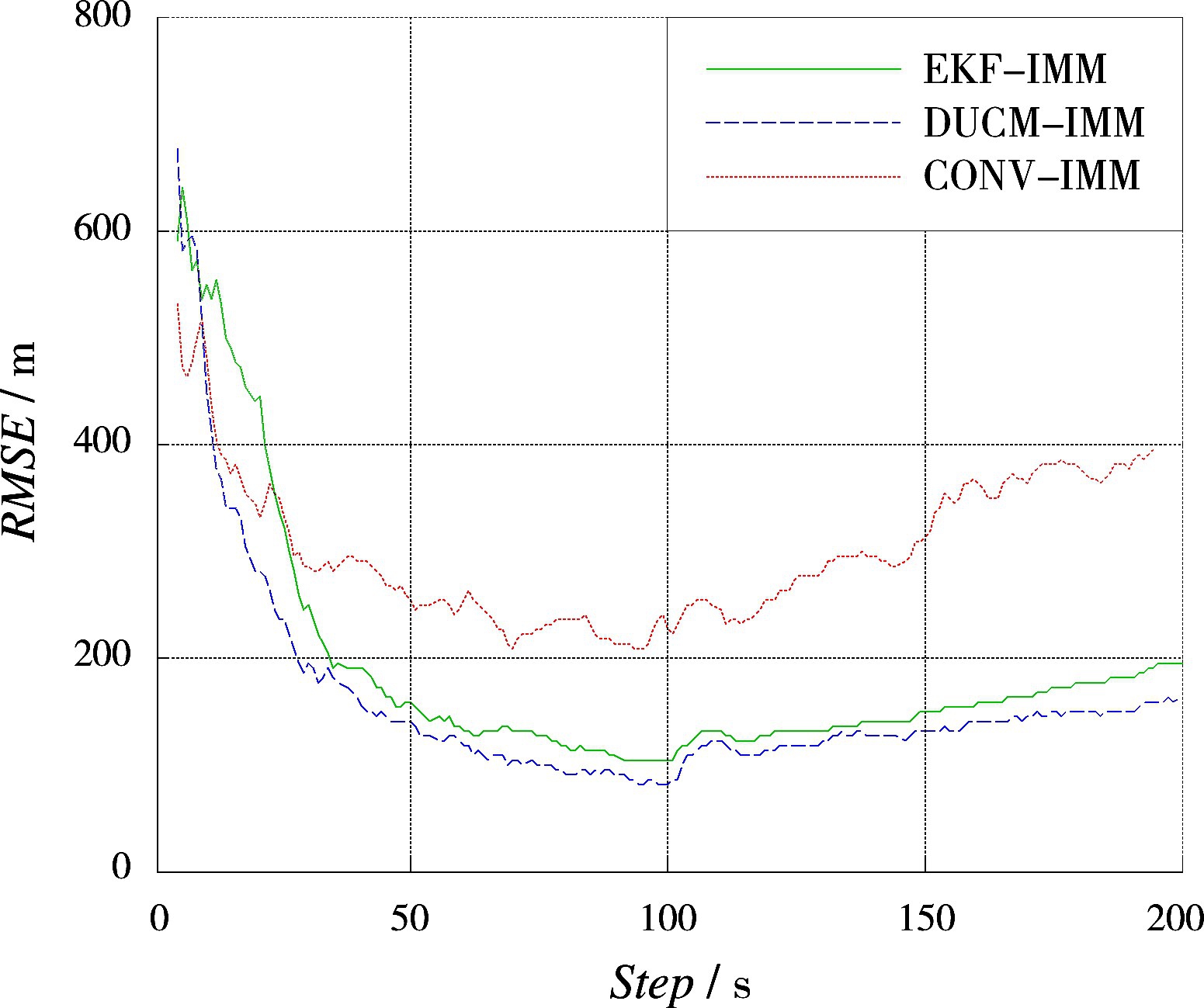
图2 场景2对应的RMSE曲线
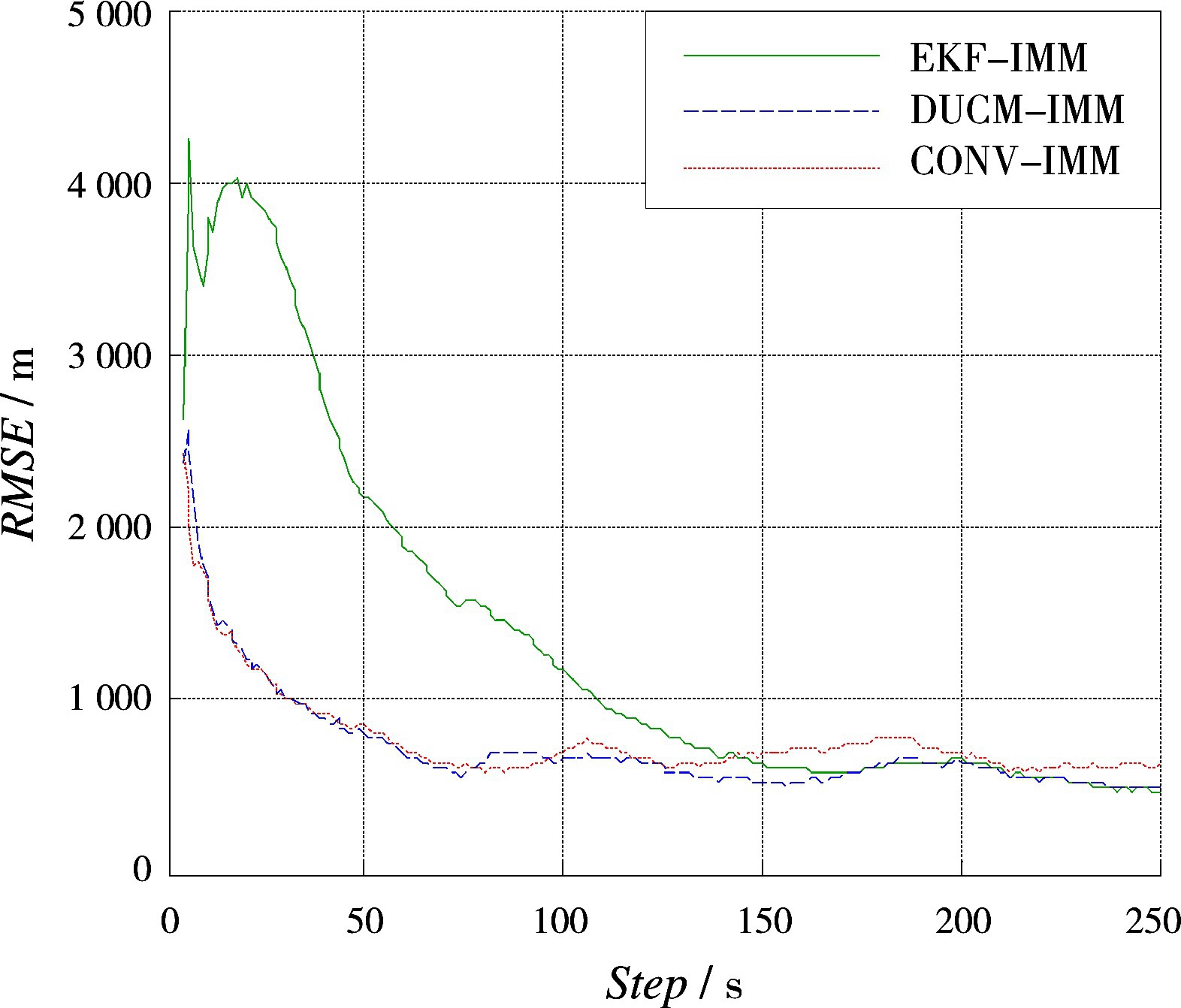
图3 场景3对应的RMSE曲线
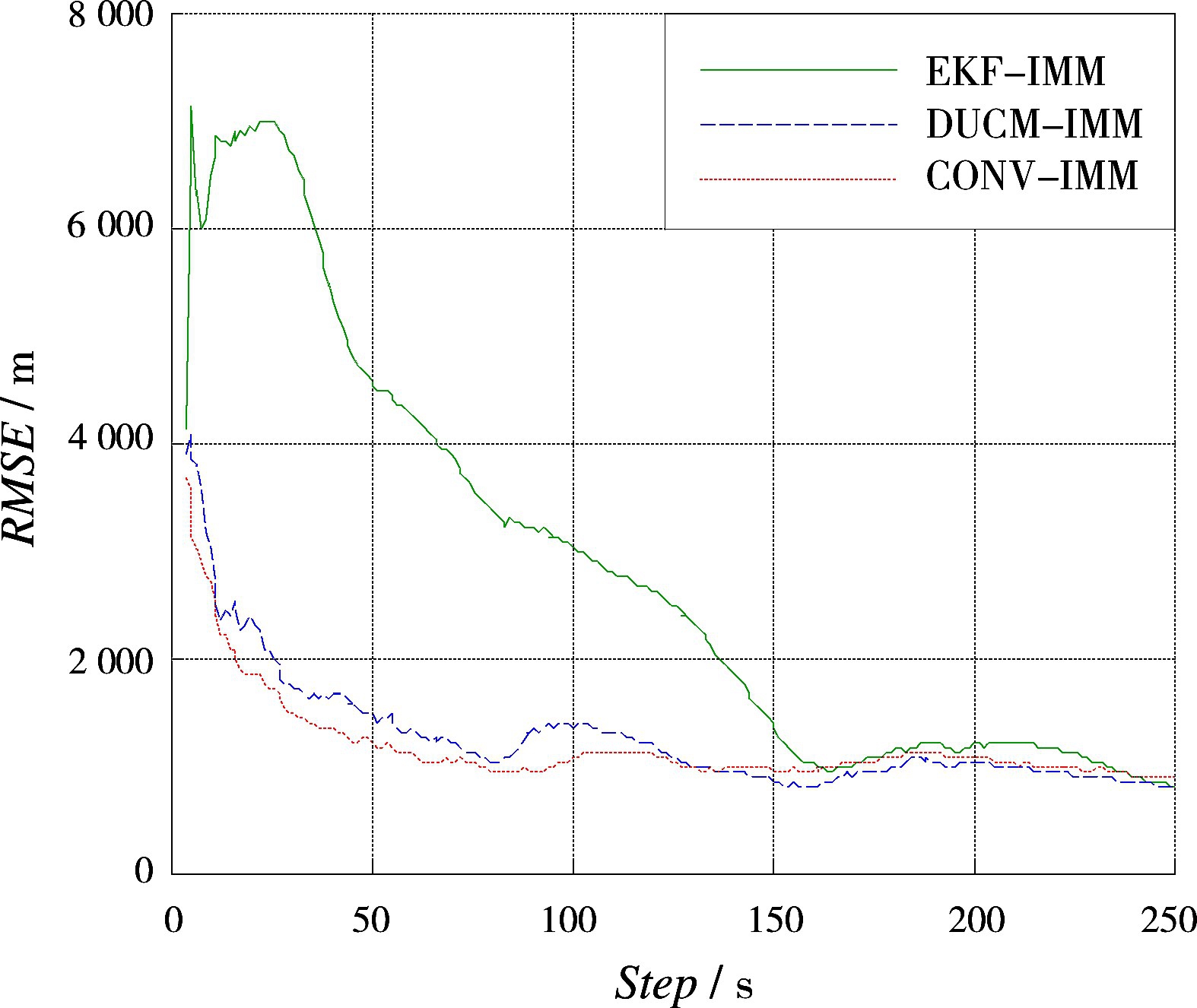
图4 场景4对应的RMSE曲线
场景1和场景2在极坐标系下获取量测信息,对应的斜距量测误差由3 m变至10 m,方位角误差由1°变至3°,其他参数不变。可以发现,EKFIMM在量测误差较大的情况下的RMES曲线收敛较慢,估计误差比DUCM-IMM的估计误差大。CONV-IMM位置估计误差最大,DUCM-IMM位置估计误差最小。这表明:在极坐标系下,与CONV-IMM算法、EKF-IMM算法相比,DUCMIMM算法跟踪性能有所改善。
场景3和场景4在球坐标系下获取量测信息,对应的斜距量测误差由5 m变至15 m,方位角误差由1.5°变至3°,其他参数不变。可以发现,EKF-IMM的RMSE曲线收敛慢,在跟踪初期估计误差较大,稳定后和DUCM-IMM位置估计误差接近。稳定后的CONV-IMM位置估计误差大于DUCMIMM位置估计误差。这表明:在球坐标系下,与CONV-IMM算法、EKF-IMM算法相比,DUCMIMM算法跟踪性能有所改善。
从所有仿真结果可以看出,由于传统量测转换会产生转换和估计偏差,CONV-IMM算法跟踪精度和模型概率变化准确度最差。EKF-IMM算法由于在线性处理过程中忽略了泰勒展开式的高阶项,导致在某些场景下收敛速度较慢。DUCMIMM算法利用预测值处理量测转换误差协方差,克服了量测转换算法固有的缺陷。它比EKFIMM跟踪精度更高,而且模型变化速度最快。
4 结束语
本文在考虑机动目标运动特性的情况下,提出了基于去相关无偏量测转换的交互多模算法。该算法以交互多模算法为基础,采用多个并行的滤波模型覆盖目标可能的运动模式,各个子滤波器采用去相关无偏量测转换方法解决系统量测与目标运动状态之间的非线性问题。通过仿真结果性能比较,该算法不仅解决了非线性估计问题,而且利用预测值消除了量测转换误差协方差和量测误差的相关性。与基于传统的量测转换交互多模型算法相比,具有更高的模型变化速度和跟踪精度。
参考文献:
[1]BAR-SHALOM Y,LIX R,KIRUBARAJAN T.Estimation with Applications to Tracking and Navigation:Theory,Algorithms,and Software[M].New York:Wiley,2001:441-466.
[2]ALI N H,HASSAN G M.Kalman Filter Tracking[J].International Journal of Computer Applications,2014,89(9):15-18.
[3]GOKCE M,KUZUOGLU M.Unscented Kalman Filter-Aided Gaussian Sum Filter[J].IET Radar,Sonar and Navigation,2015,9(5):589-599.
[4]SPITZMILLERJN,ADHAMIRR.Tracking with Estimate-Conditioned Debiased 3-D Converted Measurements[J].Intelligent Information Management,2015,2(4):1-16.
[5]SONG X,ZHOU Y,BAR-SHALOM Y.Unbiased Converted Measurements for Tracking[J].IEEE Trans on Aerospace and Electronic Systems,1998,34(3):1023-1027.
[6]DUAN Z S,HAN C Z,LI X R.Comments on“Unbiased Converted Measurements for Tracking”[J].IEEE Trans on Aerospace and Electronic Systems,2004,40(4):1374-1377.
[7]BORDONARO S,WILLETT P,BAR-SHALOM Y.Decorrelated Unbiased Converted Measurement Kalman Filter[J].IEEE Trans on Aerospace and Electronic Systems,2014,50(2):1431-1442.
