0 引言
目前关于探地雷达(Ground Penetrating Radar,GPR)电磁波在层状体系中的传播模型和介电特性模型反演缺乏一套严谨的理论,这严重制约了GPR无损技术的发展,使得GPR信号分析一直依赖简化公式或根据经验人工调试参数。现有研究成果大多数只能确保结构层单层厚度的精确检测,对结构层多层厚度及结构层参数反演的研究和其他道路指标的检测结果不尽人意。因此,开展高效准确的反演优化策略研究,探索层状结构GPR检测反演理论及其工程应用具有重要意义。
现有分层介质参数反演的手段主要分为时域和频域[1]两个方面。时域反演中传统的参数反演算法包括通过估计的回波信号幅度和时延等信息进行介质参数反演的剥层(Layer Stripping)反演法和基于电磁模型参数优化过程理论的高斯牛顿(Gauss Newton)反演法[2],Caorsi和Stasolla提出一种基于能量比的层剥离技术(Energy-Based Layer Stripping)能够在不同工作环境下重构分层介质的几何和电性能参数,但要求相邻的两个回波信号之间的时间间隔比发射脉冲持续时间长[3]。频域反演在薄层介质更具优势,秦瑶等利用电磁波在层状体系中的传输函数反演出地下层结构的厚度和广义反射系数[4],但这种方法无法解析出地下层的电性参数。
有鉴于此,本文结合时间延迟完备字典和稀疏自适应匹配追踪算法(Sparse Adaptive Matching Pursuit,SAMP)[5],以及基于能量比的层剥离技术提出了一种新的分层介质参数反演算法。该算法能够对探地雷达信号进行稀疏分解,估计信号的反射系数和时间延迟,并在此基础上实现分层介质的厚度和介电常数的估计。克服了层剥离估计精度较低和反卷积算法执行时间长等缺点,具有较短的执行时间和较高的估计精度。
1 解决方案
1.1 稀疏分解模型
GPR接收信号x(t)可建模为分层介质的广义反射系数矢量a(t)与雷达发射信号s(t)的卷积加上测量噪声及模型误差n(t),写成矩阵形式:
式中,X=[x(t1),x(t2),…,x(tN)]T,S=[s(t-τ1),s(t-τ2),…,s(t-τNT)]是一个经过Ψ描述后的与延时相关的托普利兹矩阵,α=[α1,α2,…,αNT]T,N=[n(t1),n(t2),…,n(tN)]T,广义反射系数可以通过去卷积计算α=S-1X[6]。不过这种方法很费时。利用稀疏表示(Sparse Representation,SR)[7]可以很有效且快速地解决这个问题,SR是利用一个过完备字典S∈RN×NT,N＜NT中的少量原子线性的表示一个原始信号,即
式中,P0是一个NP-Hard[8]问题。实际应用中,一般采用贪婪算法或凸松弛算法解决此问题。
1.2 构造过完备字典
SR的关键步骤是构造过完备字典,过完备字典的类型有多种,本文采用匹配字典,以与信号最匹配为原则构造原子,减少了搜索匹配原子过程中的计算量。
为了求解式(1),假设探测场景的每个网格都是均匀的,则每一个网格点的目标回波信号时延是可以计算的,则接收信号可以表示为
式中,X=[x(t1),x(t2),…,x(tN)],t1为起始测量时间,tN=t1+(N-1)Δt,Δt为采样时间间隔,N为时间采样总数。则N×NT维的矩阵Ψ的第j列可表示为
式中,τ(πj)为收发器到第j个网格点目标的双倍程时延,在不需要已知发射信号幅度的条件下,只需计算成像场景中各网格点到收发器的双程时延即可构造需要的字典。
1.3 基于稀疏约束的广义反射系数和时延估计
根据GPR信号传播理论,当雷达波在地下传播时,只有在不连续介质交界面处才会产生反射,因此广义反射系数矢量α(t)是稀疏的,从而可以利用该先验信息,将传统的盲估计问题转化为稀疏约束下的优化问题,即
式(5)可以被基于过完备字典的稀疏分解方法求出,SAMP算法的具体求解过程如下:
输入:N×NT的时延过完备字典Ψ,N×1维观测向量X,步长S。
输出:信号的稀疏表示系数估计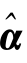
,含有各目标时延参数的原子集合Ψt1。
1)初始化r0=X,Λ0=Ø,L=S,t=1;
2)计算u=abs[ΨTrt-1](即计算〈rt-1,φj〉,1≤j≤NT),选择u中L个最大值,将这些值对应的Ψ的列序号j构成集合Sk(列集合序号);
3)令Ck=Λt-1∪Sk,Ψt={φj}(for allj∈Ck);
4)求X=Ψtαt的 最 小 二 乘 解:
5)从^αt中选出绝对值最大的L项记为
,对应的Ψt中的L列记为ΨtL,对应的Λ的列 序号记为ΛtL,更新集合F=ΛtL;
6)更新残差
7)如果残差rtnew=0,则停止迭代进入第8)步;如果 ‖rtnew‖ ≥ ‖rt-1‖2,更新步长L=L+S,返回第2)步继续迭代;前面两个条件依次都不满足,则Λt=F,rt=rtnew,t=t+1,如果t≤M则停止迭代进入第8)步,否则返回第2)步继续迭代;
8)重构所得
在ΛtM处有非零项,其值分别为最后一次迭代所得
注:得到
后,利用过完备字典可得重构信号
中的原子对应的时间参数即为各分界面的反射时延;
反射系数矢量则对应了各个回波的点反射率。
1.4 基于层剥离技术的分层介质参数反演
探地雷达收发系统距离分层介质上表面高度为d0,分层介质为K层水平分层的均匀非磁性介质。假设发射信号为s(t),x1(t)为第i-1层和第i层交界面的反射信号,εi和di分别为第i层的介电常数和厚度,在TM极化方式下,第i-1层和第i层交界面处的反射系数和双向透射系数分别为
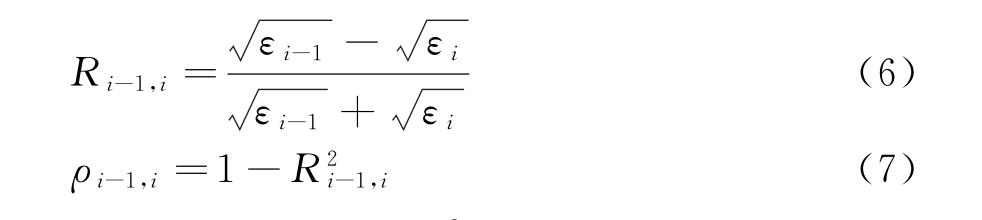
定义广义反射系数
(即点反射率)为各层反射回波与雷达发射波的电场强度之比,则利用传输线理论,可推导出每层的广义反射系数和接收信号模型,可公式化为
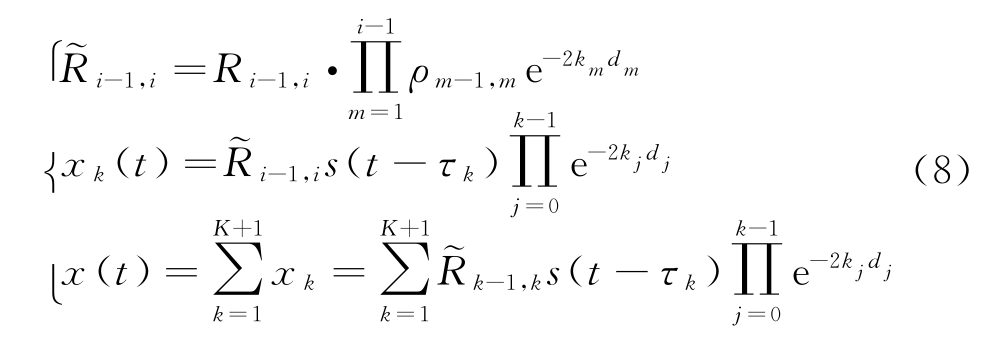
式中,ρm-1,m为第m-1层和第m层交界面处的双向透射系数,km,kj为电磁波在第m层和第j层介质中的波数,dm,dj为第m层和第j层介质厚度,τk为第k层界面反射信号的双倍程时延。估计出信号的时间延迟和广义反射系数之后,就可以利用层剥离算法(Layer Stripping)反演出每层介质的介电常数和厚度,其详细的反演过程如下:
1)由反卷积算法或SAMP算法估计反射系数矢量和各层界面时延;
2)通过公式
计算d0;
3)确定
和d0之后可以确定反射系数R0,1,进而可以通过公式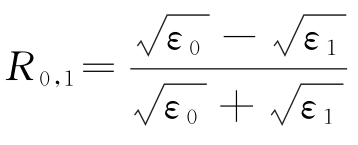
求出ε1;
4)通过公式
确定ρ0,1;
5)知道τ1,τ2和ε1后可以估算出d1和k1,再由公式
求出R1,2;
6)由公式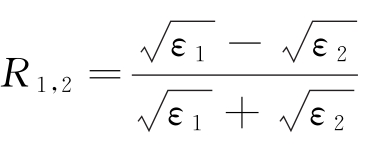
求出ε2;
7)整个参数反演过程就是以上几个步骤的重复迭代过程。
2 实验结果分析
2.1 回波信号有重叠时参数反演结果
探测场景各层的参数为L0(ε0=1.0,d0=0.40 m),L1(ε1=6.0,d1=0.05 m),L2(ε2=10.0,d2=0.19 m),信号幅度和时延估计结果如图1所示。
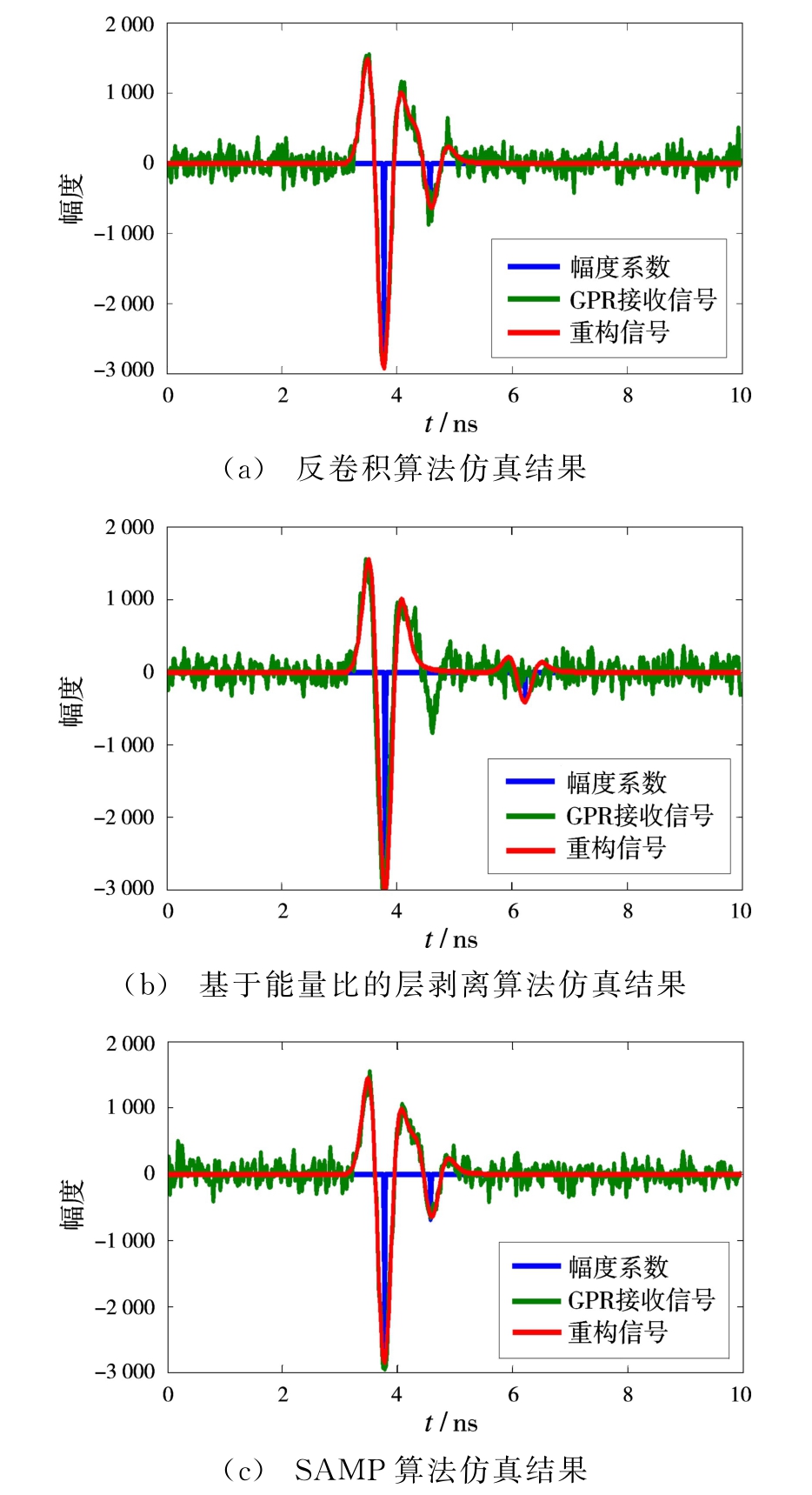
图1 3种算法在回波信号有重叠情况下的信号重构和时延估计结果
表1给出了3种方法的参数反演结果和所需要的执行时间。
表1 回波信号有重叠时3种方法反演结果和所需要的执行时间
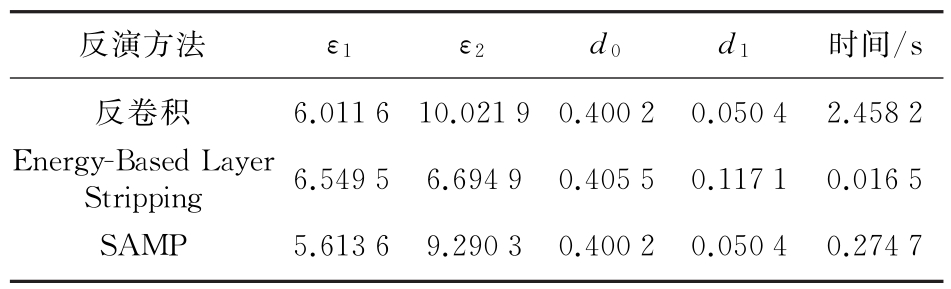
根据表中结果可知,当回波信号有重叠的情况下,反卷积方法对介质参数的估计结果是最精确的但很费时,Energy-Based Layer Stripping方法执行时间最短,但估计结果不精确,而SAMP方法估计结果及所需的执行时间都是比较合适的。因此,与反卷积和Energy-Based Layer Stripping方法相比SAMP方法有着明显的优势。
2.2 时间分辨率对处理结果的影响
定义BΔτ=B(2dε/c)为信号的时间处理分辨率,B为信号带宽,Δτ为能够区分两个反射信号的最小时间延迟。在实验中,给定带宽时,d1和ε1决定了回波信号是否有混叠。图2给出了当ε1=6.0固定不变,改变层厚度d1时回波信号幅度和时延估计结果,相应的各层介质参数反演结果如表2所示。
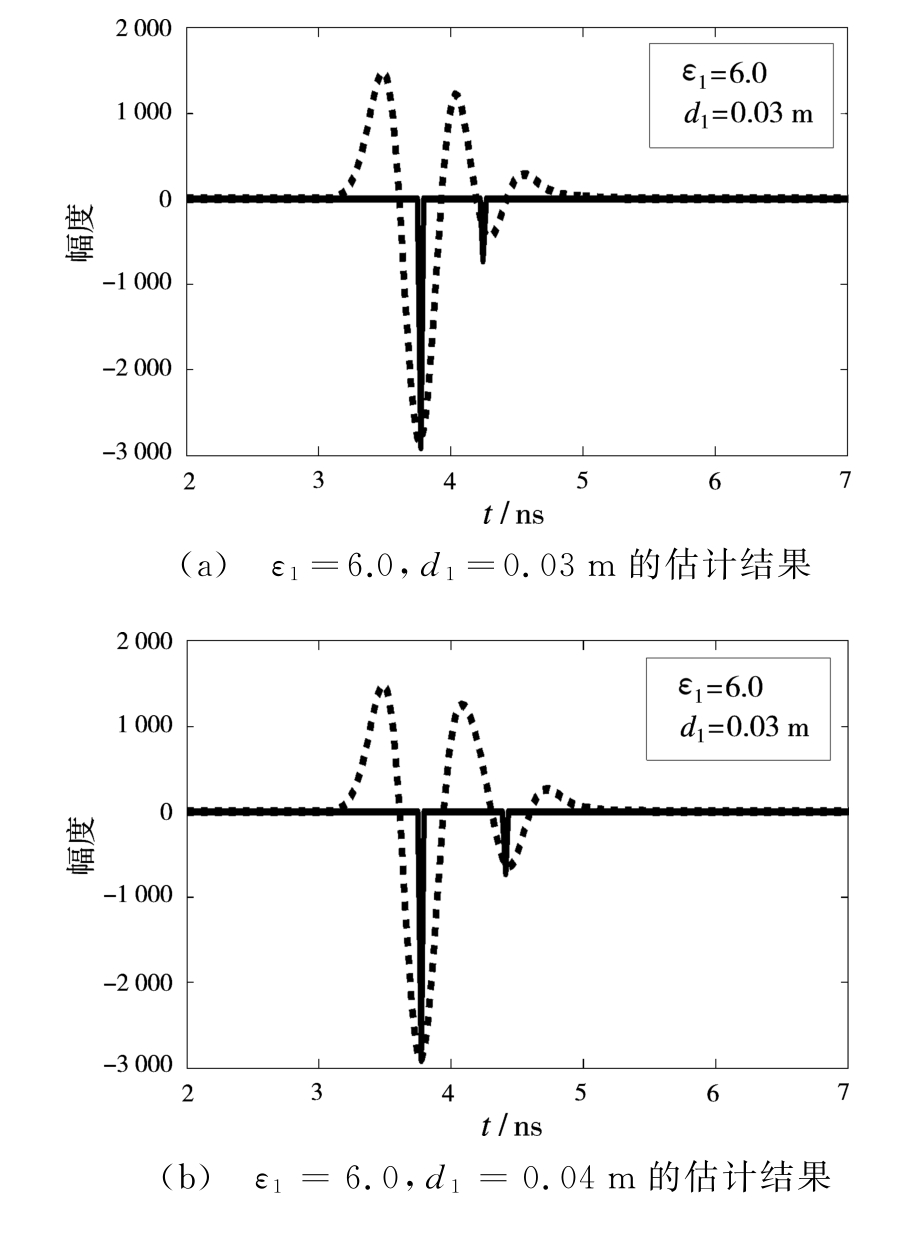
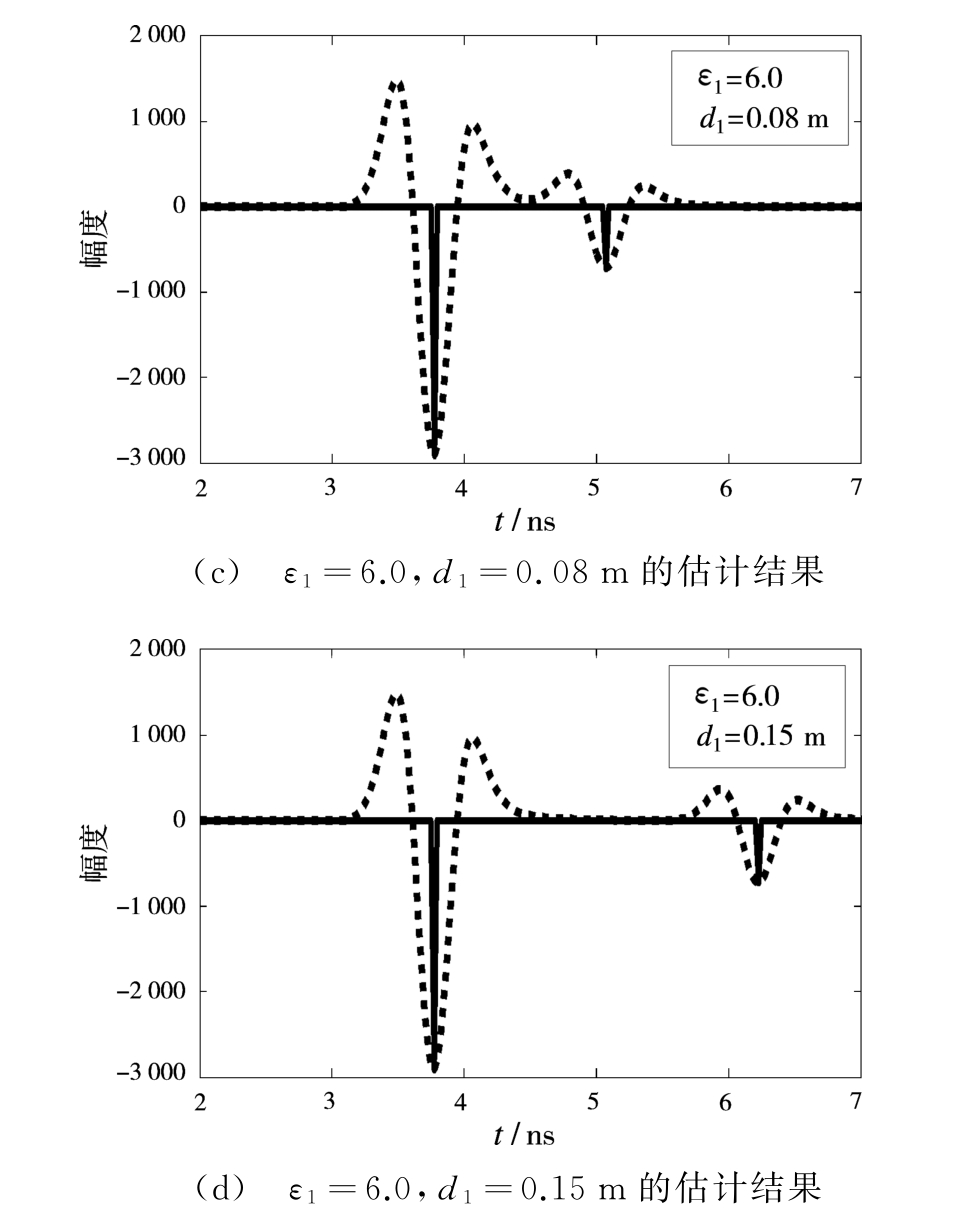
图2ε1=6.0固定不变,d1变化时回波信号幅度和时延估计结果
表2ε1=6.0不变,d1变化时薄层介质参数反演结果
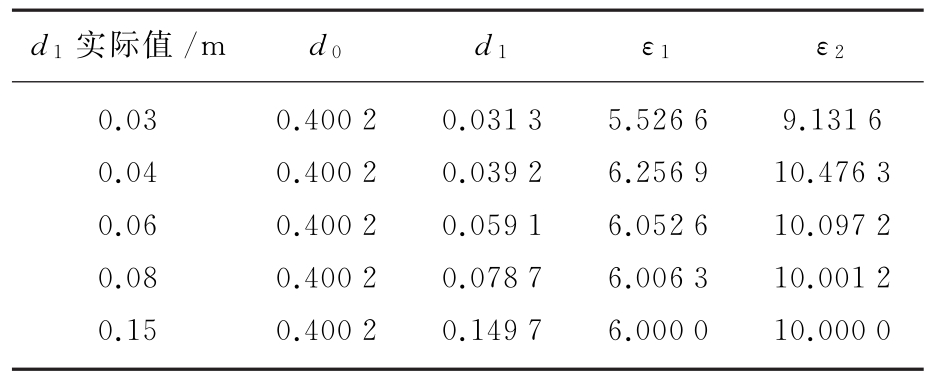
根据表中的参数反演结果,图3给出了参数估计误差与d1的关系曲线图,从图3可以看出当ε1不变时,分层介质参数估计误差总的趋势是随d1增大,即BΔτ增大而减小。
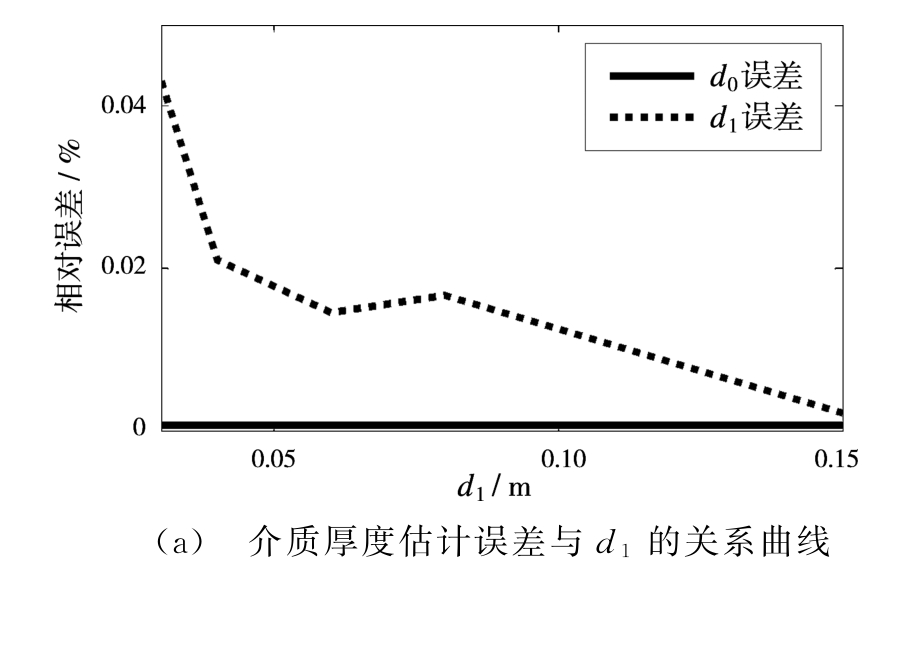
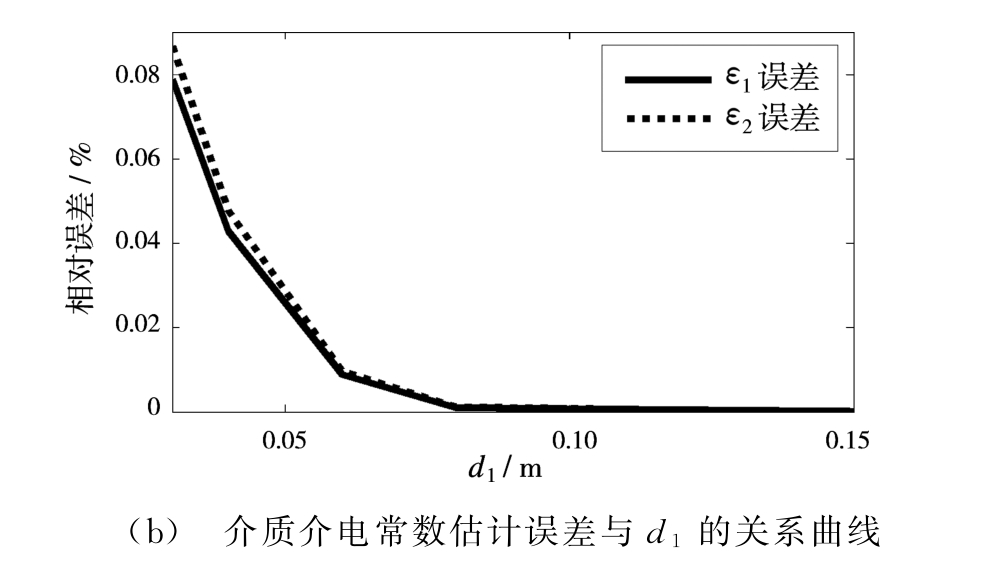
图3 参数估计误差与d1的关系曲线
相同地,图4给出了当d1=0.08 m固定不变,ε1变化时回波信号时延和幅度估计结果,相应的参数反演结果如表3所示,图5给出了参数估计误差与ε1的关系曲线图。
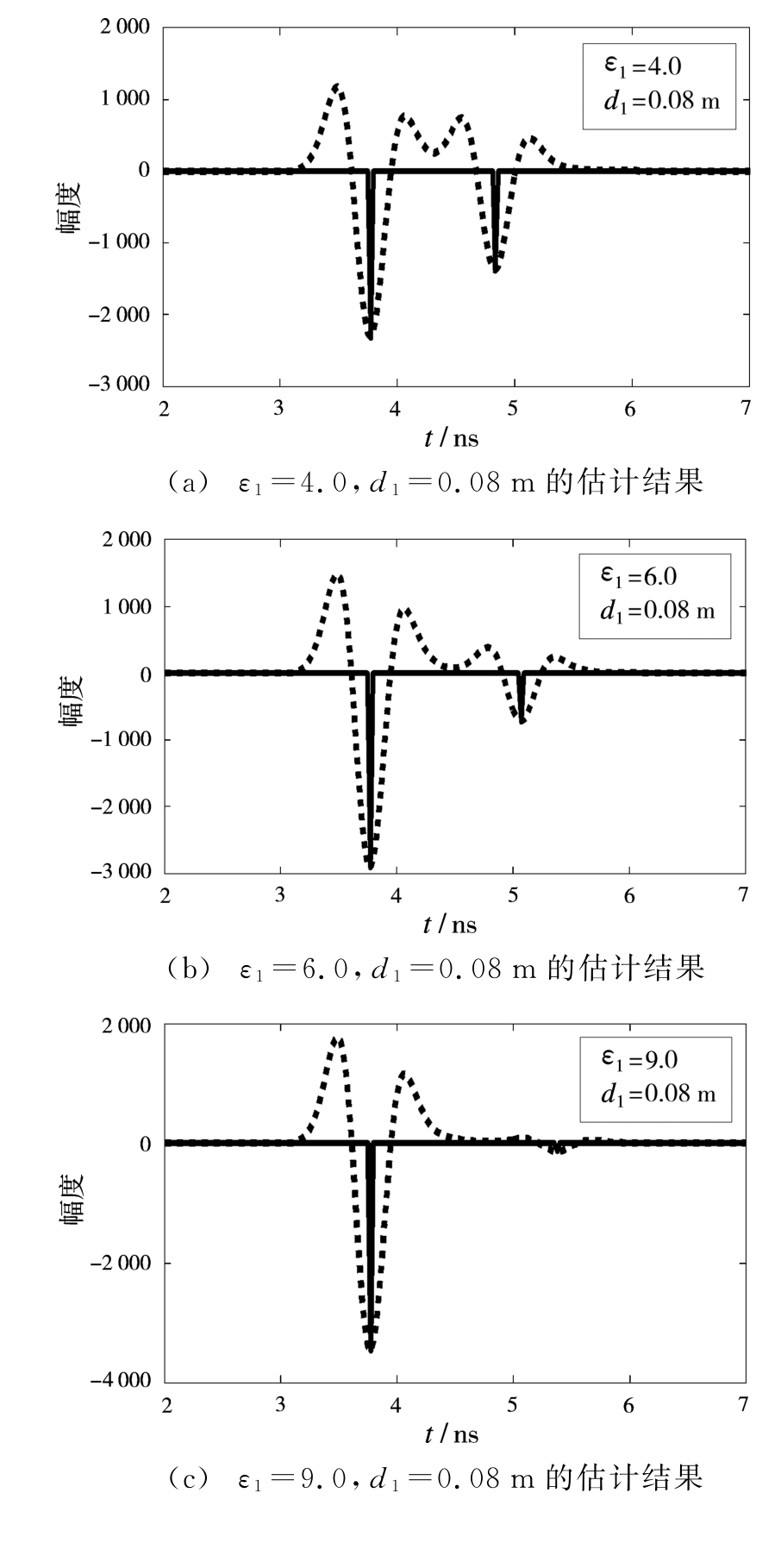
图4d1=0.08 m固定不变,ε1变化时回波信号幅度和时延估计结果
表3d1=0.08 m不变,ε1变化时薄层介质参数反演结果
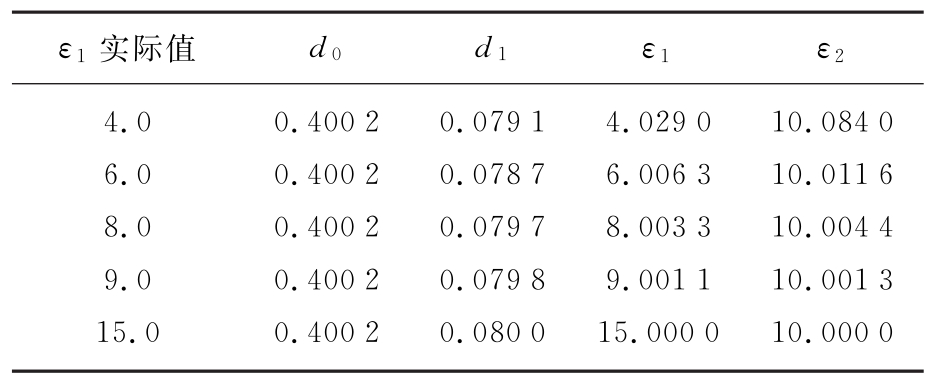
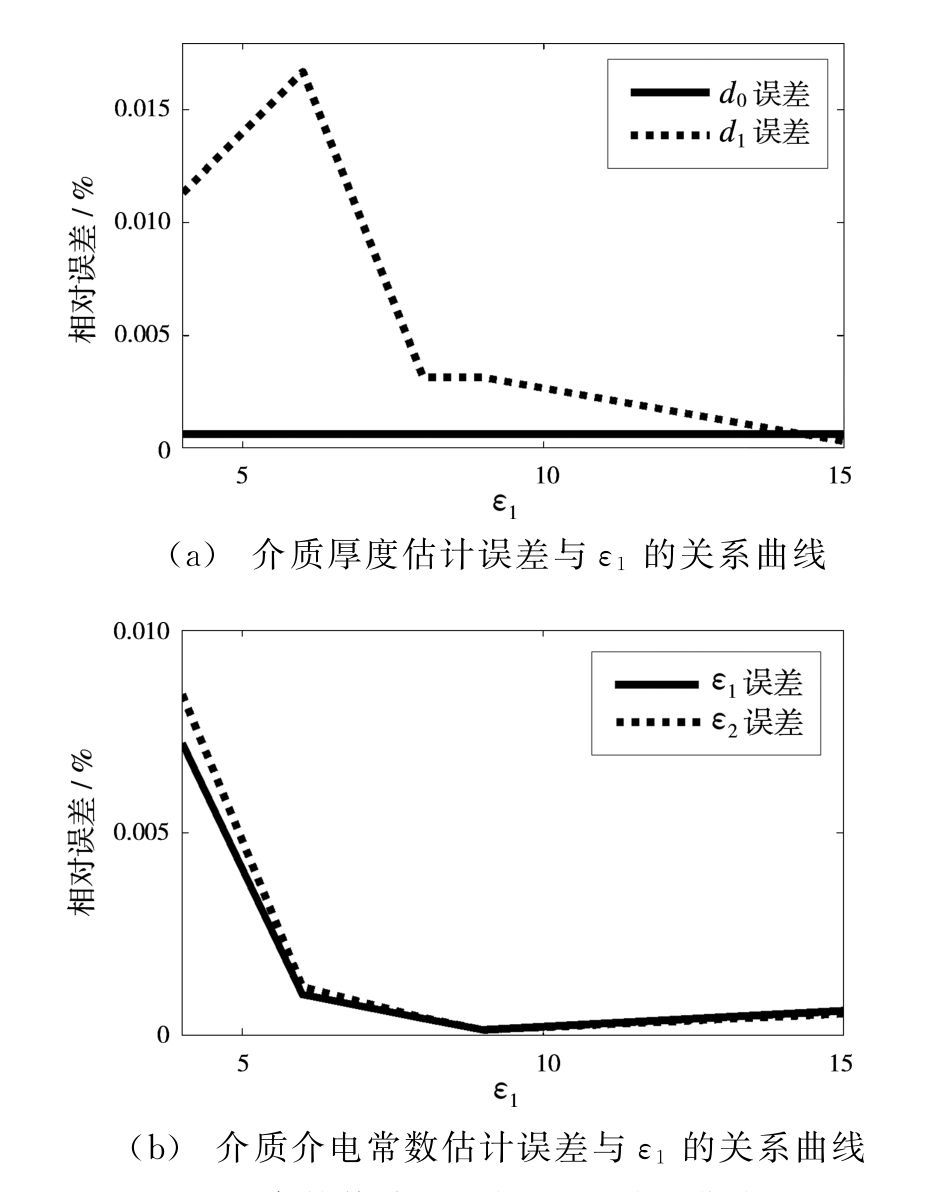
图5 参数估计误差与ε1的关系曲线
由图5可知,d1固定不变时,随着ε1增大即BΔτ的增大,ε1,ε2的估计误差减小。而厚度的估计误差与ε1的变化不成比例关系,但总的趋势是误差随BΔτ增大而减小。
3 结束语
本文主要研究GPR信号在分层介质中的传播模型和各层介质的参数反演问题。研究结果表明,SAMP使用过完备字典中少量的原子就能估算出回波信号时延和幅度,大大减少了运算时间。在此基础上利用Layer Stripping方法反演各层介质的参数。与传统的反卷积方法和单纯的Energy-Based Layer Stripping方法相比,该方法具有执行时间短和估计精度高等优点。
参考文献:
[1]HUANG Zhonglai,ZHANG Jianzhong.Determination of Parameters of Subsurface Layers Using GPR Spectral Inversion Method[J].IEEE Trans on Geoscience and Remote Sensing,2014,52(12):7527-7533.
[2]LIU Guangdong,ZHANG Kaiyin.A Time-Domain Gauss-Newton Inversion Algorithm for Solving Two-Dimensional Electromagnetic Inverse Scattering Problems[J].Acta Physica Sinica,2014,63(3):1-15.
[3]CAORSI S,STASOLLA M.A Layer Stripping Approach for EM Reconstruction of Stratified Media[J].IEEE Trans on Geoscience and Remote Sensing,2014,52(9):5855-5869.
[4]QIN Y,WANG Q.Using GPR Spectrum Inversion Method to Improve Recognition Ability of Thin-Layer[J].International Journal of Digital Content Technology and Its Applications,2012,6(10):136-143.
[5]康乃馨,何明浩,王冰切,等.基于压缩感知的多径LFM信号参数估计[J].雷达科学与技术,2016,14(3):291-296.KANG Naixin,HE Minghao,WANG Bingqie,et al.Parameter Estimation of Multipath LFM Signal Based on Compressive Sensing[J].Radar Science and Technology,2016,14(3):291-296.(in Chinese)
[6]ZHAO S,SHANGGUAN P,AL-QADI I L.Application of Regularized Deconvolution Technique for Predicting Pavement Thin Layer Thicknesses from Ground Penetrating Radar Data[J].NDT&E International,2015,73(3):1-7.
[7]郑纯丹,周代英.稀疏分解在雷达一维距离像中的应用[J].雷达科学与技术,2013,11(1):55-58.ZHENG Chundan,ZHOU Daiying.Research on High Resolution Range Profile Based on Sparse Decomposition in Radar[J].Radar Science and Technology,2013,11(1):55-58.(in Chinese)
[8]SHAO W,BOUZERDOUM A,PHUNG S L.Sparse Representation of GPR Traces with Application to Signal Classification[J].IEEE Trans on Geoscience and Remote Sensing,2013,51(7):3922-3930.
