0 引言
利用雷达探测并跟踪海面目标通常会受到海面杂波的影响[1]。当海杂波的强度较大时,由于经过海杂波反射后的雷达信号平均电平较高,目标检测受杂波和干扰信号幅度的影响,检测性能大大下降[2]。当雷达发射的波束较窄并且入射角度较小时,海杂波的反射信号可能变为“尖峰”回波信号,容易产生假目标[3]。在雷达处理中广泛采用脉冲间非相参积累技术,在目标回波强度弱于海杂波的条件下,探测性能不佳甚至失效,难以完成对小目标的监视[4]。
由于海杂波回波信号的多普勒频率分布较广,应用AMTI及其他频域滤波方法将产生一个问题。海杂波较广的多普勒频率分布使得测量杂波中心频率十分困难,较广的海杂波多普勒频率影响了杂波中心频率的测量。在海杂波背景下,传统的检测方法是建立精确的海杂波模型,主要的海杂波建模方法包括基于统计理论的方法[5-8]和基于分形理论的方法[9-11]。但不同海面的精确模型不同,同一海面不同雷达的精确模型也不相同,因此建立精确的海杂波模型方法不具有通用性。近几年随着人们对海杂波研究的深入,又提出一些新的方法。如文献[12]基于改进的Hough变换,通过对连续多脉冲的信号进行距离-时间维的排列,并进行时间向的二次采样,对采样后的采样点进行平滑得到子图,对平滑子图应用边缘检测然后进行Hough变换,在Hough域通过两级门限检测目标。该方法不依赖于海杂波模型,具有较高的启发性,但需要进行二次采样,计算量较大,较难满足雷达的实时性要求。
针对这种情况,本文提出一种基于多普勒频率相关性检测的抑制海杂波方法,本方法利用目标与海杂波在频率上的相关性差异,通过相关性检测门限区别目标与海杂波。本方法不依赖于海杂波模型,具有较好的通用性,实测海杂波数据的检验结果验证了该方法的正确性。
1 强海杂波背景下的目标检测
这里针对某远程预警雷达进行分析。该雷达发射线性调频脉冲,雷达回波经过海面及目标的散射后被雷达接收,接收到的回波经过脉冲压缩处理得到一维距离维数据。在该距离维数据中,目标信号与海尖峰信号都呈现为一小段尖峰,海杂波信号呈现为大能量的一段区域。将脉冲按发射时间排列,得到时间-距离维的信号。
在同一雷达波束宽度内,连续的多个脉冲里目标的多普勒频率基本保持不变。这是因为目标不会在十分短的时间内发生速度突变。而海杂波和海尖峰与海况有关且持续时间较短[13],海杂波的多普勒频率在连续几个脉冲内有较大变化。针对这一特点,在两级自适应滤波处理基础上增加频率相关性检测门限,可以在海杂波背景下检测出目标。为了算法描述的需要,下面结合实测海杂波数据进行分析说明。
1.1 实测海杂波数据分析说明
本文所用实测海杂波数据来源于中国东海岸某城市使用的一部远程预警雷达,该雷达发射线性调频脉冲信号。实测数据为该雷达在远程机扫模式下测得的低掠海角回波信号。将连续的M个脉冲按时间维进行排列,每个脉冲的采样点数为L,得到距离-时间维信号Pkl={pkl},pkl表示第k个脉冲的第l个采样点,其中k=1,2,…,M,l=1,2,…,L。本次试验中共采集10组数据,每一组数据包含471个脉冲,每个脉冲4 414个采样点。图1(a)是由一组数据组成,从图1(a)可看出,在第100~300个脉冲、1 400~3 300个采样点存在较大能量的海杂波,其能量大于60 dB。其中第302脉冲含有目标,如图1(b)所示。其中1 425采样点处为目标,而采样点1 724和1 691处为海杂波。由图1(b)可知,目标幅度为74.01 dB,采样点1 724处海杂波的幅度为56.51 dB,采样点1 691处海杂波的幅度为55.23 d B。
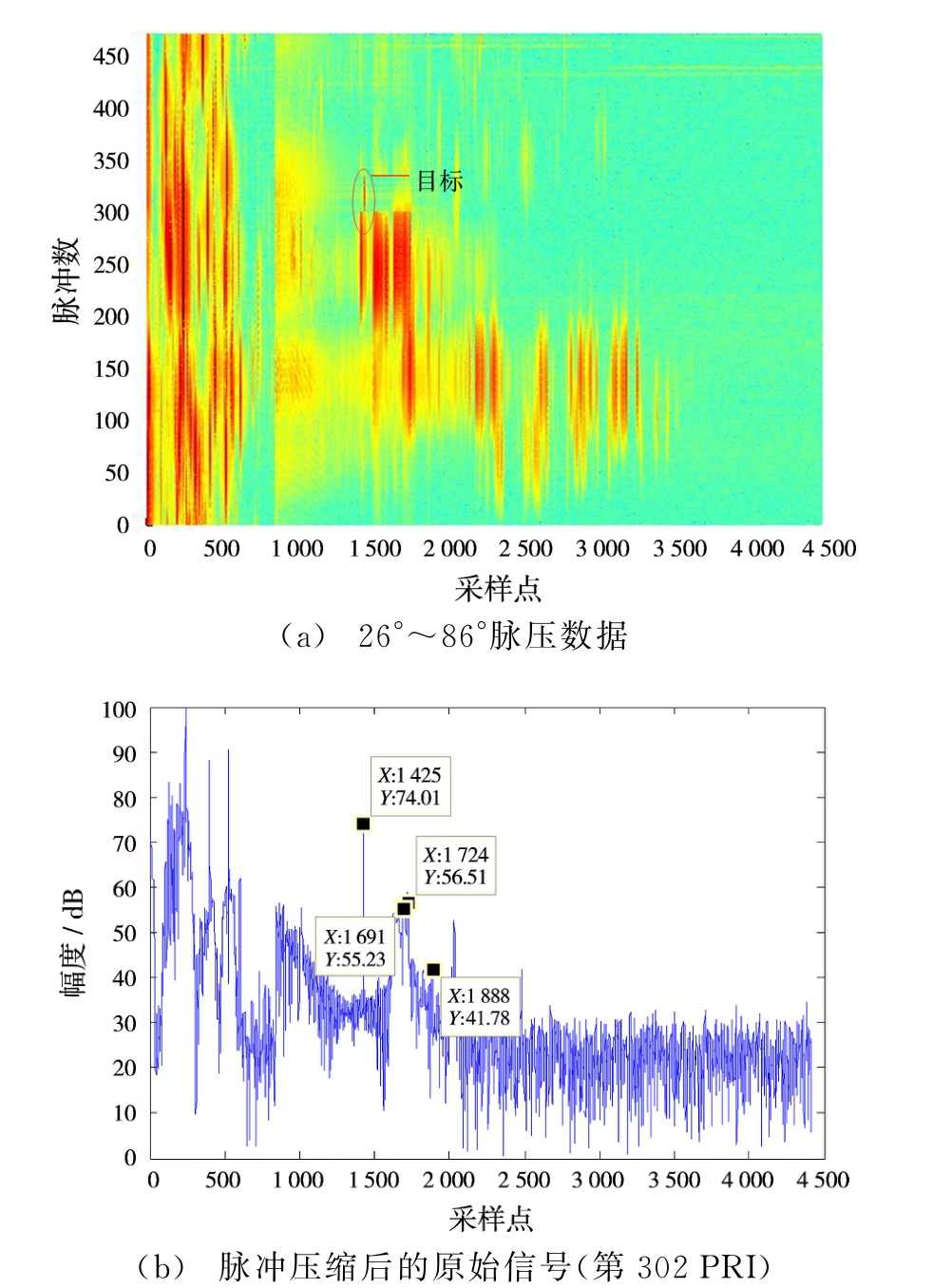
图1 海杂波脉压信号
1.2 两级自适应滤波处理算法
现有雷达采用的是传统AMTI滤波器与两级自适应滤波处理。AMTI处理在应对杂波频率与零频率差别较大时,杂波处的滤波器凹口无法设计较深,对较快运动速度的杂波不能很好地滤除。两阶自适应滤波器通过地物杂波滤波器,再进行自适应杂波滤波器滤除运动杂波,相较AMTI可以保证高速杂波处的滤波器凹口深度较深。为了保证对运动杂波多普勒频率的正确估计,需要先将脉冲信号经过地物杂波滤波器,以滤除地杂波的干扰。地物杂波滤波器系数w1,w2,…,wm,其中m为滤波器的阶数。地物杂波滤波器需要在零点有较深的凹口,且有较陡的上升曲线以保证零频率外的信号没有被抑制。本文以五阶FIR滤波器为例。
将脉压后的数据经过地物杂波滤波器,所得的对消后的信号满足下式:
式中,Skl为第k个脉冲、第l个采样点对消后的值,P=[pkl,…,p(k+m-1)l]为第k到第k+m-1个脉冲、第l个采样点的值,W=[w1,…,wm]为对应m个脉冲的对消系数。
上述实测数据经过式(1)对消后,得到对消后的距离-时间维信号。海杂波具有一定的速度,使用地物杂波滤波器不能滤除海杂波,因此需要进行二级滤波处理。
通过隔周测频[14]方法估计运动杂波多普勒频率中心与谱宽,设计二级杂波自适应滤波器,对消处理后的信号如图2(a)所示。通过图2(a)与图1(a)对比可知,自适应动目标滤波器进行动目标显示不能将强海杂波区域抑制。根据图2(b)与图1(b)的对比也可看出,强海杂波的能量并没有因为设计自适应动杂波滤波器而滤除。
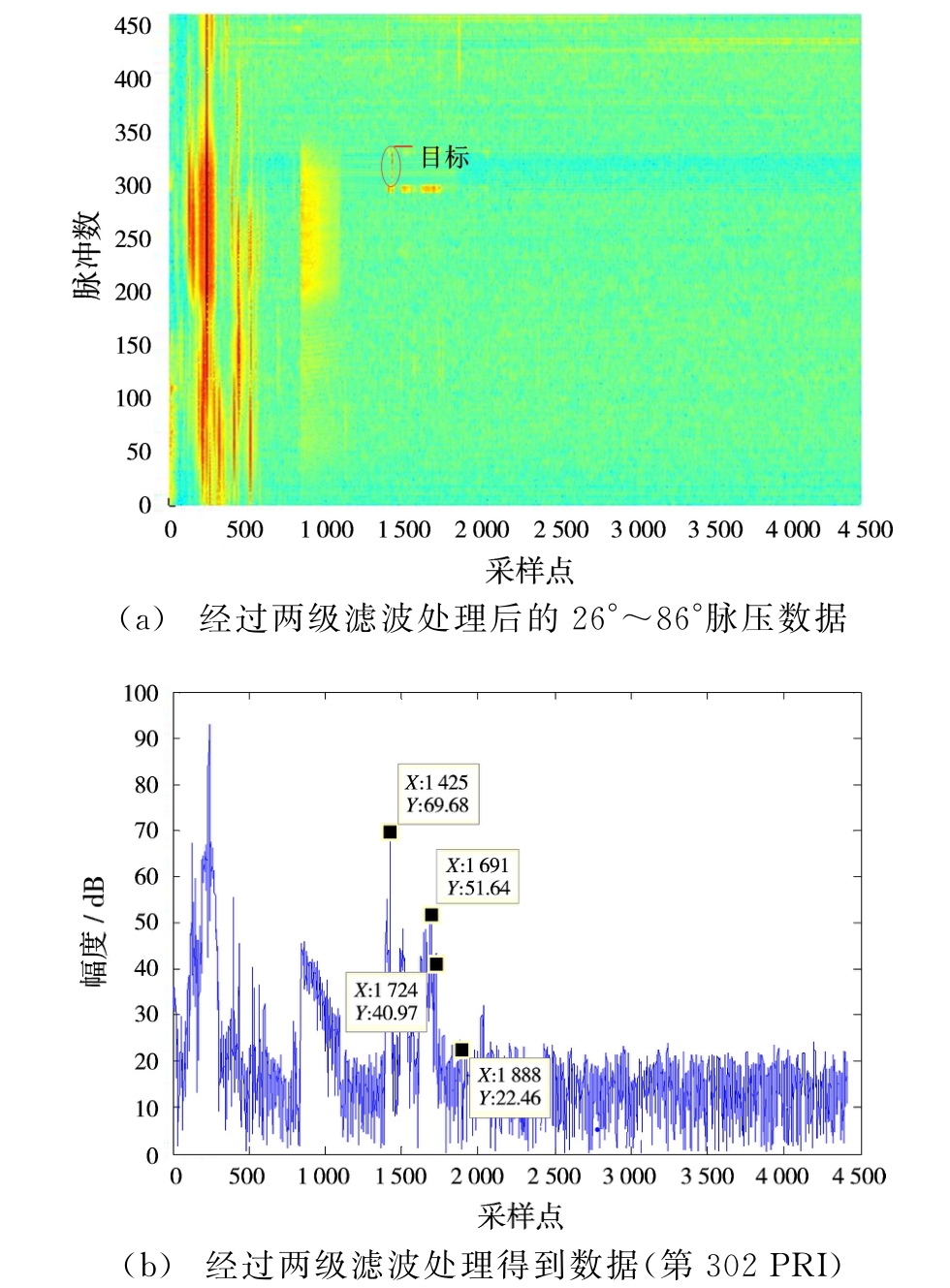
图2 两级滤波处理后的数据
1.3 多普勒频率相关性检测方法
在连续多个脉冲时间内,目标的速度不会在几个微秒时间内发生突变,因此目标在连续几个脉冲中的多普勒频率具有很强的相关性,通过实测数据的实验,目标在连续5个脉冲中的多普勒频率相关性基本维持在0.98以上。而海杂波在很短时间内其多普勒相关性较高,但若时间稍长其多普勒频率相关性会减弱很多,而目标在一个波束宽度内的多普勒频率相关性都保持在较高水平。
对连续多个脉冲的目标长度采样点两两进行互相关变换。假设一个脉冲目标长度多普勒频率为wi1,wi2,…,wik,其中wik为i个脉冲、第k个采样点对应的多普勒频率,1~k为目标电平宽度。选取M个脉冲,两两进行互相关运算为例:
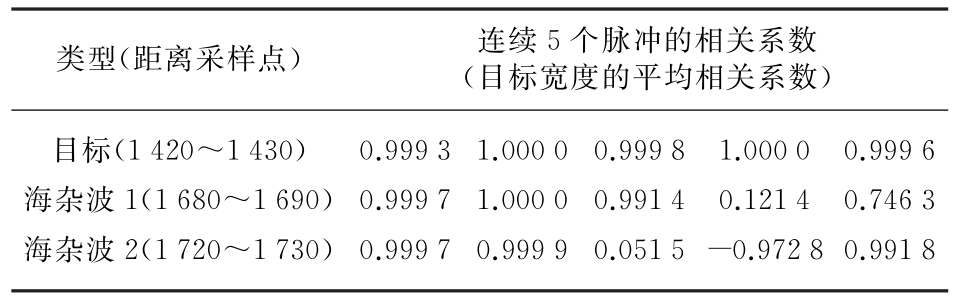
式中,Xi=[wi1,wi2,…,wik],Xi+1=[w(i+1)1,w(i+1)2,…,w(i+1)k]。Xi,Xi+1为两个连续脉冲间的目标采样宽度的多普勒频率点。对雷达回波脉压后得到的距离-时间维信号滑动应用式(2),即得到距离-时间维信号两两的相关性。再经过目标宽度门限筛选出在目标宽度门限范围内满足相关性高的采样点,筛选出的采样点作为两阶滤波处理后的目标门限判别方式。针对第302 PRI信号,目标点位置为1 425采样点处,目标宽度为10个采样点。由表1可知,目标、海杂波1、海杂波2在目标宽度内的相关性。
表1 目标与杂波相关性(归一化平均相关系数)
雷达回波脉压后的距离-时间维信号经过多普勒频率相关性检测后,进行两级自适应滤波处理。滤波后的距离-时间维信号经过拟目标点筛选,将
表1中,目标在连续5个采样点中的相关性都接近于1,而两处海杂波的相关性则不稳定。在一个波束宽度内,若采样点相关性都较强,便记录为拟目标点。不在拟目标点的信号进行幅度归一,信号幅度归一即保证信号的相位不变,只将幅度值归一到一个平均噪声值。得到最终处理后的信号,如图3(a)所示。存在目标的第302 PRI的脉冲信号经过多普勒频率相关方法处理后如图3(b)所示。对比图3(a)、图2(a)及表1可知,海杂波在一个波束宽度内多普勒频率相关性有较大波动,而目标在此区间基本保持较高的相关性,因此经过多普勒频率相关方法处理后的脉压信号中,海杂波信号已经被归一化到平均噪声中,后期进行恒虚警检测就可以筛选出目标。
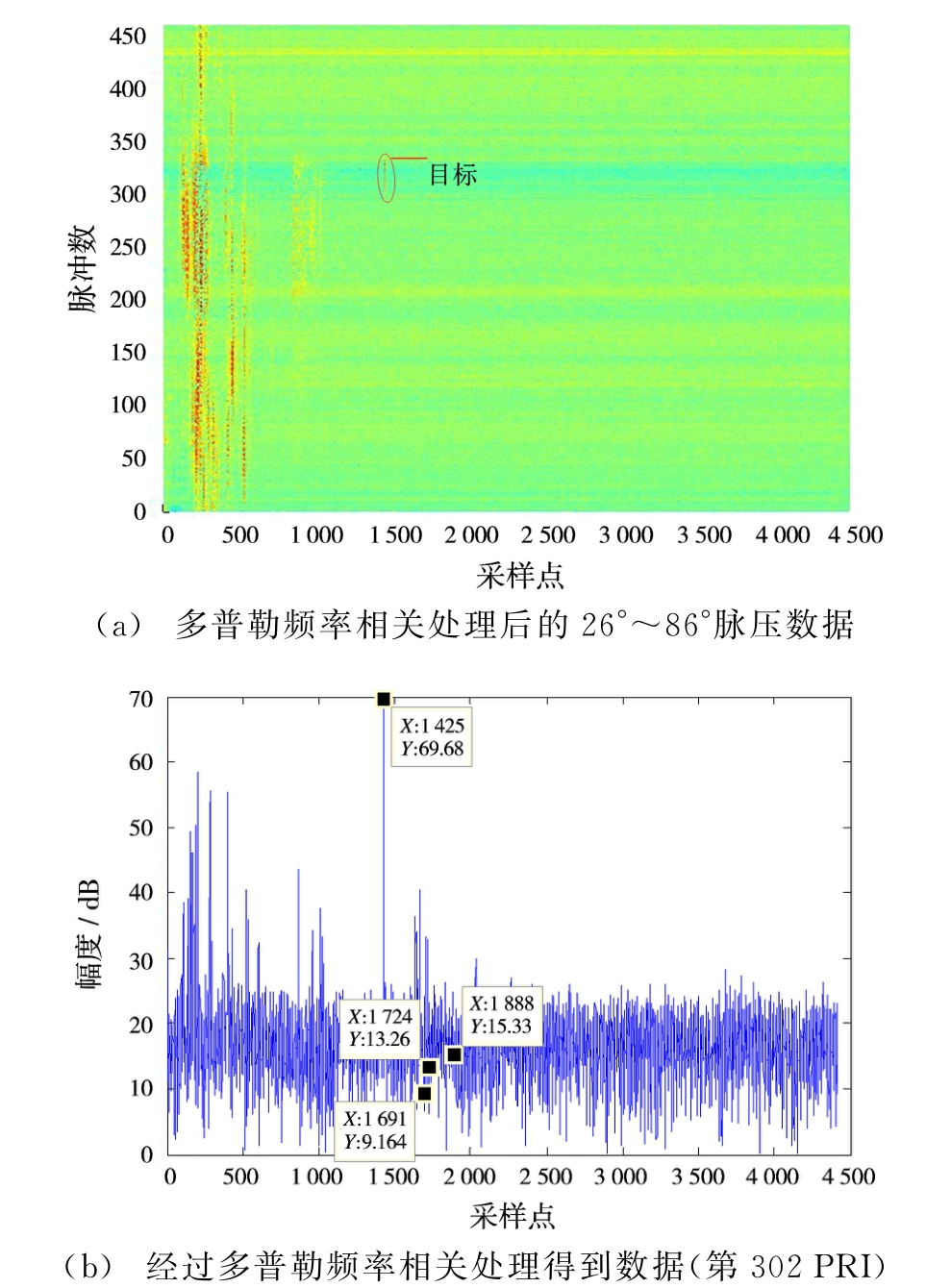
图3 多普勒频率相关方法处理后的数据
2 实测数据结果及分析
为了验证本文所提方法的正确性和有效性,这里利用实测的海杂波数据对本文方法的性能进行实验验证。多普勒频率相关法的处理流程如图4所示。在实测数据Data Number1中加入两个具有不同速度的目标A1,A2进行仿真目标在强海杂波背景下的情况。两模拟目标的径向速度分别为650 km/h(目标A1)与883 km/h(目标A2),距离雷达219.75 km。实验雷达波束宽度5°,机扫方式一个波束内共35个连续脉冲。含有目标A1和目标A2的两组脉冲分别为第241~245 PRI和第301~305 PRI。目标位置在第1 425采样点附近。对这两组脉冲进行多普勒测频。
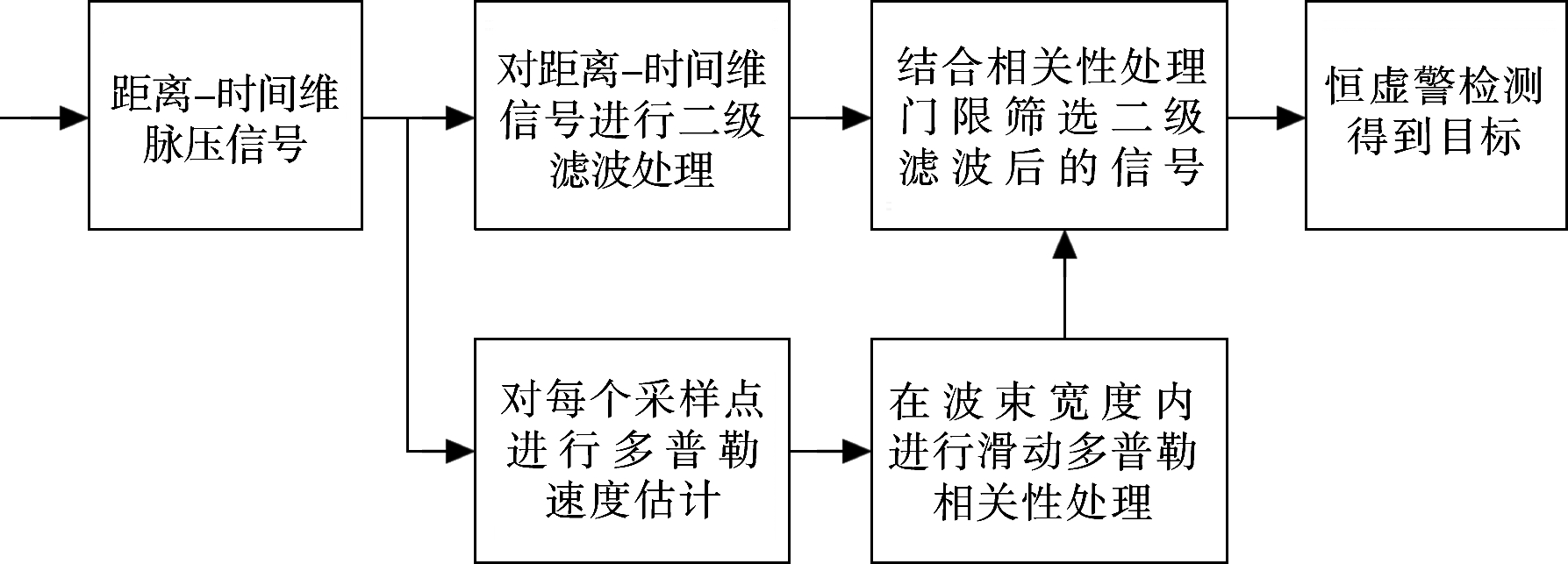
图4 多普勒频率相关算法流程图
两组脉冲进行多普勒频率相关处理,以连续5脉冲进行滑动相关处理。两组脉冲处理后的相关性如图5所示。由图5可知,目标处采样点的相关性均在0.98之上,保持在较高水平。从图5(a)可以看出,由于海杂波的频率与海况有关且持续时间较短,连续多组脉冲之间的相关性并不稳定,因而海杂波的多普勒频率相关性不能稳定在一个固定值附近。经过多普勒频率相关筛选后的采样点即为拟目标点,经过多普勒频率相关处理后剔除了部分杂波分量。之后对距离-时间维信号进行两级滤波处理。
两个目标处信号仅经过二级滤波的两个目标信号脉冲分别如图6(a)、图6(c)所示,而经过多普勒频率相关性方法处理的信号如图6(b)、图6(d)所示。两种方法对两目标的改善因子如表2所示。
表2 两级滤波对消与多普勒相关性对消的改善因子
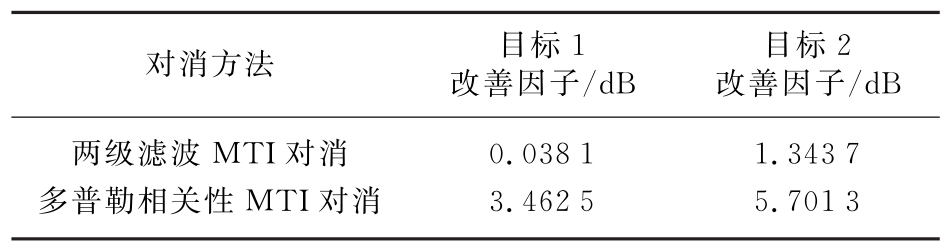
多普勒频率相关算法的改善因子较传统两级滤波MTI算法的改善因子增强了3 d B左右。对比图6(a)和图6(b)、图6(c)和图6(d)可以发现,经过多普勒频率相关算法可以抑制大部分强海杂波,该方法对于滤波器无法滤出的海尖峰等易形成假目标的海杂波具有较强的剔除能力,对大片的低速海杂波则经过两级滤波将其滤除。通过实验验证了该方法可以在强海杂波环境下有效地抑制杂波,提高了雷达对目标的检测概率。
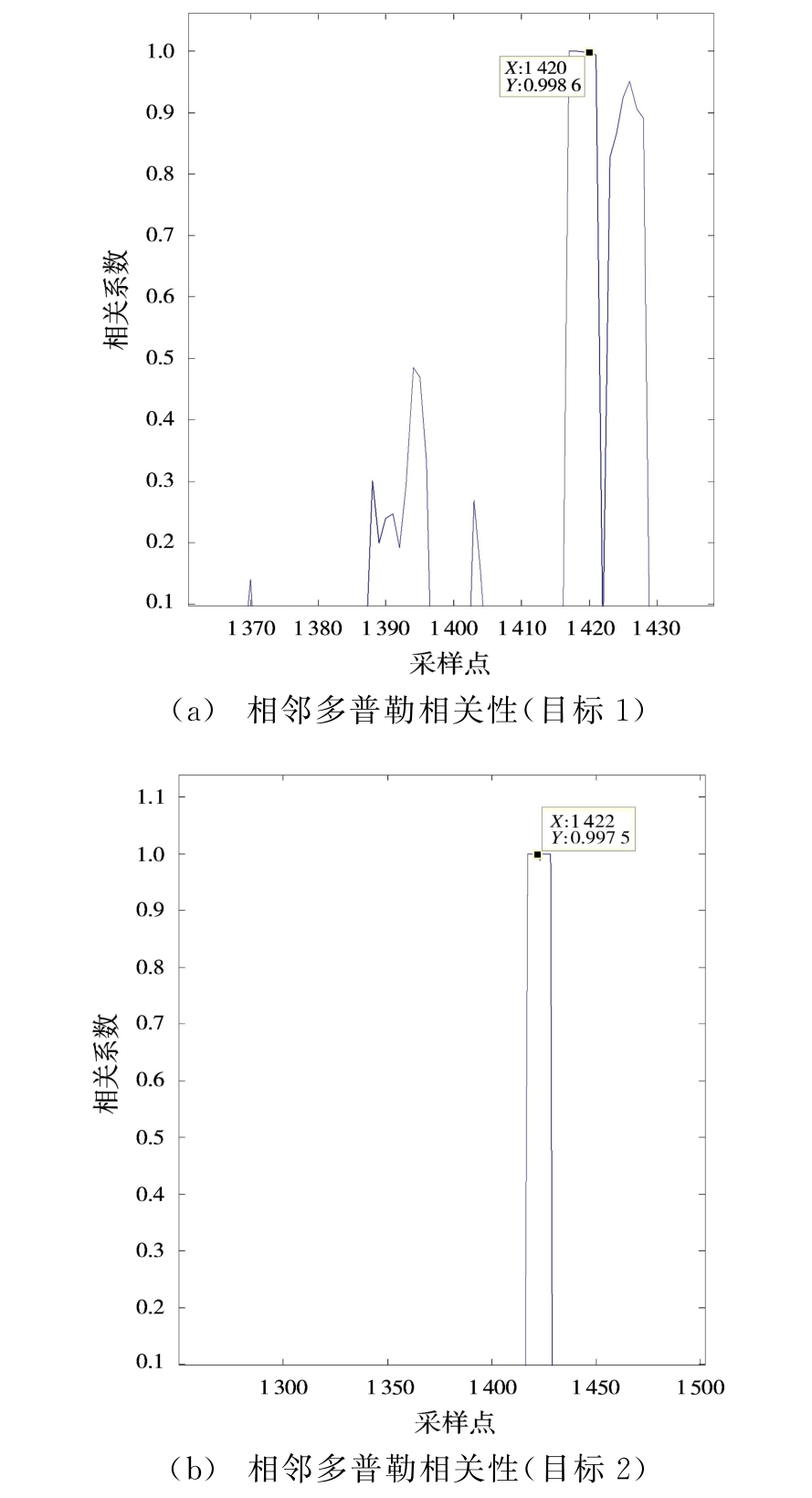
图5 目标脉冲的相关性
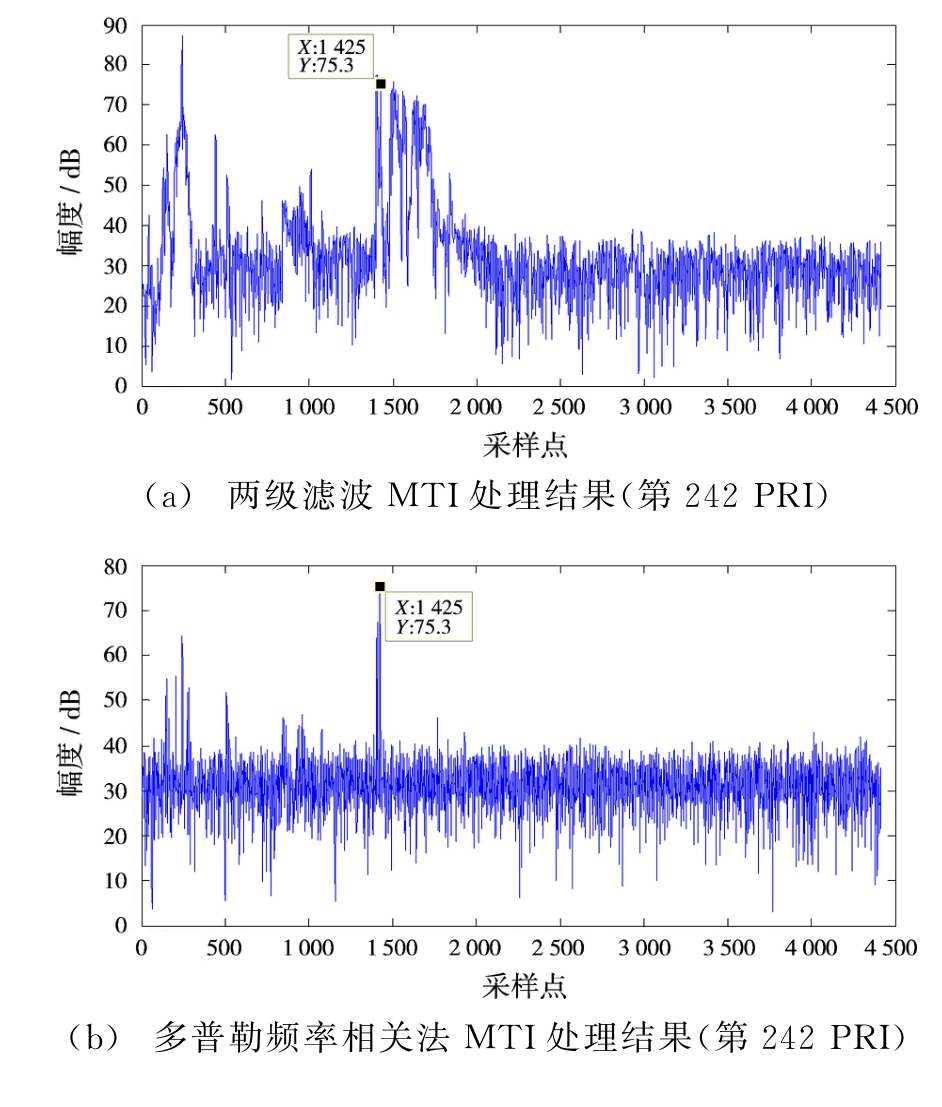
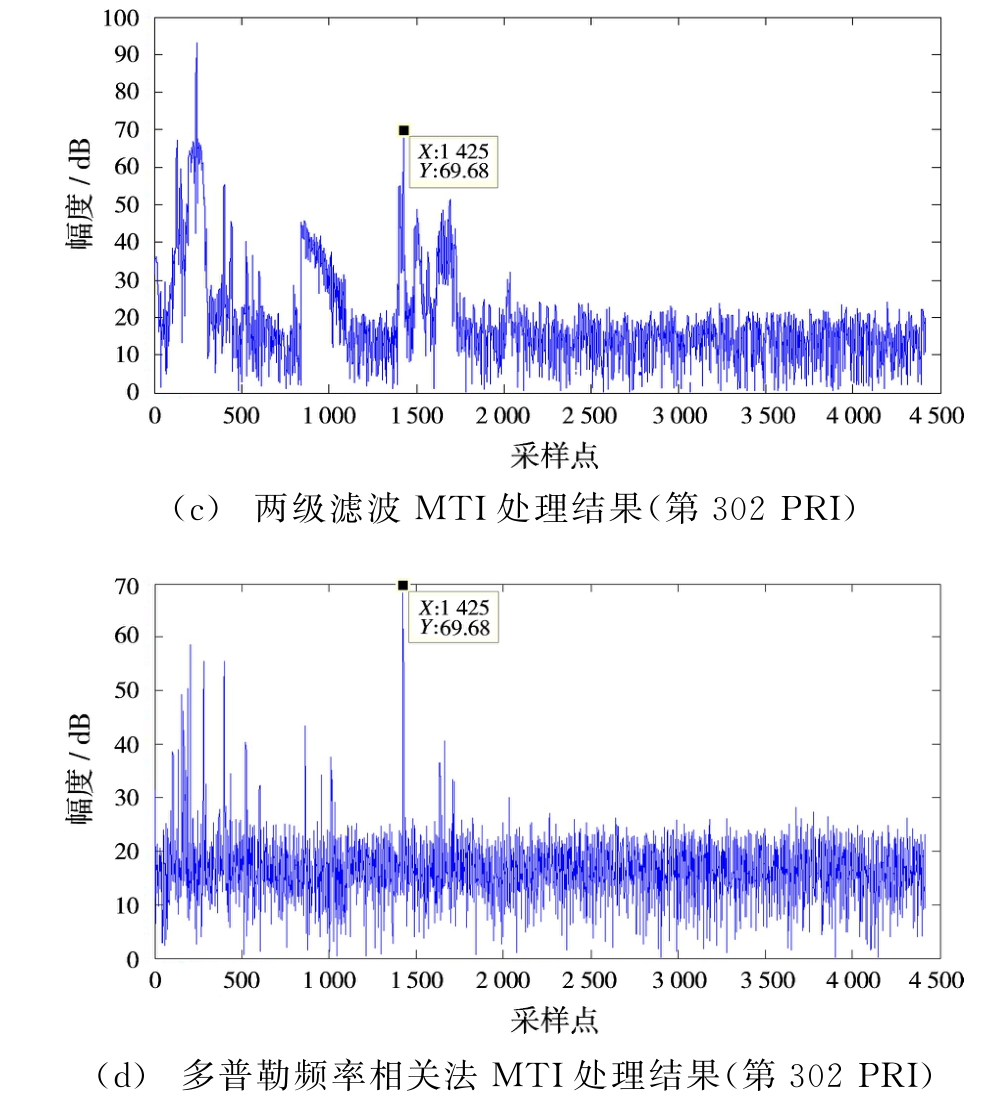
图6 传统二级滤波MTI对消处理结果与多普勒频率相关MTI对消处理结果比较
3 结束语
本文提出了一种改进型的两级滤波处理方法,该方法不依赖于海杂波模型。根据强海杂波中目标在连续多脉冲中多普勒频率相关性较高,海杂波在连续脉冲中相关性有波动这一特点,应用多普勒频率相关方法,计算出每个脉冲的多普勒频率,通过波束宽度及连续较高的相关性筛选出拟目标位置。对距离-时间维信号进行两级滤波处理,结合拟目标筛选得到目标。该方法可以在强海杂波背景下检测出运动目标,且由于计算量较低,具有较高的工程应用。实测数据的处理结果验证了该方法的有效性和实用性。当海杂波多普勒频率相关性与目标很接近时,该方法很难剃除这一类的杂波,这一类杂波表现为假目标。后续需要进行更深层次的研究,寻找去除这类海杂波的方法。
参考文献:
[1]何友,黄勇,关键,等.海杂波中的雷达目标检测技术综述[J].现代雷达,2014,36(12):1-9.
[2]曾浩,李洁,鉴福升.强海杂波环境下目标检测方法对比分析[J].雷达科学与技术,2015,13(1):33-36.ZENG Hao,LI Jie,JIAN Fusheng.Comparative Analysis of Target Detection Methods in Strong Sea Clutter Background[J].Radar Science and Technology,2015,13(1):33-36.(in Chinese)
[3]GRECO M,STINCO P,GINI F.Identification and Analysis of Sea Radar Clutter Spikes[J].IET Radar,Sonar and Navigation,2010,4(2):239-250.
[4]司军,赵中兴,吴俭,等.基于时间相关性的海面小目标检测技术[J].雷达科学与技术,2016,14(3):261-266.SI Jun,ZHAO Zhongxing,WU Jian,et al.Detection Technique of Dim Target in Sea Clutter Based on Time-Coherent Characteristic[J].Radar Science and Technology,2016,14(3):261-266.(in Chinese)
[5]王小英,陈常龙,尹俊平.正态分布和瑞利分布混合情形下的参数估计及分类问题[J].数学建模及其应用,2016,5(3):25-30.
[6]谭龙,陈秋菊,吴惟诚,等.远程预警雷达海杂波信号仿真[J].电子信息对抗技术,2016,31(4):79-82.
[7]马红星,陈思佳.水面杂波背景的统计MIMO雷达检测方法研究[J].雷达科学与技术,2015,13(5):479-484.MA Hongxing,CHEN Sijia.Statistical MIMO Radar Detection Approaches Against Water Clutter[J].Radar Science and Technology,2015,13(5):479-484.(in Chinese)
[8]CARRETERO-MOYA J,GISMERO-MENOYO J,BLANCO-DEL-CAMPO A,et al.Statistical Analysis of a High-Resolution Sea-Clutter Database[J].IEEE Trans on Geoscience and Remote Sensing,2010,48(4):2024-2037.
[9]鲍星星.基于加权组合的海杂波多重分形建模方法[J].电子设计工程,2016,24(4):32-34.
[10]王磊,金丹,察豪.实测海杂波数据的多重分形特性分析[J].现代雷达,2016,38(10):32-35.
[11]刘宁波,关键,张建.基于分形可变步长LMS算法的海杂波中微弱目标检测[J].电子与信息学报,2010,32(2):371-376.
[12]左磊,李明,张晓伟,等.基于改进Hough变换的海面微弱目标检测[J].电子与信息学报,2012,34(4):923-928.
[13]PANAGOPOULOS S,SORAGHAN J J.Small-Target Detection in Sea Clutter[J].IEEE Trans on Geoscience and Remote Sensing,2004,42(7):1355-1361.
[14]陈伯孝.现代雷达系统分析与设计[M].西安:西安电子科技大学出版社,2012:246-247.
