0 引言
多输入多输出(Multiple Input Multiple Output, MIMO)雷达是一种采用多发射天线发射特定波形信号集，并利用多接收天线进行特定匹配处理的雷达系统。基于波形分集思想，MIMO雷达可获得相比传统相控阵雷达更多的自由度，因此能够扩展阵列孔径、提高参数分辨性能、改善目标检测性能等，从而逐渐成为未来雷达的发展趋势之一[1-2]。理想的发射波形是获取MIMO雷达体制优势的关键。MIMO 雷达波形研究主要从正交发射波形优化设计、发射方向图综合等方面展开[3-4]。正交发射波形优化主要是指优化设计正交波形信号，使发射信号具有良好的自相关和互相关特性。已有文献采用模拟退火算法[5]、遗传算法[6]、循环算法[7]、约束非线性规划算法[8]等设计不同编码方式的正交波形。发射方向图综合是指通过合理设计发射信号波形，灵活控制MIMO雷达合成发射方向图；主要通过合成发射波形的互相关矩阵[9]和发射波束域矩阵[10]等途径来实现。本文主要研究正交发射波形优化问题，设计良好时域相关特性的空间合成信号以获取更好的脉压性能。
正交频分(Orthogonal Frequency Division, OFD)信号[11]是MIMO雷达中一类常用的正交波形信号，具备优异的探测性能。通常OFD信号可设计为正交频分线性调频(Orthogonal Frequency Division-Linear Frequency Modulation, OFD-LFM)信号和正交频分相位编码(Orthogonal Frequency Division-Phase Coded, OFD-PC)信号。OFD-LFM信号是指在每个通道子载波上调制LFM信号，文献[12-13]详细分析了最小化OFD-LFM信号间互相关影响的参数关系，给出了频谱重叠时限制自相关旁瓣性能的原因；文献[14]从接收波束形成再进行时空匹配滤波的信号处理方式来分析其旁瓣分布情况，并设计了相应的优化方法。MIMO雷达中对OFD信号的研究主要集中在OFD-LFM信号上，对OFD-PC信号的研究相对比较欠缺。文献[15]讨论了OFD-PC信号在MIMO雷达中的应用优势，并对其脉冲压缩性能进行了分析。文献[16]提出采用脉间频率捷变的方法降低距离旁瓣。本文针对OFD-PC信号距离旁瓣问题，考虑一种脉内优化方法，对OFD-PC空域合成信号的自相关函数进行详细分析，提出一种全新的基于空时联合优化的非均匀间隔OFD-PC波形优化设计方法。与文献[16]不同，本文方法仅对单个脉冲信号进行优化，脉冲与脉冲之间的相参性不受破坏。通过最小化发射信号相关矩阵与单位阵误差来实现发射功率方向图全向逼近；同时，以自相关峰值旁瓣水平(Auto-correlation Peak Sidelobe Levels, APSL)作为目标函数，最小化空域合成信号的APSL，以保证感兴趣方向上期望的信号时域特性。基于该方法建立MIMO雷达中OFD-PC波形与发射功率方向图联合优化模型，实现了空域合成信号时域旁瓣抑制与方向图全向逼近的目的，对提高MIMO雷达中目标检测能力极具实际意义。
1 OFD-PC信号模型及空时特性
MIMO雷达中OFD-PC波形的基本信号形式如图1所示。假设发射阵列是阵元间距为d，阵元数为Ne的均匀线阵；每个发射阵元发射中心频率为f1,f2,…,fNe的载波脉冲信号，每个载波脉冲上调制码元宽度为T、编码长度为Q的相位编码序列，脉冲宽度为Te=T·Q。载波间隔Δf和码元宽度T满足Δf=1/T。
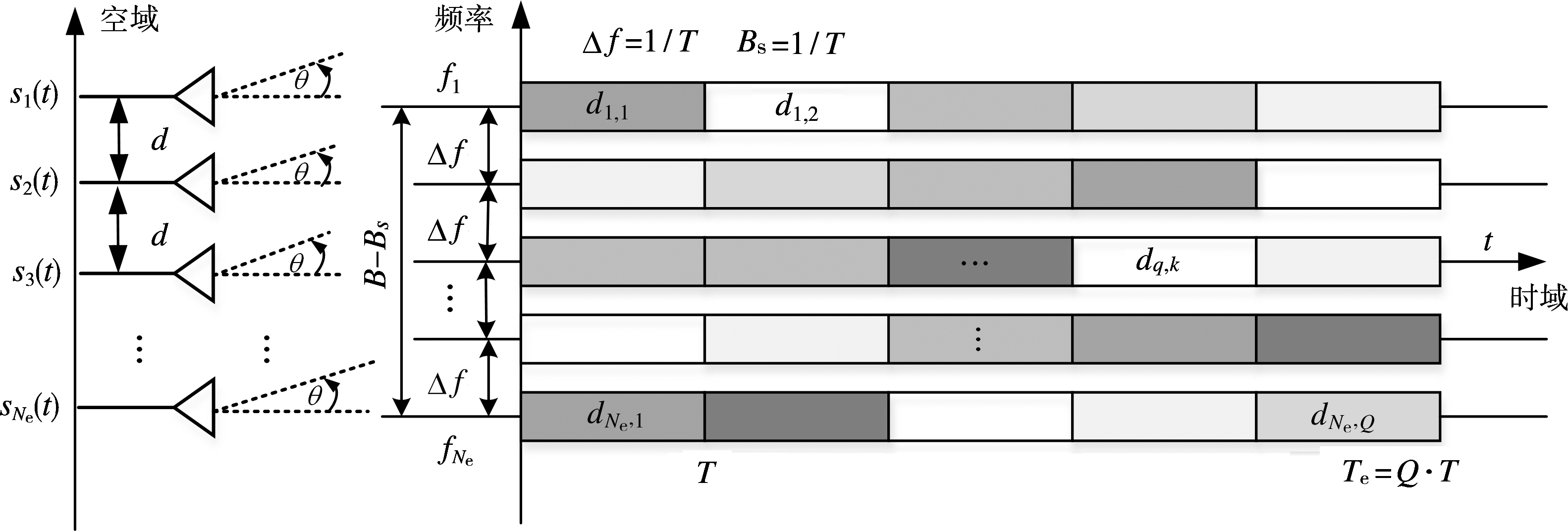
图1 OFD-PC信号形式
假设MIMO雷达中第k个通道发射的载波相位编码波形信号为sk(t)，可表示为
(1)
式中：d0,k,d1,k,…,dq,k,…,dQ-1,k为相应的相位编码序列；f0为中心载频， Δf为各载波信号中心频率的间隔；ck=k-(Ne+1)/2， (k=1,2,…,Ne)为载波频率编码， rect(t)=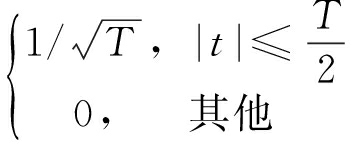
为矩形脉冲函数。假定Bs为单个载波上调制的相位编码信号带宽，则Bs=1/T； 此时OFD-PC空域合成信号的总带宽B=Bs+(Ne-1)·Δf。
不考虑传播衰减，位于远场方向θ处目标在t时刻被照射的空域合成信号为
(2)
式中：(·)T表示转置；
表示选取阵列中心为参考点的发射阵列导向矢量，λ为波长；
空间相位编码序列c1,c2,…,cNe和载波频率编码序列一致；s(t)=[s1(t),s2(t),…,sNe(t)]T表示t时刻各通道发射信号构成的列向量。合成信号y(θ,t)在总脉冲宽度Te内的平均功率为
(3)
式中， (·)*表示共轭， (·)H表示共轭转置，R=
s(t)sH(t)dt/Te表示发射信号的协方差矩阵。pE(θ)反映时间Te内雷达在空间各处的电磁能量分布情况，称为发射功率方向图。不难证明：当T·Δf为整数时，不同通道发射信号相互正交，R为单位矩阵，发射功率方向图pE(θ)为一全向函数，信号能量空间均匀分布。可实现对整体探测环境的各向同性照射而不需要波束扫描，因此可获得长时间相干累积，有利于对目标的检测。
假定信号处理结构为通过时空匹配滤波[17]实现目标检测，利用接收波束形成得到目标方向，因此可认为目标检测时匹配滤波前信号为y(θ,t)。目标检测性能不仅受信号y(θ,t)能量因素影响，还受到y(θ,t)匹配滤波后距离旁瓣影响；前者由pE(θ)的分布特性体现，后者由y(θ,t)的时域相关特性反映。下面主要分析信号y(θ,t)自相关函数特性，在接收端进行匹配滤波处理前需对y(θ,t)进行基带混频，可直接假设中心载频f0=0 Hz。根据式(2)，方向θ处合成信号y(θ,t)自相关函数可表示为
f(θ,τ)=
y(θ,t)y*(θ,t+τ)dt=
0(τ)+
s(τ))+
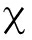h(τ))
(4)
函数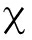v(τ)可写为
ej2πvΔfq1T·e-jπvΔf(τ-mT)·
sinc(πvΔf(T-|τ-mT|))·
(5)
式中，v=-(Ne-1),…,-1,0,1,…,(Ne-1)，τ表示相关时延。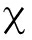v(τ)中包含载波调制相位编码序列非周期自相关函数Rk(m)。若每个发射天线发送相同相位编码序列，Rk(m)可写为
(6)
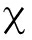v(τ)主要反映空间θ处合成信号相关函数f(θ,τ)的时域特性，对f(θ,τ)的主瓣宽度及旁瓣水平起决定性作用，从而影响最终的目标检测性能。f(θ,τ)可看成是对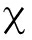v(τ)函数的加权求和，加权函数Wv(τ)定义为
(7)
Wv(τ)主要反映空间θ处f(θ,τ)的空域特性。所以f(θ,τ)可改写为
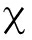v(τ)
(8)
2OFD-PC空域合成信号的波形优化分析
根据式(8)，对影响空域合成信号自相关函数特性因素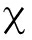v(τ)和Wv(τ)两部分进行分析。
1) 根据式(4)，f(θ,τ)中
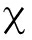0(τ)主要影响近区主旁瓣分布(将时延范围(-T,T)称作旁瓣近区，之外为远区)展开为
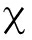0(τ)|=
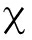|W0(τ)|·|0(τ)|
(9)
(10)
(11)
|W0(τ)|为近似sinc函数，最高峰值点位于τ1=n1/Δf，n1∈Z，较低峰值点位于τ2=
(2n2+1)/(2NeΔf)，n2∈Z。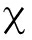0(τ)可看作2Q-1个自相关移位项相加。当m=0，|τ|<T时，主瓣最高峰值为Ne，较高旁瓣幅度由函数
和(2n+1)/2NeΔf共同约束；当m≠0，|τ-mT|<T时，|B0(τ)|最高旁瓣是由主瓣最高峰值平移mT位置，其幅值由主瓣最高峰值乘以
常用伪随机序列Rk(m)≪Rk(0)，m≠0，因此|τ-mT|<T内最高旁瓣幅度得到较大衰减。
2) 根据式(4)，f(θ,τ)后两项主要影响近远区低旁瓣分布，其中|Wv(τ)|为
(12)
|Wv(τ)|高峰值点位于τ1=n1/Δf，较低峰值点位于τ2=(2n2+1)/2(Ne-v)Δf。当|τ-mT|<T时|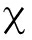v
约束旁瓣高度。此时Rk(m)幅值较小，旁瓣峰值较低。
综上所述，Rk(m)与Δf影响着近远区旁瓣电平分布情况。选择自相关性能较优的相位编码序列必然带来空域合成信号的直接优化效果；而如果对Δf进行随机选择，此时Δf≠1/T，信号正交性被破坏，旁瓣分布固定位置将会打乱，同相累加的可能性减小，高旁瓣分布情况有望改善。为此进行相应仿真分析验证该想法的可行性。设等频率间隔Δf=1/T=2 kHz，非均匀频率间隔为7个互不相同且和为B-Bs=14 kHz的随机数，信号均采用M伪随机序列。图2给出了等间隔与非均匀间隔OFD-PC空域信号发射功率方向图对比。等间隔OFD-PC信号发射功率方向图各向同性，而对于非均匀间隔OFD-PC信号，由于Δf≠1/T，信号不再严格正交，发射能量非均匀分布，发射功率方向图呈现波动。图3中非均匀间隔OFD-PC空域合成信号自相关函数已经不存在明显较高的旁瓣。所以OFD-PC载波频率的随机化能够有效降低距离旁瓣。那么如何在信号正交性破坏程度较小的前提下，选择最优的载波频率，改善不同方位上OFD-PC空域合成信号的自相关性质，需要进一步研究。
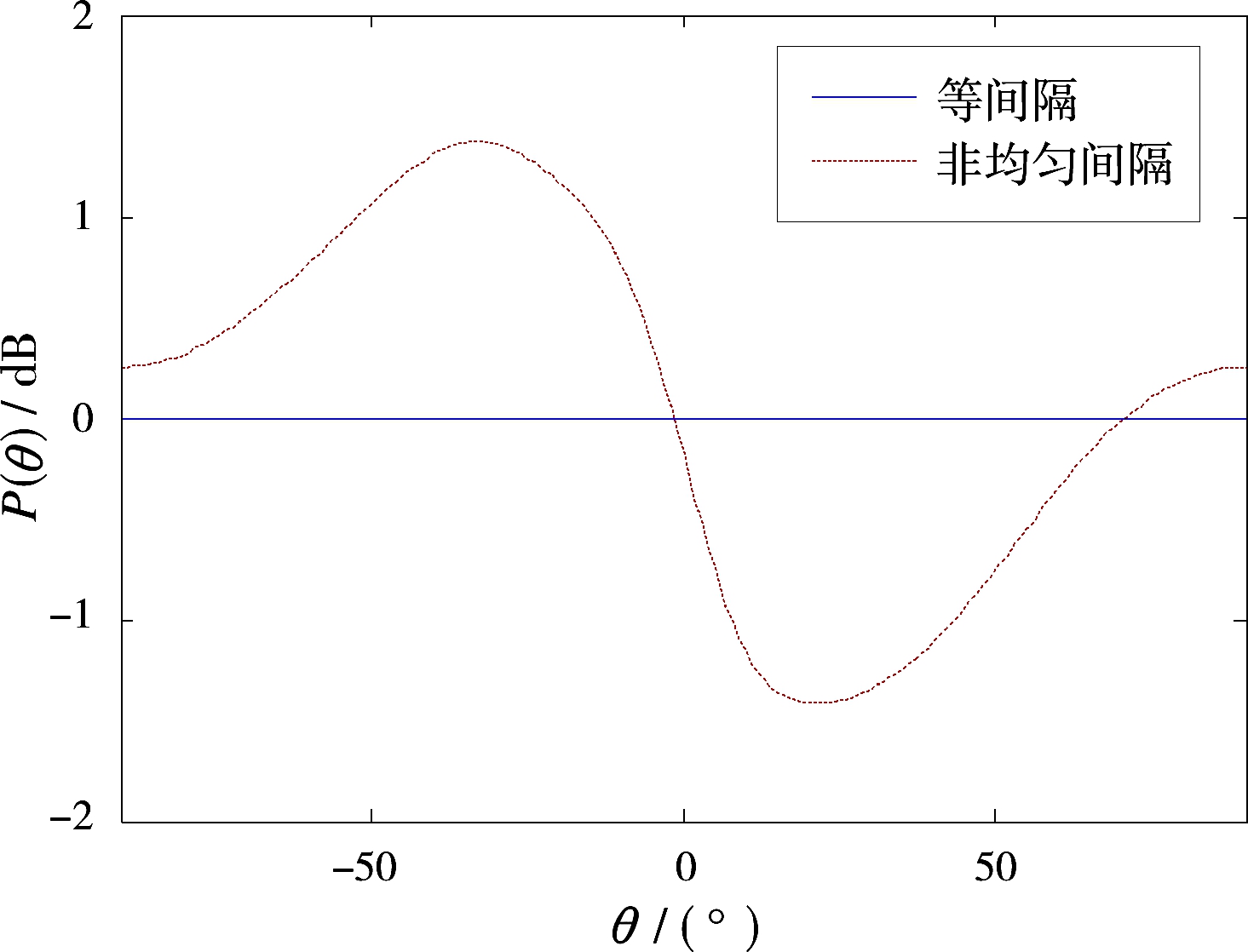
图2 发射功率方向图对比
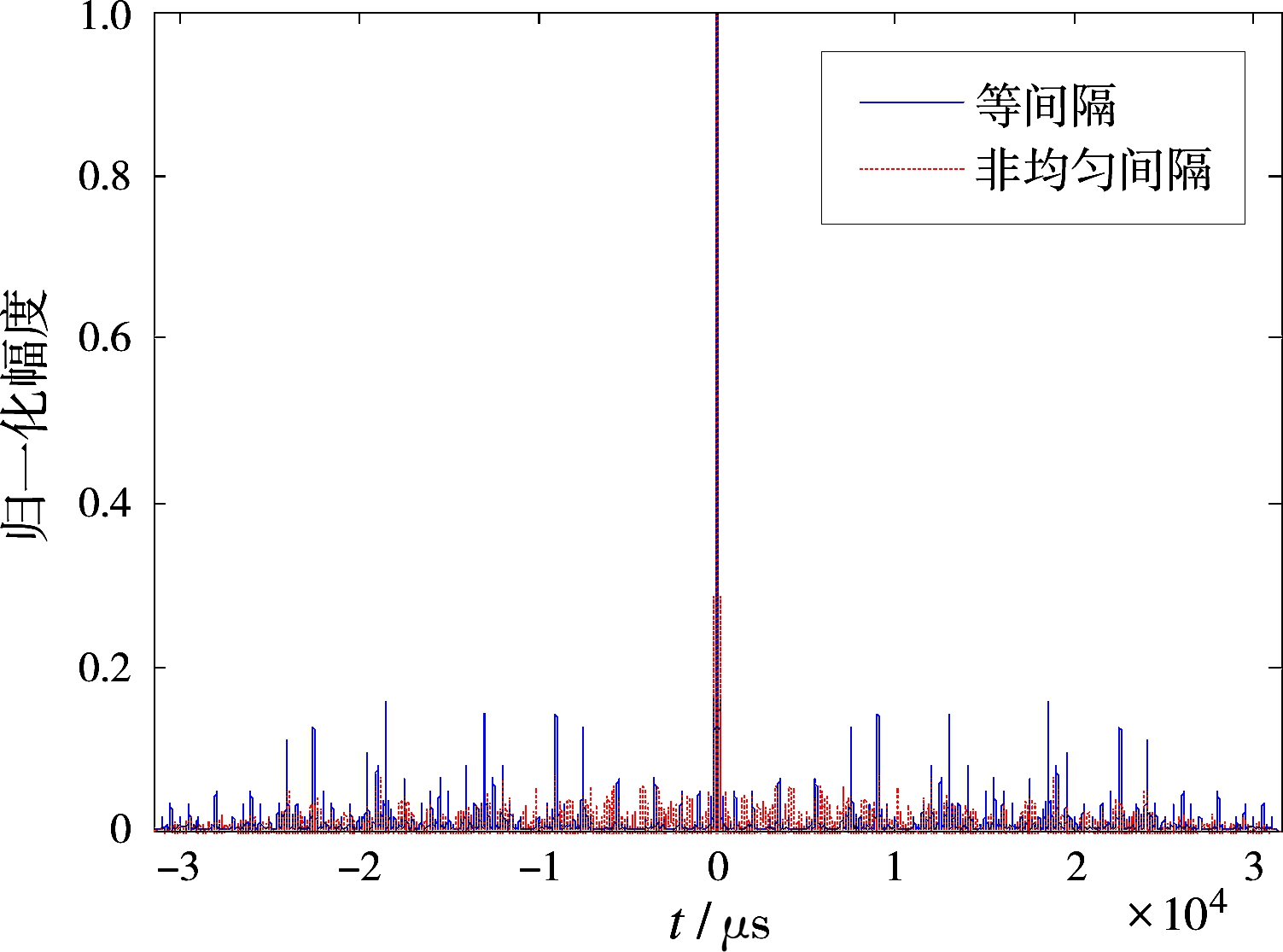
图3 空域合成信号自相关函数对比
3OFD-PC空域合成信号的波形优化设计方法
根据以上分析，提出较为完备的波形优化策略，一方面直接选用具有较好非周期自相关特性的相位编码序列来优化OFD-PC空域合成信号；另一方面在此基础上进一步优化设计一种非均匀间隔OFD-PC波形，并约束该波形信号的正交性，建立合理全面的优化模型，确保所设计波形在功率方向图逼近全向的前提下，获取最低的自相关旁瓣电平。
3.1 相位编码序列的优化选择
根据上节的分析，相位编码序列自身的自相关性质优劣将直接影响主旁瓣比的高低。前文中M序列是一种常用的伪随机编码序列，自相关旁瓣水平较高，这里选择一种自相关性能优异的多相编码序列GQ(Goutelard Q-Ary Sequences)全序列进行优化对比。当然，此处仅仅通过举例的方式证明编码序列优化选择的有效性和必要性，并不针对编码序列的最优选择展开讨论。GQ全序列[18]由法国Goutelard于1996年提出，具备优异的非周期自相关性能，在短波段远程遥感、雷达、通信等领域有着广泛的应用。图4给出了GQ全序列和M序列自相关函数对比情况。显然，GQ全序列的自相关旁瓣远低于M序列的自相关旁瓣。分别用GQ全序列和M序列调制OFD-PC波形的载波信号，得到两种空域合成信号自相关函数，如图5所示。由图可知，GQ全序列调制的OFD-PC合成信号自相关旁瓣要远低于M序列。因此，选择具有较好非周期自相关特性的相位编码序列来调制OFD-PC波形，可有效降低空域合成信号自相关函数旁瓣电平，这是一种最直接的波形优化方式。
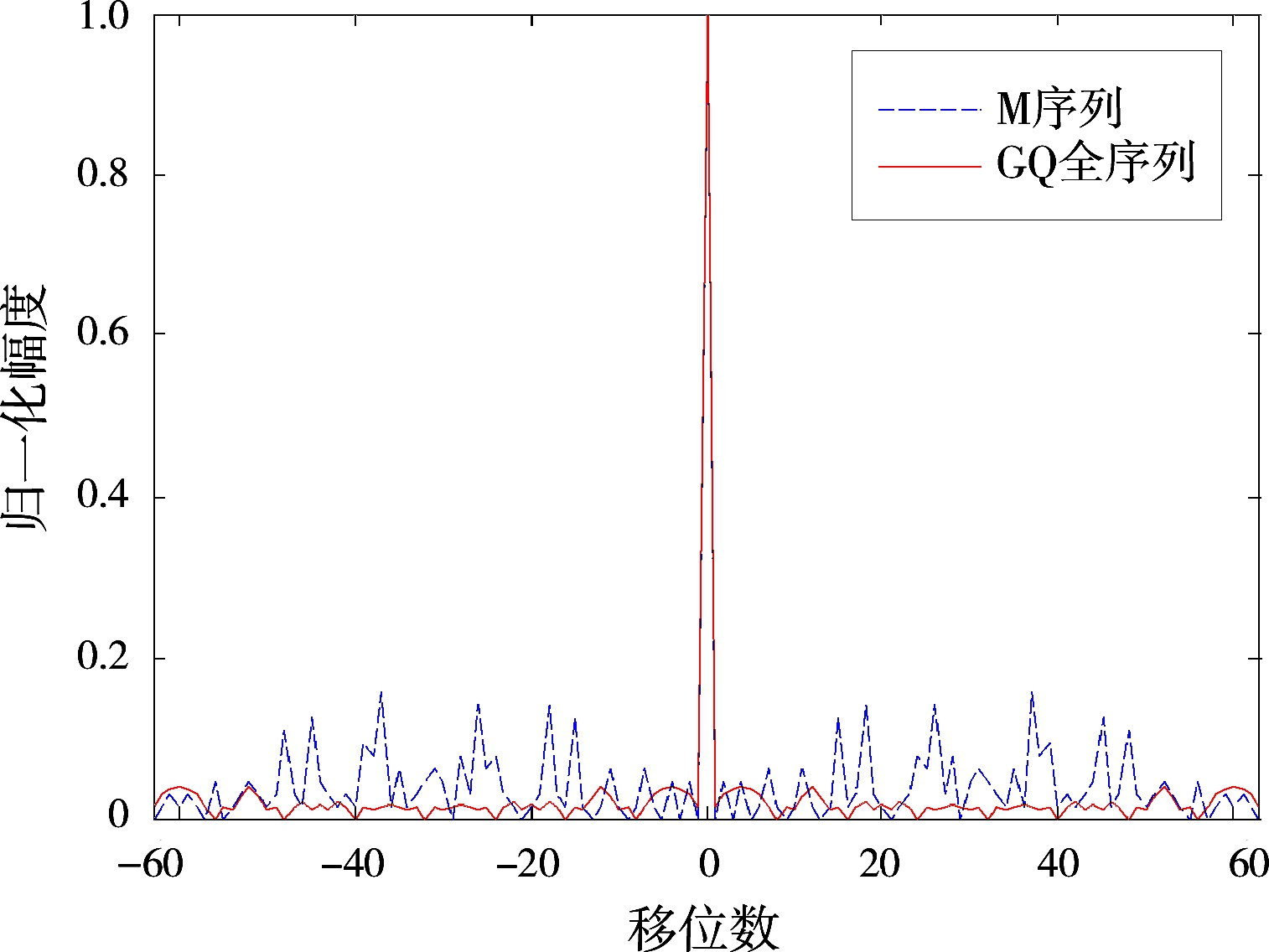
图4 序列自相关函数对比
图5 序列调制下OFD-PC信号自相关函数对比
3.2 非均匀间隔OFD-PC的优化设计
基于上述分析，设计一种非均匀间隔OFD-PC波形，此时， Δf1, Δf2,…,ΔfNe-1是在总带宽一定情况下的随机取值，由于Δf≠1/T，不同载波信号之间可能存在频谱重叠。传统OFD-PC信号中各载波信号间频率间隔为Δf=1/T，因此在MIMO雷达中OFD-PC波形将获取全向的发射功率方向图。当进行非均匀频率间隔优化以获取脉压性能提高时，必然破坏发射功率方向图的全向性。为了在空域与时域特性矛盾中取得合理折中，需要建立合理的波形优化模型。
为了将非均匀间隔OFD-PC空域合成信号自相关旁瓣限制在较低水平，选择空域合成信号的最大APSL作为目标函数。考虑f(θi,τ)对称性，最优化区间设为0<τ≤Te。将整个搜索空间划分为θ1,θ2,…,θK，在每个空间角度上进行最优化搜索。由式(3)可知，发射功率方向图由发射信号相关矩阵决定，为使发射功率方向图接近全向，需要约束发射信号相关矩阵逼近单位阵。基于以上讨论，建立非均匀间隔OFD-PC的波形优化模型：
(13)
最优化搜索变量为Δf=[Δf1, Δf2,…,ΔfNe-1]T， 即Ne-1个载波信号中心频率间隔组成的列向量。K表示空间搜索角度数。代价函数限制自相关函数旁瓣区域最大APSL最小，从而将整体旁瓣压制在较小的水平。第一个约束条件中ε用来控制发射功率方向图与理想全向方向图的逼近程度，ε的合理选取能够使自相关旁瓣的抑制与方向图的逼近达到合理折中；第二个约束条件是合成信号总带宽保持不变，从而保证波形主瓣宽度恒定。假定OFD-PC信号处理结构为先接收波束形成后时空匹配滤波，这里暂不考虑空域合成信号的空域互相关性能。需要说明，式(13)的目标函数为非凸函数，具有非线性约束，很难求得最优解，本文采用序列二次规划[19]法进行求解。
4 结果分析
假设MIMO雷达中发射阵列是阵元数为Ne=8，阵元间隔为半波长的均匀线阵。每个载波编码信号码元时宽为T=500 μs，带宽为Bs=1/T。规定OFD-PC发射信号总带宽为B=Ne/T，对应载波频率间隔Δf=1/T的情况；最优化变量Δf=[Δf1, Δf2,…,ΔfNe-1]T需满足频率间隔之和为B-Bs的约束条件。仿真分析中波形性能主要从发射功率方向图和空域合成信号的自相关来体现。设定空间搜索范围为[-90°，90°]，对该范围内搜索角度进行离散采样，分别在-90°,-89°,…,90°等角度处进行波形最优化搜索。分别对M序列与GQ全序列调制的OFD-PC信号进行波形优化，并尽量保证序列长度一致，选用M序列码长Q=63；GQ全序列码长Q=64。发射功率方向图逼近误差取ε=0.1，得到基于M序列和GQ全序列的OFD-PC空域合成信号发射功率方向图分别如图6和图7所示。为方便对比，图中也给出了文献[15]和文献[16]中优化设计波形的相应性能。文献[15]中波形信号载波频率等间隔分布，空域合成信号完全正交，发射功率方向图为全向均匀分布。文献[16]中采用脉冲间载波频点捷变方式，但仍满足Δf=n/T，所以发射功率方向图也为均匀全向。对于本文方法优化设计的非均匀间隔OFD-PC波形，由于载波频率间隔不相等且不为1/T，能量分布不再是严格各向同性，但因为在优化过程中利用逼近误差ε进行约束，使得信号的相关矩阵在相应的区间内逼近单位阵，所以其发射功率方向图仍保持着近似全向，这也证明了所提优化方法中该约束有效性。
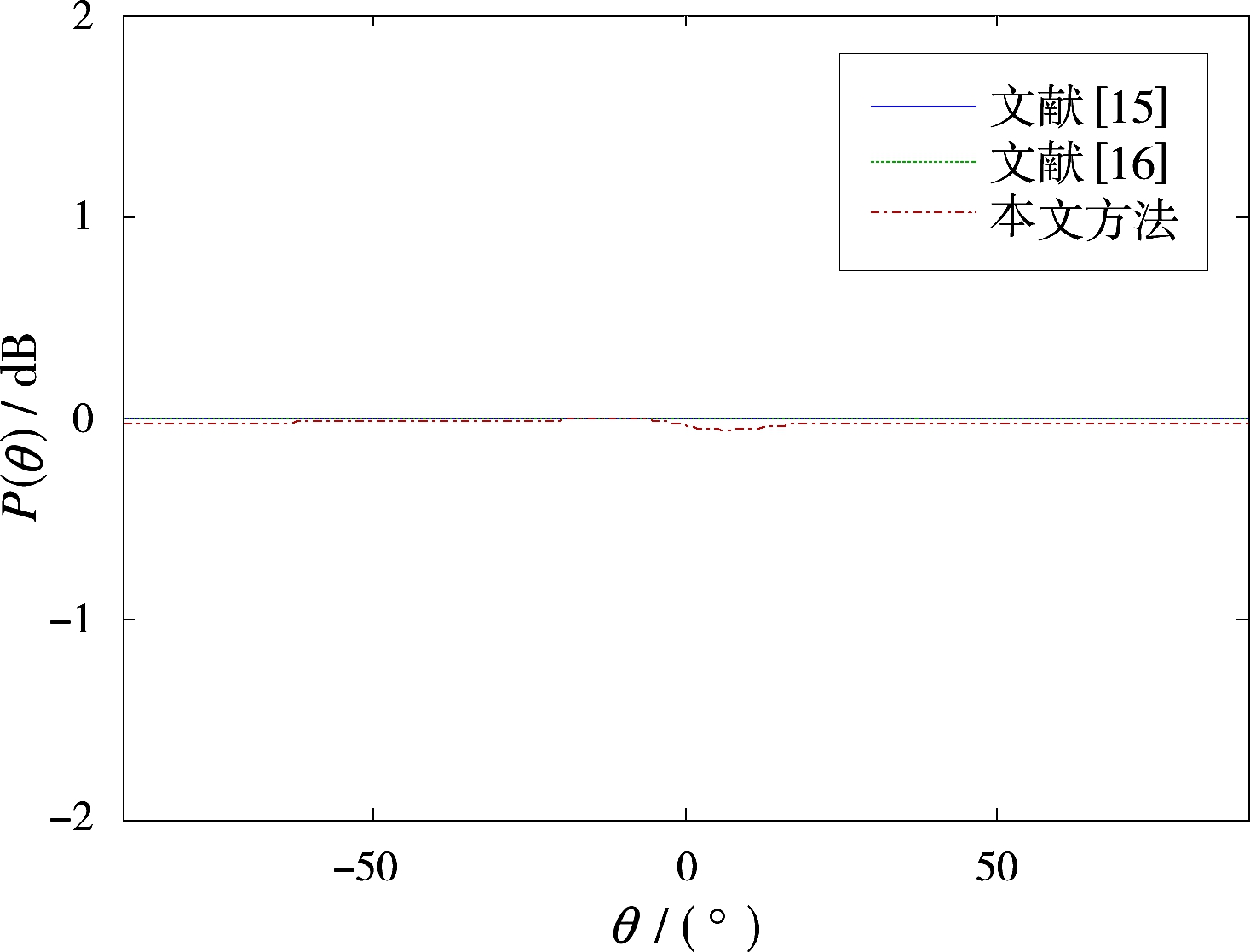
图6 M序列发射功率方向图对比
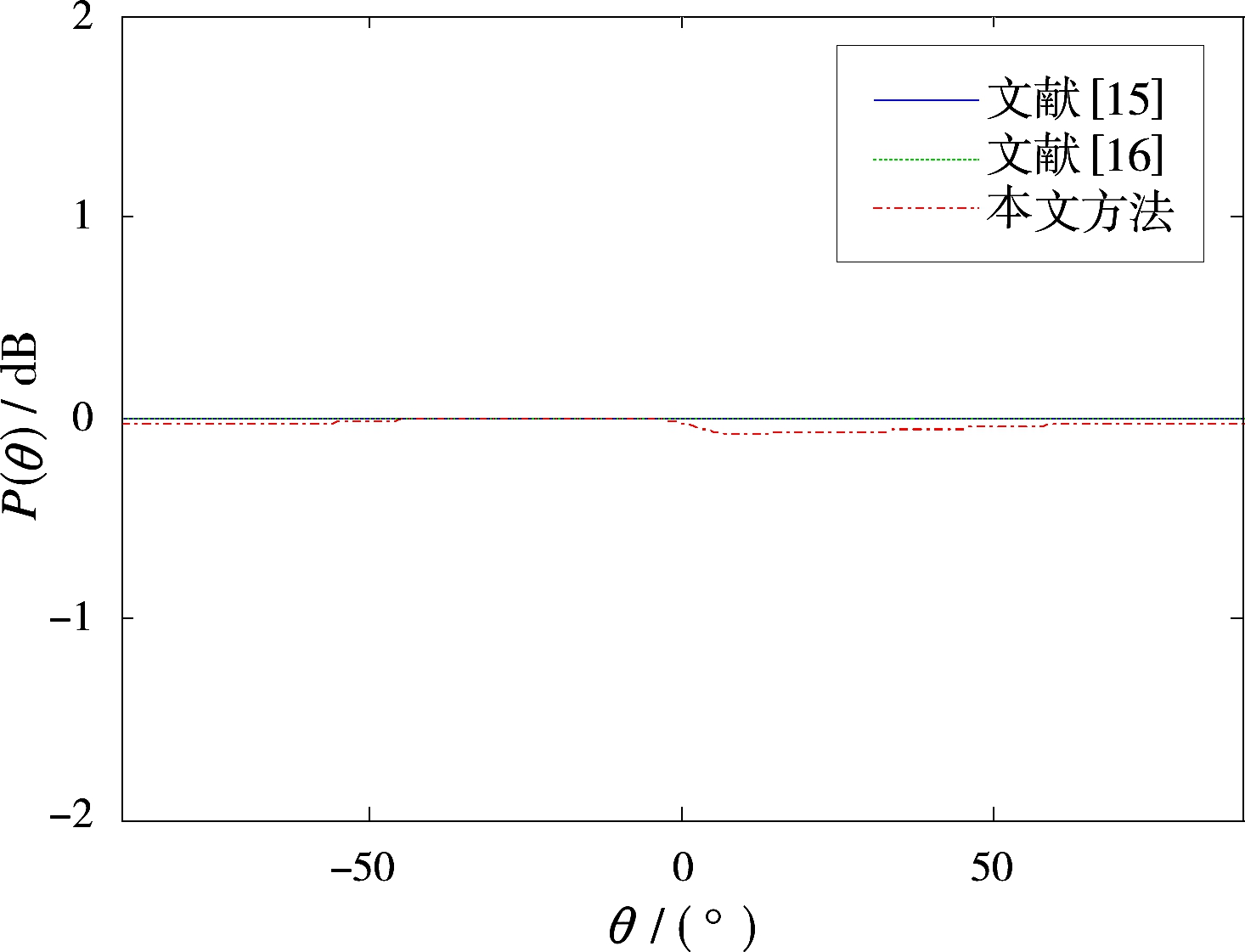
图7 GQ全序列发射功率方向图对比
图8和图9分别给出在采用本文方法优化基础上，基于M序列与GQ全序列OFD-PC空域合成信号在(-T,T)内的自相关函数与文献[15-16]方法在近区的旁瓣对比情况。由图可知，最优搜索OFD-PC信号载波频率间隔后得到的非均匀间隔OFD-PC信号的近区旁瓣相对于文献[15]方法有较大程度的降低，并与文献[16]方法起到相似的优化效果，而波形主瓣宽度基本保持不变。图10和图11分别给出了基于M序列与GQ全序列OFD-PC空域合成信号在(-Te,Te)内的自相关函数对比情况。由图可知，在整个延迟范围内，本文方法设计的波形相比文献[15-16]有着更低的旁瓣，而对比图10和图11可以看到，基于GQ全序列的非均匀OFD-PC信号旁瓣降低程度要高于基于M序列的非均匀OFD-PC信号。
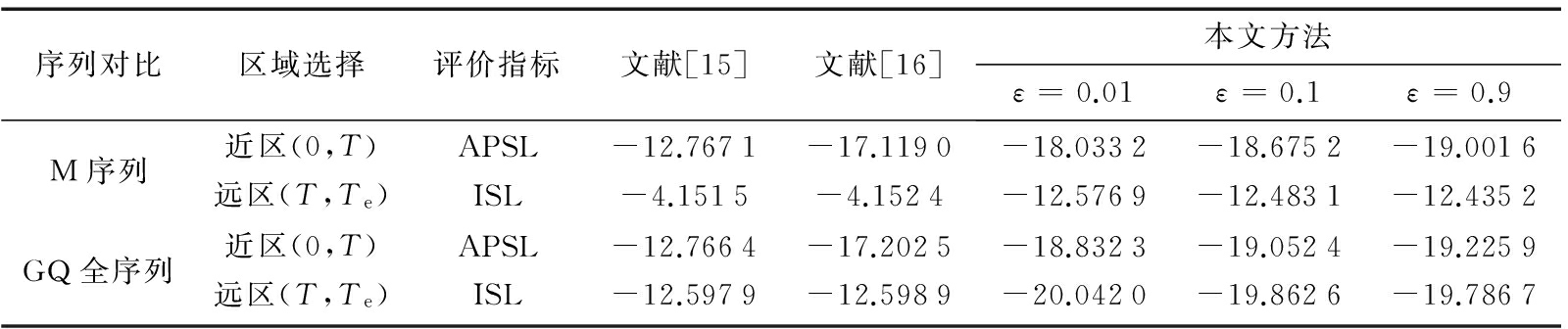
为对本文波形优化方法旁瓣改善性能进行定量分析，将不同仿真条件下旁瓣降低程度进行了总结，如表1所示。发射功率方向图逼近误差取3种情况：ε=0.01,ε=0.1,ε=0.9，得到基于M序列和GQ全序列的OFD-PC空域合成信号在近区和远区的旁瓣改善值。由表可知： 1) GQ全序列对比于M序列在近区幅值降低程度相对较小，即相位编码序列自相关性能的优劣对近区的影响较小。但对相同序列，根据图8、图9与表1数据对比，本文提出设计方法随着ε的增大并在可控范围内，对比文献[15]，近区旁瓣峰值APSL(Auto-Correlation Peak Sidelobe Levels)(APSL=10 log10[max sidelobe power/(peak response)2])最大降幅可达6 dB，脉压性能得到进一步提升，降低了虚警概率。2) GQ全序列对比M序列在远区积分旁瓣电平ISL(Integrated Sidelobe Levels)(ISL=10 log10[total sidelobe power/(peak response)2])降幅可达2 dB左右，即对于自相关性能越好的相位编码序列，其远区积分旁瓣电平相比文献[15-16]改善程度越明显。针对相同序列，根据图10、图11与表1数据分析对比，本文提出设计方法随着ε增大并在可控范围内，远区积分旁瓣电平降幅仍然可达7 dB左右，较好的优化远区的能量累积。综上所述，对于文献[15]近远区旁瓣优化的固有局限性以及文献[16]在远区能量分布较大的劣势，本文提出的非均匀间隔波形优化设计方法对近区旁瓣与远区能量优化能力都得到较大的提升。
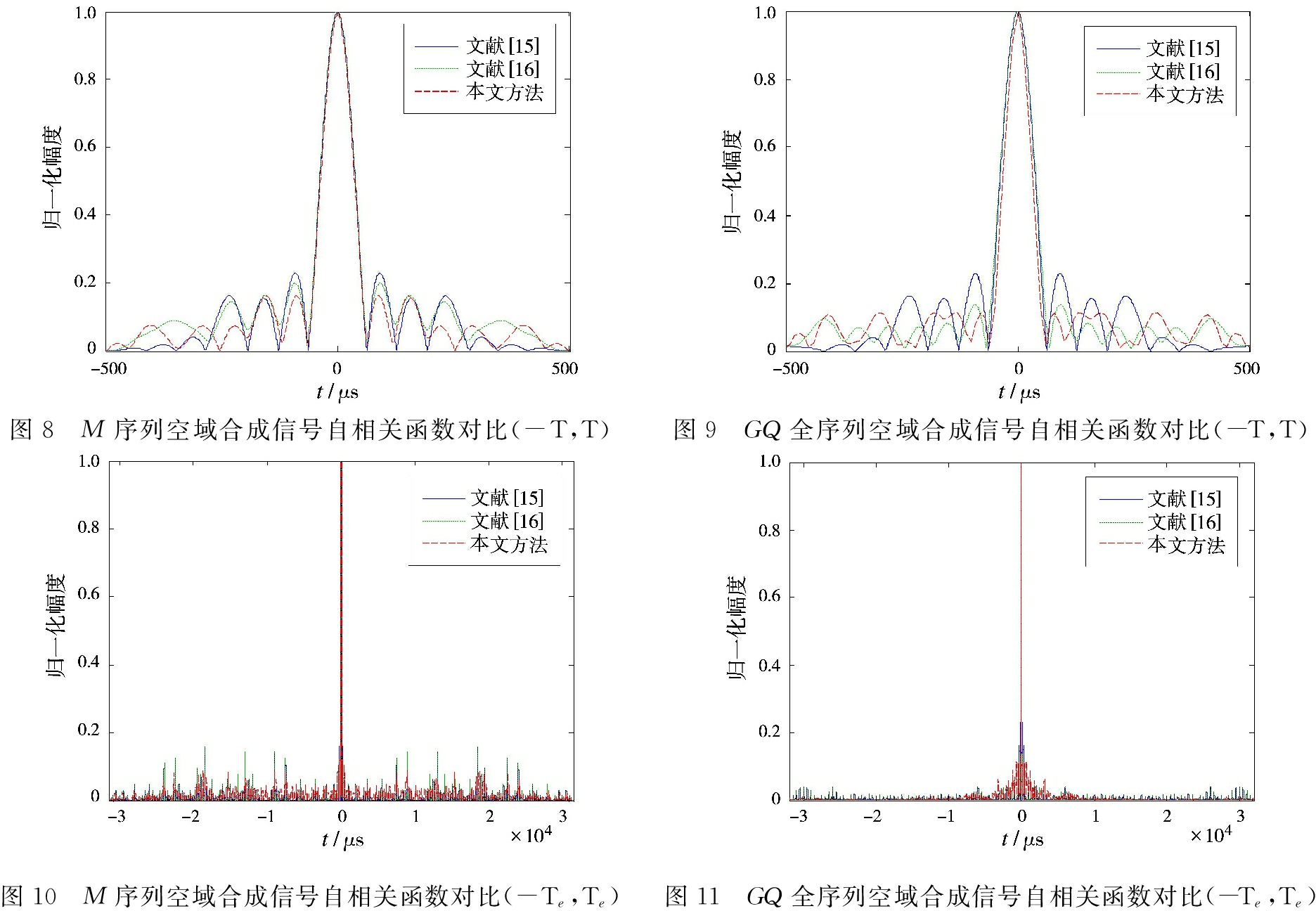
表1 波形优化设计前后APSL，ISL值对比 dB
因本文研究的发射波形结构为OFD-PC信号，不同发射天线发射的波形信号可以实现完美正交，但是此时空域合成信号的自相关主旁瓣峰值比较低，本文所提波形优化方法通过优化频点间隔来降低旁瓣，此时OFD-PC信号子载波间隔非均匀并且不满足正交条件，发射波形信号的正交性受到破坏，但是本文在波形优化的同时，限制了这种破坏程度，从而发射波形集间的互相关性能仍然保持在较优的水平。与此同时，这里也给出空域合成信号在不同方位的互相关性能分析。以M序列为例，图12给出文献[15]中等间隔波形及本文方法所设计的优化波形在-73°与3°空域合成信号的互相关性能对比。从图中可以看出，由于信号频率等间隔的影响，文献[15]空域合成信号的互相关在零延迟附近(非零延迟)有较高峰值。虽然本文方法优化中约束了频率间隔的波动幅度，但不同方位上空域合成信号互相关性能仍得到较好的改善。
图12 空域合成信号互相关对比
由于信号间的频率间隔影响OFD-PC信号的多普勒容忍性，所以将本文方法设计波形与等间隔波形的多普勒容忍性进行对比，比较结果如图13所示。从图中可以看出，本文方法设计波形多普勒容忍性比等间隔波形要差，特别是在fdT≥1时，随着fdT增大，周期性峰值点都有较大的降低。因此，如何保证MIMO雷达中OFD-PC信号的多普勒容忍性，并实现波形的空时频联合优化是下一步亟待研究的问题。
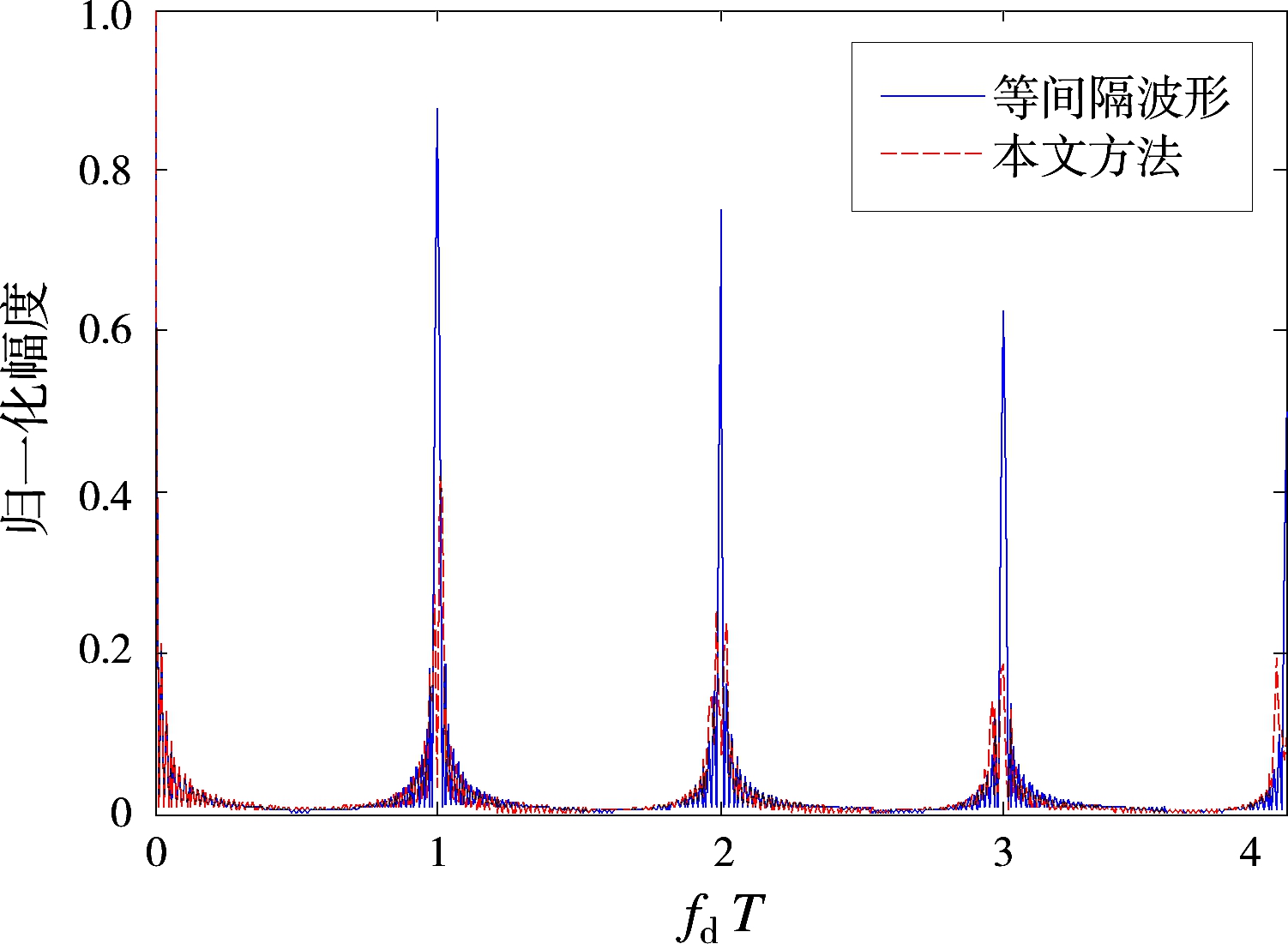
图13 空域合成信号多普勒容忍性对比
5 结束语
为优化MIMO雷达中OFD-PC波形的脉冲压缩性能，本文提出一种降低OFD-PC空域合成信号距离旁瓣的波形优化设计方法。一方面，通过选择非周期自相关性能优异的相位编码序列直接优化降低距离旁瓣；另一方面，在此基础上进一步提出一种非均匀间隔OFD-PC的MIMO雷达发射波形设计方法。建立合理的空时联合优化模型，最优化求解各载波信号的频率间隔，实现了OFD-PC空域合成信号脉冲空时综合性能的优化。所设计波形脉压性能得到较大提升，发射功率方向图接近全向，对MIMO雷达中目标检测能力的提升具有重要意义。然而，本文的优化模型求解复杂度仍然较高，如何建立更高效、更全面的空时频联合优化模型有待进一步研究。
参考文献：
[1]陈浩文,黎湘,庄钊文. 多发多收雷达系统分析与应用[M]. 北京：科学出版社, 2015.
[2]DUAN Xiang,LIU Zhou,LIU Hongming,et al.Research on Bistatic MIMO Radar Search Processing Method[J].Journal of Signal Processing, 2013, 29(3):319-325.
[3]曹思扬,郑元芳. 雷达波形研究发展现况与趋势[J]. 雷达学报, 2014, 3(5):603-621.
[4]CUI G,LI H,RANGASWAMY M.MIMO Radar Waveform Design with Constant Modulus and Similarity Constraints[J].IEEE Trans on Signal Processing, 2014, 62(2):343-353.
[5]潘浩. 基于模拟退火算法的雷达正交多相码信号设计[J]. 黑龙江科技信息, 2016(15):101.
[6]MEHANY W,JIAO L,HUSSIEN K.Orthogonal Discrete Frequency-Coding Waveform Design Based on Modified Genetic Algorithm for MIMO-SAR[C]∥9th IEEE Conference on Industrial Electronics and Applications,Hangzhou:IEEE, 2014:1082-1086.
[7]HE H,STOICA P,LI J.Designing Unimodular Sequence Sets with Good Correlations:Including an Application to MIMO Radar[J].IEEE Trans on Signal Processing, 2009, 57(11):4391-4405.
[8]胡亮兵,刘宏伟,吴顺君. 基于约束非线性规划的MIMO雷达正交波形设计[J]. 系统工程与电子技术, 2011, 33(1):64-68.
[9]ZHANG X,HE Z,RAYMAN-BACCHUS L,et al.MIMO Radar Transmit Beampattern Matching Design[J].IEEE Trans on Signal Processing, 2015, 63(8):2049-2056.
[10]FRIEDLANDER B.On Transmit Beamforming for MIMO Radar[J].IEEE Trans on Aerospace and Electronic Systems, 2012, 48(4):3376-3388.
[11]WANG Wenqin.Large Time-Bandwidth Product MIMO Radar Waveform Design Based on Chirp Rate Diversity[J].IEEE Sensors Journal, 2015, 15(2):1027-1034.
[12]胡蜀徽,唐佳,王志华,等. 正交频分LFM信号MIMO雷达的距离维高分辨[J]. 雷达科学与技术, 2014, 12(6):585-591.
[13]陈正中,李小波,梁浩,等. 正交频分LFM信号的MIMO雷达的匹配滤波技术[J]. 雷达科学与技术, 2013, 11(2):197-202.
[14]赵永波,水鹏朗,刘宏伟,等. 基于线性调频信号的综合脉冲与孔径雷达波形设计方法[J]. 电子学报, 2010, 38(9):2076-2082.
[15]陈伯孝,张守宏. 基于相位编码的稀布阵综合脉冲孔径雷达的脉冲压缩性能分析[J]. 电子科学学刊, 1998, 20(1):50-55.
[16]陈伯孝,张守宏. 降低稀布阵综合脉冲孔径雷达距离旁瓣的方法研究[J].西安电子科技大学学报, 1997, 24(增刊):103-108.
[17]皮强. 综合脉冲与孔径雷达跟踪处理技术研究与工程实现[D]. 西安：西安电子科技大学, 2011.
[18]GOUTELARD C.Les Sequences GQ Sequences Q-Aire Orthogonales a Correlation Parfaite[J].
Digital Communications Systems:Propagation Effects,Technical Solutions,Systems Design,1996, 28(1):1-13.
[19]王旭,周生华,刘宏伟,等. 一种空时联合优化的MIMO雷达波形设计方法[J]. 西安电子科技大学学报(自然科学版), 2014, 41(3):41-48.
