0 引言
随着科技的不断发展，卫星通信逐渐成为一种不可替代的重要通信方式，卫星通信系统具有通信距离远、保密性好、通信容量大、传输速度高而且通信的覆盖范围大、性能稳定、信息传递质量高、机动性灵活、频带宽等优势。由于卫星通信相比其他通信方式有着巨大的优势，近年来卫星通信在通信领域的作用愈来愈显得不可替代。运动平台相控阵卫星自跟踪系统是针对导弹等高速运动平台与中继卫星之间稳定的双向传输需求，开展弹载平台二维有源相控阵卫星跟踪技术的研究[1]。
由于运动载体在移动中机动性的存在，在任何时候将可能产生姿态上偏转角度，从而导致所使用的卫星与天线波束指向出现偏差，导致信息传输的质量下降甚至无法连接。因此在自跟踪系统中目标的角度测量是其关键技术之一，角度搜索/角度捕获过程、角度跟踪过程都需要应用到角度测量，角度测量精度直接影响到角度跟踪精度。
现有的单脉冲角度测量方法主要有相邻波束直接比幅、相邻波束直接比相、基于和差波束测角算法等。相邻波束直接比幅法测角精度较低，在运动目标较远的情况下，并不适用于跟踪系统；相邻波束比相法的测角精度和信噪比有很大关系，低信噪比时，测角误差会很大；基于和差波束的测角算法虽然能较好地适用于跟踪系统，但是并不能提高输出信号的信噪比，对系统之后的信号处理帮助不大。近年来，一些基于空间谱估计思想的测角方法也得到重视。这一类方法可以对多个信号方向进行估计，但其运算量通常较大，难以实现[2]。
本文研究正是在上述背景下产生，重点研究了运动平台相控阵卫星跟踪系统的角度测量算法和系统测角精度，详细研究了若干因素对测角精度的影响，并且给出了提高测角精度的措施[3]。
1 系统总体设计方案简介
运动平台相控阵卫星跟踪系统的硬件组成框图如图1所示，系统由发射阵列天线、接收阵列天线、射频前端通道模块、自跟踪基带单元信号处理模块、主波控单元模块、电源和外部时钟等部分组成。接收阵列天线在射频前端分为4个子阵，每个子阵由8×8的阵元组成，子阵中阵元按半波长等间距排列。接收阵列天线合成的4路信号进行模拟下变频处理以后，得到中频频率为140 MHz、带宽为6 MHz的信号，分别通过SMA接口送入数字板。自跟踪基带单元模块利用外部时钟提供的100 MHz采样率对4路信号进行采样，得到中心频率为40 MHz、信噪比为-8 dB的信号。由于之后信号处理需要用到接收信号的相位信息，A/D采样以后，经过FPGA对4路信号进行数字下变频处理，得到4路复信号。自跟踪基带单元模块同时根据运动平台主机提供的载体姿态角度信息和目标的引导信息完成目标的搜索捕获过程、角度测量、基带信号和波束形成等。测的目标角度估计值通过uPP通信接口送入DSP中进行角度跟踪滤波处理。DSP将跟踪滤波处理后的角度估计值和系统的状态信息返给FPGA，控制系统的工作状态。 FPGA将波束指向信息给主波控单元，确保运动平台上收发阵列天线的波束始终实时对准卫星[4]。
图1 运动平台相控阵卫星自跟踪系统组成框图
2 相控阵卫星跟踪系统测角算法
2.1 阵列形式与坐标定义
接收天线阵列和天线阵面坐标示意图如图2所示，图中每个小方格由8个阵元组成，其中阵元Z轴垂直纸面向外。系统测试角度示意图如图3所示，方位角(-90°～90°)为信号来波方向在XOY平面上投影与X轴的夹角，俯仰角(-90°～90°)为信号来波方向与Z轴的夹角[4]。
图2 接收天线阵面及坐标示意图
图3 调试角度坐标示意图
2.2 系统测角直接法
信号的入射方向单位向量为
r=[sinθcosφ,sinθsinφ,cosθ]T
(1)
为了方便起见，这里以子阵1为参考，则子阵2，3，4的坐标向量为
p2= [0,Dy,0]
p3= [Dx,0,0]
p4= [Dx,Dy,0]
(2)
其中，子阵2,3,4相对于子阵1的信号相移分别为
φ
(3)
φ
(4)
φ+Dysinθsinφ]
(5)
设运动平台相控阵波束指向角为(θ0,φ0)，由于阵列天线每个阵元的移相器移相，这样每个子阵的波束指向相位分别为
φ0
(6)
φ0
(7)
φ0+Dysinθ0sinφ0]=
φ20+φ30
(8)
经过子阵数字移相器后，子阵2、子阵3、子阵4接收信号的相位差分别为
Δφ2=φ2+φ20=
[sinθsinφ-sinθ0sinφ0]
Δφ3=φ3+φ30=
[sinθcosφ-sinθ0cosφ0]
(9)
Δφ4=Δφ3+Δφ2
(10)
由式(10)可得
sinθsinφ=sinθ0sinφ0-Δφ2λ/2πDy
sinθcosφ=sinθ0cosφ0-Δφ3λ/2πDx
(11)
因此有
(12)
由式(12)可得
(13)
也可以表示成
(14)
2.3 系统测角间接法
结合式(12)有
φ0=sinθsinφ=
sin(θ0+Δθ)sin(φ0+Δφ)=
(sinθ0cosΔθ+cosθ0sinΔθ)·
(sinφ0cosΔφ+cosφ0sinΔφ)
(15)
φ0=sinθcosφ=
sin(θ0+Δθ)cos(φ0+Δφ)=
(sinθ0cosΔθ+cosθ0sinΔθ)·
(cosφ0cosΔφ-sinφ0sinΔφ)
(16)
当测角很准的时候，如果信号来波方向角度与波束指向的偏差较小，式(15)可以变成
φ0Δφ+cosθ0sinφ0Δθ+
cosθ0cosφ0ΔθΔφ
(17)
类似可得
φ0Δφ+cosθ0cosφ0Δθ-
cosθ0sinφ0ΔθΔφ
(18)
结合上两式可得
Δφ
(19)
估计的来波方向则由下式可得：
φ0+Δφ
(20)
2.4 系统实际处理方法
假设每个子阵结构完全相同，子阵1为相位参考点，子阵1输出信号为y1(n)=z1(n)+v1(n)，v1(n)为子阵1输出的噪声，则L个阵元所有信号合成：
(21)
式中， Δγ=γ0-γ，γ0为每个阵元移相器控制波束扫描的相位，γ为信号入射方向的空间实际相位。
则子阵2、子阵3、子阵4输出分别为
y2(n)=z1(n)ejΔφ2+v2(n)
y3(n)=z1(n)ejΔφ3+v3(n)
y4(n)=z1(n)ejΔφ4+v4(n)
(22)
因为
(23)
y12(n)=y1(n)+y2(n)+v1(n)+v2(n)=
z1(n)(1+ejΔφ2)+v12(n)
(24)
y34(n)=y3(n)+y4(n)+v3(n)+v4(n)=
z1(n)ejΔφ3(1+ejΔφ2)+v34(n)
(25)
由上述两子阵输出的互相关，有
φ2)|z1(n)|2e-jΔφ3+vφ3(26)
y13(n)=y1(n)+y3(n)=z1(n)(1+ejΔφ3)+
v13(n)
y24(n)=z1(n)ejΔφ2(1+ejΔφ3)+v24(n)
(27)
同理求上述两个子阵输出的互相关有
φ3)|z1(n)|2e-jΔφ2+vφ2(28)
一般来说，在信号积累以后信噪比得到提高，噪声功率远远小于信号功率，所以上式中噪声功率可以忽略，此时可以分别求出Aφ3和Aφ2的相位，但是需要注意，此时Aφ3和Aφ2的相位Δφ3与Δφ2之间的关系为
Δφ3=-∠Aφ3, Δφ2=-∠Aφ2
(29)
理论上，累积快拍数N足够大，角度测量的精度比较理想[4]。
2.5 测角仿真基本思想
在这里假设任一子阵内共有M行、N列，共MN个阵元，pmn=[dm,dn,0]为第(m,n)阵元的坐标。假设入射波到达阵元pmn的时间比到达参考点p00的时间超前[5]，即该阵元相对于参考信号点延迟为
(30)
相应的信号相移为
φ+dnsinθsinφ]
(31)
当波束指向角度为[φ0,θ0]时，对应的移相值为
φmn0=
φ+dnsinθsinφ]
(32)
第(m,n)个阵元的信号表示为
xmn(t)=s(t)ej(φmn-φmn0)+vmn(t)
(33)
因为每个子阵有MN个阵元，则其中任意一个子阵的合成信号为
(34)
为描述简单起见，方便以后算法推导。可令s(t)=1，并设为合成信号以后的噪声v(t)，有
(35)
通过上式可以求出合成信号的幅度。根据仿真设置信噪比，根据信噪比的计算公式可以得出理想高斯白噪声的功率，从而得出4个子阵的输出信号y1(t),y2(t),y3(t),y4(t)。
2.6 测角仿真情况
分别考虑在理想情况下SNR对系统测角精度的影响。在下面的仿真中，方法1为系统测角直接法，方法2为系统测角间接法。
仿真1：假设信号从(θ,φ)=(35°,15°)方向入射进来。阵元之间间距为半波长。当测向时，数字移相器控制波束指向的是(θ+1°,φ+1°)≈(36°, 16°)。信号的SNR从-20 dB变化到40 dB。仿真中采用的快拍数是16 384。仿真结果是基于500次独立实验。
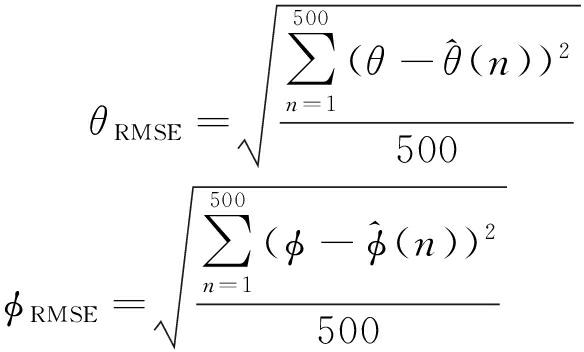
(36)
式中，
和
分别表示第n次试验时估计出的俯仰角和方位角。仿真结果如图4所示。
图4 测向RMSE随SNR变化曲线图(波束指向与目标入射角的差值是1°)
通过图4可以清楚地看出，在波束指向与信号来波方向存在偏差的情况下，方法1和方法2测角的偏差都随着信噪比的增加而逐渐降低。方法1测得俯仰角偏差优于方法2。
仿真2：假设信号从(θ,φ)=(35°,15°)方向入射过来。阵元之间间距为半波长。其中信噪比为-20 dB，积累快拍数为16 384，方位角波束和俯仰角波束同时与信号偏角从-5°变化至5°。其他条件同仿真1条件相同。
通过图5可以看到，当波束指向与信号偏差较小的时候系统的方位角和俯仰角测角精度都很高。当系统的波束指向和信号方向偏差较大时，方法1的俯仰角测角精度将好于方法2。而两种方法的方位角测角精度基本一致。
图5系统测角误差随波束指向与信号方向偏角变化曲线
仿真3：通过前两次的仿真可以看出，方法1比方法2更加适用于系统。所以再次研究方法1测向精度在不同幅度和相位误差情况下随SNR变化情况。本次仿真除了增加了幅相误差不一致以外，其他条件和仿真1一样。本次仿真的幅相误差分别为[4dB, 5°]， [1dB, 5°]， [4dB, 1°]， [1dB, 1°]。
从图6和图7可以看出，幅相误差对角度的测量具有影响，在信噪比较低的情况下，幅相误差影响较大。相位误差的影响要大于幅度误差的影响。
图6存在幅相误差时方位角估计误差随信噪比变化曲线
图7存在幅相误差时俯仰角估计误差随信噪比变化曲线
3 系统测角精度分析与精度提高方法
3.1 噪声误差
噪声误差是由于阵列天线将噪声和信号一起接下来，加上通道中由于电子的热运动引起的误差等，其中反映噪声误差的大小是信噪比[6]。接收机的额定噪声功率N0=
通过提高信噪比可以显著地抑制噪声干扰。目标偏离波束指向θ0位置取决于：
(37)
式中，K(θ)表示接收机噪声引起的归一化差信号，其误差为δΔ，假设接收机通道的信噪比为(S/N)Σ，则δΔ的表达式为
(38)
此时随机噪声引起的测角误差为
(39)
可以将接收的信号通过匹配滤波器，使输出的信噪比达到最大，从而抑制噪声功率。本系统的测角算法具有脉冲积累的效果，因为每个阵元都是独立不相关的，所以工程上认为噪声为独立不相关的高斯噪声，在积累的过程中，信号可以叠加起来，噪声反而会被抑制，从而提高信噪比。
(40)式中，N为积累的个数。可见通过积累提高信噪比。
3.2 幅相不一致
各种非理想因素造成阵列各通道的幅相不一致主要分为通道间的不一致和通道内不同频率的幅相响应不一致[7]。通过第2节的仿真也可以看出幅相不一致对测角精度的影响。
由于通道内幅度不一致引起的系统测角误差：
σ3=θBlnKA/2.772 6
(41)
由于通道内相位不一致引起的系统测角误差：
(42)
误差减少措施为：幅相误差可以通过信号的通道均衡来处理，本系统采用的通道校准技术是找出系统通道的失配系数，通过补偿的方法来实现[8]。
3.3 波束扫描误差
由相控阵雷达阵列的波束图可知：
F(θ)≈
(43)
由辛格函数曲线可知，当
时，可以查出x=±0.443π：
(44)
(45)
式中，θ0.5为波束在法线方向时的半功率波束宽度，λ为波长。此时的测角误差为σ5=0.02θB。
3.4 数字移相量化误差
数字移相器的位数决定了移相器所提供的量化误差。通过查阅资料知道k位的数字移相器[9]，其产生的最小相量为Δφ=2π/2k。因此，若用移相器修正馈线通道之间的相位差，则修正后剩余的最大相位误差为
(46)
这一相位误差的均方根值σΔφ按均匀分布的相位误差计算，应为
(47)
通过推导可以计算出波束指向误差与移相器位数k的关系为
(48)
4 结束语
本文针对运动平台相控阵卫星跟踪系统的背景下，主要提出跟踪系统的设计和角度测量算法的方案。结合相控阵天线特点，在传统的单脉冲测角的基础上，改进了比相测角算法。并且对比仿真了两种测角算法的性能，仿真结果和理论推导一致，该算法能提高输出信噪比的效果、测角精度准确，能够很好地解决卫星跟踪系统中角度测量的工程需求。详细研究了若干因素对测角精度的影响，并且适当地给出了改进测角精度的措施。本文从事的工作是闭环自跟踪系统中的关键技术之一，为开展弹载平台二维有源相控阵卫星跟踪技术的研究奠定了基础。
参考文献：
[1]张海成,杨江平,王晗中. 大型跟踪测量雷达的卫星标定方法研究[J]. 雷达科学与技术, 2014, 12(5):470-472.ZHANG Haicheng,YANG Jiangping,WANG Hanzhong.Study on Satellite Calibration Method for Tracking and Instrumentation Radar[J].Radar Science and Technology, 2014, 12(5):470-472.(in Chinese)
[2]张健. 基于通信信号的单脉冲测角算法实现[D]. 西安：西安电子科技大学, 2014.
[3]甘明. 基于相控阵天线单脉冲测角算法的精度研究[J]. 现代电子技术, 2013, 36(7):89-93.
[4]姜雯献,李朝海. 相控阵跟踪系统测角与角度跟踪算法[J]. 雷达科学与技术, 2015, 13(2):190-194.JIANG Wenxian,LI Chaohai.The Algorithms for Angle Measurement and Angle Tracking of the Tracking System in Phased Array Radar[J].Radar Science and Technology, 2015, 13(2):190-194.(in Chinese)
[5]姜义成,喻春曦. 一种改善单脉冲雷达测角精度的新方法[J]. 雷达科学与技术, 2009, 7(5):380-383.JIANG Yicheng,YU Chunxi.A Novel Approach for Angle Measuring Precision Improvement in Monopulse Radar System[J].Radar Science and Technology, 2009, 7(5):380-383.(in Chinese)
[6]杨雪亚,刘张林. 子阵级和差波束形成及测角方法研究[J]. 中国电子科学研究院学报, 2015, 10(1):82-86.
[7]张海成,杨江平,王晗中.大型跟踪测量雷达的卫星标定方法研究[J]. 雷达科学与技术, 2014, 12(5):470-472.ZHANG Haicheng,YANG Jiangping,WANG Hanzhong.Study on Satellite Calibration Method for Tracking and Instrumentation Radar[J].Radar Science and Technology, 2014, 12(5):470-472.(in Chinese).
[8]方棉佳,吕涛. 单脉冲和差波束测角的精度研究[J]. 雷达科学与技术, 2013, 11(6):645-649.FANG Mianjia,LYU Tao.Research on Precision of Angle Measurements in Monopulse Sum-Difference Beams[J].Radar Science and Technology, 2013, 11(6):645-649.(in Chinese)
[9]UMRANI A W,DUBEY V K.Effect of Angle-of-Arrival on Transmit Diversity and Beamforming Systems Under Correlated Fading[J].Electronics Letters, 2015, 41(6):293-294.
