0 引言
二维波达方向估计在阵列天线应用中是非常重要的研究方向。当前有关该问题的研究大多假定噪声为高斯白噪声[1]，但实际应用中，例如当回波中存在大反射面引起的闪烁或由海浪等造成的尖峰干扰时，噪声是相关的。此外，由于低空多径效应的存在，使得天线接收的回波经常是相干的[2]。在这些情况下，最常用的子空间类算法，如MUSIC算法、ESPRIT算法等性能将急剧下降。因此，相关噪声环境或相干信源的2D-DOA已受到广泛关注[3-4]。文献[5]通过所构造四阶累积量矩阵的特征值及其特征向量就可以直接获得近场源方位参数的估计，适用于任意高斯噪声环境，但是不能分辨相干信源。文献[6]采用FBSSD算法，解决了相干信源的分辨问题，但是没有分析相关噪声的影响。为解决上述问题，本文提出了一种基于四阶累积量的空间平滑(Cumulant-Based Space Smoothing, CSS)算法，该算法可以实现相关噪声环境中对相干信源的二维测向。
1 阵列结构和信号模型
如图1所示，假设阵列由两个相同的M阵元的平行均匀线阵X和Y组成，X和Y间距为dy，阵元间距为d。假设N个目标的方位角和俯仰角分别为{(θ1,φ1),…,(θN,φN)}，噪声为零均值的高斯色噪声，则X，Y阵接收到的信号可表示为
X(t)=A S(t)+NX(t)
(1)
Y(t)=A Φ S(t)+NY(t)
(2)
式中，
A=[a1,a2,…,aN]
ai=[exp(-jT1i),…,exp(-jTMi)]T
Tki=2π(k-1)dcosθisinφi/λ
Φ=diag{φ1,φ2,…,φN}
φi=exp(-j2πdysinθisinφi/λ)
式中，X(t)和Y(t)为M×1维的接收数据，S(t)为N×1维的发射数据，NX(t)和NY(t)为M×1维的相关噪声，λ为工作波长。
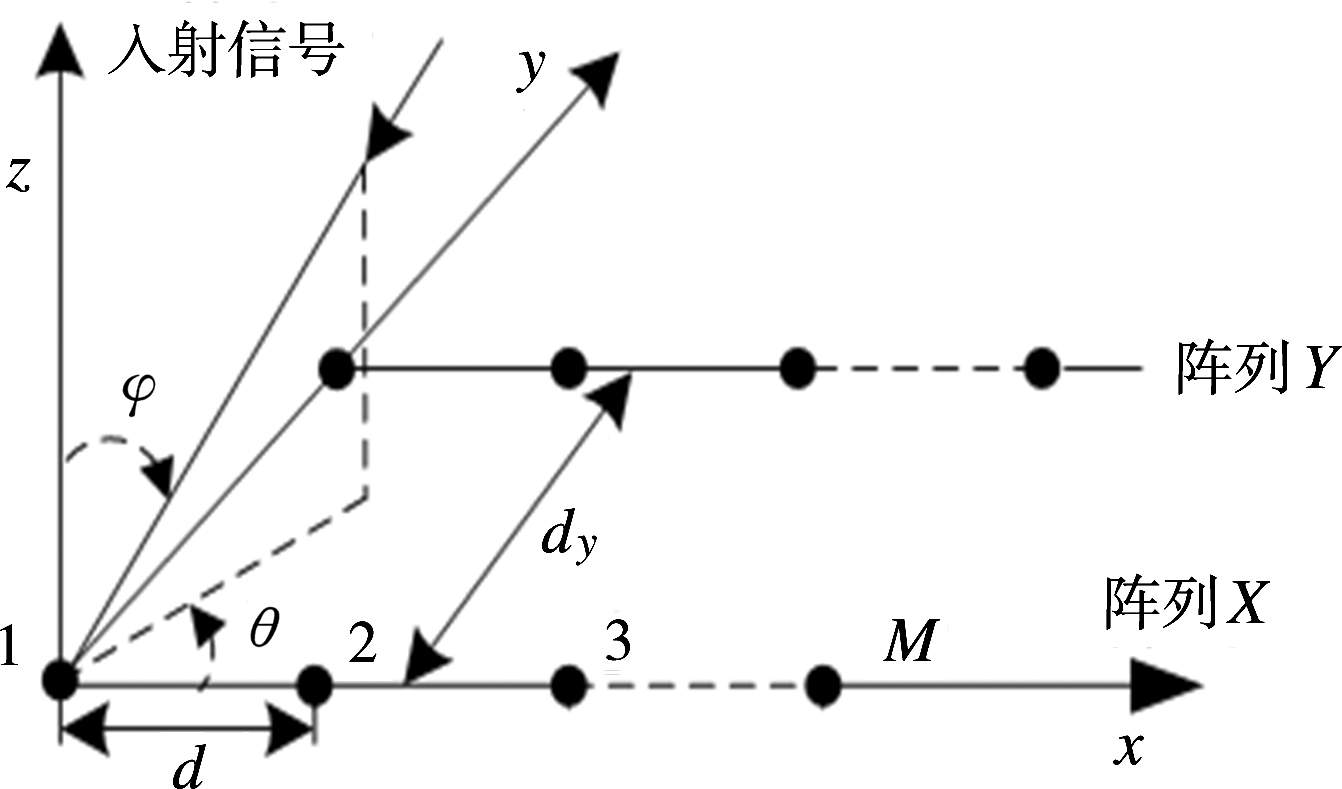
图1 双线性平行阵列结构
2 基于四阶累积量的2D-DOA算法
设xm(t)和ym(t)分别为线阵X,Y的第m阵元的接收数据，将式(1)、式(2)划分成P=M-L+1个子阵，L是平滑子阵的阵元数。有
Xi(t)=[xi(t),xi+1(t),…,xi+L-1(t)]T
(3)
Yi(t)=[yi(t),yi+1(t),…,yi+L-1(t)]T
(4)
则式(3)、式(4)可进一步改写为
(5)
(6)
式中，
D=diag{exp(-jTD1),…,exp(-jTDN)}
TDk=2πdcosθksinφk/λ,k=1,…,N
为了解决相关噪声的问题，定义L×L维的四阶累积量矩阵
和
且第m行第n列元素分别为
(7)
(8)
式中，xl,j(t)和yl,j(t)为Xl(t)和Yl(t)的第j个元素，xl(t)为(0,0)处的接收数据。
因此，2P个四阶累积量矩阵可以写为
(9)
(10)
式中，
Λ=diag{γ4,u1|b(1)|2,…,γ4,uK|b(K)|2}
对式(9)、式(10)作平滑处理，有
(11)
(12)
式中，
若子阵阵元数L>N，则当平滑数P≥N时，矩阵RSS满秩。
定义平滑的波达方向矩阵CS为
CS=Cy×[Cx]+
(13)
式中，
式中，λi，vi为Cx的非零特征值及特征向量。
通过对接收矩阵CS特征分解，得到矩阵AS,Φ，可以求出信源的2D-DOA，该算法不需要谱峰搜索，并且方位角、俯仰角可以自动配对。
3CSS算法的基本处理流程
根据以上的分析，将CSS算法的基本处理流程归纳如下：
Step 1：利用式(7)、式(8)、式(11)和式(12)计算平滑的四阶累积量矩阵Cx和Cy，然后对Cx进行特征分解，依据盖尔圆准则确定信源个数N。
Step 2：通过式(13)计算平滑波达方向矩阵CS。
Step 3：对CS特征分解，取前N个大特征值为
其特征向量为
N)。
Step 4：利用上一步求得的
和并根据式(9)、式(10)和式(13)可得
λ/2πd
(14)
(15)
式中，
为向量
的第j个元素。
Step 5：联立求解式(14)、式(15)，可得信号的方位角及俯仰角
4 算法性能仿真与分析
4.1 算法的2D-DOA性能
假设观测的相干源角度为(10°,40°)，(20°,50°)和(60°,30°)，采用双线性12阵元的天线，平滑次数P=5，距离d和dy均为半波长。信噪比为10 dB，快拍数为1 000，噪声为相关噪声，Monte-Carlo实验次数为50。图2(a)、图2(b)给出了2D-DOA情况，图2(c)给出了角度配对情况。
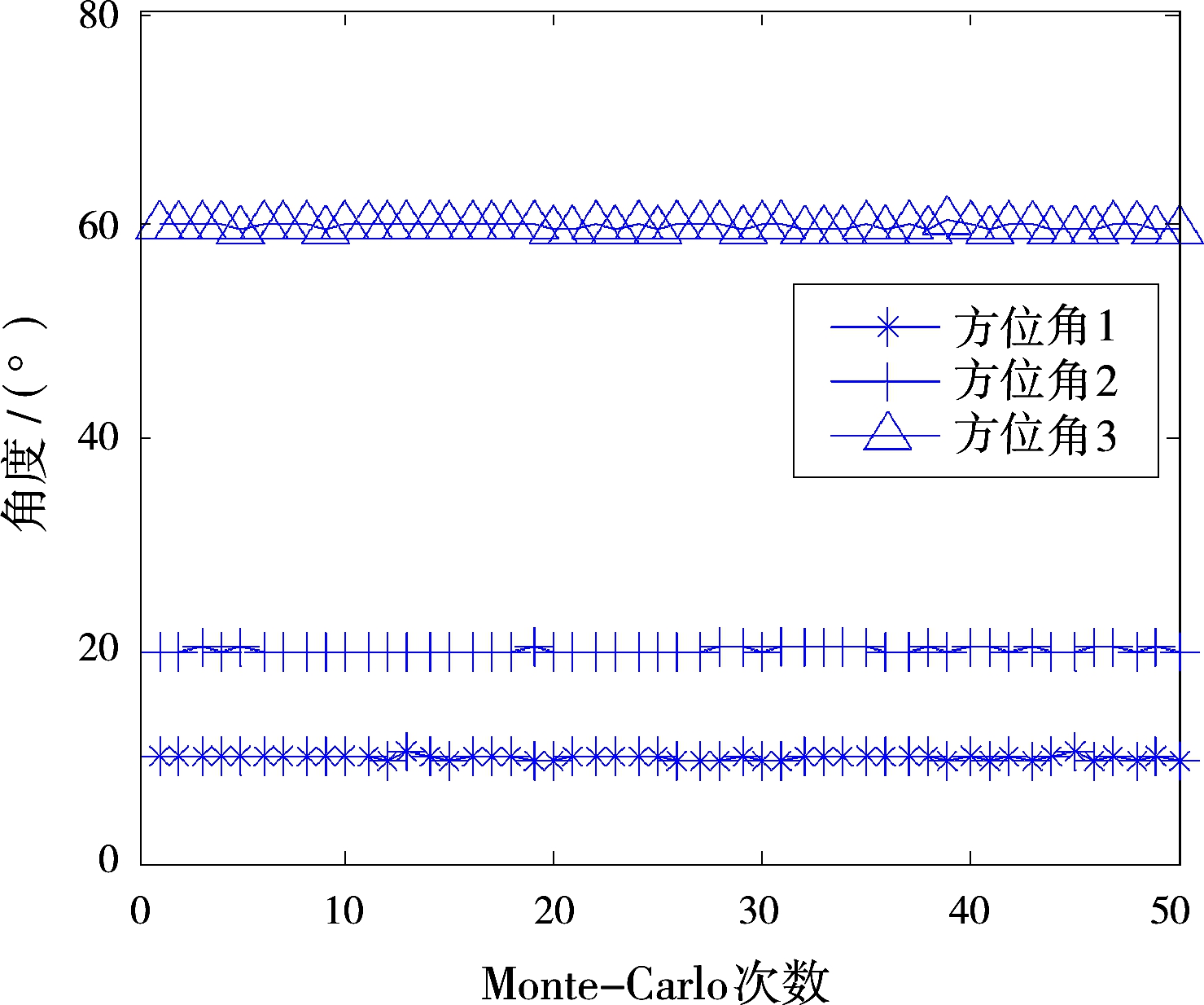
(a)方位角估计结果
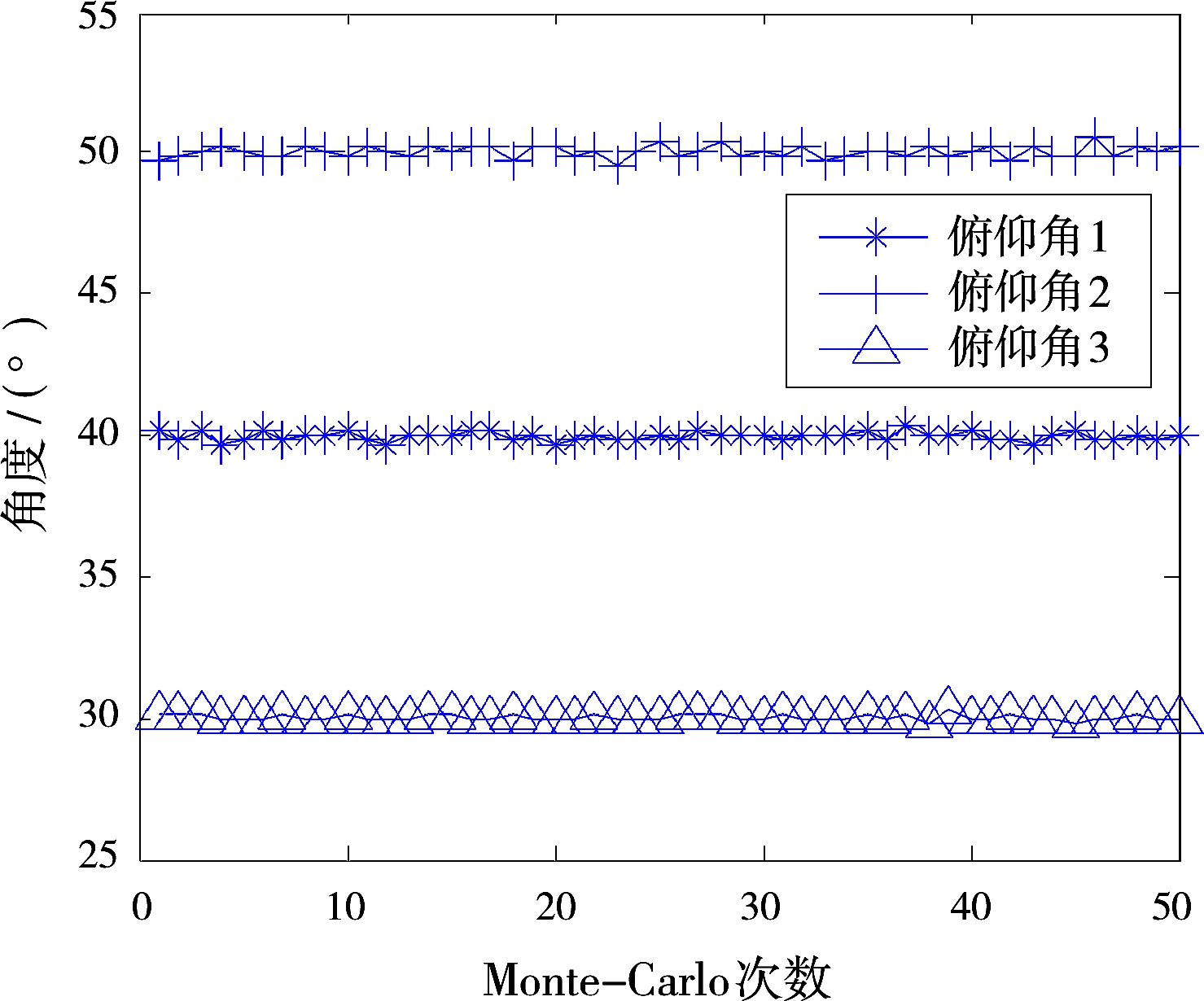
(b)俯仰角估计结果
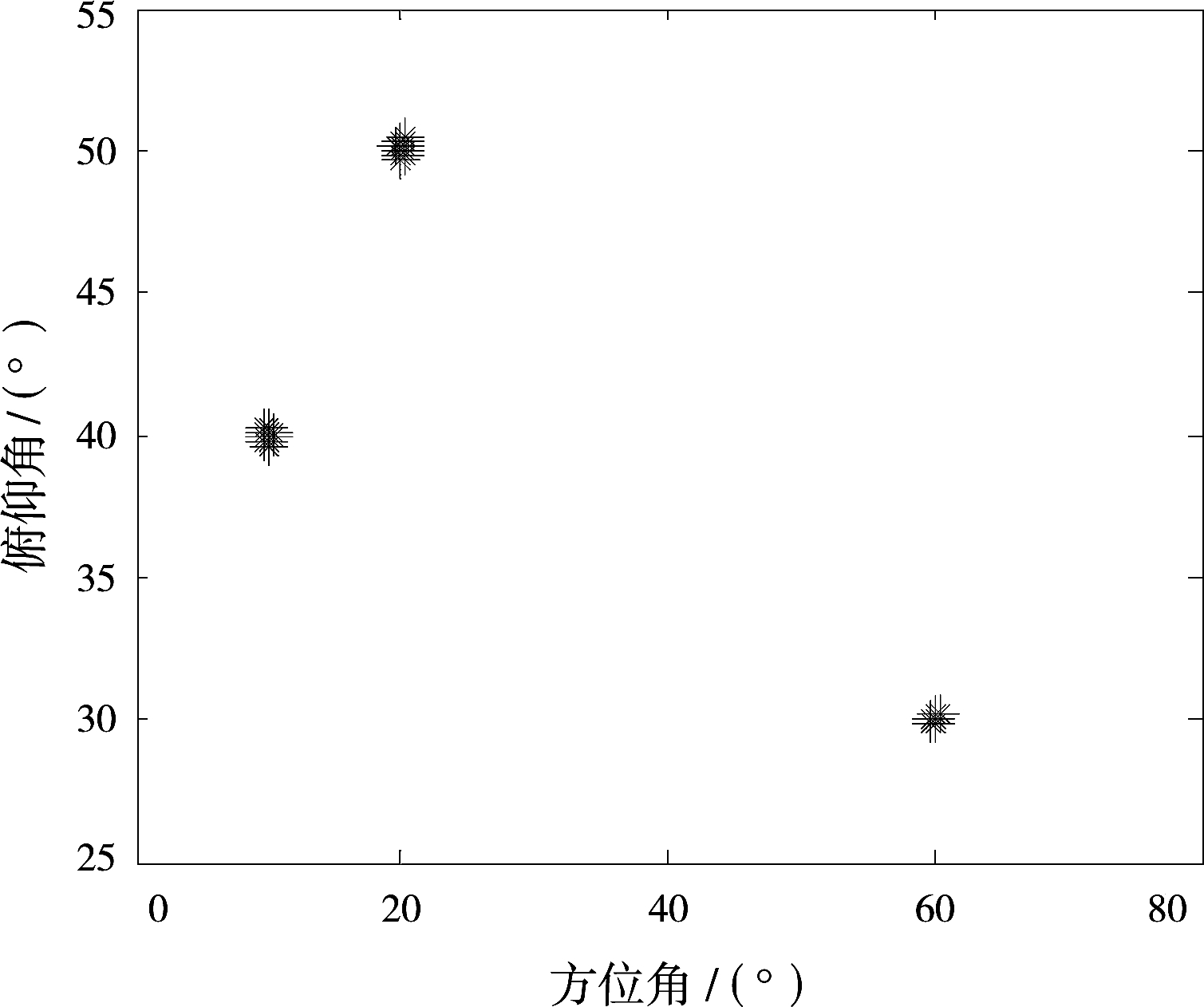
(c)二维角度的配对结果
图2算法对信源二维到达角的估计
从图2可以看出，所提方法可以对多信源实现2D-DOA，并且可以实现估计角度的自动配对，可以解决相关噪声下相干信源的2D-DOA问题。
4.2 算法不同信噪比的统计性能
取信噪比的范围由0dB到30dB，阵列设置和其他参数不变。图3(a)、图3(b)分别给出了不同信噪比下2D-DOA的偏差、方差。
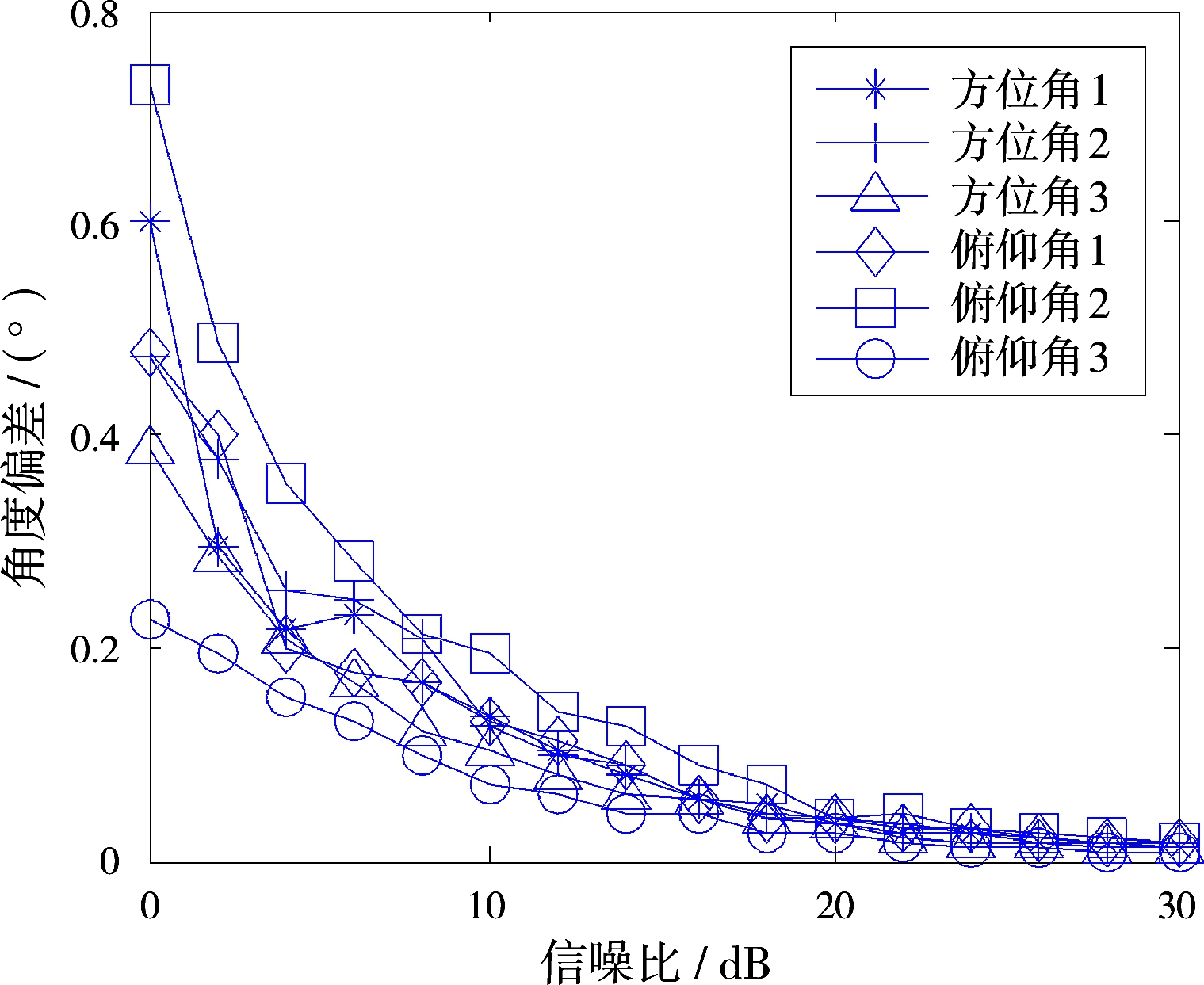
(a)二维角度的偏差
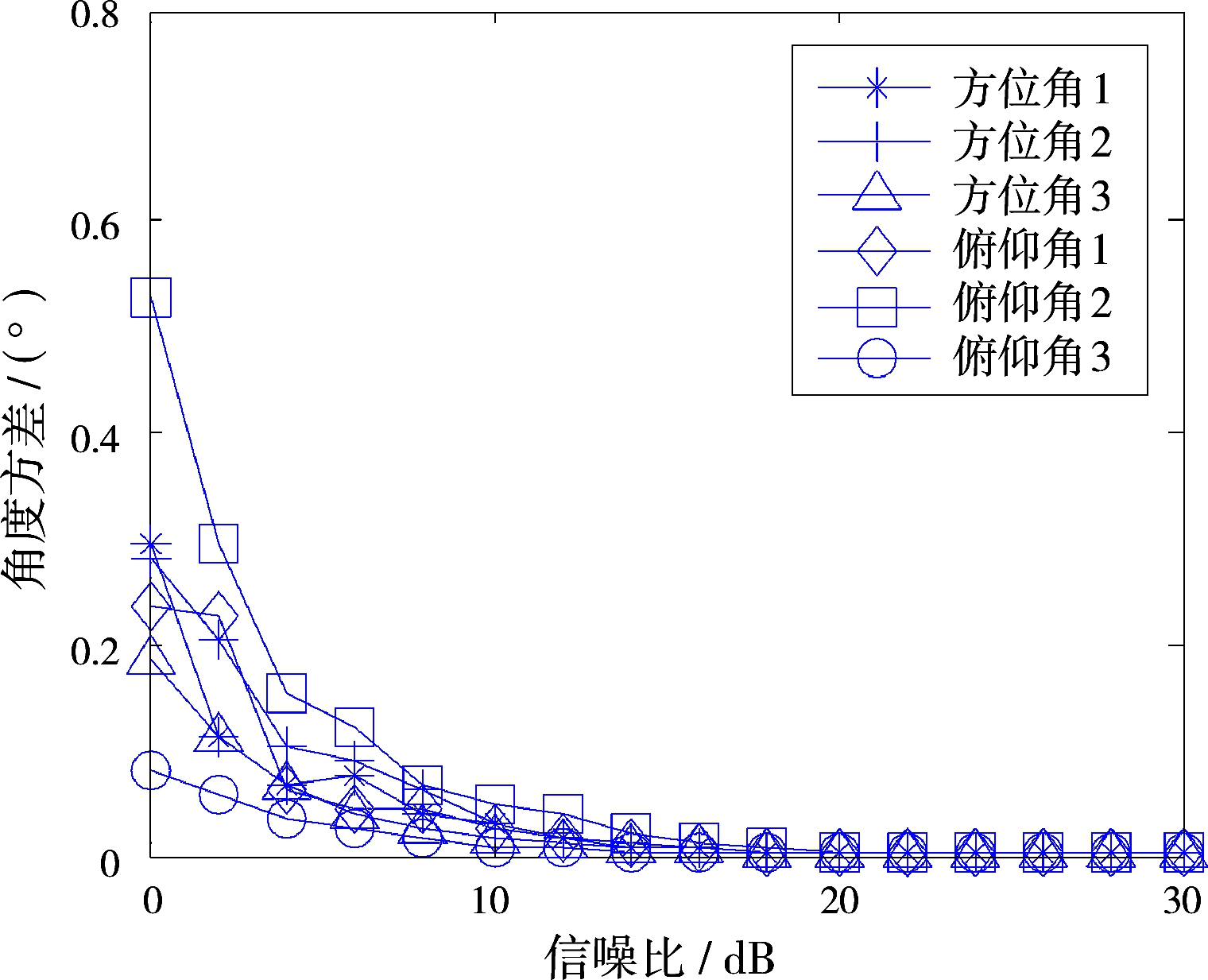
(b)二维角度的方差
图3算法在不同信噪比下的统计性能
由图3可见，所提CSS算法适用于低信噪比的2D-DOA情况，并且随着信噪比的提高，2D-DOA的偏差和方差逐渐减小；并且由于信源3与其他两个信源的角度间隔较大，所以其2D-DOA估计的精度略高一些。
5 结束语
本文将四阶累积量和空间平滑相结合，提出了一种新的CSS算法。该算法采用两个平行的均匀线阵作为传感器，通过特殊定义的四阶累积量矩阵对接收空域数据进行平滑处理，实现了相关噪声环境下对相干信源的二维波达方向的估计，并且所估计信源的二维波达方向能够自动配对，最后通过蒙特卡罗实验证明了所提CSS算法的有效性。
参考文献：
[1]符博博,郑娜娥,胡捍英. 单基地MIMO雷达中基于改进传播算子的二维DOA估计算法[J]. 信号处理, 2016, 32(4):438-443.
[2]SHI Junpeng, HU Guoping, LEI Teng. DOA Estimation Algorithms for Low-Angle Targets with MIMO Radar[J]. Electronics Letters, 2016, 52(8):652-654.
[3]WANG Shuangling, HE Qian, HE Zishu, et al. Waveform Design for MIMO Over-the-Horizon Radar Detection in Signal Dependent Clutter and ColoredNoise[C]∥IET International Radar Conference, Xi’an:IET, 2013:14-16.
[4]王鹏,邱天爽,李景春,等. 基于四阶累积量的近场源多参数联合估计[J]. 大连理工大学学报, 2015, 55(6):625-630.
[5]叶中付. 空间平滑差分方法[J]. 通信学报,1997, 18(9):1-7.
[6]石和平. 阵列信号处理中的DOA估计关键技术研究[D]. 天津：天津大学, 2015:12-32.
