0 引言
线性调频连续波(Linear Frequency Modulated Continuous Wave, LFMCW)雷达具有距离分辨率高、不存在距离测量盲区、方向性好、角度分辨率高、发射功率低等很多优良性能,特别是近些年,固态微波毫米波器件取得前所未有的进步,FMCW雷达通过采用毫米波集成技术实现近程探测,大大缩小了体积和成本,因此其得到快速的发展和应用。
LFMCW雷达系统通过测量发射信号和回波之间的差频信号频率提取目标参数信息。目前国内外提出了许多频率估计算法应用于LFMCW雷达距离测量,研究的重点主要在测量精确度和工程实现方面。提高探测精确度的主要实现方法是提高对差频信号的准确估计,目前已提出多种方法,在时域上有自相关法、极大似然估计法等,但是运算量很大,实时处理性能差,不便于工程实现。更多实现方法是在频域上利用借助FFT技术测量差频频率使得LFMCW雷达系统进一步地简化,但同时带来FFT的栅栏效应,使得差频信号频率不能与FFT的量化谱线重合,测量误差较大。文献[1]利用信号频谱的最大两根谱线进行插值对频率进行估计,被称作Rife算法。当信号频率位于两相邻量化频率之间的中心区域时,估计精度很高,估计方差接近克拉美-罗限(CRLB);在信号频率接近量化频率点时误差较大。文献[2]基于Rife算法通过FPGA实现LFMCW雷达测距,在一定程度上提高了测距精度,但没有解决Rife算法的不足。文献[3]利用M-Rife算法基于FPGA实现对Rife算法的优化,性能稳定,但是需要频谱平移并反复计算修正频谱,使得计算量较大。文献[4]提出Jacobsen算法,使用FFT计算后的实、虚部代替FFT模值进行插值。同时FPGA技术近年飞速发展,集成了专用的信号处理IP核为LFMCW雷达信号处理提供了新的手段和硬件支持。针对Rife算法和Jacobsen算法各自特点,本文提出一种基于两种算法的联合频率估计方法,应用于三角波调制的LFMCW雷达,精度高、计算量少且性能稳定,适合在FPGA上实际工程应用。
1 测量方法
1.1 测距测速原理
LFMCW雷达利用发射信号与接收信号混频输出的差拍信号计算得出目标距离信息。理想情况下的差频信号存在规则区间和少量的非规则区间,目标信息主要体现在规则区间的差频信号上,因此本文主要对规则区间差频信号进行采样处理。
LFMCW雷达主要采用波形有锯齿波和三角波,其中三角波可以解调出目标的多普勒频移。其差频信号与距离R、速度v的关系为
(1)
(2)
式中,c为光速,T为三角波调制周期, ΔF为信号频带宽度,fbu,fbd分别为上扫频和下扫频阶段差频信号频率。
1.2 算法流程
设对差频信号采样后的离散信号为X(k),采样频率为fs。Rife算法主要根据最大和次大两根谱线进行频率估计:
(3)
(4)
式中,谱线最大值X(k0)对应位置为k0。k1为次最大值位置,k1=k0+i。当次大值位于最大值左边时,i=-1;次大值在最大值右边,i=1。通过估计上下扫频两段差频信号频率,再利用式(1)、式(2)计算目标参数。
Jacobsen算法利用FFT频谱最大的3根谱线来对频率估计值进行校正,并使用FFT计算后的复数结果代替FFT模值进行插值估计,以一定计算量代价改善谱峰的估计精度。Jacobsen算法对离散差频信号的频谱最大值位置搜索,确定频率估计偏差为
(5)
式中,X(k0-1),X(k0+1)为最大谱值两侧相邻谱线。然后通过式(3)计算差频估计频率,再通过式(1)、式(2)计算目标参数。
结合Rife算法和Jacobsen算法各自特点以及相关性,提出一种联合算法兼顾计算量和精确度。本文提出的LFMCW雷达测距联合算法流程如下:
1) 对三角波型差频信号上下扫频的规则区间进行AD采样,取得离散数字信号。
2) 采用Rife频率估计算法,估计的频率偏差为δ1。
3) 判断估计频率与量化频率相对位置。当|δ1|≥δR,令δ=δ1。δR相当于一个门限值。否则进行步骤4)。
4) 用式(5)Jacobsen算法计算频率估计偏差δ2,令δ=δ2。
5) 用式(3)计算差频估计频率,再用式(1)、式(2)计算目标参数。
1.3 性能分析
在Matlab中Rife算法作蒙特卡罗仿真,信号频率从0.995MHz到1.000 5MHz等间隔的1 001个频率点,采样频率fs=4 MHz, 信噪比SNR=5 dB。对每个频率点作1 000次蒙特卡罗仿真,0.996 1 MHz,1 MHz,1.003 9 MHz分别为3个量化频率点。Rife频率估计算法中插值偏移量δ对频率估计误差的影响如图1所示,Rife算法能在一定程度上减少因为能量泄漏和栅栏效应引起的频率估计错误,但是当被估计频率位于两相邻量化频率的中心区域时精度很高,位于量化频率点附近时频率估计性能较差。由图1可知,当待估频率在0.995 5~0.996 6 MHz,0.999 4~1.000 6 MHz 和1.003 3~1.004 5 MHz时,频率估计误差较大,其区间边界所对应的量化频率偏差δ分别为0.149 4和0.145 0,0.156 0和0.150 6,0.150 0和0.149 4。在中量化频率偏差δ与门限δR判断中,一般选取最大偏差为δR,同时由于误差存在和方便在FPGA中计算,因此在本联合算法中门限δR取0.2。
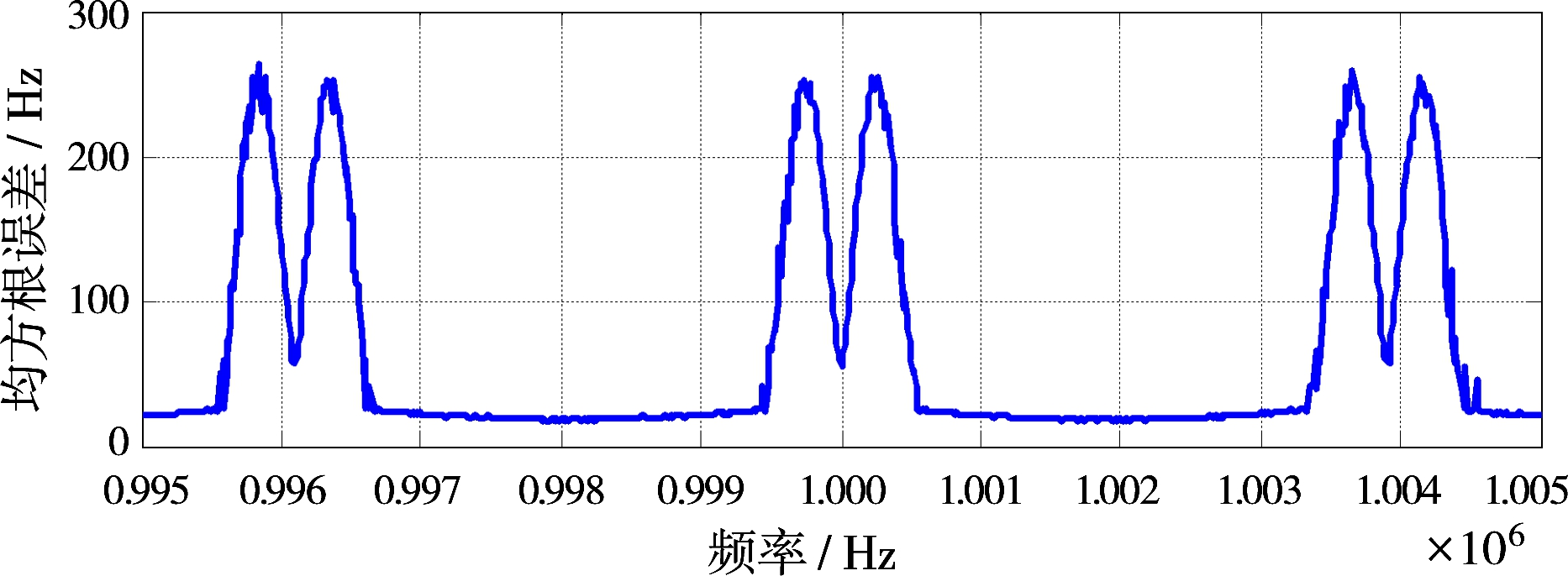
(a)不同频率下Rife算法频率估计误差
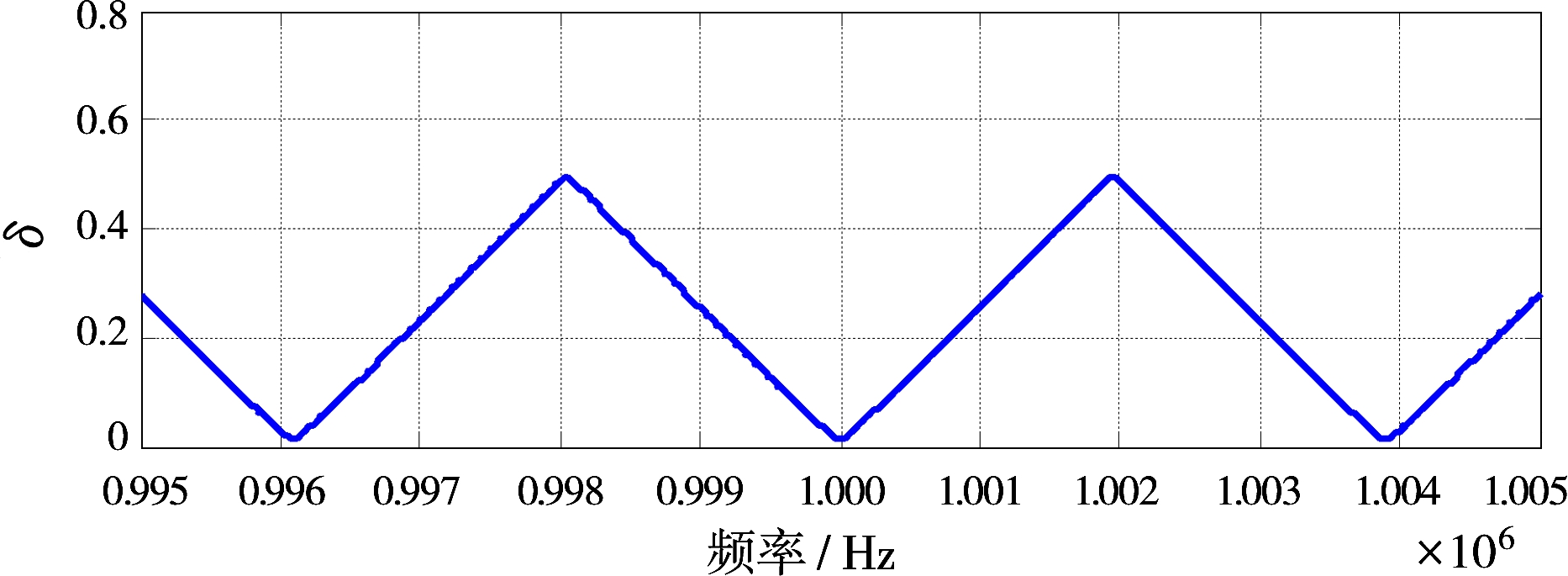
(b)不同频率下δ的取值变化
图1 δ对频率估计误差的影响
通过Matlab仿真,在信噪比SNR=-5, 0和5 dB环境下对比Rife算法和Jacobsen算法与联合估计算法的均方根误差和待估计频率之间的关系,如图2所示。当SNR>0 dB时 ,该算法频率的估计精度在量化频率点附近Jacobsen算法比Rife算法比较有很大提高,同时在两个相邻量化频率的中心区域内Rife算法仍然具有较强估计能力,因此联合算法结合两种算法在不同区间内的各自估计性能优势,对比已有的两种单一算法可以在整段频率区间都能取得较好的估计值。
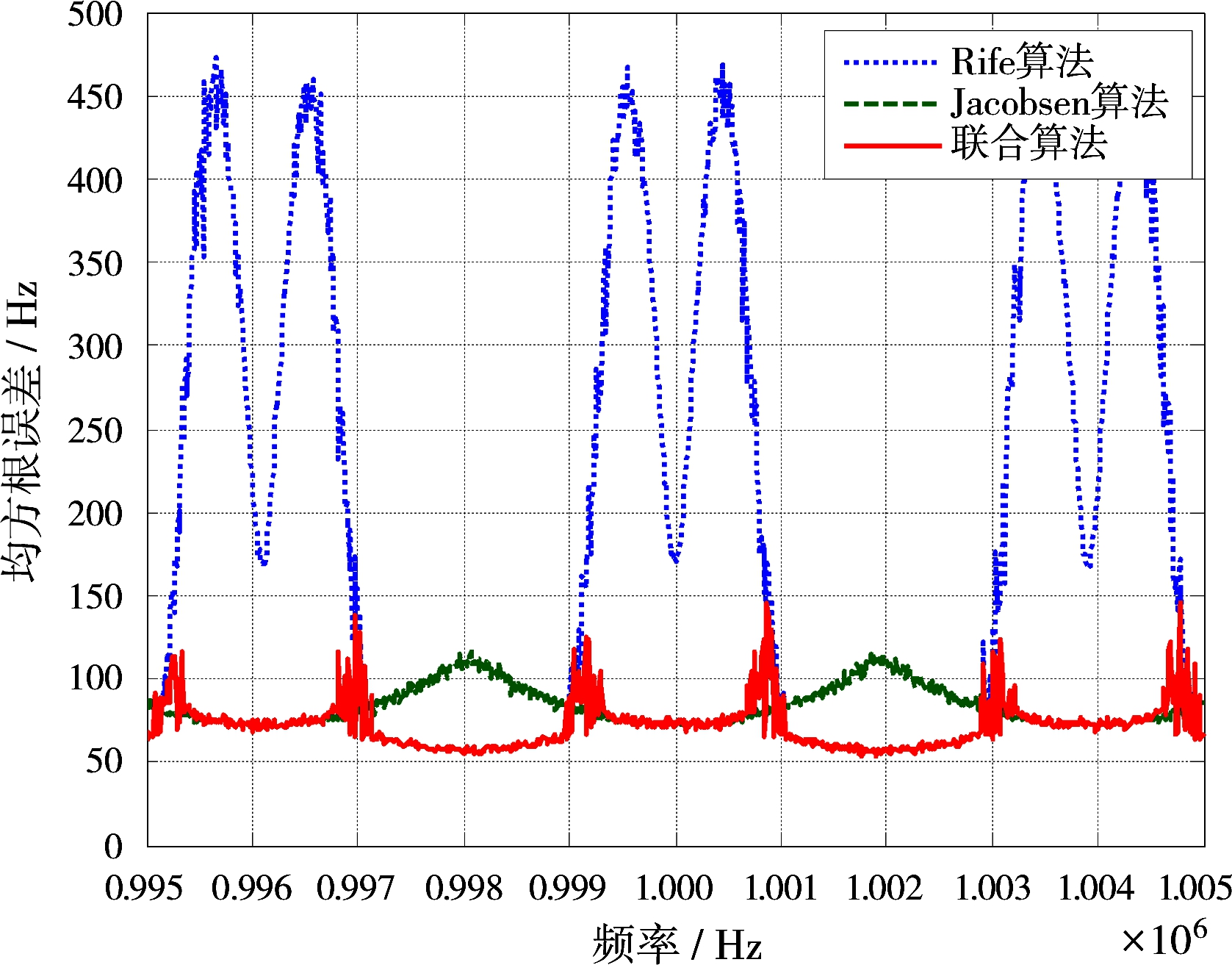
(a)SNR=-5 dB
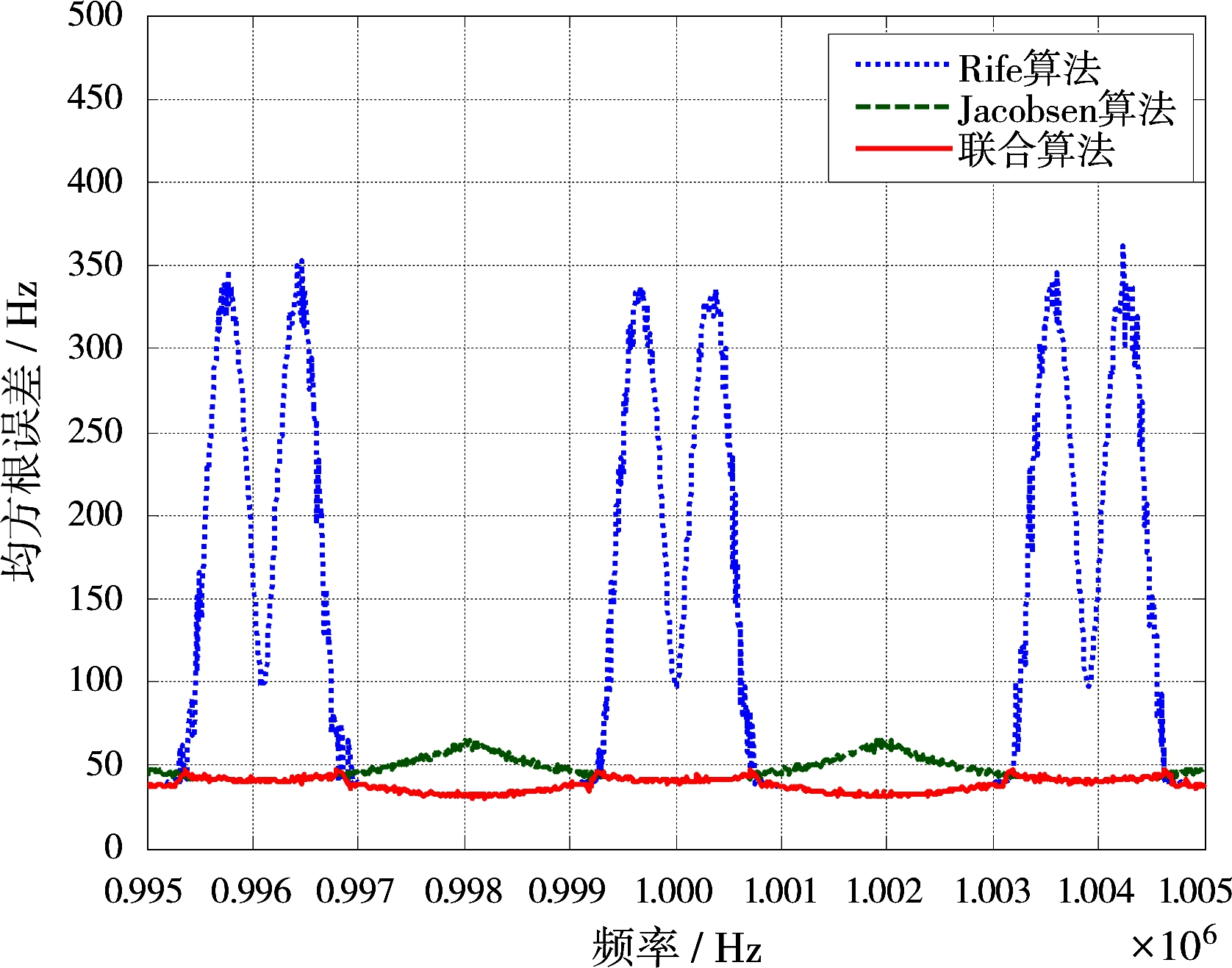
(b)SNR=0 dB
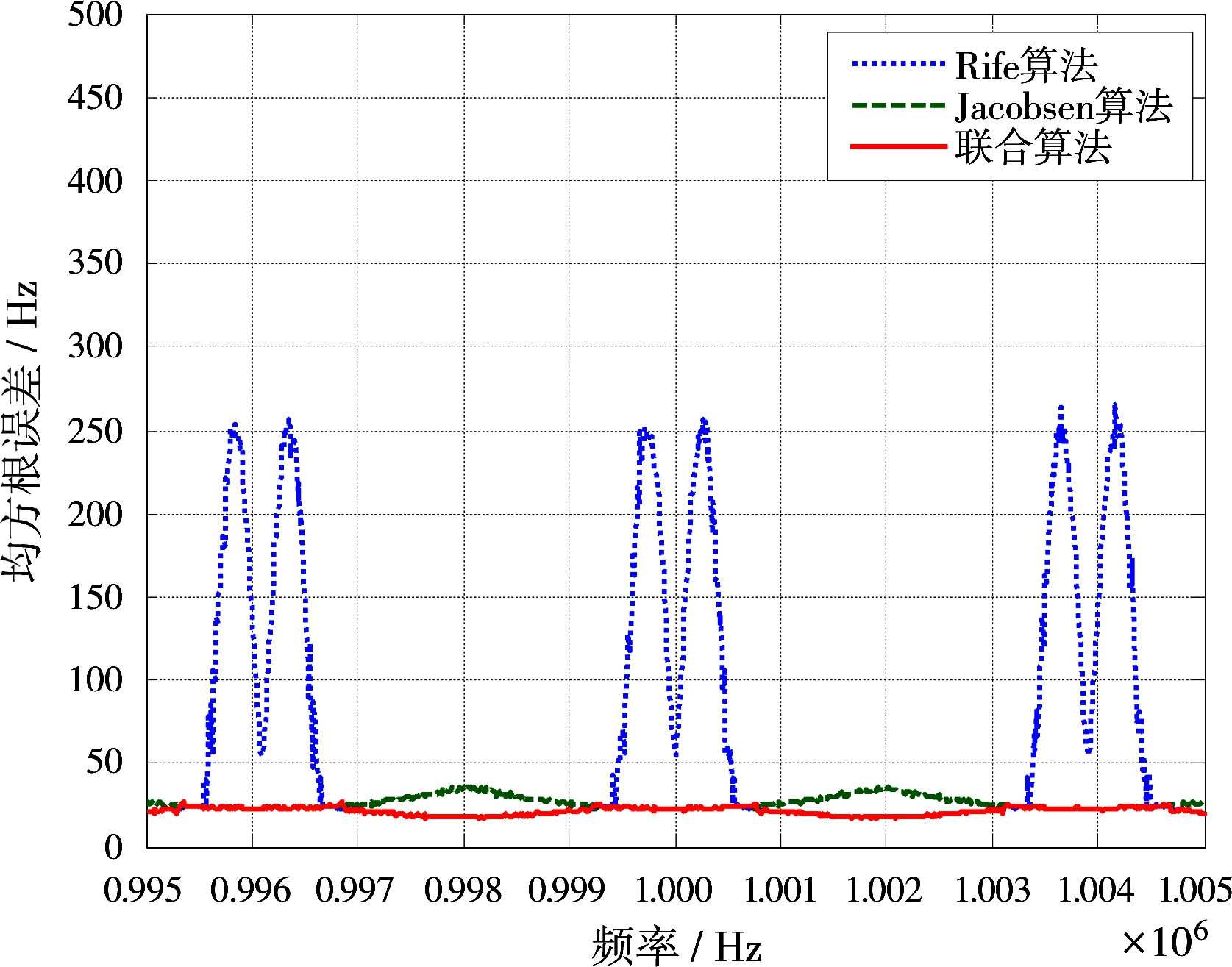
(c)SNR=5 dB
图2算法估计性能比较
1.4 算法计算量分析
表1列出了各个算法的运算量情况。联合算法需要判决插值偏差δ与门限δR的大小,选择不同算法进一步处理,所以联合算法的计算量介于Rife算法和Jacobsen算法之间,因此联合估计算法计算量相对较小。
表1 各算法运算量对比

2 算法实现
2.1 FPGA实现
本设计中可编程逻辑器件FPGA选用Altera公司的Cyclone IV系列EP4CE30F23C8N芯片,基于Quartus II软件采用Verilog HDL语言对算法整体实现,经过综合后得到的RTL结构模型如图3所示。
程序主要包括AD采样模块、FFT模块、PLL模块、频率估计模块和目标参数计算模块。各主要模块功能如下:
1) AD采样模块根据奈奎斯特采样定理由最远目标距离的差频信号频率确定采样频率,且控制只采集差频信号规则区的有效信息。PLL模块控制ADC的采样频率,采样位数为16位。
2) 采样后数字信号直接进入FFT模块,FFT由Quartus II软件的MegaWizard Plug-In Manager生成FFT-IP核,FFT控制模块起信号控制作用。FFT后信号可直接输出实部、虚部,同时可经过取模模块输出功率值。FFT 运算点数为1 024点。
3) 频率估计模块首先对功率值搜索,得到最大值和左右相邻值,并求出次大值,同时记录各自位置,然后采用联合估计算法读出信号频率信息。
4) 目标参数计算模块保留上下扫频的差频信号估计频率,通过式(1)、式(2)计算得出目标参数信息。
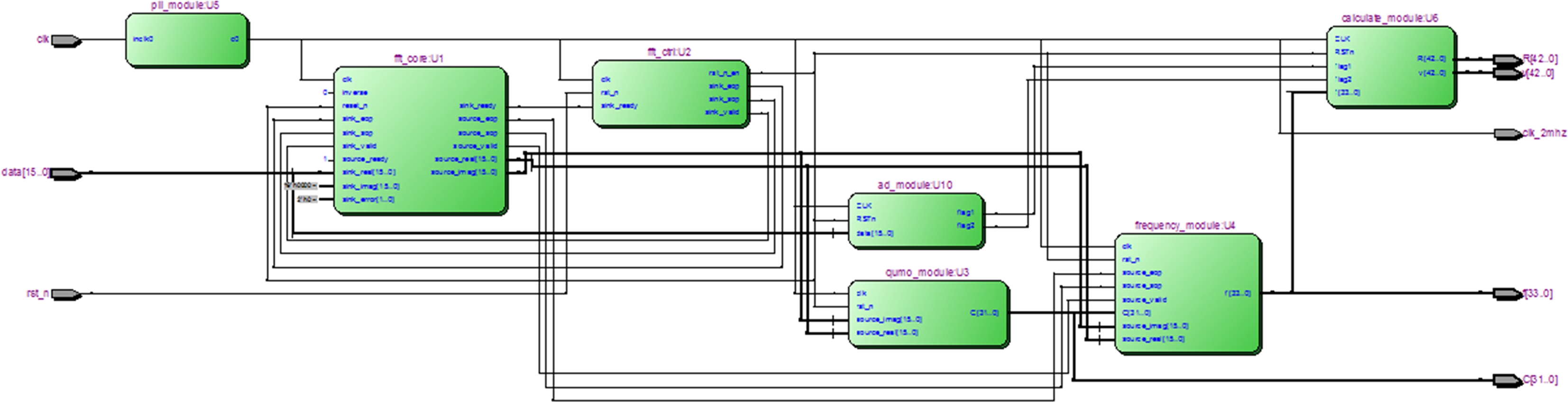
图3 RTL设计图
2.2 FPGA资源消耗
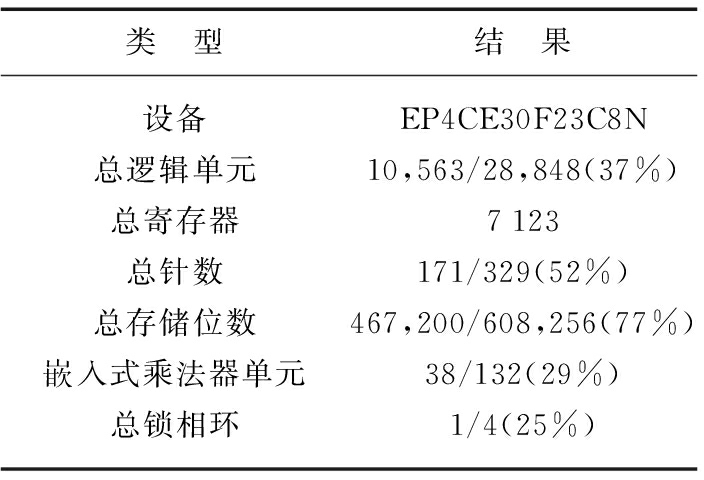
通过Quartus II 对LFMCW雷达系统算法进行编译,得到 FPGA资源消耗情况如表2所示。应用联合频率估计算法的雷达系统整体逻辑资源占用较少,系统有富余资源用于测量算法的进一步优化改进和雷达系统FPGA部分其他模块设计。
表2 FPGA资源消耗表
3 算法验证
测试选取LFMCW雷达信号中心频率f0=37.5 GHz(波长λ=8 mm),调频带宽B=1 GHz,调频周期T=10 ms。测试固定目标取20~30 m,步长为1 m。采样频率fs=0.5 MHz。通过固定目标测试结果如表3所示。在不考虑目标运动方向的前提下,设定运动目标的距离和速度,得到目标估计距离和速度信息如表4所示。
表3 测距结果
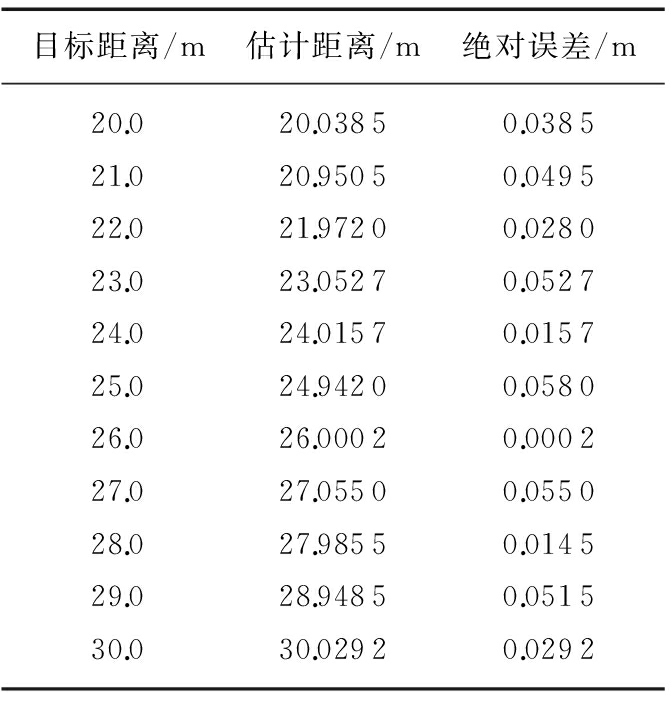
表4 测速结果
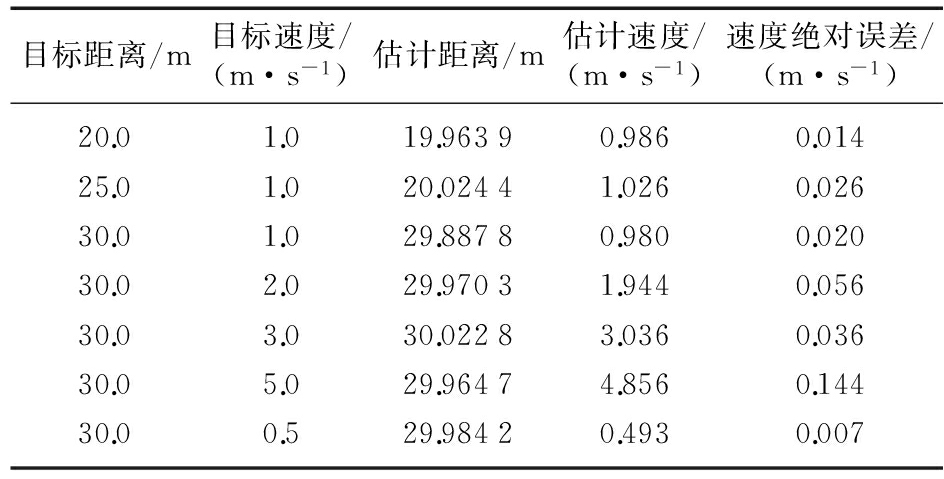
由表3得出,利用联合算法对差频信号经估计,在近距距离测量距离估计绝对误差小于0.06 m。由表4得出,利用三角波调制调频连续波特性,可以同时得出目标速度信息,速度误差小于0.20 m/s。通过SignalTapⅡ软件实时捕捉目标结果如图4所示,目标参数信息可以显示出来,在保证精确度同时具备实时性。
图4 目标参数实时结果
4 结束语
本文提出了Rife算法与Jacobsen算法的联合频率估计算法,通过Jacobsen算法补足Rife算法在量化频率点附近测距精度低的缺点,实现在整段频率区间都能取得较高频率估计性能;其次结合三角波调制LFMCW雷达特点,实现雷达精确测距和测速。基于FPGA硬件模块化设计实现LFMCW雷达系统,在探测范围内目标速度和距离参数都能取得较好的精确度,而且计算量相对较小,具备较高的稳定性和实时性,可以在LFMCW雷达中直接应用。
参考文献:
[1]RIFE D C, VINCENT G A. Use of the Discrete Fourier Transform in the Measurement of Frequencies and Levels of Tones[J]. The Bell System Technical Journal, 1970, 49(2):197-228.
[2]詹启东,涂亚庆. 基于Rife法的线性调频连续波雷达测距算法及实现[J]. 兵工学报, 2014, 35(5):748-752.
[3]王旭东,刘渝,邓振淼. 基于修正Rife算法的正弦波频率估计及FPGA实现[J]. 系统工程与电子技术, 2008, 30(4):621-624.
[4]QUINN B G. Estimation of Frequency, Amplitude, and Phase from the DFT of a Time Series[J]. IEEE Trans on Signal Processing, 1997, 45(3):814-817.
[5]孙峰,朱莉,张超,等. 毫米波LFMCW雷达测距关键算法研究[J]. 微波学报, 2015(S2):197-202.
[6]CANDAN C. A Method for Fine Resolution Frequency Estimation from Three DFT Samples[J]. IEEE Signal Processing Letters, 2011, 18(6):351-354.
[7]严鑫,黄永明,王海明,等. LFMCW车载防撞雷达信号处理模块研究[J]. 雷达科学与技术, 2016, 14(5):498-504. YAN Xin, HUANG Yongming, WANG Haiming, et al. Research on Signal Processing Module of LFMCW Automotive Anti-Collision Radar[J]. Radar Science and Technology, 2016, 14(5):498-504.(in Chinese)
[8]吴珊珊,胡国兵,丁宁,等. 正弦波频率估计结果的可靠性评估算法研究[J]. 现代雷达, 2015, 37(3):31-35.
