0 引言
多输入多输出(Multiple Input Multiple Output,MIMO)雷达是一种新型体制雷达,它使用多个发射天线发射互相正交信号探测目标,同时利用多个接收天线接收目标反射的回波信号并进行相干处理[1]。MIMO雷达与相控阵雷达相比能形成具有更多阵元的虚拟阵列,获得了更多的发射自由度,提高了空间分辨率,增加了可估计的最大信源数,以及参数估计的精度也有所提高[2],使得MIMO雷达在弱目标检测、干扰抑制、提高分辨率等方面具有明显的优势。其研究主要包括波形设计研究、空时自适应处理、目标检测参数估计等方面[3]。天波电离层发射模式与地波绕射传播模式组合的工作模式具有威力大、系统灵活、覆盖范围广等特点[4]。由于电离层具有分层特性,天波超视距雷达(Over-The-Horizon Radar,OTHR)信号在电离层中传播时经常发生多径传播或多模传播效应,严重影响天波OTHR对目标的检测、定位等性能[5]。而基于MIMO体制的天波OTHR利用MIMO雷达灵活的波束形成能力,尽最大可能消除天波超视距雷达中来自不同空间方位的多径、多模杂波[6]。天地波雷达也同样存在多径传播效应或多模传播效应,因此,研究将MIMO模式运用到天地波雷达中,MIMO技术与天地波组网雷达相结合,就将两者的优势结合在一起,使得系统的发射自由度得到提高,并且提高了参数估计的精度和空间分辨率,增加了可估计的最大信源数,同时还具有探测范围广且系统较为灵活等优势。
目标角度的估计问题一直是阵列信号处理的一项重要内容。针对天波MIMO、地波MIMO的参数估计,学者们纷纷展开了研究。文献[7]研究了天波MIMO雷达二维波达角估计问题,并提出了一种嵌套平行阵下基于子空间的二维DOA估计。文献[8]以“发射阵列为均匀线阵,接收阵列为L阵”作为模型,提出了基于ESPRIT算法估计出目标的三维角度信息,即可实现对目标在三维空间的定位。但是这不仅只局限于天波MIMO,还对阵形有要求。文献[9]采用单次快拍数据构建一组Toeplitz矩阵重构出新的协方差矩阵并进行centro-Hermitian矩阵变换,转化为实矩阵,运用ESPRIT算法估计出目标的发射角和接收角。文献[10]研究了在L型阵列下运用三阶张量分解法实现目标三维角度和多普勒频率的联合估计以及多目标定位。但是上述文献研究的都是天波MIMO的目标角度估计方法。文献[11]利用发射分集平滑 (Transmission Diversity Smoothing,TDS)对回波数据解相干的方法,该方法仅研究了用于单基地地波MIMO雷达的情况,只能估计出一个角度。文献[12]提出一种地波MIMO的基于二维多重信号分类算法的多目标DOD和DOA联合估计。文献[13]基于ESPRIT提出一种RTRESPRIT算法用于地波MIMO的联合角度估计。文献[14]利用发射阵和接收阵的旋转平移不变结构,采用ESPRIT算法估计地波MIMO目标的收发角。但是这些文献涉及的是地波MIMO的目标角度估计。目前国内外研究天地波MIMO多目标探测的相关文献很少。
天地波MIMO雷达具有光明的前景,本文提出了将MIMO雷达与天地波一体化相结合的工作模式,以双L型阵列为例,实现天地波MIMO多目标角度估计的仿真。本文建立了基于L型阵的天地波MIMO的回波模型,采用MUSIC算法完成多目标角度估计。最后验证了实现的天地波MIMO雷达仿真的有效性。
1 天地波MIMO雷达信号模型
天地波混合组网模式下的定位方法:天/地波联合传播模式下,高频无线电波通过自由空间斜入射到电离层,经电离层反射后通过自由空间到达海面,再经海面以表面波形式传播到接收站。天地波MIMO雷达系统如图1所示。
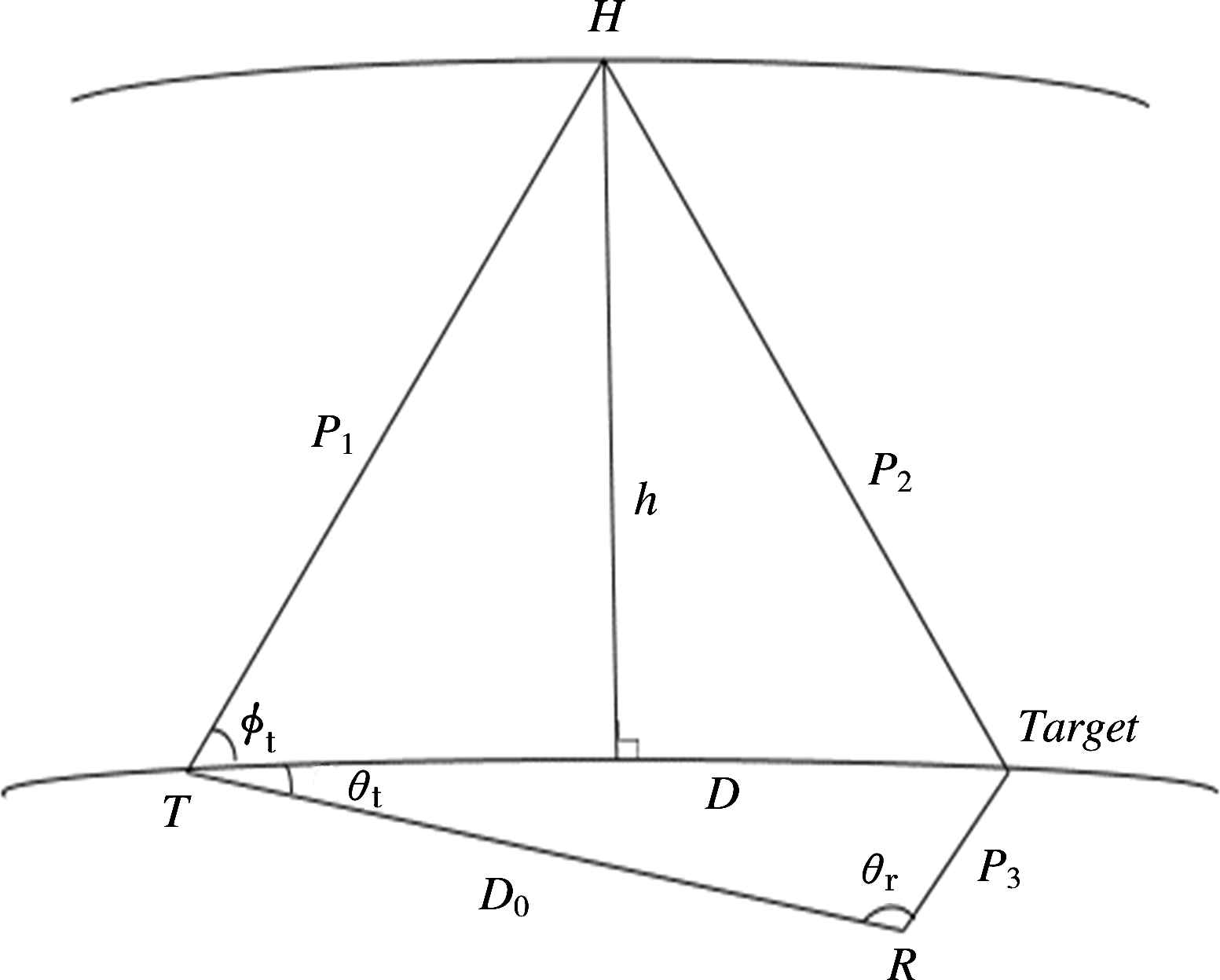
图1 天地波组网探测示意图
天地波传播模式结构图如图1所示,其中:T站为天波发射站;R站为地波接收站;Target为目标位置;D0为天波发射站到地波接收站的距离,是已知的;D为天波发射站到目标的距离;ϕt为发射俯仰角;θt为发射方位角;θr为目标与基线之间的夹角(方位角),可测出。P=P1+P2+P3为信号时延对应的传播距离,即群距离;P3为目标与地接收站的距离;h为电离层的高度。当不考虑电离层斜侧有P1=P2,群路径P可由时延测出。
于是问题就简化为:已知D0,P,θr,求解P3。可以得出平面坐标下的定位方程(忽略地球曲率):
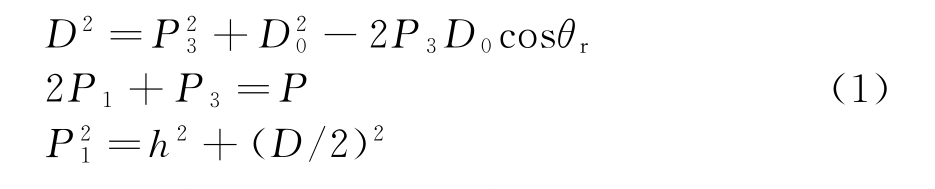
假设发射阵和接收阵列都是L型阵列,阵元间距均为半波长,发射阵列包含M_t个阵元,M_t=M_t1+M_t2-1,其中M_t1个阵元位于X轴,M_t2个阵元位于Y轴;接收阵列包含M_r个阵元,M_r=M_r1+M_r2-1,其中M_r1个阵元位于X轴,M_r2个阵元位于Y轴。假设远场空间有K个目标,第k个目标相对于发射阵列的方位角和俯仰角为(ϕtk,θtk),即为发射角,相对于接收阵列的方位角为θrk,即为接收角,k=1,2,…,K,如图2所示。
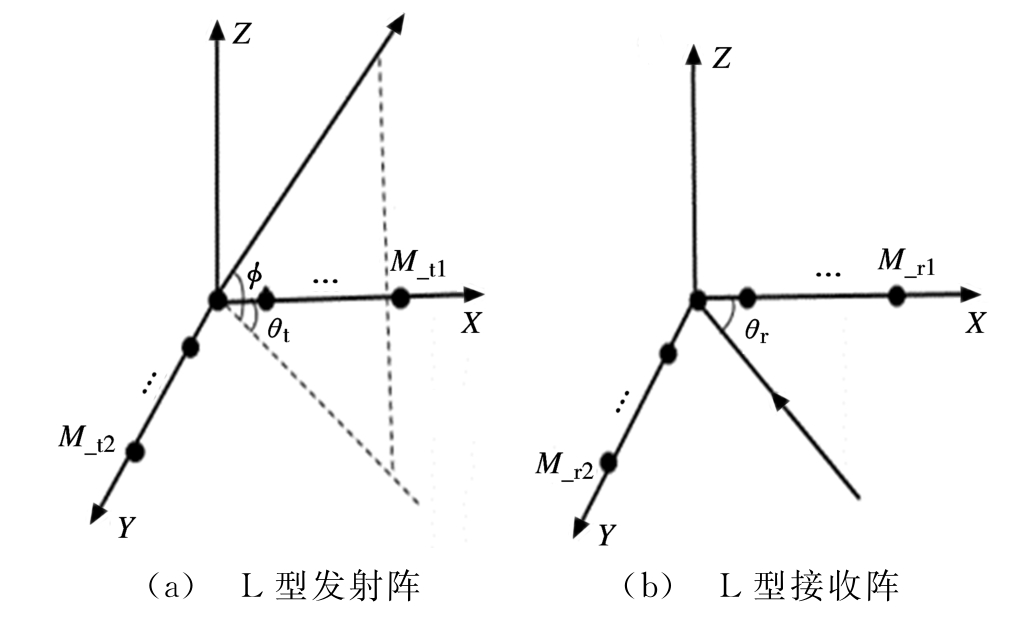
图2 L型发射阵及接收阵示意图
设发射阵元的位置为(xm,ym),m=1,2,…,M_t,发射正交信号为矢量s(t)=[s1(t),s2(t),…,sM_t(t)],考虑到正交性,有下式成立:
式中,∗为共轭运算符,c为常数。假设目标位于俯仰角为ϕt、方位角为θt的远场处,如果不考虑传输过程中的损耗,则第m个发射阵元的发射信号sm(t)到达目标时的信号为
式中,τm为第m个阵元相对于参考阵元到达目标的时延:
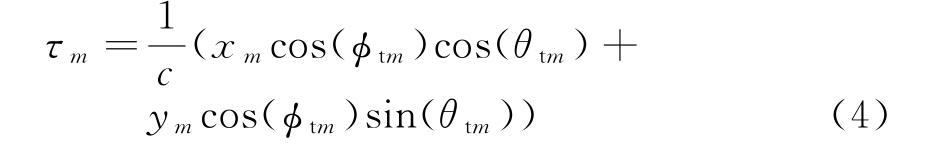
式中,c为光速,(xm,ym)为第m个发射阵元的坐标。假设发射信号为窄带信号,则有
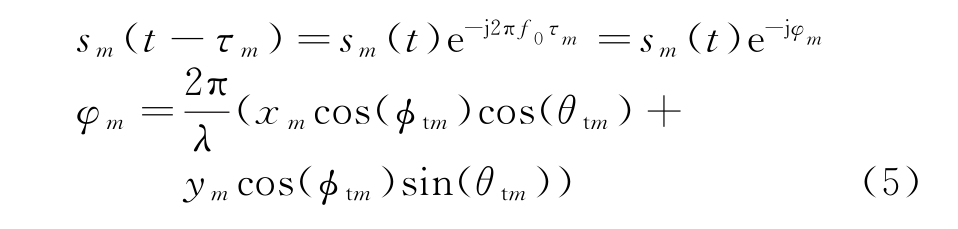
第m个信号从发射到目标处的传播时间为
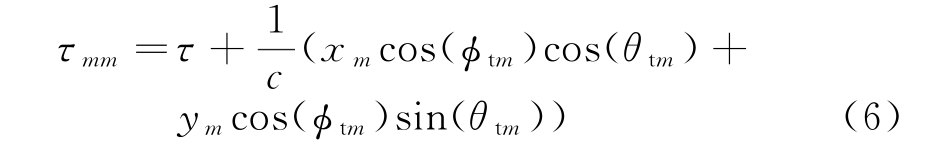
式中,τ=R/c,R为发射参考阵元到目标的距离。
则发射阵元的导向矢量为
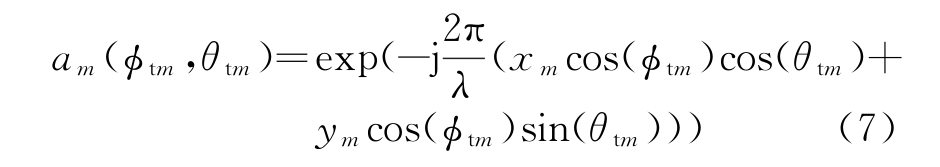
am(ϕtm,θtm)为发射导向矢量的第m个元素,m=1,2,…,M_t。如果不考虑目标多普勒效应,那么目标接收到的正交信号为各个发射阵元的叠加,所以上式可以改为
照射到目标的正交信号为
Xn(t)信号经过目标发射到海面,再经海面以表面波形式传播到接收站。假设目标散射系数为β,则第n个接收阵元接收到的信号为
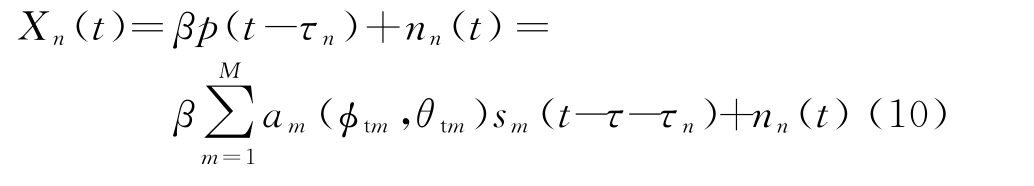
式中,![]() 为第n根接收天线接收到的噪声。考虑到发射信号的总带宽远小于其中心频率且阵元孔径较小,假设窄带条件成立,上式可以近似为
为第n根接收天线接收到的噪声。考虑到发射信号的总带宽远小于其中心频率且阵元孔径较小,假设窄带条件成立,上式可以近似为
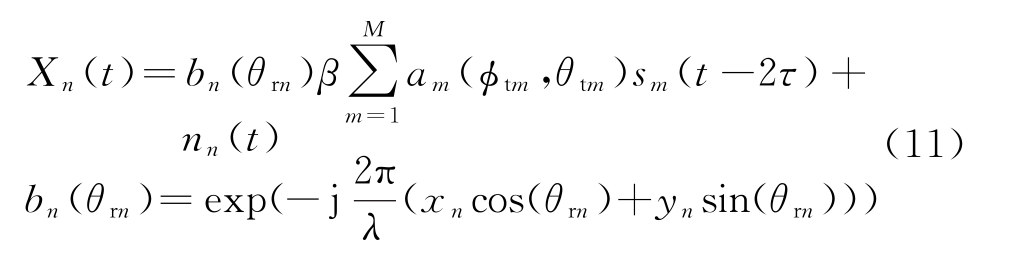
假设L为脉冲周期内的采样点数,Ts为采样间隔,那么L个回波信号矢量为
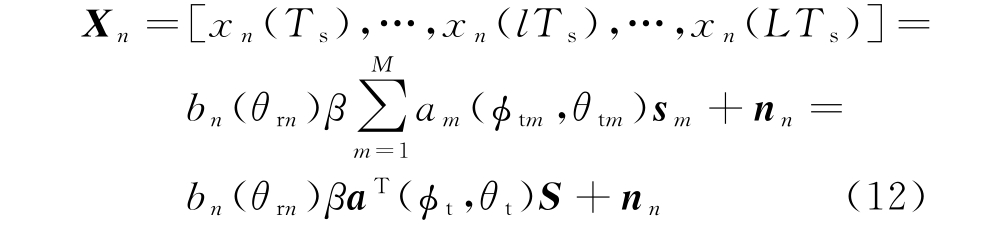
式 中,S=[s1,…,sM_t]T,nn=[nn(Ts),…,nn(LTs)]。如果有K个目标,在多目标情况下总的接收信号为
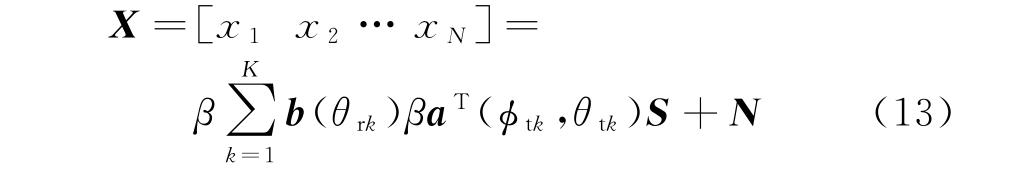
式 中,bn(θk)=[b1(θk),b2(θk),…,bN(θk)]T,N=[nn1,nn2,…,nnM_r]那么X为M_r×L维的回波数据矩阵。
将式(13)写成矩阵形式,在这里假设目标散射系数相同,都为β,则有
式中:X为接收数据;S为发射阵元发射的信号;N为接收的噪声矩阵;A=At⊗Ar,At=[at(ϕt1,θt1),at(ϕt2,θt2),…,at(ϕtK,θtK)]为发射导向矢量矩阵,Ar=[br(θr1),br(θr2),…,br(θrK)]为接收导向矢量矩阵,at(ϕt,θt)为发射导向矢量,br(θr)为接收导向矢量。
2 目标角度估计
由于天地波MIMO雷达各发射阵元发射的是正交信号,因此能够在发射端和接收端之间形成多个相互独立的通道。每个通道的目标回波系数都是互不相关的,故接收信号是由反射的多个发射信号的不同时延的叠加。在接收端使用匹配滤波器,让接收到的信号与发射端发射的信号分别进行匹配滤波,由于正交性,可以分离出发射信号。然后对经过匹配滤波后的数据作多普勒变换,然后进行角度估计。
MUSIC算法的基本思想:通过对阵列接收数据协方差矩阵进行特征分解,划分成2个相互正交的子空间,由信号导向矢量张成的信号子空间和与信号子空间正交的噪声子空间。然后利用这两个子空间的正交性来构造空间扫描谱,通过谱峰搜索得到信号的来波方向。
对式(14)的信号使用M USIC算法进行谱估计。首先求阵元接收信号的协方差矩阵,即
对RXX进行特征值分解
计算出噪声子空间特征矢量矩阵UN。AA为联合矢量,那么可以通过最小化搜索实现目标的角度估计,即
式中,AA=AAt⊗AAr,AAt是关于发射俯仰角和发射到达角的,AAr是关于到达角的。
3 仿真试验与分析
为验证天地波MIMO雷达多目标角度估计的有效性,共设计了4组仿真试验。
仿真1 天地波雷达系统结构参数为两站距离D=713 km,电离层高度h=200 km,天地波MIMO的阵形如图2所示,M_t=3,M_r=5,阵元间距为半波长,仿真信噪比(SNR)为20 d B,采样点个数为512。假设远场空间中有5个目标,发射信号完全正交。对应目标1的到达角为75°,对应目标2的到达角为95°,对应目标3的到达角为115°,对应目标4的到达角为130°,对应目标5的到达角为145°。普通相控阵雷达接收天线为5时,最多可估计出4个目标,图3显示了对5个空间目标仿真实验M USIC空间谱图,由图可知,M USIC算法在天地波MIMO多目标角度估计中具有良好的角度估计性能。
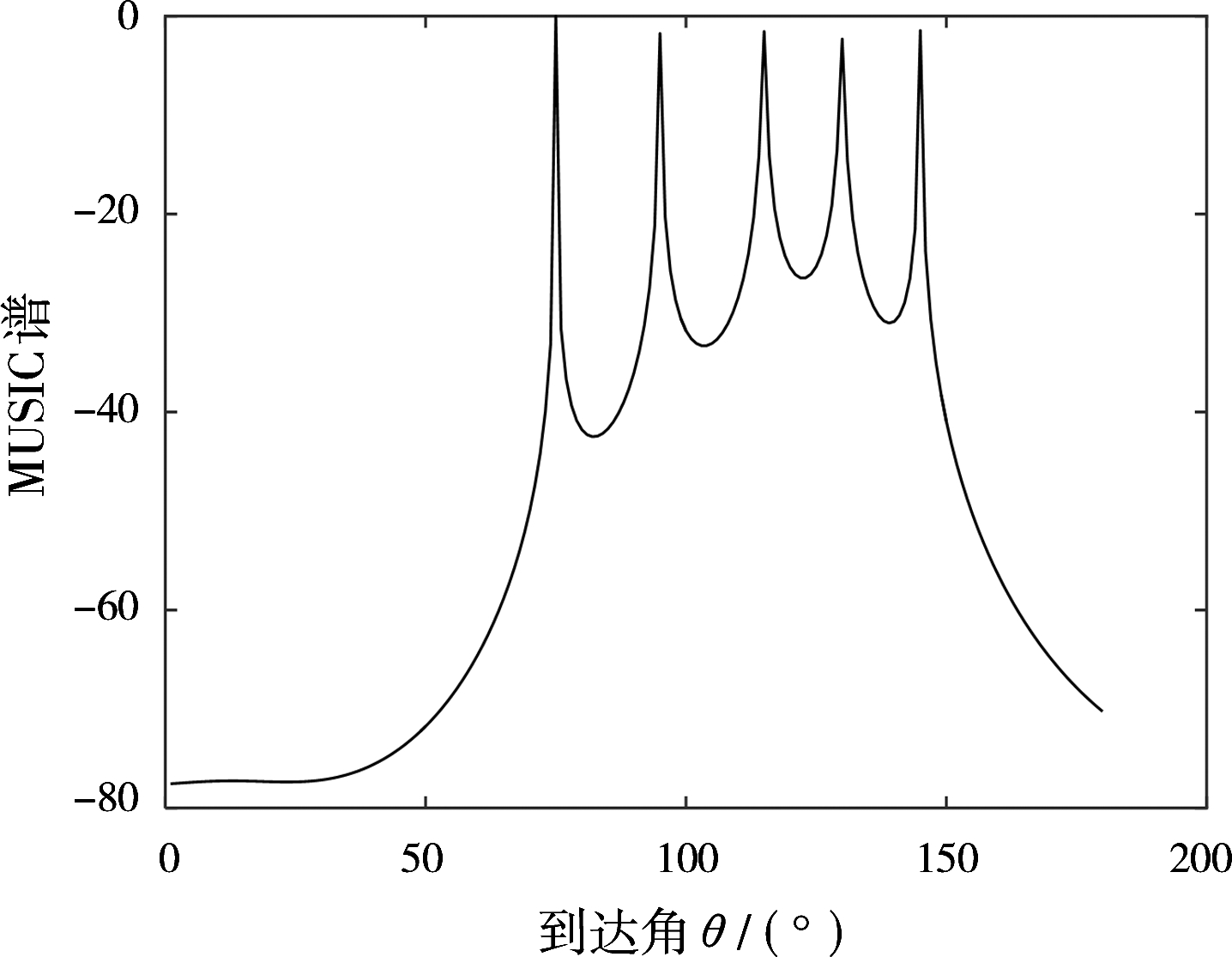
图3 5个目标的MUSIC空间谱
仿真2 为了说明目标估计角度分辨率的性能。仿真参数设置为天地波雷达系统结构参数为两站距离D=713 km,电离层高度h=200 km,天地波MIMO的阵形如图2所示,M_t=3,M_r=5,阵元间距为半波长,仿真信噪比(SNR)为20 d B,采样点个数为512。假设远场空间中有2个目标,发射信号完全正交。对应目标1的到达角为110°,对应目标2的到达角为112°。图4显示了对2个空间目标仿真实验MUSIC空间谱图,由图可知,MUSIC算法在天地波MIMO多目标角度估计中估计出两个相距较近的目标角度是有效可行的。
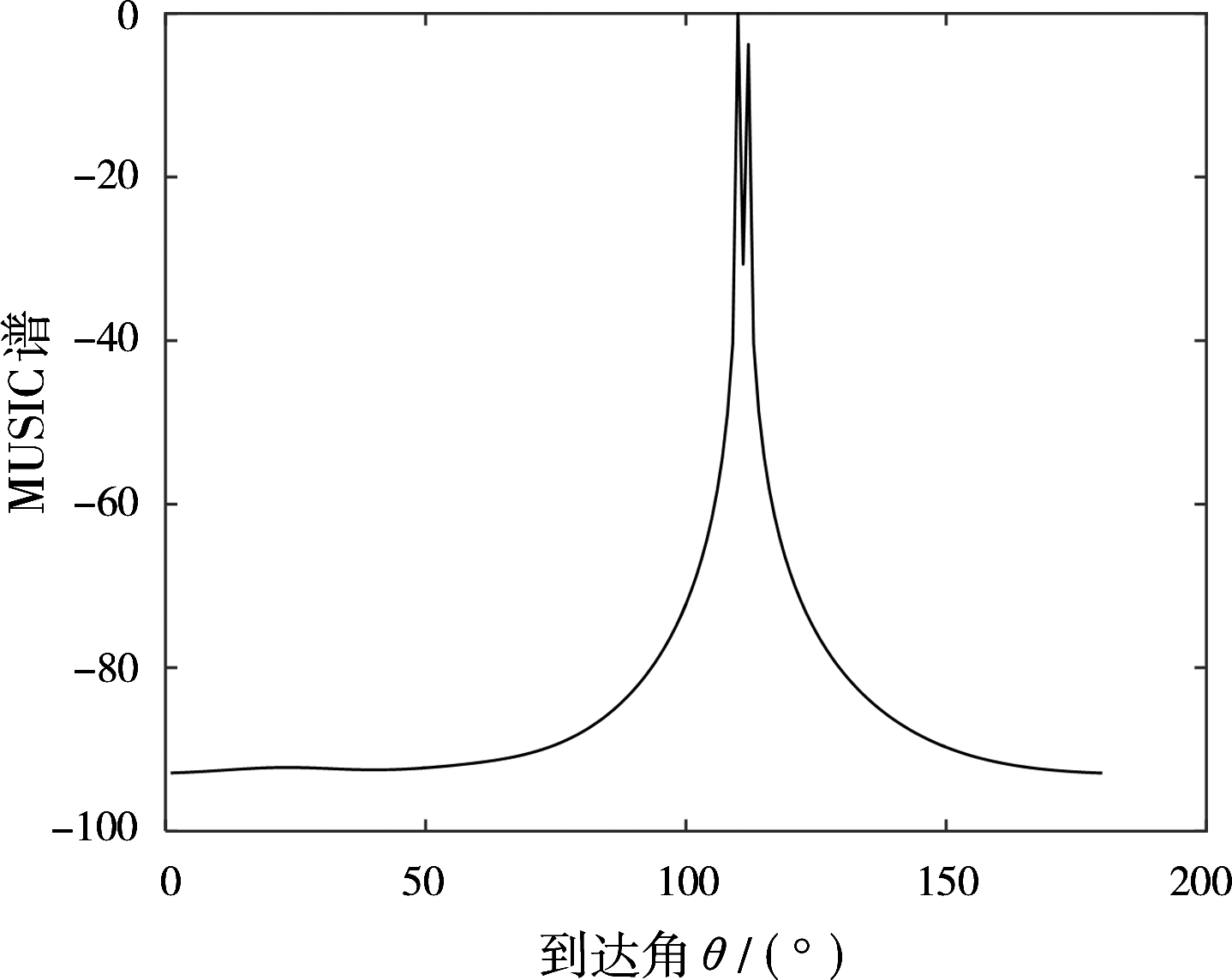
图4 2个目标的MUSIC空间谱
仿真3 对不同信噪比(SNR)对角度分辨率的影响进行分析评估。仿真参数设为信噪比从0 dB按步长1 dB增长到20 dB,采样点个数为512,M_t=3,M_r=5,设置两个估计目标。图5给出了目标在不同的信噪比(SNR)对角度分辨率的影响曲线。从图中可以看出,角度分辨率是随信噪比的增大而提高的。
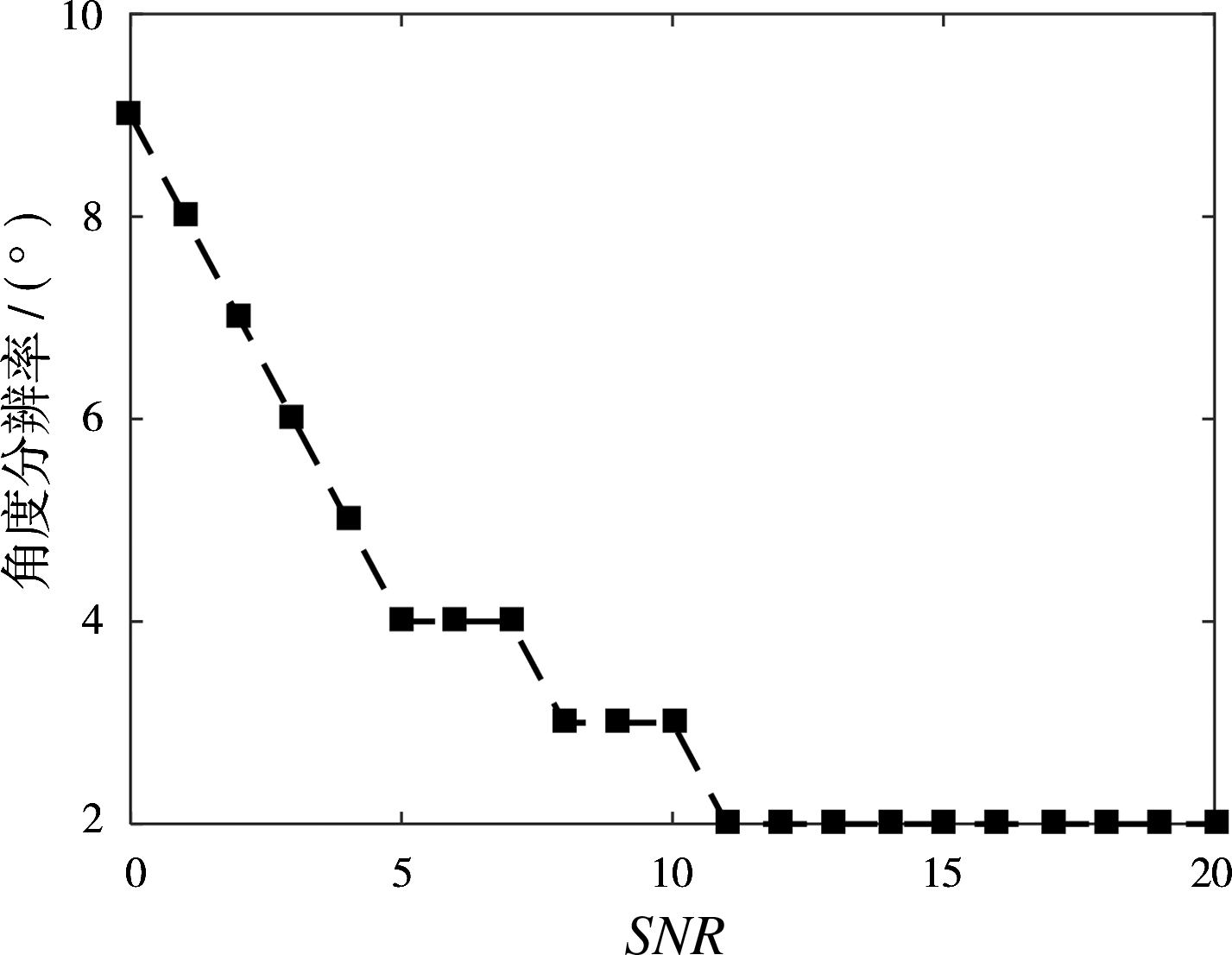
图5 2个目标时角度分辨率随SNR的变化
仿真4 对不同的接收阵元数对多目标角度的估计的影响进行分析评估。仿真参数设为M_t=3,到达角分别为110°和115°。信噪比从0 dB按步长1 dB增长到20 dB,采样点个数为512。M_r=3,M_r=5,以及M_r=8,结果为100次Monte-Carlo实验统计结果,图6给出了目标在不同接收天线数下目标估计成功率随信噪比的变化曲线。从图中可以看出,在一定的信噪比范围内,目标估计成功率是受接收天线数的影响的。
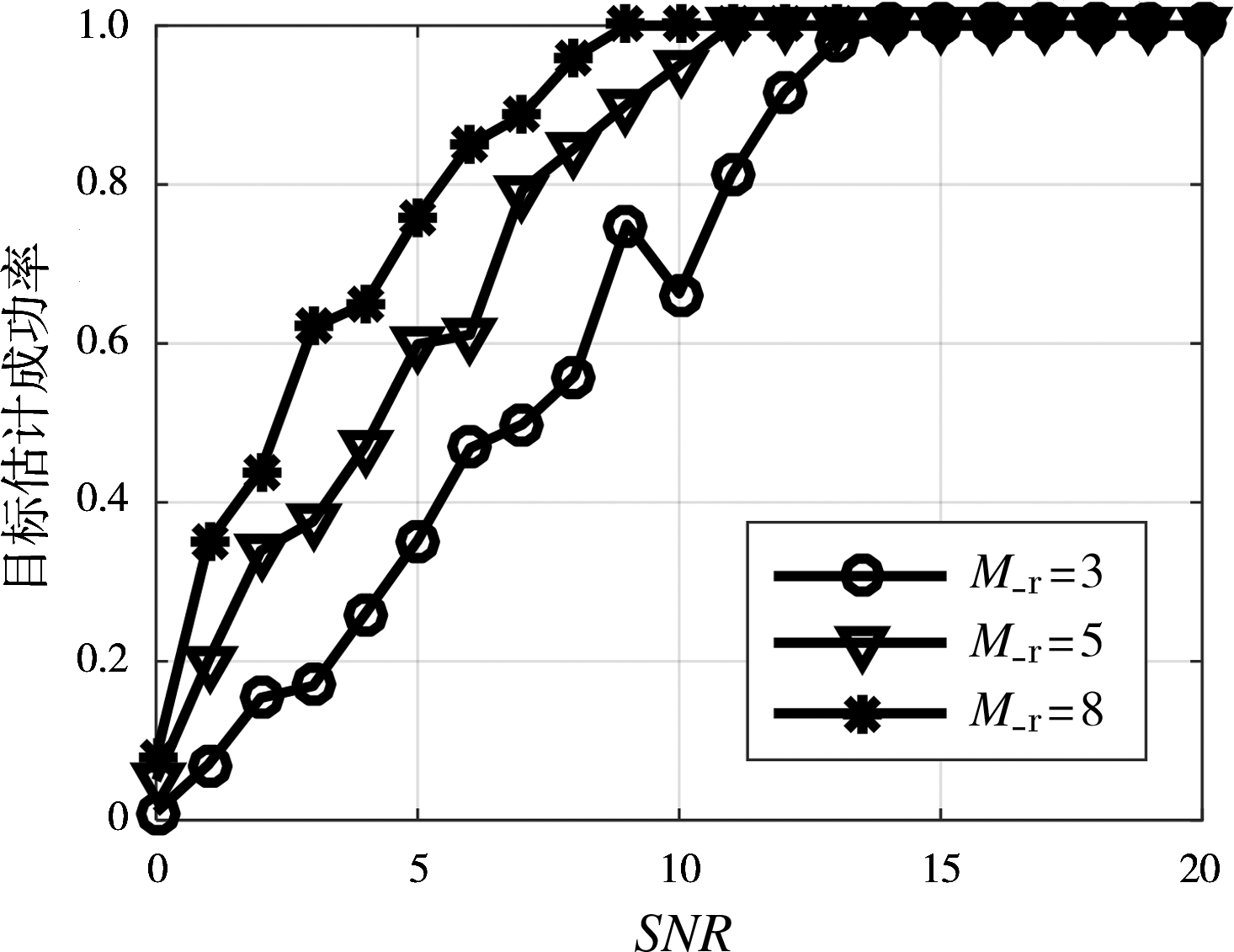
图6 目标估计成功率随SNR和接收天线的变化曲线
4 结束语
本文将MIMO技术与天地波组网模式相结合,研究了天地波MIMO雷达的信号模型。以双L阵配置下的天地波MIMO雷达为例,介绍了利用MUSIC算法进行目标角度估计的方法,并进行了仿真试验。仿真结果表明,运用MIMO技术的天地波雷达增加了可估计信源数,还提高了目标角度分辨能力。天地波MIMO雷达将MIMO技术与天波电离层发射模式和地波绕射传播模式组合相结合,具有重要的研究意义。
参考文献:
[1]LESTURGIE M.T06:MIMO Radar[C]∥IEEE Radar Conference,Cincinnati,OH:IEEE,2014:33.
[2]李仙茂,董天临,黄高明.MIMO雷达及其特性综述[J].现代防御技术,2015,43(4):125-130.
[3]FRANKFORD M T,STEWART K B,MAJUREC N,et al.Numerical and Experimental Studies of Target Detection with MIMO Radar[J].IEEE Trans on Aerospace and Electronic Systems,2014,50(2):1569-1577.
[4]焦培南,杨龙泉,凡俊梅.短波天波反射/地波绕射组合新传播模式及其可能应用[J].电波科学学报,2007,22(5):746-750.
[5]叶聪.基于MIMO体制的天波超视距雷达信号与数据处理算法研究[D].成都:电子科技大学,2013.
[6]李茂.MIMO-OTH雷达参数估计与干扰抑制研究[D].成都:电子科技大学,2015.
[7]李建峰,张小飞.MIMO雷达嵌套平行阵下基于子空间的目标二维波达角估计[J].系统工程与电子技术,2017,39(3):522-528.
[8]WU Yuebo,YANG Jingshu,WANG Jiang.A Method for Multi-Target 3D Localization in Bistatic MIMO Radar[J].Journal of Electronics and Information Technology,2010,33(10):2483-2488.
[9]陈群,张旭.双基地MIMO雷达相干多目标快速定位算法[J].电子信息对抗技术,2015,30(2):10-15.
[10]王翔.双基地MIMO雷达信号处理及阵列设计技术研究[D].南京:南京理工大学,2014.
[11]TABRIKIAN J,BEKKERMAN I.Transmission Diversity Smoothing for Multi-Target Localization[C]∥IEEE International Conference on Acoustics,Speech and Signal Processing-Proceedings,Philadelphia,PA:IEEE,2005:1041-1044.
[12]ZHANG Xiaofei,XU Lingyun,XU Lei,et al.Direction of Departure(DOD)and Direction of Arrival(DOA)Estimation in MIMO Radar with Reduced-Dimension MUSIC[J].IEEE Communications Letters,2010,14(2):1161-1163.
[13]王克让,何劲,贺亚鹏,等.MIMO雷达DOD和DOA联合估计算法:RTR-ESPRIT[J].航空学报,2012(5):893-901.
[14]CHEN Duofang,CHEN Baixiao,QIN Guodong.Angle Estimation Using ESPRIT in MIMO Radar[J].Electronics Letters,2008,44(12):770-771.
