0 引言
穿墙雷达成像(Through-the-Wall Radar Imaging,TWRI)是一种能够使用电磁波的传播特性获取墙后场景信息,对墙后隐藏目标进行检测、识别、成像的新型技术,在军事和民用方面具有广阔的应用前景[1-2]。目前大多算法假设墙体参数已知,但在实际场景中,墙体参数(如墙体厚度和介电常数)是未知的或者有一定程度的不确定性。而这种墙体参数的不确定性将导致重建图像模糊、位置偏移。文献[3]通过调整基于图像域滤波方法的墙体参数,取峰度值最大时对应的墙体参数用于成像,从而获取了较好的墙后目标聚焦图像。文献[4]通过分层介质格林函数将墙体参数的影响考虑进去,得到图像熵值随着聚焦时间的动态变化图,当熵最小时,输出相应的成像结果。文献[5]通过构造墙体实测与理论散射场之间误差的代价函数,使用非线性优化来求解墙体参数。归纳起来,上述研究实际上是一种最为直观的搜索法的自聚焦方法。在给定墙体参数的候选范围后,依据某种寻优准则的代价函数,如图像峰度值最大化、图像熵值最小化、墙体参数最小化误差等计算诸多参数候选值的结果,然后依据寻优准则搜索最佳值。
近年来,压缩采样突破了奈奎斯特采样的限制,由于目标的成像空间具有稀疏性,为了降低数据采集的时间、存储量和数据量,TWRI可采用压缩感知理论进行稀疏信号的重建[6-9]。文献[7]则是在压缩感知理论的基础上,利用稀疏场景中目标具有的结构聚类特性,充分考虑了扩展目标像素间的结构信息,通过Gibbs采样方法,获得了高分辨成像。文献[8]采用块稀疏压缩感知方法,根据建筑物内部墙体和外部墙体的位置特点来构造稀疏字典,获得了较好的成像结果。但是这些方法都是假设为已知的墙体参数成像,而当墙体参数的先验信息不准确时会导致成像性能差。尽管可以采用如前所述的依照图像聚焦度寻优准则找到最优解的全局搜索法进行求解,其优点是不会受到求解过程中局部较小值等问题的困扰,缺点是计算量大、运算效率不高,有一定的局限性。
本文通过建立结构化贝叶斯压缩感知分层模型,构建以墙体厚度和介电常数为参数化字典的稀疏表示模型,引入针板(Spike-and-Slab)先验表征扩展目标的结构稀疏性以充分利用扩展目标像素间的结构信息。在此基础上,对未知墙体参数的字典矩阵对墙体参数进行一阶泰勒级数展开,然后采用变分法分层交替迭代得到目标散射系数和墙体参数。与前述的方法相比,该方法引入参数化字典解决了目标位置偏移和图像模糊的问题,又可以充分利用扩展目标像素间的结构信息,实现了未知墙体参数下的自聚焦成像。
1 信号模型
假设均匀介质墙的厚度为d,相对介电常数为εw。在实际情况下这两个参数是未知的,设为Θ=[d,εw]T。在方位向和距离向上将成像区域Ω=[xmin,xmax]×[zmin,zmax]离散划分为NxNz个像素点。令σ(j,l)(j=1,…,Nx,l=1,…,Nz)表示加权指示函数,若目标在第(j,l)个像素点上,则σ(j,l)≠0,反之σ(j,l)=0。将σ(j,l)按照顺序排列构成维数为NxNz的列向量σ,则第n根天线回波信号的离散模型为
式中,yn=[yn(t1),…,yn(tM)]T,An(Θ)为M×NxNz的矩阵,设s(t)为发射的脉冲信号,则An(Θ)第m行的元素为s(tn,m-τn,1),…,s(tn,mτn,NxNz)。第n根天线到第o个像素点间的总传播时 延[3]τn,o为
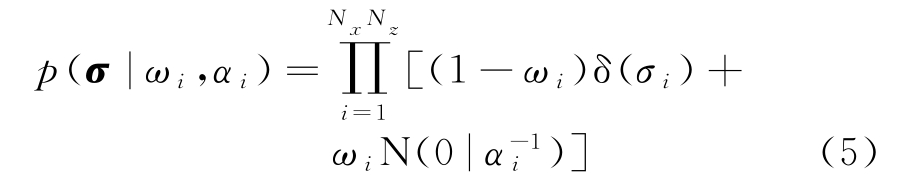
式中,i∈{1,…,NxNz},δ(σi)为在σi处的狄拉克δ函数,αi为高斯密度函数的反方差,服从Gamma分布,即αi|c′,d′～Gamma(c′,d′),ωi为第i个散射点处散射系数σi是非零值的先验概率大小。为了便于推断分析,用◦表示向量Hadamard内积[7]。令σ=θ◦λ,则式(5)变为
式中,φn,o≈arctan(|xn-xo|/|zn-zo|),c为光速。将N根天线信号进行堆叠组合,则所构造的离散模型可以表示为
式 中,
表示从y中选择Q1Q2≪MN形成的矢量,根据文献[6]构造测量矩阵Φ,并由此得到大小为Q1Q2×1的测量数据(或稀疏成像)参数化字典稀疏表示模型为
对于扩展目标,成像区域除了散射点满足稀疏性之外,非零目标散射点与周围散射点之间还存在依赖关系。令每个网格上目标散射点满足针板先验稀疏模型[7],即
式中,ωi为伯努利分布的参数,其值较大时,对应的σi为非零的概率越大,其值较小时,对应的σi倾向于为零的概率越大。对于实际的穿墙成像,扩展目标相邻像素间的结构信息模式如图1所示的3种结构聚类模式。不同的聚类模式选择对应ωi的不同选择形式
可通过相应的Beta分布求解,即
式中,k的取值对应不同的聚类模式,g(k)=1/1+e4-Sk,h(k)=e4-Sk/1+e4-Sk,(s1=0,s2=1,s3=2)。当g(1)＜h(1)时,ωi趋向0,σ趋向0;当g(2)＞h(2)时,ωi趋向1,σ趋向非0;当g(3)=h(3)时,ωi趋向0.5,σ趋向0和非0的几率相等[9]。
图1 相邻像素间3种不同的聚类模式
2 自聚焦结构稀疏成像方法
假设加性噪声e与σ无关,服从高斯分布
则观测信号矢量y的似然函数为
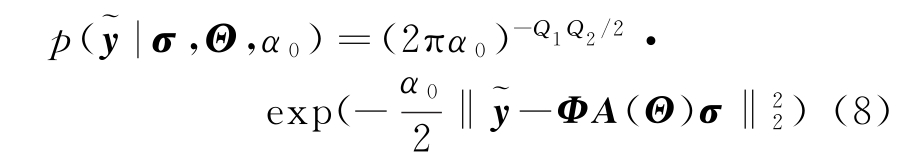
式中,α0服从参数为a′,b′的Gamma分布,即α0|a′,b′～Gamma(a′,b′)。相比于文献[7]的Gibbs采样方法的计算复杂度高,变分推断方法通过最大化变分下界逼近原先的边缘似然度,具有较高的运算效率。根据文献[10]中的方法,后验概率分布可表示为
而边缘似然度p(~y)不具有解析的形式,可将θ,λ,α0,α,ω视为隐变量,d,εw视为参数,由变分法可得到后验概率的近似分解[10]如式(10),从而进行交替迭代推断求解,即
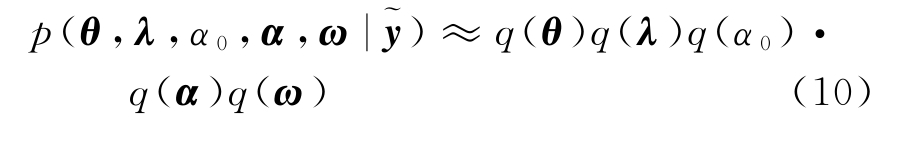
2.1 隐变量θ,λ,α0,α,ω的估计
根据之前相关参数的先验,可以直接计算各随机变量服从的后验概率分布和相应的均值,从而得到θ,λ,α0,α,ω的估计,即
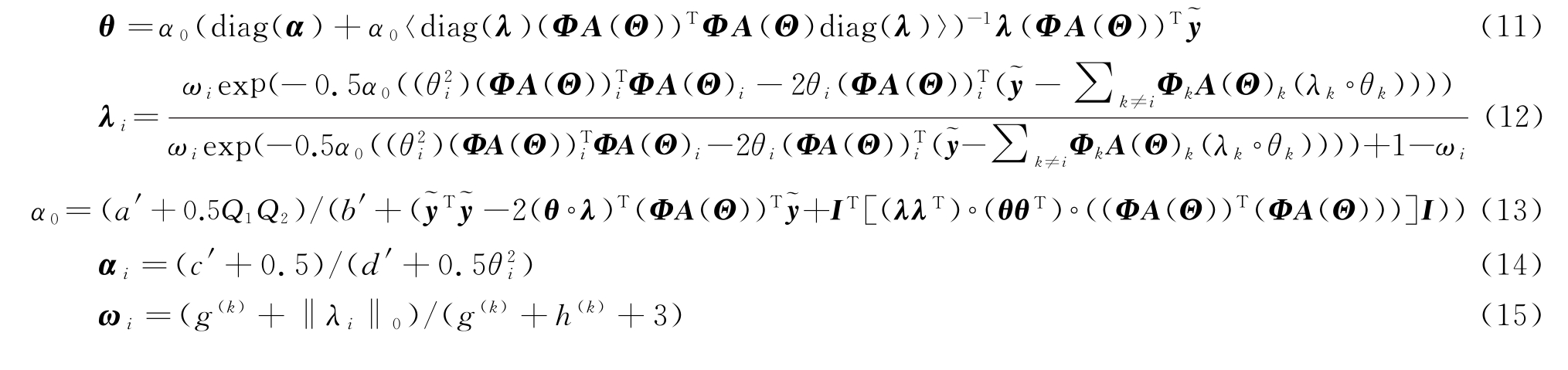
2.2 参数d和εw的估计
根据贝叶斯期望最大化准则,为了更精确地估计d,εw,通过最大化取对数后的联合概率密度函数的期望来求解,表示为
进而转化为式(17)的凸优化问题,通过最小化残差,更新d,εw:
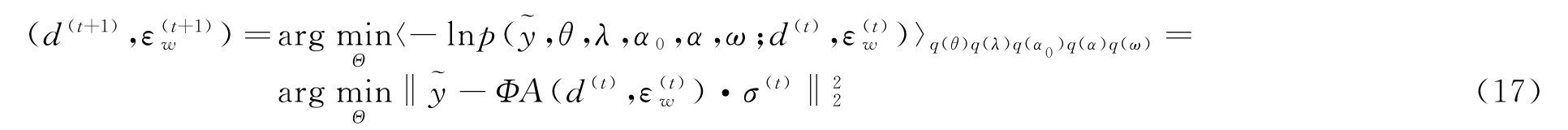
式中,t为迭代次数。可以将A(d,εw)关于Θ近似按一阶泰勒级数展开,则式(17)的求解变为
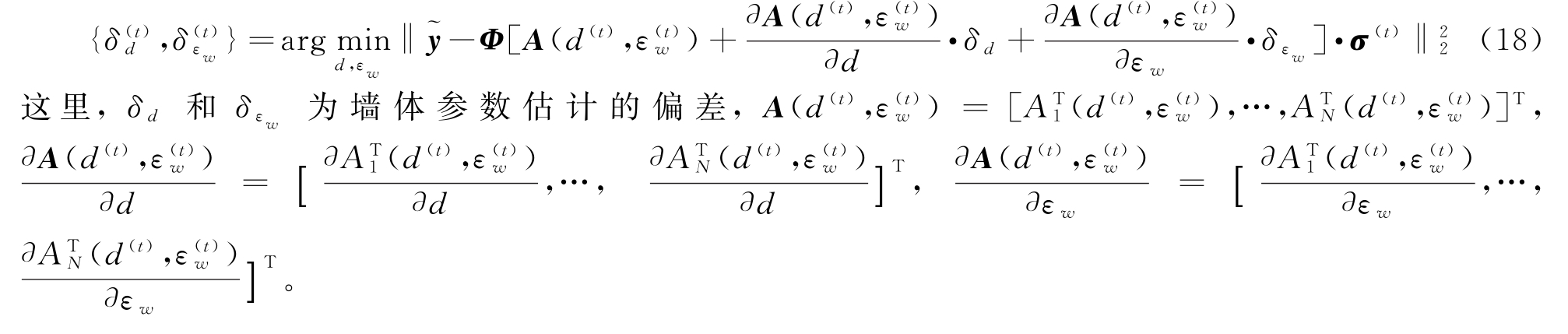
根据文献[11]的求解方法,可以得到δd,δεw的估计为
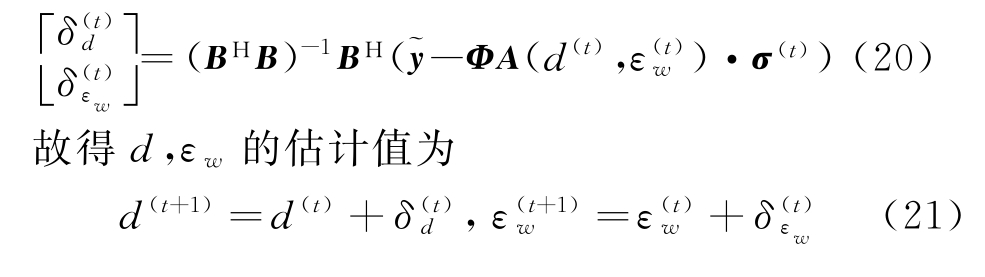
2.3 算法实现
算法的具体流程如表1所示。根据文献[12]设置模型参数和初值θ(0),然后循环迭代式(11)、式(12)、式(13)、式(14)、式(15)、式(21),直到满足收敛条件,最后输出准确的墙体参数d,εw和散射系数σ,重构出高分辨的扩展目标图像。算法的计算复杂度主要来自循环迭代的第1步,为O((Q1Q2)3NxNztmax)。令X={θ,λ,α0,α,ω},可以证明Kullback-Leibler距离
X,Θ)]和式(17)中负的对数联合概率密度函数的期望
分别随着X和Θ单调递减,直至达到收敛点,因而算法的收敛性也得到了保证。
表1 算法流程
3 仿真与实验结果分析
3.1 仿真结果分析
利用电磁仿真软件XFDTD产生仿真数据,模型如图2所示。采用25个收发共置单元组成的天线阵列,阵元间距为0.04 m,距离墙壁为0.2 m。各天线的发射信号均为高斯脉冲信号,中心时刻和有效宽度均为1 ns。为了模拟实际情况,设置墙体的长度为1.6 m,高度为2 m,电导率为0.01 S/m,厚度为0.2 m,相对介电常数为6.4。两个矩形目标的长0.3 m,宽0.2 m,均位于墙后1.4 m处。
图2 XFDTD仿真模型
从仿真的25个阵元中随机选择20个,每个阵元随机选200个频点,按表1中设置各参数的初值。假设d,εw的初值分别为0.25和5.5,迭代次数为10次。图3给出了仿真迭代过程中的成像结果,图中虚线框表示真实目标的位置,经过4次迭代后的自聚焦,获取了较准确的墙体参数,消除了图像模糊和虚假像,得到了准确位置的高分辨扩展目标图像。由图4(a)可知迭代收敛后,d为0.21 m,εw为6.32,接近真实值。迭代过程中相应的性能指标[7]变化如图4(b)和图4(c)所示,可以看出本文方法在迭代过程中ENT,RMSE,MFOD逐渐变小直至收敛,TCR逐渐变大到收敛。这里,ENT从0.551逐渐减小到0.456,反映该图像的杂波越来越少;RMSE从0.872逐渐减小到0.765,表明观测值与真值之间的偏差越来越小,预测的准确性越来越高;MFOD从0.064逐渐减小到0.053,反映该扩展目标区域的边缘平滑性越来越好;TCR从12.30 dB逐渐增大到15.28 dB,反映成像的聚焦度越来越高,图像越来越清晰。
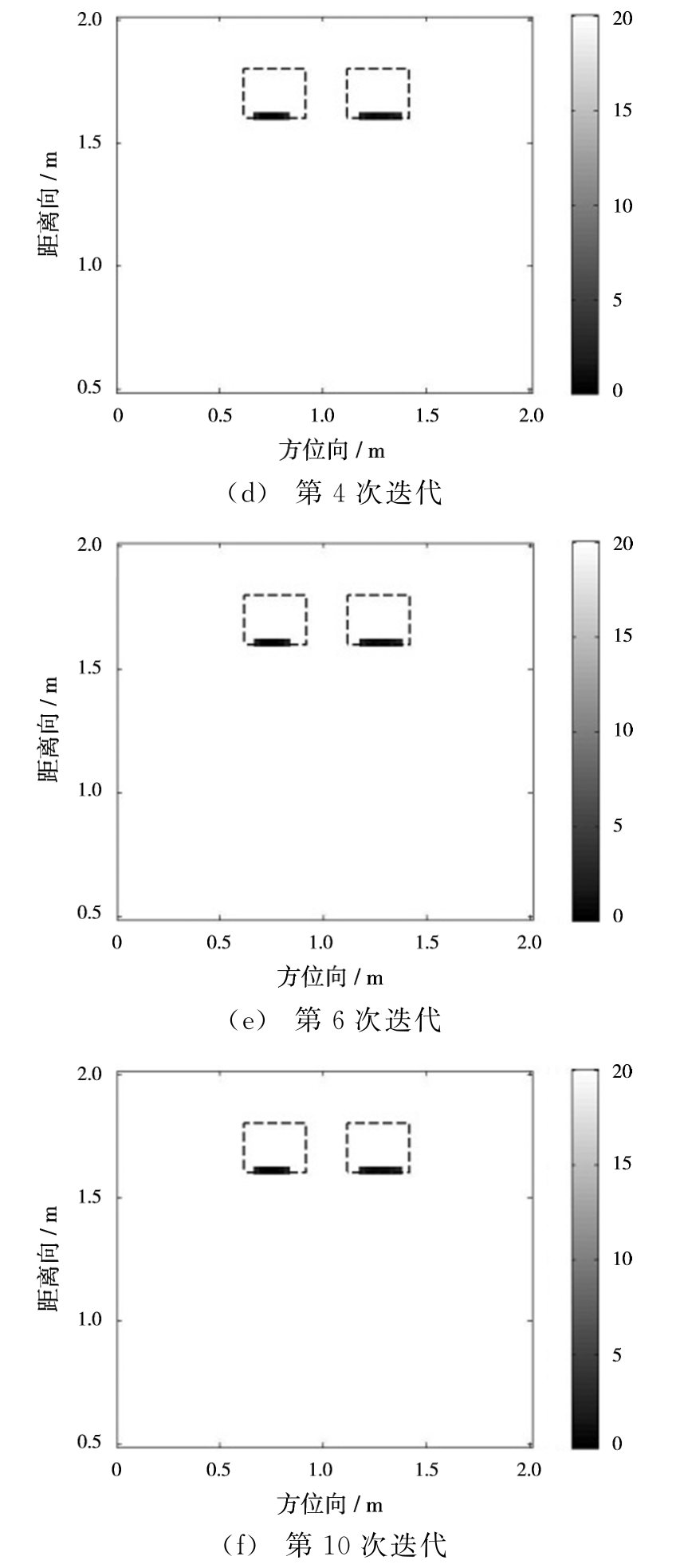
图3 迭代过程中成像
图4 迭代过程中墙体参数及算法性能指标变化情况
3.2 实验结果分析
穿墙实验场景使用美国GSSI公司的探地雷达SIR-20搭建,如图5所示。实验场景的墙体为均匀实心砖墙,墙后实验对象是文件柜,高为1.8 m,宽为1 m,位于墙后1.4 m处。选择中心频率为1 GHz的喇叭天线,平放在实验桌上,距离墙前壁0.2 m处,沿着墙体平行方向,从-0.6 m处到0.6 m每隔0.04 m水平扫一次,共扫描31个测量点。在每个测量点各测量2次,包括有文件柜和无文件柜的两种情况。SIR-20系统的参数设置:每道采样1 024点,每秒60道,时间窗17 ns。将每个测量点采集的多道数据取平均去噪、滤波以及自动增益控制等信号处理,然后将有文件柜场景的处理结果与无文件柜场景的处理结果相减,得到较好的文件柜回波信号。
图5 实验场景图
采用自聚焦成像,在未知墙体参数下预设的墙体参数d为0.30 m,εw为5,通过自聚焦5次迭代就收敛,获取的墙体参数d为0.18 m,εw为7.2,与测量的墙体参数真实值d为0.20 m,εw为7.0很接近。图6给出了迭代过程中的实验成像结果,可以看出在迭代过程中消除了图像模糊和位置偏移,减少了虚假像,扩展目标图像变得清晰。
图6 实验结果图
4 结束语
本文提出的穿墙雷达自聚焦稀疏成像方法充分考虑了扩展目标相邻像素间的结构信息,将墙体参数引入到贝叶斯压缩感知模型中,通过变分法推理得到墙体参数预设初值与真实值的偏移量,进行循环迭代更正了墙体参数。仿真和实验结果表明,相比常规算法解决了目标位置偏移、模糊和散焦问题,实现了未知墙体参数下高分辨的扩展目标自聚焦成像。
参考文献:
[1]YEKTAKHAH B,SARABANDI K.All-Directions Through-the-Wall Radar Imaging Using a Small Number of Moving Transceivers[J].IEEE Trans on Geoscience and Remote Sensing,2016,54(11):6415-6428.
[2]LI G,BURKHOLDER R J.Hybrid Matching Pursuit for Distributed Through-Wall Radar Imaging[J].IEEE Trans on Antennas and Propagation,2015,63(4):1701-1711.
[3]JIN T,CHEN B,ZHOU Z.Image-Domain Estimation of Wall Parameters for Autofocusing of Throughthe-Wall SAR Imagery[J].IEEE Trans on Geoscience and Remote Sensing,2013,51(3):1836-1843.
[4]LI F,LI L.Refocusing Through the Unknown Building Wall with a Filtered Backprojection Algorithm[C]∥European Conference on Synthetic Aperture Radar,Nuremberg,Germany:VDE,2012:631-634.
[5]SOLIMENE R,SOLDOVIERI F,PRISCO G,et al.Three-Dimensional Through-Wall Imaging Under Ambiguous Wall Parameters[J].IEEE Trans on Geoscience and Remote Sensing,2009,47(5):1310-1317.
[6]晋良念,申文婷,钱玉彬,等.组合字典下超宽带穿墙雷达自适应稀疏成像方法[J].电子与信息学报,2016,38(5):1047-1054.
[7]WU Q,ZHANG Y D,AHMAD F,et al.Compressive-Sensing-Based High-Resolution Polarimetric Through-the-Wall Radar Imaging Exploiting Target Characteristics[J].IEEE Antennas and Wireless Propagation Letters,2015(14):1043-1047.
[8]AMIN M G,AHMAD F.Determining Building Interior Structures Using Compressive Sensing[J].Journal of Electronic Imaging,2013,22(2):381-388.
[9]QIN S,ZHANG Y D,WU Q,et al.Structure-Aware Bayesian Compressive Sensing for Near-Field Source Localization Based on Sensor-Angle Distributions[J].International Journal of Antennas and Propagation,2015(1):1-15.
[10]YANG L,ZHAO L,BI G,et al.SAR Ground Moving Target Imaging Algorithm Based on Parametric and Dynamic Sparse Bayesian Learning[J].IEEE Trans on Geoscience and Remote Sensing,2016,54(4):2254-2267.
[11]CHEN Y C,LI G,ZHANG Q,et al.Motion Compensation for Airborne SAR via Parametric Sparse Representation[J].IEEE Trans on Geoscience and Remote Sensing,2017,55(1):551-562.
[12]SUN L,WANG T,LU X,et al.ISAR Imaging for Micromotion Targets Using the Hierarchical Bayesian Prior[C]∥5th Asia-Pacific Conference on Synthetic Aperture Radar,Singapore:IEEE,2015:545-549.
