0 引言
海杂波背景下的目标检测一直是个难题。由于海面的反射作用,雷达接收的回波信号包含大量海杂波能量,使得目标易被淹没。而且当高分辨雷达以低擦地角照射粗糙海面时,雷达回波信号甚至会出现“海杂波尖峰效应”[1-2],容易产生假目标。不同于简单的地杂波,海杂波随着雷达极化方式、雷达分辨率、天线视角、海情、风向等多个因素的变化而呈现明显的非平稳性、非高斯性[3]。虽然学者们又陆续采用对数正态分布、韦布尔分布和K分布等非高斯海杂波模型[4]拟合海杂波实现目标检测,但由于雷达和海情的诸多变因,这种根据实测海杂波数据研究先验杂波统计特性[5-6],并建立具体海杂波模型实现目标检测的方法[7]效果仍然欠佳,且不具通用性。传统雷达信号处理中,一般是通过动目标显示(Moving Target Indicator,MTI)、动目标检测(Moving Target Detection,MTD)等频域滤波方式抑制杂波,实现目标检测。但由于海杂波多普勒频率分布范围十分广泛,使其杂波频谱中心的测量及其谱宽的估计成为难题[8]。不同于传统雷达信号处理设计自适应滤波器方式,文献[9]基于海杂波和目标信号在时间相关性上的差异,采用成组非相参积累的杂波图迭代算法,抑制强海杂波,实现海面小目标检测。但由于海杂波的非平稳性,多次杂波图迭代的结果波动性较大,不具有通用性。
针对这种情况,本文提出了一种基于两级多普勒频率相关性判别的海杂波抑制方法。根据目标和海杂波的多普勒频率相关性差异,依次对时间-距离二维多普勒频率进行时间相关性判别、空间相关性判别二值化处理。从而筛选出满足相关性要求的区域,即为目标区域,其他相关性低的区域视为海杂波区域。由此区分目标和杂波,进而实现强海杂波背景下的运动目标检测。该方法不依赖于具体的海杂波模型,具有较好的通用性,且海杂波抑制效果明显。通过大量实测海杂波数据的实验结果验证了该方法的正确性。
1 多普勒频率相关性判别
雷达回波信号在时间上和空间上都是相关的[10-11],且目标和海杂波的相关性存在差异,如多普勒频率相关性的差异。本文由此提出多普勒时间相关性和多普勒空间相关性的概念。由于目标运动的平稳性使其多普勒频率在时间和空间上都表现出很强的相关性,而海杂波由于海浪的冲击突变使其在连续脉冲间或时间-距离区域块间的多普勒相关性较弱。根据雷达回波信号的多普勒频率在时间和空间上的相关性差异,区分出目标和海杂波,从而实现海杂波抑制。
1.1 多普勒时间相关性判别
多普勒时间相关性是指对时间-距离二维雷达回波信号,其同距离单元、不同脉冲间信号的多普勒频率在时间测量上表现出的关联特性。用相邻两脉冲间多普勒序列的相关系数来定量描述多普勒时间相关性的大小。设一个脉冲连续距离单元的多普勒频率为fi1,fi2,…,fik,其中fik为第i个脉冲、第k个距离单元对应的多普勒频率。对m个距离单元长度的相邻两脉冲间信号的多普勒序列求取相关系数:
式中,Xik=[fi(k+1),fi(k+2),…,fi(k+m)],X(i+1)k=[f(i+1)(k+1),f(i+1)(k+2),…,f(i+1)(k+m)],Xik,X(i+1)k表示相邻两脉冲第k+1个至第k+m个距离单元的多普勒频率序列,Cov(Xik,X(i+1)k表示这两序列的协方差,D(Xik),D(X(i+1)k)分别表示这两序列各自多普勒频率的方差。根据求出的相关系数ρ的大小,可以判断同距离单元相邻两脉冲间的多普勒时间相关性大小。设置多普勒时间相关性系数门限为某个定值,当ρik大于等于该门限定值时,则认为第i个脉冲、第k个距离单元的位置点具有多普勒时间相关性,反之则认为该点处不具有多普勒时间相关性。
通过对时间-距离二维雷达回波信号的多普勒频率滑动,可求得全部位置点同距离单元相邻两脉冲间的多普勒相关系数,再根据相关系数门限判断各位置点是否具有多普勒时间相关性,并对二维多普勒频率作二值化处理。若某位置点具有多普勒时间相关性,则将该位置点的多普勒值重置为1值,反之则将该点的多普勒值重置为0值。
1.2 多普勒空间相关性判别
多普勒空间相关性是指对二维回波信号,在不同距离单元、不同脉冲间信号的多普勒频率之间的关联特性。本文的多普勒空间相关性判别是对前面多普勒时间相关性判别处理后得到的二值化多普勒值进行的。由于目标和海杂波多普勒频率的相关性差异,经多普勒时间相关性判别二值化处理后,海杂波区域大部分的多普勒值已被置为0值,目标区域的多普勒值大多被置为1值。但由于海杂波的突变性,经多普勒时间相关性判别后的杂波区域仍会存在部分散落的1值多普勒,而对于目标区域的连续脉冲主瓣序列,其每个主瓣基本都至少伴有一个1值多普勒副瓣。根据这种区域块相关性特点,可由连续脉冲的1值多普勒副瓣搜索出连续目标脉冲主瓣,称为“连续拟目标主瓣序列”,并认为以该序列位置为中心构成的矩形区域块具有多普勒空间相关性。
设经过多普勒时间相关性判别二值化处理后的一个脉冲某连续3个距离单元的多普勒值为fi(k-1),fik,fi(k+1),其中fik为第i脉冲、第k个距离单元对应的多普勒值。设
若Fik≠0,即fi(k-1),fik,fi(k+1)不全为0值,而是至少有一个1值多普勒,则认为fik所处“有效目标主瓣”。若
即Fik,F(i+1)k,…,F(i+m)k全都不为0时,则认为fik,f(i+1)k,…,f(i+m)k处在几个连续脉冲的“有效目标主瓣”,称之为“连续拟目标主瓣序列”。再以fik,f(i+1)k,…,f(i+m)k序列位置为中心向四周扩展两个距离单元或两个脉冲构成矩形区域块,即以f(i-2)(k-2),f(i+m+2)(k+2)两位置为对角线两点构成矩形区域块,称该矩形区域块具有多普勒空间相关性。
通过对多普勒时间相关性判别二值化处理后的二维多普勒值滑动,可以搜索出全部的“连续拟目标主瓣序列”,即可找出全部的具有多普勒空间相关性的目标区域块,而剩下的区域即为杂波区域。然后对二值化的多普勒值再次重置,将具有多普勒空间相关性的目标区域块内的多普勒值全部重置为1值,同时将其他杂波区域的多普勒值全部重置为0值。
2 两级多普勒相关性判别的海杂波抑制技术
由于目标运动的平稳性和海杂波冲击的突变性,目标和海杂波的多普勒频率相关性在时间和空间上都存在差异。表现为运动目标及其区域具有多普勒时间相关性和多普勒空间相关性,而海杂波区域相关性较低,由此区分目标和海杂波,多普勒相关性判别方法如第1节内容所述。基于上述,本小节提出了一种基于两级多普勒相关性判别的海杂波抑制技术。
图1为两级多普勒相关性判别的海杂波抑制方法的整个算法流程。雷达接收到的海杂波回波信号先经过脉冲压缩和脉冲重排,得到时间-距离二维信号,脉压后的海杂波数据先通过有限冲击响应滤波器(Finite Impulse Response,FIR)滤除地杂波,再经隔周测频[12]估算得到时间-距离二维多普勒频率,并依次经过多普勒时间相关性判别、多普勒空间相关性判别二值化重置,将杂波区域的多普勒频率全部重置为0值,将目标区域块的多普勒值全部重置为1值。最后根据二维多普勒值的二值化分布,将分布1值多普勒的目标区域信号全部保留,同时将分布0值多普勒的杂波区域信号全部归一成平均噪声电平。从而抑制了海杂波,实现了强海杂波背景下的目标检测。
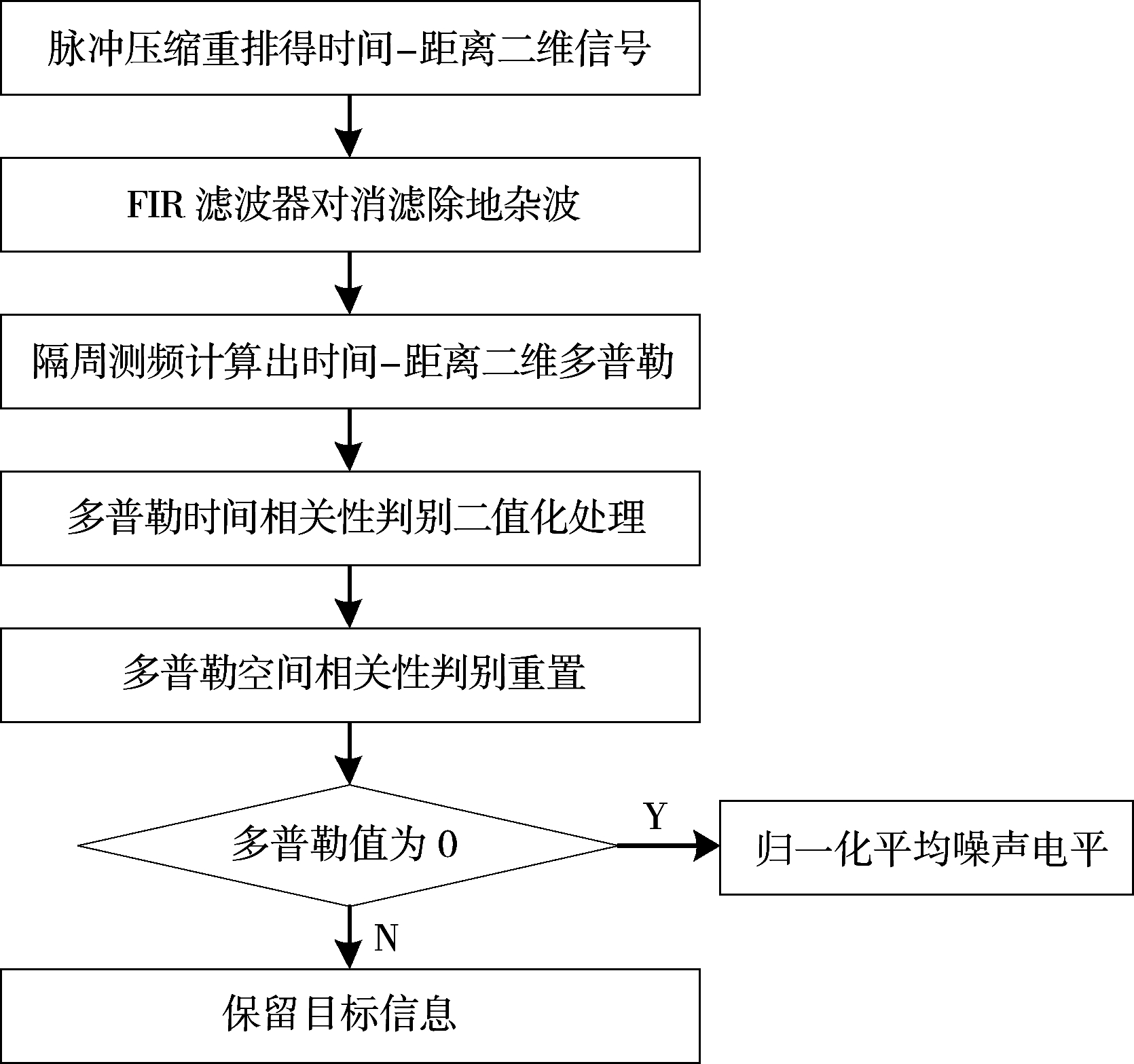
图1 两级多普勒相关性判别算法流程图
2.1 FIR滤波器滤除地杂波
在进行两级多普勒相关性判别之前,先将脉压后的雷达回波数据通过零频凹口的FIR滤波器,以除去地杂波对后续多普勒判别处理的影响。对于FIR滤波器设计,在时域其实质为寻找合适的滤波权系数,在频域即为设计与杂波多普勒中心所对应的凹口滤波器。凹口中心为零频的FIR滤波器即可用于滤除零频地杂波。经FIR滤波器的脉冲信号满足下式[13]:
式中,X=[xij,x(i+1)j,…,x(i+m-1)j]为第i脉冲到第i+m-1脉冲,即连续m个脉冲、同距离单元j处的信号序列,W=[w1,w2,…,wm]为m阶FIR滤波器权系数序列,Sij为第i脉冲、第j距离单元处信号通过此FIR滤波器后的数值。由式(4),将脉压后的时间距离二维海杂波数据经过m阶零频FIR滤波器除去地杂波,再进行后续两级多普勒相关性判别处理。
2.2 两级多普勒相关性判别实现海杂波抑制
对已经滤除过地杂波的二维海杂波数据进行隔周测频,计算得到时间-距离二维多普勒频率值。由式(1)对二维多普勒频率滑动运算,求得全部位置点同距离单元相邻两脉冲间的多普勒相关系数。再根据设置的定值相关系数门限判断各位置点是否具有多普勒时间相关性,并将各点的多普勒值二值化处理。若某位置点具有多普勒时间相关性,则将其多普勒值重置为1值,反之则将该位置点的多普勒重置为0值。
由于目标和海杂波多普勒频率的相关性差异,经多普勒时间相关性判别二值化处理后的二维多普勒值,在海杂波部分大多已被置为0值,但还有个别的1值多普勒零散分布。而目标区域附近的1值多普勒点基本呈不规则块状分布,且偶尔会被0值多普勒点隔断。再由式(2)和式(3)对时间相关性判别二值化处理后的二维多普勒再次滑动,可搜索出全部的“连续拟目标主瓣序列”位置,并分别以这些序列位置为中心向周围扩展两个距离单元或脉冲,即可找出全部具有多普勒空间相关性的矩形目标区域,剩下的区域全部视为海杂波区域。再将这些矩形目标区域内的多普勒值全部重置为1值,而将海杂波区域内的多普勒值全部置为0值。
经过对多普勒频率进行两级相关性判别二值化重置,得到目标区域内多普勒全为1值、海杂波区域内多普勒全为0值的0-1多普勒分布。最后根据得到的二维多普勒0-1分布,将分布1值多普勒的目标区域内信号全部保留不变,而将分布0值多普勒的海杂波区域信号全部归一成平均噪声电平,由此抑制杂波,检测出强海杂波背景下的运动目标。为了验证本文所提方法的正确性和有效性,下面使用实测的海杂波数据对所述方法的性能进行实验验证。
3 实测数据处理结果分析
本文使用的实测海杂波数据来源于中国东海岸某城市使用的一部远程预警雷达。实测数据为该雷达在远程机扫模式下测得的低掠海角回波信号。该雷达发射线性调频脉冲,脉冲信号经海面和目标的散射被雷达接收。将雷达接收到的一维连续脉冲回波信号先进行脉冲压缩处理,再按时间维进行脉冲重排,得到时间-距离二维回波信号。
本次实验中共采集10组雷达回波数据,每组数据包含200个脉冲,每个脉冲包含4 414个距离单元。图2(a)为其中一组回波信号经脉压处理和脉冲重排后得到的时间-距离二维海杂波数据。可见前2 000个距离单元内存在大片海杂波区域,且能量很高,大于80 d B。其中第100~108脉冲的第550和第2 025距离单元分别为人为注入的两个模拟对空实验目标。目标A的径向速度为945.07 km/h,距离雷达82.5 km,目标B的径向速度为781.2 km/h,距离雷达318.75 km。图2(b)为图2(a)中第103脉冲的海杂波数据,其中第550和第2 025距离单元处分别为模拟目标A和目标B,两目标幅度均为77 d B左右。
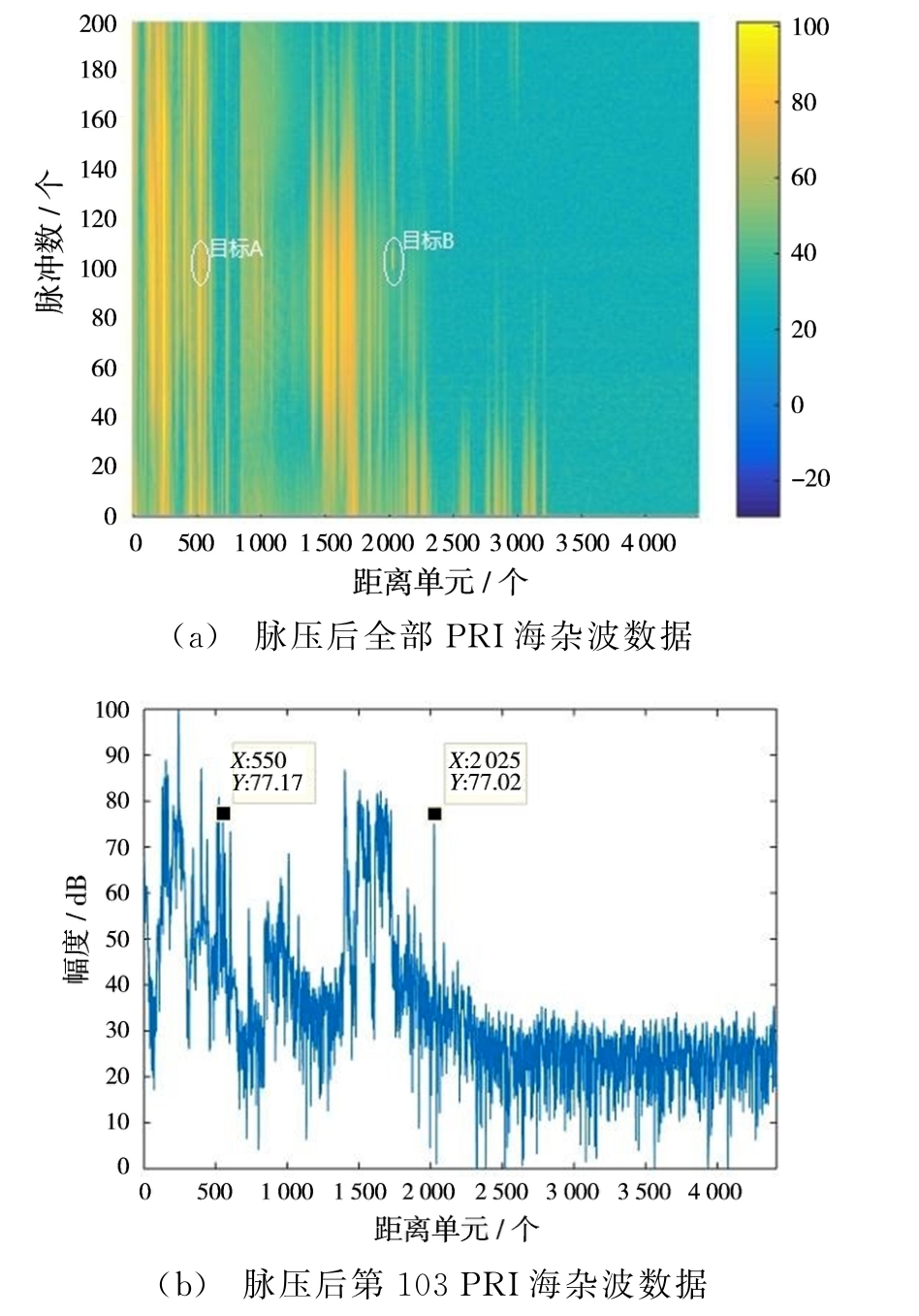
图2 脉压后的海杂波信号
传统雷达频域滤波技术一般是通过设计两级自适应动目标显示(Automatic Moving Target Indicator,AMTI)对消器[14]抑制杂波。图3为运用传统两级AMTI滤波方式处理图2海杂波数据后的结果图。先通过地物杂波滤波器滤除掉地杂波,再设计自适应运动杂波滤波器滤除运动杂波。但由于海杂波频谱范围分布较广,自适应运动杂波滤波器难以准确地估计海杂波的频谱中心和谱宽,这使得滤波效果欠佳。从图3(b)可以看到前1 000距离单元内仍然存在大量没被滤除的海杂波,且两目标的幅值较之前都有所降低。可见传统两级自适应滤波器虽然能滤除一定的海杂波,但并不能将强海杂波区滤除干净,且运动杂波滤波器凹口还有可能造成目标信号一定程度的损失。

图3 经过传统两级自适应滤波器处理后的脉压数据
而采用本文提出的两级多普勒相关性判别的海杂波抑制技术,杂波抑制效果十分显著。将图2中的脉压海杂波数据先通过五阶FIR滤波器对消滤除地杂波,然后经隔周测频求取时间-距离二维多普勒频率,再依次进行两级多普勒相关性判别,其中先进行多普勒时间相关性判别二值化处理。先求得同距离单元相邻脉冲间多普勒频率相关性系数。图4中可见目标A和目标B距离单元附近的多普勒相关系数都比较高,均高于0.97,而目标距离单元外的杂波处多普勒相关系数明显较低。经大量实验研究表明,多普勒时间相关系数门限可取到0.96~0.98之间。此处设置相关系数门限为0.97,将相关系数高于该门限的位置点的多普勒都置为1值,将低于该门限的位置点的多普勒全置为0值,以便后续进一步处理多普勒空间相关性判别。
多普勒时间相关性判别后,再对二值化处理的二维多普勒值进行多普勒空间相关性判别。表1为经多普勒时间相关性判别二值化后时间-距离二维多普勒频率的第100~106脉冲的部分多普勒值数据。其中第550距离单元附近为A目标区,第890距离单元附近为海杂波区。观察表1,根据第1.2节所述的多普勒空间相关性判别可以看出,目标区第550距离单元第100~106脉冲,这连续7脉冲主瓣各自都至少有一个1值多普勒副瓣,故称此处为连续7脉冲“拟目标主瓣序列”。并以此序列位置为中心向四周扩充两个脉冲或两个距离单元,即以第98脉冲第548距离单元、第108脉冲第552距离单元两位置点为对角线构成矩形目标区域块,并将此目标区域内所有多普勒重置为1值。而第890距离单元杂波区附近的1值多普勒点成明显的零散分布,不具有空间相关性,故将杂波区的多普勒值全部重置为0值。

图4 同距离单元相邻两脉冲间多普勒相关系数
表1 时间相关性判别后的二值化多普勒值

最后根据两级多普勒相关性判别处理后得到的二值化多普勒值分布,将分布1值多普勒的目标区域信号全部保留,而将0值多普勒的杂波区信号全部归一成平均噪声电平,结果如图5所示,可见大片强海杂波区域被抑制,两目标被检测出来。对比图3和图5处理效果,可见两级多普勒相关性判别的海杂波抑制方法处理效果比传统两级AMTI滤波的海杂波抑制效果显著。

图5 经过两级多普勒相关性判别处理后的脉压数据
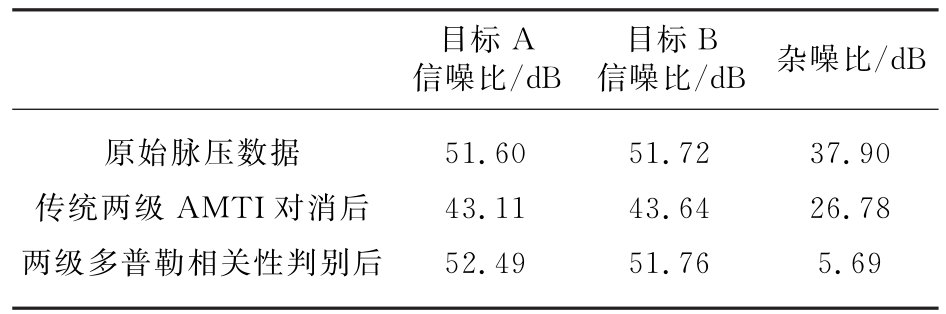
表2为传统两级AMTI滤波和本文两级多普勒相关性判别处理抑制杂波前后的信噪比和杂噪比。传统两级AMTI对消后目标信噪比有一定损失,目标A由原来的51.60 dB变成43.11 d B,目标B由原来的51.72 dB变成43.64 d B,海杂波虽有一定程度抑制,但杂噪比仍然很高,为26.78 d B。而两级多普勒相关性判别处理后目标的信噪比基本没有损失,且海杂波抑制效果显著,杂噪比降到5.69 dB。由此可见本文两级多普勒相关性判别技术抑制海杂波的有效性。
表2 海杂波数据的信噪比和杂噪比
4 结束语
本文提出了一种基于两级多普勒相关性判别实现海杂波抑制的算法。根据目标和海杂波在连续脉冲间及二维区域间的多普勒相关性差异,将隔周测频所估算得到的多普勒频率依次经过多普勒时间相关性判别、多普勒空间相关性判别,最后根据相关性二值化重置后的多普勒值,将分布1值多普勒的目标区域块信号保留,并将0值多普勒的海杂波区域块信号全部归一成平均噪声电平。该方法可以实现强海杂波背景下的运动目标检测,海杂波抑制效果显著,且不依赖于具体的海杂波模型,具有良好的通用性。实测海杂波数据的实验处理也验证了该方法的正确性和有效性。
参考文献:
[1]GRECO M,STINCO P,GINI F.Identification and Analysis of Sea Radar Clutter Spikes[J].IET Radar Sonar&Navigation,2010,4(2):239-250.
[2]ROSENBERG L.Sea-Spike Detection in High Grazing Angle X-Band Sea-Clutter[J].IEEE Trans on Geoscience and Remote Sensing,2013,51(8):4556-4562.
[3]李东宸,水鹏朗,许述文.块白化杂波抑制的海面漂浮小目标检测方法[J].西安电子科技大学学报(自然科学版),2016,43(6):21-26.
[4]曾浩,李洁,鉴福升.强海杂波环境下目标检测方法对比分析[J].雷达科学与技术,2015,13(1):33-36.
[5]XIN Z,LIAO G,YANG Z,et al.A Deterministic Sea-Clutter Space-Time Model Based on Physical Sea Surface[J].IEEE Trans on Geoscience and Remote Sensing,2016,54(11):6659-6673.
[6]CARRETERO-MOYA J,GISMERO-MENOYO J,BLANCO-DEL-CAMPOÁ,et al.Statistical Analysis of a High-Resolution Sea-Clutter Database[J].IEEE Trans on Geoscience and Remote Sensing,2010,48(4):2024-2037.
[7]FARSHCHIAN M.Target Extraction and Imaging of Maritime Targets in the Sea Clutter Spectrum Using Sparse Separation[J].IEEE Geoscience and Remote Sensing Letters,2017,14(2):232-236.
[8]丁昊,李建忠,安昕,等.实测海杂波数据的多普勒谱特性[J].雷达科学与技术,2012,10(4):400-408.
[9]司军,赵中兴,吴俭,等.基于时间相关性的海面小目标检测技术[J].雷达科学与技术,2016,14(3):261-266.SI Jun,ZHAO Zhongxing,WU Jian,et al.Detection Technique of Dim Target in Sea Clutter Based on Time-Coherent Characteristic[J].Radar Science and Technology,2016,14(3):261-266.(in Chinese)
[10]HOLDSWORTH D A.Spatial Correlation Analysis Revisited:Theory,and Application to“Radar Backscatter Model”Data[J].Radio Science,1999,34(3):629-641.
[11]WALSH E J.Pulse-to-Pulse Correlation in Satellite Radar Altimeters[J].Radio Science,1982,17(4):786-800.
[12]陈伯孝.现代雷达系统分析与设计[M].西安:西安电子科技大学出版社,2012:230-231,246-247.
[13]HU Z,LIU L.Applications of Wavelet Analysis in Differential Propagation Phase Shift Data De-Noising[J].Advances in Atmospheric Sciences,2014,31(4):825-835.
[14]ISPIR M,CANDAN C.On the Design of Staggered Moving Target Indicator Filters[J].IET Radar Sonar&Navigation,2016,10(1):205-215.
