0 引言
在雷达辐射源信号分选识别研究中,SVM以其较强的训练和识别能力得以广泛应用,其原理是通过核函数将样本从不可分的低维空间映射至可分的高维空间中,实现非线性不可分问题向线性可分问题的转化[1]。但实际应用中,SVM中核函数性能各异,且对不同的模型参数有着不同的学习感知能力,因此,对核函数性能进行有效评估已显得尤为重要。
当前,常用的核函数有线性核(Linear)、多项式核(Poly)、高斯核(RBF)、多层感知核(Sigmoid)以及多项式核与高斯核凸组合的核函数(Pobf)。在常用的评估方法中,K-CV和LOO及其评估上界[2-5]是一种基于分类器的核函数评估方法,主要通过将特征参数分为K组,取K-1组进行训练,剩下一组进行测试,并将此过程循环K次,最终将测试结果误差作为SVM的评估准则,但是LOO法误差计算过程繁杂、开销较大,难以适用实际需求;文献[6]提出了一种依据识别结果综合应用多种统计量的评估方法,包括配对t测试方法、纠正重复采样t测试方法,该类方法将统计方法运用其中,却存在着计算量大、难以满足实际应用需求的弊端;核排列、核极化、局部核极化[7-10]是几种常用的独立于分类器的核函数评估方法,这类方法更多地关注了核函数对样本从低维空间映射到高维空间的实际分类能力,但并未考虑到核函数的泛化性能。这些方法在对核函数进行评估时,仅从某一方面对核函数进行评估,并不具备全面性。因此,后续的研究者们又提出了一种基于多指标的核函数评估方法[11],以可分离性、稳定性和复杂性为指标,并通过Mercer理论[12]来对各指标进行度量。但该指标体系中,可分离性指标是通过度量特征参数在核空间上的相似性而得出,其本质属于特征参数相似性,并非核函数的可分离性;复杂性指标,仅考虑了核函数参数个数对分类器的影响,忽略了参数维度对核函数的影响。
为此,本文提出一种新的支持向量机核函数评估方法,首先构建了以核函数相似性、稳定性和复杂性为评估指标的评估体系,并给出各个指标的计算准则,然后利用层次分析法对不同应用场景下的评估指标赋予权值,其次利用指标评分函数对各指标予以评分,最后通过权重矩阵和指标评分矩阵对各评估对象以综合打分的方式进行评估。将新的评估方法分别应用至雷达辐射源信号实时处理和事后处理两种不同的应用背景中,该评估方法的有效性与可行性得以验证。
1 评估指标的建立与计算
评估指标的构建是进行评估工作的前提与基础。指标的选取应当在基于用户实际应用需求的背景下,遵循目的性、科学性、系统性等原则。但是在实际评估中,由于评估指标会受到各种复杂因素的影响,难以满足以上所有指标选取准则。因此,针对核函数性能的实际情况,从以下3个方面来构建核函数评估指标:
1)对核函数性能的直接度量即核函数对特征参数的识别率。因此,在构建理想核函数基础上,通过计算其他核函数所确定最优超平面与理想核函数所确定最优超平面之间的位置关系来间接地对核函数的识别性能予以度量。
2)在实际侦察环境中,侦察接收机所侦获的脉冲个数随机性强且难以控制。因此,选用稳定性指标来量化样本容量对核函数抗扰动能力的影响。
3)在实际应用中,核参数的个数、维数直接影响核函数性能的优劣。因此,选用复杂度特征来对核函数的复杂性进行描述。
依据上述指标,完成核函数评估指标体系的构建。支持向量机核函数评估指标体系如图1所示。
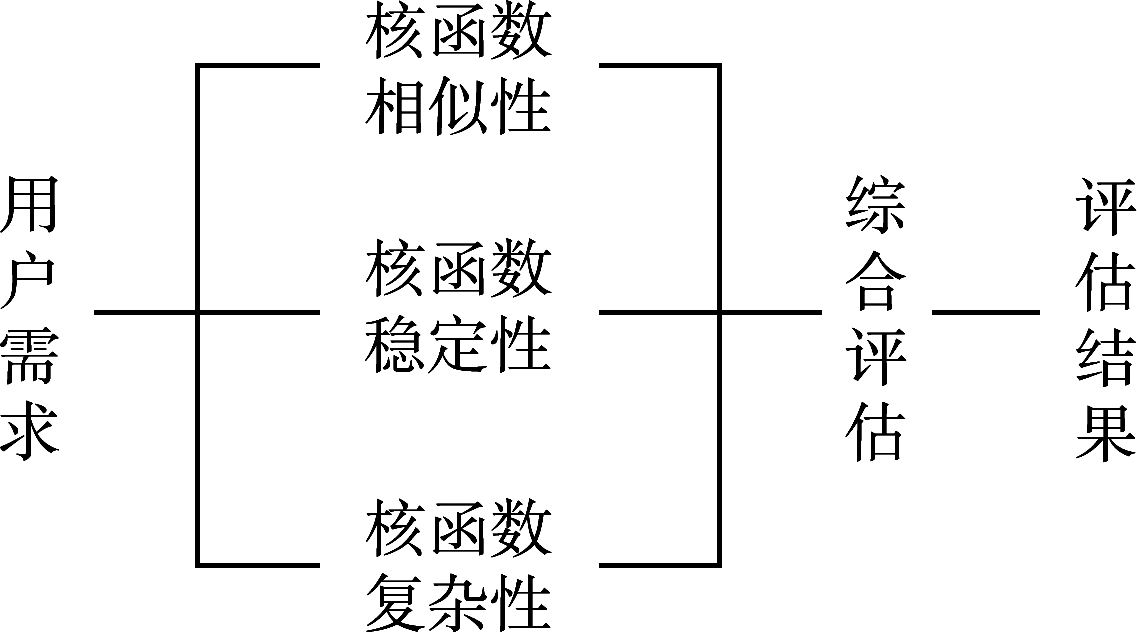
图1 支持向量机核函数评估指标体系
目前,常用的核函数中Poly核、Sigmoid核属于全局性核函数,具有较强的全局泛化性;而RBF核属于局部性核函数,具有较好的局部拟合性;Pobf核既具有较强的全局泛化能力,也同时具备较强的局部拟合能力[13]。因此,为了充分考虑各核函数的性能,选用模拟条件无信噪比环境下识别率最高的线性混合核函数为理想核函数,记为Id Kernel。
式中,λi(i=1,2,3,4)为对应核函数系数,其中
1.1 相似性
相似性是用来描述在训练识别样本已定条件下,各类核函数所构造的最优超平面与理想核函数所构造的最优超平面位置之间的关系。如图2所示的支持向量机可分情形下的可分曲线示意图中,记有一组线性可分的训练样本集
其中ai为第i个样本,yi∈(-1,1)为第i个样本的分类标签,超平面方程表示的就是能够把两类样本分开的方程。最优超平面不仅能够最大限度地将不同类样本予以区分,还使得样本到该平面的距离最大,即样本间间距最大,如图中虚线X所示。方程表示为
图2 支持向量机可分情形下的可分曲线
若将该平面分别向样本方向进行平移,当碰到某个样本点时停下,得到平面X1,X2,这两个平面称为支持平面,落在这两个平面上的样本点就是支持向量。则两条直线可用以下公式表示:
从式(2)可得出,不同核函数所确定的最优超平面的不同之处在于各平面的斜率和截距不同,因此可以用不同核函数所确定的最优超平面与理想核函数所确定的最优超平面之间的斜率和截距的相似性来确定两类超平面之间的相似性,从而间接描述核函数之间的相似性。
记K,B是理想核函数所确定的最优超平面的斜率矩阵和截距矩阵;Kp,Bp是其他核函数所确定的最优超平面的斜率矩阵和截距矩阵。
其中,两类最优超平面的斜率相似性Ck和截距相似性Cb分别为
因此,最优超平面的相似性定义为C=t1·Ck+t2·Cb,其中,t1=t2=0.5。
核函数的相似性不仅能够有效地刻画不同核函数所确定的最优超平面之间的位置关系,还能对核函数的分类能力予以度量。
1.2 稳定性
SVM对样本的分类识别是一个样本量不断增加的学习过程,而核函数的分类性能直接决定SVM分类能力。在传统核函数性能评估中,诸如留一法、交叉验证法仅从训练样本的完整性予以度量,并未充分考虑核函数的泛化性能。基于此,本文将鲁棒度作为度量核函数稳定性的评估指标。
假设分类函数f(x)在点x处能够正确分类,若f(x)在点x处的梯度越小,则f(x)在点x处的稳定性越好,记f(x)在点x处的抗扰动能力函数为
式中,‖∇f(x)‖代表了f(x)点x处值的变化率。
因此,可以将函数f(x)鲁棒度R(f)定义为抗扰动能力函数R(f,x)在边界支持向量集上的平均值,记为
式中,N表示边界支持向量的个数,由上节支持向量的定义可得。
鲁棒度有效度量了核函数对样本容量的抗扰动能力[14]和对样本集的正确预测能力,鲁棒度越大,分类函数对预测样本的正确预测能力越强;反之,越差。
1.3 复杂性
复杂性指标为定性指标,无法使用特定的函数对其进行量化。因此,利用渐近时间复杂性T(n)=O(f(n))作为核函数复杂性的度量指标。其中,f(n)代表算法中频度最大的语句频度。
根据经验,建立指标到评分值的映射表,如表1所示。
表1 指标-评分值映射表
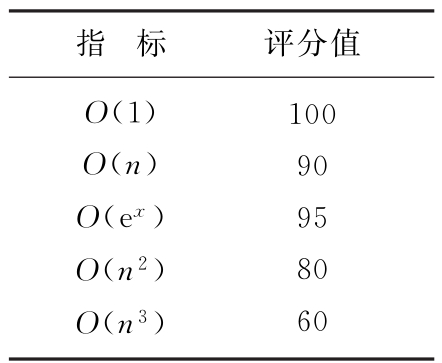
其中,O(1)是常数,O(n)是线性,O(ex)是幂指数,O(n2)是二次阶,O(n3)是三次阶。由于在RBF核函数中,其核参数数值变化对核函数的时间复杂度影响极小,因此对O(ex)的评分值为95分。
2 基于用户需求的核函数评估模型
Step1:根据所给出的指标计算规则对指标原始值进行计算,构建评价矩阵C=(aij)m×n,其中m为评价目标数,n为属性指标数。
Step2:矩阵规范化。利用向量规范化zij=
对评价矩阵C予以数据预处理,得到规范化决策矩阵
Step3:确定指标的评分值。在实际应用中,相似性和稳定性指标可用凸递增函数来描述,其评分值随着实际数值的增加而增加,因此其评分函数如式(7)所示:
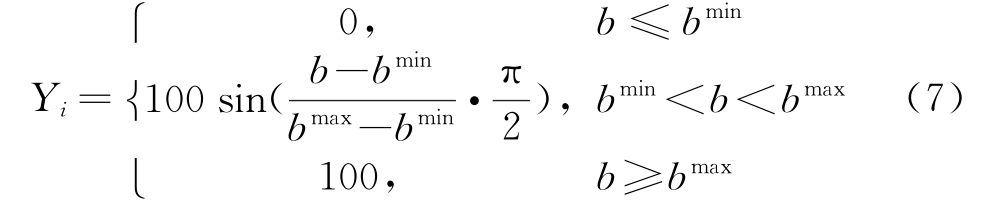
式中,bmax和bmin代表指标值b的满意点和无效点。
Step4:确定评估指标权重W。在雷达辐射源信号识别过程中,可以分为实时处理和事后处理两大类。实时处理时,侦察接收机所截获的雷达信号信噪比低,且对样本的稳定性和复杂性有较高的要求;而事后处理时,对稳定性和复杂性则要求低,识别率才是关键。因此,用户可根据实际应用需求,利用层次分析法对各评估指标的权重予以确定。
Step5:对各评估对象进行综合评分。S=W·Y,W代表各评估指标的权重,Y代表评估对象各指标的评分值。
Step6:对评估方案进行排序。根据评估方案的总体的评分值,依次对各方案进行排序。
3 应用分析
假定在雷达信号样式和特征参数已定的情况下,选用单载频、频率捷变、线性调频、非线性调频、频率编码、二相编码、四相编码、线性调频和二相编码、线性调频和四相编码、相位编码和频率编码十种信号所提取的相像系数、熵值、小波包和复杂度四种信号脉内特征参数,分别在-5,0,5,10,15和20 d B信噪比环境下对这10种信号各取100组数据进行学习,另选取150组数据进行测试,可以得到其识别测试结果,如表2所示,记识别率、识别时间、复杂度为F1,F2,F3。并由式(7)可以得到其评分矩阵,如表3所示。
表2 识别测试结果
表3 评分矩阵
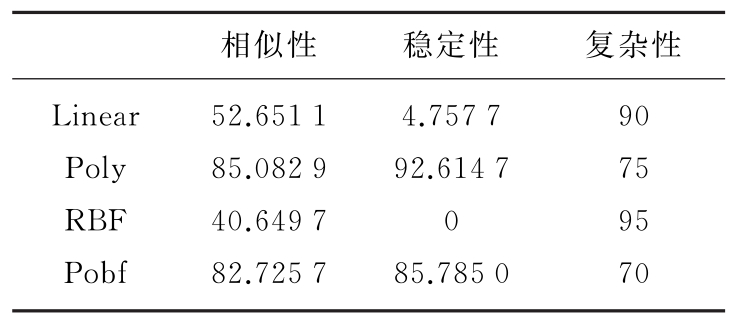
理想核函数在无信噪比条件下的识别率为94%,相比于Linear核、Poly核、RBF核、Sigmoid核在无信噪比条件下识别率最高,相应的核函数系数λ=(0.3,0.49,0.2,0.01)。对Linear核、Poly核、RBF核、Sigmoid核,以及Poly核和RBF核所构成的混合核Pobf核进行评估。由于Sigmoid核在实际应用中识别率过低,不能达到正常使用需求,因此将Sigmoid核予以删除,主要对Linear核、Poly核、RBF核、Pobf核进行评估。其中,Pobf=0.5·Poly=0.5·0.5·RBF。
由实验可得4种核函数的相似性指数为[0.396 6,0.727 8,0.299 4,0.696 8];稳定性指数为[3 285.1,81 852,3.720 1×10-4,71 277]。
1)实验1:基于雷达辐射源信号实时处理的核函数性能评估
实时处理时判断矩阵如表4所示。
表4 实时处理时判断矩阵
此时,该判断矩阵的特征值为λ=3.007 0,一致性指标CI=0.003 5＜0.1。因此,此矩阵的一致性可以接受,并由此得到的指标权重为W=(0.158 8,0.403 0,0.438 2)。并根据表3的评分矩阵可以得出各核函数的总体的评分值:Linear核函数为49.716 3,Poly核函数为83.699 9,RBF核函数为48.084 2,Pobf核函数为78.382 2。因此选用Poly核函数。
由表1中的识别测试结果可知,在信噪比小于10 dB时,时间复杂度由小到大依次是RBF核、Linear核、Poly核和Pobf核;但RBF核和Linear核的稳定性较差。尽管Poly核在0 dB和-5 dB时时间复杂度较大,但当信噪比大于0 dB时,其时间复杂度呈现骤降趋势,且其识别准确率也较为可观。因此,评估结果符合实际应用需求。
2)实验2:基于雷达辐射源信号事后处理的核函数性能评估
事后处理判断矩阵如表5所示。
表5 事后处理时判断矩阵
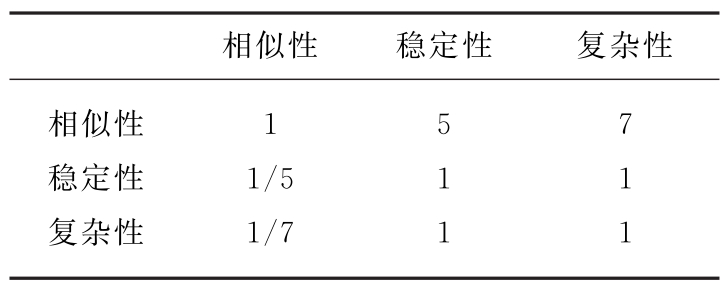
此时,该判断矩阵的特征值为λ=3.012 6,一致性指标CI=0.006 3＜0.1。因此,此矩阵的一致性可以接受,并由此得到的指标权重为W=(0.747 1,0.133 6,0.119 4)。根据表3的评分矩阵可以得出各核函数的总体的评分值:Linear核函数为50.717 3,Poly核函数为84.893 8,RBF核函数为41.712 4,Pobf核函数为81.623 2。在实际应用中选用Poly核函数。
由表1可以看出,当信噪比大于10 dB时Poly核的识别准确总体上比Pobf核略高,且稳定性和时间复杂度较为稳定。因此,评估结果符合实际应用需求。
4 结束语
支持向量机核函数性能的优劣直接影响着雷达辐射源信号分选识别效果。因此,本文提出了一种新的支持向量机核函数性能评估方法,该方法首先构建了一套以相似性、稳定性、复杂性为评估指标的评估体系,并基于用户实际需求利用层次分析法对各评估指标赋予不同权重,最后利用综合打分的方式对各评估对象的性能予以评估。将该方法运用至支持向量机核函数性能评估的仿真应用中,仿真结果验证了该评估方法的可行性和有效性,具有一定的实际应用参考价值。
参考文献:
[1]白璐,徐立祥,崔丽欣,等.图核函数研究现状与进展[J].安徽大学学报(自然科学版),2017,41(1):21-28.
[2]CHAPELLE O,VAPNIK V,BOUSQUET O,et al.Choosing Multiple Parameters for Support Vector Machines[J].Machine Learning,2002,46(1/2/3):131-159.
[3]JOACHIMS T.Estimating the Generalization Performance of a SVM Efficiently[C]∥Seventeenth International Conference on Machine Learning,Stanford,CA:Morgan Kaufmann,2000:431-438.
[4]JAAKKOLA T S,HAUSSLER D.Exploiting Generative Models in Discriminative Classifiers[C]∥Conference on Advances in Neural Information Processing Systems,Massachusetts:MIT Press,1998:487-493.
[5]宋小彬,蒋晓瑜,汪熙,等.基于改进Joachims上界的SVM泛化性能评价方法[J].电子学报,2011,39(6):1379-1383.
[6]王泳,胡包钢.应用统计方法综合评估核函数分类能力的研究[J].计算机学报,2008,31(6):942-952.
[7]WANG Tinghua,TIAN Shengfeng,HUANG Houkuan,et al.Learning by Local Kernel Polarization[J].Neurocomputing,2009,72(13/14/15):3077-3084.
[8]BARAM Y.Learning by Kernel Polarization[J].Neural Computation,2005,17(6):1264-1275.
[9]NGUYEN C H,HO T B.Kernel Matrix Evaluation[C]∥20th International Joint Conference on Artificial Intelligence,Hyderabad,India:[s.n.],2007:987-992.
[10]易序峰,吴坚,喻高航.基于自适应梯度算法的SVM核极化参数选择方法[J].赣南师范学院学报,2015,36(6):23-27.
[11]JING Xu,HE Minghao,HAN Jun,et al.A Comprehensive Estimation Method for Kernel Function of Radar Signal Classifier[J].Chinese Journal of Electronics,2015,24(1):218-222.
[12]李琼,陈利.一种改进的支持向量机文本分类方法[J].计算机技术与发展,2015,25(5):78-82.
[13]胡燕燕,李东生,张诗佳.凸组合核函数的支持向量机高光谱图像分类[J].激光与红外,2016,46(5):627-633.
[14]张鹏,倪世宏,谢川.支持向量机增量学习中模型参数选择问题研究[J].空军工程大学学报(自然科学版),2011,12(5):5-9.
