0 引言
未来作战中,由于各类新型抗干扰技术在现代雷达中的应用[1],使得与雷达发射波形不匹配的干扰信号不能获得相应的处理增益,很大程度上降低了压制或者欺骗干扰的效果。为应对新型抗干扰样式所带来的威胁,迫切需要对新型干扰技术进行研究。现代雷达多采用具有大时宽-带宽积信号,而线性调频脉冲信号(Linear Frequency Modulation,LFM)在雷达中是使用最为广泛的一种大时宽-带宽积信号,针对LFM脉冲压缩雷达的干扰方法研究是目前电子战领域研究的热点。
LFM脉冲信号是脉内相干的,这种脉内相干性使其在距离 多普勒频移之间存在强耦合作用,这种距离-多普勒之间的相互影响会引起距离随着多普勒频移的视在漂移而产生测距误差[2]。因此,如果在转发干扰信号时适当地叠加一个多普勒频移量,回波信号经过匹配滤波处理后就可在真目标附近产生一个假目标,假目标的位置随着频移量大小的变化而变化。频移干扰是现代干扰样式中一种对付LFM脉冲压缩雷达较为有效的手段。许多学者对移频干扰进行了研究分析。文献[3-4]分析了移频干扰技术,得出了移频干扰可以实现距离欺骗的结论。文献[5-7]针对常规移频干扰存在可被识别的特征,给出了特征隐藏的随机移频、正弦波移频、阶梯波移频和线性函数移频等新型移频干扰样式,通过改变移频量(移频量按函数形式变化),可产生不同位置、不同形状的多假目标干扰效果。但当雷达调频斜率改变时,以上移频干扰技术产生的假目标位置将在不同位置发生距离跳变的现象,雷达方可根据该特点对假目标进行剔除,使干扰失去效果。本文所推导的延时-变脉宽移频干扰是通过对接收信号进行延时和倍乘调制,使干扰信号的产生不依赖于调频斜率,以达到隐藏特征的目的。与常规移频干扰技术相比,具有如下特点:干扰信号与雷达信号具有很好的匹配性;同等干信比条件下,可降低对干扰机发射功率的要求;克服了常规移频干扰在对抗雷达调频斜率改变时干扰失效的缺点。
1 LFM信号移频干扰原理
随着数字射频存储器(Digital Radio Frequency Memory,DRFM)技术的成熟和应用,DRFM可实现移频干扰技术。其原理是:首先DRFM对截获到的雷达发射信号进行存储,干扰需要时DRFM复制出原雷达信号,上变频时通过给上变频本振调制一个附加的频移量,从而产生假目标干扰信号[8]。假设线性调频雷达发射的雷达信号表达式为
式中,T为脉宽,k为调频斜率,且k=B/T,B为信号带宽,BT为脉冲压缩比,u(t)为信号复包络,其表达式为
根据信号匹配滤波理论,雷达接收到回波信号后在接收机中进行脉冲压缩。匹配滤波器的单位冲激响应为x∗(t0-t),式中t0为匹配滤波器物理可实现条件决定的附加延时[9]。则线性调频信号经脉冲压缩后输出响应的振荡包络为
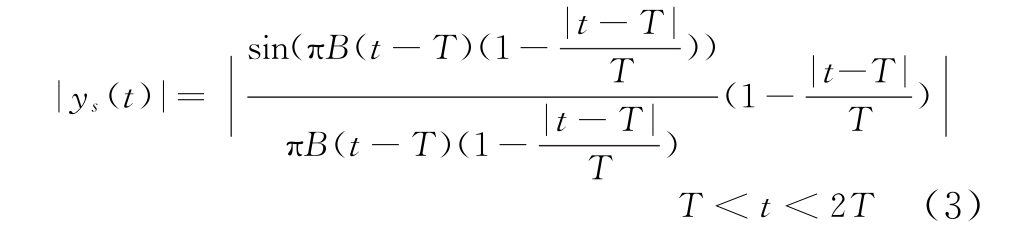
干扰机对截获的雷达信号移频后转发,干扰信号进入雷达接收机,在匹配滤波器的输入端表现为x(t)的频率发生了fd的频移,因此,移频干扰信号为
式中,fd为附加的频移量。式(4)经过匹配滤波后的输出信号为
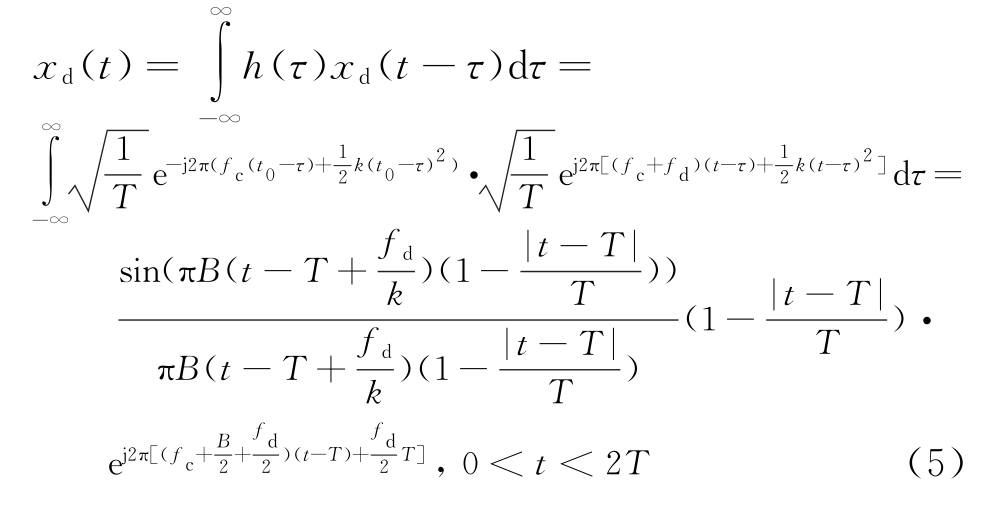
由式(5)可知,移频干扰经匹配滤波后的输出信号是一个单频振荡,其中心频率为fc+B/2+![]() 振荡包络为
振荡包络为

假设雷达脉宽T=10μs,带宽B=10 M Hz,fd分别为1.0,3和-0.8 M Hz画图,如图1所示。

图1 移频干扰脉压输出波形
由图1可知,干扰信号中的频移量使雷达受到了距离欺骗干扰效果,具体表现为假目标回波相对地发生前移或后移。当fd=0时,脉压输出在输入脉冲结束时刻T出现主峰,主峰宽度为[-1/B,1/B],输出信号包络按sinc函数规律衰减;从式(5)和图1可知,当fd≠0时,主峰偏移到Δt=T-fd/k处(fd>0主峰导前,fd<0则主峰导后),即其延时和频移之间存在耦合作用,使得输出主峰展宽,幅度按三角包络下降,干扰功率出现失配损失,且fd的值越大,失配越严重[10],表现在假目标能量越小。根据式(5)知,移频量fd使雷达受到距离欺骗的同时,还使干扰信号匹配滤波后单频振荡的中心频率发生了fd/2的改变。因此,移频干扰产生的假目标的中心频率偏移真实目标,如果是单个假目标,则很容易被雷达识别,这也是常规移频干扰的主要缺点。
2 延时-变脉宽移频干扰
从上一节的分析可知,移频干扰信号与真实目标回波信号相比,干扰信号经匹配滤波后中心频率发生了fd/2的改变,这种中心频率变化的特征可作为一种雷达抗干扰的潜在方法。目前,一种有效的方法是实施干扰时使用变化的移频量来隐藏该特征,防止干扰被识别和滤除。许多学者通过对频移量fd的调制和改变让频移量发生变化以隐藏该特征,主要包括阶梯波移频、线性函数移频和随机数移频等新型移频干扰样式。但以上干扰技术均有一个共同的缺点,移频量按一定的规律线性递增或线性递减变化,当雷达调频斜率改变时,所产生的假目标将在多个不同距离进行跳变,可被雷达准确识别和剔除。因此,如何较好地隐藏移频量的变化成了移频干扰研究的重点。
由Δt=T-fd/k可知,假目标与真目标的距离只与频移量fd和调频斜率k的大小有关,而与其他参数无关。因此,若要知道移频量与假目标距离差之间的一一对应关系,就必须知道调频斜率的大小,且在对付具有不同调频斜率的频率分集雷达时,干扰产生的假目标由于存在假目标位置随调频斜率捷变而发生距离跳变的现象,将使得干扰完全失效。雷达参数不变,取fd=1 M Hz,分别取调频斜率k,k/2,k/3作仿真。为便于分析,仿真中对不同调频斜率下的匹配滤波输出都作了归一化处理,如图2所示。

图2 不同调频斜率下的常规移频干扰
由图2可知,移频量相同时,调频斜率不同会造成假目标与真目标之间的距离差发生变化,且调频斜率不同引起频移量的不同导致假目标信号幅度也不同,仿真结论与理论分析一致。因此,针对常规移频干扰技术的不足,若使干扰信号移频量fd随雷达调频斜率k的变化而变化,而延时量Δt不随k发生改变,则可避免假目标位置随调频斜率变化的特点,使干扰信号在对付雷达调频斜率改变时仍有效。延时-变脉宽移频干扰的思想是:首先分别对雷达信号及其延时信号进行整数倍频谱扩展,然后利用后者对前者进行时域脉冲压缩,可以产生前移或后移假目标干扰,无需检测雷达调频斜率,能够克服常规移频干扰存在的可被识别的特征。
为简化分析,考虑载频为零时的情况,将线性调频信号重写为
式中,A(t)为矩形包络函数:
取时延量τ,则原信号经时延变换后可表示为

移频干扰分为正向移频和负向移频,分别可产生超前假目标和拖后假目标干扰,以正移频干扰为例讨论干扰信号的产生原理。由式(10)可知,将式(10)左边恢复为常规移频干扰信号表现形式,并引入移频干扰分量,需要对式(10)进行等式变换。将式(10)两边同乘以A(t),由式(7)可得

对式(11)两边取平方,得
再将式(12)两边同乘以x-2(t-τ)x(t),即
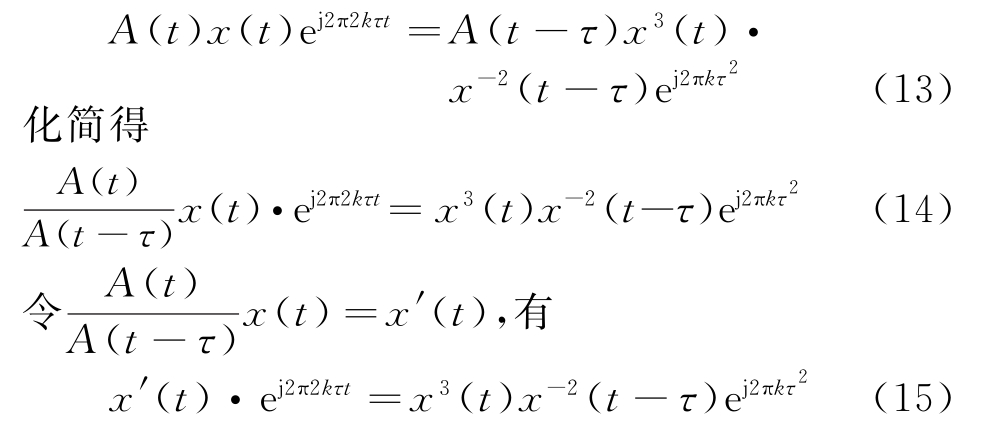
从式(14)、式(15)可以看出,线性调频信号经过延时和倍乘变换后,等式左边即为常规移频干扰的表达式,其区别仅在于参数的取值范围略有不同,等式中x′(t)·ej2πkt2τ较x(t)脉冲宽度减小τ,即干扰信号前沿长度为τ的小部分被截掉,截断后的脉冲宽度变为T-τ,干扰信号载波频率fc+2kτ,频移量2kτ,线性调频信号与延时变脉宽调制后的信号如图3所示。其中,频移量随调频斜率变化,将2kτ代入Δt=T-fd/k得Δt=T-2kτ/k=T-2τ,若延时量取值不变,Δt的值也就不变。故当雷达调频斜率改变时,频移量随之改变,使得调频斜率不会对Δt=T-fd/k造成影响,有效避免了常规移频干扰技术假目标与真目标之间的距离差随调频斜率改变而发生变化的现象。令式(15)右边为干扰信号,则延时-变脉宽移频干扰信号可表示为
根据式(16)可以看出,通过延时和倍乘调制,可使干扰信号的产生不依赖于调频斜率,无需检测调频斜率大小就可实现假目标欺骗干扰的效果,可有效避免常规移频干扰假目标位置随调频斜率改变而发生距离跳变的现象。需要指出的是,式中ej2πkτ2项代入相关参数计算后为一固定常数,只对干扰信号幅度造成影响,而对干扰信号频率不会产生影响。同理,若将式(12)两边同乘以x-2(t-τ)x-1(t)可以产生负移频延时-变脉宽移频干扰信号。
3 仿真实验
对特征隐藏的三角波移频和延时-变脉宽移频干扰进行对比仿真,以验证干扰的有效性。雷达参数同上,三角波移频中,将脉宽T均分为两段,即三角波周期为1,干扰机起始频率设为1 M Hz,调频斜率在时段[0,T/2]内为5 k Hz,在(T/2,T]内为-5 k Hz,干信比JSR1=8;延时-变脉宽移频干扰中,以正移频干扰为例,设延时量τ=1μs,干信比JSR2=4,分别以调频斜率k,k/2,k/3作对比仿真,如图4所示。

图3 线性调频与延时变脉宽调制信号
由图4可以看出,当干信比分别大于等于8和4时,三角波移频可产生覆盖前移多个假目标干扰,但当雷达调频斜率分别取k,k/2,k/3时,三角波移频干扰产生的假目标位置与预定位置发生了偏移,抗干扰方可根据该特点对假目标进行剔除,而延时-变脉宽移频干扰产生的假目标位置不随调频斜率的改变,且干信比一定时其干扰信号功率较大,合理控制延时量大小,可使雷达难以从目标中区分出真目标。由此可知,针对固定调频斜率雷达而言,三角波移频干扰可以形成覆盖前移假目标干扰的效果,但雷达若采取调频斜率捷变来对抗假目标干扰时,三角波移频干扰由于假目标位置发生改变而失去干扰效果,而延时-变脉宽移频干扰假目标位置不发生改变,仍具有欺骗干扰的效果。

图4 延时变脉宽与三角波移频干扰方法对比
4 结束语
移频干扰是一种针对线性调频脉冲压缩雷达的距离多普勒频率间存在耦合的特点进行攻击的转发式干扰。它通过对截获的雷达发射信号调制一个附加的频移量后转发给雷达,以达到欺骗干扰的效果。本文首先分析了常规移频干扰技术的不足,在此基础上仿真分析了一种改进的延时 变脉宽移频干扰方法,并将该方法同三角波移频干扰作对比仿真。仿真结果表明延时 变脉宽移频干扰具有假目标位置不随雷达调频斜率改变而发生距离跳变的特点,可有效避免常规移频干扰在对付具有不同调频斜率的频率分集雷达时干扰失效的问题。仿真结论对移频干扰技术的研究具有一定的实用性。
参考文献:
[1]兰俊杰,陈蓓,王冰切,等.对组网雷达的分布式干扰效能评估[J].火力与指挥控制,2011,36(9):195-198.
[2]王雪松,肖顺平,冯德军,等.现代电子战系统建模与仿真[M].北京:电子工业出版社,2010:179-186.
[3]吴永刚,郭树旭,任磊,等.现代线性调频雷达干扰新技术研究[J].计算机仿真,2013,30(11):11-14.
[4]许阳超.脉压雷达有源干扰问题研究[D].成都:电子科技大学,2014.
[5]张克舟,李青山,张恒,等.LFM脉冲压缩雷达的随机移频多假目标干扰技术研究[J].电光与控制,2014,21(8):106-109.
[6]孟超普,程林,王秀锦.对线性调频脉压雷达的改进移频干扰研究[J].舰船电子对抗,2016,39(3):1-6.
[7]顾成虎,曲丽娜.LFM脉冲压缩雷达的移频干扰技术研究[J].哈尔滨商业大学学报,2015,31(3):350-353.
[8]刘明均.基于DRFM的数字化干扰系统设计与实现[D].西安:西安电子科技大学,2013.
[9]宫健,金虎兵,郭艺夺.一种多域复合调制的雷达灵巧干扰新方法[J].雷达科学与技术,2016,14(2):117-120.
[10]黄翀鹏,王剑,徐保国.线性调频脉冲的移频干扰性能研究[J].系统工程与电子技术,2013,35(5):935-939.
