0 引言
按照目标与雷达之间的距离划分,电磁散射可分为远场散射和近场散射。在远场区域,电磁波采用平面波近似,其雷达散射截面(RCS)计算方法已经较为成熟[1-7]。在近场区域,电磁波为球面波,远场区域的计算方法已经不再适用,随着高频段雷达应用的逐渐增多,目标体越来越多地处于近场区域。近场RCS的分析预估已经成为电磁散射研究的重要课题[8-9]。
国内外一些学者对近场RCS的计算进行了研究。其计算思路主要有两种:一种是将物体表面剖分成小面元,用远场RCS计算方法分别计算各小面元的RCS值,然后通过相位叠加得到总的散射场,是从部分到整体的思路[10],DEMACO公司研发的NCPTD和CPATCH软件采用的就是此方法。另外一种是以物理光学法(PO)为基础,通过散射场积分方程在无远场近似的情况下推导得出,该方法是从整体到部分的思路[11]。图形电磁学(GRECO)是以物理光学法(PO)和物理绕射理论(PTD)为基础,利用了计算机图形加速卡的一种快速的远场RCS计算方法,该方法充分利用了计算机硬件的优势,由计算机硬件完成最困难、最费时的遮挡和消影工作。
在远场RCS计算中,GRECO法在互遮挡判断上的优势是极具吸引力的,但是,在近场条件下,目标体照射区域和雷达与面元之间的距离将随雷达与目标体之间距离的变化而变化,其照射区域和面元到雷达的距离无法通过远场图形电磁学中的方向性光源和图形硬件中的深度缓存获得,因此,传统的图形电磁学无法直接应用于目标体的近场RCS计算。因此,如何把图形电磁学在遮挡判断上的优势应用在目标的近场RCS计算中,是十分有价值和有意义的工作。该文通过将OpenGL中的光源设置为位置性光源,同时对目标体进行二次光照,每次光照设置不同的衰减系数,从而得到面元与点源之间的距离。最后,以平板、球体等目标体在不同距离下的雷达散射截面的计算为例,验证了该方法的有效性和准确性。
1 近场RCS图形电磁学计算公式
设D为一理想导体材料的目标体,如图1所示,S为光照区表面,设表面单位单元为ds,点源P与ds的距离为r。其表面法相为n,入射电场方向为i,散射场方向为s。假设物体表面只有被入射波照射到的区域才有感应电流的存在。
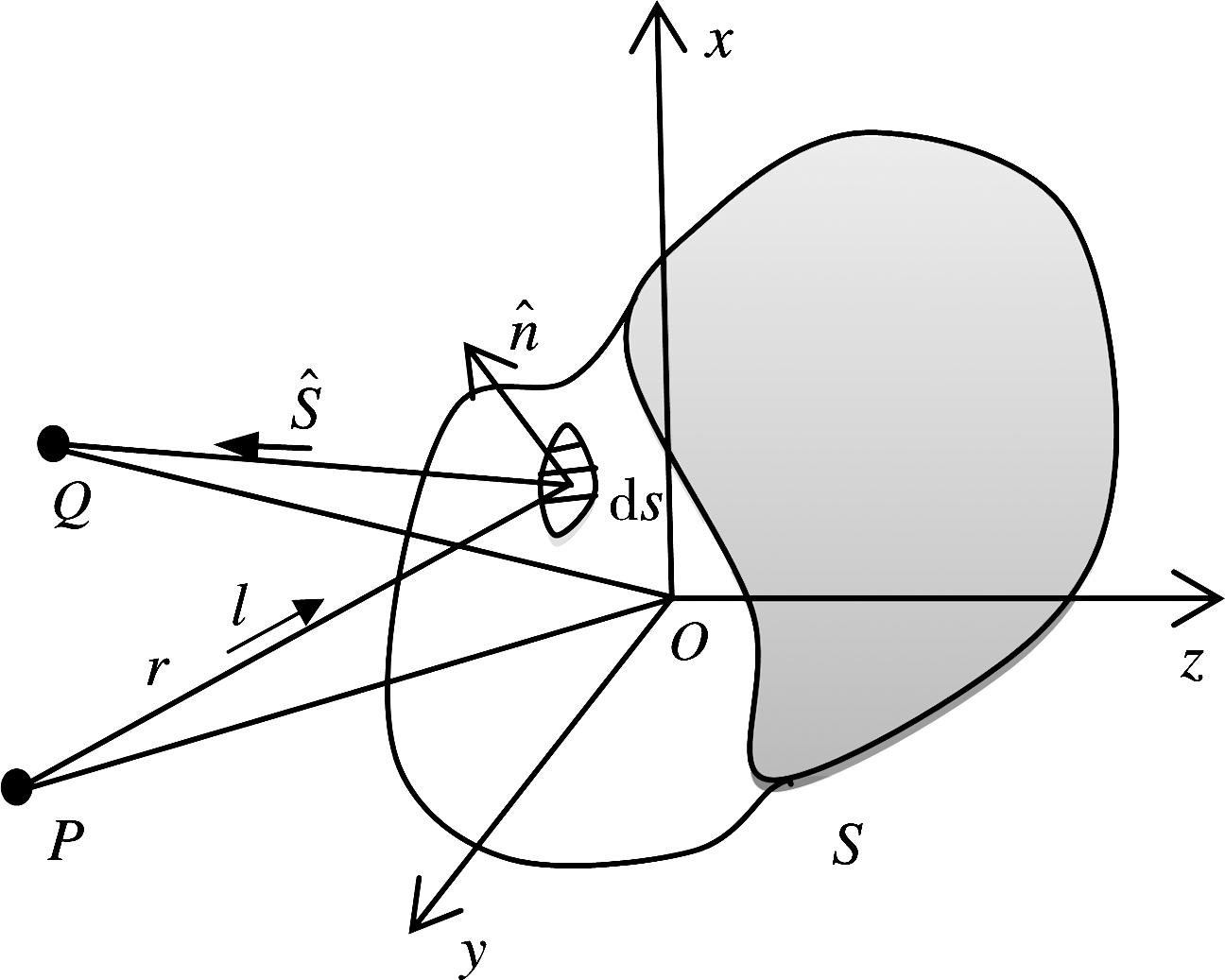
图1 散射示意图
根据麦克斯韦方程,对无远场近似的散射场积分方程进行推导可得
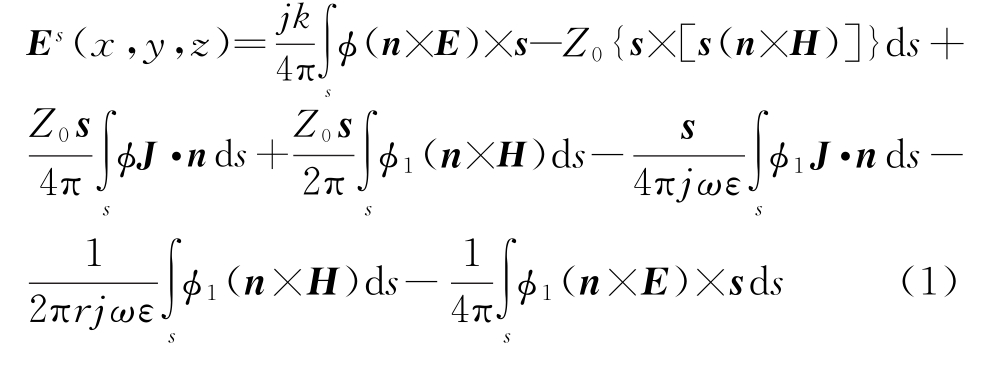
式中,Es为目标体散射电场,E和H分别为总电场和总磁场,Z0为波阻抗
假设物体表面的曲率半径远大于波长,考虑极化因素,由散射场积分方程可得
式中,Es(Q)为接收雷达处散射电场,由于是球面波入射,因此:
由式(2)和式(3)可得
近场雷达散射截面可定义为
式中,R为源点到目标体中心的距离。
由式(4)和式(5),可以得到如式(6)所示的近场RCS的计算表达式:
式中,Δs为每个剖分面元的面积,r为源点到面元的距离,elm代表面元。由式(6),结合图形电磁学可得近场RCS的图形电磁学计算公式为
式中,l表示每一方形像素所在屏幕上的线度,l/cosθ则表示该像素所代表的原目标面ds的线度。与远场RCS图形电磁学计算公式进行对比可知,近场图形电磁学中与远场图形电磁学所需不同的参数为点源到目标体面元的距离r和照射区域Spixel。如图2所示,源1和源2分别为相同方位角下,不同距离位置的源点,由图中可见,近似平面波照射时,光照区域不随距离产生变化,同时Z1和Z2可以通过深度缓存得到,当为球面波时,点源到面源的距离随点源与目标体的距离产生变化,无法通过深度缓存获得。
2 近场RCS图形电磁学计算方法
图2 近场入射与远场入射示意图
使用图形电磁法计算目标RCS时,首先要把模型显示在计算机屏幕上。采用图形软件可以建立3D的目标体,并对其进行三角网格剖分,如图3所示,使用自编的STL文件读入接口把模型文件转换成目标表面的网格点坐标,就可以方便地用OpenGL函数把目标表面显示出来。对单个部件,可以用OpenGL中填充三角形函数gl Vertex3f把相邻两个剖面的对应点形成的三角形区域填充起来,这样顺序填充就可以把相邻两剖面间的部分填充成三角面元组成的曲面,如此循环,就可以把整个部件显示出来。循环读入显示各个部件的文件,就可以完整地表示模型的全部表面。
图3 目标体三角剖分模型
2.1 光照区域Spixel
通过OpenGL将光源设置为位置性光源,光源位置信息通过模型视图矩阵进行变化,并以视觉坐标的形式存储,光照区域将随光源位置的不同自动进行光照区域判断,结合深度缓存自动进行遮挡处理,从而得到准确的光照区域,利用OpenGL将消隐后的目标图像显现在计算机屏幕上,如图4所示,照射区域随源点与目标体距离变化而变化。
图4 通过近场GRECO法获得的光照区域
2.2 点源到面元的距离r
完成光照设置后,对应于三角面元的像素颜色可以通过图形硬件的颜色缓冲区得到,像素颜色为三角面元顶点颜色的均值。OpenGL中顶点颜色的完整计算公式为
式中,emissionmaterial和ambientlightmodel×ambientmaterial分别为材料发射光和全局环境光
为衰减因子,其中d为面元顶点到光源的距离,kc,kl,kq为衰减系数,(max{L·n,0})×diffuselight×diffusematerial为散射光成分,(max{s·n,0})shininess×specularlight×specularmaterial为镜面光成分。将光照设置中保留散射光成分,其他成分设置为零。顶点颜色可表示为
假设面元3个顶点的颜色分别为C1,C2,C2,则直接读取的像素颜色为
分别设置不同的衰减系数,对目标体进行二次光照:
第一次光照设置衰减系数分别为kc=1,kl=0,kq=0,可得到
第二次光照设置衰减系数分别为kc=0,kl=1,
可得到
设d1,d2,d3分别为顶点距源点的距离,其中d1为最大距离。通过OpenGL可以直接读取Cpixel1,Cpixel2,其值分别为
式中
由式(13)、式(14)可得
式中,Rmin为源点距目标体中心的最近距离,一般情况下,n取3,则误差为
由式(7)可知相位误差为
从图5可以看出,当R大于10 m时,误差可以忽略不计。
图5 随距离变化的计算相位误差
因此,当R＞10 m时,式(15)可以近似为
结合
可得
3 计算结果及分析
1)目标体为半径1.0 m的球体,如图6所示。入射频率1 000 MHz,计算间隔1 m。
由图7可以看出,本文的计算结果与解析法的计算结果吻合较好,最大误差小于0.5 dB,验证了方法的有效性和准确性。其RCS值随着距离的增大而减小,其减小速度随着距离的增大而减慢。当距离满足远场条件时,其值与远场RCS解析解基本相同,验证了方法的正确性。
图6 球体计算模型
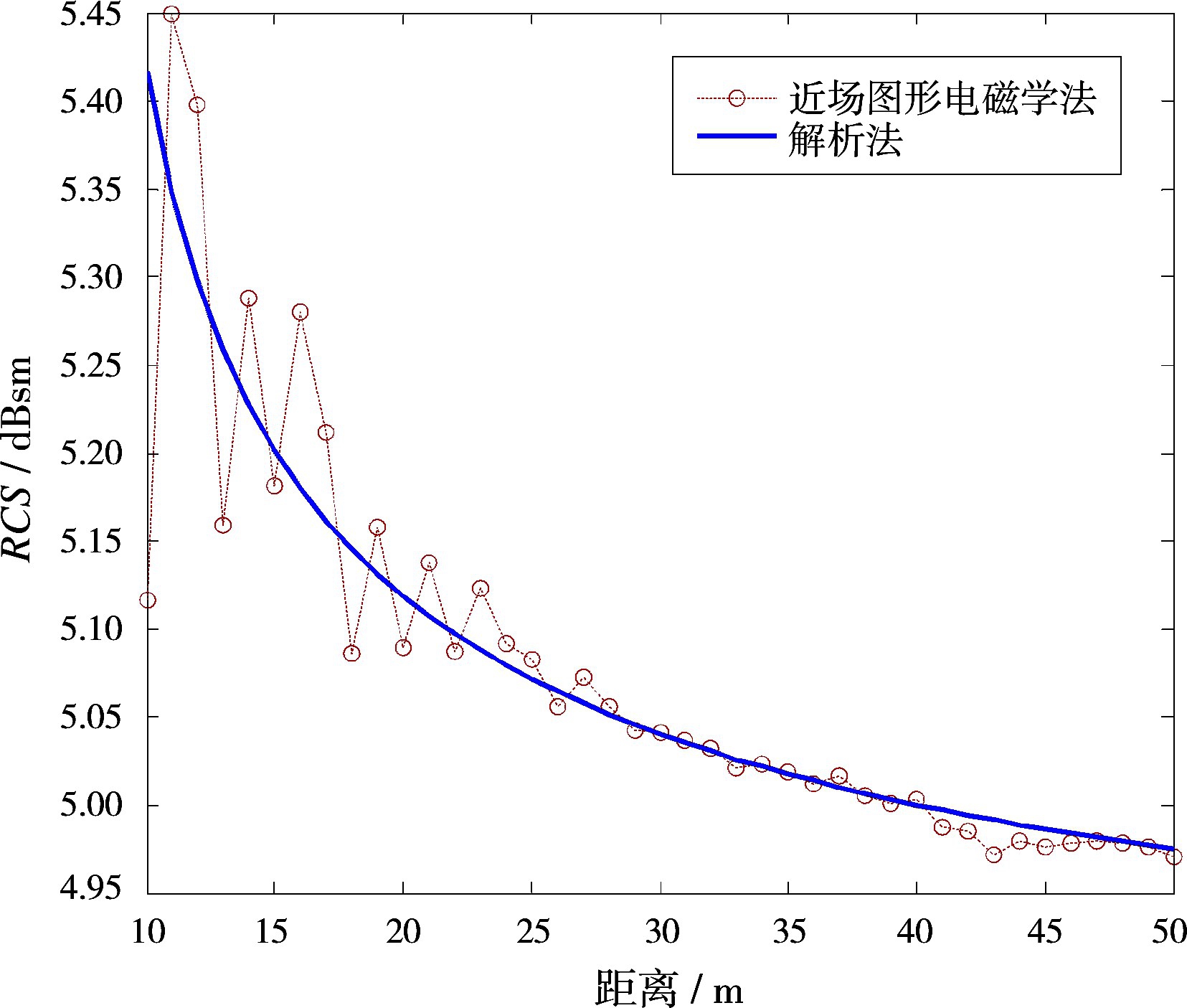
图7 近场GRECO计算结果与解析解对比
2)目标体为2 m×2 m的平板,如图8所示,计算频率为1 000 MHz,计算间隔为1 m。计算结果如图9所示。
由图9可以看出,该方法计算结果与解析法计算结果较好吻合,最大误差0.6 dB。满足远场条件时,计算结果与远场解析解基本相同,最大误差小于1 d B,验证了方法的正确性。
图8 平板计算模型
图9 平板近场GRECO计算结果与解析解对比
3)目标体由0.5 m半径的半球和高1.5 m的锥体组成。如图10所示,计算频率1 000 MHz,计算间隔为1 m。计算结果如图11所示,当距离满足远场条件时,计算结果与远场RCS计算结果吻合,验证了方法的正确性。
图10 锥体计算模型
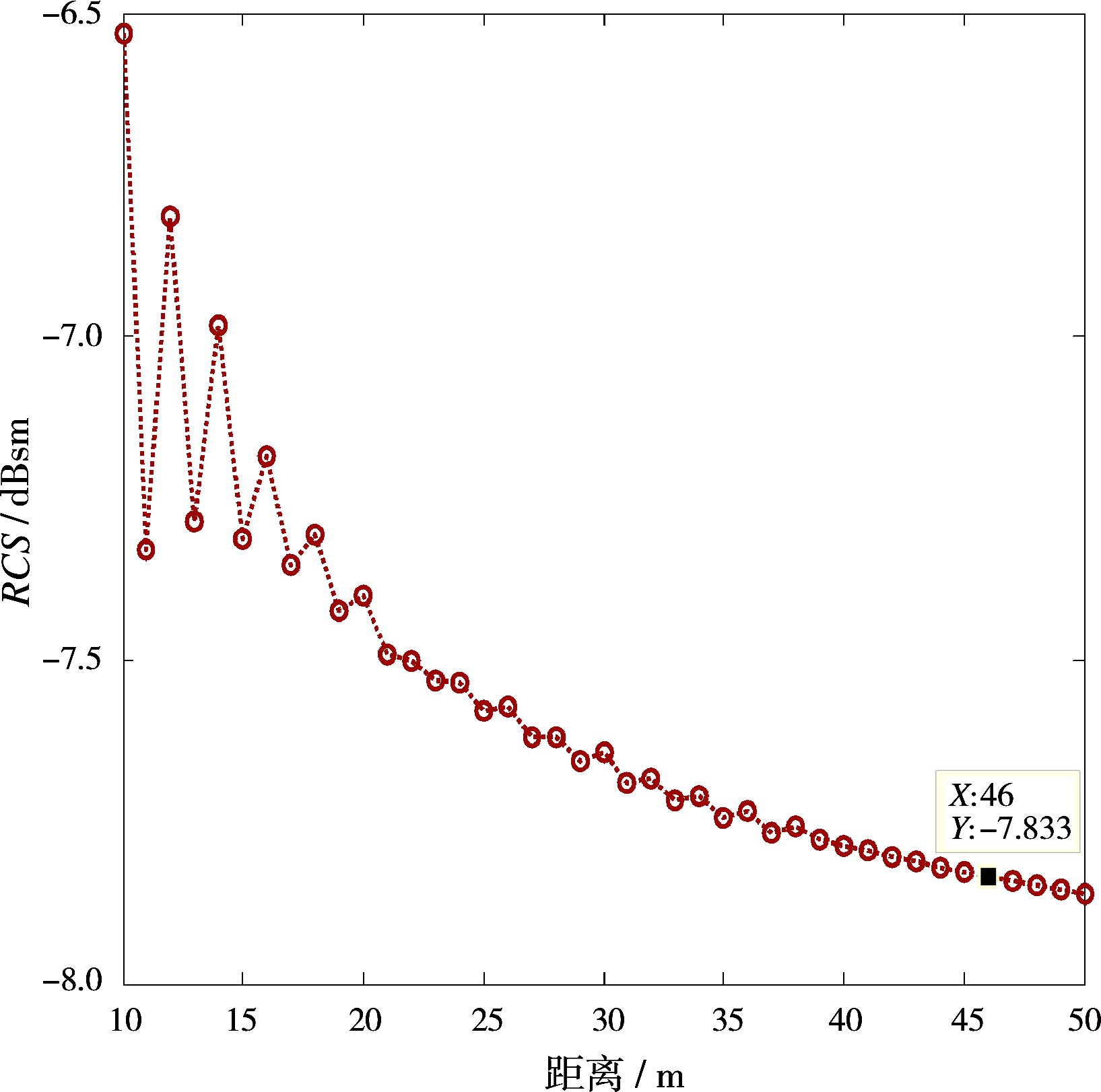
图11 锥体近场GRECO法计算结果
4 结束语
本文研究了远场GRECO法在近场RCS计算时存在的问题,在此基础上推导了近场RCS的计算公式,提出了一种近场GRECO法。该方法将OpenGL中的光源设置为位置性光源,同时对目标体进行二次光照,每次光照设置不同的衰减系数,从而得到面元与点源之间的距离。通过以上参数的求解,结合原有图形电磁学法计算了平板、球体等目标体在不同距离下的雷达散射截面,并与解析解进行了比较,验证了方法的有效性和准确性。
参考文献:
[1]苏建勋,李增瑞.体面积分方程(VSIE)分析任意复杂频率选择结构[J].中国传媒大学学报(自然科学版),2015,22(4):11-15.
[2]陈俊,曲长文,杨俭,等.基于并行MLFMA的SAR舰船目标RCS计算[J].雷达科学与技术,2013,11(4):368-374.CHEN Jun,QU Changwen,YANG Jian,et al.RCS Computation of Vessel Target in SAR Image Based on Parallel MLFMA[J].Radar Science and Technology,2013,11(4):368-374.(in Chinese)
[3]庄亚强,张晨新,张小宽,等.典型隐身飞机动态RCS仿真及统计分析[J].微波学报,2014,30(5):17-21.
[4]刘珺,赵志钦.基于Open MP的色散介质FDTD并行程序设计[J].电子科技,2015,28(7):21-23.
[5]孔勐,陈明生,张忠祥,等.基于压缩感知结合HFSS软件求解目标单站RCS问题[J].微波学报,2015,31(3):7-10.
[6]徐剑盛,周万城,罗发,等.雷达波隐身技术及雷达吸波材料研究进展[J].材料导报,2014,28(9):46-49.
[7]JALALI H.Linear Contact Interface Parameter Identification Using Dynamic Characteristic Equation[J].Mechanical Systems and Signal Processing,2016(66/67):111-119.
[8]BHALLA R,LING H.Near-Field Signature Prediction Using Far-Field Scattering Centers Extracted from the Shooting and Bouncing Ray Technique[J].IEEE Trans on Antennas and Propagation,2000,48(2):337-338.
[9]JENG S K.Near-Field Scattering by Physical Theory of Diffraction and Shooting and Bouncing Rays[J].IEEE Trans on Antennas and Propagation,1998,46(4):551-558.
[10]LI Jing,LI Xiangjun.An Efficient Algorithm for Near Field RCS of Electrically Large Dynamic Targets[C]∥International Conference on Information Science and Technology,Nanjing:IEEE,2011:413.
[11]POULIGUEN P,DAMIENS J F,HEMON R,et al.RCS Computation in Near Field[C]∥International Conference Days on Diffraction,St Petersburg,Russia:IEEE,2006:252-265.
