0 引言
在对雷达进行方位标定时,很多时候采用的是方向盘反觇标定。由于方向盘本身就存在定北误差,因此方向盘反觇标定方法标定误差较大,且实施过程较为复杂,所需时间较长。标定误差的存在则会从源头上导致测量数据的不准确,大大降低了雷达测量数据的可信度和准确度,同时实施过程的复杂度也导致实际操作的不便。因此,寻找便捷高效的雷达方位标定方法具有极为重要的现实意义。
目前,在雷达偏差校正领域已有诸多研究[1-9]。文献[1]介绍了多雷达组网中对异步雷达数据的误差校正;文献[2]介绍了一种新的实时优化雷达偏差的方法,上述方法均是利用高精度雷达的数据对其他雷达的误差进行估计,并对雷达进行校正;文献[3]提出采用GPS数据对雷达进行误差校正,针对同一个目标3种不同精度传感器数据进行比较,进行雷达误差校正;文献[4-5]提出了ADS-B与雷达联合误差校正方法,该方法校正精度较高,但对标校利用的航迹选择有严苛的要求,工程应用较为困难,且算法复杂度高,实施性较差。
针对实际需求和现有算法的不足,本文提出了基于多直线融合的雷达误差标定算法,基于雷达侦察方位误差可以等同于雷达侦察航迹与实际航迹的夹角这一原则,该算法利用ADS-B数据集作为标定数据集,ADS-B数据集以GPS为基础,其定位精度完全满足雷达对标定数据的要求[4-5]。该算法首先利用航迹相似度匹配原则选择雷达与ADS-B获得的匹配数据集对;然后基于直线可信度判断算法对ADS-B数据集进行直线集拆解,与该直线集对应完成雷达数据集的拆解,进而计算直线对的夹角集;最后结合直线的可信度对夹角集进行统计平均,获得雷达标定误差角。该算法设计过程中充分考虑了航迹选择难度的问题,可以适用于所有雷达侦察和ADS-B航迹数据集。本文所采用的方法直接以电轴为基准,省去了光轴与电轴的对准,避免此类误差的出现,也避免了由于方向盘本身存在的定北误差而引起的雷达标定误差。同时,该算法也避免了标定过程对航迹选择的限制问题,大大提高了其使用过程的便捷性和适应性,非常有利于雷达的调试和战地标校。
1 传统雷达系统误差标定方法
如文献[1-5]所述,传统的雷达误差校正方法是利用最优估计方法对雷达斜距、方位和仰角进行全面校正。目前,基于ADS-B标定雷达系统误差的方法通常将ADS-B航迹数据(以下简称“ADS-B数据”)作为目标真值,转换到雷达坐标系下,在时间上与雷达侦察航迹数据(以下简称“雷达数据”)对准后求得斜距差、方位差及仰角差,再作平均,即估算出雷达测距、测方位及测仰角的系统误差。
设雷达数据点r=(ρr,φr,θr),航迹R=[r1,r2,…,rn];转换到雷达坐标系下得ADS-B数据点a=(ρa,φa,θa),A=[a1,a2,…,an]。则雷达侦察误差ε=[Δρ,Δφ,Δθ]可由下式计算:
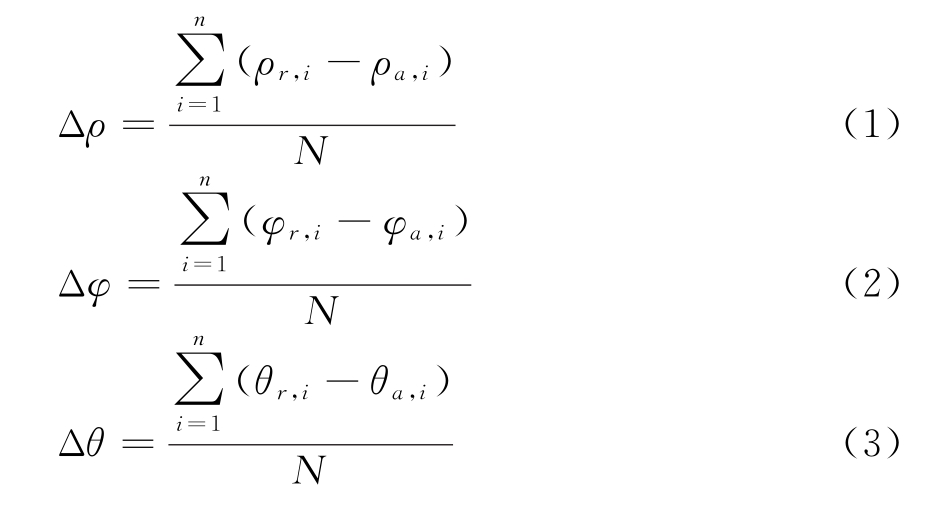
上述算法简单,计算方便,但对参与计算的航迹数据要求较高,要求雷达数据和ADS-B数据实现严格的时间同步,而在实际工程应用中不可能实现,导致上述算法的实用性较差。
在上述算法的基础上,文献[5]提出了另一种改进算法,该算法建立在选定特定航迹数据上,标定原则:1)对雷达径向飞行的直线航迹对雷达的侦察方位影响最小,利于标校雷达侦察方位误差;2)等距离飞行航迹(以雷达为中心进行圆周飞行)对雷达测距影响最小,利于标校雷达的测距误差。
基于上述两条原则,在雷达误差标校中首先选择该种类型的两种航迹目标,然后利用上述算法可以得到雷达的侦察误差值。该种算法的优点是不必考虑雷达数据与ADS-B数据严格同步的问题,同时可以得到较高的误差标定精度,其缺点是在实际工作中无法找到真正意义上的径向和圆周飞行航迹,导致算法几乎没有实用价值。
为改进上述两种算法存在的缺点,提出了基于多直线融合的雷达误差标定算法,该算法可以很好地克服上述两种算法的不足,在保证误差标定精度的基础上大大提高算法的实用性。
2 基于多直线融合的雷达误差标定算法
2.1 算法基础
如果飞行器以直线飞行,则雷达侦察到的航迹也为直线。设雷达侦察方位误差为Δφ,则雷达侦察到的航迹与飞行器的航迹夹角为Δφ,如图1所示。

图1 雷达侦察航迹与飞行器真实轨迹夹角
由上述基本原理可知,在雷达侦察方位误差标定中如果能找到完全直线飞行的航迹,只要通过直线拟合,并计算两直线间的夹角即可。但在实际应用中,基本上没有完全按直线飞行的目标,同时飞行器的飞行路线真值也难以获得,考虑到ADS-B数据的误差完全可以满足雷达标校误差的需求,下述算法利用ADS-B数据集作为标定航迹真值。同时对飞行器的航迹进行多段直线拟合,使其更逼近于飞行器的航迹,并分别计算各段直线的夹角,通过合理的加权计算,最终实现雷达侦察方位误差的标校。
2.2 直线拟合和航迹拆解
2.2.1 直线拟合
设某一待拟合的航迹段共有n个航迹点P=[(y1,x1),(y2,x2),…,(yn,xn)],直线拟合就是求取这些点的拟合直线y=ax+b,式中a,b为两个待定参数,a代表截距,b代表斜率。
利用最小二乘拟合算法,可得

此时计算偏差的平方和最小,其值为
2.2.2 航迹拆解
在实际应用中,飞机航迹一般意义上不是严格的一条直线,所以拆解飞机航迹为多段直线,L=[l1,l2,…,lk],对应偏差平方和E=[e1,e2,…,ek]。
定义:参与直线拟合最少点数为pmin,同时点集拟合的最大偏差平方和为emin。
则给定一点集P=[(y1,x1),(y2,x2),…,(yn,xn)],拟合成直线集L=[l1,l2,…,lk],其中k<n,算法过程如下:
1)在P点集中从拟合起始点选择p个点参与拟合,单直线首次选择取p=pmin;
2)分别利用式(4)、式(5)和式(6)计算对应的拟合直线的截距、斜率和方差e;
3)判断e是否小于emin,如果小于emin,则选择点数p=p+1,返回步骤1);如果e大于emin,并且p大于pmin,则该线段拟合点数为p-1,点集对应上次参与集合的点集,同时存储拟合结果,结果包括参与的点集、截距、斜率和偏差平方和,否则剔除该点集和拟合结果;
4)设置参与拟合的起始点,当剩余的点集小于pmin时,结束拆解算法,否则返回1)。
经过航迹拆解算法后,可得直线集L=[l1,l2,…,lk],E=[e1,e2,…,ek],对应点集P变为[P1,P2,…,Pk]。
2.3 航迹数据集粗处理(野值点剔除)
为了剔除雷达测量数据中的野值点以获取稳健的直线参数最佳估值a,b,本文采用门限过滤的方法进行野值点剔除:
1)利用整体最小二乘法计算a,b的初始值;
2)利用计算出的a,b值,根据下式计算出每个点至拟和直线的距离di:
3)计算标准偏差:
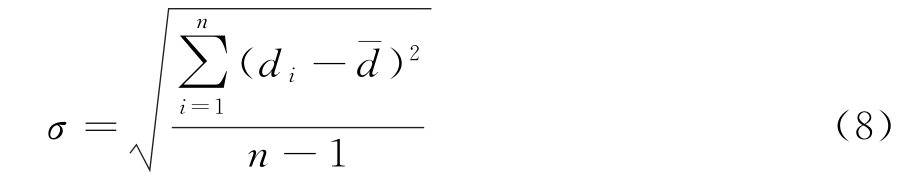
式中:
4)当di>2σ时,此点被认为是野值点,删除,反之,则保留;
5)利用所有保留下来的点重新计算a,b;
6)重复2)~5)步直到剩下所有点的di都在规定的阈值之内,即di都小于2倍的标准偏差时为止。
2.4 雷达标定误差校正流程
第一步:选择轨迹数据。由于ADS-B数据集远远密集于雷达侦察航迹数据,所以以雷达侦察航迹数据为基准选择参与计算的航迹,一般选择雷达侦察的航迹数据不少于雷达探测距离的1/2。根据雷达扫描速度推算出其应具有的点数Num,当雷达侦察航迹数据点数大于Num时,该航迹可以参与误差的标定,同时选择与雷达侦察航迹数据靠近的ADS-B航迹数据集。
第二步:坐标系转换。由于ADS-B数据的数据格式主要为经度、纬度和高度,雷达数据格式为斜距、方位角、高度,两种数据格式不一致,因此需要将数据转换到以雷达站为中心的(x,y,z)直角坐标系中,考虑到高度标定单独进行,则分别得到ADS-B和雷达航迹点集如下:
式中,雷达航迹点集数m小于ADS-B航迹点集数n。
第三步:轨迹匹配度判断。在考虑点集时间戳的情况下,Pa和Pr变为

以Pr为基础,依次取其点(yr,xr,tr),在Pa中寻找与tr最靠近的点(ya,xa,ta),计算它们的距离![]() 由此可得到
由此可得到![]() 时,dmin为定义的匹配阈值,两直线匹配,否则返回第一步。
时,dmin为定义的匹配阈值,两直线匹配,否则返回第一步。
第四步:航迹点集集合粗处理。利用基于门限过滤的野值点剔除方法对两个航迹数据粗处理,得到参与误差标定的两航迹点集集合Pa和Pr。
第五步:ADS-B航迹数据拆解。首先利用直线拟合和航迹拆解算法对Pa进行航迹拆解,得到直线集合La、偏差平方和Ea和点集变形Pa,La=[la1,la2,…,lak],Ea=[ea1,ea2,…,eak],Pa=[Pa1,Pa2,…,Pak]。
第六步:雷达航迹数据拆解。基于Pa=[Pa1,Pa2,…,Pak],从1到k分别找出雷达航迹数据Pr中与Pai对应分线段对应的航迹子集Pri,雷达航迹数据变为Pr=[Pr1,Pr2,…,Prk],分别计算雷达航迹数据的Lr和Er,Lr=[lr1,lr2,…,lrk],Er=[er1,er2,…,erk]。
第七步:分直线夹角计算。利用直线夹角公式求出相应分航迹段间的夹角集R=[θ1,θ2,…,θk],其中θi=arctan[(ari-aai)/(1+ariaai)]。
第八步:误差角计算。根据Er=[er1,er2,…,erk]计算直线夹角计算因子B=[βr1,βr2,…,βrk],![]()
第九步:雷达侦察系统误差角计算。按照上述步骤分别从ADS-B和雷达态势图中选取具有代表性的不同航向的多组对应航迹,计算雷达标定误差角,然后再求其统计平均值,最终得到雷达的标定误差。
3 结果分析
为了验证算法的性能,本文利用实测数据进行雷达标定误差校正的实验分析。在一段时间内同时利用雷达和ADS-B获取空中目标的空情数据,然后利用MATLAB软件按照前面所介绍的方法进行误差校正,并对数据进行分析,分别选取2条不同航迹进行处理,如图2所示。图中“+”线为ADS-B航迹数据,“∗”线为雷达原始航迹,“o”线为对雷达标定误差进行校正之后的航迹,“☆”线为利用ADS-B航迹高度代替雷达获取高度数据的航迹。
从两幅图中校正前后的航迹对比可以看出,如果不进行标定误差校正,在雷达跟踪的航迹与ADS-B获取的目标真实飞行轨迹存在很大差别,如果该雷达数据被使用将会产生严重后果。而经过本方法对雷达标定误差进行校正之后,该航迹与目标真实航迹基本一致。
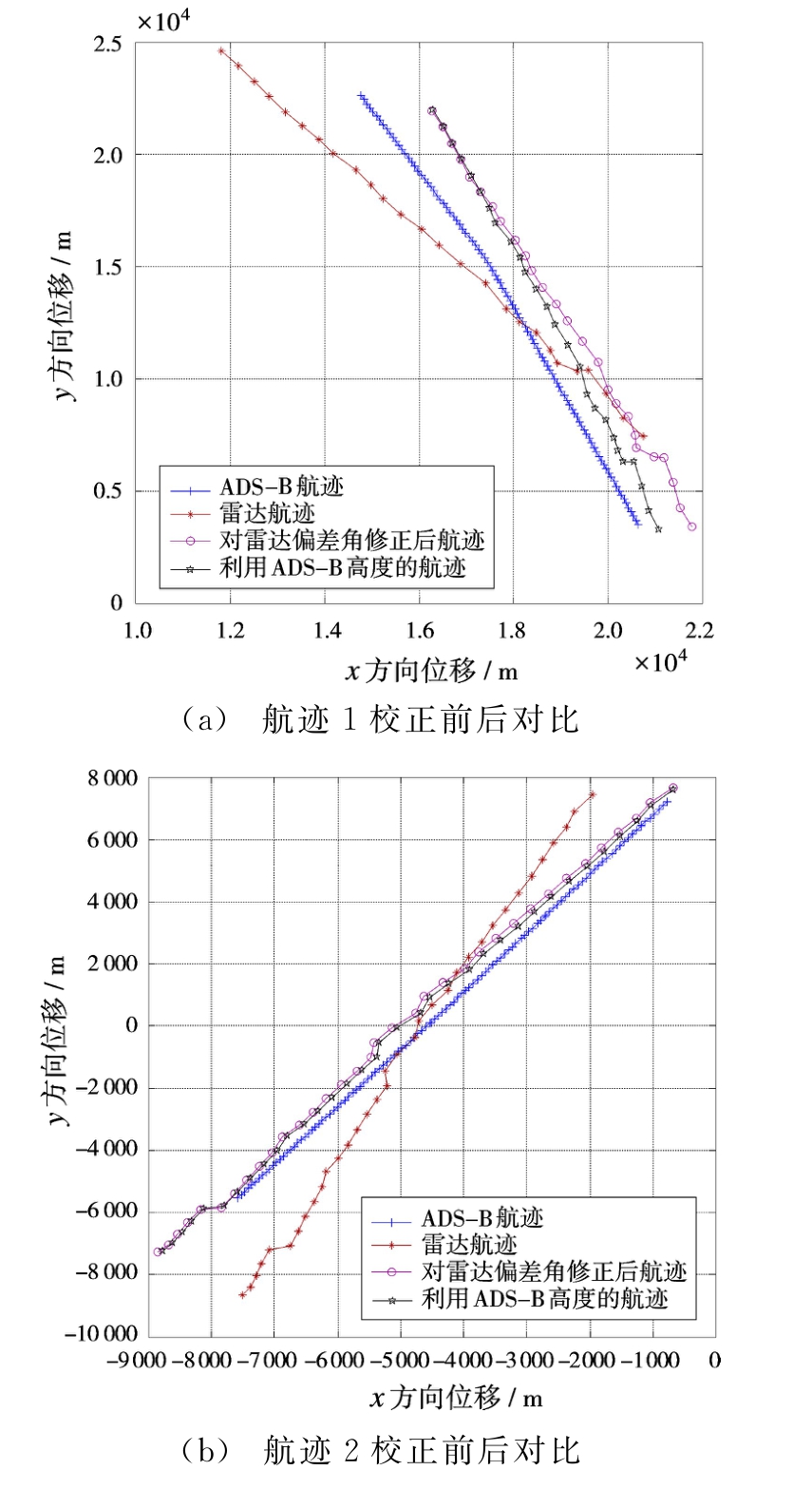
图2 航迹校正结果
4 结束语
针对利用方向盘对雷达进行反觇标定存在的标定误差,本文提出利用ADS-B航迹数据对该误差进行校正。由于ADS-B数据具有很高的精度和稳定性,在配置较好的天线情况下可以稳定持续接收到500 km以内的民航飞机航迹,因此以民航飞机(协作目标)的航迹数据作为研究对象和参考标准。本文利用ADS-B技术对空中目标精准定位、稳定跟踪的优点,提出了一种雷达标定误差校正新方法。该算法利用ADS-B数据集作为标校真值,采用基本的直线拟合方法,同时考虑到航迹对标校的影响,算法的实现既保证了误差标定的科学性,同时大大降低了算法的计算复杂度。通过实测数据进行定量分析证明,该种方法设计简单、操作方便,实施性很高,且对雷达标定误差的校正效果非常明显,非常适用于工程应用领域。该算法已在实际装备中得到了较好的应用,收到了很好的效果。
参考文献:
[1]RAFATI A,MOSHIRR B,SALAHSHOOR K,et al.Asynchronous Sensor Bias Estimation in Multisensory-Multitarget Systems[C]∥IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems,Heidelberg,Germany:IEEE,2006:402-407.
[2]PORTAS J A B,HERRERO J G,VELA G M.New Approach to Online Optimal Estimation of Multisensor Biases[J].IEE Proceedings:Radar,Sonar and Navigation,2004,151(1):31-40.
[3]PORTAS J A B,HERRERO J G,VELA G M.Radar Bias Correction Based on GPS Measurements for ATC Applications[J].IEE Proceedings:Radar,Sonar and Navigation,2002,149(3):137-144.
[4]HE You,ZHU Hongwei,TANG Xiaoming.Joint Systematic Error Estimation Algorithm for Radar and Automatic Dependent Surveillance Broadcasting[J].IET Radar,Sonar&Navigation,2013,7(4):361-370.
[5]张涛,唐小明,金林.ADS-B用于高精度雷达标定的方法[J].航空学报,2015,36(12):3947-3956.
[6]张青竹,张军,刘伟,等.民航空管应用ADS-B的关键问题分析[J].电子技术应用,2007,33(9):72-74.
[7]官云兰,周世健,张立亭,等.稳健整体最小二乘直线拟合[J].工程勘察,2012,40(2):60-62.
[8]RAJA ABDULLAH R S A,SALAH A A,ISMAIL A,et al.Experimental Investigation on Target Detection and Tracking in Passive Radar Using Long-Term Evolution Signal[J].IET Radar,Sonar&Navigation,2016,10(3):577-585.
[9]张海成,杨江平,王晗中.大型跟踪测量雷达的卫星标定方法研究[J].雷达科学与技术,2014,12(5):470-472.

