0 引言
超宽带穿墙雷达是一种针对建筑物内隐藏目标进行非侵入式探测的新型雷达，可以实现对建筑物内隐藏目标的探测、定位和成像[1-2]。建筑物布局成像技术是穿墙雷达在实际中的重要应用，在灾难救援与反恐巷战等领域具有重要应用价值。目前，对于建筑物布局成像方法已经有了深入研究，并提出了很多性能良好的成像方法。
文献[3]将墙体的连续块状物理特性与稀疏字典结合，利用压缩感知的方法反演出建筑物的内部结构，但求解过程涉及大型矩阵的操作，运算过程复杂且耗时。文献[4]利用Jump-Diffusion算法估计未知的建筑结构布局信息(墙体的数量、位置、长度和方位等参数)，但该方法得到的初始目标结构模型不佳且迭代过程需要解决电磁建模问题。对此，文献[5]利用建筑物布局的回波信号可以建模为基本散射体(平板、二面角和三面角)响应之和的思想，将匹配理论代价函数的最大似然估计分解为两步算法：用于检测建筑物布局的基本散射体的稀疏重建算法和更新散射体中心属性的局部代价函数的非线性最小化算法，这在一定程度上降低了计算复杂度，但运算速度仍然较慢。事实上，建筑物布局成像一般采用迭代方法，即从成像的初始估计去逐步逼近建筑物布局的真实结构[4-5]，通常是以BP算法作为成像的初始估计，然后经过二次处理获得墙体分布成像。文献[6]利用BP算法得到初次成像并对墙体图像进行连通域检测，然后根据墙体前后表面距离得到约束条件，最后在该约束下假定墙体参数并对其进行二次补偿成像，但该处理方法步骤繁琐、计算量大且成像耗时。
由以上分析可知，高效稳健的恢复算法仍然是建筑成像中的关键问题。若要实现对建筑物墙体目标连续清晰成像，并减少成像处理时间，在成像算法中就必须充分利用墙体的连续块状的物理特性，同时还要避免大型矩阵运算操作。本文以LASSO模型为基础，将墙体的连续块状的物理特性引入稀疏表示模型中，然后在优化最小化框架(MM)下构造稳健的优化目标函数[7]，进而推导墙体成像算法的迭代式。为了进一步提高运算速度，在迭代计算过程中利用墙体回波的时移特性把对字典的直接运算操作逐步分解成对时域信号与相关量的卷积运算，因而缩短了信号处理时间。与现有的成像方法对比，本文方法在实现墙体图像的连贯清晰成像的同时，也大幅提升了成像速度。
1 信号模型
在步进频体制MIMO天线阵列配置下，由J个发射阵元、K个接收阵元对建筑布局场景进行数据采集，得到的观测数据有M=J×K组，对步进频信号进行插零和补零处理，经IFFT变换得到N点时域脉冲序列r(nTs)，这里的Ts=1/(Δf(N-1))为采样时间间隔。此外，将成像场景的方位向和距离向分别划分为Gx和Gy个像素。令L=M×N，P=Gx×Gy，根据文献[3]可得墙体回波数据稀疏表示模型为
z=ψσ+e
(1)
式中，z∈CL×1为观测数据向量，e∈CL×1为加性噪声向量，σ∈CP×1为场景墙体的后向散射系数向量，ψ∈CL×P为字典矩阵。由于墙体在整个成像空间具有稀疏性，所以基于式(1)的模型可将其成像视为稀疏线性回归问题，其可以使用LASSO模型估计σ[8]，但这种方法得到的墙体图像轮廓不模糊且不连贯。很显然，墙体是具有连续块状特性的扩展目标，所以将这种特性与稀疏线性回归模型相结合，可以有效解决上述问题。将像素网格在方位向的单个像素处理转化为对像素块处理，如图1(a)所示。假设在第y个距离向，将对应的方位向划分为S=Gx/lx个像素块，每个像素块包含lx个像素网格，则该距离向上像素σ与像素块β的关系可以表示为
β(s)(y)=
1,2,…,Gx,y=1,2,…,Gy
(2)
式中，F[s]表示第s个像素块(s=1,2,3,…,S)。依据式(2)，则整个成像区域被划分为B=S×Gy(b=1,2,3,…,B)个像素块，用β表示为
β=[β(1)(1)…β(S)(1)β(1)(2)…β(S)(2)…
β(1)(Gy)…β(S)(Gy)]T
(3)
这样，β与σ的关系可以通过一个块特性矩阵A来表示，即
σ=Aβ
(4)
这里的A有P行B列，且具有块特性，例如A的第b列位置(b-1)×lx+1～b×lx的元素为1，其他为0，如图1(b)所示。
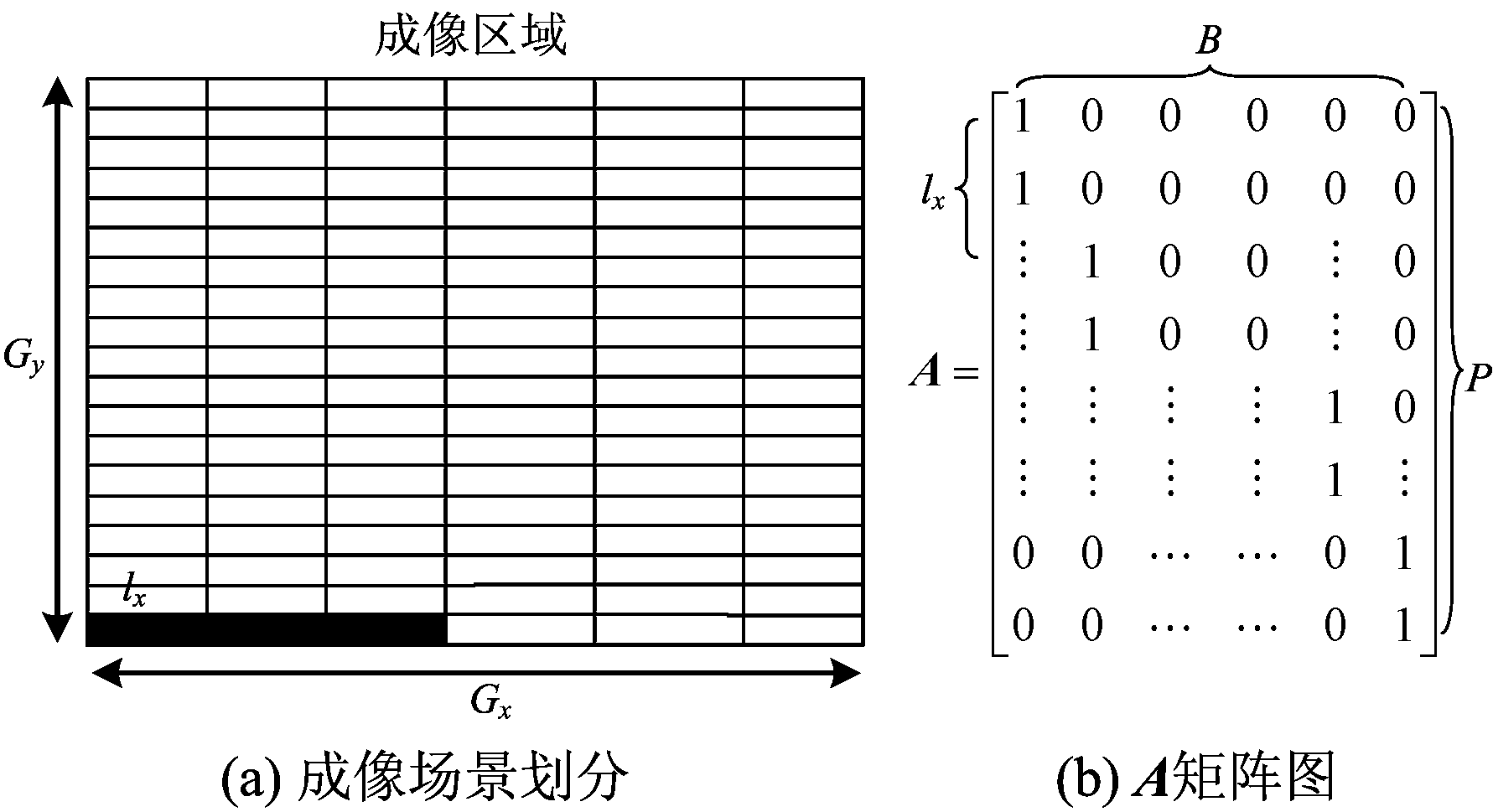
图1 像素网格划分与块特性矩阵
根据式(4)和式(1)，新的字典矩阵Φ与ψ,A的关系为Φ=ψA，此时Φ∈CL×B，对应的墙体成像的LASSO模型的目标函数表示为
(5)
可以通过优化最小化技术(MM)来最小化LASSO模型的目标函数[9-10]，进而估计出稀疏系数。
2 优化最小化框架下的成像算法
2.1 算法描述
由以上分析可以看出，求解式(5)的关键在于目标函数的优化函数。根据文献[11]的MM方法，可得其优化目标函数为
L1(β,β(i))=
(6)
式中，zl表示观测向量z中的第l个元素，Φlb表示Φ中第l行第b列的元素，clb为1/rl(Φlb≠0，rl为Φ中第l行的非零元素个数之和
表示第i次迭代后β中第b个像素块的值，
表示向量[Φβ]中的第l个元素。对式(6)关于βb求偏导，并令其为0，可得到第b个像素块的值为
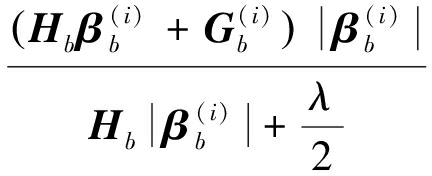
b=1,2,3,…,B
(7)
式中，
可以看出，
的计算由Hb,Gb决定，而Hb,Gb的计算又与Φ有关，但因Φ的维数很大，所以关于的迭代过程不仅需要很大的存储空间，而且需要很大的计算量。参考文献[11]的方法，利用Φ结构中元素的时移特性来避免针对Φ的直接构造，将其用回波信号直接表示，并结合卷积思想修正迭代公式。因为Φ=ψA，所以Φ的运算与ψ密切相关。在雷达成像过程中，ψ描述了电磁波传播过程中的时延信息和衰减。用Λm表示第m组收发阵元到所有网格点的衰减系数向量，Λm=diag(αm(1),αm(2),…,αm(P))，这里的αm(p)表示到第p个像素网格的分量。另外，用Dm表示第m组收发阵元下包含墙体回波时延信息的矩阵，它的第n行第p列元素为r(n,τm(p))=r(nTs-τm(p))，其中τm(p)为收发阵元位置到像素网格点的时延。为了方便后续算法的处理，对其离散取整为nm(p)=round(τm(p)/Ts)。综合以上分析可知，第m组收发阵元的ψm=[DmΛm]，而所有收发阵元的
把ψ和A的每一元素代入式(7)的
展开可得
(8)
式中，Kb={(b-1)lx+1∶blx|b=1,2,3,…,B}表示第b个像素块对应的像素位置集合，αm(ub)，τm(ub)分别表示第m组收发阵元下第b个像素块的衰减系数和时延集合，
τm(ub))。令
则式(8)变为
(9)
式中,
令ω[n]=p(nTs)，由于r(nTs)是对称的，所以ω[n-k]=ω[k-n]。利用卷积，式(9)中的
可写为
(10)
因为
而zm[n]已知，所以
的计算由
决定，而
的计算与τm(ub)有关。由于{τm(p)∈τm(ub)|p∈ub}，将τm(p)离散取整为nm(p)，根据哈希表原理，从nmin到nmax中找出{k:τm(p)∈τm(ub)|p∈ub}对应的值，利用卷积对进行处理，可得
(qm·ω)[n]
(11)
式中,
令
则qm[k]可重新定义为
那么qm[k]的值就是满足k=nm(Kb)时累加集合
中对应的元素。从以上分析可以看出，对大矩阵Φ的直接操作逐步分解成对时域信号与相关量的卷积运算，因此只需要对qm[k]作简单统计运算，并结合式(9)～式(11)就可以以较快的速度得到
由于Hb和
具有类似的结构，所以以同样的方式对Hb进行推导，可得
Hb=
(12)
式中，γm[n]定义为字典矩阵Φ中第n行的非零元素个数之和，h[n]=p2(nTs)。可以看出，只要计算出γm就可以求出Hb。由于不能预先通过构造矩阵Φ来计算γm，不能通过统计的方法得到γm，所以必须要根据信号时移特性进行处理。如果存在一个正整数C使得C≪N，那么具有N个采样点的r(nTs)在满足|n|<C时，其值为零[11]。由此可以推出，当满足|nTs-τm(p)|≤CTs时，Φm中的第(n,p)个元素不为0，对其取整后为|n-nm(p)|≤C。同时，时延nm(p)还要满足0≤nm(p)≤N-1。综上可知，当时延nm(p)满足max(0,n-C)≤nm(p)≤min(n+C,N-1)时，才能保证Φm中的第(n,p)个元素不为0。令
其中
和
分别表示如下：
进一步，将γm[n]表示为
(13)
式中，
{b=1,2,…,B∶k=nm(Kb)}，而|Sk|表示集合中满足条件的元素个数。
2.2 算法实现
综上所述，将BP成像结果σ作为解的初始值，求出对应的β作为迭代条件代入迭代公式中，在第i次迭代过程中，分别构造m组收发阵元下对应第b个像素块的
和Hm(b)，然后根据式(9)和式(12)得到
和Hb，最后代入到式(7)迭代计算。通过迭代求解，满足终止条件得到β后反向求出得到最终的σ，即成像结果。算法流程如表1所示。
表1 算法流程
3 实验结果与分析
为验证算法性能，使用实验室搭建的多通道雷达系统对两个真实场景进行实验探测。使用6个超宽带喇叭天线组成非均匀线性阵列，天线孔径合成为2 m，且天线阵列中心离地1.1 m，系统发射1～2 GHz的步进频率信号，步进频率5 MHz，步进点数N=201。实验场景如图2所示，图2(a)所示的场景是一个长5 m、宽4 m、墙体厚度0.2 m的半封闭房间，其场景示意图如图2(b)所示，实验系统摆放在墙体正中位置，天线阵列距离墙体0.5 m进行探测。图2(c)所示的场景是一个包含门窗的小房间，其长宽均为2.4 m，门宽0.8 m，窗户宽度1 m且距离地面1.3 m，其场景示意图如图2(d)所示，由于实验场景限制，实验系统摆放在房间的偏左位置，天线阵列距前墙1.5 m进行测量。
图2 实验场景与示意图
将系统采集的回波数据经去噪、杂波相消和自动增益控制等信号处理得到的目标回波，运用本文方法对上述实验数据分别进行成像，成像结果如图3所示。从图3(a)和图3(b)可以看出，本文方法得到的墙体边缘连贯清晰，墙体轮廓特征较强，且图像杂波较少。为了看出算法的收敛情况，图3(c)给出了不同场景成像结果的一阶差分均值法[12](Mean of First Order Difference，MFOD)与迭代关系的变化图。从图3(c)可以看出，随着迭代增加，MFOD的值逐渐减小，最后趋于平缓，说明图像边缘轮廓变化趋于稳定，图像逐渐连贯清晰，说明随迭代次数增加，算法收敛。采用文献[8]和本文方法进行成像比较，由于文献[8]采用的是L1正则化方法，在LASSO模型中并未将墙体的特性加以考虑，从图3(d)和图3(e)可以看出，文献[8]方法得到成像墙体是离散的点，轮廓特性不明显，聚焦性较差，并且在前后墙之间出现较多的杂波。
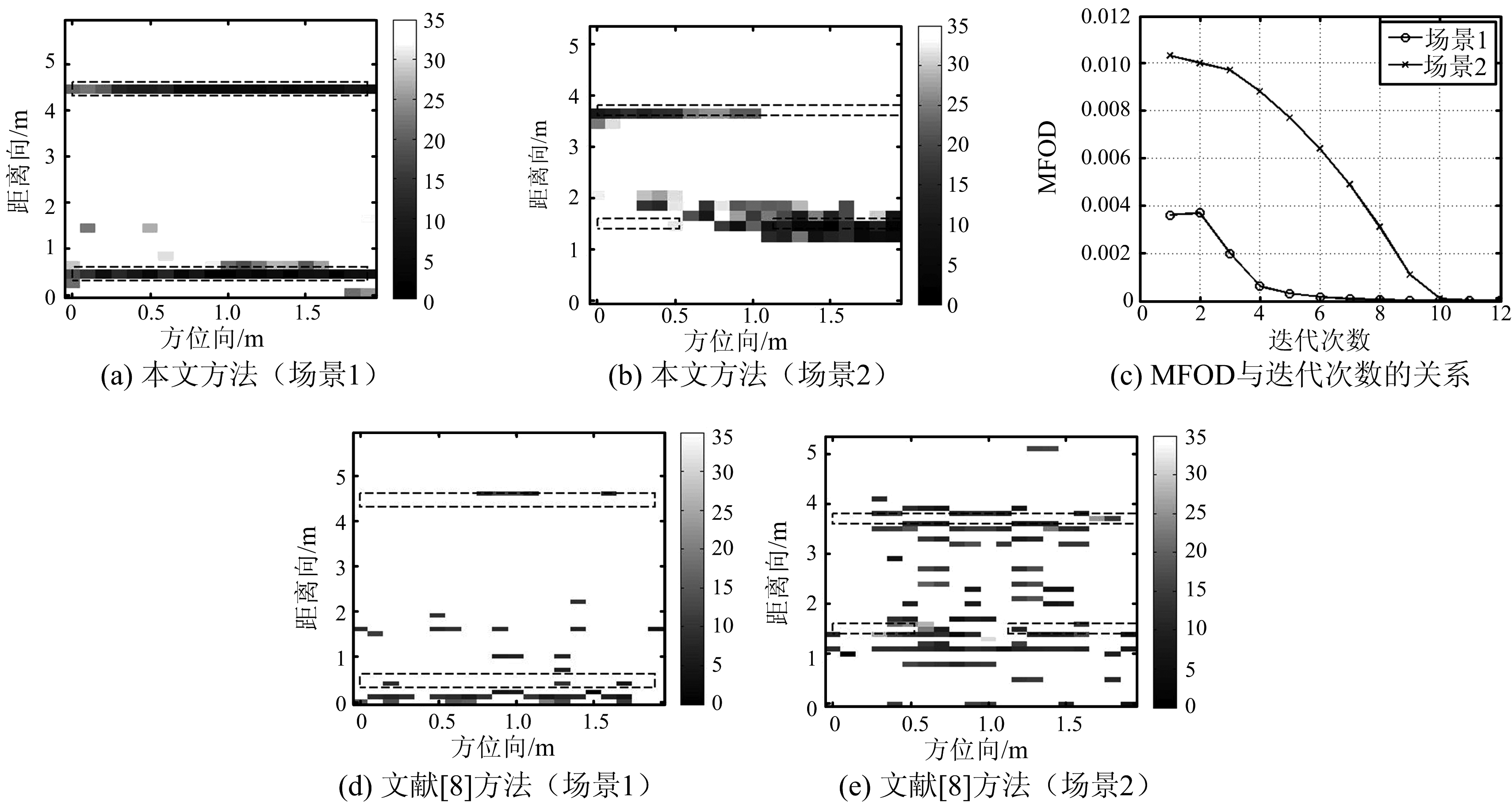
图3 成像结果与分析
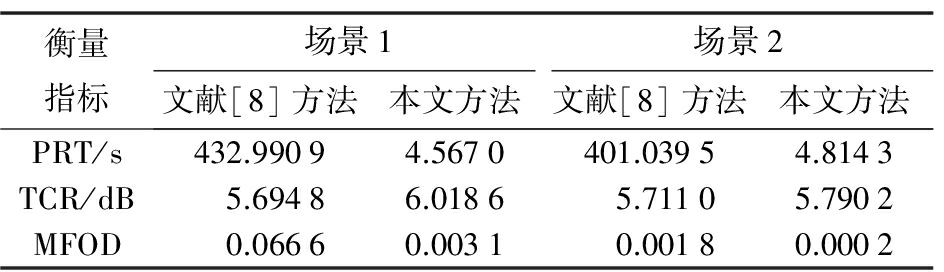
为了直观比较文献[8]方法和本文方法的成像性能，对两个场景成像效果进行定量分析，分别利用程序运行时间(Program Running Time，PRT)、目标杂波比[13](Target-to-Clutter Ratio，TCR)以及一阶差分均值法(MFOD)评估两种算法的性能。比较结果如表2所示，从中可以看出，本文方法在两个场景中的PRT值比文献[8]方法小了约100倍，说明算法运行速度得到了极大提高。TCR用来评估墙体成像的聚焦性，两个场景中本文方法得到的TCR的值都较大，说明本文方法成像的聚焦性能较好。此外，两个场景中的MFOD值都几乎提升了一个数量级，说明本文方法得到的墙体图像边缘轮廓明显、区域平滑。
表2 算法性能比较
4 结束语
将墙体连续块状的物理特性引入信号模型，解决了墙体轮廓模糊、边缘不连贯问题，实现了建筑墙体连续成像。利用MM构造稳健的优化函数，同时利用时域信号时移特性构建卷积，避免构造成像字典形成的大矩阵运算，从而较大幅度上减少算法处理时间。通过对两个不同场景的实验加以验证。在下一步工作中，围绕对未知建筑物墙体分布中时延精确补偿的问题进行研究，从而满足穿墙建筑物布局成像的实际要求。
参考文献：
[1] LIU Jiangang, KONG Lingjiang, YANG Xiaobo, et al. Refraction Angle Approximation Algorithm for Wall Compensation in TWRI[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(7):943-946.
[2] YEKTAKHAH B, SARABANDI K. All-Directions Through-the-Wall Radar Imaging Using a Small Number of Moving Transceivers[J]. IEEE Trans on Geoscience and Remote Sensing,2016,54(11):6415-6428.
[3] LAGUNAS E, AMIN M G, AHMAD F, et al. Determining Building Interior Structures Using Compressive Sensing[J]. Journal of Electronic Imaging, 2013, 22(2):381-388.
[4] NIKOLIC M M, ORTNER M, NEHORAI A, et al. An Approach to Estimating Building Layouts Using Radar and Jump-Diffusion Algorithm[J]. IEEE Trans on Antennas and Propagation, 2009, 57(3):768-776.
[5] ERTIN E, MOSES R L. Through-the-Wall SAR Attributed Scattering Center Feature Estimation[J]. IEEE Trans on Geoscience and Remote Sensing, 2009, 47(5):1338-1348.
[6] 姚雪,孔令讲,苏玲霞,等. 一种适用于穿墙雷达建筑布局成像算法[J]. 雷达科学与技术, 2015, 13(1):27-32.
YAO Xue, KONG Lingjiang, SU Lingxia, et al. A New Algorithm for Through-Wall-Radar Building Layout Imaging[J]. Radar Science and Technology, 2015, 13(1):27-32.(in Chinese)
[7] HUNTER D R, LANGE K. A Tutorial on MM Algorithms[J]. The American Statistician, 2004, 58 (1):30-37.
[8] OGWORONJO H C, ANDERSON J M M, NDOYE M, et al. Anl1-Regularized Least Squares Algorithm for Reconstructing Step-Frequency Ground Penetrating Radar Images[C]∥IEEE Radar Conference, Philadelphia, PA: IEEE, 2016:17-20.
[9] YU D, WON J H, LEE T, et al. High-Dimensional Fused Lasso Regression Using Majorization-Minimization and Parallel Processing[J]. Journal of Computational and Graphical Statistics, 2015, 24(1):121-153.
[10] YANG Yi, ZOU Hui. A Coordinate Majorization Descent Algorithm forl1Penalized Learning[J]. Journal of Statistical Computation and Simulation, 2014, 84(1):84-95.
[11] NDOYE M, ANDERSON J M M, GREENE D J. An MM-Based Algorithm forl1-Regularized Least-Squares Estimation with an Application to Ground Penetrating Radar Image Reconstruction[J]. IEEE Trans on Image Processing, 2016, 25(5):2206-2221.
[12] 晋良念,申文婷,钱玉彬,等. 组合字典下超宽带穿墙雷达自适应稀疏成像方法[J]. 电子与信息学报, 2016, 38(5):1047-1054.
[13] TIVIVE F H C, BOUZERDOUM A, AMIN M G. A Subspace Projection Approach for Wall Clutter Mitigation in Through-the-Wall Radar Imaging[J]. IEEE Trans on Geoscience and Remote Sensing, 2015, 53(4):2108-2122.
