0 引言
机载雷达前视成像在复杂地形回避、自主着陆和精确制导等方面具有重要意义。一般情况下,机载雷达在对地面目标成像时,常常采用多普勒波束锐化(DBS)技术或合成孔径雷达(SAR)技术,但当目标位于前视位置时,等距离线与等多普勒线非正交,上述方法失效,无法实现前视成像[1-2]。
目前,解决机载雷达前视盲区问题的方法主要有实波束成像技术[3-4]、单脉冲成像技术[5]、双基地SAR成像技术[6]等。实波束成像技术受天线波束宽度和作用距离的限制,难以得到较高的方位分辨率。单脉冲成像方法将单脉冲测角和波束扫描相结合来提高图像方位分辨率,但当一个波束内同时存在多个目标时,无法精确区分目标。双基地SAR也能实现前视成像,但需要解决系统的同步问题并且不同的空间几何关系对成像算法的要求也不同,难以找到通用的成像算法。可见,现有的雷达前视成像技术,虽然有各自的优点,但在实际应用时面临着多目标分辨率差或计算复杂度高等难题。
本文将阵列信号处理中的超分辨技术引入前视成像中。相较于传统单通道雷达,阵列接收系统具备更高的空域自由度,采用相应的超分辨信号处理技术能获得更高的空间分辨率,故可用于前视条件下雷达成像方位分辨率的改善。
然而,现有的超分辨算法,如MUSIC算法[7-8]等,需要采用独立样本实现接收信号自相关矩阵的估计,在实际处理中,往往选取接收信号相邻距离门数据作为训练样本。但在雷达成像模式下,不同距离门所对应的场景不同,故采用相邻距离门估计必然会导致距离分辨率的损失。此时,需考虑采用相邻脉冲信号作为训练样本实现某距离-脉冲单元相关矩阵的估计,但在一般条件下,相邻脉冲间地面回波信号相关性极强。因此,采用上述思路实现前视成像时,面临的一个关键问题即为相干信源的空间谱估计问题。
基于上述分析,本文在解相干处理的基础上,提出了一种基于改进MUSIC算法的阵列雷达前视成像算法。首先利用各通道回波数据样本估计协方差,对所得协方差进行修正以及空间平滑去相干,随后采用MUSIC算法估计空间谱,再根据载机运动、波束扫描等参数,将每个距离门-脉冲的谱曲线进行累积,最终获得前视图像。
1 阵列雷达信号模型
阵列雷达是将多个天线单元按照一定规律排列,并通过施加激励来获得预设辐射结果的一类特殊天线。由于接收的回波信号的性质只与其阵元的相对位置有关,按照天线单元的排列方式,可将其分为均匀线阵、圆阵、面阵和任意阵列。本文以均匀线阵为例,假设雷达接收天线阵元是全向辐射和等增益的。
图1给出了简化的二维机载阵列雷达前视成像几何模型。距离向的分辨可以通过脉冲压缩来实现,本文要解决的问题是方位分辨,也就是阵列信号处理中的超分辨空间谱估计。
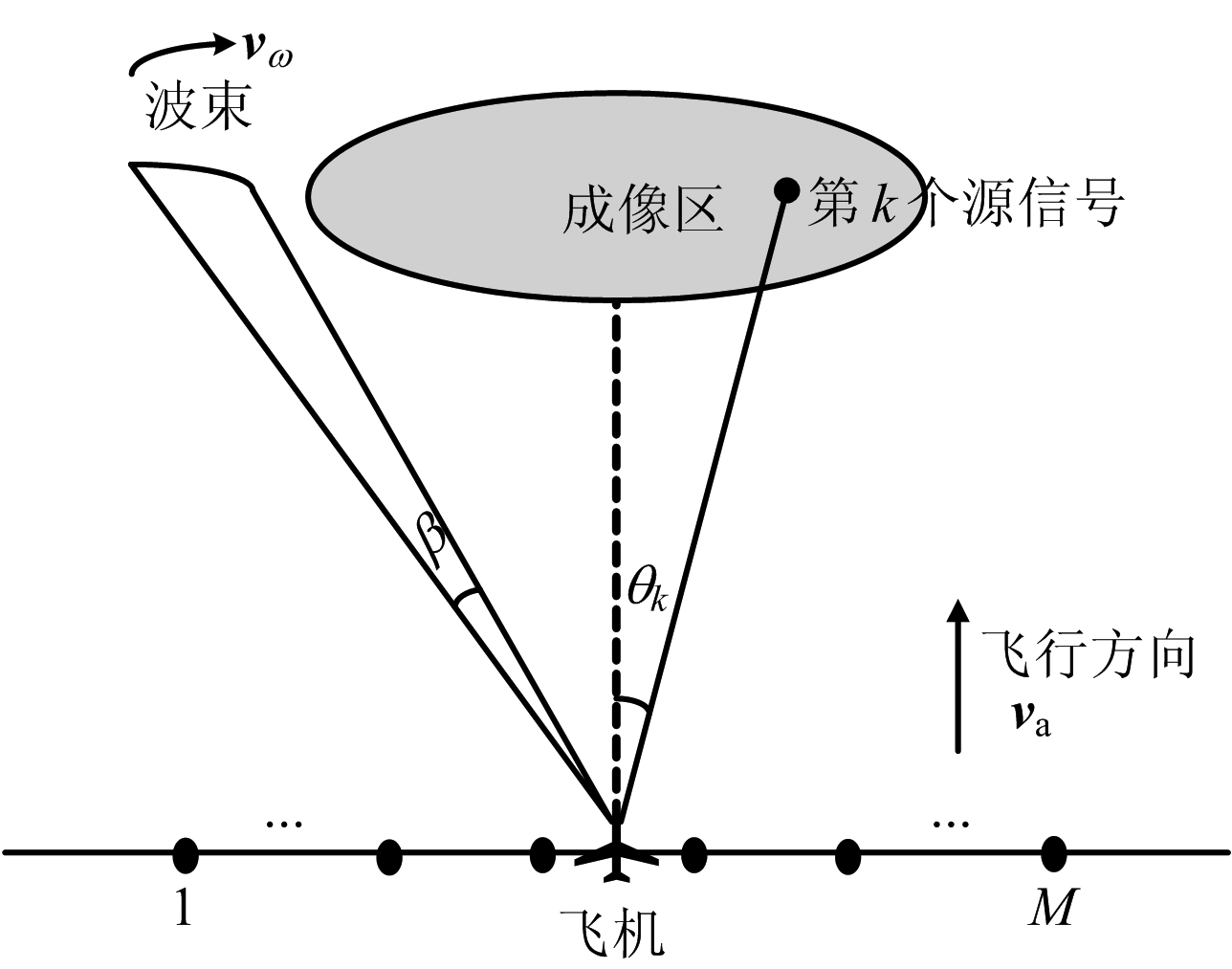
图1 阵列雷达前视成像几何模型
假设成像区有K个窄带目标信号,其波达方位角分别为θ1,θ2,…,θK。等间距直线阵由相同的M个阵元构成,每个阵元的位置为0,d1,…,dM-1,且M>K,则第m个阵元的输出为
(1)
式中,t=1,2,…,L,L为时间采样数,sk(t)为接收到的第k个源信号,nm(t)为阵元上的高斯白噪声,θk为第k个源信号的波达方位角,λ为信号波长。定义θk的导引矢量为
(2)
那么,阵列输出信号可用如下矩阵形式表示:
X(t)=A(θ)S(t)+N(t)
(3)
由式(3)知,阵列协方差矩阵可表示为
R=E[XXH]=AE[SSH]AH+E[NNH]=
ARSAH+RN
(4)
式中,RS为信号协方差矩阵,RN为噪声协方差矩阵。由于噪声服从零均值高斯分布,假设功率为σ2,有下式成立:
R=ARSAH+RN=ARSAH+σ2I
(5)
式(5)的协方差矩阵R在实际应用中无法直接得到,一般情况下,数据协方差矩阵R可用样本协方差矩阵![]() 代替,即
代替,即
(6)
可以证明![]() 是R的最大似然估计,当采样值L→∞时,两者是一致的。
是R的最大似然估计,当采样值L→∞时,两者是一致的。
当信源互不相关时,MUSIC算法可以有效分辨来波方向,获得超分辨空间谱。然而,若将该方法直接用于雷达成像中(即对距离脉冲压缩后每个距离门的多通道数据采用MUSIC算法获取超分辨空间谱)却面临很大困难。这是由于该算法需要独立同分布样本实现协方差矩阵的精确估计,而在以往处理中,往往选取相邻距离门数据作为训练样本完成估计。而在成像处理中,由于不同距离门地面场景不同,故在获取某个距离门空间谱(即方位图像)时,训练样本无法从相邻距离门获取。在这种条件下,只能考虑在慢时间域选取训练样本,即选用同距离相邻脉冲的信号作为样本估计协方差矩阵[9]。然而,地面散射点回波信号在不同脉冲间相关性极强,导致采用该样本估计所得协方差矩阵RS并非对角阵,即秩rank(RS)<K,此时,传统MUSIC算法中信源不相干的前提无法满足,直接导致算法失效。
2 改进的MUSIC算法
由上一节可知,阵元回波相邻脉冲相关性极强,采用该样本估计所得协方差矩阵的秩亏损。这时,传统的MUSIC算法失效,所以需对其作出改进。在这种前提下,本文先对阵列协方差矩阵进行修正和空间平滑,再用MUSIC算法进行超分辨空间谱估计并最终实现机载阵列雷达的前视成像[10-11]。
2.1 协方差矩阵的修正
通常情况下,![]() 是Hermite矩阵而不是Toeplitz矩阵,对
是Hermite矩阵而不是Toeplitz矩阵,对![]() 进行修正,得到Toeplitz的协方差矩阵的估计值RX,使信号协方差的秩恢复为rank(RX)=K,从而能有效地估计出信号的超分辨空间谱。
进行修正,得到Toeplitz的协方差矩阵的估计值RX,使信号协方差的秩恢复为rank(RX)=K,从而能有效地估计出信号的超分辨空间谱。
令Iv为M×M维反向单位矩阵,即

(7)
且令
(8)
式中,![]() 为
为![]() 的共轭,RX为Hermite的Toeplitz矩阵,且RX为
的共轭,RX为Hermite的Toeplitz矩阵,且RX为![]() 的无偏估计。
的无偏估计。
2.2 空间平滑技术
空间平滑是处理相干或强相关信号的有效办法,一般来说,空间平滑只适用于均匀线阵[12]。在MUSIC算法之前先用空间平滑技术对协方差矩阵进行预处理,能得到更加精准的超分辨空间谱。其原理是以滑动方式将原线阵分成若干个重合子阵,并对各子阵协方差矩阵加权取平均代替原来意义上的协方差矩阵。
如图2所示,通过滑动方式,M元的等距线阵被分成P个子阵,每个子阵阵元数为N,其中N=M-P+1。定义第p个前向子阵的输出为
![]() [xp(t),xp+1(t),…,xp+N-1(t)]T=
[xp(t),xp+1(t),…,xp+N-1(t)]T=
AMDp-1s(t)+np(t)
(9)
式中,AM为N×K维的方向矩阵,其列为N维的导引矢量aM(θi),i=1,2,…,K。
(10)
所以第p个前向子阵的协方差矩阵为
![]()
![]()
(11)
定义前向空间平滑后协方差矩阵为
(12)
同样,后向空间平滑的协方差矩阵为
(13)
式中,Rb为Rf的共轭倒序阵,它们服从共轭倒序不变性。因此,双向空间平滑后的矩阵可以表示为
(14)
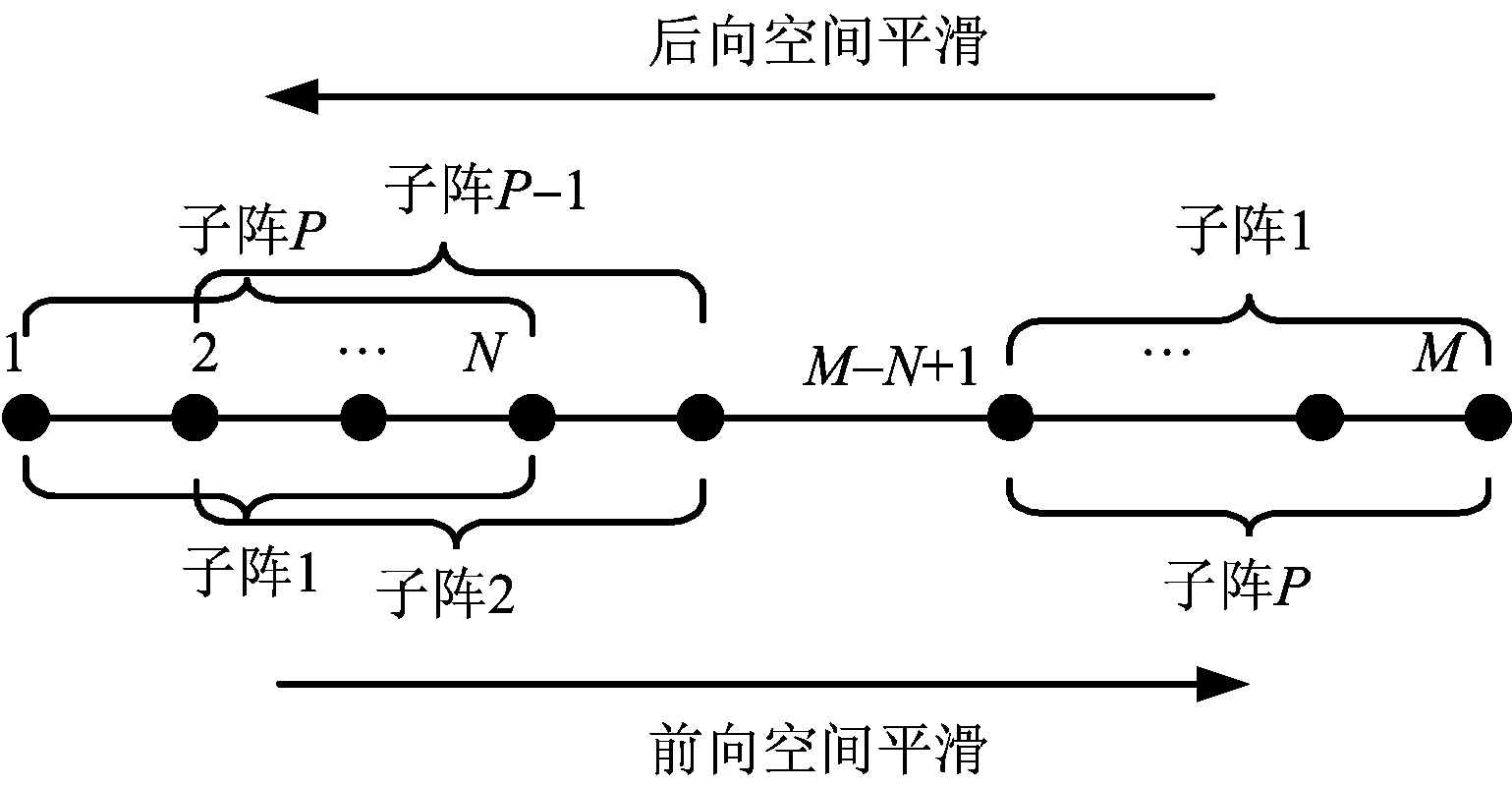
图2 空间平滑示意图
当子阵阵元数N≥K,子阵数P≥K时,单向空间平滑后协方差矩阵满秩;当2P≥K时,双向空间平滑后协方差矩阵满秩。单向的空间平滑需要K个子阵能使协方差恢复成满秩,而双向平滑只需要K/2个子阵就能使协方差矩阵恢复成满秩。当有K个信号源,每个子阵的阵元数N= K+1时,双向平滑只需要M=1.5K个阵元,而单向平滑则至少需要M=2K个阵元。也就是说,在阵元数相同的情况下,双向平滑比单向平滑能分辨更多的信号源。本文采用的是双向空间平滑。
MUSIC算法在确定噪声子空间时需要提前知道信源数,而在实际应用中,信源数往往是未知的,所用要先进行信源估计[13]。根据特征空间的分析可知,数据协方差矩阵的大特征值数目对应于信源数目,其他小特征值相等,所以可以根据大特征值的数目来确定信源数,但在实际中,由于快拍数、信噪比等的影响,根本无法明显区分大小特征值。因此,本文采用盖氏圆方法,该方法不需要知道特征值的大小就能估计出信源数。
在对样本协方差矩阵进行修正以及空间平滑后得到协方差矩阵R′,之后估计信源数,再对R′进行分解,有
[N,S,U]=SVD(R′)
(15)
取UN=N(:,K+1:N)为噪声子空间,然后再用MUSIC算法进行超分辨空间谱估计。
3 基于超分辨技术的阵列雷达前视成像算法
在上文研究的基础上,本节提出了基于超分辨技术的阵列雷达前视成像算法,该算法通过多通道接收信号,并采用改进的MUSIC算法对回波信号逐距离门、脉冲进行空间谱估计,然后根据平台运动参数、天线扫描参数在距离-方位域实现信号积累,以提高成像区特征目标的方位精度的方式提高整个图像的方位分辨率。
综上所述,基于超分辨技术的阵列雷达前视成像算法流程图如图3所示,算法主要步骤如下:
1)对阵列接收的数据进行脉冲压缩处理,并进行距离徙动校正;
2)逐距离门-脉冲处理数据,首先由相邻脉冲样本估计协方差矩阵![]() 并对其进行修正及平滑处理得到维数为N×N的协方差矩阵R′;
并对其进行修正及平滑处理得到维数为N×N的协方差矩阵R′;
3)利用盖氏圆方法估计信源数K,并对R′进行特征分解,以N-K个小特征值对应特征向量组成噪声子空间;
4)搜索信号来波方向θ,计算该距离门-脉冲回波对应的空间谱曲线;
5)根据波束扫描等参数,将每个距离门的谱曲线进行累积,最终形成距离-方位图像。
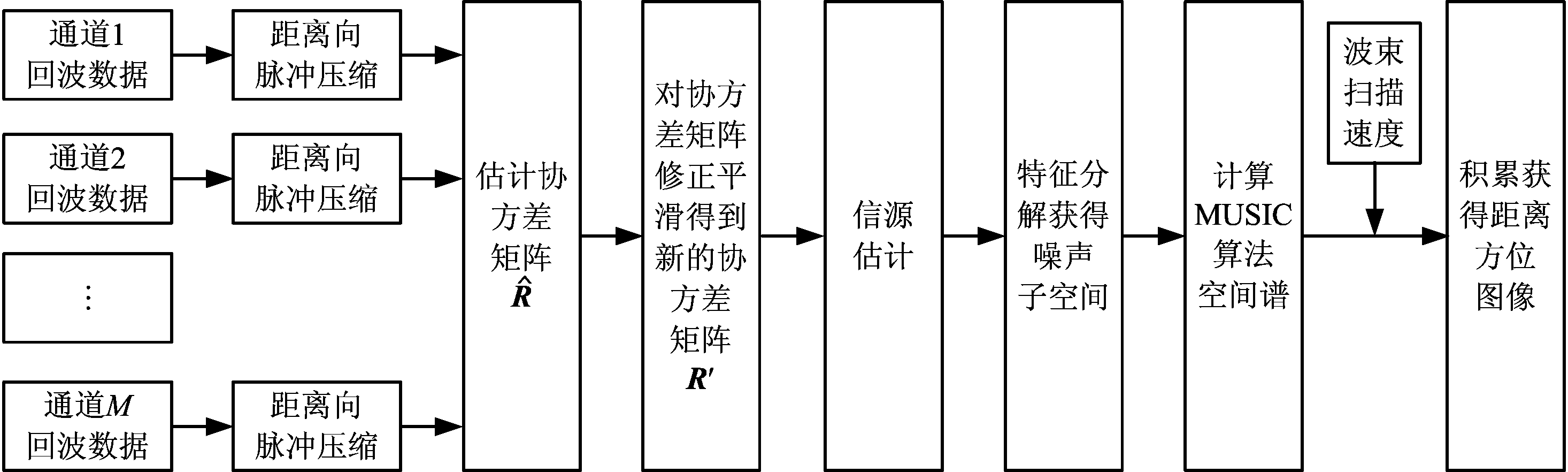
图3 超分辨成像算法信号处理流程图
4 仿真及实测数据处理结果
为了验证本文所提基于超分辨技术的阵列雷达前视成像算法的有效性,本节分别进行了点目标以及场景的前视成像仿真实验。
在点目标仿真实验中,在成像区放置了5个点目标,R=[900 m,900 m,900 m,700 m,1 100 m]和θ=[-1°,0°,1°,0°,0°](相对于飞行方向)分别为距离和方位角度,可见,3个点位于同一距离不同方位角度上。其余仿真参数(点目标)如表1所示。图4给出了本文方法的成像结果,图5给出了同一距离门3个点目标的方位剖面图。可以看出,同一距离门的3个目标成像处理后分别位于-1°,0°和1°位置,证明了该方法能够有效地分辨主瓣波束内多个目标,为机载雷达前视成像提供了可行性。
为了进一步对算法的成像效果进行验证,选用了一幅高分辨率SAR图像作为地面仿真场景,由该图像仿真生成阵列雷达回波信号并进行成像处理。仿真场景为机场跑道区域,对应的SAR图像如图6(a)所示,仿真部分参数如表1(场景)所示。本文方法成像结果如图6(b)所示,可见,成像结果中机场跑道分辨明显,强散射目标清晰可见,前视成像效果较好。
表1 仿真实验系统参数列表
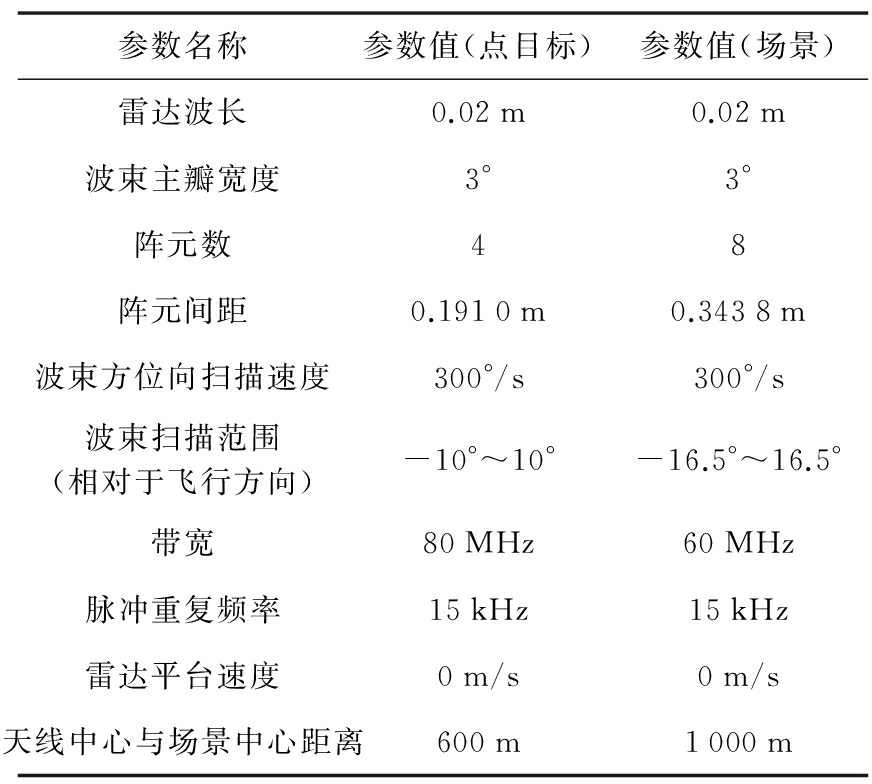
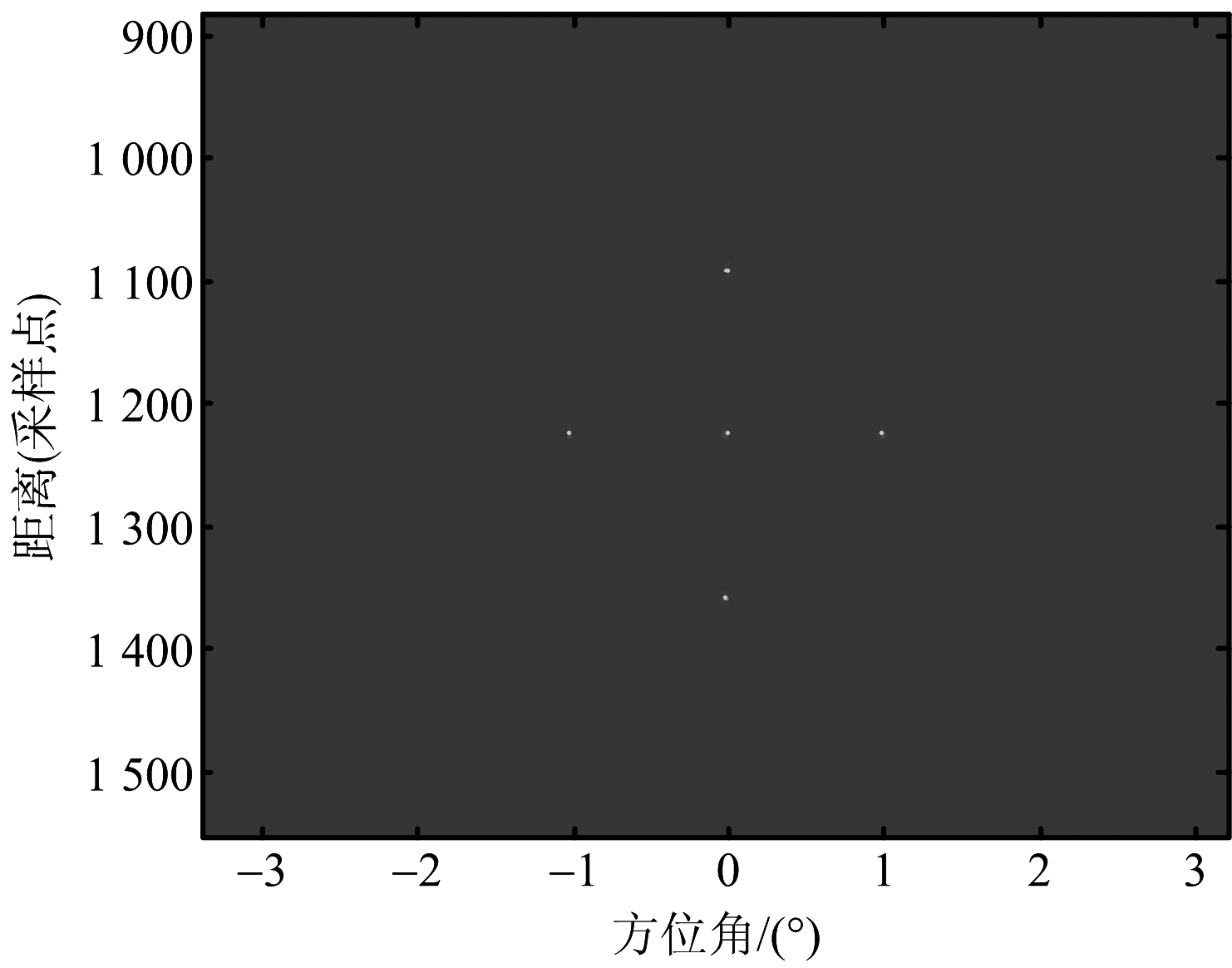
图4 点目标超分辨成像结果
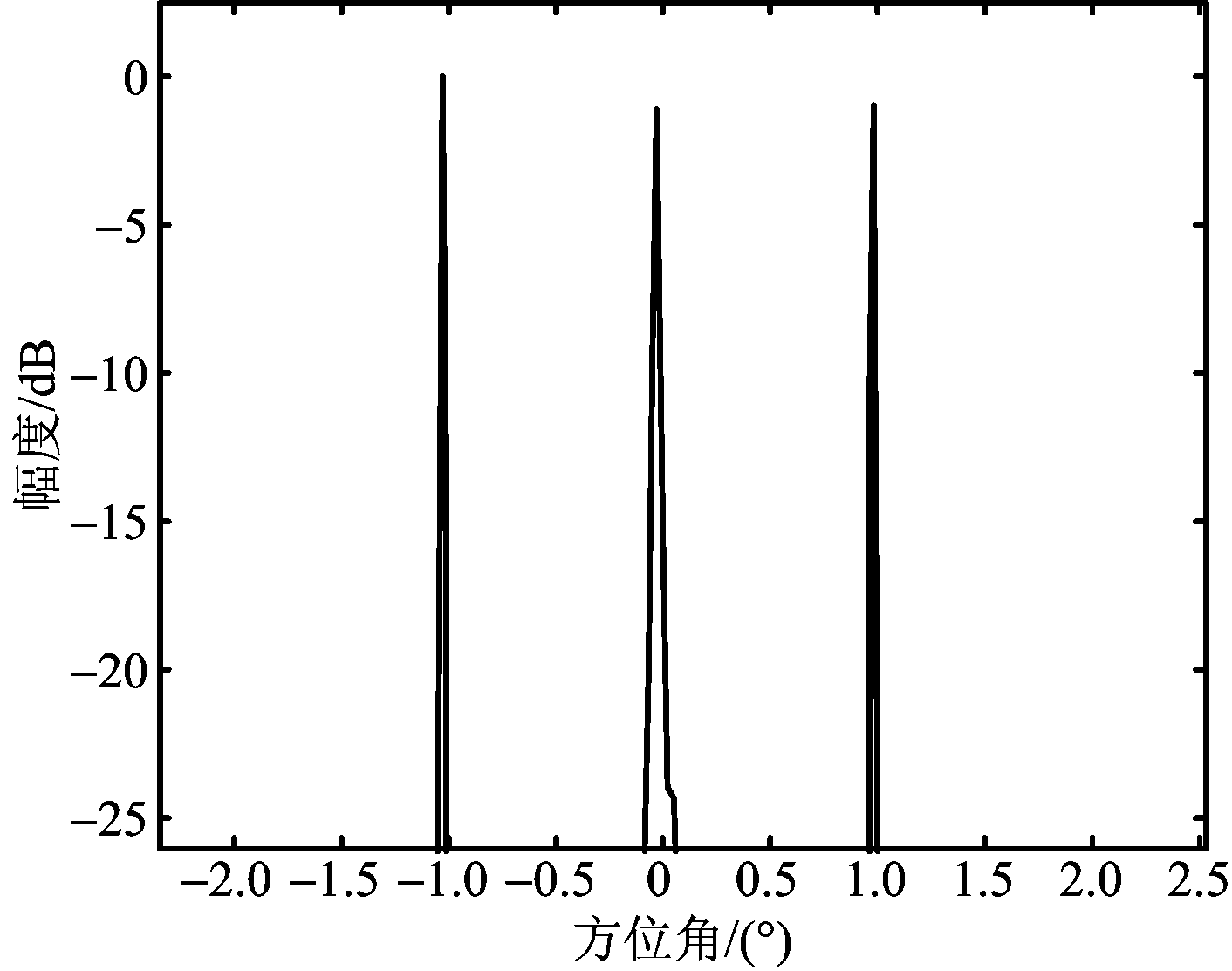
图5 点目标剖面

图6 地面仿真场景成像结果
为了对本文算法在实际处理中的效果进行验证,采用该算法对一组机载雷达实测数据进行了成像处理。该数据由某型相控阵雷达录取,方位接收通道数为4。成像场景为海面区域,数据录取时,成像区有多艘舰船在行驶,主要系统参数如表2所示。图7首先给出了和波束的实波束成像结果,可以看出,由于天线波束宽度的限制,实波束成像图方位分辨效果极差,几乎无法分辨舰船目标。图8给出了本文算法的成像结果,相较于实波束成像,该算法方位聚焦效果良好,可以清晰地分辨每艘船的位置,分辨率显著提升。为了展示该算法对波束中多目标的分辨效果,图9给出了同一距离门两艘舰船的方位剖面图,可以看出,本文算法能分辨同一波束内多个目标,前视成像效果良好。
表2 实测数据系统参数列表

图7 海面场景实波束成像结果
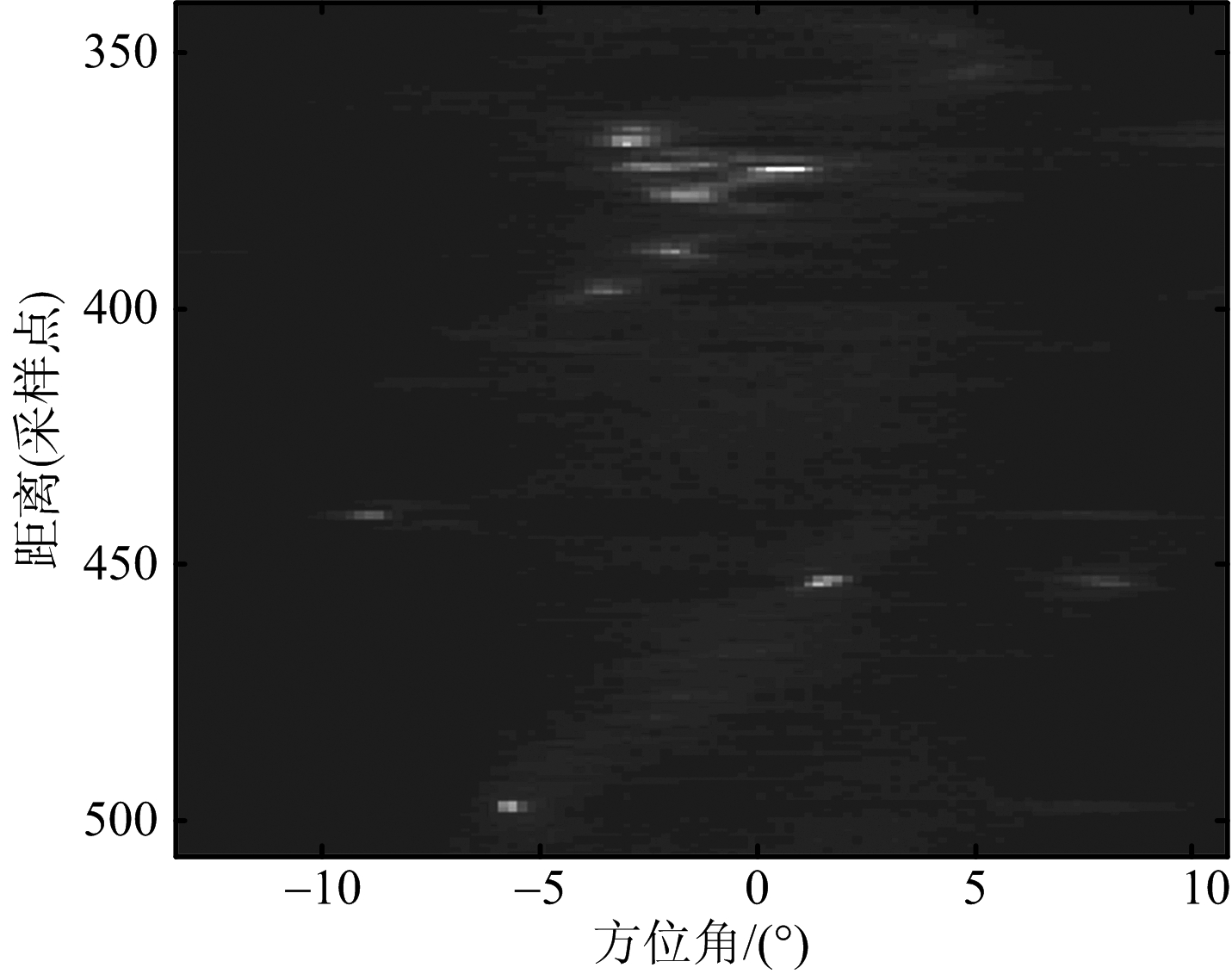
图8 海面场景超分辨成像结果
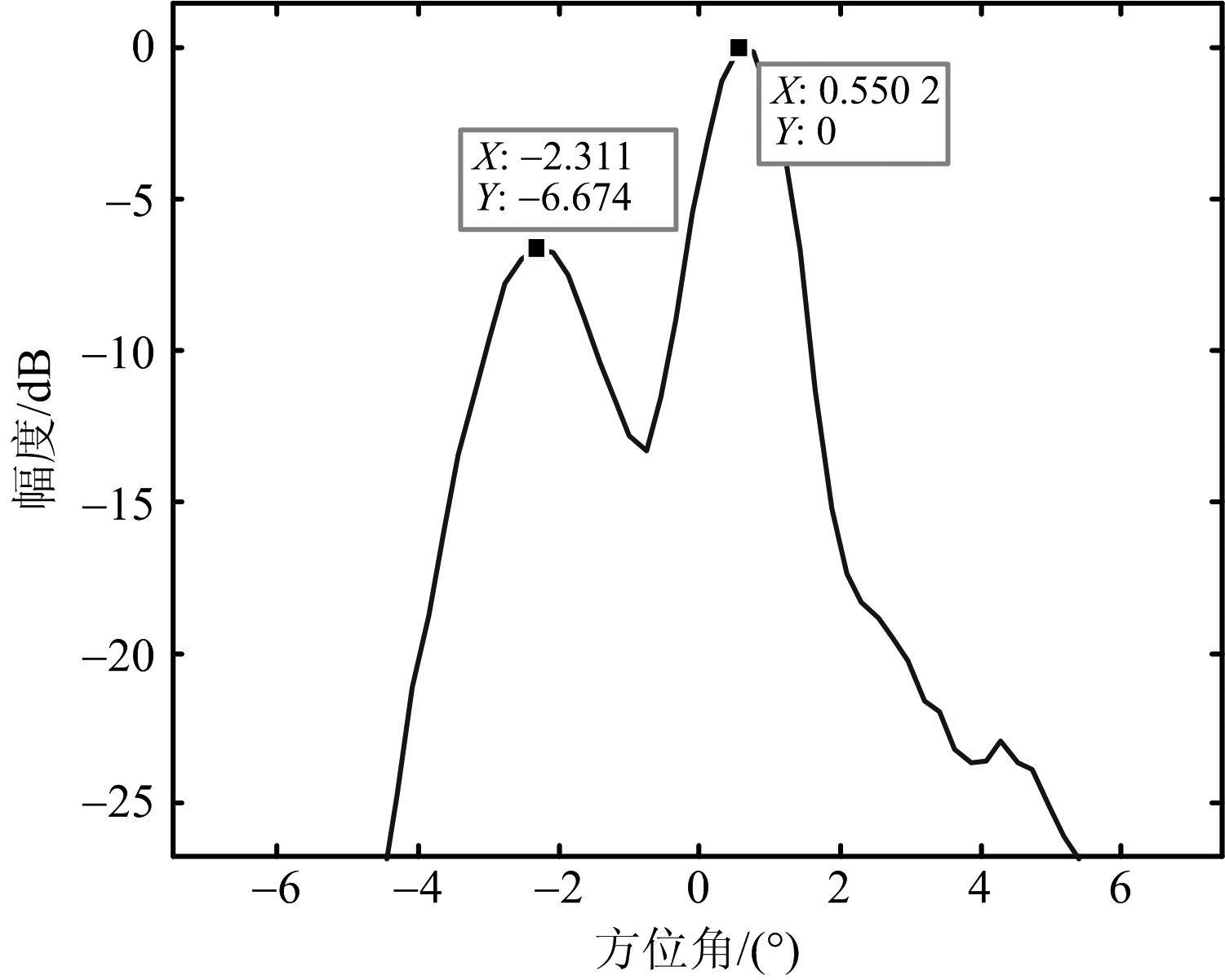
图9 点目标剖面
5 结束语
本文采用基于超分辨技术的阵列雷达算法有效地解决了机载雷达前视成像的盲区问题。该算法通过对接收的各通道回波数据进行样本协方差估计,并对该协方差进行修正及空间平滑等处理,最后用改进的MUSIC算法实现雷达超分辨前视成像。仿真及实测数据处理结果表明,该算法能有效提高前视成像方位分辨率。
参考文献:
[1] 庞礴, 代大海, 刑世其, 等. 前视SAR成像技术的发展和展望[J]. 系统工程与电子技术, 2013, 35(11):2283-2290.
[2] WANG Yanwei, SUN Yijun, LI Jian, et al. Adaptive Imaging for Forward Looking Around Penetrating Radar[J]. IEEE Trans on Aerospace and Electronic Systems, 2015, 41(3):922-936.
[3] 温晓杨, 匡纲要, 胡杰民, 等. 基于实波束扫描的相控阵雷达前视成像[J]. 航空学报, 2014, 35(7):1977-1991.
[4] 杨志伟, 贺顺, 廖桂生. 机载单通道雷达实波束扫描的前视探测[J].航空学报,2012, 33(12):2240-2245.
[5] 吴迪, 杨成杰, 朱岱寅, 等. 一种用于单脉冲成像的自聚焦算法[J]. 电子学报, 2016, 44(8):1962-1968.
[6] QIU Xiaolan, HU Donghui, DING Chibiao. Some Reflections on Bistatic SAR of Forward-Looking Configuration[J]. IEEE Geoscience and Remote Sensing Letters, 2008, 5(4):735-739.
[7] WEN Fei, WAN Qun, FAN Rong, et al. Improved MUSIC Algorithm for Multiple Moncoherent Subarrays[J]. IEEE Signal Processing Letters, 2014, 21(5):527-530.
[8] ZHAO Guanhua, FU Yaowen, ZHUANG Zhaowen. Imaging by Root-MUSIC for Forward-Looking Radar with Linear Array[C]∥ International Conference on Wireless Communications and Signal Processing, Hangzhou:IEEE, 2013:1-6.
[9] CHEN Hongmeng, LI Ming, WANG Zeyu, et al.
Sparse Super-Resolution Imaging for Airborne Single Channel Forward-Looking Radar in Expanded Beam Space via lp Regularisation [J]. IEEE Electronics Letters, 2015, 51(11):863-865.
[10] KIDERA S, SAKAMOTO T, SATO T. Super-Resolution UWB Radar Imaging Algorithm Based on Extended Capon with Reference Signal Optimization [J]. IEEE Trans on Antennas and Propagation, 2011, 59(5):1606-1615.
[11] ZHANG Dong, ZHANG Yongshun, HU Xiaowei, et al. Fast OMP Algorithm for 3D Parameters Super-Resolution Estimation in Bistatic MIMO Radar[J]. Electronics Letters, 2016, 52(13):1164-1166.
[12] PHAM G T, LOUBATON P, VALLET P. Performance Analysis of Spatial Smoothing Schemes in the Context of Large Arrays[J]. IEEE Trans on Signal Processing, 2016, 64(1):160-172.
[13] 司伟建, 朱瞳, 张梦莹. 色噪声背景下基于特征空间的信源估计新方法[J]. 系统工程与电子技术, 2011, 33(8):1713-1717.


