0 引言
合成孔径雷达(SAR)对地观测已经由早期的定性分析逐渐走向定量化应用,而SAR定标技术就是其中的关键。全极化SAR系统通过测量目标场景中每个分辨单元内的全极化散射回波进而获得其全部极化散射特性,能提供比单极化SAR更丰富的信息,但全极化SAR系统获取的数据会受到极化串扰、极化通道幅相不平衡等系统误差的影响,只有经过极化定标才能够进行定量化数据应用[1-5]。
极化合成孔径雷达(Polarimetric SAR, Pol- SAR)定标算法目前主要分为3类:点目标定标算法[1,4-6]、分布目标定标算法[4-5]、混合点目标和分布目标的定标算法[2,4-5,7]。点目标定标算法是3类算法中开展最早、研究最多的一类算法。Whitt算法[1]不需要对雷达系统失真矩阵作任何假设,用于定标的目标也只需要满足很少的限制条件,在定标目标的选择上有很大的灵活性,是点目标定标算法中的典型代表,受到了广泛应用[8]。在Whitt算法中对特征值次序对应关系进行选择有一个重要判断条件[1],本文研究并证明了该判断条件在有些情况下失效,将无法唯一求解得到系统失真矩阵的真值。本文进而基于一组特定极化定标器组(三面角反射器、0°和45°二面角反射器)给出了特征值次序对应关系错误会对失真矩阵求解结果产生的影响,并提出了新的判断条件和解决方法,对Whitt算法进行了改进。最后,利用中国科学院电子学研究所研制的一部机载PolSAR系统的极化外定标实验数据进行验证,实验结果表明改进后的算法具有更好的有效性和稳健性。
1 Whitt算法
一般的点目标定标算法,要么假定待测目标具有某种特性,要么假定雷达系统的失真矩阵具有某种特殊形式,这些假设都会带来一些应用限制,而Whitt算法则不需要对雷达系统失真矩阵作任何假设,用于定标的目标也只需要满足很少的限制条件,在定标目标的选择上有很大的灵活性,实验室环境和野外环境都可以使用[4]。
PolSAR系统的极化定标模型可表示为
M=![]()
AejφRST
(1)
式中,M为系统测量得到的目标观测矩阵,S为目标的真实散射矩阵,R和T分别为系统接收和发射失真矩阵,A为系统绝对幅度增益因子,φ为系统绝对相位。
采用式(1)模型,考虑真实散射矩阵已知的3个不同点目标的极化测量,则有
Mi=AejφiRSiT, i=1,2,3
(2)
Whitt算法要求至少有一个点目标的散射矩阵是可逆的,所以不妨假设目标1的散射矩阵可逆,即S1和M1可逆。矩阵M2和M3都左乘![]() 得到如下相似变换:
得到如下相似变换:
MT1=![]()
(3)
MT2=![]()
(4)
以上两式中只包含矩阵T,与矩阵R无关,且MT1和ST1、MT2和ST2为两对相似矩阵。
MT1和ST1矩阵的特征值和特征向量满足如下关系:
(5)
式中,![]() 和ΛT1分别为矩阵ST1和MT1的特征值构成的对角矩阵,XT1和YT1分别由ST1和MT1的特征向量构成。这些特征值和特征向量矩阵之间有如下关系成立:
和ΛT1分别为矩阵ST1和MT1的特征值构成的对角矩阵,XT1和YT1分别由ST1和MT1的特征向量构成。这些特征值和特征向量矩阵之间有如下关系成立:
(6)
同理,MT2和ST2矩阵的特征值和特征向量满足:
(7)
(8)
考虑到构成XT1和YT1、XT2和YT2的特征向量具有任意的尺度因子,分别选取尺度因子CT1和CT2后进行求解,根据以上方程组最终可求得发射失真矩阵T。
同理,矩阵M2和M3都右乘![]() 则有
则有
MR1=![]()
(9)
MR2=![]()
(10)
类似求解矩阵T的过程,可求得接收失真矩阵R。
失真矩阵R和T求出以后,代入式(2),就能求出绝对幅度增益因子A,由散射矩阵的第mn个元素得到
(11)
选择理论散射矩阵最准确的定标目标,可以获得A的最好估计。详细求解过程可参考文献[1]。
2 Whitt算法存在的问题及其影响
Whitt算法求解系统失真矩阵R和T的方法是类似的,这里以求解T为例。求解T时涉及到两对相似矩阵MT1和ST1、MT2和ST2,这两对相似矩阵的特征向量所分别构成的矩阵YT1和XT1、YT2和XT2是求解的关键。以矩阵XT1和YT1为例(下面称为特征向量矩阵),由特征值构成的对角阵![]() 和ΛT1(下面称为特征值矩阵)的对应次序决定了特征向量矩阵的对应关系,而它们理论上需要满足式(6)。但因为特征值矩阵和特征向量矩阵都是分别求解的,所以Whitt算法中提出了一个判断条件对特征值矩阵
和ΛT1(下面称为特征值矩阵)的对应次序决定了特征向量矩阵的对应关系,而它们理论上需要满足式(6)。但因为特征值矩阵和特征向量矩阵都是分别求解的,所以Whitt算法中提出了一个判断条件对特征值矩阵![]() 和ΛT1进行对应次序的判断和修正。
和ΛT1进行对应次序的判断和修正。
记![]() 判断条件如下:
判断条件如下:
ΛT1=

(12)
Whitt算法中通过式(12)对ΛT1和![]() 的对应次序进行判断和修正,也对特征向量矩阵YT1和XT1进行相应操作,修正完成后应该满足式(6)。同理,对矩阵XT2和YT2也进行类似操作以满足式(8)。当两对相似矩阵的特征值矩阵和特征向量矩阵都各自对应时,Whitt算法才可以唯一求解得到失真矩阵T的真值。如果特征向量矩阵的对应关系是错误的,求解结果将是不正确的。求解失真矩阵R类似。
的对应次序进行判断和修正,也对特征向量矩阵YT1和XT1进行相应操作,修正完成后应该满足式(6)。同理,对矩阵XT2和YT2也进行类似操作以满足式(8)。当两对相似矩阵的特征值矩阵和特征向量矩阵都各自对应时,Whitt算法才可以唯一求解得到失真矩阵T的真值。如果特征向量矩阵的对应关系是错误的,求解结果将是不正确的。求解失真矩阵R类似。
经研究发现式(12)在有些情况下是失效的,也即通过式(12)并不能对特征值次序的对应关系进行判断和修正,所以Whitt算法求解得到的系统失真矩阵并不一定是真值。比如,将Whitt算法求解需要的3个参考极化定标器依次选择为三面角反射器、0°和45°二面角反射器,该判断条件就是失效的。下面将给出证明。
2.1 针对判断条件无效的证明
假设![]() 和ΛT1的次序是对应的,则由式(6)可得
和ΛT1的次序是对应的,则由式(6)可得
(13)
容易得到
(14)
进而有
(15)
选定一组常用的极化定标器组:三面角反射器、0°和45°二面角反射器,并用S1,S2,S3依次表示其理论散射矩阵。根据Whitt算法对参考目标的要求,容易证明这3个目标是满足要求的。
根据特征值的相关定义,容易求得任意角度α下的二面角反射器理论散射矩阵的特征值都是±1。不妨令![]() 根据式(14)可得
根据式(14)可得
(16)
根据式(15)和式(16)可得
(17)
式(17)就是式(12)中的判断条件,可见Whitt算法的判断条件失效了,根据式(12)并不能判断和修正特征值矩阵的对应次序。因为由特征值构成的对角矩阵中特征值的次序是任意排列的,故上述对应次序实际上是随机的,Whitt算法无法正确求得系统失真矩阵的真值。
2.2 判断条件失效对系统失真矩阵求解结果造成的影响
前面已经说明,Whitt算法求解发射失真矩阵T时涉及到两对相似矩阵MT1和ST1、MT2和ST2,它们对应的特征值矩阵分别是ΛT1和![]() 和
和![]() 同理,求解接收失真矩阵R时也涉及到两对相似矩阵MR1和SR1、MR2和SR2,它们对应的特征值矩阵分别记为ΛR1和
同理,求解接收失真矩阵R时也涉及到两对相似矩阵MR1和SR1、MR2和SR2,它们对应的特征值矩阵分别记为ΛR1和![]() 和
和![]() 为了方便叙述,将ΛT1和
为了方便叙述,将ΛT1和![]() 和
和![]() 称为第一组特征值矩阵,ΛT2和
称为第一组特征值矩阵,ΛT2和![]() 和
和![]() 称为第二组特征值矩阵。
称为第二组特征值矩阵。
依然选定三面角反射器、0°和45°二面角反射器作为Whitt算法所需的3个参考目标,并用S1,S2,S3依次表示其理论散射矩阵。根据式(1)和Whitt算法的求解过程,可得到特征值矩阵的不同对应次序下,系统失真矩阵的求解结果,具体 如下。
2.2.1 仅第一组特征值矩阵的次序不对应
当ΛT1和![]() 次序不对应,而ΛT2和
次序不对应,而ΛT2和![]() 次序对应时,可求得发射失真矩阵为
次序对应时,可求得发射失真矩阵为
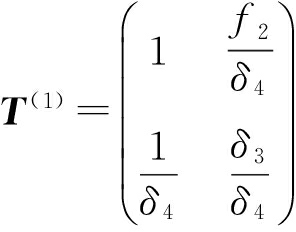
(18)
同理,当ΛR1和![]() 次序不对应,而ΛR2和
次序不对应,而ΛR2和![]() 次序对应时,可求得接收失真矩阵为
次序对应时,可求得接收失真矩阵为
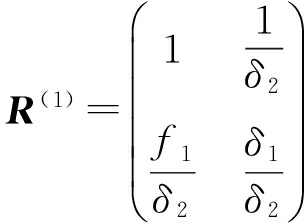
(19)
2.2.2 仅第二组特征值矩阵的次序不对应
当ΛT1和![]() 次序对应,而ΛT2和
次序对应,而ΛT2和![]() 次序不对应时,可求得发射失真矩阵为
次序不对应时,可求得发射失真矩阵为
(20)
同理,当ΛR1和![]() 次序对应,而ΛR2和
次序对应,而ΛR2和![]() 次序不对应时,可求得接收失真矩阵为
次序不对应时,可求得接收失真矩阵为
(21)
2.2.3 第一组和第二组特征值矩阵的次序都不对应
当ΛT1和![]() 和
和![]() 次序都不对应时,可求得发射失真矩阵为
次序都不对应时,可求得发射失真矩阵为
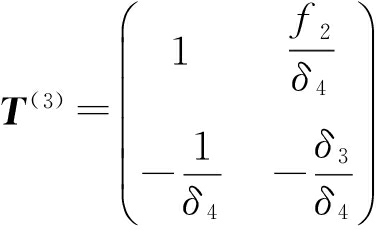
(22)
同理,当ΛR1和![]() 和
和![]() 次序都不对应时,可求得接收失真矩阵为
次序都不对应时,可求得接收失真矩阵为
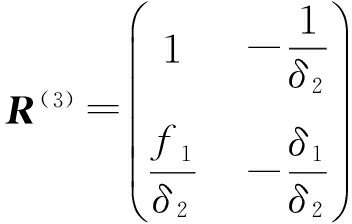
(23)
![]()
![]() 都是单独求解的,其特征值的排列次序是任意的。因为Whitt算法的判断条件是无效的,所以这些特征值矩阵的对应次序关系是随机的,由此求得的系统失真矩阵T和R可能是上述结果中的任意一种。
都是单独求解的,其特征值的排列次序是任意的。因为Whitt算法的判断条件是无效的,所以这些特征值矩阵的对应次序关系是随机的,由此求得的系统失真矩阵T和R可能是上述结果中的任意一种。
3 针对Whitt算法的改进
Whitt算法中的核心公式是式(6)和式(8),这两个公式中的特征值都可以分别求得,但对应次序需要判断条件加以确定。当这两个公式得以满足时,Whitt算法能够求得失真矩阵的真值。式(6)和式(8)中的相位φ1,φ2,φ3与目标特性等很多复杂因素相关,不可预知,故式(6)和式(8)实际上是欠定的。如果不附加新的条件,Whitt算法将无法给出正确的特征值对应次序,也就无法求得失真矩阵的真值。根据第2节的结果,Whitt算法求解得到的系统失真矩阵T和R各自有4种解,其中只有1种是真值。
以T为例,当第一组特征值矩阵的对应次序错误时,T的求解结果为式(18)或式(22),其HV通道串扰大小是f2/δ4,VH通道串扰大小是1/δ4。当仅有第二组特征值矩阵的对应次序错误时,T的求解结果为式(20),其串扰大小和真值是一致的。考虑到实际情况下,系统发射失真矩阵的串扰δ3,δ4的大小是远小于0 dB的,一般小于-15 dB,而式(18)或式(22)的求解结果中串扰大小近似为真值的倒数,是远大于0 dB的,一般大于+15 dB。所以在原Whitt算法基础上,可首先任意给定ΛT1和![]() 和
和![]() 的次序,并假定它们是对应的,求解得到矩阵T。然后对T的串扰大小进行判断,可设置阈值1为0 dB。如果串扰值大于0 dB,则只需要修改ΛT1和
的次序,并假定它们是对应的,求解得到矩阵T。然后对T的串扰大小进行判断,可设置阈值1为0 dB。如果串扰值大于0 dB,则只需要修改ΛT1和![]() 的次序,并重新计算矩阵T;如果串扰值小于0 dB,则说明ΛT1和
的次序,并重新计算矩阵T;如果串扰值小于0 dB,则说明ΛT1和![]() 的次序一定是对应的,无需作更改。经过此次判断后,能够实现ΛT1和
的次序一定是对应的,无需作更改。经过此次判断后,能够实现ΛT1和![]() 次序的正确对应。此时还剩下ΛT2和
次序的正确对应。此时还剩下ΛT2和![]() 的对应关系不确定。
的对应关系不确定。
当仅有第二组特征值矩阵的对应次序错误时,T的求解结果为式(20),此时串扰大小和真值是一致的,而通道不平衡为-f2,和真值互为相反数。考虑到通道不平衡的真值f2的相位是没有先验信息的,所以无法直接给出判断条件来修正ΛT2和![]() 的对应关系。
的对应关系。
至此,改变第二组特征值矩阵的对应次序可分别得到矩阵T的两个解,一个是真值,另一个是式(20)表示的T(2)。同理,也可分别求得矩阵R的两个解,一个是真值,另一个是式(21)表示的R(2)。
假定任意目标的散射矩阵是Starget,相应的观测矩阵是Mtarget。用上述求得的系统失真矩阵对Mtarget进行校准,重点关注校准结果中不同通道间的相互关系,故暂不考虑绝对幅度增益因子A。
当选取的系统失真矩阵是T和R的真值,则Mtarget的校准结果是该目标散射矩阵的真值Starget,记为![]()
当选取T(2)和R进行校准,注意到T(2)=![]() 可得
可得
(24)
当选取T和R(2)进行校准,注意到![]() 可得
可得
(25)
当选取T(2)和R(2)进行校准,可得
(26)
式(24)和式(25)的求解结果中VV通道数值是真值的相反数,而式(26)中VV通道是真值而交叉通道数值是真值的相反数。式(24)~式(26)的结果可以通过考察对一个22.5°二面角反射器的校准结果加以排除,方法如下:1)使用上述修改判断条件后的Whitt算法分别求得T和R的两个求解值;2)提取22.5°二面角反射器的观测矩阵数据;3)任选一组T和R的求解值对其进行极化校准;4)首先,设置阈值2为90°,并考察校准后散射矩阵的VV通道相位大小,如果在180°附近(即大于阈值2)则将该组T,R求解值保留并跳转到5),如果在0°附近(即小于阈值2)则舍弃并跳转到6);5)然后,设置阈值3为90°,并考察校准后散射矩阵的HV或VH通道的相位大小,如果在0°附近(即小于阈值3)则将该组T,R求解值保留,如果在180°附近(即大于阈值3)则舍弃;6)重复步骤3)和5),最终可筛选出唯一一组T,R求解值,该组求解值即为系统失真矩阵的真值。
如果由于条件限制没有22.5°二面角反射器数据可用,则可用任意一个三面角反射器数据进行替代,不过筛选结果会有局限,方法如下:1)使用上述修改判断条件后的Whitt算法分别求得T和R的两个求解值;2)任选一个三面角反射器;3)任选一组T和R的求解值对其进行极化校准;4)考察校准后散射矩阵的VV通道相位大小,如果在0°附近则将该组T,R求解值保留,如果在180°附近则舍弃;5)重复步骤3)和4),最终可得到两组T,R求解值。
注意到,相比于利用22.5°二面角反射器进行筛选,利用三面角反射器最终只能筛选出两组T,R求解值,即真值T,R或T(2),R(2)且无法进一步判别。使用T(2),R(2)对任意目标进行极化校准会对交叉通道引入相位翻转,如果极化校准后的其他应用不需要利用交叉通道相位,则任选一组失真矩阵求解值皆可,否则仅利用三面角反射器数据无法提供所需要的结果。
改进后的Whitt算法流程如图1和图2所示,这里假设有可用的22.5°二面角反射器。如果没有22.5°二面角反射器,则可以利用三面角反射器进行替代,将图2进行适当修改即可。
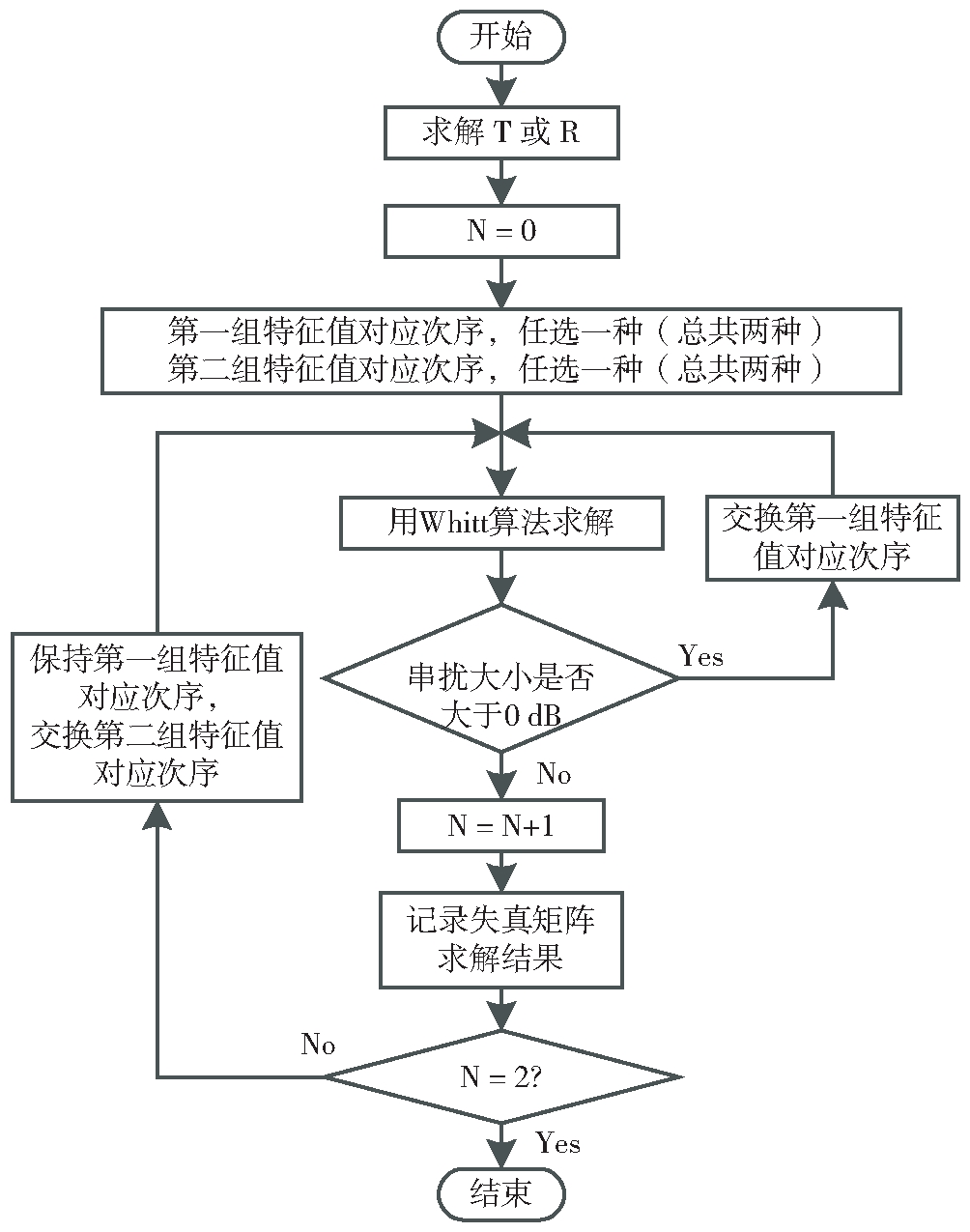
图1 利用新的判断条件分别求解系统失真矩阵T和R
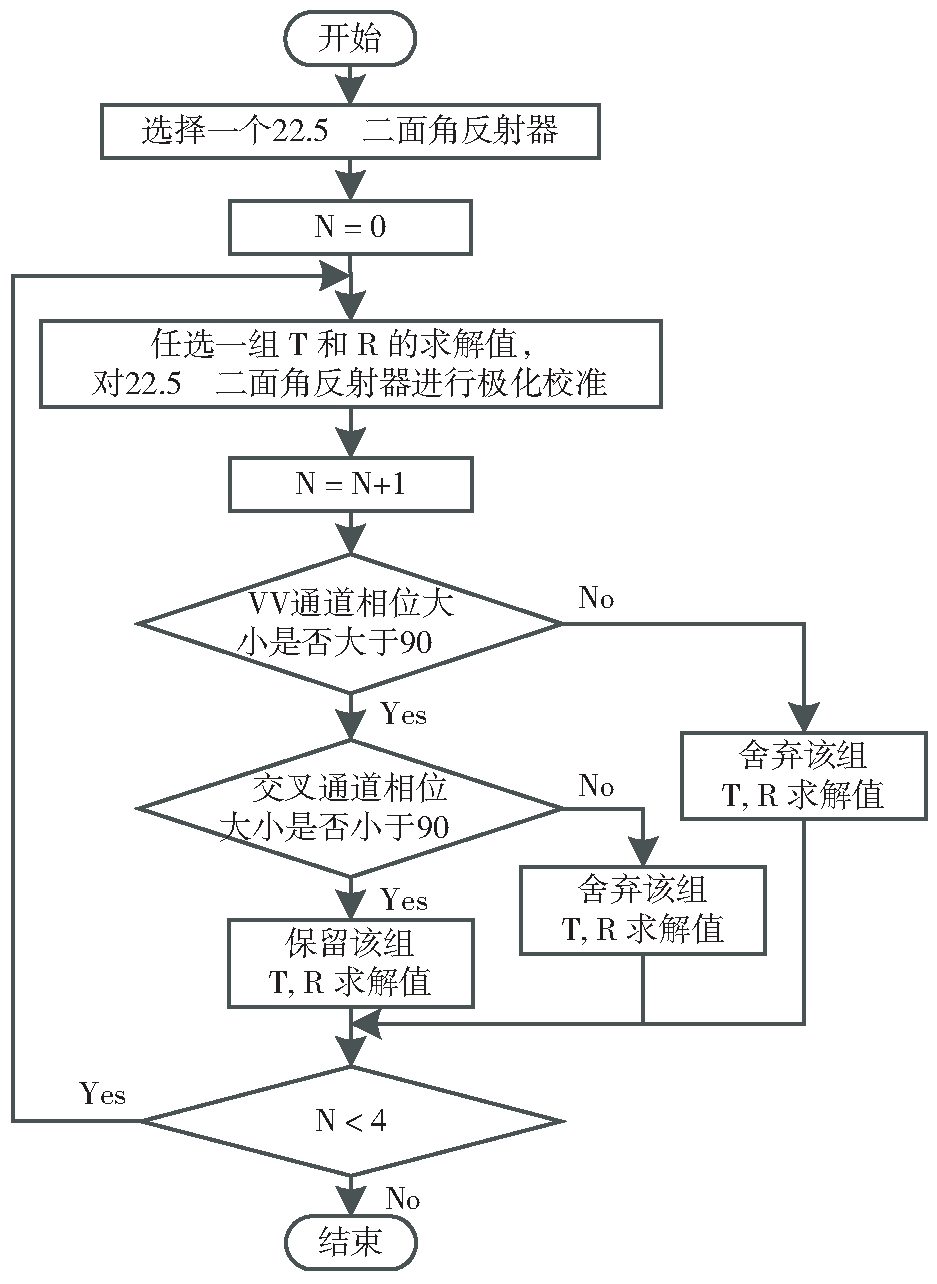
图2 选择系统失真矩阵T和R求解值的方法
4 实验验证和结果分析
Whitt算法的推导是在不考虑噪声N的情况下进行的,见式(1),但实际系统和环境是广泛受到噪声和杂波影响的。在利用Whitt算法对实际数据处理时,首先需要对定标器的加工和布设误差进行准确标定,其方法可参考文献[9],另外,定标器的信杂比等系统误差也会对处理结果产生影响,相关内容可参考文献[6, 8]。
本文利用中国科学院电子学研究所研制的一部机载PolSAR系统所采集的全极化数据对改进算法进行了实验验证。由于该定标场中并未布设22.5°二面角反射器,故本节利用三面角反射器数据进行系统失真矩阵的筛选。如第3节所述,使用三面角反射器数据进行筛选会得到两组失真矩阵T,R,并得到两组极化校准结果,本节中分别记为改进算法的校准结果1和2。本数据的测绘区域为外定标场,其中布设了若干角反射器,分布情况如图3所示。编号1的3个定标器从上往下依次是三面角反射器、0°和45°二面角反射器,本文将其作为Whitt算法所需的3个参考目标来进行极化定标参数求解;编号2~编号4是检测用三面角反射器,用作检验极化校准效果。
在极化定标前先对数据进行辐射定标,然后利用改进的Whitt算法求解系统失真矩阵。利用求得的定标参数对编号2~编号4的定标器进行极化校准并考察校准效果,最后对整幅图像进行极化校准并生成Pauli基合成图(红色:HH-VV;绿色:2HV;蓝色:HH+VV)。
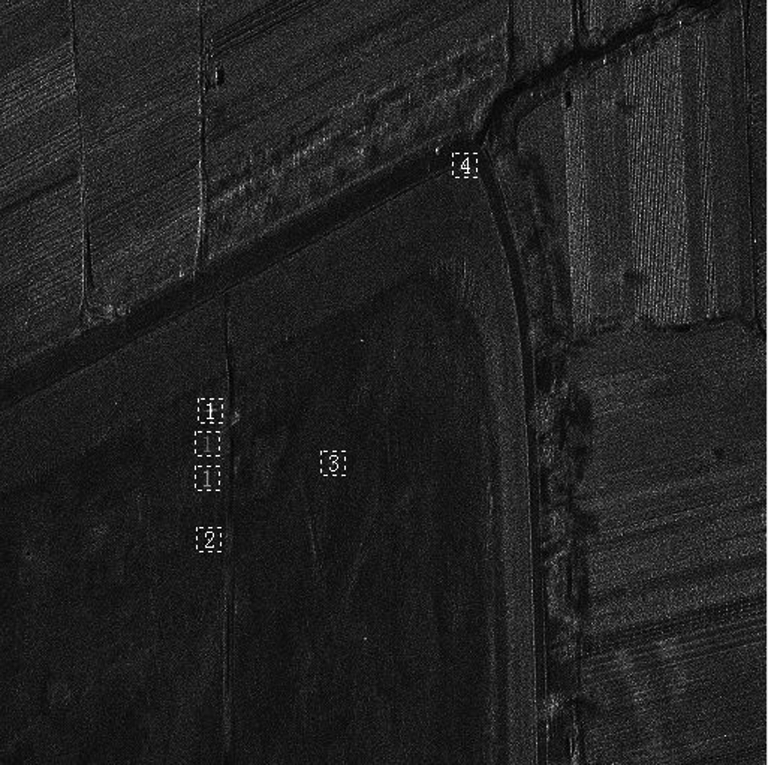
图3 外定标场中定标点分布情况
表1是编号2~编号4的检测用三面角反射器的极化校准结果。改进算法的校准结果1和2分别对应改进Whitt算法求解得到的两组系统失真矩阵。采用原Whitt算法的校准结果,幅度不平衡全都大于2 dB,相位不平衡都在-180°~-170°之间,这是由于极化校准时使用了错误的系统失真矩阵求解值所导致的,符合之前的理论分析。要说明的是,使用原Whitt算法并不是都会得到这么差的结果,而是判断条件的失效导致校准结果会随机出现多种可能中的一种,这里恰好对应了一种不正确的结果。采用改进算法的校准结果(包括校准结果1和2),幅度不平衡全都优于0.6 dB,相位不平衡全都优于6°,可以看到改进算法在幅度、相位不平衡方面有了显著提升。在串扰方面,原Whitt算法和改进算法相比于定标前都提升不大,编号3甚至还出现了变差的情况,这主要是受到定标器自身信杂比等系统误差的影响,可通过在今后布设定标器时选择更合理的定标场地等方面进行解决。总体而言,串扰大小除一个为-24.9 dB外全部优于-27 dB,满足该机载试验系统的设计要求。表1中所示结果符合本文前述的理论分析。
表1 检测用三面角反射器的极化校准结果
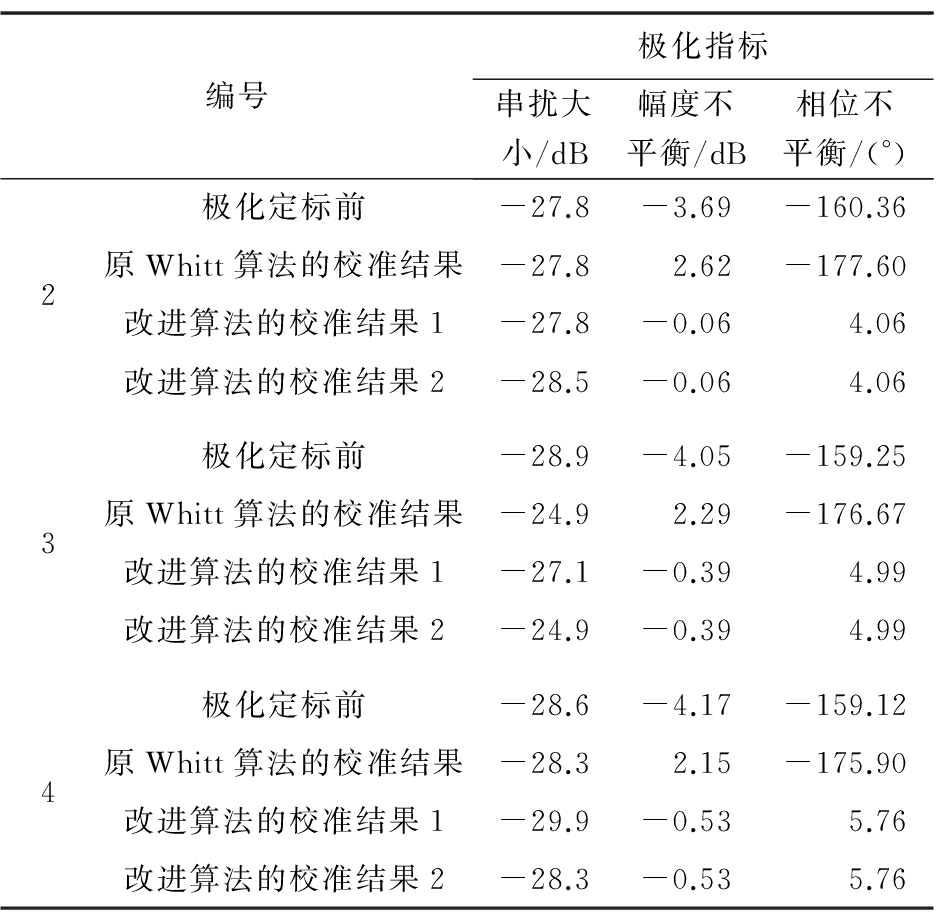
图4是利用极化校准前数据合成的伪彩图,图5是采用原Whitt算法的校准结果,图6和图7是分别采用改进算法求得的两组不同系统失真矩阵进行校准的结果。图5与图4相比变化不大,这是因为原Whitt算法的判断条件是无效的,所以其求解得到的系统失真矩阵是多种可能组合中的某一种,利用其进行极化校准并不能保证得到正确解,图5显然对应其中的一种错误情况。图6和图7所示校准结果符合典型地物的散射特性,比如裸地呈现蓝色、植被呈现绿色、建筑物呈现红色等。同时根据前述说明,校准结果1和2只在交叉通道相位上不同,而这不影响Pauli分解和伪彩图合成的结果,所以图6和图7基本是一致的。实验结果表明,利用该改进算法进行极化定标参数求解具有更好的有效性和稳健性。

图4 极化校准前

图5 采用原Whitt算法的校准结果

图6 采用改进算法的校准结果1

图7 采用改进算法的校准结果2
5 结束语
本文发现Whitt算法中对特征值对应次序进行判断的条件在某些情况下不成立并给出了证明。基于一组特定极化定标器组(三面角反射器、0°和45°二面角反射器)给出了特征值次序对应关系错误会对失真矩阵求解结果造成的影响。提出了新的判断条件和解决方法,对Whitt算法进行了改进。利用中国科学院电子学研究所研制的一部机载PolSAR系统进行了极化外定标实验验证,实验结果表明,利用该改进算法进行极化定标参数求解具有更好的有效性和稳健性。考虑到点目标极化定标算法在机载极化数据处理中的广泛应用,以及三面角反射器和二面角反射器在外场实验中的简单易用和广泛布设,本文对使用Whitt算法进行极化定标和处理有一定的参考意义。
参考文献:
[1] WHITT M W, ULABY F T, POLATIN P, et al. A General Polarimetric Radar Calibration Technique[J]. IEEE Trans on Antennas and Propagation, 1991, 39(1):62-67.
[2] FORE A G, CHAPMAN B D, HAWKINS B P, et al. UAVSAR Polarimetric Calibration[J]. IEEE Trans on Geoscience and Remote Sensing, 2015, 53(6):3481-3491.
[3] 郭睿. 极化SAR处理中若干问题的研究[D]. 西安: 西安电子科技大学, 2012.
[4] 席育孝. 多极化合成孔径雷达定标技术研究[D]. 北京: 中国科学院研究生院, 2002.
[5] 张红,王超,刘萌,等. 极化SAR理论、方法与应用[M]. 北京: 科学出版社, 2015.
[6] 熊维族. 系统误差对点目标极化散射测量的影响[J]. 现代雷达, 2007, 29(6):9-12.
[7] 廖露,李平湘,杨杰,等. 一种基于分布式目标互易性判断的SAR极化定标改进方法[J]. 武汉大学学报(信息科学版), 2015, 40(8): 1042-1047.
[8] ZHANG Lintao, HONG Jun, MING Feng, et al. Application Study of the Airborne Polarimetric SAR Calibration Using Passive Point Targets[C]∥ International Conference on Remote Sensing, Hangzhou: IEEE, 2010:447-450.
[9] 王宇,李焱磊,周良将,等. 非理想定标器条件下的机载P波段极化SAR定标方法: 201110346856.0[P]. 2013-05-08.





