0 引言
早期雷达进行目标的波达方向估计主要采用数字波束形成(DBF),而DBF的角度分辨率和天线的孔径成反比,也就是说,为了能够达到较好的角度分辨率,需要增大雷达天线的阵列孔径,但当角度分辨率要求很高时,再增大阵列孔径就难以实现了。对于米波雷达来说,在低仰角区直达波和多径信号均位于同一波束宽度内,导致无法分辨,最终导致测角模糊[1]。也就是说,采用DBF测角算法简单、运算速度快,但是只能够测出目标大致方向,但是测角精度无法满足雷达系统要求。为了能够提高测角精度,弥补DBF低仰角区测角不足,学者们研究出了一类子空间拟合算法:最大似然(ML)算法,这种算法在目标信噪比(SNR)较低、快拍数较少的条件下,相比于其他算法而言,可以达到更好的测角性能。但是,ML算法实现过程中,需要进行空域的多维搜索,所以运算量较大。为了减少运算量,学者们对该算法进行了改进,最终形成了合成导向矢量(SVML)算法[2-3]。基于上述DBF和SVML算法的优缺点分析,本文采用DBF算法与SVML算法相结合,先用DBF算法估测出目标大致方位,然后再采用SVML进行精测。即采用DBF算法减少角度搜索范围,再利用SVML算法在低仰角区的测角优势,加快测角速率并提高测角精度。
针对测角过程中SVML算法需要进行多维空域搜索,整个计算过程时间复杂度较高这一问题,GPU引入通用计算,通过并行运算提高运算效率[4-5]。相对CPU而言,GPU一方面具有很强的数据并行处理能力,另一方面则具有很高的数据处理带宽,一经研发便被广泛应用于通用计算机领域。2006年11月,英伟达公司推出一种新的并行编程模型和指令集架构的通用计算架构CUDA,CUDA架构的一大优势就是能够利用GPU的并行计算引擎完成许多复杂任务的计算。它包含一个让开发者能够使用C语言作为高级编程语言的软件环境,使得熟悉标准编程语言的程序员保持一个比较低的学习曲线[1,6]。除此之外,相对CPU而言,GPU将更多的资源用于数据运算,而非缓存和数据流控制,使GPU的浮点计算能力和内存带宽都远高于CPU,所以对于密集型以及高度并行化的计算,GPU优势明显。本文中将GPU用于目标的波达方向估计,利用GPU特有的CUBLAS矩阵处理库,提高测角速率,实现数据的实时处理。
1 DBF与SVML算法基本原理
1.1 算法性能分析
图1为DBF和SVML算法的测角结果对比。通过对实测数据进行仿真分析得到:当来波方向大于2.5°时,两种算法的误差均为0.2左右,但当角度小于2.5°时,DBF测角误差达0.599,而SVML算法测角误差为0.063。
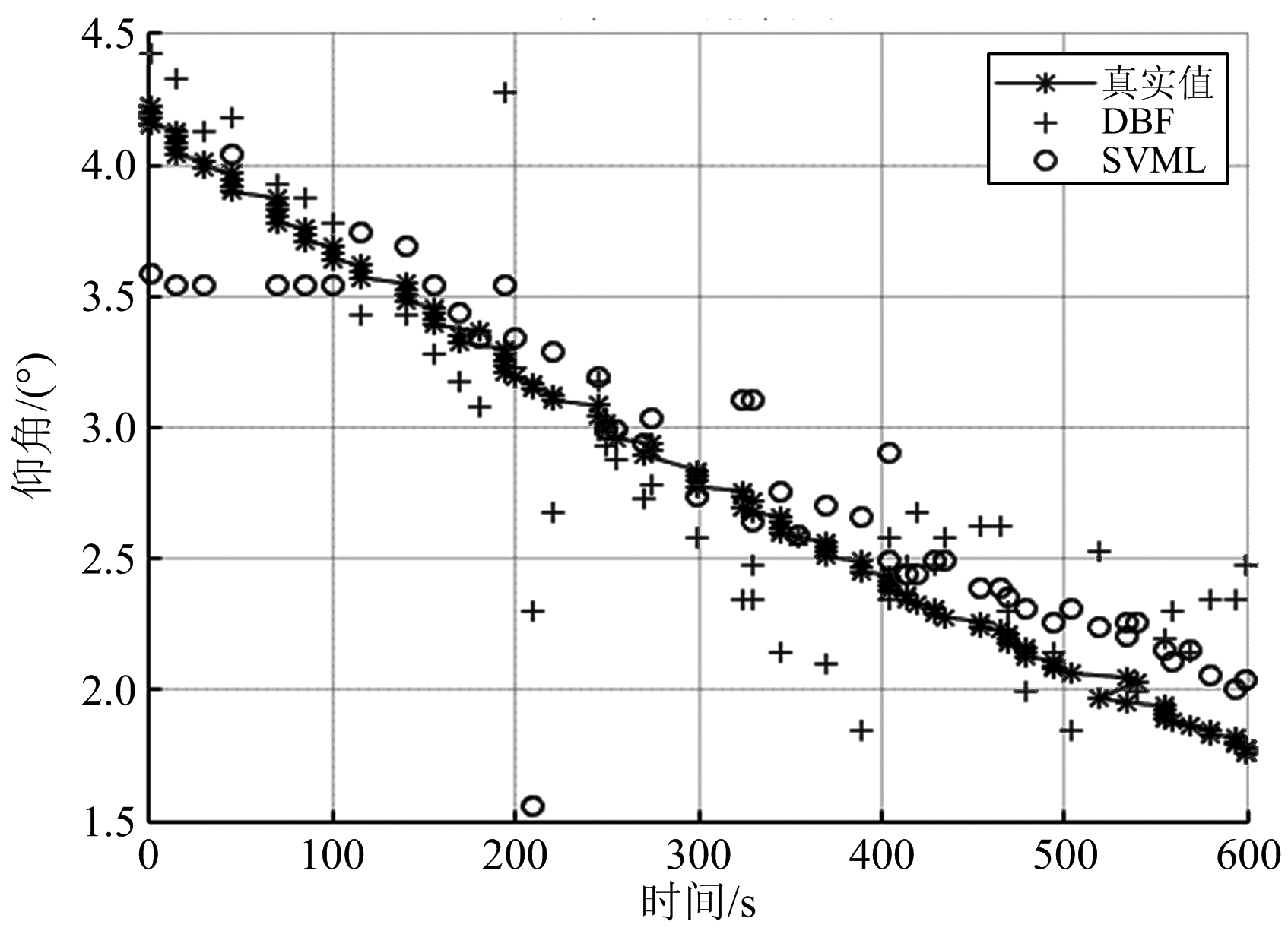
图1 测角结果对比
以上数据验证了在高仰角区DBF算法和SVML算法均能取得较好的测角效果,但是相对而言,DBF测角算法更简单、速度更快,所以高仰角区采用DBF算法测角。低仰角区SVML的测角误差更小、测角精度更高。
具体而言,如图2和图3所示,以目标真实仰角分别为5.5°和0.8°为例来进行讨论。图2和图3均采用的是某目标的实测数据。图2中目标真实仰角为5.5°。可以看出,当目标在高仰角区时,采用两种算法均可较为准确地估计其来波方向。从图2(b)可以看出,SVML的波瓣比DBF更窄,因此相对DBF算法而言,角度分辨率更高一些。图3中目标的真实仰角为0.8°。从图3(b)可以看出,SVML的波瓣比DBF更窄。因此,当目标处于低仰角区时,对于DBF算法来说,直达波反射波都处于一个波束宽度内,很难进行分辨,进而导致角度模糊,而SVML算法的波瓣使其对直达波和反射波有更高的分辨率。
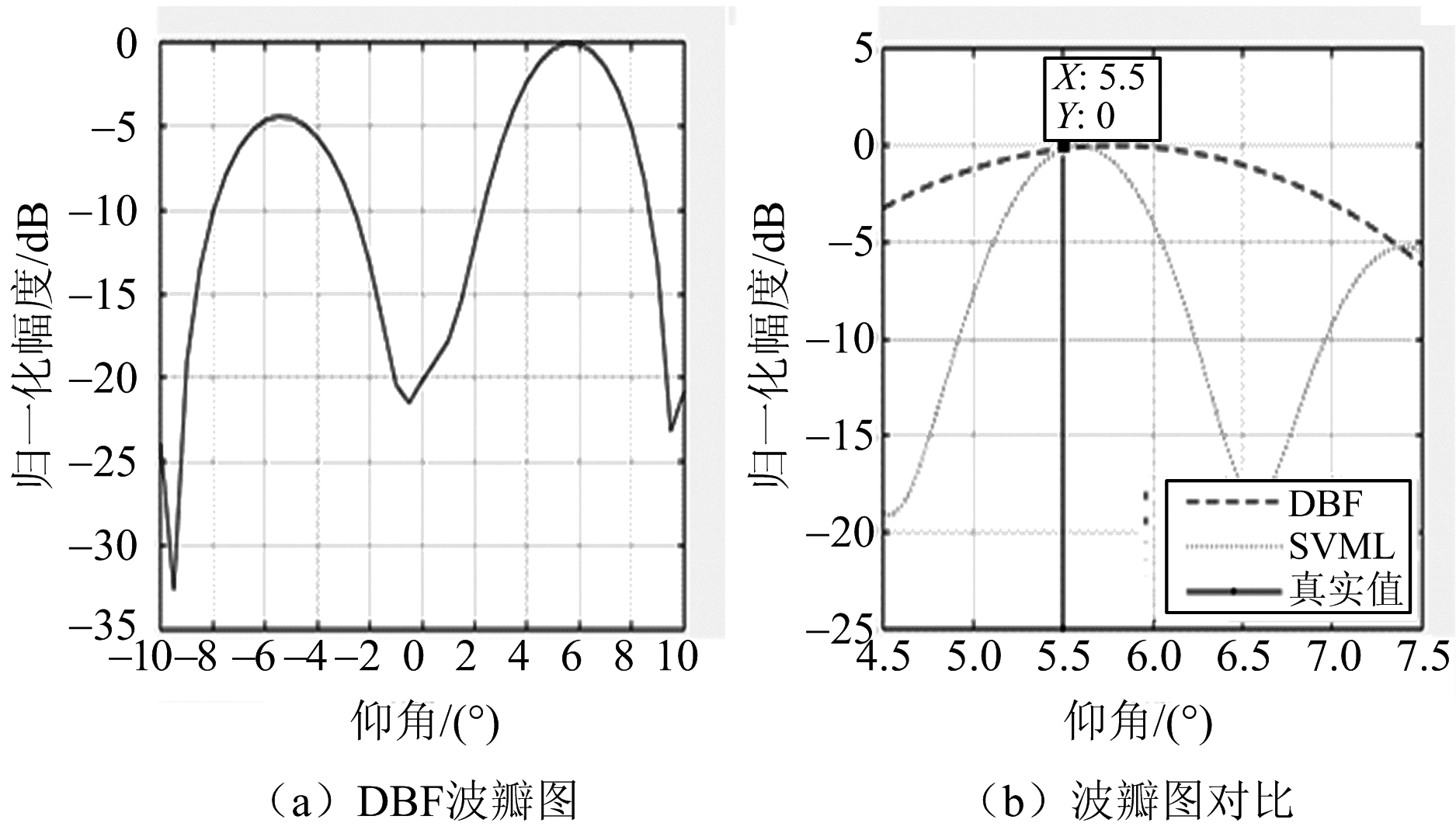
图2 测角结果分析(目标真实仰角为5.5°)
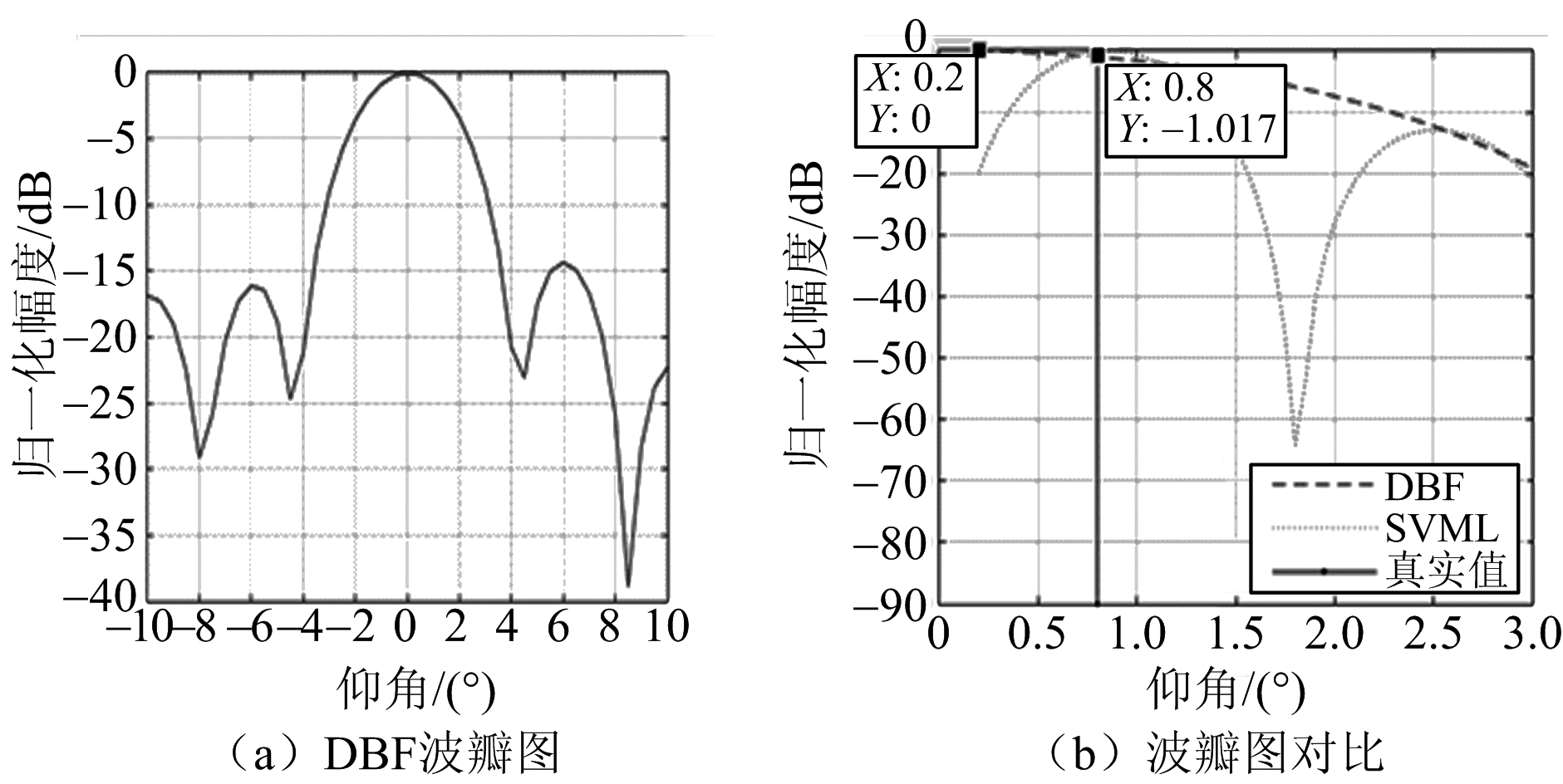
图3 测角结果分析(目标真实仰角为0.8°)
基于上述仿真分析可得,在高仰角区直接采用DBF算法进行测角就可以满足雷达系统的要求,但是在低仰角区测角不能满足分辨率要求,测角结果出现很大误差。虽然SVML算法的窄波瓣使其拥有更高的测角精度,但是该算法复杂度高、运算实时性差。所以本文中采用DBF和SVML相结合的混合测角方法,一方面为了提高低仰角区的测角精度,另一方面则是为了提高测角速率。
1.2 DBF算法基本原理
DBF方法是指采用数字信号处理方法,针对某一方向的雷达回波信号,通过对因为传感器在空间位置的不同而引起的传播波程差导致的相位差进行补偿,最终实现同相叠加,使该方向上接收到的能量最大,形成该方向上的波束,以实现期望信号的接收[7-8]。进一步地,可以通过改变权值来实现波束扫描。在实际工程实现中,因为目标的高度测量只与目标的仰角相关,与方位角无关,所以,数字波束的形成只进行仰维的。另外,工程只为了使波束能够指向空间的不同方向,可以通过改变阵元权值来实现,然后,分别针对每个入射角θ来计算DBF模值,达到对空域搜索的目的。
阵列输出信号模型为
Y(t)=W1×NX(t)N×P
(1)
W=[1,ejκdsinθ,…,ejκd(N-1)sinθ]
(2)
式中,W表示导向矢量,X(t)表示经过A/D采样和数字脉冲压缩处理后的雷达回波信号,κ=2π/λ表示雷达波数,d表示相邻阵元间距离,N表示阵元数,P表示脉冲数。假设搜索的仰角范围为α∈[α1,α2],令α1<α2,入射角θ每隔一定的步进Δθ遍历搜索[α1,α2],并计算[α1,α1+Δθ,…,α2]对应的幅度值,最大的DBF幅度值对应的α为入射角θ的仰角位置。
1.3 SVML算法基本原理
合成导向矢量(SVML)算法是在ML的基础上作了一些改进,以提高其测角速率[9-10]。SVML算法的准确性与安放雷达附近的地形息息相关,该算法充分考虑了地形反射系数、目标与雷达的直达距离以及雷达天线的高度等信息[11]。当合理利用雷达附近地形信息对测角结果进行修正,就可以较为准确地计算出目标的波达方向。SVML算法的基本思想是[12-13]:首先,通过采集到的雷达回波信息,对雷达周围360°方位对应的地形信息进行估计,为后续地形修正做好数据准备;其次,利用等效的球面模型和目标的相关参数信息,一方面,计算得到反射波的角度,另一方面,计算出直达波与反射波的波程差;然后,根据入射角计算得到直达波和反射波的导向矢量,再根据上述得到的反射系数和波程差计算得到合成导向矢量[14];最后,根据计算得到的导向矢量进一步计算得到关于入射角的SVML函数,搜索找出最大谱峰对应的角度,即为所求目标仰角。
根据等效的球面模型计算得到的目标高度ht为
(3)
目标与天线的地心夹角φ及水平距离g为
(4)
g=φ(re+hr)
(5)
综合式(3)~式(5)得
(6)
式(6)的解为
(7)
(8)
(9)
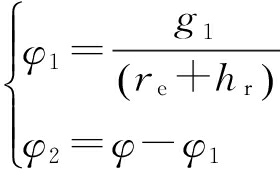
(10)
得到反射路径ri1和ri2为
(11)
(12)
式(13)中,Δr为反射路径ri1和ri2计算得到的反射波与直达波的波程差:
Δr=ri1+ri2-rd
(13)
得反射角θi为
(14)
根据Δr和θi计算得到的合成导向矢量a(θ):
a(θ)=![]()
(15)
式中,ad(θ)表示直达波的导向矢量,ai(θ)表示反射波的导向矢量,ρ表示反射系数,常取-0.95。然后,利用a(θ),计算正交投影矩阵P(θ):
P(θ)=a(θ)[aH(θ)a(θ)]-1aH(θ)
(16)
最后,求入射角θ的最大似然函数为
(17)
式中,R为回波信号的自相关矩阵。
需要注意的是,SVML算法与雷达附近地形要求很严格,其测角精度也受地形影响严重,只有当地形匹配时,也就是对测角结果进行合适的地形修正时,该算法的测角精度才高。因此在使用SVML算法时,建立合适的地形数据是必要的[15]。
2 CUDA编程模型
CUDA编程模型中,主要包含3个重点抽象:线程组层次,即一组线程构成线程块,一组线程块构成线程格,实现多层次并行结构;共享存储器,主要用来实现线程间通信以及加速并行计算;栅栏同步,其主要作用是实现程序流程按照指定顺序执行,得到期望结果[16]。根据CUDA线程划分的特点,可以将复杂问题进行划分,先划分为较大且独立的子问题,在线程块内执行;然后,将每个子问题划分为更小的子问题,在线程内进行处理[17];最终,通过多层次并行,实现通用计算加速。
综上所述,在CUDA编程架构下,一段代码被分为两部分进行执行,分别为在CPU上执行的主机代码和在GPU上执行的设备代码。通常在主机端将数据进行初始化,数据准备好后,通过PCIE总线复制到设备端完成运算,设备端完成计算后,将计算结果再复制回主机。在整个计算过程中,CPU因为具有很多缓存单元以及流控制单元,主要负责整个算法流程控制,而GPU因为具有很多运算单元,则主要负责一些复杂运算。CUDA编程模型如图4所示。所有线程同时运行相同的Kernel并根据各自的线程ID接入不同的内存地址进行运算,最终达到并行运算的目的。
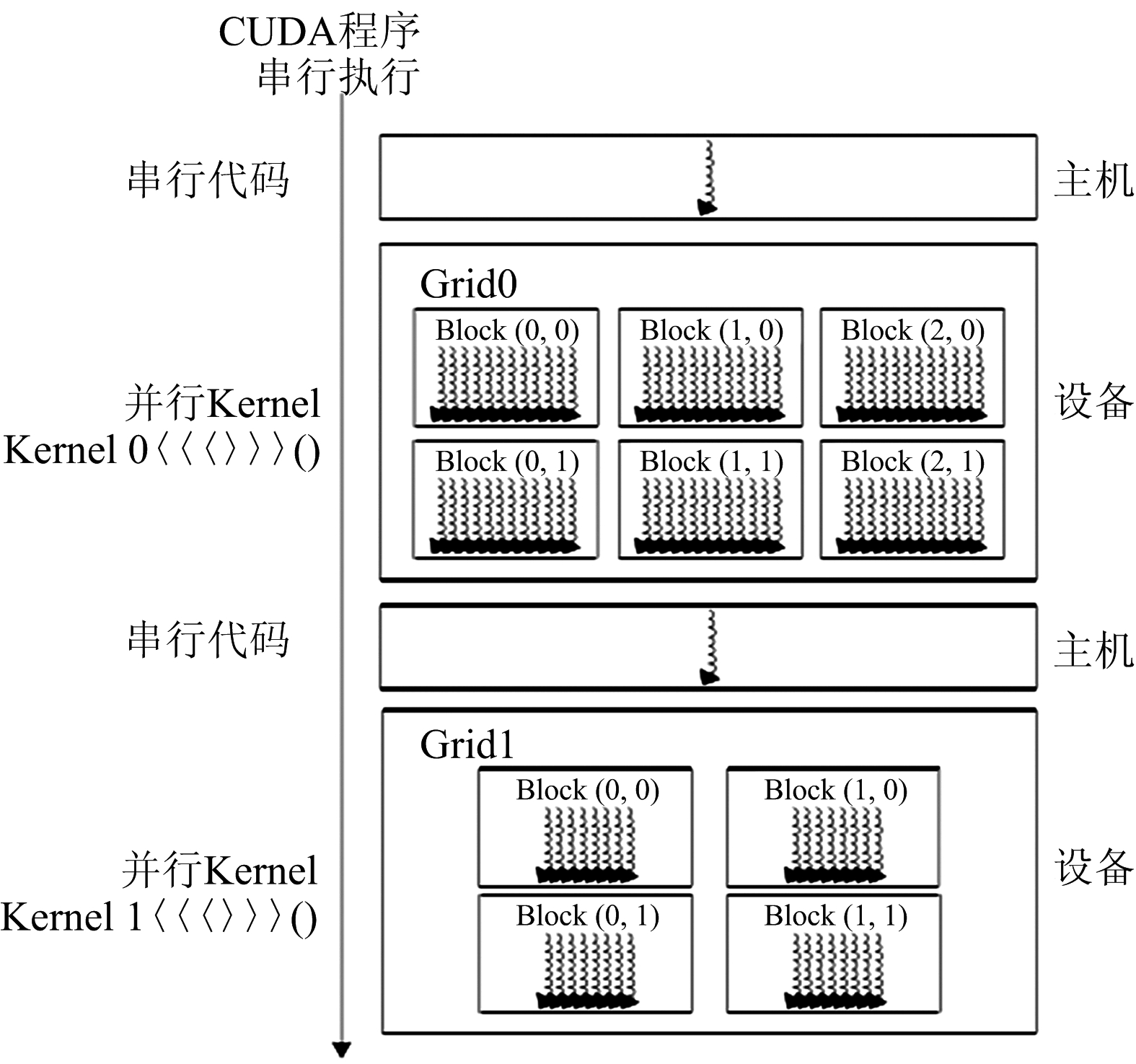
图4 CUDA编程模型
接下来介绍整个测角流程。首先,主机端采用相应的内存管理函数为数据分配CPU端所需的内存以及数据在GPU端所需的显存,并实现数据初始化。数据初始化完毕后,将数据复制到GPU,由设备代码完成主要计算过程。在GPU上,先进行DBF粗测。为了降低副瓣对测角结果的影响,DBF粗测前进行加窗处理。这里可以采用线程块索引(blockIdx)来控制测角数目,线程索引(threadIdx)来控制脉冲数,充分利用块内线程可以相互通信这一特点,加快运算效率。即DBF粗测完成后,得到目标波达方向的大致范围,接着采用SVML算法进行精测。SVML算法的主要流程如图5所示,首先要根据地球模型计算反射角和相位差,然后进行最大似然估计,最终找出最大似然值所对应的角度值就是要估计的波达方向。
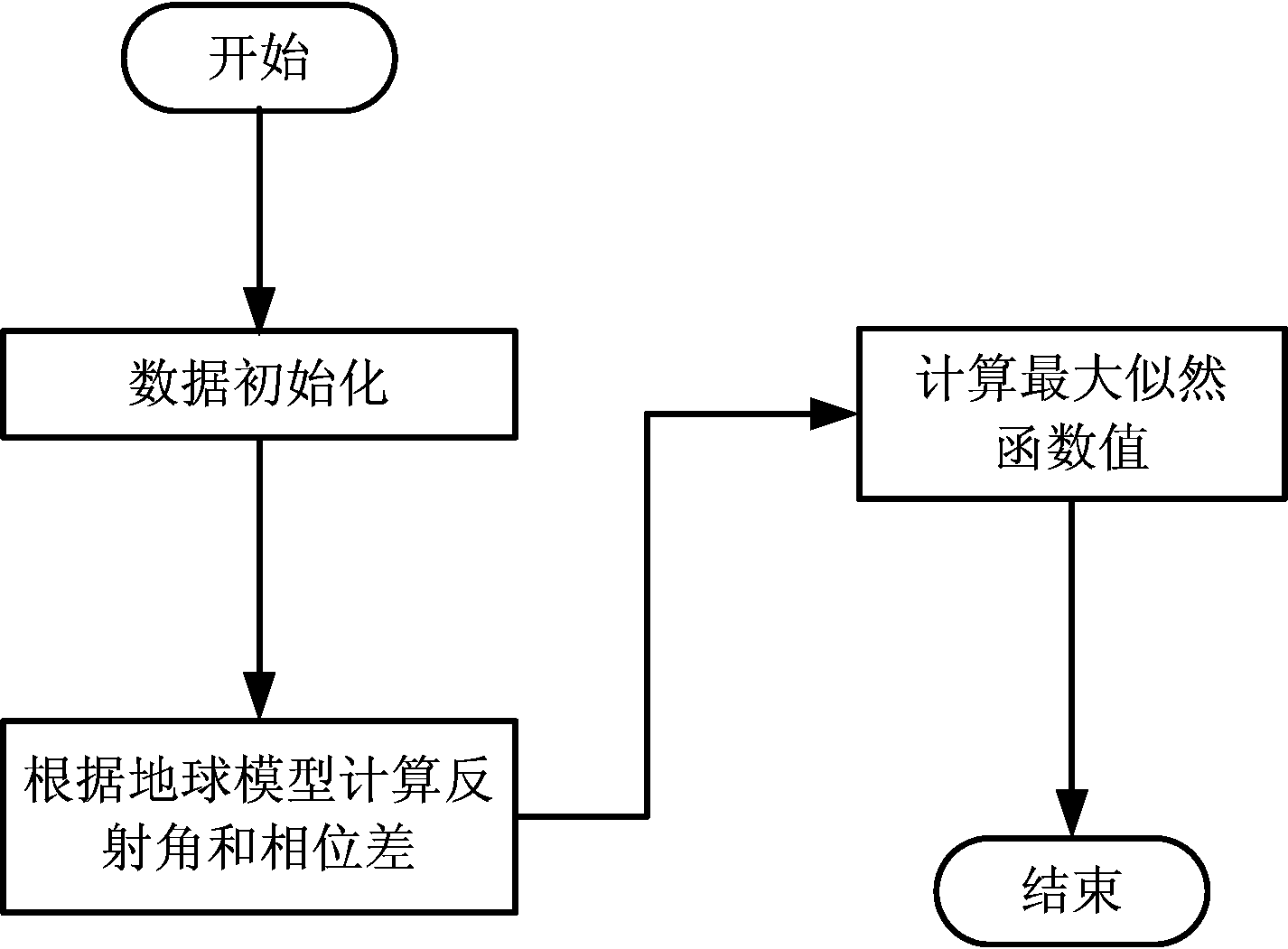
图5 SVML算法流程图
每个线程计算一个似然值,也就是说,每个线程进行如图5所示的流程,最终每个线程计算得到一个似然值。即可以采用以下索引方式:
int tid=threadIdx.x+blockIdx.x*blockDim.x;
while(tid<ang_num){
∥ang_num为搜索角度数目
/**根据地球反射模型计算反射角和相位差
/**计算最大似然函数值
tid+=blockDim.x*gridDim.x;}
经过上述分析,可以得出整个测角流程,如图6所示。
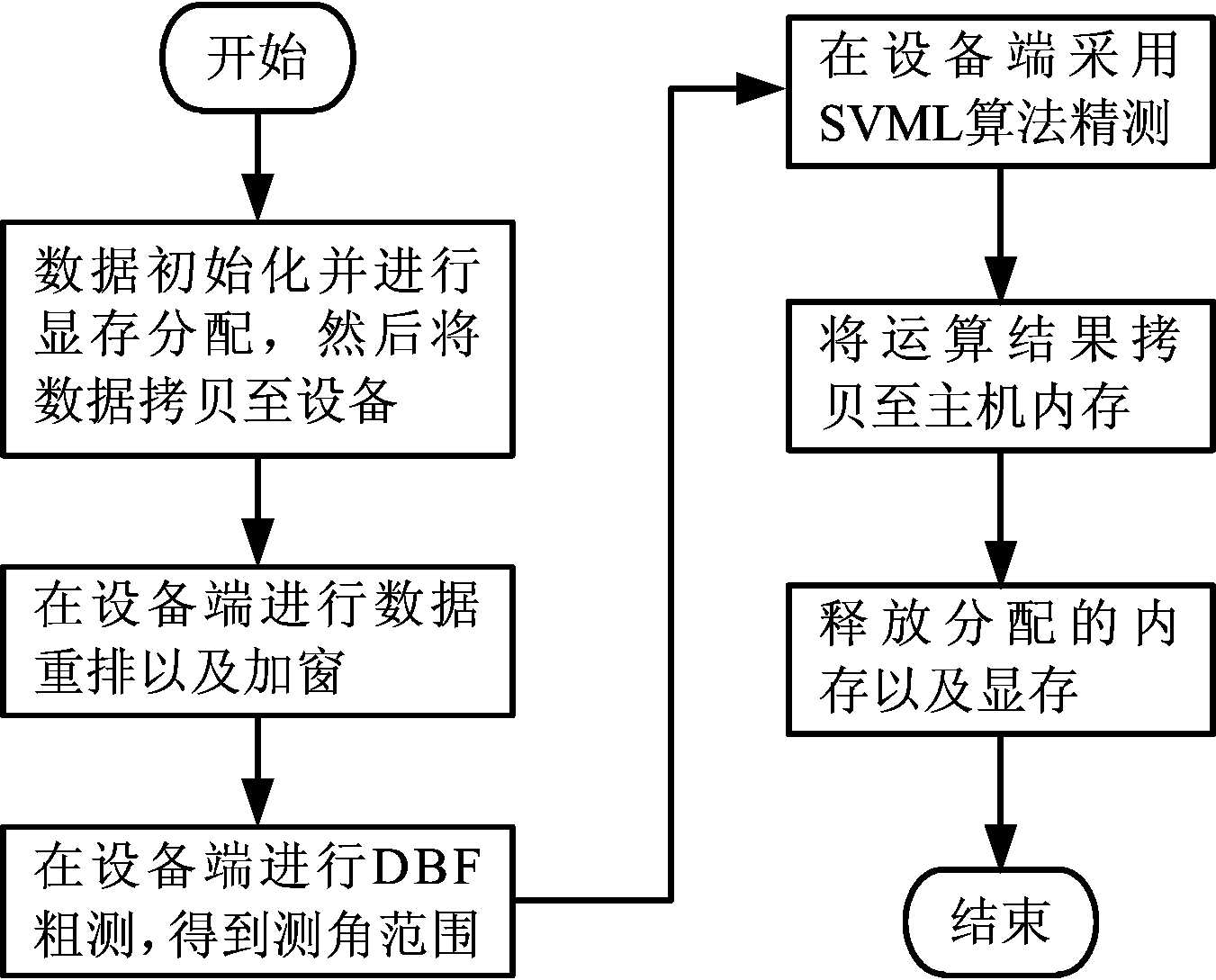
图6 DBF和SVML算法混合侧向流程图
3 仿真结果及分析
本次仿真采用的操作系统为Windows 7 SP1,显卡是计算能力为2.0的NVIDIA Tesla C2050,该显卡支持双精度浮点运算,满足雷达系统对精度的要求。本文中,为了提高运算精度,数据处理均采用双精度浮点数。
例如该设计中对某一目标的真实仰角为1.4°,则对应DBF粗测结果如图7和图8所示。
图7 CPU上DBF粗测结果
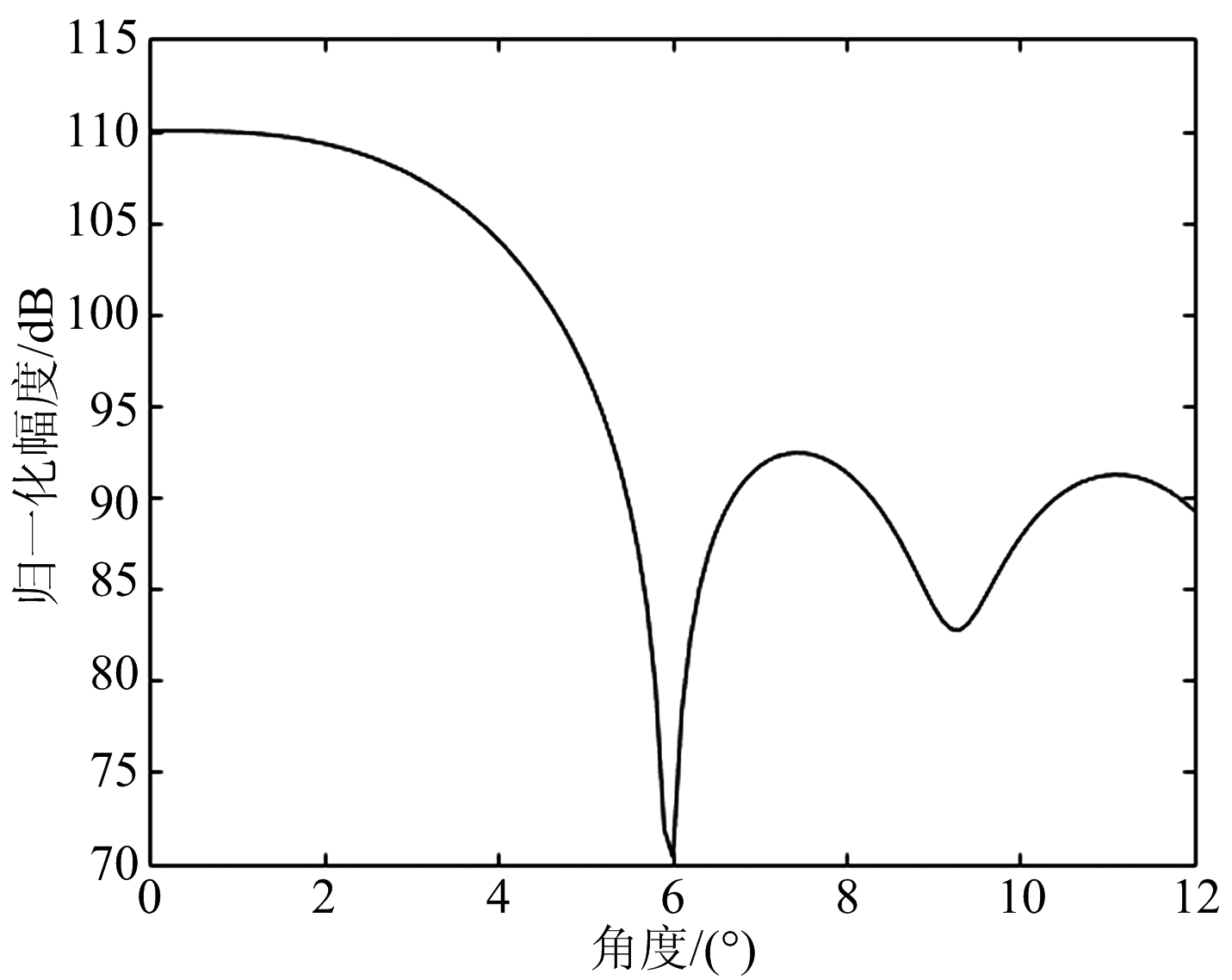
图8 GPU上DBF粗测结果
从图7和图8可以看出,GPU上DBF粗测结果同CPU一致,并且在低仰角区时,波束形成结果相差甚微,所以很难根据波束形成结果确定对应角度,从而出现测角模糊。采用混合测角方法以及GPU并行计算,减小了运算量,加快运算速率。SVML谱图如图9和图10所示。
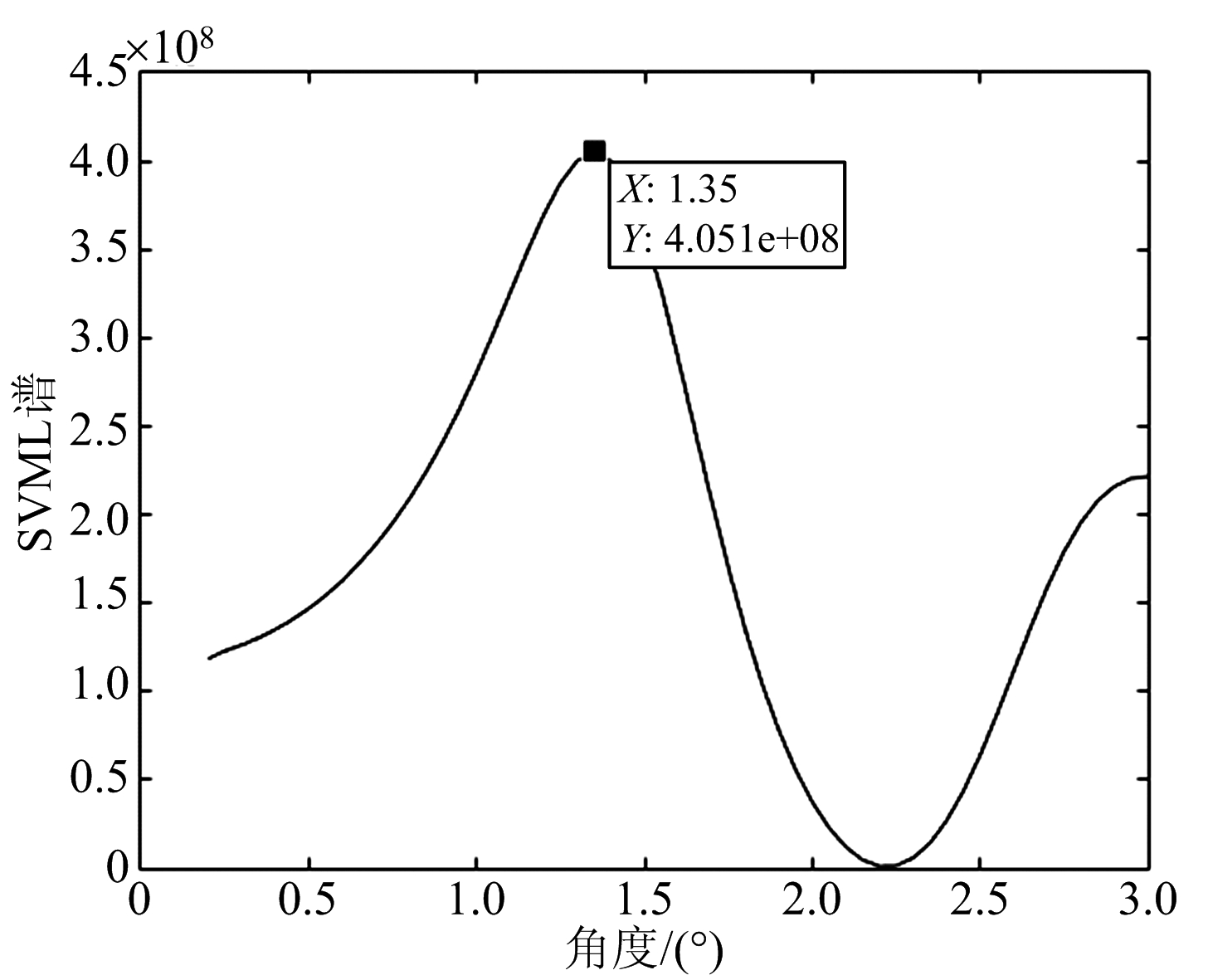
图9 CPU上SVML谱图
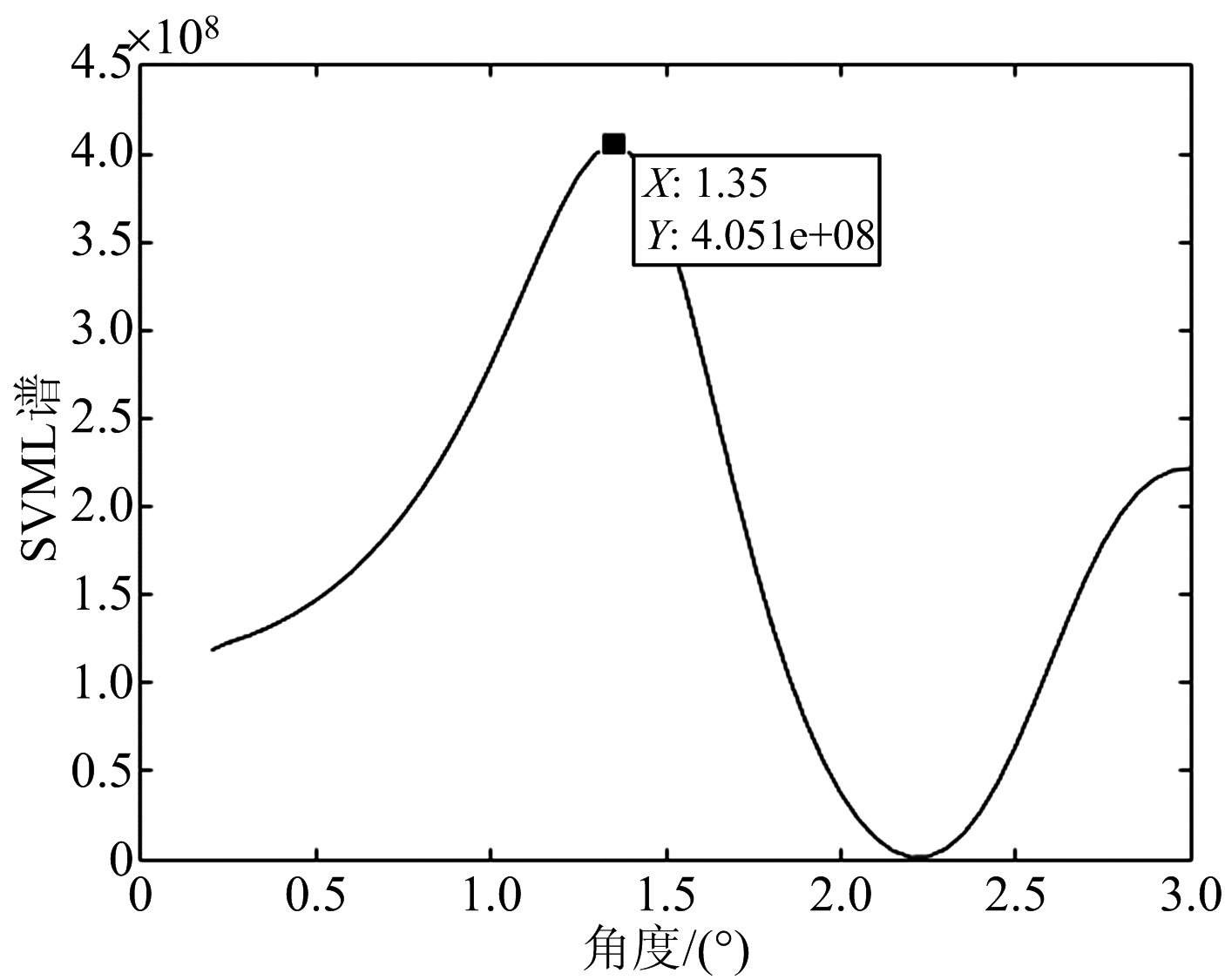
图10 GPU上SVML谱图
图9和图10分别表示CPU,GPU上生成的SVML谱图,图11则是在原值基础上换算成分贝值得到的。从图中可以看出,在CUDA平台上利用GPU进行波达方向估计结果与CPU上估计结果是一样的,但是通过测量可以发现,两者的处理速度有很大差别。表1所示为处理相同数据CPU与GPU所用时间对比。
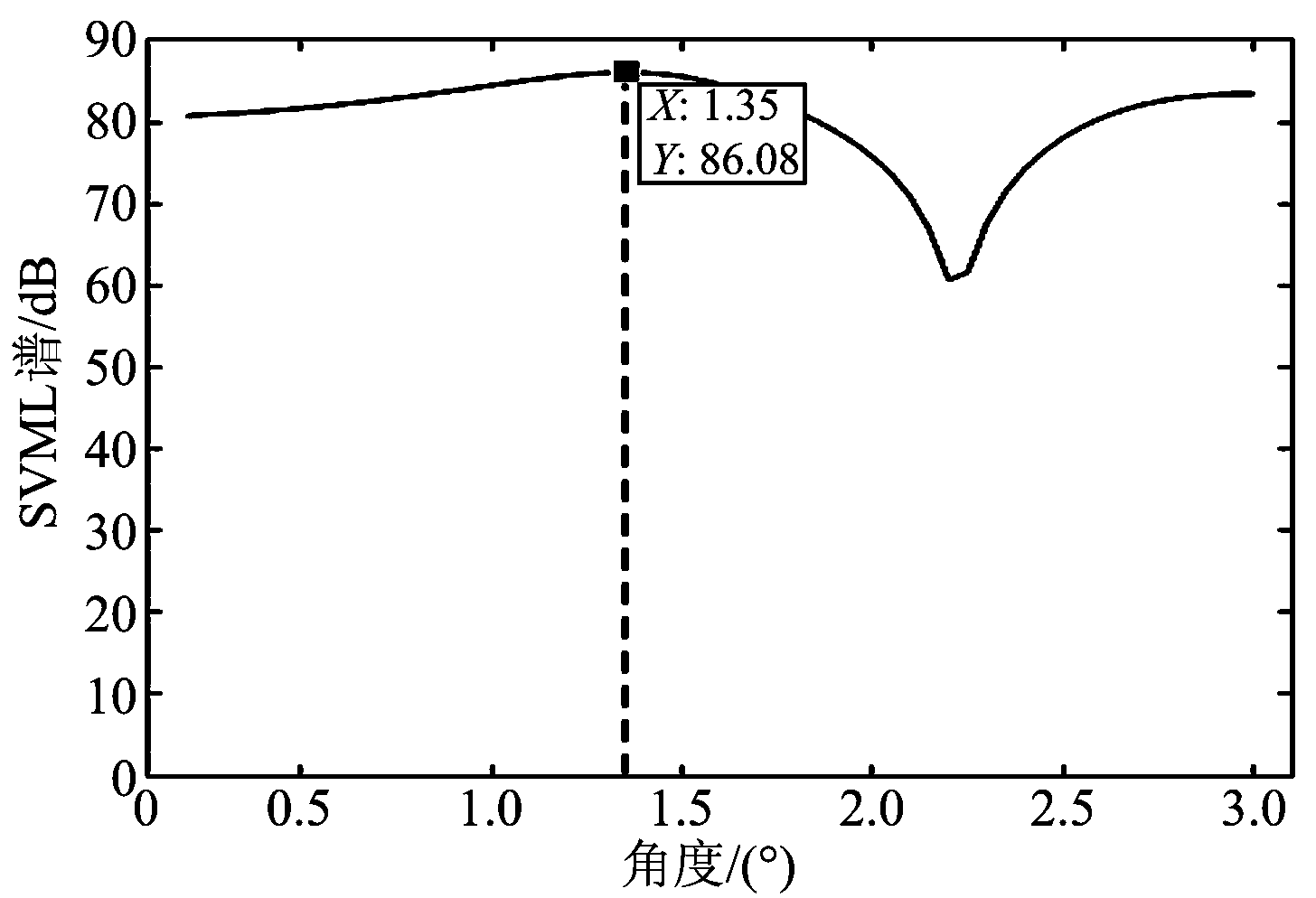
图11 SVML谱图
表1 CPU与GPU所运行时间对比
ms
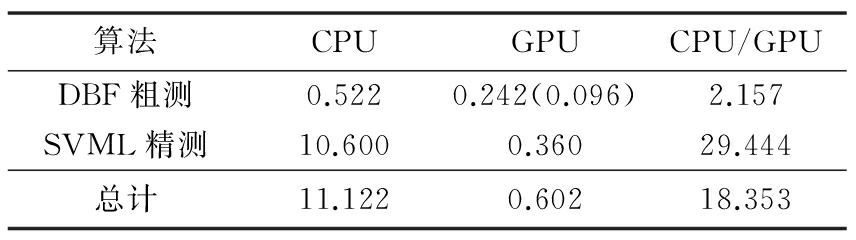
从表1可以看出,GPU比CPU的数据运算效率更高。要说明的是,DBF粗测一栏括号内数字表示总时间0.242 ms内有0.096 ms用于数据传输,也就是说,GPU有很大一部分时间都是用在数据传输上,所以,在GPU运算过程中,应当尽量减少数据传输时间。
4 结束语
实验表明,通过在GPU上估计来波方向,不仅达到了和CPU上一样的效果,而且加快了运算速度,提高了运算效率。但是在CUDA程序中,主机与设备之间的数据传输会耗费很多时间,所以,可以采用以下3种方法减少传输时间。
方法1:尽量减少在主机和设备之间进行数据传输,尽量减少传输的数据量。
方法2:可以采用纹理存储器来保存一些地形数据、窗函数、角度搜索表等,可以使用纹理内核函数来读取纹理存储器。因为纹理存储器带有缓存机制且只读,所以速度很快。
方法3:可以采用流来实现计算与数据传输的重叠,即支持设备重叠功能的GPU能够在执行一个CUDA C核函数的同时,还能在设备与主机之间执行复制操作。
总的来说,利用CUDA处理数据相比CPU而言,很好地满足了目前信息处理对高精度、实时性、大数据的要求。
参考文献:
[1] 董玫. 米波雷达测高算法及应用研究[D]. 西安: 西安电子科技大学, 2008.
[2] SHAN T J, KAILATH T. Adaptive Beamforming for Coherent Signals and Interference[J]. IEEE Trans on Acoustics, Speech and Signal Processing, 1985, 33(3):527-536.
[3] 王布宏, 王永良, 陈辉. 相干信源波达方向估计的加权空间平滑算法[J]. 通信学报, 2003, 24(4):31-40.
[4] 张庆科, 杨波, 王琳, 等. 基于GPU的现代并行优化算法[J]. 计算机科学, 2012, 39(4):304-311.
[5] SABDERS J, KANDROT E. GPU高性能编程CUDA实战[M]. 聂雪军, 等译. 北京: 机械工业出版社, 2011.
[6] 朱伟. 米波数字阵列雷达低仰角测高方法研究[D]. 西安: 西安电子科技大学, 2013.
[7] 吴向东. 米波雷达低仰角测高算法及相关技术研究[D]. 西安: 西安电子科技大学, 2008.
[8] 李娜. 几种超分辨算法在米波雷达测高中的应用[D]. 西安: 西安电子科技大学, 2013.
[9] 刘张林, 陈伯孝, 杨雪亚, 等. 米波雷达最大似然超分辨测高技术研究[J]. 雷达科学与技术, 2011,9(4):308-310.
[10] 张裕峰. 多径传播条件下的波达方向估计算法研究[D]. 合肥: 中国科学技术大学, 2010.
[11] 汪坤. 某米波雷达测高方法的改进及工程实现[D]. 西安: 西安电子科技大学, 2015.
[12] 丁鹭飞, 耿富录. 雷达原理[M]. 3版. 西安: 西安电子科技大学出版社, 2002.
[13] MAHAFZA B R. 雷达系统分析与设计: MATLAB版[M]. 2版. 陈志杰, 罗群, 沈齐, 等译. 北京: 电子工业出版社, 2008.
[14] 胡晓琴, 陈建文, 王永良. 米波雷达测高多径模型研究[J]. 电波科学学报, 2008, 23(4):651-657.
[15] 吴顺君, 梅晓春. 雷达信号处理和数据处理技术[M]. 北京: 电子工业出版社, 2008.
[16] 吴志辉, 徐小红, 朱同林. 基于CUDA的直方图问题并行优化[J]. 现代计算机, 2015(13):58-61.
[17] 刘星, 孙文君, 曹雅楠, 等. 基于GPU的异构并行环境下程序优化策略研究[J]. 湖北第二师范学院学报, 2010, 27(8):88-91.

