0 引言
雷达在对低空巡航飞行目标进行跟踪测量时，强相关的直达波和多径反射波同时进入接收波束主瓣，多径效应严重影响着低空(低仰角)目标的探测与测量[1-3]。尤其是处于地平线反射区域的超低空目标，常规的多径消除技术不能使测量雷达有效地工作于这一区域。由于直达回波和多径反射波在距离和速度上差异很小[4-5]，无法通过脉冲压缩从距离上进行分离[6]，也不能通过多普勒测速进行分离，只能考虑利用仰角差异进行分离直达回波和多径回波，并进行仰角和高度测量。
由于回波中所携带的关于目标仰角的相位信息被多径回波所破坏，单脉冲测角技术[7]会带来很大的测高误差。阵列超分辨技术已应用于多径信号的波达方向估计问题中，代表性的算法有线性预测算法[8]、空间平滑MUSIC[9](多重信号分类)算法，以及最大似然[10-11]类参数估计方法等。但是这类算法通常需要特征值分解和多维空间谱搜索。利用直达角和反射角之间的几何关系[12]，可将二维空间谱搜索降为一维空间谱搜索。但是对于大型跟踪测量雷达，处理过程仍然涉及上百个阵元的协方差矩阵计算和空间谱搜索，其运算量仍然很大，不利于工程实现。
波束域处理是一种阵列接收数据预处理的方法，通过线性变换把阵元空间合成一个或几个波束，再对合成后的波束域的数据用超分辨算法进行角度估计，因其具有运算量低、对系统误差和空间色噪声不敏感，以及降低信噪比门限等优点，近年来受到了普遍的关注。文献[4,13]介绍了波束域处理在低角跟踪的应用。
本文将波束域处理应用到最大似然算法中，利用波束域最大似然算法进行低仰角超分辨处理。通过优化多波束指向和波束形成幅度加权，形成多个俯仰交叠波束，然后使用最大似然算法对波束域数据进行空间谱搜索，通过空间谱能量最大化的角度估计目标仰角和高度。本文方法受反射多径影响小、测量精度高，且运算复杂度低，适用于低角目标的跟踪和测量。
1 信号模型
垂直放置的均匀线阵(ULA)由N个间距为d的阵元组成，阵列参考点高度为ha。假设阵地反射面为平坦反射面，远场窄带的目标回波信号分别经直达路径Rd和地面反射路径Rs入射到阵列，目标高度为ht，对应的入射俯仰角为Ψ=[φd,φs]，其中φd和φs分别为目标的直达波和地面反射波的俯仰角，如图1所示。
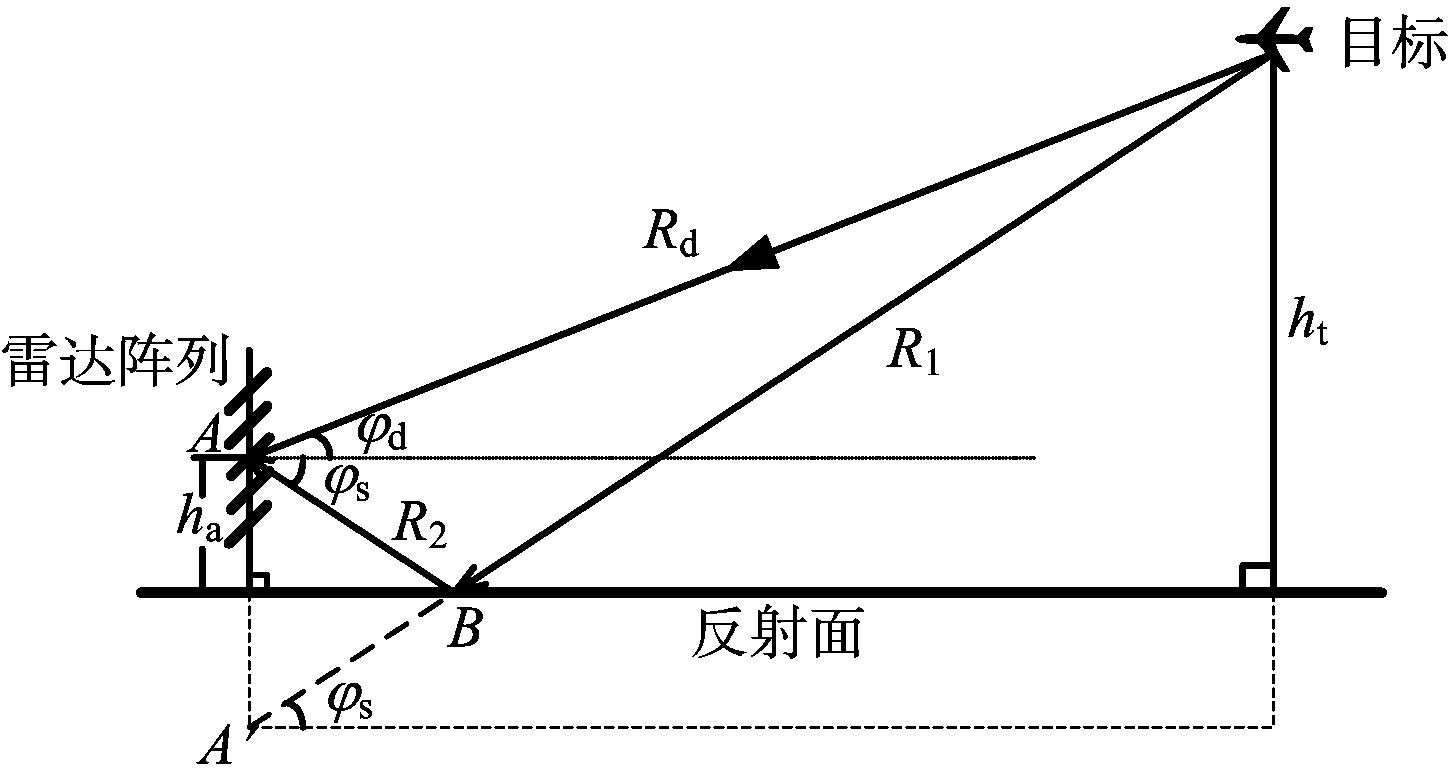
图1 阵列天线接收信号电波传播示意图
阵列接收的回波矢量为
x(t)=A(Ψ)·s(t)+n(t)=
n(t), t∈{t1,…,tL}
(1)
式中，A(Ψ)=[a(φd) a(φs)]为阵列流型矩阵， a(φd)=[1,exp(j2πd/λsin(φd)),…,exp(j2π(N-1)d/λsin(φd))]T为阵列对目标直达波的导向矢量, (·)T表示转置，a(φs)为对应反射波的导向矢量，s(t)=[s(t) ρs(t-τ)]T为目标回波复包络向量，ρ为反射区的反射系数，τ=ΔR/c为波程差引起的时延，其中ΔR=Rs-Rd=R1+R2-Rd， n(t)为与信号不相关的复高斯白噪声向量。N×L的数据矩阵X=[x(t1),…,x(tL)]表示L快拍的阵列数据。
当地面粗糙度增加到不再满足瑞利准则时，来自于目标到达粗糙面上的信号不是完全的镜面反射，同时在其他入射角上被散射，此时雷达天线接收的信号应该是镜面反射分量与漫反射分量之和。将式(1)信号模型写成矢量形式：
x(t)=(Ad+Γ⊙As)s0(t)+n(t)
(2)
式中，Ad=a(φd)，Γ为反射系数向量，⊙表示Hadamard积，As=
a(β)g(β-φs)dβ为多径反射向量之和，其中a(β)=[1,ej2πdsinβ/λ,…,ej2πd(N-1)sinβ/λ]T，g(β-φs)为多径反射角分布函数。显然，当反射面完全平坦时As=a(φs)。
2 波束域最大似然测高方法
对式(1)所示的阵列接收数据，采样数据的联合概率密度函数为
f(X)=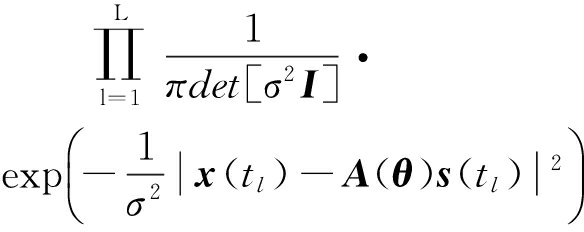
(3)
忽略常量后的对数似然函数如式(4)所示：
(4)
为了计算最大似然函数，需要根据未知参数最大化对数似然函数，首先固定θ和s，根据估计σ2使得Lf最大化，可得
(5)
把上式带回对数似然函数里，忽略常数项，则最大似然估计可以通过解下面的最大化问题得到：
(6)
因为对数函数是单调函数，则上式的最大化问题即是式(7)的最小化问题：
(7)
下面固定θ，根据s的估计使得上式最小化，可得
(8)
式中，(·)H表示厄米特共轭转置。把上式代入，可以得到式(9)给出的最小化问题：
(9)
式中，PA(θ)是由矩阵A(θ)的列向量张成的空间的投影，表达式如下：
PA(θ)=A(θ)(AH(θ)A(θ))-1AH(θ)
(10)
因此参数θ的最大似然估计可以通过最大化式(11)的对数似然函数得到：
(11)
通过下式简化：
Lf(θ)=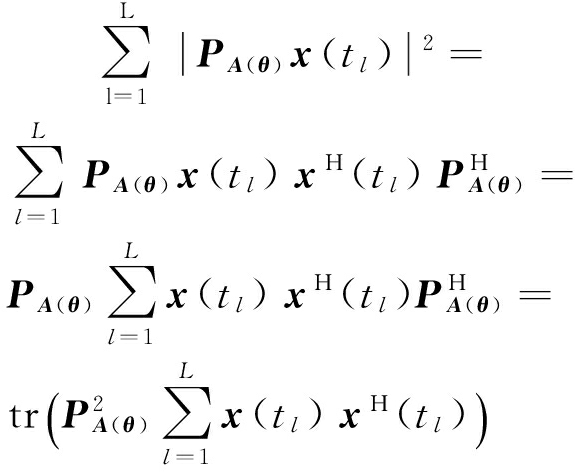
(12)
又因为投影矩阵
和
则θ的最大似然求解即最大化式(13)：
(13)
对于高频段雷达而言，俯仰维通常有几十个至上百个阵元，由于最大似然算法涉及空间谱搜索，将导致计算量巨大，不利于实时处理。波束域处理将空间阵元通过变换合成一个或多个波束，每个波束输出作为一个通道，再利用合成后的波束域数据进行超分辨测高。
将某一确定的观察俯仰角度区间[φdown,φup]等间隔分为B份，间隔Δφ=(θup-θdown)/(B-1)通过选择B个相邻的波束形成器a(θb),b=1,2,…,B，取矩阵C如下：
C=[a(θleft)a(θleft+Δθ)…a(θright)]
(14)
则正交化的波束形成矩阵为
T=C(CHC)-1/2
(15)
则波束形成后的输出为
Y=THX
(16)
对应的协方差矩阵为
RY=THRXT
(17)
3 实验结果分析
下面通过仿真和实测处理结果验证本文方法的有效性，将本文方法与和差比幅测角进行性能比较。
仿真实验中所采用的阵列是垂直放置的均匀线阵，阵元数为100，阵元间距半波长。设目标距离为345 km、高度为10 000 m、仰角φd=0.50°、多径入射角φs=-0.52°，地面反射系数ρ=-0.5。图2(a)是和差比幅测角方法和波束域最大似然超分辨算法的仰角测量误差随信噪比的变化，图2(b)是两种方法的高度测量误差随信噪比的变化。从图2(b)可以看出，与SS-MUSIC及ML算法相比，空域滤波算法的测角结果更接近于真实值。
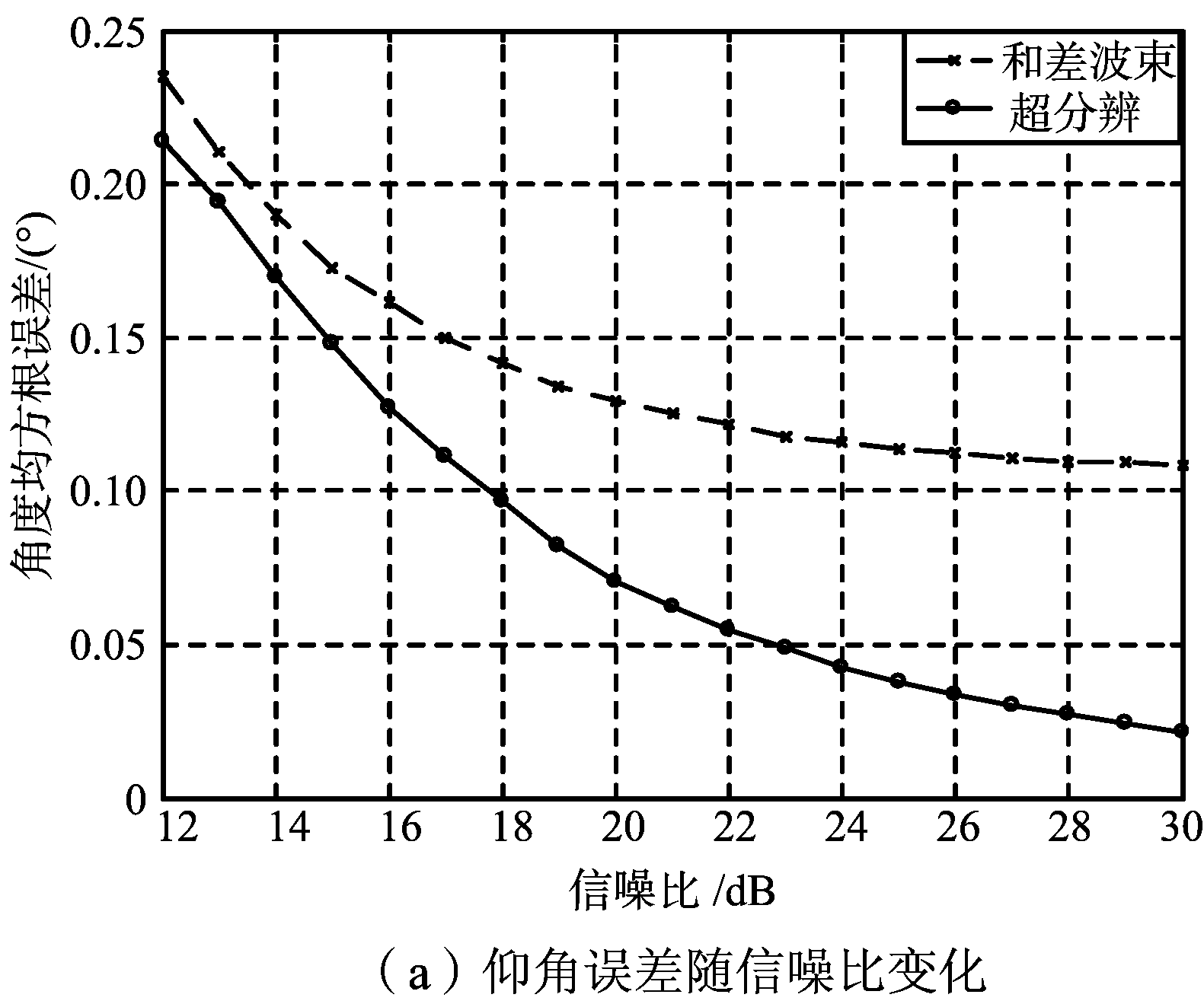
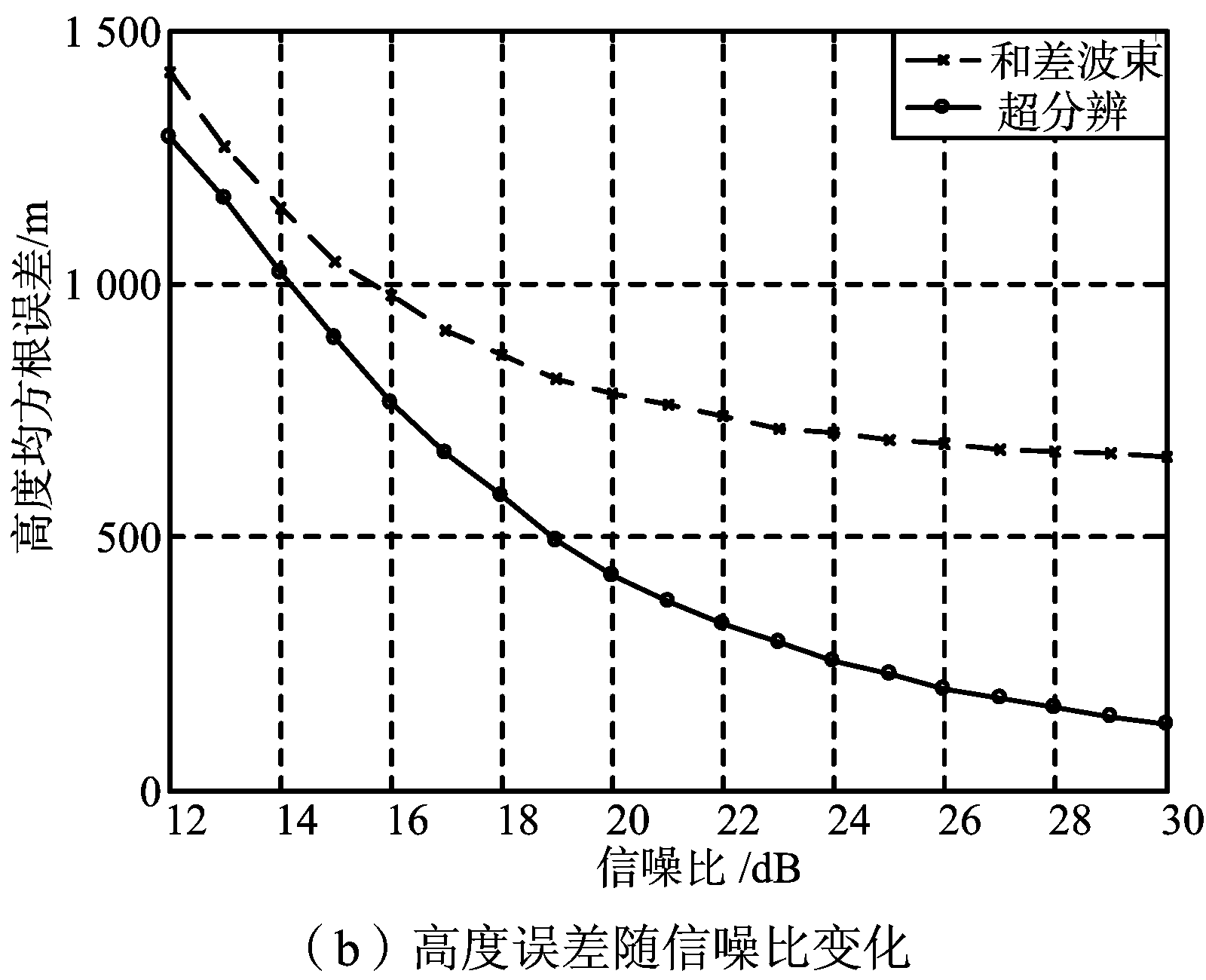
图2 仰角和高度测量结果
利用某S波段雷达采集的实测数据验证本文方法的有效性。图3是雷达对某批民航飞机的观测结果，其中图3(a)为目标仰角测量值随目标距离的变化，图3(b)为目标高度测量值随目标距离的变化，其中基于应答信号的二次雷达是目标仰角和高度的真实值。从图3可见，在低仰角时(≤1.0°)，直达回波和多径反射回波同时进入波束，多径信号影响严重，基于多波束比幅的测角方法基本失效，而本文的波束域最大似然测高方法测量的高度和目标真实高度吻合较好，在1.0°以下的低仰角区，测高均方根误差在500 m以内，显著改善了角度分辨率和测高精度。
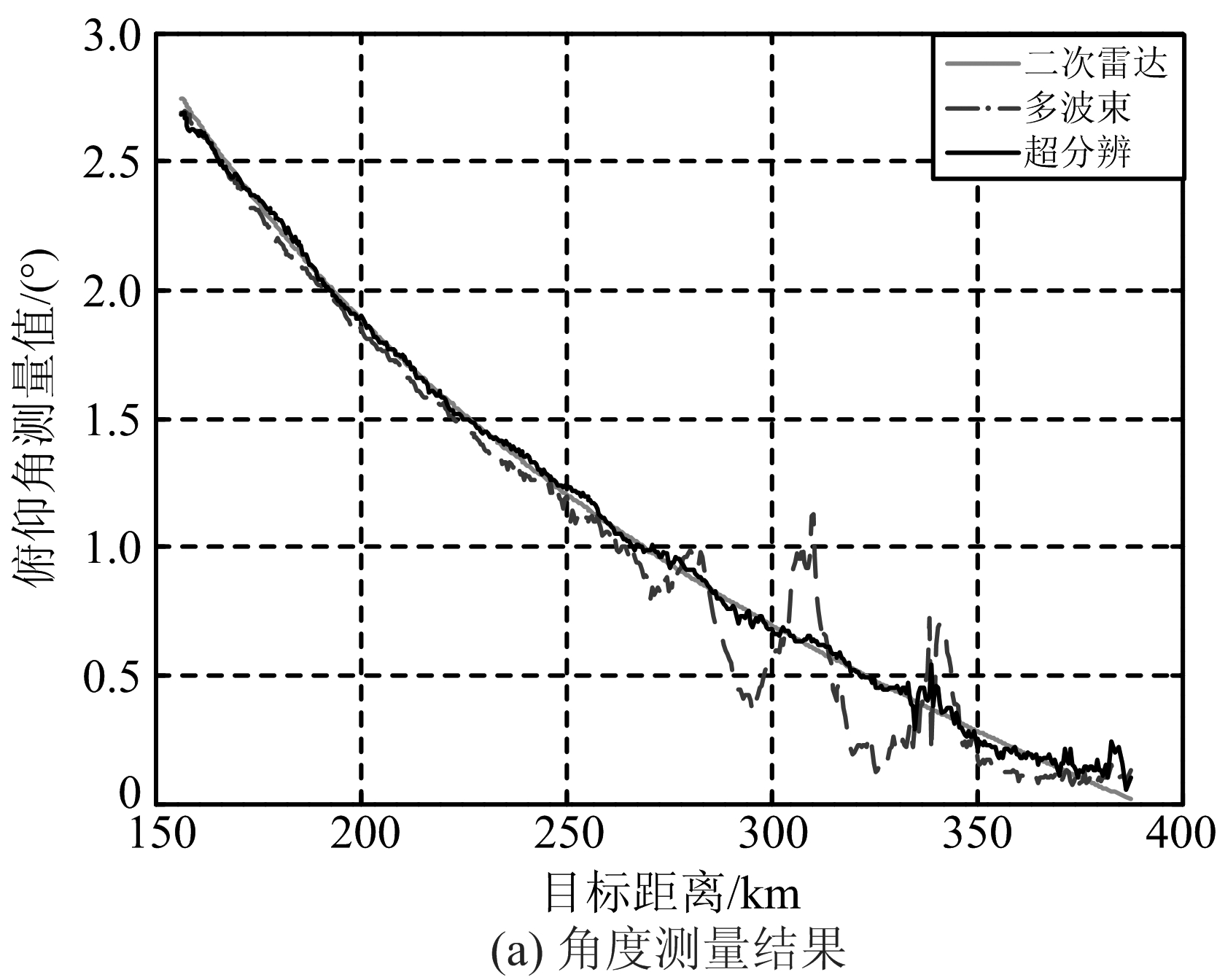
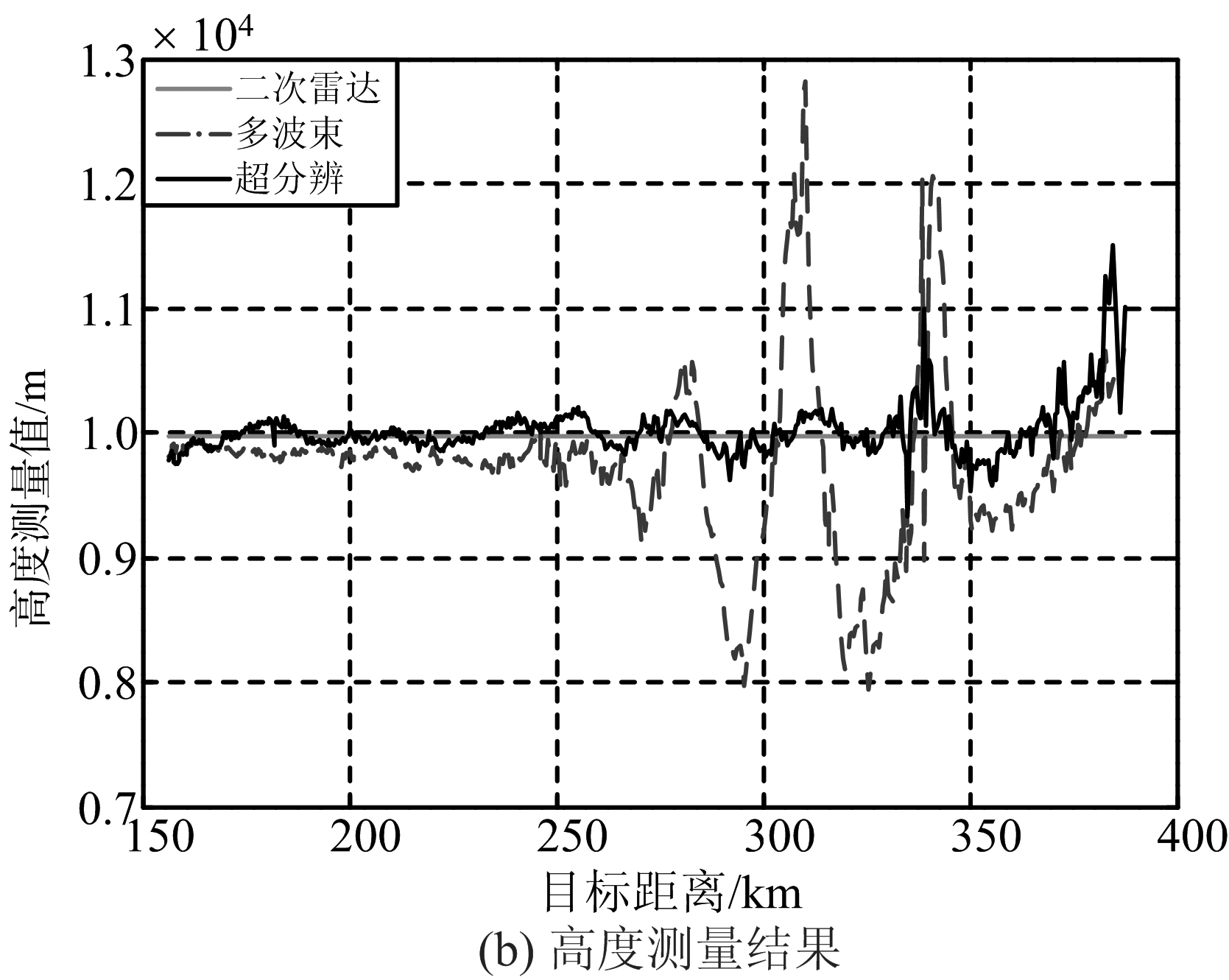
图3 实测数据处理结果
4 结束语
地面(水面)反射引起的多径信号是雷达测高中的主要难题，基于此，本文提出了波束域的最大似然测高算法。该算法对跟踪和搜索目标进行俯仰多波束覆盖，然后利用最大似然算法对波束域数据进行空间谱搜索，从而对目标仰角和高度进行估计。本文提出的方法运算复杂度低，具有较高的角度分辨率和测高精度，并通过仿真及S波段雷达实测数据分析结果得到了验证。
参考文献：
[1] HURTADO M, NEHORAI A. Performance Analysis of Passive Low-Grazing-Angle Source Localization in Maritime Environments[J]. IEEE Trans on Aerospace and Electronic Systems, 2007, 43(2):780-789.
[2] SEBT M A, SHEIKHI A, NAYEBI M M. Robust Low-Angle Estimation by an Array Radar[J]. IET Radar, Sonar and Navigation, 2010, 4(6):780-790.
[3] PARK D, YANG E, AHN S, et al. Adaptive Beamforming for Low-Angle Target Tracking Under Multipath Interference[J]. IEEE Trans on Aerospace and Electronic Systems, 2014, 50(4):2564-2577.
[4] ZOLTOWSKI M D, LEE T S. Maximum Likelihood Based Sensor Array Signal Processing in the Beamspace Domain for Low Angle Radar Tracking[J]. IEEE Trans on Signal Processing, 1991, 39(3):656-671.
[5] 杨广玉, 马晓静, 杨雪亚. 基于时-空稀疏解的方位超分辨算法[J]. 雷达科学与技术, 2014, 12(2):171-175.
YANG Guangyu, MA Xiaojing, YANG Xueya. Azimuth Super-Resolution Algorithm Based on Temporal-Spatial Sparse Solution[J]. Radar Science and Technology, 2014, 12(2):171-175.(in Chiense)
[6] GE Fengxiang, SHEN Dongxu, PENG Yingning, et al. Super-Resolution Time Delay Estimation in Multipath Environments[J]. IEEE Trans on Circuits and Systems, 2007, 54(9):1977-1986.
[7] ZHOU Bilei, LI Rongfeng, DAI Lingyan, et al. Combining Sum-Difference and Auxiliary Beam Adaptive Monopulse Algorithm at Subarray Level for Anti-Jamming[C]∥12th International Conference on Signal Processing, Hangzhou: IEEE, 2014:277-282.
[8] XIN J, SANO A. MSE-Based Regularization Approach to Direction Estimation of Coherent Narrowband Signals Using Linear Prediction[J]. IEEE Trans on Signal Processing, 2001, 49(11):2481-2497.
[9] YUAN Xin. Coherent Source Direction-Finding Using a Sparsely-Distributed Acoustic Vector-Sensor Array[J]. IEEE Trans on Aerospace and Electronic Systems, 2012, 48(3):2710-2715.
[10] BORS A G, LUO M. Optimized 3D Watermarking for Minimal Surface Distortion[J]. IEEE Trans on Image Processing, 2013, 22(5):1822-1835.
[11] SHAWASH J, SELVIAH D R. Real-Time Nonlinear Parameter Estimation Using the Levenberg-Marquardt Algorithm on Field Programmable Gate Arrays[J]. IEEE Trans on Industrial Electronics, 2013, 60(1):170-176.
[12] ZHU Wei, CHEN Baixiao. Altitude Measurement Based on Terrain Matching in VHF Array Radar[J]. Circuits, Systems, and Signal Processing, 2013, 32(2):647-662.
[13] ZOLTOWSKI M D, LEE T S. Beamspace ML Bearing Estimation Incorporating Low-Angle Geometry[J]. IEEE Trans on Aerospace and Electronic Systems, 1991, 27(3):441-458.
