0 引言
在传统单通道合成孔径雷达(SAR)成像中,由于存在最小天线面积限制,无法同时获得宽距离测绘带和高方位分辨率。多通道 SAR 系统采用数字波束形成技术(DBF)可以在保证无距离模糊的前提下,通过多普勒模糊抑制来实现高分辨宽测绘带成像[1]。方位多通道 SAR在实现高分辨率宽测绘带的过程中,需要对信号进行 DBF 解模糊,这就要求各通道的特性一致,通道位置也必须精确已知[2]。然而,对于实际星载 SAR 系统,各通道之间存在着不可避免的误差。文献[3]对单星方位多通道 SAR(Multi-Channel SAR, MC-SAR) 系统的误差源进行了分析,由于外界环境因素和通道自身的加工工艺,各接收通道的幅相特性不可能完全一致;同时,安装、制造、测量误差和天线姿态误差都会导致各通道天线相位中心位置测量也存在误差,这两类非理想因素造成了通道间的幅相不一致,将影响星载MC-SAR系统DBF解模糊性能,对成像造成严重影响。因此,通道间幅相误差必须得到校正。针对这一问题,国内外提出了多种估计通道间幅相误差的方法。文献[4]提出了距离互相关法,它需要的运算量极小,但其对系统参数有着很高的要求,需要设置单独的定标模式;文献[5]提出了二维自适应校正法,该算法复杂度很低,但是幅度校正的结果却不是很理想;文献[6]提出了基于回波数据的子空间投影法,它考虑了噪声的影响,通过信号子空间与噪声子空间正交性,估计出通道幅相误差。以上文献均是针对星载MC-SAR系统单发多收模式而提出的估计算法,没有考虑多发多收模式的情况。在多发多收模式下,每个通道都要发射和接收信号,数据量相对于单发多收模式会成倍增加。对于基于回波数据的定标方法,其估计算法的运算量会大大增加。因此,本文利用子空间估计算法,提出了一种基于发射机与接收机的定标方法,该方法只需处理天线自发自收所得到的回波,大大降低了数据量,通过将通道的发射和接收相位误差进行分离,对成像进行校正。
该方法分两次估计,首先通过SAR系统接收地面发射机对其发射的信号,估计出接收通道间的幅相误差;其次通过接收机接收系统发射的信号,估计出发射通道间的幅相误差。根据两次估计,从而得到多发多收模式下各回波所需补偿的幅相误差值。
1 方位多通道SAR多发多收模式的基本原理及回波模型
如图1所示,设系统有3个天线,沿方位向排列。3个天线的发射机同时发射相同的信号,由地面点目标反射后3个天线的接收机分别接收。
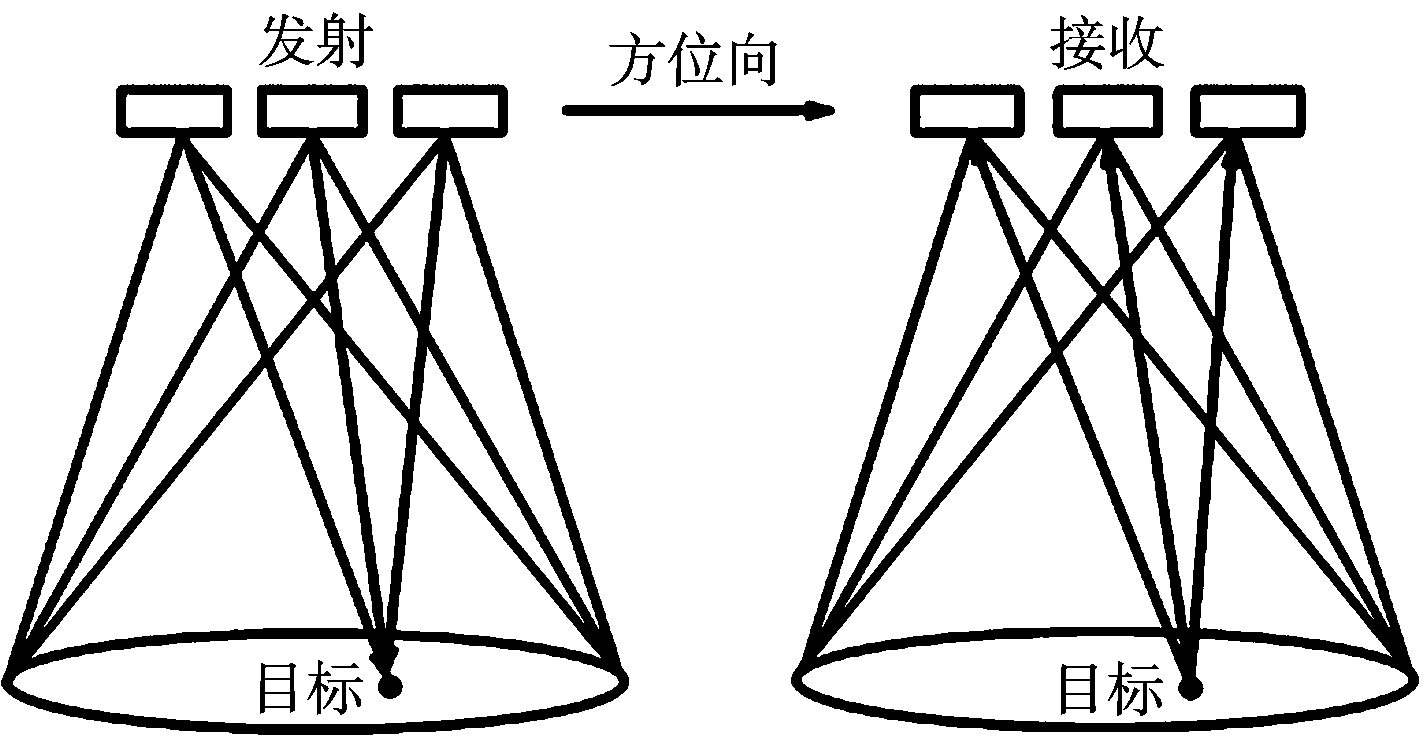
图1 多发多收模式工作原理示意图
多发多收模式下得到的回波数据可等效为单波束SAR在多个点的采样结果,文献[7]对其原理进行了详细说明。下面列出系统的回波模型。
如图1所示,假设各天线同时发射信号,经点目标反射后得到回波。设5个等效采样点分别为a,b,c,d,e,等效单通道在这5个位置得到的回波为s1,s2,s3,s4,s5,由多发多收模式原理,等效单通道在各方位位置处得到的回波信号为
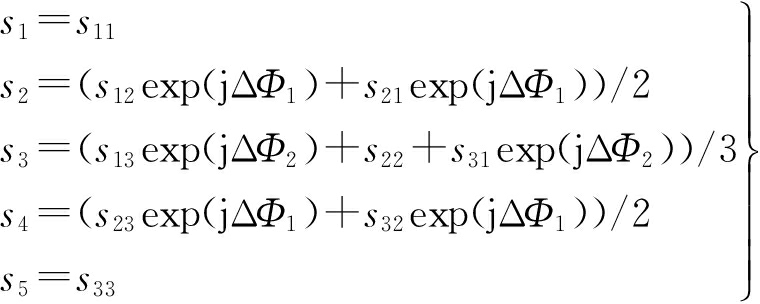
(1)
式中,sij(t)表示由第j个天线发射、第i个天线接收的回波信号。由文献[8]可知,等效过程中需补偿常数相位,分别为ΔΦ1和ΔΦ2。将每个PRT内得到的5个回波s1,s2,s3,s4,s5依次在方位向排列,即可等效为单波束SAR系统在观测时间内连续采样的结果。为方便以后的分析,将s1,s2,s3,s4,s5和sij的定义进行拓展,将s1,s2,s3,s4,s5看作沿方位向排列的5个自发自收的虚拟天线分别在观测时间内连续采样得到的回波,其中某一虚拟天线的回波用sm表示,m=1,2,3,4,5;设sij为由第j个天线发射、第i个天线接收后补偿了固定相位的回波。
2 方位多通道SAR多发多收模式的回波误差模型
在上述内容中,默认各个通道的幅相特性一致,这样在幅相特性方面,多个通道的采样可以等效为单个通道的采样;还默认实际的天线相位中心相较于测量值没有偏差,这样就可以达到等效采样位置在同一航线均匀分布的要求。然而,在工程实现时,以上两种理想条件均无法达到。由于各通道的前端组成部分,如天线、微波器件、A/D变换器等的工作性能不可能完全一致,且这种不一致性会随着外界环境的变化而改变[9],所以各通道的幅相特性会不一致。设Γnr=γnrejζnr为第n个天线接收通道的幅相特性误差,Γnt=γntejζnt为第n个天线发射通道的幅相特性误差(以第一个天线的通道为参考,则γ1r=1,ζ1r=0,γ1t=1,ζ1t=0)。
同时,实际情况下天线的相位中心也总会偏离理想位置,沿航向的通道位置误差会产生方位向的延时;沿垂直向的通道位置误差会导致通道相位误差。图2所示的是3个天线的相位中心误差。
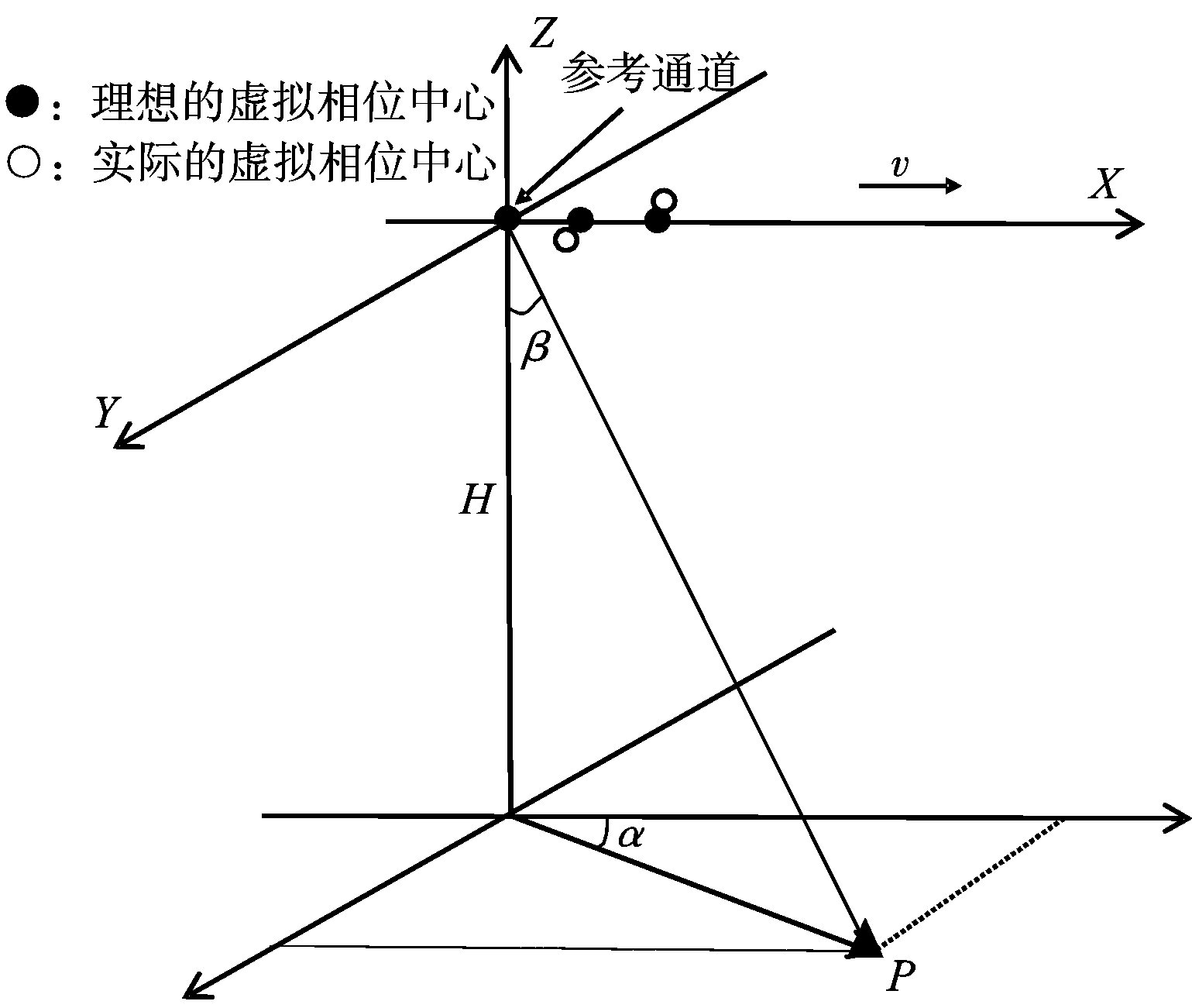
图2 相位中心误差示意图
首先定义方位向多通道SAR系统空间坐标系:X轴方向为卫星速度方向,Y轴方向垂直于X轴方向,Z轴背向地球中心。P点为目标点,设其坐标为(x,y,z),β为最短斜距矢量与Z轴负方向的夹角,α为最短斜距矢量在地面投影与X轴方向的夹角,vs为系统运行速度。图中有3个天线,天线1坐标为(0,0,0)。实心点代表天线相位中心理想位置,均在X轴上,空心点代表天线相位中心实际位置,与理想位置有偏差。设第n个天线的相位中心偏差为(Δxn,Δyn,Δzn)(以天线1为参考,则有(Δx1,Δy1,Δz1)=(0,0,0))。显然,天线相位中心位置误差会使天线与目标的距离改变,从而产生相位误差。由文献[10]:
(2)
式中,Rn为通道到点目标的距离,ΔΦenx为相位中心沿X轴方向的偏差Δxn引起的相位误差,ΔΦeny为沿Y轴方向的偏差Δyn引起的相位误差,ΔΦenz为沿Z轴方向的偏差Δzn引起的相位误差。其中,由文献[8],ΔΦenx随方位向时间t变化,而ΔΦey,ΔΦez可等效为通道的相位特性误差。由文献[10],沿航向的通道位置误差产生的方位向延时在一般的误差范围内,对系统性能没有显著影响,因此可以忽略。由此,式(1)可以改写为
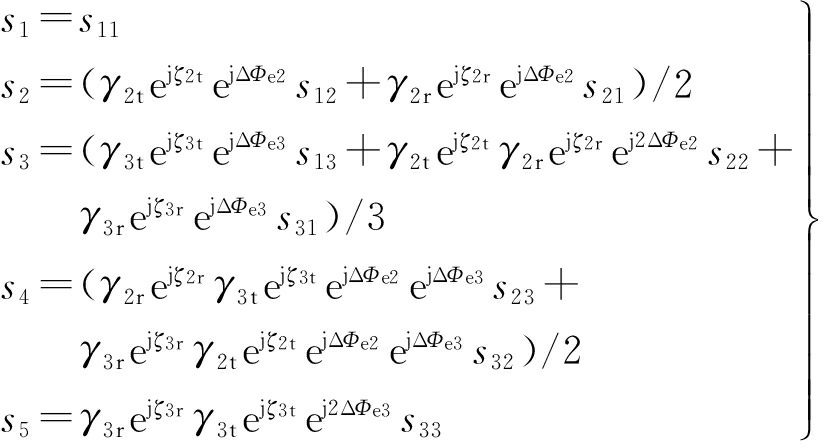
(3)
从而,得到了需要标定的幅相误差。只有得到各路回波(sij)所带的幅相误差的估计值并将误差补偿后,式(3)方可近似于式(1),实现正确的成像。
3 定标方法及信号模型
3.1 定标策略概述
对于子空间算法,一般而言都是基于回波数据进行幅相误差估计的。然而,对于多发多收模式,由式(3)可知,需要估计的幅相误差较为复杂。如果利用回波来估计,对于本文所讨论的三通道系统,则需要对9组的回波数据进行计算,运算量过大。若减少回波数,仅考虑天线自发自收所得的回波,则得不到足够的幅相误差信息来补偿成像时的回波数据。假设该系统有3个通道,通过基于回波数据的子空间算法,只能得到幅度误差γ2tγ2r,γ3rγ3t和相位误差ejζ2tejζ2rej2ΔΦe2,ejζ3rejζ3tej2ΔΦe3的估计值,在不能够分离通道发射和接收相位特性的情况下,通过自发自收下的回波所得到的估计值将不能够对成像中其他的回波进行补偿。针对这一难点,本文提出相应的定标策略。该方法只需处理天线自发自收所得到的回波,且能够将通道的发射和接收相位特性进行分离,以补偿成像中其他通道回波中的相位误差。本定标方法利用子空间算法进行幅相误差估计,假设相位中心误差固定,在地面实施两次布设,得到数据后分别进行估计。总体的定标流程如下:
1) 在地面放置发射机,对雷达发射信号。利用雷达的接收数据,估计出γ2r,γ3r,ejζ2rejΔΦe2和ejζ3rejΔΦe3。
2) 在地面放置接收机,接收雷达发射的信号。利用接收机的数据,估计出γ2t,γ3t,ejζ2tejΔΦe2和ejζ3tejΔΦe3。
3) 对成像过程中,如式(3)所示的每个回波中的幅相误差进行补偿。
3.2 基于地面发射机信号的回波模型
如图3所示,设方位多通道系统有M个通道,沿航向分布,通道间间隔为d。X轴方向为雷达运动方向,Z轴背向地球中心,Y轴垂直于X-Z平面,θ为天线下视角。
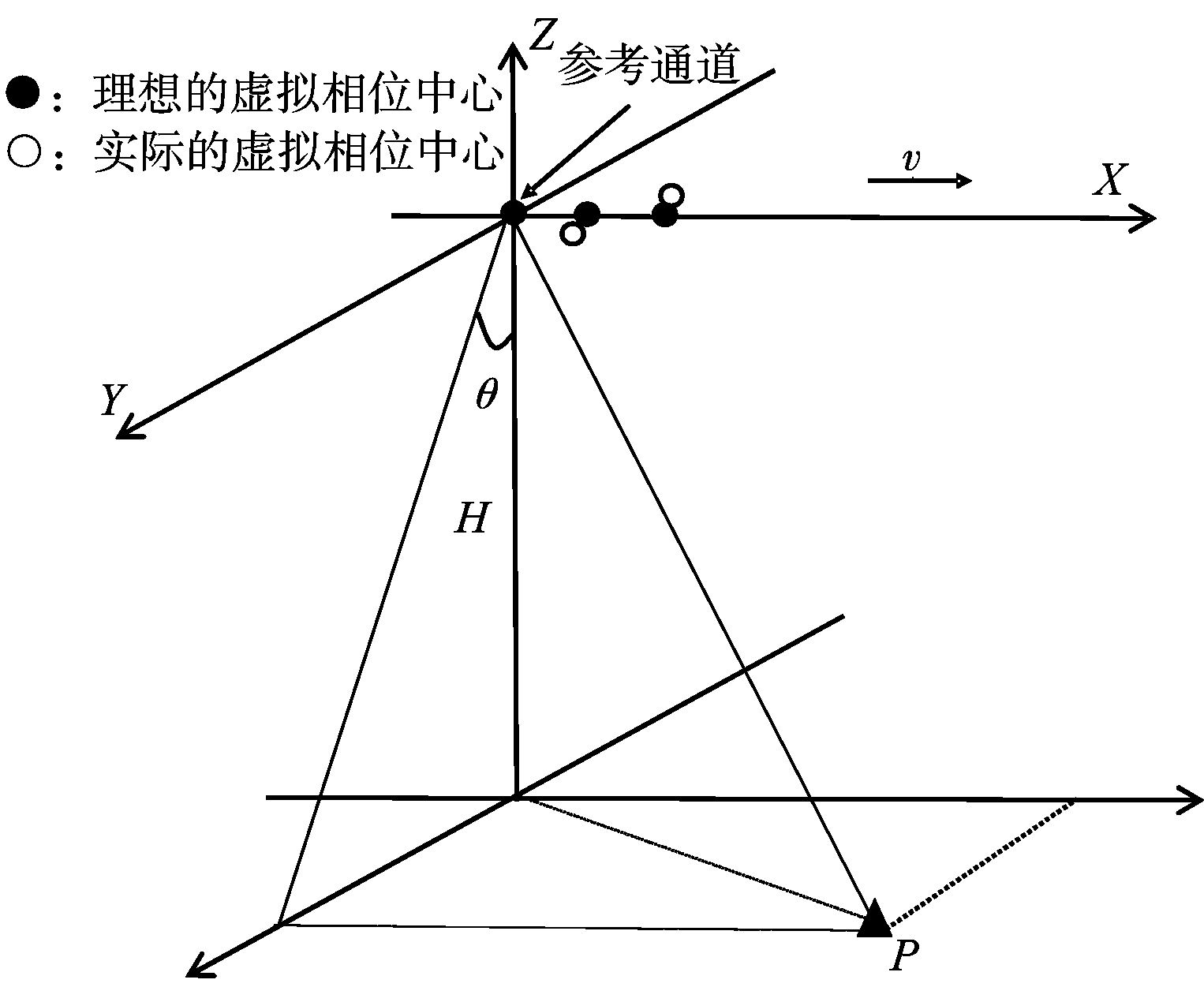
图3 基于发射机的校正方法的几何模型
假设各通道同时接收在地面P点位置的发射机发射的信号,P点坐标为(x,y,z)。设第一个通道为参考通道,坐标为(0,0,0),系统速度为v,校正源P到参考通道的距离为![]() 则参考通道接收到的回波信号为
则参考通道接收到的回波信号为
s0(τ,t)=![]()
(4)
式中,τ为方位向时间,t为距离向时间,c为光速,λ为发射信号波长,g(t)为单程天线方向图,h(τ)为天线接收到的发射信号。由文献[8],第m个通道的信号![]() 即其他通道接收到的信号近似为参考通道方位向的延时。转换到距离-多普勒域,同时考虑加性噪声,可得
即其他通道接收到的信号近似为参考通道方位向的延时。转换到距离-多普勒域,同时考虑加性噪声,可得
Sm(τ,fd)=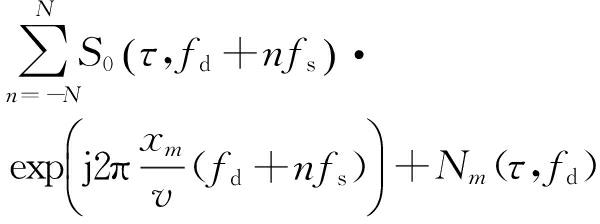
(5)
式中,fd为多普勒频率,多普勒模糊数为2N+1,fs为方位向采样频率。
将每个通道的回波用矢量形式表达,可得以下各矩阵:
S(τ,fd)=![]()
(6)
S0(τ,fd)=[S0(τ,fd-Nfs),…,
S0(τ,fd+Nfs)]T
(7)
a(fd+nfs)=![]()
(8)
A(fd)=[a(fd-Nfs),…,a(fd+Nfs)]
(9)
N(τ,fd)=[N1(τ,fd),…,Nm(τ,fd)]T
(10)
由式(5),上面各矩阵关系可表示为
S(τ,fd)=A(fd)S0(τ,fd)+N(τ,fd)
(11)
加入上节中建立的接收通道误差模型,上式改写为
S(τ,fd)=ΓrA(fd)S0(τ,fd)+N(τ,fd)
(12)
式中,
Γr=diag⎣1,γ2rejξ2rejΔΦe2,…,γmrejξmrejΔΦem」
(13)
3.3 基于地面接收机校正的信号模型
如图4所示,设方位多通道系统有M个通道,沿航向分布,通道间间隔为d。X轴方向为雷达运动方向,Z轴背向地球中心,Y轴垂直于X-Z平面,θ为天线下视角。
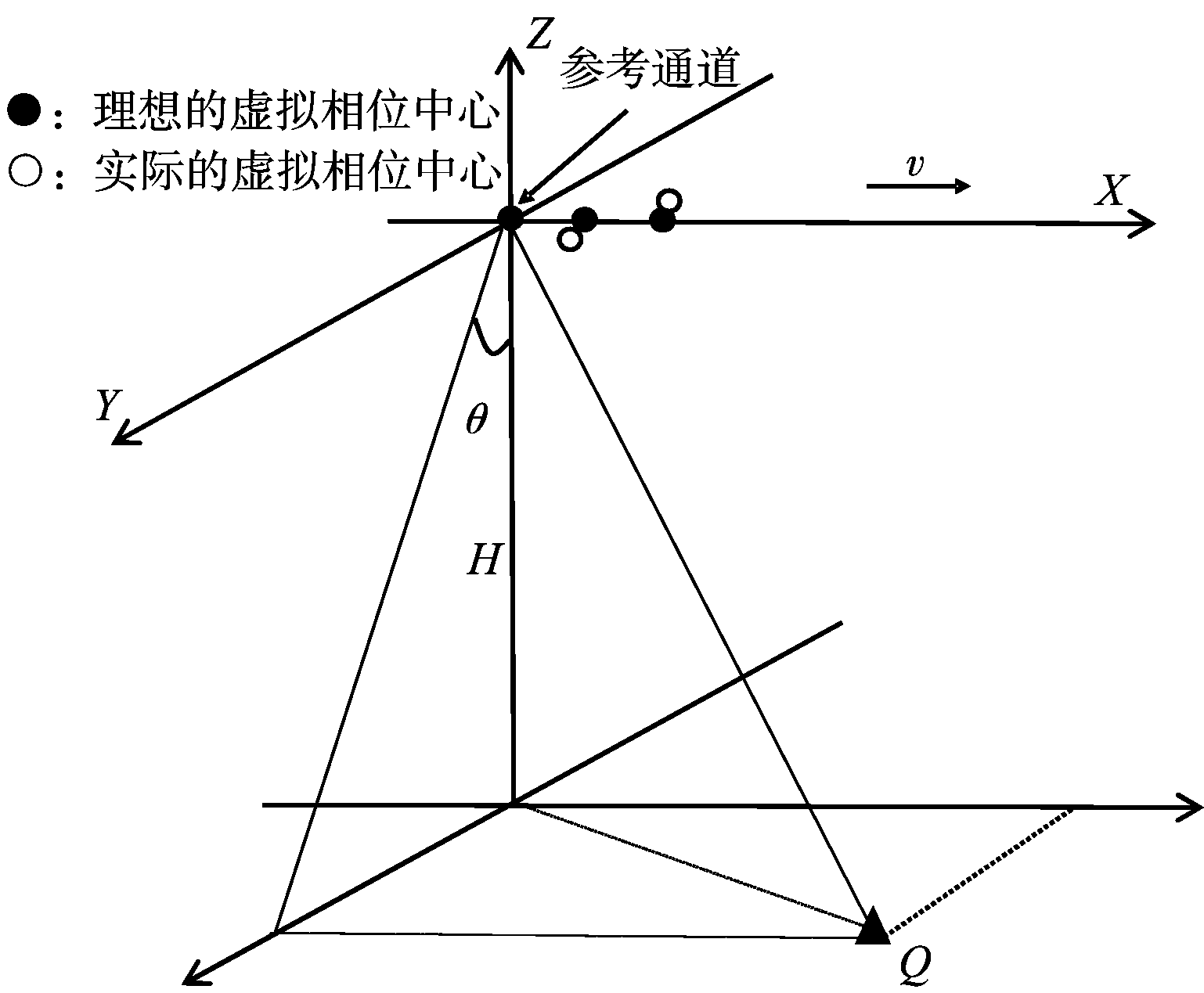
图4 基于接收机的校正方法的几何模型
假设各通道同时发射信号,则位于地面Q点位置的接收机会接收到雷达发射的信号,Q点坐标为(x,y,z)。需要说明的是,各通道的发射信号不能相关,否则无法在接收机中分离出不同天线发射的信号。由文献[7],发射前对信号进行频谱搬移则可实现在接收机中对不同信号进行分离。具体过程如下:设每个通道均发射线性调频信号,第一个通道为参考通道,坐标为(0,0,0),系统速度为v,接收机到参考通道的距离为![]() 则参考通道发至接收机的信号为
则参考通道发至接收机的信号为
(14)
设第m个通道的坐标为(xm,0,0),接收机到第m个通道的距离为![]() 则发至接收机的信号为
则发至接收机的信号为
(15)
式中,设h1(τ)的载频为fc,hm(τ)的载频为fc+(m-1)fm。
当接收机接收到信号后,信号经过带通滤波得到分离,正交解调后,各通道发射信号均搬移到基频,得到下式:
(16)
(17)
式中,h(τ)为各通道信号搬移到基频的信号。此时与利用发射机时所处理信号相同,参考上节,得到
S(τ,fd)=ΓtA(fd)S0(τ,fd)+N(τ,fd)
(18)
式中,
Γt=diag ⎣1,γ2tejξ2tejΔΦe2,…,γmtejξmtejΔΦem」
(19)
3.4 估计算法流程
由于基于发射机和基于接收机的校正方法最终所得到的信号模型均一致,只是需要估计的幅相误差大小不同,因此可以利用同样的估计算法和流程对两个信号模型进行处理,分别得到误差的估计值。算法的内容如下。
3.4.1 相位误差估计
本文的相位误差估计算法采用子空间投影算法。由文献[11],相位误差 ⎣1,ejξ2,…,ejξm」的估计值可由下面的代价函数进行最小化后得到:
(20)
式中,![]() 为信号的噪声子空间En的估计值。En可由接收信号的协方差矩阵得到。协方差矩阵RSS一般通过下式得到估计值:
为信号的噪声子空间En的估计值。En可由接收信号的协方差矩阵得到。协方差矩阵RSS一般通过下式得到估计值:
![]()
![]()
SH![]() -K+k,fd)
-K+k,fd)
(21)
3.4.2 幅度误差估计
由文献[8],利用下式来进行估计:
(22)
式中,噪声功率![]()
3.4.3 算法流程
综合上述两小节内容,算法流程可总结为:
1) 由式(21)得到接收信号协方差矩阵,进行特征分解得到信号子空间ES和噪声子空间En;
2) 由式(22)估计出幅度误差并进行补偿;
3) 将式(20)最小化估计出各通道相位误差。
4 仿真验证
4.1 估计算法仿真实验
通过计算机仿真来验证估计算法的性能,仿真采用表1中的参数,并在信号中加入30 dB噪声。由误差模型可知,垂直向相位中心误差等效为通道相位误差,因此在仿真中只加入幅度误差和相位误差,幅度误差在(0.8,1.2)范围内随机变化,相位误差弧度在(-π/2,π/2)范围内随机变化。由于本文所分析的系统通道数为3,与多普勒模糊数相等,使得估计中得不出噪声子空间。为了能够利用子空间算法,在实验中,由文献[3],设参考通道的方位采样率为其他通道的2倍,使得估计时可以把参考通道的数据等效为两个通道的采样结果,即通道数增加到4个。
表1 仿真参数
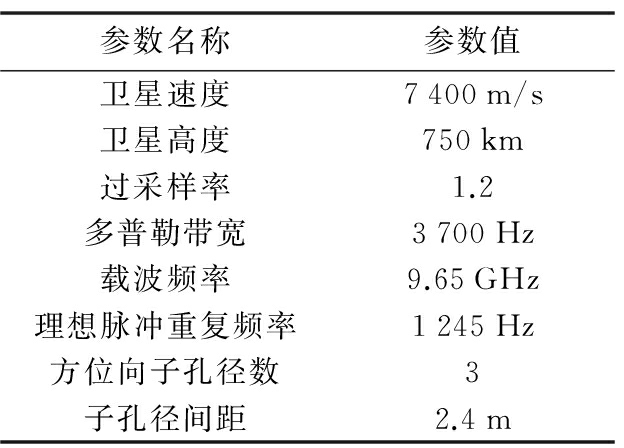
表2~表5分别统计了两个模型下幅度和相位误差估计值的结果,表中列出了3个通道,其中通道1为参考通道不含误差。第二行为仿真中加入的误差值,第三行为估计算法得到的估计值。
表2 接收通道幅度误差估计结果
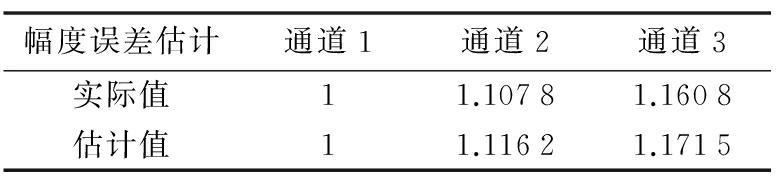
表3 接收通道相位误差估计结果

表4 发射通道幅度误差估计结果
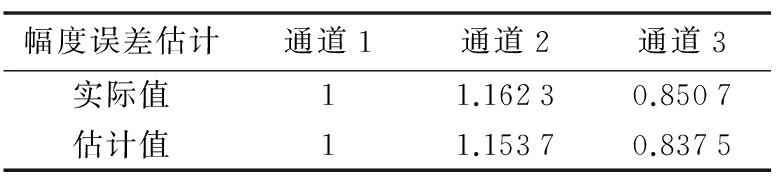
表5 发射通道相位误差估计结果
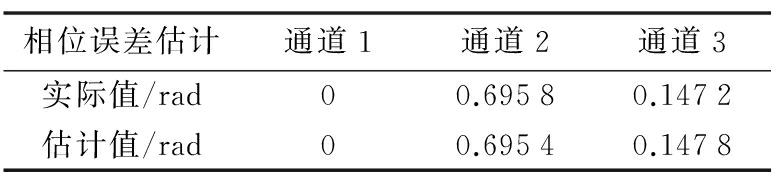
由以上各表可知,接收通道和发射通道的幅度误差估计值与设定的随机产生的幅度误差最多仅差不到0.05;相位误差估计精度可达以弧度为单位的千分位。
4.2 成像仿真实验
利用表1参数,进行点目标成像仿真,以验证该定标方法的有效性。在信号中加入30 dB噪声,并同时加入上节中随机生成的幅相特性误差和相位中心位置误差,得到点目标仿真结果。利用上节得到的幅相误差估计值,对系统的回波信号进行补偿,得到校正后的点目标仿真结果。图5(a)为校正前的点目标的方位向截面,图5(b)为校正后的点目标的方位向截面。
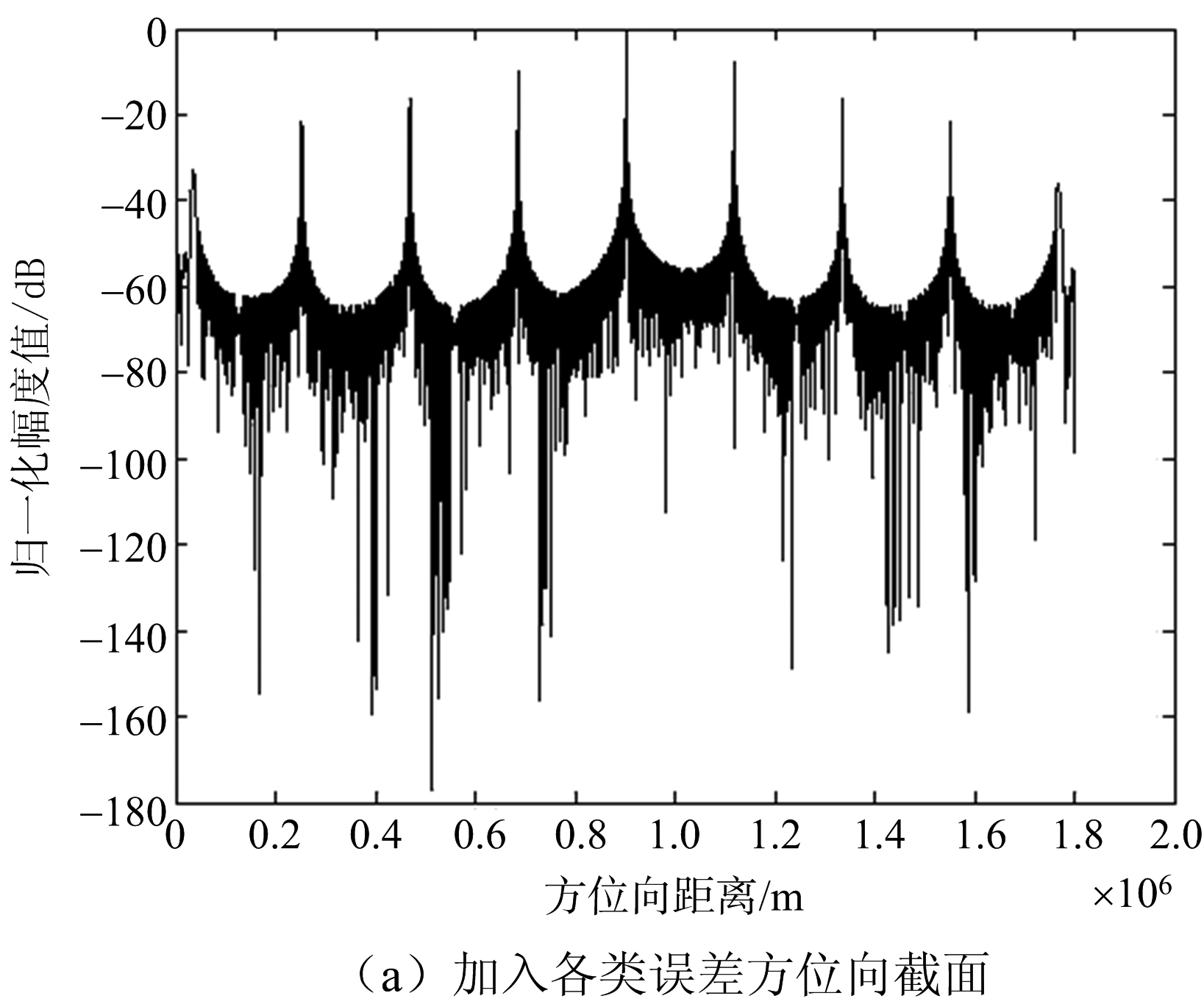
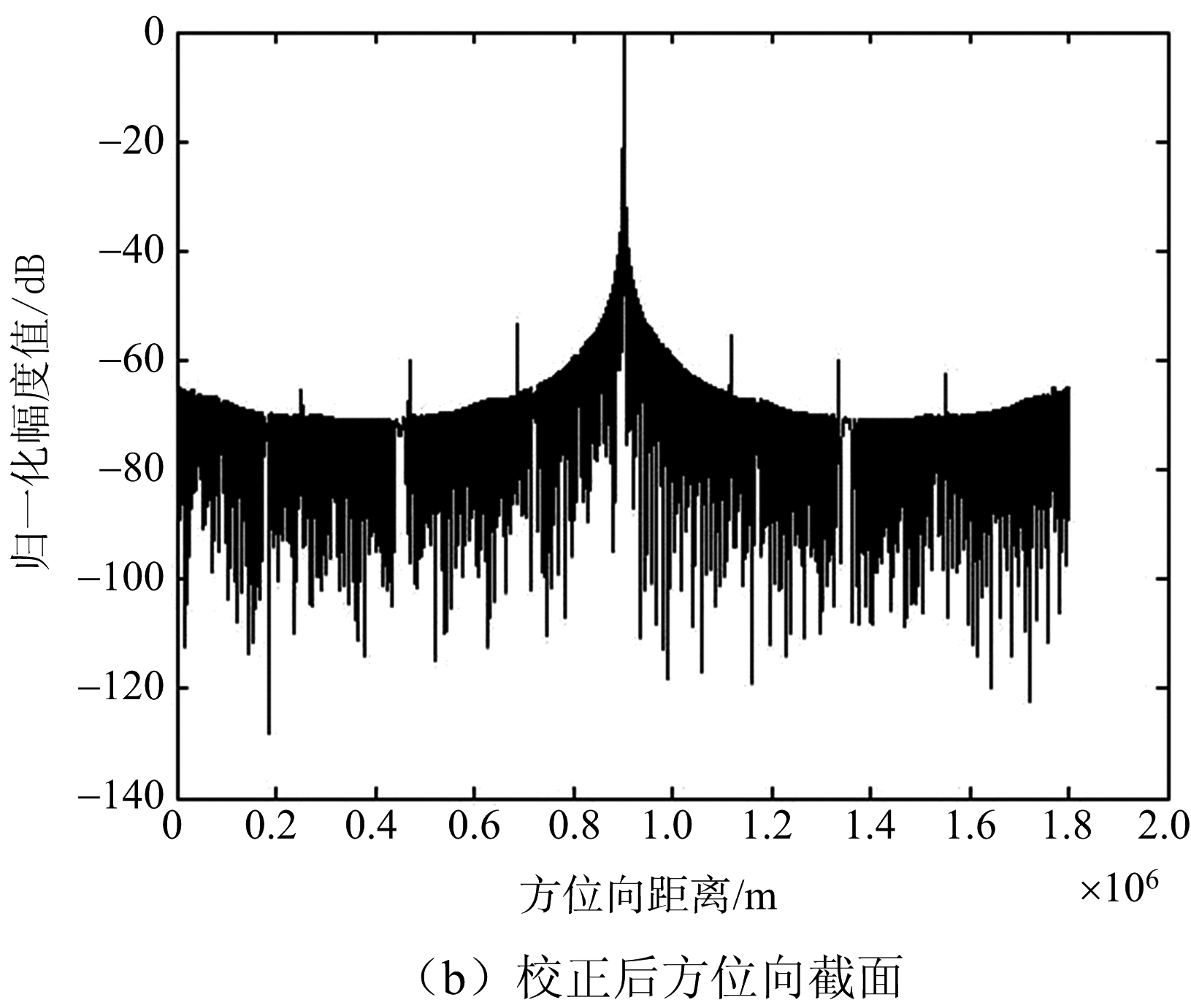
图5 校正前后方位向截面对比
由图5可以看出,幅相误差在方位向上产生了假目标,对成像产生了很大影响;而校正后,假目标得到抑制,成像结果较好。
为验证估计精度已达到要求,分别统计没有误差和校正误差后两种情况下方位向的三类成像指标(峰值旁瓣比、积分旁瓣比、分辨率),进行对比,得到表6。
表6 校正带来的成像指标变化

由表6可以看出,校正后的积分旁瓣比、峰值旁瓣比、分辨率均在可以接受的范围内,不会对成像产生影响。
5 结束语
本文利用子空间投影算法,提出了一种基于地面发射机和接收机的定标方法来估计多发多收模式下通道间的幅相误差。其利用地面布设的发射机和接收机,降低了算法的运算量,实现了收发通道相位误差分离,使得对成像的校正较为快捷。本文通过仿真实验,验证了估计算法性能上的可靠性。通过点目标仿真实验,对本文提出方法的有效性进行了验证。
参考文献:
[1] 杨桃丽, 李真芳, 刘艳阳, 等. 两种星载高分辨宽测绘带SAR系统通道相位误差估计方法[J]. 电子学报, 2013, 41(5):931-935.
[2] GEBERT N, KRIEGER G, MOREIRA A. Digital Beamforming on Receive: Techniques and Optimiza-tion Strategies for High-Resolution Wide-Swath SAR Imaging [J]. IEEE Trans on Aerospace and Electronic Systems, 2009, 45(2):564-592.
[3] 马仑, 廖桂生, 李真芳. 多通道SAR误差估计与补偿方法及其实测数据验证[J]. 电子与信息学报, 2009, 31(6):1305-1309.
[4] FISCHER C, HEER C,WERNINGHAUS R. X-Band HRWS Demonstrator: Digital Beamforming Test Results[C]∥ 9th European Conference on Synthetic Aperture Radar, Nuremberg: VDE, 2012:1-4.
[5] SIKANETA I, CERUTTI-MAORI D. Demonstrations of HRWS and GMTI with RADARSAT-2[C]∥ 9th European Conference on Synthetic Aperture Radar, Nuremberg: VDE, 2012:263-266.
[6] LI Zhenfang, WANG Hongyang, SU Tao, et al. Generation of Wide-Swath and High-Resolution SAR Images from Multichannel Small Spaceborne SAR Systems[J]. IEEE Geoscience and Remote Sensing Letters, 2005, 2(1):82-86.
[7] 宋岳鹏, 杨汝良. 应用多收发孔径实现高分辨率宽测绘带的合成孔径雷达研究[J]. 电子与信息学报, 2007, 29(9):2110-2113.
[8] 徐青. 多通道雷达系统阵列误差校正方法研究[D]. 西安:西安电子科技大学, 2011.
[9] 郜参观, 邓云凯, 冯锦. 通道不平衡对偏置相位中心多波束SAR性能影响的理论分析[J]. 电子与信息学报, 2011, 33(8):1828-1832.
[10] 马喜乐. 偏置相位中心多子带HRWS SAR技术研究[D]. 长沙: 国防科学技术大学, 2010.
[11] LI Zhenfang, BAO Zheng, WANG Hongyang, et al. Performance Improvement for Constellation SAR Using Signal Processing Techniques [J]. IEEE Trans on Aerospace and Electronic Systems, 2006, 42(2):436-452.

