0 引言
对于诸如雷达组网的多传感器信息系统,系统误差的估计和修正是其进行多源信息融合过程中最基本、最重要的问题之一。多雷达组网中主要的系统误差包括每部雷达的距离误差、方位角误差、俯仰角误差,这些偏差是系统的、非随机变化的。
常用的误差配准算法有基于球(极)投影的实时质量控制(Real Time Quality Control, RTQC)算法、最小二乘(Least Squares, LS)误差配准算法、极大似然估计(Maximum Likelihood, ML)配准算法、广义最小二乘(Generalized Least Squares, GLS)配准算法等[1-4],也有基于地心地固坐标系(Earth-Centered Earth-Fixed Coordinate, ECEF)的最小二乘(ECEF-LS)误差配准算法[5-6]和广义最小二乘(ECEF-GLS)误差配准算法[7]。多雷达系统误差的估计本质上属于多维、多峰值优化问题,而经典的遗传算法会有陷入局部最优解的不足。本文针对异地三坐标雷达组网误差配准问题,通过将多部雷达对共同目标测量数据转换到ECEF坐标系,建立误差估计的目标函数模型,将误差估计问题转换为非线性优化问题,然后将小生境技术引入遗传算法进行目标函数寻优,实现对系统误差的估计。
1 基于遗传算法的误差估计
1.1 坐标转换
假定雷达组网系统中有两部三坐标雷达,分别为雷达A和雷达B,地理坐标分别为(LA, λA, HA)和(LB, λB, HB),其中L,λ和H分别表示纬度、经度和高度。由ECEF笛卡尔坐标转换公式(1)可以得到其ECEF笛卡尔坐标分别为(xAs, yAs, zAs)和(xBs, yBs, zBs):
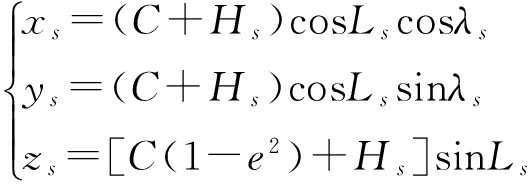
(1)
(2)
式中,e为地球偏心率,Eq为赤道半径。
假设在观测时刻k,雷达A和雷达B对目标T的观测值分别为(RAk, θAk, φAk),(RBk, θBk, φBk);雷达A的测距系统误差为ΔRA,方位角系统误差为ΔθA,仰角系统误差为ΔφA;雷达B的测距系统误差为ΔRB,方位角系统误差为ΔθB,仰角系统误差为ΔφB。如图1所示,目标在公共坐标系中的真实位置为T,由于测量误差的存在,雷达A和雷达B对目标T的测量值转换到公共坐标系下分别为TA和TB。
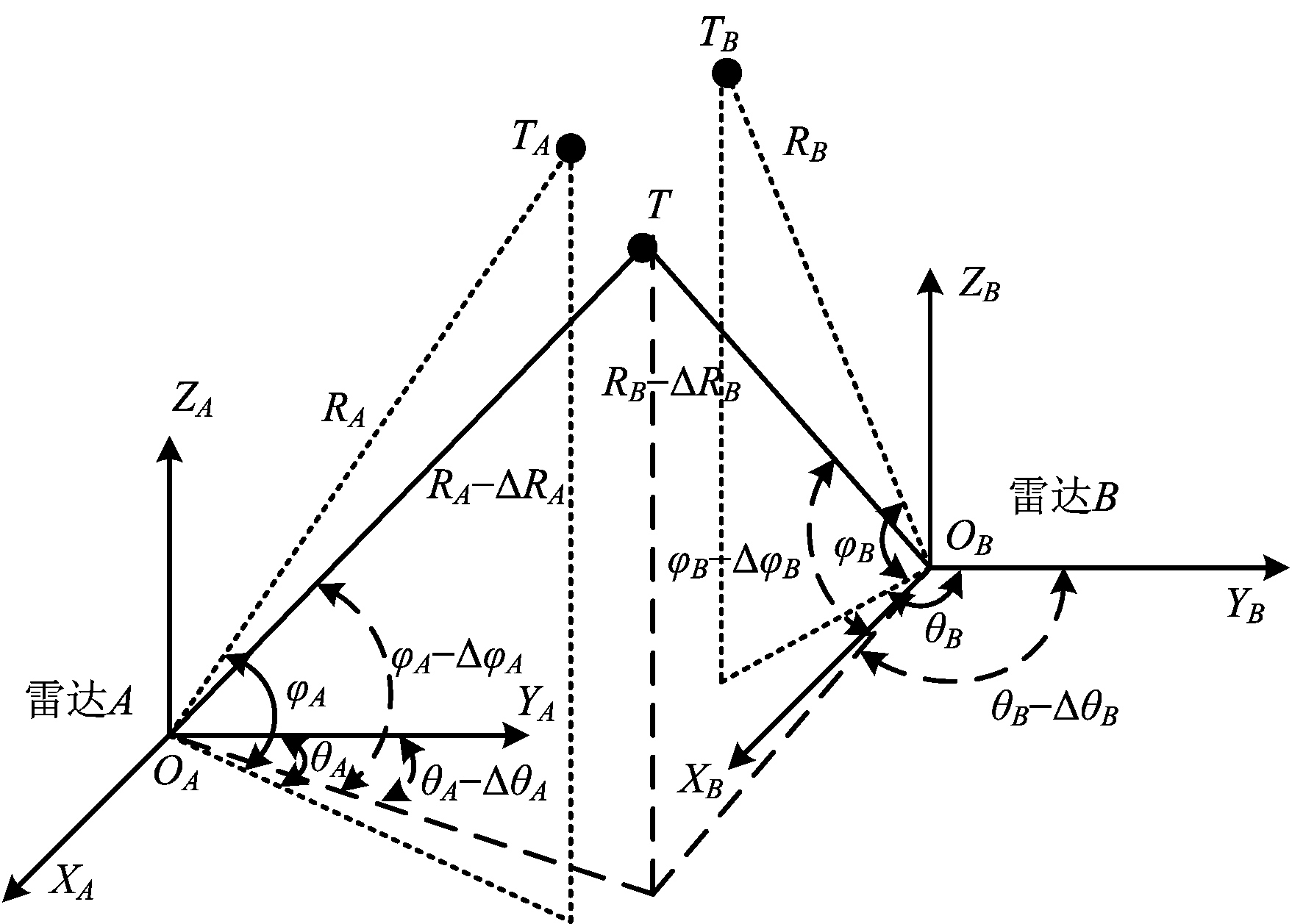
图1 空间误差配准的几何关系
那么在只考虑系统误差的情况下,目标T在雷达A和雷达B的局部坐标系中的真实坐标分别为
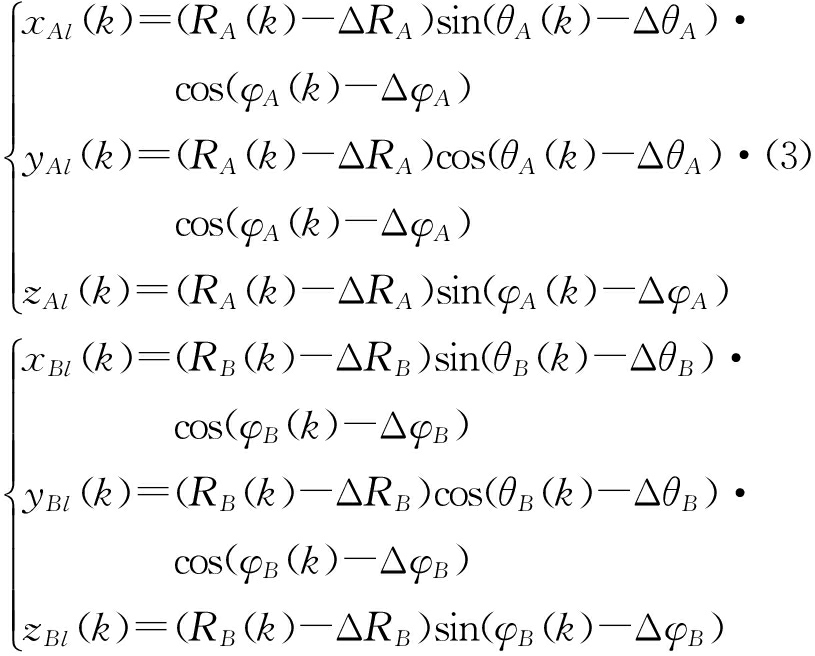
(4)
将目标的局部雷达坐标转换到以地心为原点的ECEF坐标系中:
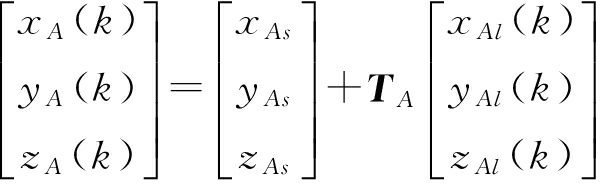
(5)
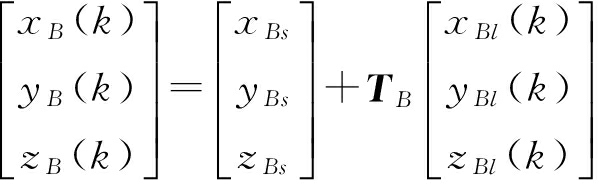
(6)
式中,TA和TB为旋转矩阵。即
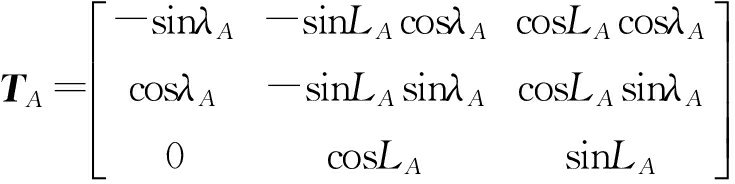
(7)
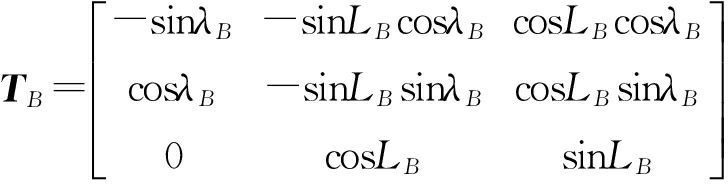
(8)
1.2 误差估计目标函数
在只考虑系统误差的情况下,在同一时刻,雷达A和雷达B对同一目标的观测点应该重合,即满足
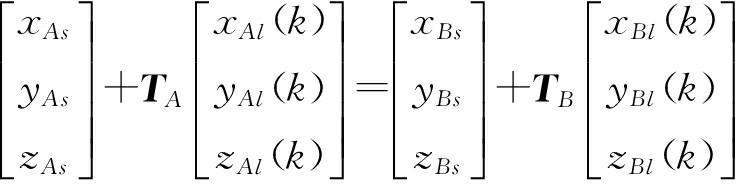
(9)
传统的基于ECEF坐标系的系统误差估计技术[5,7]通过解式(9)的方程,得到一组两雷达系统误差的解。由于式(9)是一个非线性方程组,求解比较困难,可以构造一个目标函数,用非线性优化算法估计各雷达的系统误差。令
Ψ(k)=[RA(k),θA(k),φA(k),RB(k),
θB(k),φB(k)]′
β=[ΔRA,ΔθA,ΔφA,ΔRB,ΔθB,ΔφB]′
则有
f(Ψ(k),β)=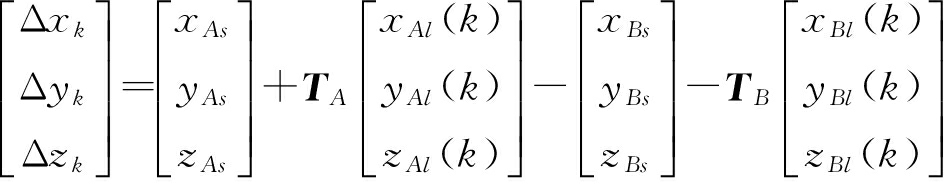
(10)
理想情况下,误差配准之后,两部雷达观测到的目标航迹都与目标的真实位置一致,但是由于存在随机误差,很难将系统误差完全修正,系统误差估计的目标变为寻找一组系统误差值,使修正之后航迹之间的欧氏距离最小。经过N次测量之后,则目标函数可以表示为
![]() (11)
(11)
式中,Ω为β的定义域。
1.3 小生境遗传算法的算法设计
遗传算法[8-9]是一种智能优化算法,它模拟生物进化过程来从庞大的搜索空间中筛选出较优秀的解。本文在遗传算法的原有结构上引入小生境技术,小生境技术是基于排挤机制的选择策略,其基本思想源于在一个有限的生存环境中,各种不同的生物为了能够延续生存,它们之间必须相互竞争各种有限的生存资源。这种策略保持了遗传算法解的多样性,同时提高了遗传算法处理多峰值优化问题的能力。
传统遗传算法寻优可以分为初始种群产生、适应度函数设计、选择、交叉、变异等过程,本文针对配准问题,引入小生境技术,设计算法过程如下:
1)初始种群产生。在雷达系统误差配准中,一般满足距离误差ΔR∈[-5 km, 5 km],方位角误差Δθ∈[-5°, 5°],仰角误差Δφ∈[-5°, 5°]。采用浮点编码的方式,随机生成n个系统误差初始解的种群{b1, b2, b3,…, bn},其中bi为一组系统误差的编码。
2)适应度函数设计。遗传算法会按与个体适应度成正比的概率决定当前群体遗传到下一代的个体,因此需根据目标函数构造适应函数,确保配准误差越小的解适应度函数值越大。利用目标函数界限的保守值这一先验信息,构造适应度函数:
(12)
式中,c≥0,c+J≥0,J为目标函数,c为目标函数界限的保守值,本文取两部雷达在同一坐标系下对同一目标观测位置的均值。
3)选择运算。对群体中的个体进行优胜劣汰操作:按与个体适应度成正比的概率决定当前群体中的各个体是否遗传到下一代。本文采用轮盘赌的选择算子,个体i被选中遗传到下一代的概率为

(13)
式中,n为种群中个体数量,Fi为个体i的适应度。
4)交叉运算。任意挑选经过选择操作后种群中的两个个体作为交叉对象,即两个父个体经过染色体交换重组产生两个子个体。本文采用离散重组的交叉算子。
5)变异运算。变异是基因上一个等位基因被另一个代替,从而产生新的遗传结构的过程。本文采用基于实值编码[10]的变异算子。
6)小生境淘汰运算。首先预先指定小生境之间的距离参数L,然后两两比较种群中各个个体之间的海明距离(或欧式距离),若这个距离小于L,则比较这两个个体的适应度大小,并对其中适应度较低的个体处以罚函数。
经过小生境淘汰运算,较差的相似个体在进化过程中被淘汰的概率大幅增加。在距离L范围内将只存在一个优良个体,从而既维护了群体的多样性,又使得各个个体之间保持一定的距离,并使得个体能够在整个约束空间中分散。
1.4 小生境遗传算法流程
针对具体的雷达组网系统误差配准,设计小生境遗传算法的流程由以下几个步骤构成:
1)算法初始化,编码并随机产生初始种群P(0),M组系统误差;
2)根据适应度函数计算个体适应度值,记忆适应度值最大的前N个个体(N<M);
3)判断终止条件,若满足,则输出结果,否则,继续步骤4);
4)按遗传策略,运用选择、交叉、变异算子作用于群体P(t),产生新群体P′(t);
5)对群体P′(t)和记忆的N个个体合并成新群体,进行小生境淘汰运算;
6)按适应度值降序排序这M+N个个体,取前M个个体作为下一代P(t+1),转到步骤2)。
小生境遗传算法的流程框图如图2所示。
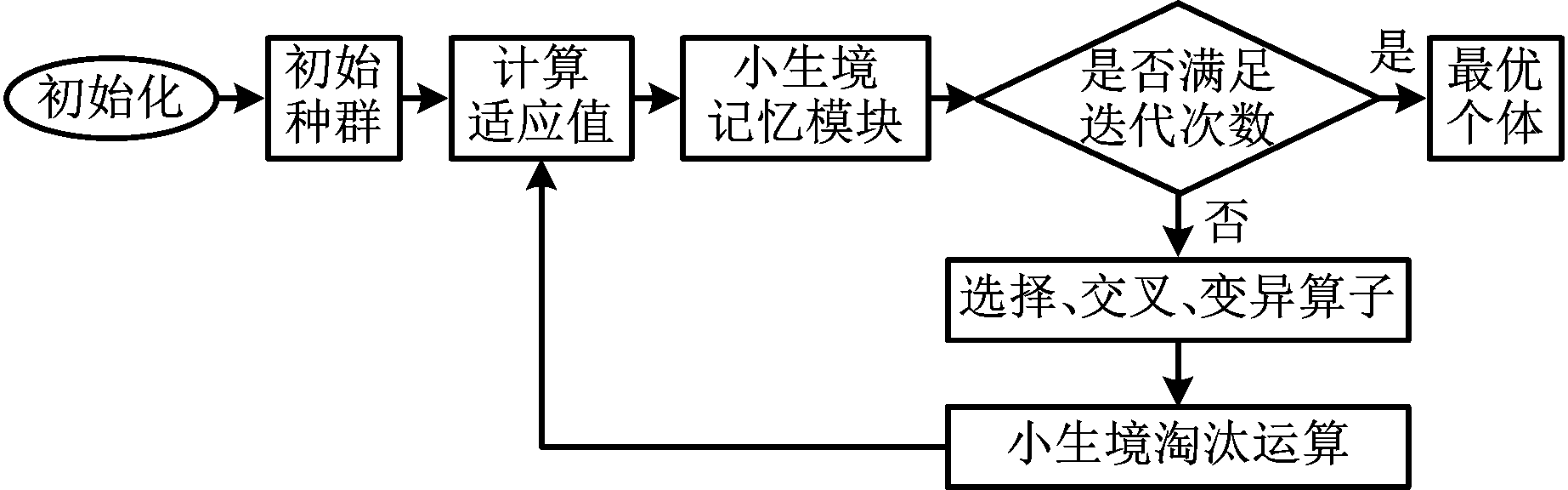
图2 小生境遗传算法流程框图
2 算法仿真与误差分析
为便于结果分析和比较,初始数据采用了文献[7-8]的结果。假设雷达A的坐标为(68.923°, -137.259°, 50.655 m),雷达B的坐标为(70.171°, -124.725°, 217.724 m),假设随机误差服从高斯分布,测距随机误差的方差为50 m,方位角和仰角随机误差的方差均为0.2°。仿真目标的飞行起点为(67.733°, 122.725°, 5 000 m),终点为(70.852°, 129.182°, 5 000 m),飞行过程中间保持200 m/s的速度。遗传算法的初始种群大小为100,迭代次数为100次,杂交概率0.6,变异概率0.16。
文中所有仿真实验均在Windows 10操作系统下Matlab 2014b平台进行。两部雷达对目标的仿真测量数据经滤波及时间对齐处理后,进行算法验证,所得结果如表1所示。
表1 两雷达系统的不同方法的仿真结果

从表1中仿真实验结果可以得出,本文算法对雷达A仿真结果的相对误差分别为0.38%,1.15%和-6.58%,对雷达B仿真结果的相对误差分别为-2.03%,2.19%和-8.07%,其相对平均误差为3.4%。而基于最小二乘法和基于传统遗传算法的雷达误差配准算法的仿真结果,其相对平均误差分别为5.37%和7.09%。本文算法估计结果比前两种算法的精度都要高,特别是对测距系统误差的估计更加准确。同时,实验过程中发现传统的遗传算法在解决多峰值优化问题时容易陷入局部最优,而基于小生境遗传算法的雷达误差配准算法不容易陷入局部最优,具有较好的数值稳定性。
对3部及以上雷达组网系统的系统误差配准,仿真估计的实施方法类同,仅需要对目标函数和适应性函数进行相应的修改。以3部为例,假设前面仿真条件不变,增加一部雷达C,其坐标为(67.500°, -123.922°, 500 m),随机误差服从高斯分布,测距随机误差的方差为50 m,方位角和仰角随机误差的方差均为0.2°。仿真结果如图2~图4所示。
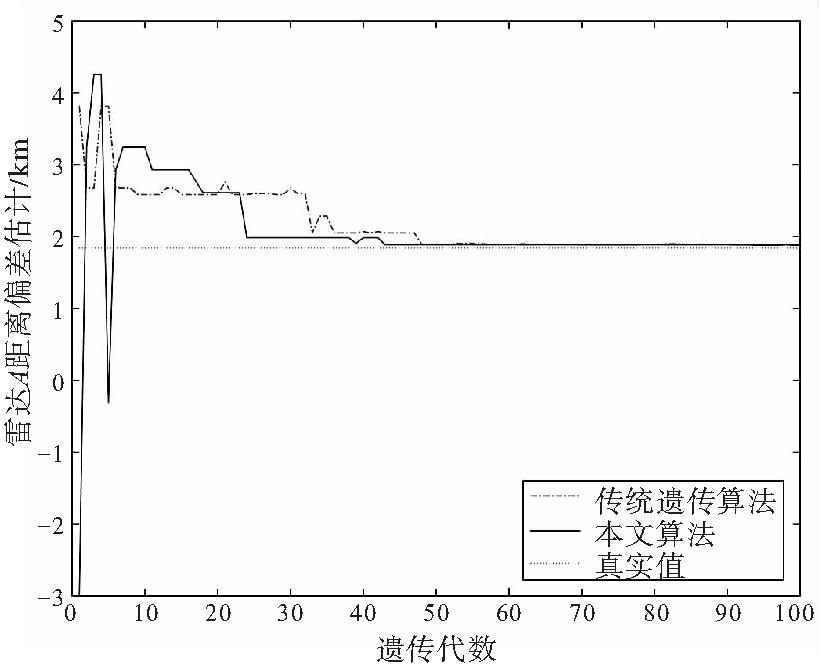
(a) 雷达A距离误差估计
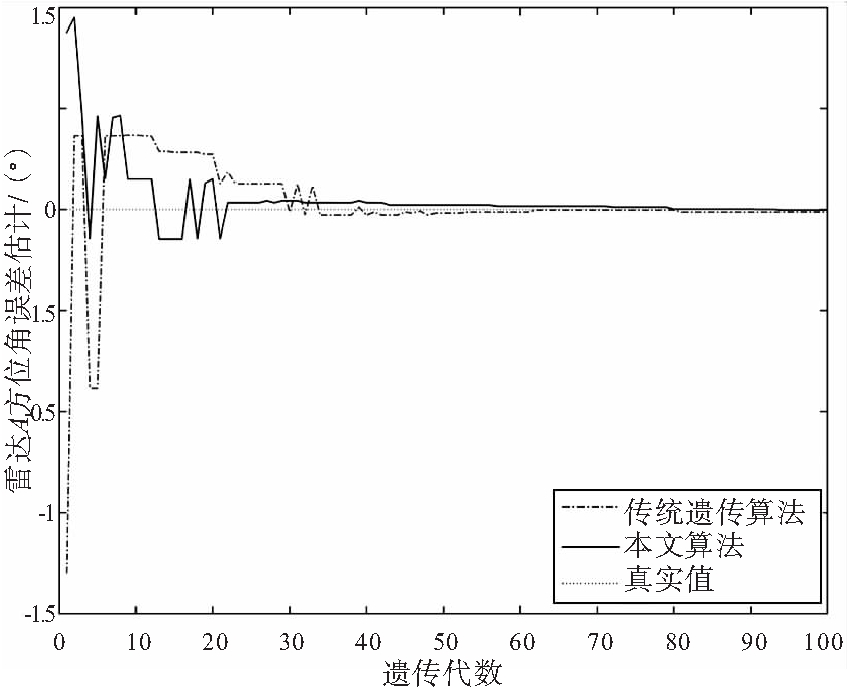
(b) 雷达A方位角误差估计
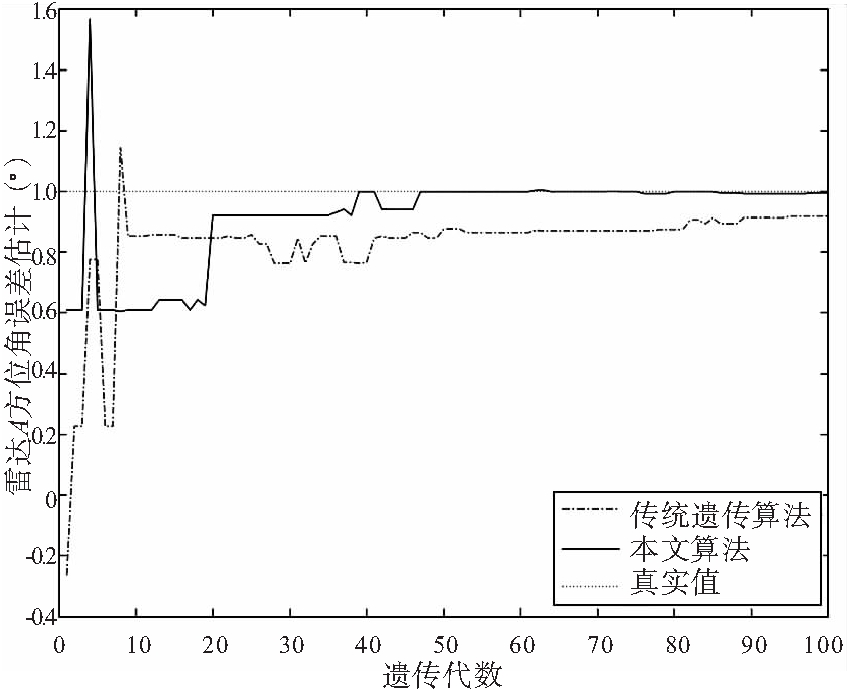
(c) 雷达A仰角误差估计
图2 雷达A距离、方位角、仰角误差仿真结果
从图2可以看出,本文算法较传统遗传算法收敛性更好。图2(c)中传统遗传算法较早陷入了局部最优,而本文算法仍具有较高的精度。

(a) 雷达B距离误差估计
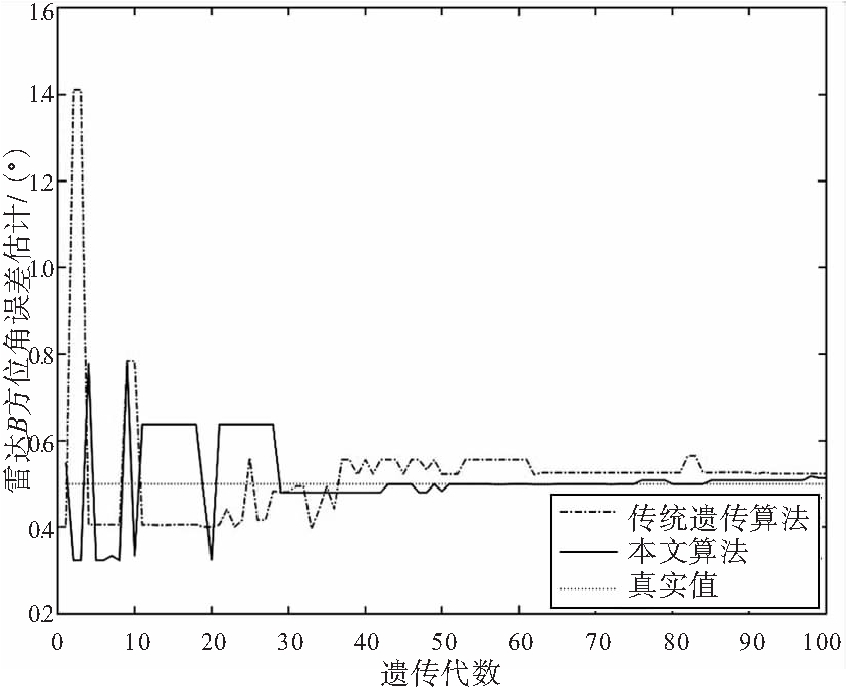
(b) 雷达B方位角误差估计
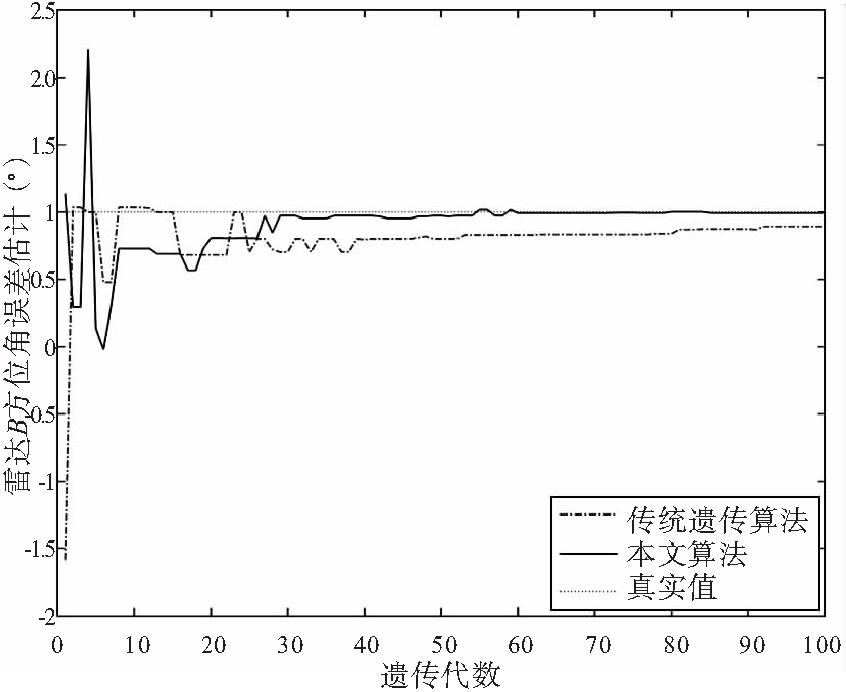
(c) 雷达B仰角误差估计
图3 雷达B距离、方位角、仰角误差仿真结果
从图3可以看出,本文算法较传统遗传算法收敛性更好,且各项仿真结果均优于传统遗传算法。图3(c)中传统遗传算法较早陷入了局部最优,而本文算法仍具有较高的精度。
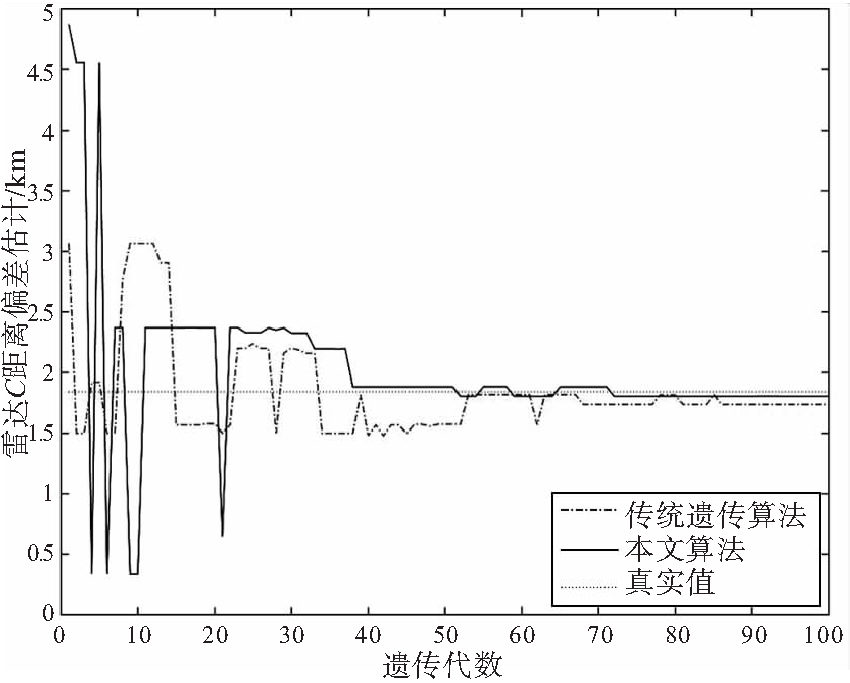
(a) 雷达C距离误差估计
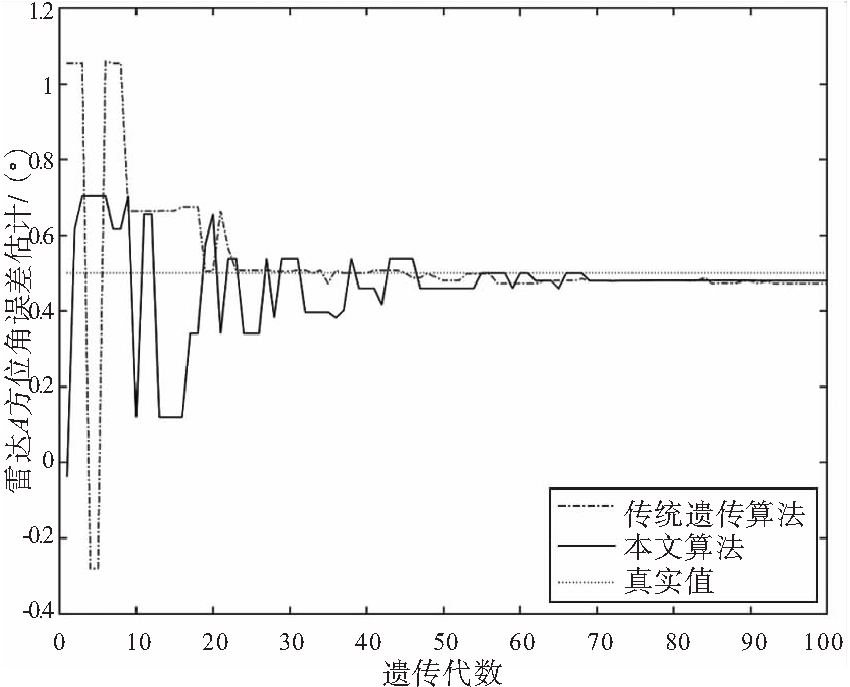
(b) 雷达C方位角误差估计
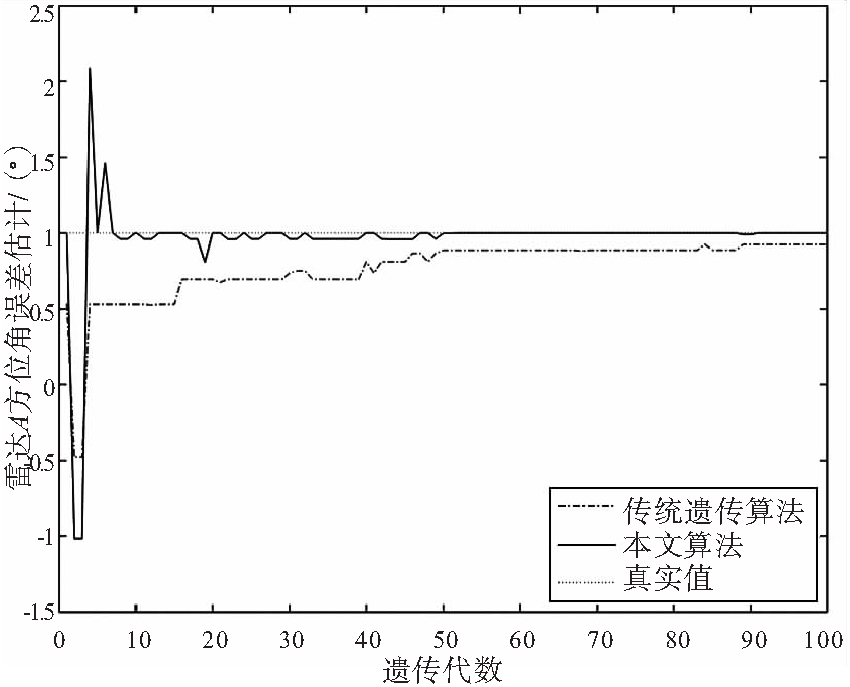
(c) 雷达C仰角误差估计
图4 雷达C距离、方位角、仰角误差仿真结果
从图4可以看出,本文算法较传统遗传算法收敛性更好,且各项仿真结果均优于传统遗传算法。综合以上结果可以得出,本文算法具有较好的全局寻优能力和收敛速度,且各项仿真结果均优于传统遗传算法。对三雷达系统误差估计的仿真结果如表2所示。
表2 对三雷达系统误差估计的仿真结果

从表2仿真结果可以得出,本文算法对三雷达系统仿真结果的相对误差均小于5%,且其相对平均误差为1.86%,而基于传统遗传算法的仿真结果的相对平均误差为6.65%。基于小生境遗传算法的雷达组网空间误差配准算法能够通过多部雷达共同观测的目标数据估计出各雷达的系统误差,限制条件少,误差估计精度较高,并且较好地克服了传统遗传算法早熟收敛和弱点,具有很高的全局寻优能力。同时,实验过程中发现,本文方法具有较高的计算复杂度,实时性较差,后期需要对如何降低其计算复杂度进行进一步研究。
3 结束语
针对异地的三坐标雷达组网误差配准问题,提出了一种基于小生境遗传算法的雷达组网空间误差配准算法。该方法在采用基于ECEF坐标系的误差配准技术的基础上,克服了将非线性方程线性化带来的误差,同时引入小生境技术,提高了遗传算法全局寻优能力和收敛速度。仿真实验结果表明,本文算法与基于ECEF坐标系的最小二乘法相比,具有更高的误差估计精度。还可以同时实现3部及以上雷达组网的系统误差配准,并且具有比较高的精度。此外,本文算法的计算复杂度较高,提高算法的实时性是下一步研究的目标。
参考文献:
[1] DU X, WANG Y, SHAN X. Robust Sensor Bias Estimation for Ill-Conditioned Scenarios[J]. Tsinghua Science and Technology, 2012, 17(3):319-323.
[2] PU W, LIU Y F, YAN J, et al. A Two-Stage Optimization Approach to the Asynchronous Multi-Sensor Registration Problem[C]∥ IEEE International Conference on Acoustics, Speech and Signal Processing, New Orleans, LA: IEEE, 2017:3271-3275.
[3] ZHOU L, LIANG Y, ZHOU J, et al. Linear Minimum Mean Squared Estimation of Measurement Bias Driven by Structured Unknown Inputs[J]. IET Radar, Sonar & Navigation, 2014, 8(8):977-986.
![]() M, MULGREW B, CLARK D E. A Cooperative Approach to Sensor Localisation in Distributed Fusion Networks[J]. IEEE Trans on Signal Processing, 2016, 64(5):1187-1199.
M, MULGREW B, CLARK D E. A Cooperative Approach to Sensor Localisation in Distributed Fusion Networks[J]. IEEE Trans on Signal Processing, 2016, 64(5):1187-1199.
[5] ZHOU Y, LEUNG H, BLANCHETTE M. Sensor Alignment with Earth-Centered Earth-Fixed(ECEF) Coordinate System[J]. IEEE Trans on Aerospace and Electronic Systems, 1999, 35(2):410-418.
[6] ZHANG F, KNOLL A. Systematic Error Modeling and Bias Estimation[J]. Sensors, 2016, 16(5):729.
[7] 董云龙,何友,王国宏,等. 基于ECEF的广义最小二乘误差配准技术[J]. 航空学报, 2006, 27(3):463-467.
[8] 张远,曲成华,戴谊. 基于遗传算法的雷达组网误差配准算法[J]. 雷达科学与技术, 2008, 6(1):65-68.
ZHANG Yuan, QU Chenghua, DAI Yi. Registration Algorithm for Radar Netting Based on Genetic Algorithm[J]. Radar Science and Technology, 2008, 6(1):65-68. (in Chinese)
[9] 付刚,王刚,王明宇,等. 基于小生境遗传算法的制导雷达误差估计[J]. 空军工程大学学报(自然科学版), 2011, 12(6):50-53.
[10] SINGH G, GUPTA N, KHOSRAVY M. New Crossover Operators for Real Coded Genetic Algorithm(RCGA)[C]∥ International Conference on Intelligent Informatics and Biomedical Sciences, Okinawa: IEEE, 2015:135-140.
