0 引言

外辐射源定位系统本身不发射电磁信号，依靠接收非合作辐射源的直达波信号与经目标散射的回波信号，通过相参处理获取目标的观测量，从中提取目标的位置信息。由于其利用辐射源的非合作性与定位体制的单发单收特性，使其具备了抗电磁干扰、抗反辐射导弹、反隐身以及对付低空和超低空突防等方面的巨大能力，保证了外辐射源定位系统在战场上的生存能力[1-2]。外辐射源定位系统在未来战场的潜力使其成为了各国军事装备研究的热点。

为更好研究单站外辐射源定位技术，确定不同战场态势下定位算法的应用范围，本文在单发单收定位体制下，给出了外辐射源定位需要的方位角(DOA)、到达时间差(TDOA)、基线距离和多普勒频移四个观测参量的获取方法，探究影响目标参量观测精度的主要因素。推导出了两种典型定位算法的几何定位精度，并分析了算法在观测精度、基线距离和目标运动状态改变的情况下，对目标几何定位精度的影响。通过分析以上仿真结果，利用子集优选的策略，给出目标在空间位置上的最优算法。

1 定位模型

在单发单收的定位模式下，定位模型如图1所示。观测站位于地面，为方便解析计算目标位置，以观测站作为坐标原点建立二维平面坐标系。在此坐标系下，假设外辐射源与目标都和接收站在同一平面,即使三者位于不同高度的运动平台，而一般情况下，三者的水平距离远大于其高度距离，故此二维模型仍然适用[3]。

图1中，L为观测站到外辐射源的基线距离，R1为观测站到目标的距离，R2为目标与外辐射源之间的距离，θT为目标相对于观测站的方位角。

2 参数测量与精度分析

外辐射源定位系统前端的主要问题就是信号的相参处理，观测站首先获得辐射源的直达波信号，再以直达波作为参考信号实现与目标回波的相参处理。通过以上方式可获得的目标观测参数有方位角、到达时间差、基线距离和多普勒频移。

2.1 方位角的测量

外辐射源定位系统测角方式与单站雷达相同，都是利用电磁波在均匀介质中的直线传播特性与天线的方向性[4]，利用比幅单脉冲技术可以获取目标方位角θT。

理论测角误差只考虑由接收机热噪声引起的误差，测角误差公式为

(1)

式中，θB为外辐射源天线波束宽度，K为误差响应曲线的斜率，E为信号能量，N0为噪声功率谱密度。

由式(1)可以看出，测角精度与信号脉宽和信噪比有关，信号脉宽与测角精度成反比例关系，信噪比与测角精度成正比例关系。在信噪比一定的前提下，信号脉冲宽度越窄，测角精度越精确。

2.2 到达时间差

到达时间差Δt是指外辐射源发射的直达波信号与经目标反射的回波信号到达观测站的时间之差，但是目标回波中包含大量直达波和多径信号，可以通过自适应相消等信号处理技术，去除目标回波中的杂波[5]，并与直达波相参得到Δt。与单站雷达测量反射回波的时间相同，到达时间差的测量精度公式如下：

(2)

式中，τ为外辐射源信号脉冲带宽，S/N为平均输出信噪比。从式(2)可以看出，由于辐射源信号是非合作信号，无法改变其脉冲宽度，为了实现对回波信号的有效检测，必须通过提高目标回波的信噪比从而提高到达时间差的测量精度，主要有相参积累和非相参积累两种方式。为方便计算分析，这里将时间差变换为距离差ΔR处理：

ΔR=cΔt

(3)

式中，c为光在空气中的传播速度。

2.3 基线距离的测量

由于外辐射源定位系统利用辐射源的非合作性，一般情况下，外辐射源的位置坐标是未知的，尤其当外辐射源位于运动平台时，位置坐标实时变化，这时就要通过双定向天线机械圆周扫描的方式，确定外辐射源与观测站之间的基线距离L，具体公式如下：

(4)

式中， d为两个定向天线之间的距离，θE为外辐射源信号入射的方位角，ω为两定向天线机械圆周扫描的速度，t为直达波信号到两天线的时间差。

式(4)中包含方位角和时间差，故对基线距离的测量精度取决于方位角和时间差的测量精度。

2.4 多普勒频移的测量

外辐射源定位系统中，多普勒频移fd指目标回波与直达波之间的频率差，其产生机理是总路径长度变化率，其中包含了目标的位置与速度信息，具体公式为

(5)

式中，λ为信号的波长。

多普勒频移的测量精度相比于单站雷达，还受到传播路径误差和目标闪烁误差的影响，这里理论误差只考虑接收机热噪声的影响，公式如下：

(6)

式中，Np为观测周期与信号脉冲周期之比，ts为信号s(t)的均方根持续时间，由式(7)确定：

(7)

由式(7)可知，通过提高信噪比与信号持续时间，可以提高多普勒频移的测量精度。

3 目标定位精度分析

外辐射源定位系统可获得的目标观测参量主要有上节讨论的方位角、到达时间差、基线距离和多普勒频移四个参数，在本文假设的二维平面内，至少需要3个参量才能实现对目标的定位，故可以利用不同的参数组合形成不同的定位算法。由于组合形式较多，在此只挑选几个常用的参数组合分析其定位算法的定位精度。

在图1的定位几何关系下，设观测站位于坐标原点，目标的状态参量为外辐射源的位置坐标为(xE,yE)，则目标观测参量可表示为

(8)

ΔR=R1+R2-L

(9)

(10)

fd=

(11)

式中，λ表示信号的波长。

(12)

(13)

在相同的定位方法下,目标位于不同的空间位置具有不同的定位精度；而在相同的空间位置上，定位方法不同，目标也具有不同的定位精度。因此，在考虑目标定位精度时，既要考虑定位方法，也要考虑目标与观测站和外辐射源之间的空间位置[6]，本文采用目标的几何定位精度作为分析定位算法优劣的衡量标准。

3.1 DOA-TDOA基线联合定位

利用方位角、到达时间差和基线距离参数信息实现对目标的定位，其观测方程为式(8)、式(9)、式(10)，根据余弦定理可知：

(14)

将式(9)代入，可得

(15)

由此可得目标的位置坐标为

(16)

在这里假设各个参数的测量误差互不相关，都是统计独立的高斯白噪声，用σθ，σΔR和σL分别表示方位角、距离差和基线距离的测量误差标准差，根据GDOP的定义式可知：

(17)

对式(15)求偏导可以得到

GDOP1=

(18)

式中：

(19)

(20)

×

(21)

(22)

(23)

×

(24)

3.2 DOA-TDOA多普勒频移联合定位

利用方位角、到达时间差和多普勒频移观测参数，其观测方程为式(8)、式(9)、式(11)。由于观测方程的非线性，无法直接求取目标的位置，故可以通过采用扩展卡尔曼等非线性滤波算法实现对目标的定位。

为求取其定位方法的GDOP，对观测方程求微分得

(25)

矩阵中各元素为

为简化计算公式，令

写成矩阵形式为

d Y=CdX

(26)

式中：

不考虑观测噪声对矩阵C的影响，可得目标位置误差向量，即式(26)的最小二乘解为

dX=(CTC)-1CTdY

(27)

由式(27)可知，目标的几何定位误差与方位角、时差和多普勒频移的观测误差，以及目标与观测站和外辐射源的位置关系有关。这里用σfd表示多普勒频移观测误差的标准差，观测误差的协方差矩阵为

(28)

则定位误差协方差矩阵为

PdX=E[dXdXT]=

[(CTC)-1CT]PdY[(CTC)-1CT]T

(29)

则几何定位精度GDOP为

(30)

4 仿真实验

为了探究本文两种定位算法的目标几何定位精度，在不同观测条件下，通过仿真实验探究观测误差和目标与外辐射源之间的空间位置关系对GDOP的影响。

4.1 DOA-TDOA基线联合定位误差仿真分析

仿真一：观测误差对GDOP的影响

仿真条件：假设接收站位于坐标原点O，外辐射源的初始位置坐标为(100,0)km，目标与外辐射源在同一平面内，各观测误差条件如表1所示。

通过图2(b)、图2(c)、图2(d)与图2(a)相比较发现，角度观测误差值提高一倍，目标的定位误差约增加为原来的两倍；距离差观测误差提高一倍，目标的定位精度几乎没有变化；基线距离观测误差提高一倍，目标的定位误差稍有增加。故在本算法定位体制下，主要影响目标定位精度的是角度观测误差，基线距离与距离差观测误差次之。

仿真二：基线距离对GDOP的影响

仿真条件：假设方位角的观测误差值为σθ=0.003 rad，距离差的观测误差值为σΔR=0.1 km，基线距离观测的误差值为σL=0.1 km，观测站位于坐标原点O，基线距离的变化值如表2所示。

图3(a)减小基线长度至70 km，使外辐射源距离观测站更近；图3(b)增加基线的长度至140 km；将以上两个目标定位的几何定位精度图与图2(a)对比发现，改变基线距离的长度，对于外辐射源附近区域定位精度影响明显，对其他区域无显著影响，基线距离越长，外辐射源附近定位精度越差。

4.2 DOA-TDOA多普勒频移联合定位

仿真一：目标速度对GDOP的影响

仿真条件：由于对目标观测的多普勒频移参量中包含目标的速度信息，所以在分析目标定位的几何定位精度时要考虑目标运动速度及运动方向。

假设方位角的观测误差值为σθ=0.003 rad，距离差的观测误差值为σΔR=0.1 km，多普勒频移的观测误差值为σfd=1 Hz，接收站位于坐标原点O，外辐射源位置坐标为(100,0)km，目标运动速度及运动方向变化如表3所示。

图4(a)中目标以(0.1,0)km/s的速度匀速运动，而图4(b)中将目标的速度大小增加为原来的二倍，速度方向不变，目标几何定位精度变大；图4(c)中令目标以速度(-0.1,0)km/s匀速运动，与图4(a)相比较，发现目标运动方向相反，几何定位精度不变；图4(d)中令目标以y轴正方向运动，发现在基线的垂线和垂线两侧附近区域定位精度较差；结合图4(e)和图4(f)分析可知，在目标运动方向与外辐射源连线区域目标定位精度较差，且几何定位精度以基线中点为中心呈中心对称分布。

结合以上仿真图分析可知，无论目标如何运动，目标在基线区域定位精度都较差。

仿真二：观测误差对GDOP的影响

仿真条件：假设接收站位于坐标原点O，外辐射源的初始位置坐标为(100,0)km，目标位于与外辐射源同一平面内，这里增加了多普勒频移观测量，故给出目标的运动状态，目标以(0.1,0 )km/s的速度匀速运动，各观测量的误差条件如表4所示。

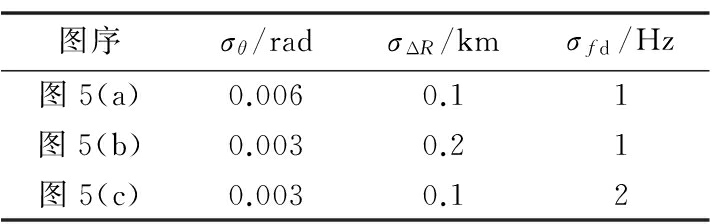
对比图5(a)与图4(a)可知，方位角观测误差增加一倍，目标几何定位精度基本不变；对比图5(b)与图4(a)可知，距离差增加为原来两倍，目标定位误差稍有增大；对比图5(c)与图4(a)可知，多普勒频移观测误差扩大一倍，目标定位误差也扩大一倍。通过以上分析可知，当利用方位角、距离

差和多普勒频移进行联合定位时，影响目标定位精度的主要因素是多普勒频移的观测误差，距离差和方位角次之。

仿真三：基线距离对GDOP的影响

仿真条件：假设方位角的观测误差值为σθ=0.003 rad，距离差的观测误差值为σΔR=0.1 km，多普勒频移的观测误差值为σfd=1 Hz，接收站位于坐标原点O，目标以(0.1,0 )km/s的速度匀速运动，基线距离变化如表5所示。

将图6(a)、图6(b)与图4(a)对比分析可知，随着基线距离的增加，目标几何定位精度降低，观测站与外辐射源附近区域定位精度变化尤为明显。

5 定位算法优化

通过对以上两种定位算法的分析发现，以上两种定位算法都是可行的，具体采用哪种定位算法实现对目标的定位，主要取决于观测站可以获得哪些目标参量，具体可以由以下几种情况：

1)当观测站采用双定向天线的机械圆周扫描的方式时，可以获得的目标参量有θT，Δt和L，此时只能利用算法一实现对目标的定位。

2)当观测站采用两部全向天线扫描时，此时可以获得的目标参数有θT，Δt和fd，此时只能利用算法二实现目标定位。

3) 当观测站利用阵列天线或者定向搜索天线时，可以获得θT，Δt，L和fd四个观测参量，此时两种算法都可以使用，因此可以将两种算法融合优化。

从仿真结果中，可以发现各自定位算法都有一定的定位盲区，为提高目标的定位精度，尽量减少目标的定位盲区，在4个观测参量都可测的情况下，可利用子集优选算法优化目标的定位精度。

首先，根据目标参数精度与目标定位几何关系，计算两种算法的几何定位精度，对比目标在各个区域的定位精度，取最高的定位精度，将此区域标记为相应的定位算法，进而给出高精度定位区域分布关系，再可通过粗略估计目标所在区域，令定位系统优化选择在此区域定位精度最高的定位算法，具体算法流程如图7所示。

由于目标运动状态复杂多变，在这里具体分析目标分别以(0.1,0)km/s和(0,0.1)km/s的速度匀速运动的两种情况。

假设方位角的观测误差值为σθ=0.003 rad，距离差的观测误差值为σΔR=0.1 km，基线距离观测误差值为σL=0.1 km，多普勒频移的观测误差值为σfd=1 Hz，基线距离设为100 km优化后的目标几何定位误差分布如图8所示。

对比图2(a)和图4(a)可以看出，优化后的定位算法，定位误差降低了一半以上，在各个区域都有较高的目标定位精度，改善了单一定位方法定位盲区多的问题。但在基线区域仍存在定位盲区，这是外辐射源单站无法克服的缺点，必须采用多站定位的方法才能克服。

6 结束语

本文研究了单站外辐射源的定位误差问题，发现目标参量的观测精度，受辐射源信号及传播途径影响较大，由于其不可控性，只能通过减少接收机热噪声和提高信号处理技术，来提高目标参量的观测精度。当可获得3个目标观测参量时，即可实现对目标的定位，此时可根据目标参量选择合适的定位算法。当4个参量都可以得到时，会出现信息的冗余，本文通过子集优选算法，提高目标在各区域的定位精度。

参考文献：

[1] CONTI M, BERIZZI F, PETRI D, et al. High Range Resolution DVB-T Passive Radar[C]// 7th European Radar Conference, Paris: IEEE, 2010:109-112.

[2] 万显荣, 梁龙, 但阳鹏, 等. 移动平台外辐射源雷达实验研究[J]. 电波科学学报, 2015, 30(2):383-390.

[3] 叶映宇, 文铁牛, 陈俊, 等. 外辐射源雷达运动目标信号特性及检测方法研究[J]. 雷达科学与技术, 2014, 12(6):604-608.

[4] 湖泽宾, 张庆庆, 张和发. 利用雷达作为外辐射源侦察定位精度分析[J]. 空军预警学院学报, 2017, 31(1):28-30.

[5] CHERNYAK V S. 双(多)基地雷达系统[M]. 周万幸, 吴鸣亚, 胡明春, 等译. 北京: 电子工业出版社, 2011.

[6] 顾晓婕, 郑恒, 田明辉. 基于多普勒/距离和的多站联合定位方法[J]. 雷达科学与技术, 2015, 13(1):81-85.