0 引言
在现代战争中,来自空中的威胁越来越大,掌握制空权、及早发现空中运动目标是夺取战争胜利的重要保证[1-3]。机载雷达在其中起着举足轻重的作用。机载雷达以高空运动平台为载体,可谓“高瞻远瞩”,较地基雷达而言,其有着更为广阔的覆盖范围,因此受到越来越多的重视。但其通常处于下视状态,面临着比地基雷达更复杂、强度更高、分布范围更广的地杂波,这使得目标的回波信号常常淹没在杂波中,对机动目标的检测与参数估计产生严重影响[4]。
空时自适应处理(Space-Time Adaptive Processing, STAP)是应用在相控阵雷达体制中的技术,能利用回波中的空时域信息实现杂波抑制。但是当目标作机动飞行时,在一个相干处理时间间隔(Coherent Processing Interval, CPI)内的机动目标回波会发生多普勒走动现象,这使得无法直接应用传统STAP方法对机动目标进行检测和参数估计[5]。尤其是当多个机动目标同时存在时,目标信号之间相互影响[6],使得对其参数估计变得困难。因此如何有效而快速地对空中多机动目标进行和检测参数估计亟待解决。
当存在空中多个目标在一个CPI内作机动飞行且加速度不变时,可将回波信号近似地看作多分量线性调频(Linear Frequency Modulation,LFM)信号[7],进而将多机动目标的参数估计问题转换为多分量线性调频信号的参数估计问题。目前,国内外针对LFM信号进行检测与参数估计的研究越来越多,包括典型的最大似然估计法、短时傅里叶变换法、离散Chirp傅里叶变换(Discrete Chirp Fourier Transform, DCFT)[8-9]、小波变换法、Wigner-Ville分布(Wigner-Ville Distribution, WVD)[10]、离散多项式相位参数估计法、分数阶傅里叶变换(Fractional Fourier Transform, FRFT)[11-12]等。上述方法多是针对单分量或多分量LFM信号的检测与参数估计,相关研究成果在工程实践中应用较为普遍,但并不能完全适用于机载雷达需要对空中多机动目标进行参数估计的情况,尤其存在以下几个关键问题:1)对弱机动目标的检测困难。例如WVD算法在检测多分量LFM信号时会产生交叉项,该交叉项容易掩盖弱机动目标信号,对于弱机动目标分量不能得到有效的估计[10]。2)需要采集大量样本,不适用于机载平台。例如FRFT算法在多机动目标检测时虽然可以有效聚积LFM的能量,并对每个机动目标进行检测和参数估计,但该方法需要的样本数较多[11-12]。3)所需计算量大、运算时间长。对于高速运动空中机动目标,过长的运算时间使得算法不能被运用到工程实践当中。例如文献[13]提出了一种基于RELAX算法的空中多机动目标检测算法,该算法虽然可以在脉冲数有限的情况下得到很好的参数估计结果,但是多次迭代使得运算量较大,不利于进行实时处理和工程运用[13]。
本文提出的NLS-RELAX参数估计方法,针对机载平台的空中多机动目标的问题。首先对复杂的地杂波进行抑制,以减弱杂波对于弱目标信号检测的影响;其次运用RELAX方法对多个目标信号进行分离,抑制强回波信号对弱回波信号的影响,使得弱机动目标回波信号可以被有效地从多个机动目标回波的叠加信号中检测出来;最后利用非线性最小二乘(NLS)的方法估计机动目标的参数,来减少RELAX方法多次迭代带来的大量运算,提高参数估计的效率。
1 数据模型
本节首先给出机载雷达信号回波模型。设载机速度为VR,飞行高度为H,雷达天线系统由N阵元均匀线阵(也可是由面阵经过微波合成的等效线阵结构)组成,脉冲重复频率为fr,天线阵元间距d=0.5λ,其中λ为雷达发射脉冲的波长。若雷达在一个相干处理时间间隔内发射K个脉冲,设xnk为第n个阵元在第k个脉冲上对应的复采样值,则每一距离门上的接收数据可用如下一个N×K的矩阵来表示:

(1)
将式(1)中的数据矩阵X按列排成一个NK×1的列向量,记为xl,用于表示第l个待检测单元的NK×1维空时快拍数据[14],其表达式为
xl=sl+cl+nl
(2)
式中,sl为第l个距离单元内的目标信号成分,cl为杂波,nl为加性高斯白噪声。sl可表示如下:
(3)
式中,Nt为该距离单元内机动目标的个数,btk为第k个目标回波幅度,a(utk,ωtk)为第k个目标的空时导向矢量,且有
a(utk,ωtk)=a(utk)⊗a(ωtk)
(4)
式中,⊗表示Kronecker积,utk=2πdcosψtk/λ和ωtk=4πVcosψtk/λfr分别为归一化的空间频率和时间频率。a(utk)为第k个目标空域导向矢量, a(ωtk)为第k个目标的时域导向矢量,二者都为K×1维列向量[15],分别表示为
a(utk)=[1,ej2π·1·dcosψtk/λ,…,ej2π·(N-1)·dcosψtk/λ]T
a(ωtk)=[1,ej2π·1·fdk/fr,…,ej2π·(K-1)·fdk/fr]T
(5)
式中,ψtk表示第k个目标的来向角,fdk表示第k个目标的多普勒频率。
若目标存在多普勒走动时,目标回波的多普勒频率发生变化,此时机动目标的时域导向矢量[15]为
a(ωtk)=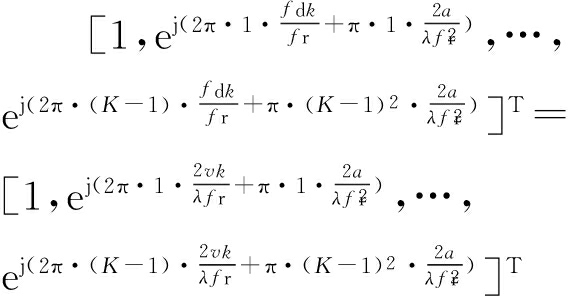
(6)
由式(6)可知,匀加速目标的时域导向矢量可分为多普勒频率项和频率调频项两部分,即当目标作匀加速运动时,其回波信号为LFM信号[15]。
2 基于NLS-RELAX的空中多机动目标检测和参数估计方法
针对机载平台的空中多机动目标之间互相影响导致参数估计受影响的问题,本文提出一种基于NLS-RELAX的参数估计方法。该方法借鉴RELAX思想的同时结合了NLS方法,在保证有效地抑制信号之间相互影响的前提下,能够获得更好的参数估计结果。下面对该方法进行展开介绍。
2.1 NLS-RELAX方法
在理想情况下,对雷达接收数据进行杂波抑制后的数据中只含有目标信号和噪声信号,可直接对杂波抑制后的数据进行目标的检测和参数估计。由于机载雷达在一个CPI内发射的脉冲采样点数有限,大大降低了直接利用时频分析方法估计机动目标参数的精度。
基于非线性最小二乘的机动目标检测方法的核心思想是构造一个目标信号模型,使其和杂波抑制后数据具有最小的“平方和”距离[16]。NLS方法较之重构时间采用技术,在获得良好的参数估计精度情况下,大大减少了运算量。
针对机载平台的下视状态使得目标淹没在复杂的地杂波中的问题,首先利用杂波协方差矩阵求逆来进行地杂波抑制[16],得到杂波抑制后的数据:
(7)
式中,x为雷达接收到的总回波信号,![]() 为利用参考单元的样本估计得到的杂波和噪声协方差逆矩阵。
为利用参考单元的样本估计得到的杂波和噪声协方差逆矩阵。
利用杂波抑制后所得的数据来进行机动目标信号模型的重构[16],具体如下式:
xz=btk·a(utk,ωtk)=bt·a(ωtk)⊗a(utk)=
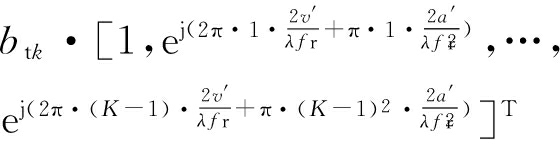 ⊗
⊗
(8)
式中:btk表示机动目标回波幅度;a(utk)是一个维列向量,表示空域导向矢量;a(ωtk)是一个K×1维列向量,表示时域导向矢量。机动目标的未知参数包含于a(ωtk)中,即a(ωtk)中包含机动目标的初始速度v′和加速度a′。
将式(8)重构所得的机动目标的信号模型与杂波抑制后的数据进行匹配,利用NLS方法来进行参数估计,构造代价函数[16]:
![]()
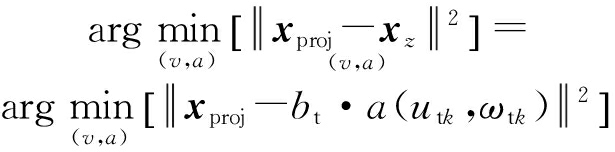
(9)
式(9)所示代价函数取得最小值时所对应的参数即为所求参数的估计结果[16]。
但利用式(9)估计目标的参数需要对目标信号的幅度进行估计,加大了参数估计的运算复杂度。为了解决这一问题,避免对目标信号幅度进行估计,利用文献[13]提出的简化算法对目标的初始速度和加速度进行估计,此时代价函数可表示为
![]()
![]()
a(utk,ωtk)]-1·a(utk,ωtk)H·xproj}
(10)
NLS在检测单个目标时能够得到很好的检测与估计效果,但当待检测单元存在多个机动目标时,弱目标信号分量会受到强目标信号分量的影响,加大了参数估计的难度。RELAX算法可以从雷达回波中分离多个机动目标,通过迭代搜索从中提取机动目标成分,其核心思想是根据各信号分量的强度,按照由强到弱的次序,逐个估计出各信号分量的参数,并根据参数估计的结果,依次从观测信号中消去其他信号分量后进行估计,将估计结果反复迭代,直至两次迭代过程的估计结果的相对变化量低于某一阈值。从而提高对多分量信号的检测与估计的有效性和可靠性。
虽然文献[11]中将重构时间采样技术和RELAX结合,在待测单元内存在多个目标时,仍然能够获得很好的参数估计结果,但由于重构时间采样技术的运算量较大,经由RELAX迭代过程后运算量成倍增大,这使得该方法很难被投入实际应用。因此,本文提出了NLS-RELAX方法,结合了非线性最小二乘和RELAX对空中多个机动目标进行检测和参数估计,该方法利用非线性最小二乘来估计机动目标的参数,减少了RELAX方法中多次迭代带来的大量运算,提高了参数估计的效率。
2.2 算法流程
为了讨论方便,本文假设待检测距离单元内存在两个机动目标,利用上节方法结合RELAX思想对两个机动目标进行参数估计,图1所示为本文方法的具体流程图。
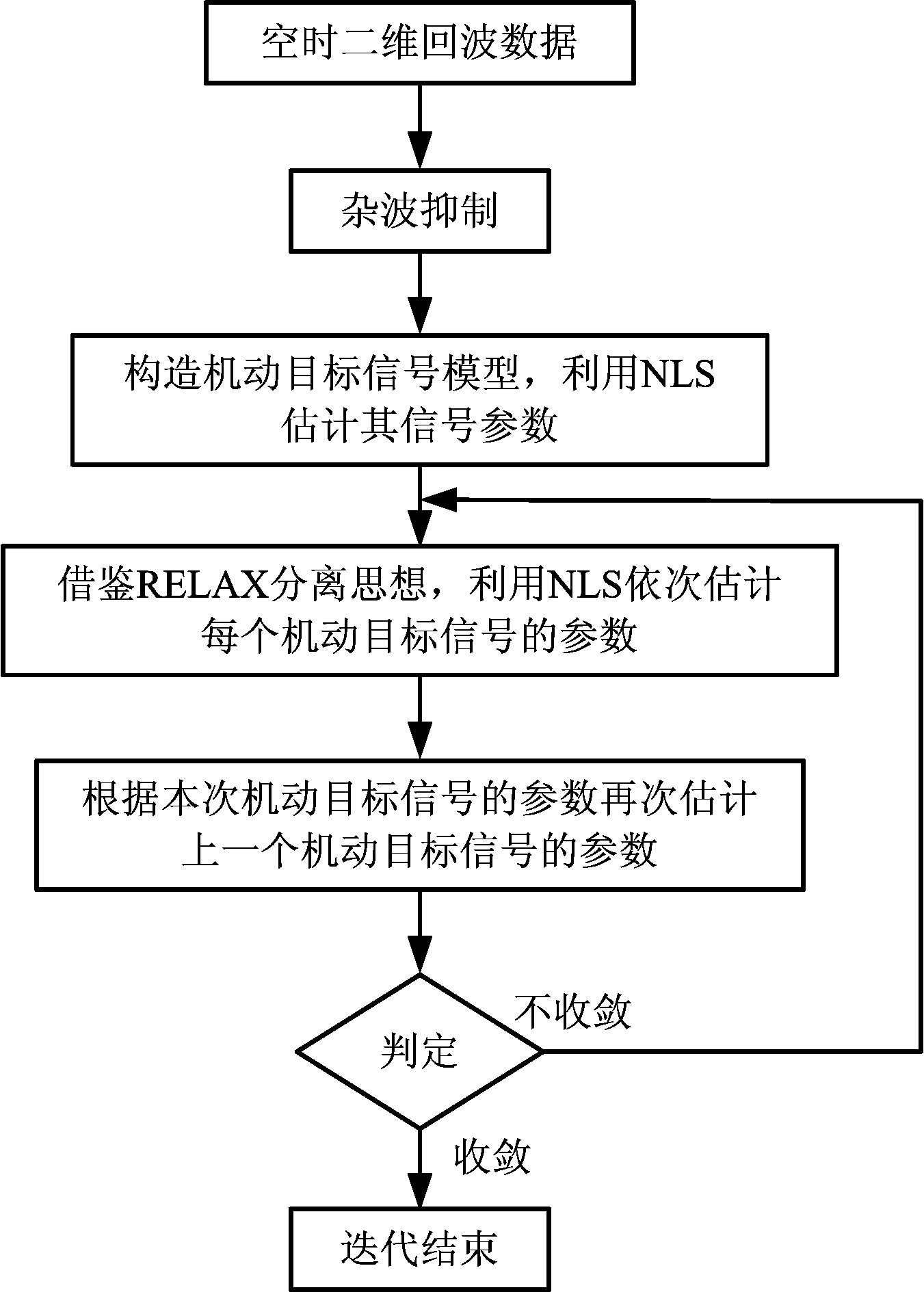
图1 基于NLS-RELAX的空中多机动目标检测与参数估计方法
具体步骤如下:
步骤1 进行杂波抑制。
首先利用式(7)对地杂波进行抑制,得到杂波抑制后的数据。
步骤2 估计第一个机动目标信号分量的参数。
利用NLS方法对第一个机动目标信号进行参数估计,由式(10)得到第一个机动目标信号的参数估计值![]() 其中
其中![]() 为第一个机动目标信号的估计速度,
为第一个机动目标信号的估计速度,![]() 为第一个机动目标信号的估计加速度。采用文献[8]的方法,利用分数阶傅里叶变换估计第一个机动目标信号的幅度
为第一个机动目标信号的估计加速度。采用文献[8]的方法,利用分数阶傅里叶变换估计第一个机动目标信号的幅度![]()
步骤3 估计第二个机动目标信号分量的参数。
根据第一个机动目标信号参数的估计值![]() 以及信号的数据模型构造第一个机动目标信号的数据
以及信号的数据模型构造第一个机动目标信号的数据![]() 利用RELAX算法的分离思想从消除杂波后的数据中减去重新构造的第一个机动目标信号,可得
利用RELAX算法的分离思想从消除杂波后的数据中减去重新构造的第一个机动目标信号,可得
(11)
xproj1为从杂波抑制后的数据中减去重新构造的第一个机动目标信号后的数据,对其进行能量检测,如果还能检测到目标信号,重复步骤2方法,对剩余信号中能量最强的机动目标信号进行参数估计,得到剩余信号中能量最强机动目标信号的参数估计值![]() 及
及![]() 其中,
其中,![]() 为第二个机动目标信号的估计速度,
为第二个机动目标信号的估计速度,![]() 为第二个机动目标信号的估计加速度。
为第二个机动目标信号的估计加速度。
步骤4 重新估计每个机动目标信号分量的参数。
从杂波抑制后的数据中减去步骤3中重新构造的第二个机动目标信号数据可得
(12)
利用式(11)方法对第一个机动目标信号的参数重新进行估计,重复步骤3估计第二个机动目标信号的参数。
重复步骤4,当每个机动目标的参数估计结果与其上一次参数估计结果变化量低于某一设定阈值,认为其收敛,即判定当前估计的参数是该机动目标的参数估计结果。
3 仿真结果及分析
仿真的雷达平台采用机载正侧阵雷达平台,载机高度为10 km,速度为120 m/s,雷达工作波长为0.32 m,雷达脉冲重复频率为1 500 Hz,雷达距离分辨率为20 m,天线系统采用16阵元64脉冲的均匀线阵。设定杂噪比为50 dB,信噪比为0 dB。假设两个机动目标均处于同一个待测单元内,方位角均处于90°,第一个机动目标信号的初始速度v1=67.99 m/s,加速度a1=99.9 m/s2,幅度bt1=1;第二个机动目标信号初始速度v2=45.99 m/s,加速度a2=68.99 m/s2,幅度bt2=0.7。本文估计均方根误差进行了500次蒙特卡洛实验,并将实验结果所得的均方根误差与克拉美罗界(Cramer Rao Bound, CRB)进行对比。
图2(a)为回波信号的功率谱,由于空中平台运动以及不同方位的地面散射体相对平台的速度各异,同时由于杂波分布范围广、强度大,导致地杂波呈现很强的空时耦合特性,机动目标信号很大程度被地杂波信号所淹没。图2(b)为杂波抑制后的功率谱,可以清楚地看出处于零频附近的杂波被有效抑制掉,两个机动目标均能突显出来,初始速度越大,其对应的机动目标离杂波脊越远,可见,目标一离杂波脊最远,目标二离杂波脊最近。图2(c)为多机动目标参数估计过程中减去目标一后的功率谱。图2(d)为多机动目标参数估计过程中减去目标二后的功率谱。

图2 不同情况下的功率谱
图3和图4是利用5种方法估计得到的参数均方根误差与CRB的比较结果图,其中图3分别为机动目标一的初始速度均方根误差和加速度均方根误差与CRB的比较结果图,图4为机动目标二的初始速度均方根误差和加速度均方根误差与CRB的比较结果图。可见,本文方法在不同的信噪比下都可以有效地估计出两个机动目标信号的参数,在信噪比较低的情况下,本文算法较单个阵元估计方法和非相干估计方法,更接近CRB,性能更好,并能得到与RTS方法相当的参数估计结果。
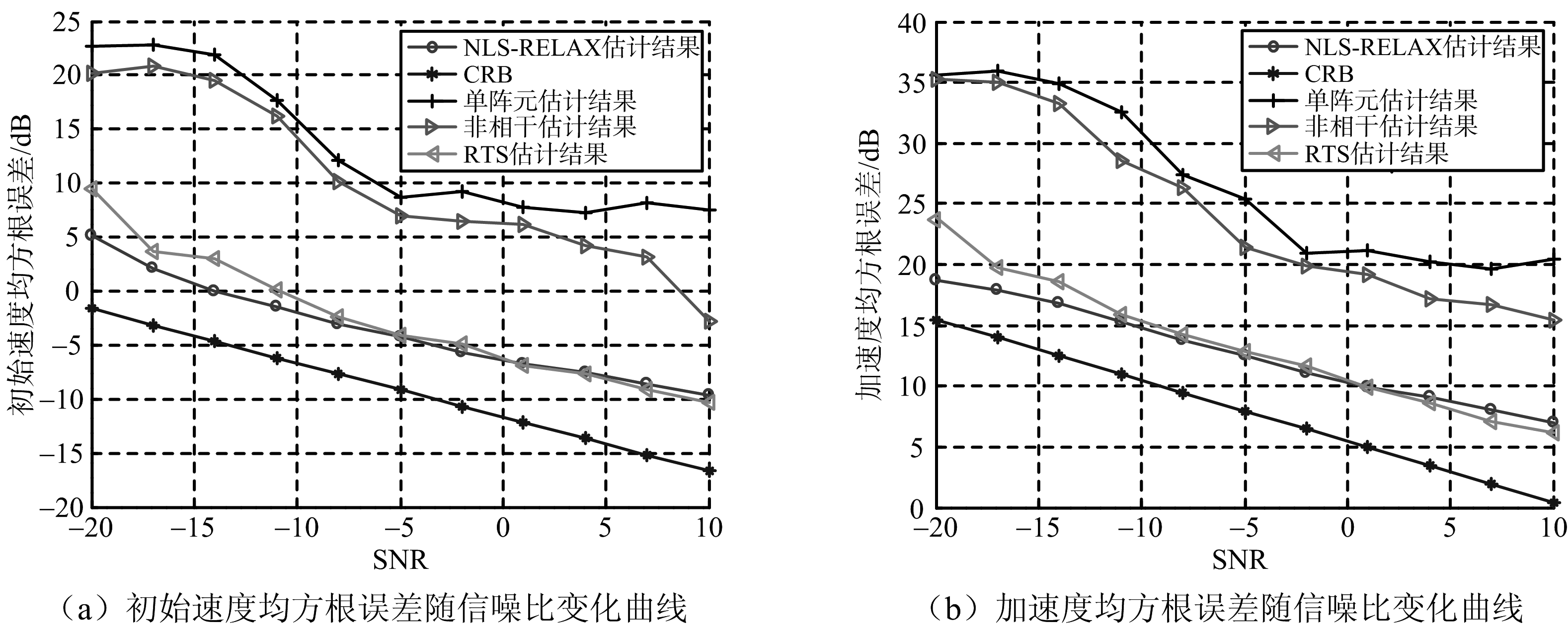
图3 机动目标一参数均方根误差随信噪比变化曲线
表1给出了本文方法和RTS方法参数估计所需运算量的比较,其中Ns表示估计斜方差矩阵时所需训练样本数,[vc,vz]表示机动目标初速度的搜索范围,vrg表示搜索长度,Δv表示搜索步长,[ac,az]表示机动目标加速度的搜索范围,arg表示搜索长度,Δa表示搜索步长,[pc,pz]表示分数阶傅里叶变换的阶数搜索范围,prg表示搜索长度,Δp表示搜索步长。
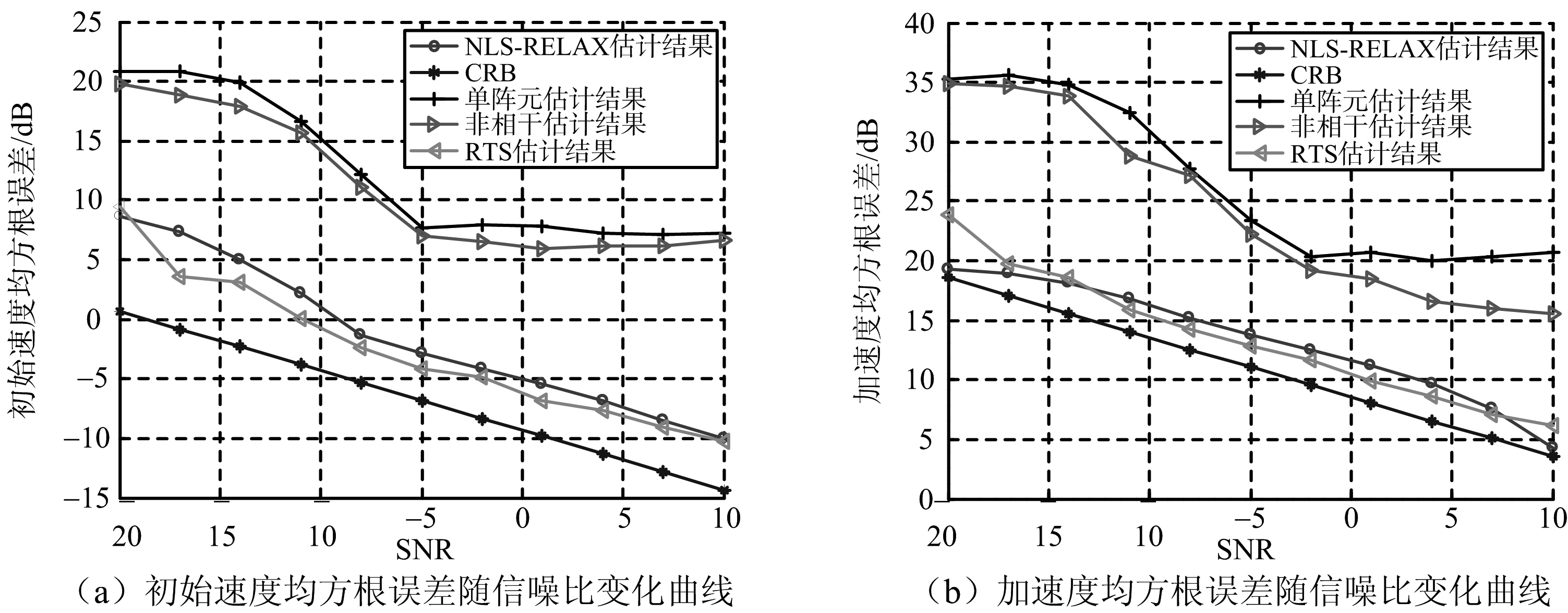
图4 机动目标二的参数均方根误差随信噪比变化曲线
表1 运算量比较
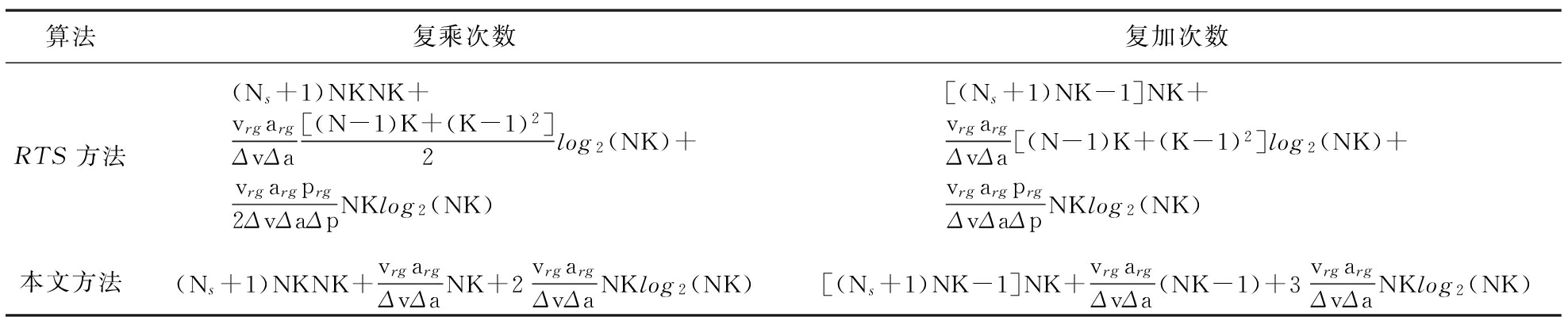
表2给出了本文方法和RTS方法进行一次蒙特卡洛实验的运算时间对比。仿真实验采用Matlab R2014a软件进行仿真,计算机参数为Inter(R)Core(TM) I 7-6700处理器;主频:3.40 GHz;内存:4 GB。可见,本文方法较之RTS方法,在达到相当的参数估计结果的情况下运算效率有着显著提高。
表2 运算时间比较

4 结束语
本文提出了一种NLS-RELAX的空中多机动目标参数估计方法,该方法借鉴了RELAX思想,对多个机动目标有效分离,并利用NLS算法构造代价函数,通过重构目标信号的空时导向矢量,使其与杂波抑制后数据具有最小“平方和”对每个机动目标信号的参数进行估计。在达到与RTS相当的参数估计结果下,大大减少了运算量。仿真实验表明,该方法在待检测单元内存在多个机动目标且在脉冲点数有限的情况下,对于每个机动目标都能获得很好的参数估计结果。
参考文献:
[1] KLEMM R. Principle of Space-Time Adaptive Processing[M]. 3rd ed. Hertfordshire:IET, 2006:1-133.
[2] DAVIS M E. A History of Battlefield Surveillance Radar[C]∥IEEE Radar Conference, Arlington, VA:IEEE, 2015:1345-1350.
[3] 丁鹭飞, 耿富录. 雷达原理[M]. 3版. 西安:西安电子科技大学出版社, 2002:1-24.
[4] RICHARDS M A. 雷达信号处理基础[M]. 邢孟道, 王彤, 李真芳, 等译. 北京:电子工业出版社, 2008:1-39.
[5] 王永良, 彭应宁. 空时自适应信号处理[M]. 北京:清华大学出版社, 2001:1-57.
[6] 罗守贵, 金林. 机载预警雷达的发展趋势分析[J]. 现代雷达, 2008, 30(12):1-5.
[7] 江莉. 线性调频类LPI雷达信号参数估计算法研究[D]. 西安:西安电子科技大学, 2016.
[8] ZUK J, ROSENBERG L. Efficient FFT Method for Modelling Performance of Radars with Scan-to-Scan Feedback Integration[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing, South Brisbane, QLD:IEEE, 2015:1817-1821.
[9] ZHANG Guiping, JIA Yunxiang, FU Gang. Optimization of Coherent Integration Algorithm on Uniformly Accelerated Goal Based on B-DCFT[C]∥3rd International Conference on Materials Engineering, Manufacturing Technology and Control, [S.l.]:Atlantis Press, 2016:979-982.
[10] 王露. 基于子带分解WVD的雷达信号时频分析方法[J]. 现代导航, 2016, 7(6):442-447.
[11] 陈艳丽, 郭良浩, 宫在晓. 简明分数阶傅里叶变换及其对线性调频信号的检测和参数估计[J]. 声学学报, 2015, 40(6):761-771.
[12] 杨潇. 基于FRFT的非平稳信号分析方法研究[D]. 成都:电子科技大学, 2015.
[13] 李海, 王小寒, 吴仁彪. 基于RELAX的空中多机动目标检测与参数估计[J]. 航空学报, 2013, 34(4):873-881.
[14] ZHU Shengqi, LIAO Guisheng, YANG Dong, et al. A New Method for Radar High-Speed Maneuvering Weak Target Detection and Imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 11(7):1175-1179.
[15] 李海, 吴仁彪, 王小寒. 基于非线性最小二乘的空中机动目标检测方法[J]. 电子信息学报, 2012, 34(9):2143-2148.
[16] 王小寒. 基于重构时间采样的机动目标检测研究
[D]. 天津:中国民航大学, 2012.

