0 引言
军用通信及电子战设备在使用过程中,为了感知全局信息往往需要侦听并解调多个频道上的信号,这要求接收机具有多信道的处理能力。
多信道接收机的主要难题是需要对整个频段进行搜索监听,以确定在哪个信道上出现信号。如果按常规的超外差接收机设计,采取逐信道移频滤波的方式进行监听,往往会遗漏或丢失部分信道上的信号,即无法进行全概率信号截获[1]。
在通信、雷达及电子对抗领域利用软件无线电手段对数字域信号处理流程进行变形,可以获得基于多相滤波器组的信道化接收机[2-3]。该接收机能有效将数据流由串行处理转化为N通道的降采样并行处理[4-5],但其缺陷是信道带宽和降采样后的采样率在数值上相等,这不利于后续的时间同步处理[6]。
为了改变多相滤波器组的输出采样率,国外有学者提出基于嵌入式变采样多相滤波器组的信道化接收机[7],但该类文献仅在Z域上描述了嵌入式变采样多相滤波器组的原理,缺少一套完善的数字时域分析与实现方法。本文首先在数字时域引入移位偏量q以对嵌入式变采样多相滤波的原理进行详细推导,并依据推导结果比较总结出易于实现的方法,确立了可行的嵌入式变采样多相滤波器组的信道化接收机架构,最后通过仿真证明了该方法的有效性。
1 多相滤波器组的结构及原理
1.1 传统信道化接收机存在的问题
如图1所示,传统超外差信道化接收机在中频信号后对每个频道分别移频,再通过多个固定带宽的低通滤波器进行滤波,获取不同频道上的信号。
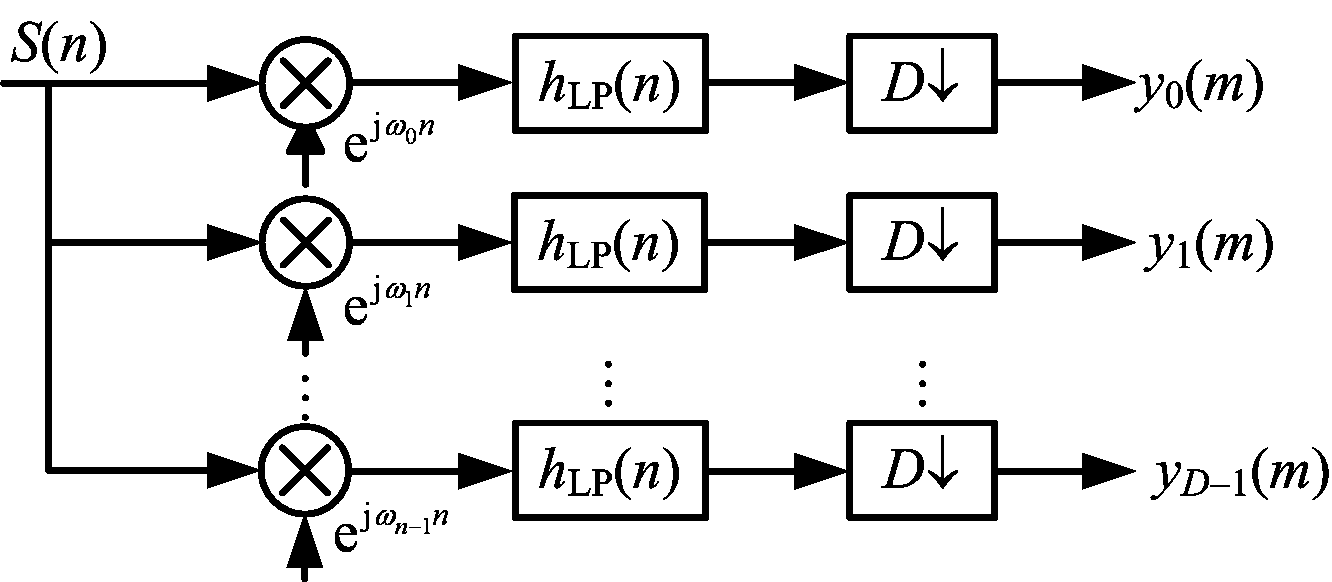
图1 传统多信道接收机构架
由于多信道接收机的总系统带宽要远大于频道带宽,因此经过低通滤波后往往进行降采样以减小后续处理压力。当系统需要解调多个信道上的信号时,需要N通道并行处理,若能将降采样过程提到低通滤波以前,则能大大提高系统的实时处理能力。为此在软件无线电领域,提出了基于多相滤波器组的信道化接收机。
1.2 基于多相滤波器组的信道化接收机
文献[4]对多相滤波器组的信道化接收机的原理及实现方法进行了详尽描述,本文2.1节将在此基础上进行变采样变形,因此本节引用该文的主要公式及结论,以便和2.1节中的推导进行对比。
对于如图2所示的N频道通信系统(此处N为偶数),频道移频频率ωk(k=0,1,2,…,N-1)为
(1)
![]()
图2 N通道系统中频示意图
通过ωk将第N-k频道上的信号移到零频。通过低通滤波提取该频道上的信号。若滤波后系统进行D倍降采样且N=D,则输入信号S(n),低通滤波器hLP(n)和输出信号yk(m)的相互关系为
yk(m)={S(n)ejωkn·hLP(n)}|n=mD=
ejωk(mD-iD-p)hLP(iD+p)
(2)
定义:SP(m)=SP(mD-p),hP(m)=hLP,(mD+p),则
yk(m)=![]()
ejωk(m-i)DhP(i)]e-jωkp
(3)
令
xP(m)=![]()
[SP(m)ejωkmD]·hP(m)
(4)
则
(5)
将![]() 代入式(4)得
代入式(4)得
(6)
最终可得
yk(m)=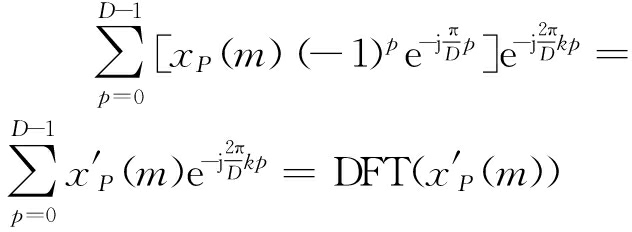
(7)
一般取D为偶数,则基于多相滤波器组的信道化接收机系统模型如图3所示。
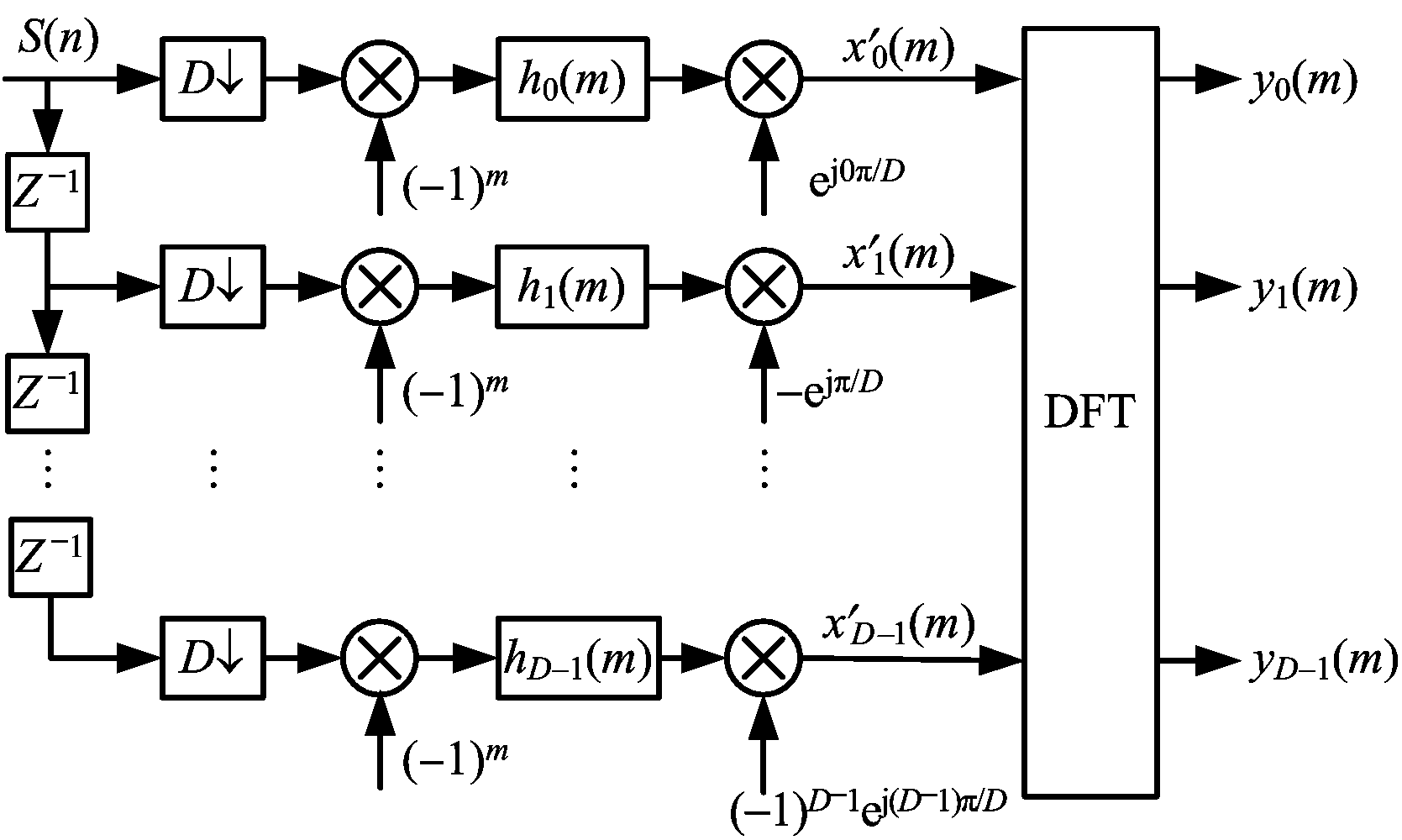
图3 多相滤波接收机数学模型
在图3的构架中![]() 即对第p通道的信号进行滤波后乘以移相系数
即对第p通道的信号进行滤波后乘以移相系数![]() 然后再进行DFT处理。
然后再进行DFT处理。
由于进行如上推导的前提条件是降采样系数D和频道数N相等,因此降采样后的单频道采样率fs′在数值上等于频道带宽Bd。
工程上为了便于信号时间同步的恢复,最优采样率fsopt=2Ba(Ba为码元速率)。因此若多相滤波接收机的fs′=2Ba,则要求Bd=2Ba。对于常用的调相方式(BPSK,QPSK等)经过升余弦滚降滤波后,要求的最小频道带宽为Bd=1.2~1.5Ba。因此若按最优采样率设计系统会造成频道的浪费,而按最优频道带宽设计则系统在时间同步恢复的过程中需要引入复杂的插值算法。
2 嵌入式变采样多相滤波器组信道化接收机
为了同时满足对采样率和频道带宽的要求,需要改变fs′,通过数据内插和分数倍抽取的方法可以改变采样率[8],但这需要引入额外的计算且在低信噪比环境下插值算法的质量会降低。若采用嵌入式变采样,依据数学推导通过在多相滤波器组的构架上进行变化,使通道采样率和通道带宽解耦,则可以获取更为准确的变采样效果且硬件实现也更为简单。文献[9]在两个特定嵌入式变采样条件下对多相滤波器组信道化接收机的结构变化进行了说明,但并未给出结构变化的原因与数学推导,也缺少通用的变采样处理方法。因此若要将变采样理论运用于工程实现,需要在离散时域推导出一种可行的变采样多相滤波器组架构,这正是本文的研究重点。
对于变采样系统而言取n=mD+q(q为移位偏量),若需求的降采样倍数为D′,则控制q随m变化,即q=m(D′-D)可满足变采样要求。文献[10]已在Z域论证了引入移位偏量后变采样多相滤波器组的信道化接收机在理论上的可行性,但由于q是周期时变的参数,引入该参数后不能直接套用原滤波器构架。
2.1 嵌入式变采样多相滤波器组的数学模型推导
引入移位偏量q后,式(2)变化为
yk(m)={S(n)ejωkn·hLP(n)}|n=mD+q
(8)
相对于式(2),式(8)中的q既可以引入到 S(n)ejωkn中,也可以引入到hLP(n)中。下面分别对这两种引入方式进行推导,并比较其在工程实现上的难易程度。
若将q引入到S(n)ejωkn中,则式(2)变化为
yk(m)=![]()
ejωk(mD+q-iD-p)hLP(iD+p)
(9)
定义:Sp_q(m)=S(mD-p+q),hp(m)=hLP(mD+p),则
yk(m)=
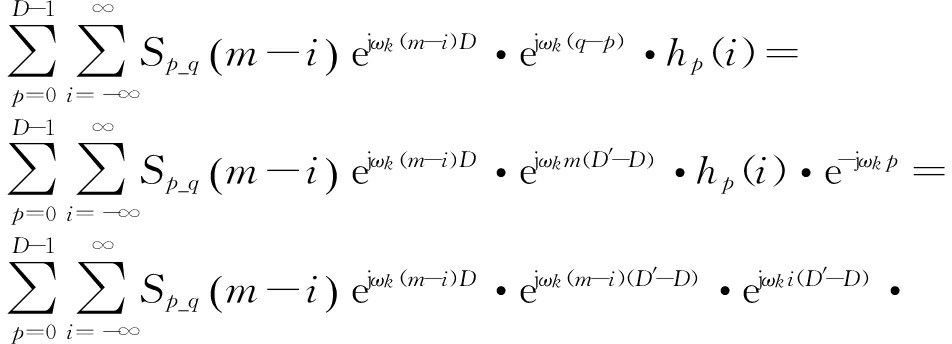
hp(i)·e-jωkp=
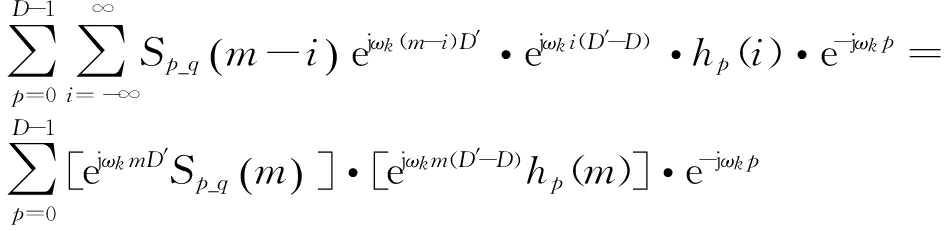
(10)
令
Xp_q=ejωkmD′Sp_q(m)·ejωkm(D′-D)hp(m)
(11)
则
(12)
对比式(4)和式(11)可见,若将q引入到 S(n)ejωkn中,则进行多相滤波之前输入数据和多相滤波器滤波系数都要乘以相应的相移因子。且将![]() 代入到式(11)中发现,由于 N≠D′,因此不同频道(即k取不同值)的相移因子并不相等,这给硬件处理带来了额外的复杂度,因此将q引入到S(n)ejωkn中,不易于工程实现。
代入到式(11)中发现,由于 N≠D′,因此不同频道(即k取不同值)的相移因子并不相等,这给硬件处理带来了额外的复杂度,因此将q引入到S(n)ejωkn中,不易于工程实现。
若将q引入到hLP(n)中,则式(2)变化为
yk(m)=![]()
hLP(iD+p+q)
(13)
定义:hp_q(m)=hLP(mD+p+q),则
xp_q(m)=![]()
(14)
根据式(4)~式(7)的推导,可得
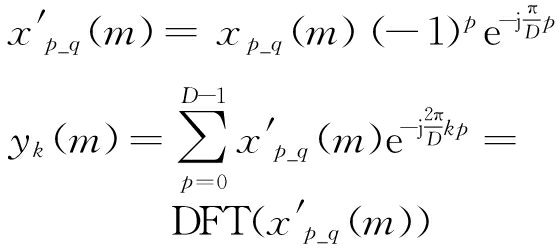
(15)
由式(15)可见,若将q引入到hLP(n)中,则相对于1.2节的推导,其变化只体现在多相滤波器的移位上,由于移位偏量q=m(D′-D)是时变的,所以信道化接收机的结构也会变化,下节将推导出将q引入到hLP(n)中的工程实现方法。
2.2 嵌入式变采样项滤波器组的工程实现方法
将q引入到hLP(n)后,为便于分析首先将滤波的移动滑窗过程体现在hLP(n)中。下面以D=8,D′=6来说明这个过程。
图4为卷积滑窗相邻的两个状态,其中D(n)为输入数据,输入数据以8个相邻数据为一列(对应8个频率通道),实线框为滤波器覆盖的数据部分(滤波器为32阶),其步进为6。

图4 滤波滑窗前后状态对比
由图4可见,由于滤波器的滑窗步进D′≠D,则每个频率通道的滤波器系数并不固定,由于工程上往往把滤波器系数放入固定位置的寄存器中,变化的系数并不利于工程实现,因此将滑窗过程体现在输入数据上更易于工程实现。
以D′<D(为同时满足最优采样和最小频道带宽要求,往往要求D′<D,若D′>D可作类似推导)来进行实现说明。将输入数据SP(m)乘以相移系数ejωkmD后得到缓存数据R(nn)|nn=mD+p,p∈[0,D-1]。每个周期将D′个缓存数据即 R(nn-D′+1)~R(nn)推入到滑窗寄存器中,其过程如下:
滑窗寄存器的状态更新等效于将前一状态下第1行到D-D′行所有列的数据搬移到第D′+1到D行的所有列,然后将前一状态第D-D′+1行到第D行的第1列到n-1列的数据搬移到第1行到D′行的第2列到n列,最后将经过移相的D′个数据放入第1列的第1行到D′行。
图5(a)和图5(b)给出D′=6,D=8,低通滤波器总长度N=32(多相滤波单通道长度n=4),一次数据更新前后,滑窗寄存器的前后状态。
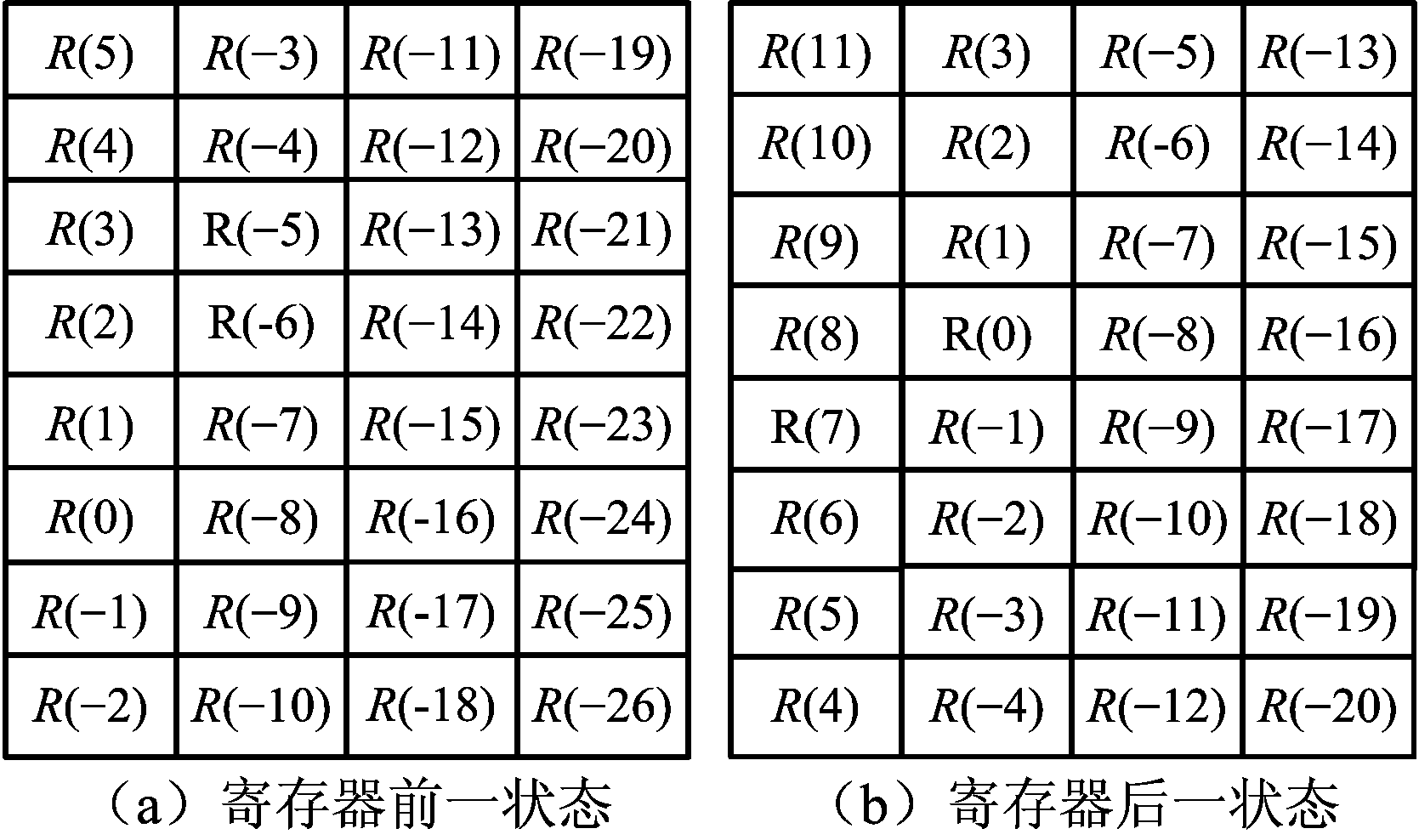
图5 寄存器状态转换
由于滤波器系数没有变化,因此要将滤波结果映射到与之对应的频道上必须将滤波后的数据进行旋转。由于q=m(D′-D),因此每次滤波后数据的旋转位数为n_r=mod(m|D′-D|,D)(mod为取余运算符),而滤波后数据的旋转周期为per_r=LCM(D′,D)/D′(LCM为最小公倍数运算符)。
图6给出基于输出旋转的变采样多相滤波的工程实现方法示意图。
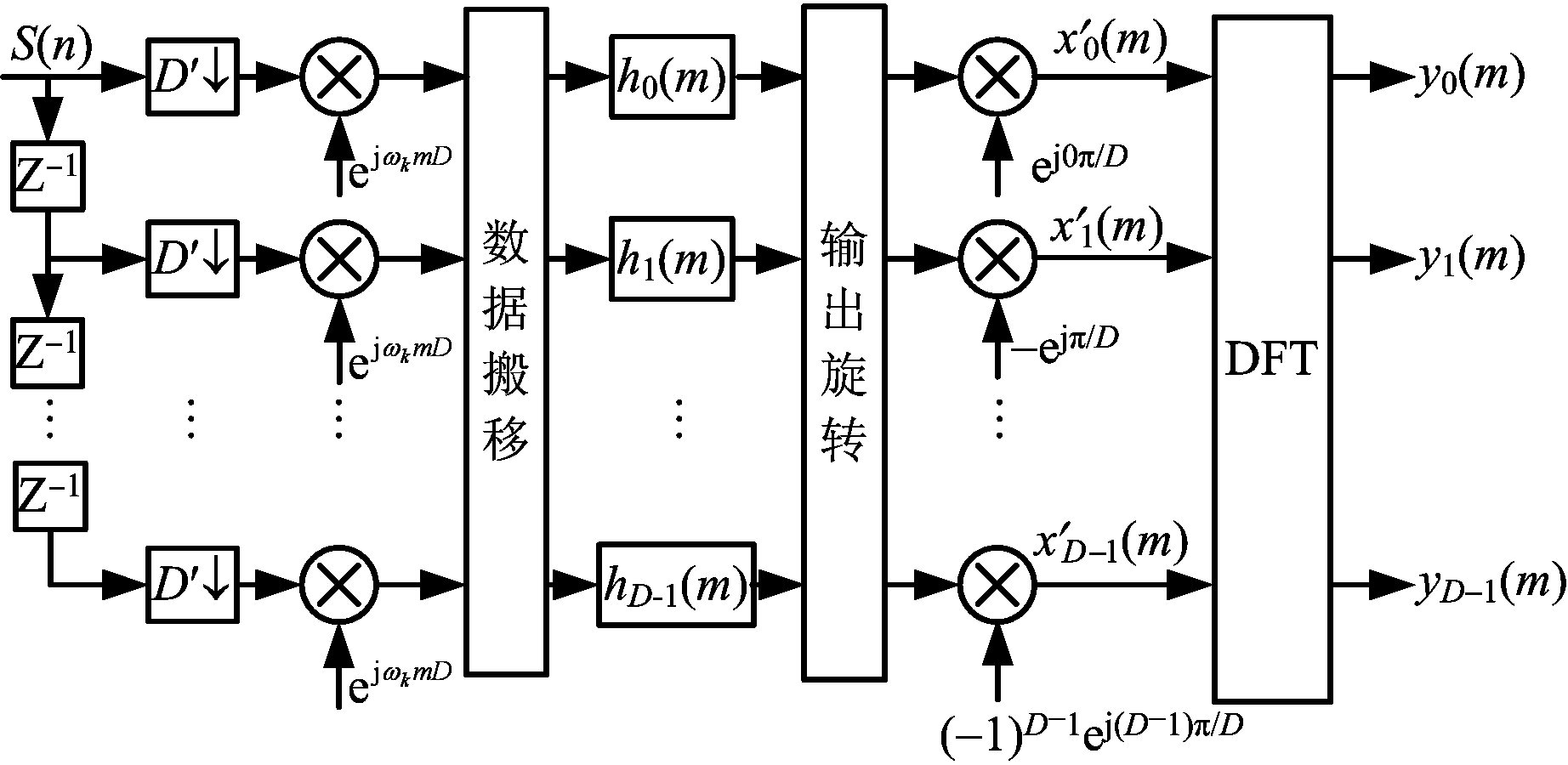
图6 变采样多相滤波器组数学模型
由图6可见,根据工程需要设置D′可实现变采样的目的。对比图3和图6可见,按本节推导方法实现的嵌入式变采样多相滤波器组信道化接收机相对于原信道化接收机的主要变化在于滤波前的数据搬移和滤波后的输出旋转。
3 计算机仿真及工程验证
3.1 嵌入式变采样多相滤波器组的仿真验证
在Matlab 8.1仿真环境下模拟16频道通信系统,系统零中频复信号带宽B=24 MHz(频道带宽B_chan=1.5 MHz),系统采样率fs=24 MHz(即按最优频道带宽设计)。模拟信号为码元时宽T=1 μs的第5频道QPSK信号(中频频率为 -3.75 MHz)码元速率Baud=1 MHz,对信号进行升余弦滚降滤波(滚降系数r=0.25)。
低通滤波器为640阶FIR滤波器(多相滤波器组单通道为40阶),低通滤波器幅频响应如图7所示。

图7 低通滤波器幅频响应
由图7可见,低通滤波器的归一化通带带宽为1/16,阻带的抑制效果在20 dB以上。
比较信号通过多相滤波器组(16倍降采样)和嵌入式变采样多相滤波器组(12倍降采样)后的输出信号频谱和时域波形。
图8为多相滤波器组第5通道信号归一化频谱,由于降采样倍数为16,则通道采样率为1.5 MHz;图9为变采样多相滤波器组第5通道信号归一化频谱,由于降采样倍数为12,则通道采样率为2 MHz。
由图8可见,信号在0.75 MHz的频谱幅度相对于中心频率的频谱幅度降低53 dB;由图9可见,信号在0.75 MHz内的频谱和图8(a)基本相同,从0.75 MHz到1 MHz为旁瓣区。
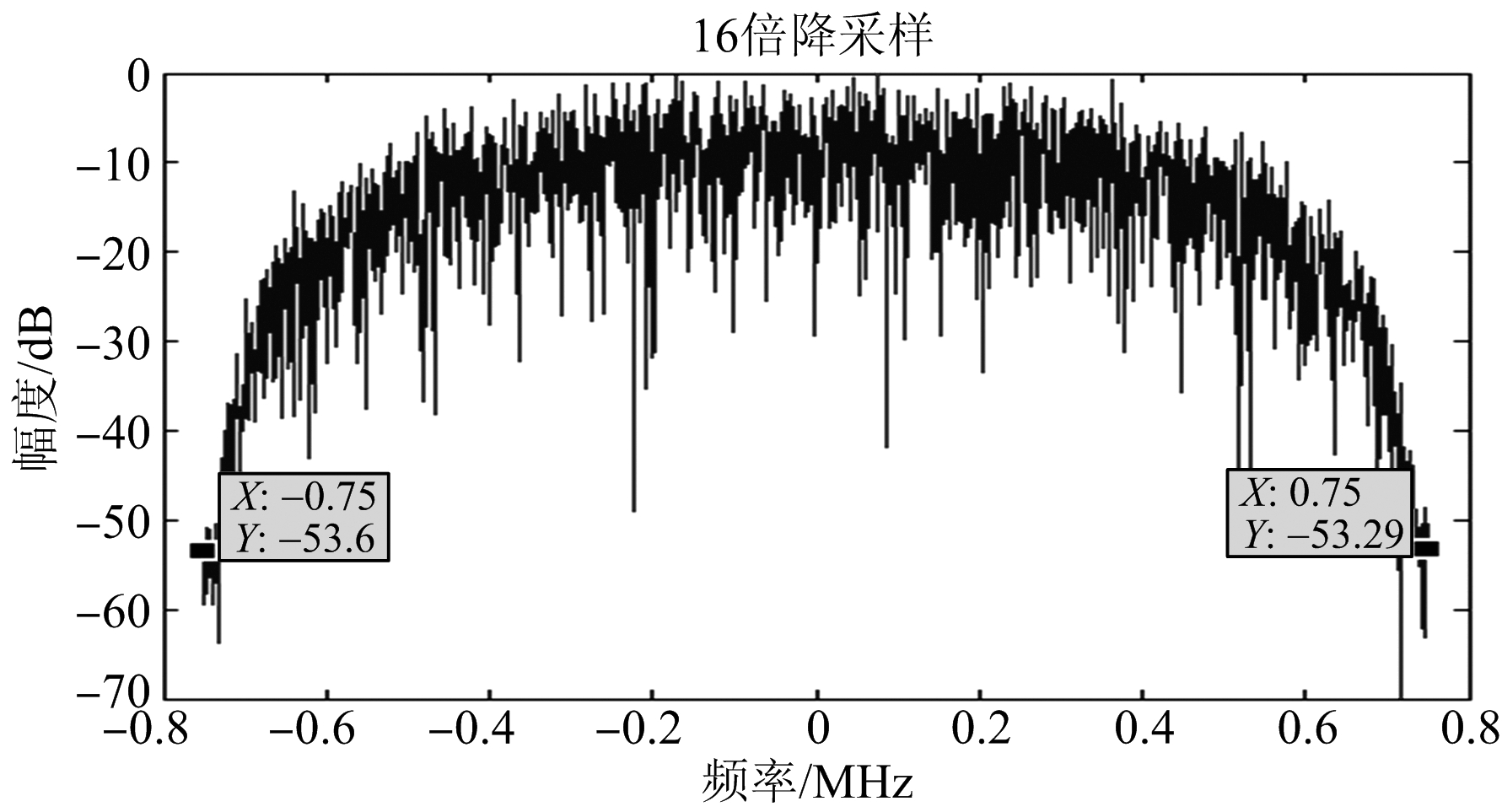
图8 多相滤波第5通道归一化频谱
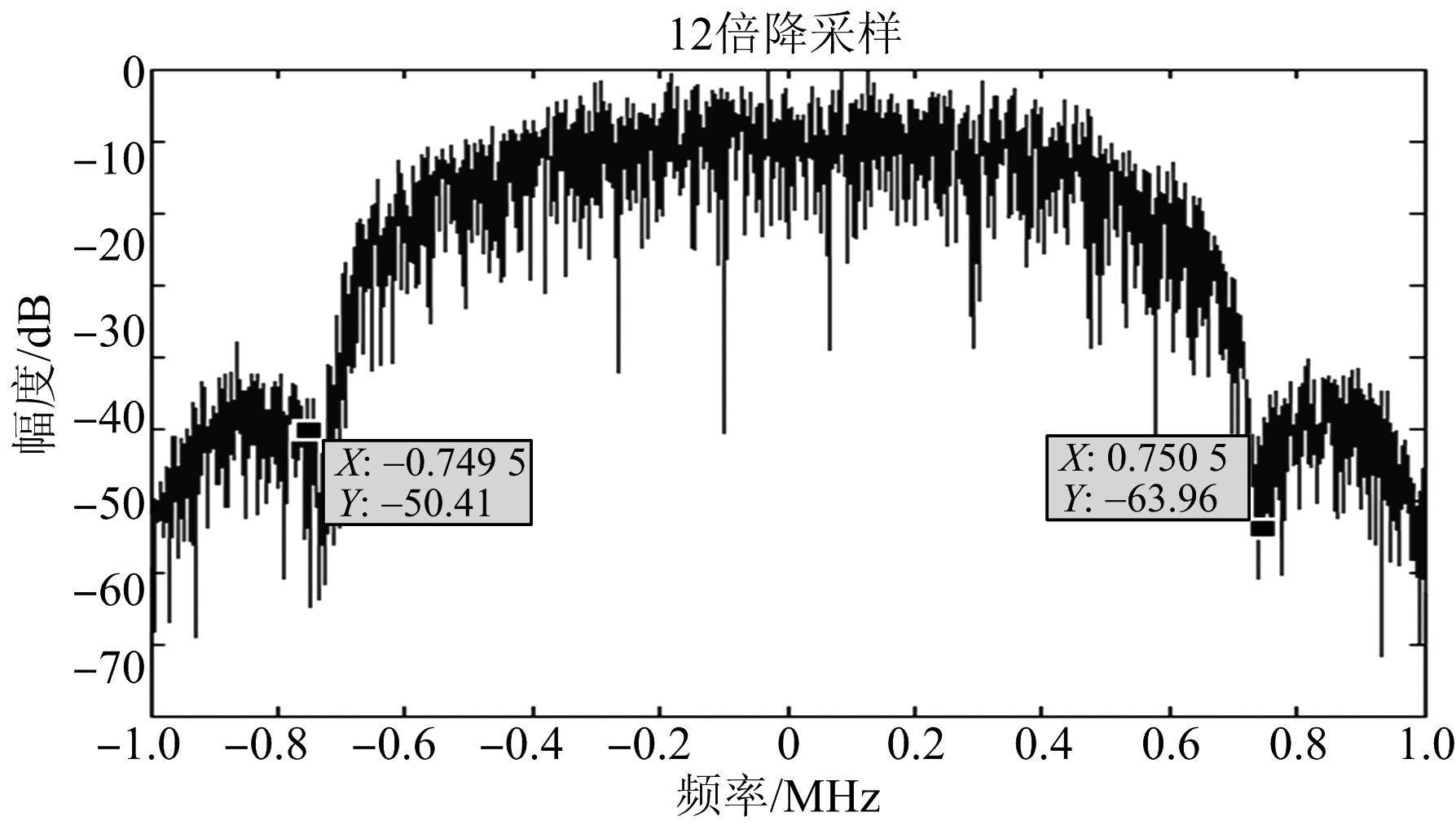
图9 变采样多相滤波第5通道归一化频谱
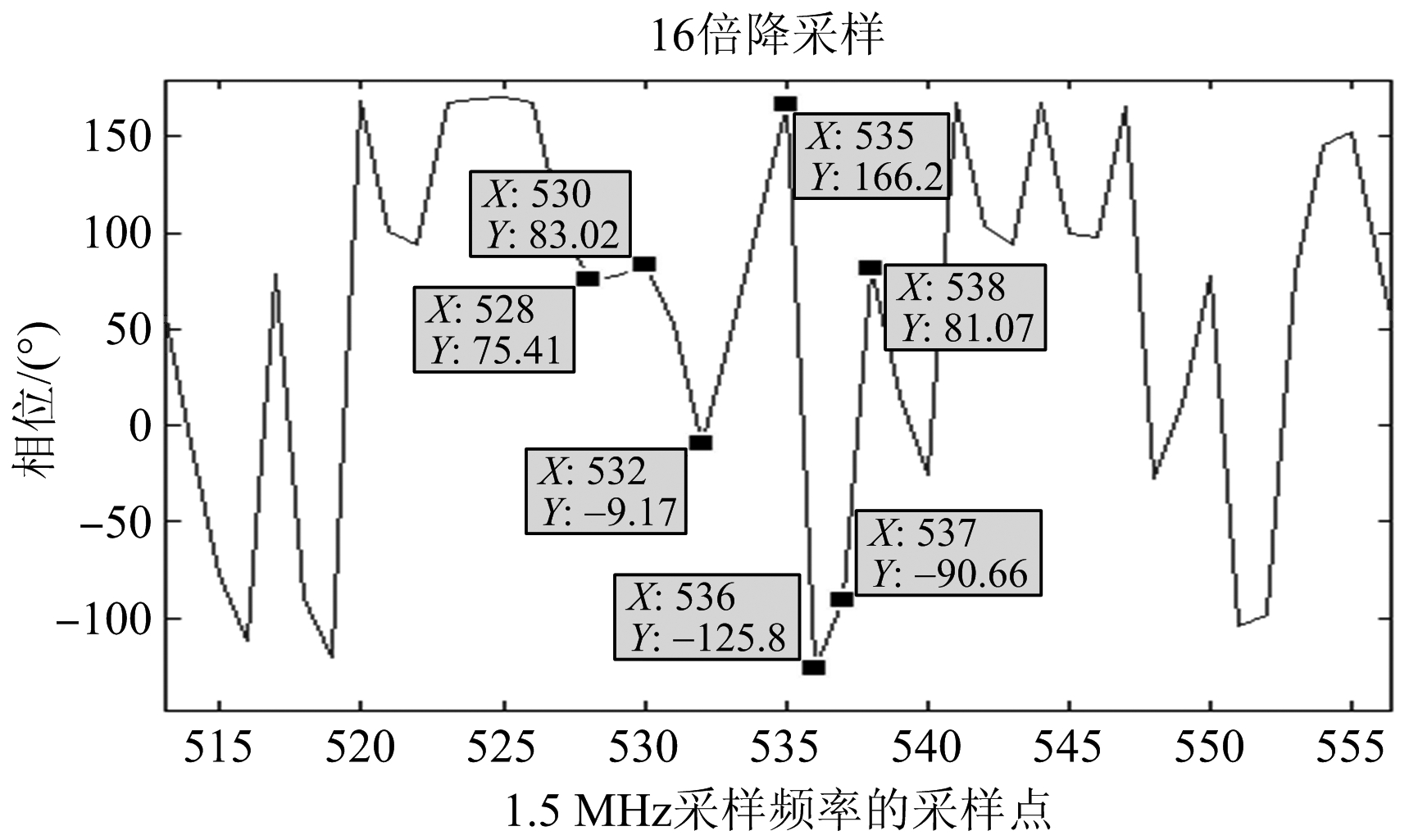
图10 多相滤波第5通道时域输出相位
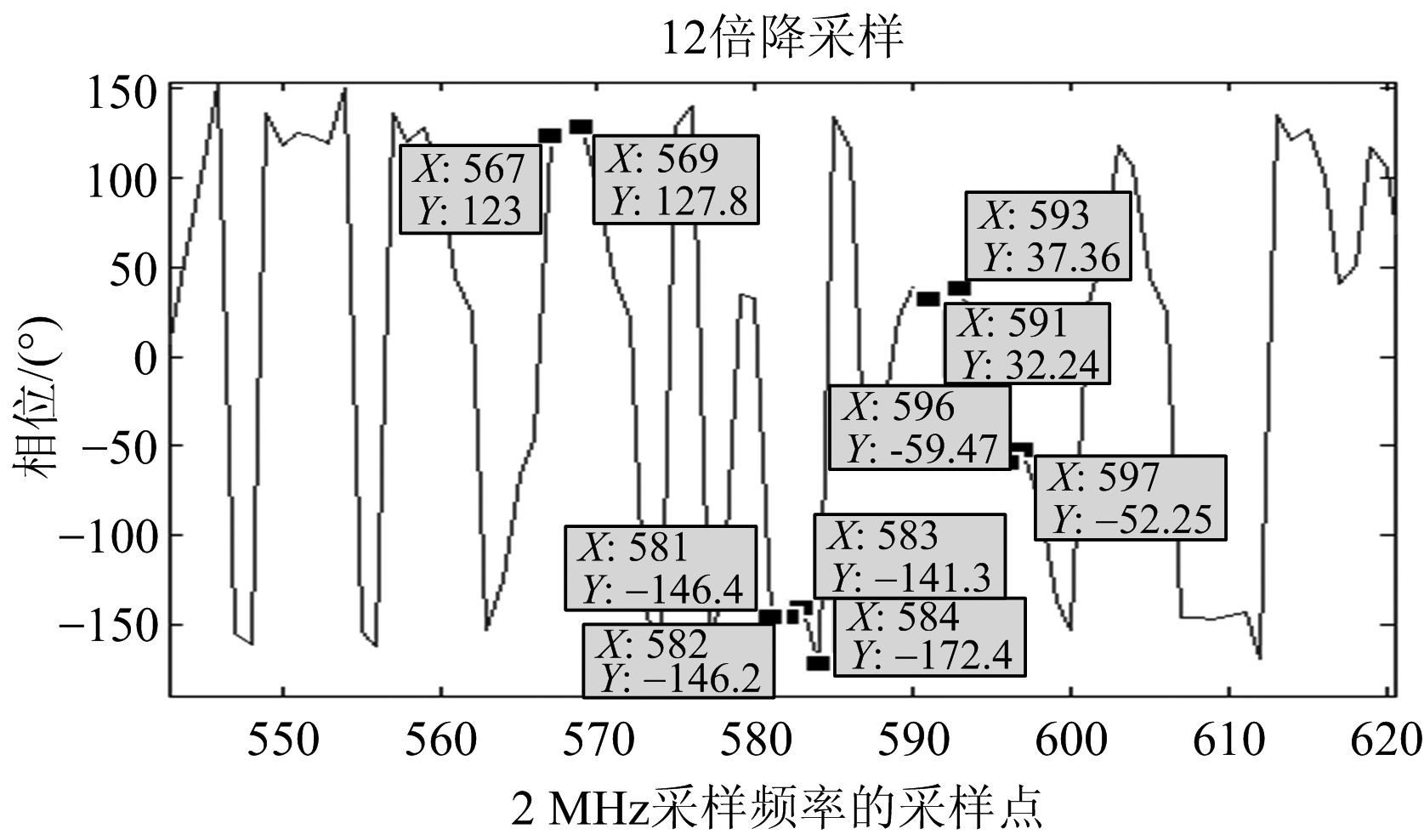
图11 变采样多相滤波第5通道时域输出相位
由图10和图11可见,输出的信号为相位间隔90°的QPSK信号。图10中信号输出采样率为1.5 MHz,而QPSK码元速率为1 MHz,即平均每个码元被采样1.5次,因此有的码元被采样1次,而有的码元被采样2次,不利于时间同步过程中的最优采样点恢复。图11中信号输出采样率为2 MHz,即每个码元被采样2次,因此能够方便地利用插值算法进行最优采样点恢复。
3.2 嵌入式变采样多相滤波器组的工程验证
利用多频道单音信号的串行输入并行输出,可直观验证嵌入式变采样多相滤波器组的工作效果。
在如图12所示的软件无线电平台上搭建超外差多通道电台系统。通过嵌入式变采样多相滤波器组将DDC后的中频输入信号划分到16个频道上,并将降采样率变化为12,通过功率控制使得信号进入多项滤波器组时的信噪比为SNR=10 dB。系统输入信号由7,8,9三个连续频道上的单音信号组成,通过检测并行输出端这3个频道上信号的相位来验证嵌入式变采样多相滤波器组的工作效果。

(a) 前端 (b) 信号处理板
图12 软件无线电射频前端及信号处理板
图13为输入信号相位,由于输入信号包含3个单音信号,因此相位变化剧烈。图14为3通道的并行输出信号相位,相位分别稳定在一个固定值(-118°,118°,-5.7°)上下振动,该振动是由低通滤波器及噪声造成,相位抖动的均方根统计值为σ=6°。由图14可见,3个相邻信道上的信号并没有出现彼此串扰的现象,因此认为变采样多相滤波器组的工程实现得以验证。
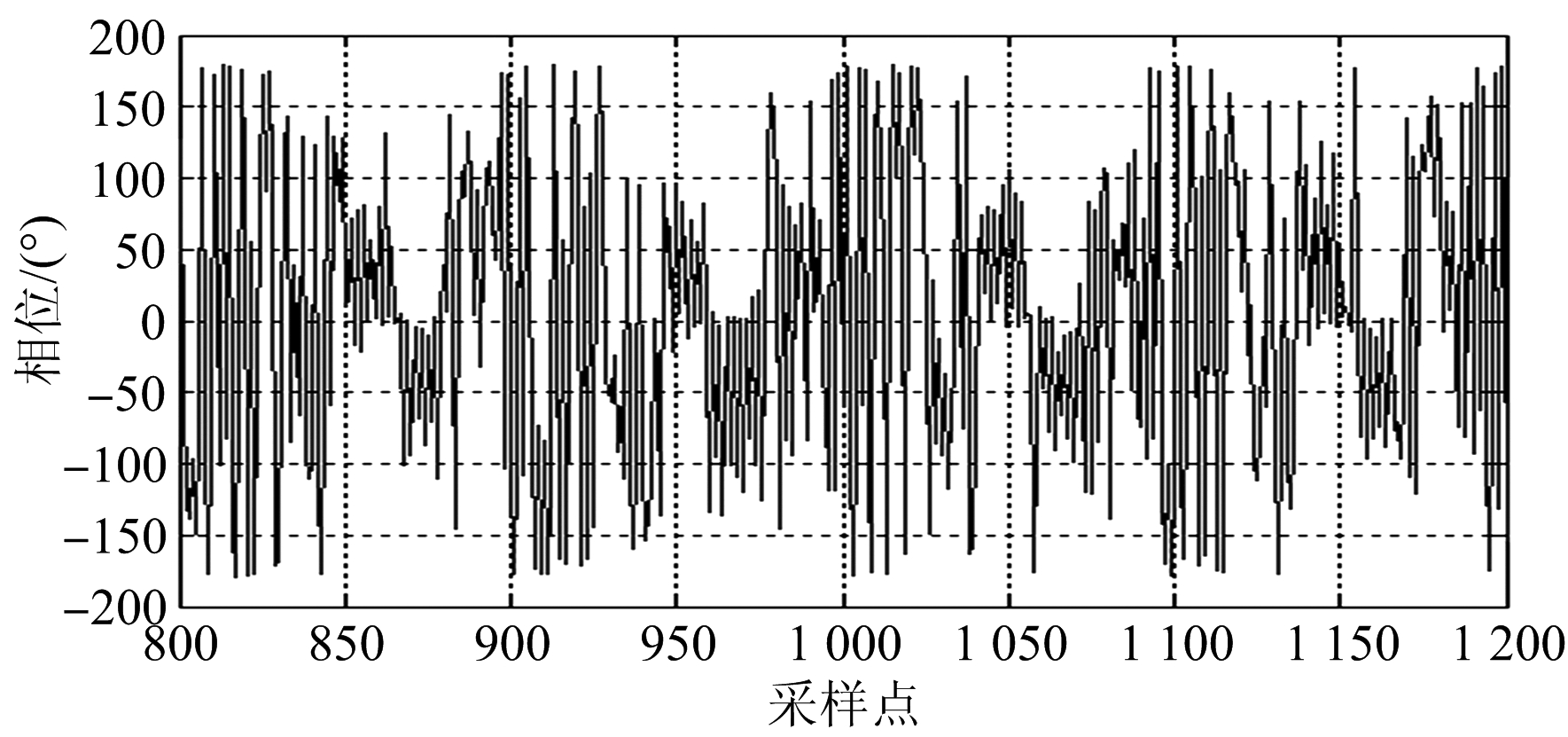
图13 输入串行信号相位
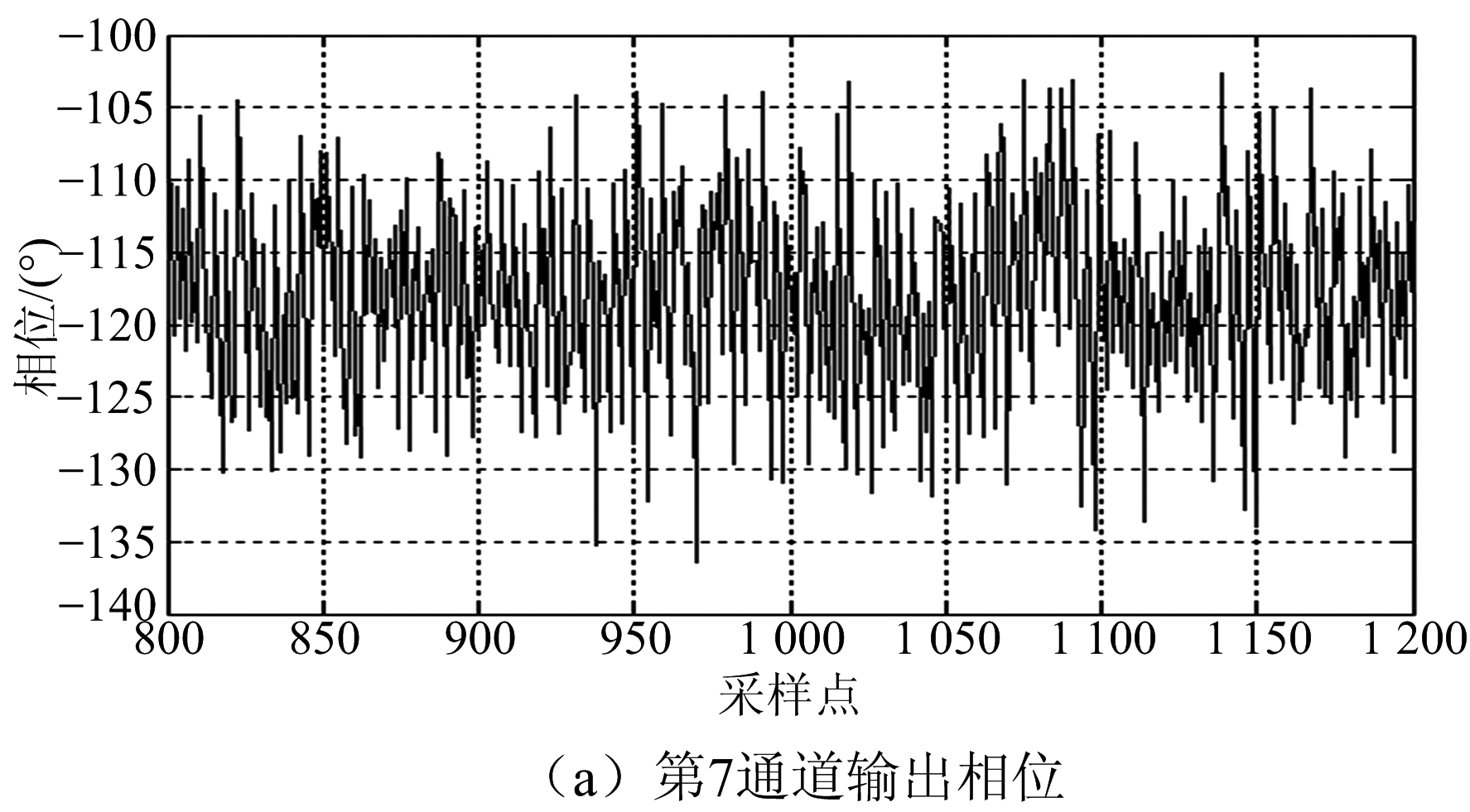
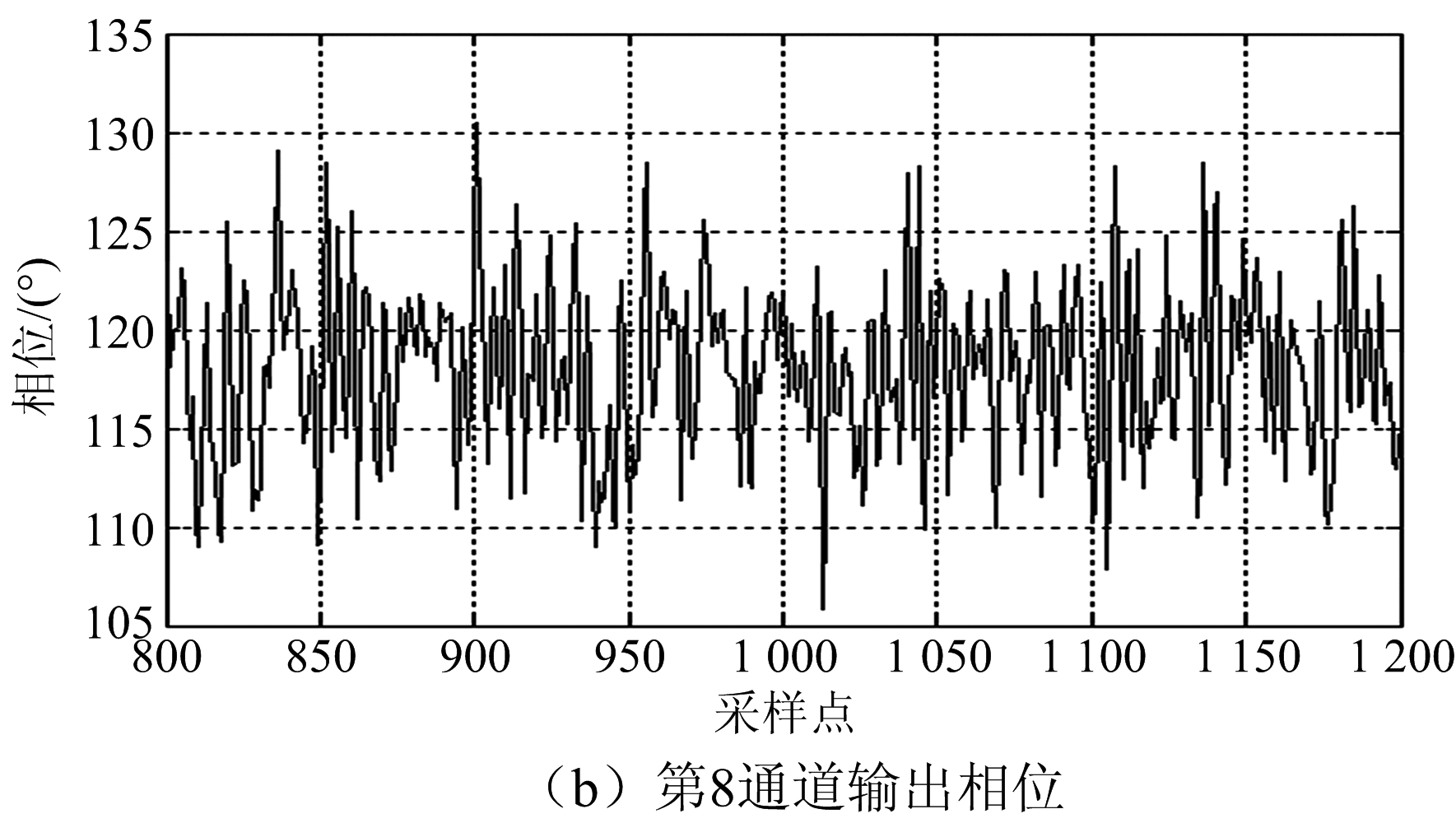
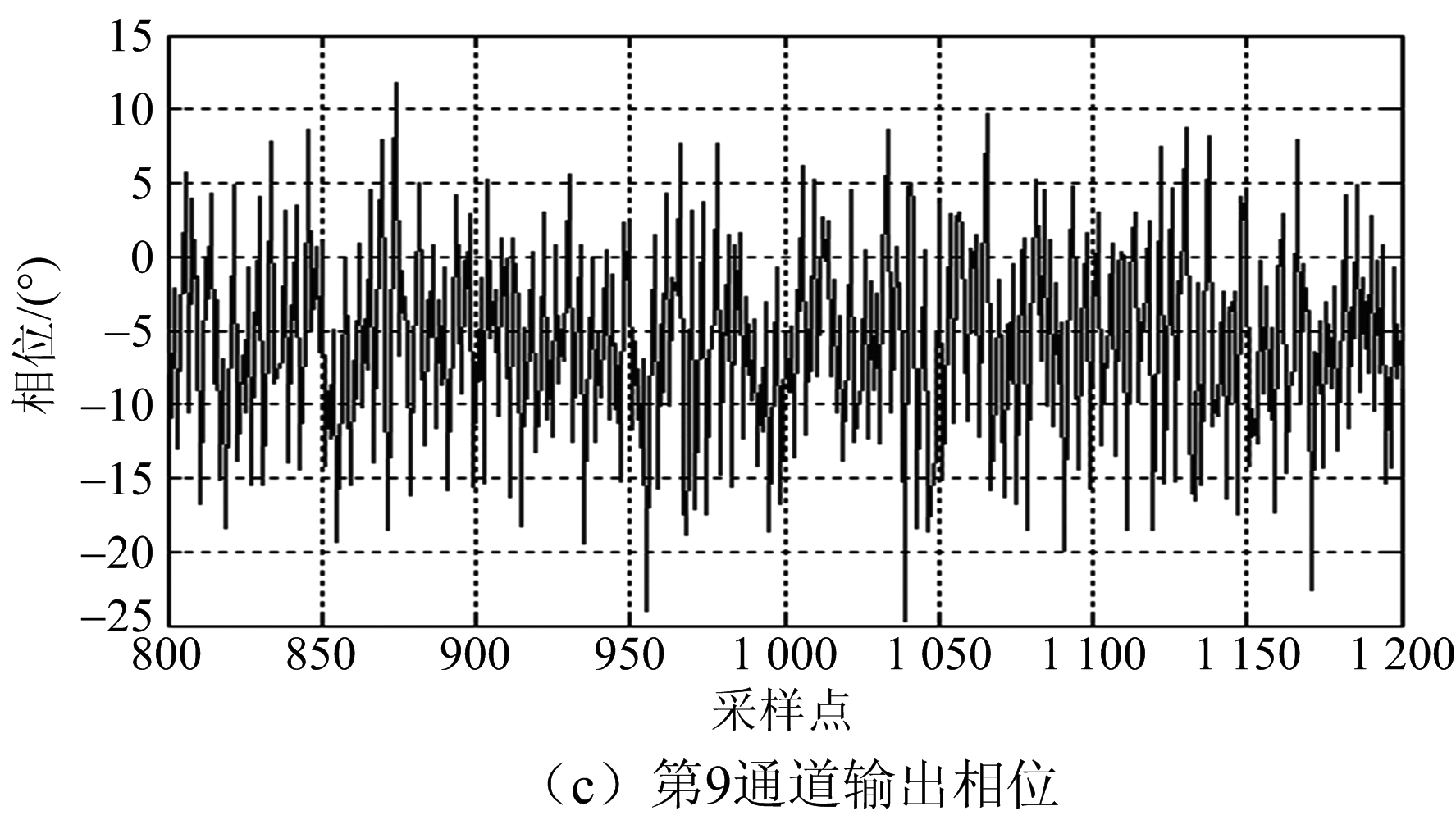
图14 输出并行信号相位
4 结束语
本文针对多相滤波器组的降采样系数N和频道数D在数值上相等,导致输出频道带宽和采样率相等,从而造成最优带宽和最优采样率无法兼容的问题,引入移位偏量q,提出基于嵌入式变采样多相滤波器组的完善时域分析与实现方法。该方法采用数据搬移滑窗、输出翻转的方式,简化了嵌入式变采样多相滤波器组相对于原多相滤波器组的结构变化,能灵活实现D′倍降采样。通过对一个QPSK系统的变采样多相滤波器组信道化接收机进行仿真,验证了本文论证方法的可行性与有效性,另外通过实物平台的工程实现对该方法进一步地验证。
参考文献:
[1] 苏翔, 傅其祥, 李永祯, 等. 宽带数字信道化接收机技术的热点和发展趋势[J]. 航天电子对抗, 2014, 30(1):32-35.
[2] HARRIS F, VENOSA E, CHEN X. Polyphase up Converter Channelizers Enable Fully Digital Multi-Carrier Frequency Hopping Modulators[C]∥ IEEE Military Communications Conference, Tampa, FL: IEEE, 2015:831-835.
[3] 陈永东, 郭天天, 刘桂生, 等. 基于多相滤波器的多测速雷达角跟踪方法研究[J]. 遥测遥控, 2016, 37(3):44-47.
[4] 罗星华, 苏涛. 基于多相滤波器组的信道化接收机的分析[J]. 火控雷达技术, 2008, 37(2):33-38.
[5] 唐宏, 赵春晖, 张朝柱. 一种基于多相滤波器组的信道化接收机设计方法[J]. 应用科技, 2006, 33(6):8-10.
[6] HARRIS F, DICK C. Performing Simultaneous Arbitrary Spectral Translation and Sample Rate Change in Polyphase Interpolating or Decimating Filters Intransmitters and Receivers[C]∥Software Defined Radio Technology Conference and Product Exposition, San Diego, CA: [s.n.], 2002:313-317.
[7] AWAN M, MOULLEC Y L , KOCH P, et al. Polyphase Filter Banks for Embedded Sample Rate Changes in
Digital Radio Front-Ends[J]. ZTE Communications, 2011, 9(4):3-9.
[8] 卜祥元, 方金辉, 范星宇, 等. 基于抽取滤波器多相分解的多速率采样模块设计[J]. 北京理工大学学报, 2014, 34(2):187-191.
[9] HARRIS F J, DICK C, RICE M. Digital Receivers and Transmitters Using Polyphase Filter Banks for Wireless Communications[J]. IEEE Trans on Microwave Theory and Techniques, 2003, 51(4):1395-1412.
[10] AWAN M, MOULLEC Y L, KOCH P, et al. Hardware Architecture of Polyphase Filter Banks Performing Embedded Resampling for Software-Defined Radio Front-Ends[J]. ZTE Communications, 2012, 10(1):54-62.
