李朋1,2,3，刘小军1,2，方广有1,2,3
( 1.中国科学院电磁辐射与探测技术重点实验室， 北京 100190； 2.中国科学院电子学研究所， 北京 100190； 3.中国科学院大学， 北京 100049)
摘要：针对深空次表层探测雷达相邻帧道数据相似的特性，提出了一种对相邻帧道差值数据进行分块自适应量化的算法 —— 帧间差分分块自适应量化(Frame Difference Block Adaptive Quantization，FD-BAQ)。该算法首先对数据进行分块，然后进行帧间差分，并对差值数据或原始数据进行Lloyd-Max量化，最后用量化后的数据进行重构。在选择对差值数据或原始数据进行量化时，提出用数据方差作为量化误差的衡量指标，当子块差值数据方差小于原始数据方差时，对差值数据进行量化来替代对原始数据量化，否则直接量化原始数据，从而大幅减小量化误差。将该方法与已有改进型BAQ算法比较，实验结果表明，在相同压缩比条件下，FD-BAQ算法在数据域和图像域均能取得更好的压缩效果。
关键词：次表层探测雷达； 帧间差分； 分块自适应量化； 量化误差
深空探测任务中，次表层探测雷达[1-2]作为重要载荷被搭载于环绕器或巡视器中，用于获取被探测星体次表层以下地质结构和分层等信息。随着高分辨雷达技术[3-5]的发展，雷达带宽和数据量急剧增加。然而，深空数据存储容量和有效下行带宽有限，故需要针对深空次表层探测雷达数据特点，设计有效的压缩算法，将数据压缩后下传。
分块自适应量化(Block Adaptive Quantization，BAQ)[6]是针对雷达数据近似服从高斯分布的统计特性，基于Lloyd-Max量化器设计的自适应量化算法。它首次在美国“麦哲伦”号金星探测器搭载的SAR雷达数据压缩任务中被提出，由于其工程实现简单，随后被广泛应用。BAQ算法的广泛应用引起了众多学者的关注，并陆续发展了一系列的改进算法。文献[7]提出一种自适应比特分配BAQ算法，通过对不同块数据分配不同量化比特提高压缩性能;文献[8-10]分别介绍了DCT-BAQ算法、FFT-BAQ算法和DWT-BAQ算法，并分析了这几种基于变换域的改进算法的压缩性能；文献[11]在一个压缩系统中集成多个不同压缩比的BAQ量化器，为雷达数据压缩提供不同压缩比的选择。虽然这些改进算法的压缩性能优于BAQ算法，但改进的同时增加了大量的计算复杂度，使得这些算法没有得到实际工程应用。
本文针对分块自适应量化压缩性能较低、其改进算法计算复杂度高不适合工程应用的问题，提出了一种基于帧间差分的分块自适应量化压缩算法。该算法利用次表层探测雷达相邻帧数据相似的特点，对相邻帧数据进行差分，并利用Lloyd-Max量化器对差值数据进行量化，最后用量化后的差值数据重构原始数据。实验结果表明，本文算法在不增加计算复杂度的同时，量化误差大幅减小，算法压缩性能提升明显。
本节首先介绍了次表层探测雷达数据模型，然后分析了次表层探测雷达数据的帧间相似性。
为方便表述，以搭载在巡视器上的次表层探测雷达为例介绍雷达数据模型。当巡视器行进到某一位置，次表层探测雷达向星体次表层发射电磁波，电磁波经过介质分界面会反射和散射产生回波，对雷达接收到的回波进行采样处理，这样获得的数据存储为一帧数据。然后，随着巡视器行进到另一位置，雷达继续发射电磁波，并再次获取该相邻次表层的雷达回波采样数据，存储为下一帧数据。
最终，随着巡视器的行进，可以获取若干帧沿地表相邻次表层的雷达回波采样数据，如图1所示，其中，Fn为第n帧的一道数据，xij为第i帧中第j个采样数据。
图1 深空次表层探测雷达帧间数据模型
通常，星体次表层以下地质结构和分层信息沿地表是缓变的，并且相邻次表层中物质的电磁反射和散射特性也基本相同。次表层探测雷达在两个相邻位置发射相同的雷达信号，经过相似的次表层区域反射和散射的雷达回波具有相似性，使得次表层探测雷达相邻帧数据具有相似性。
为分析差分量化的数据重构误差，建立如下帧间差分量化模型。模型主要包括以下两部分：Section-1是差分量化部分，通过差分、重构和量化的循环过程获得所有量化后的差值数据；Section-2是重构部分，利用第一帧原始数据和量化后的差值数据，以递归方式获得所有重构的原始帧数据。用Fi表示第i帧原始数据，
表示Fi的重构帧数据；Di表示Fi与帧间的差值数据，
表示量化后帧间差值数据；Q[]表示量化过程，Qi表示对帧间差值数据的量化误差。
帧间差分量化模型Section-1：量化
Step 1：初始化
，
Step 2：量化、重构、帧间差分循环过程
fori=2,3,4,…,N-1
Fi+Qi
end
Step 3：获得最后一帧重构数据
帧间差分量化模型Section-2：重构
Step 1：初始化
Step 2：重构过程
fori=2,3,4,…,N
end
通过帧间差分量化模型可以发现，获得所有量化的差值数据后，只需第一帧原始数据，就可以通过循环递归方式重构所有原始帧数据。并且，第i帧数据的重构误差为Qi：
(1)
值得注意的是，Qi表示对差值数据的量化误差，而式(1)中对Fi的重构误差即为Qi。也就是说，通过帧间差分量化模型，在接收端重构的帧数据与原始帧数据的误差仅是对帧间差值数据的量化误差，而非直接对原始帧数据进行量化产生的误差。次表层探测雷达数据压缩中，如果能使得对差值数据的量化误差远小于对原始数据的量化误差，则可以大幅减小量化误差，提高压缩性能。
通常，数据的量化误差主要取决于数据的方差和动态范围，方差和动态范围越小，量化误差越小。深空次表层探测雷达相邻帧数据具有相似性，理论上相邻帧差值数据的方差和动态范围小于原始帧数据。但是，当次表层结构变化剧烈或某一帧数据出现错误等情况发生时，帧间差值数据的方差和动态范围可能会大于原始帧数据，使得对帧间差值数据的量化误差大于对原始帧数据的量化误差，造成算法性能的不稳定。
为保证算法稳定性，当考虑对帧间差值数据或原始帧数据进行量化时，需要对二者的量化误差大小进行准确判断。这里，采用数据方差作为量化误差大小的判断准则。文献[12]中分析了Lloyd-Max量化器的均方量化误差：
·
fX(x)dx
(2)
式中，右边第一项
表示量化器输入数据的方差，右边第二项表示量化器输出电平的二阶矩，[bj-1,bj]和yj分别表示第j个量化区间的边界和输出量化电平，fX(x)表示量化器输入数据的概率密度函数，M表示量化区间数量。
本文算法使用Lloyd-Max量化器对差值数据或原始数据进行量化。根据式(2)可以发现，在量化器选定的前提下，量化器输入数据的方差是影响量化器均方误差的决定性因素。因此，将量化器输入数据的方差作为衡量量化误差的判断准则，数据方差越小表明均方量化误差越小。值得注意的是，使用Lloyd-Max量化器时需要求解数据的方差，这里引入这个判断准则，只增加了一个比较过程，不会增加额外的计算复杂度。
算法的原理框架如图2所示，算法流程如下：
1) 将每帧数据进行均匀分块，长度为L的帧数据均分成若干长度为K的子块数据，用(x1,x2,x3,x4,…,xL)表示任意一帧数据，分块过程如式(3)所示：
(x1,x2…,xK,xK+1,xK+2,…,x2K,…,
xL-K+1,xL-K+2,…,xL)→
(x1,x2,…,xK)∪(xK+1,xK+2,…,x2K)∪…
∪(xL-K+1,xL-K+2,…,xL)
(3)
2) 将当前处理的第i帧块数据Fi与相邻前一帧块重构数据
进行差分，获得帧间差值数据Di：
3) 计算当前帧块数据Fi和差值Di的方差，
表示帧间差值数据Di的平均值，
表示帧块数据Fi的平均值。
4) 判断
与
的大小，如果
，将差值数据Di进行Lloyd-Max量化，并获得量化差值数据
否则，将原始帧块数据Fi进行Lloyd-Max量化获得
5) 重构：若Lloyd-Max量化器输出为，则重构数据不变；若Lloyd-Max量化器输出为，则用式(7)重构数据，并将传递到帧间差分模块。
6) 将当前帧块数据设置为Fi+1，返回步骤2)。
图2 帧间差分分块自适应量化算法原理框图
本文采用中国科学院电子学研究所研制的某高分辨次表层探测雷达采集的数据进行仿真实验，选取尺寸为4 096×2 000的回波数据作为实验数据，共计2 000帧数据，每帧4 096个采样点，数据经A/D量化后以16 bit有符号位存储。为了分析本文算法性能，选取目前应用广泛、工程计算复杂度相当的BAQ算法进行对比实验。另外，文献[7]提出了一种自适应比特分配BAQ改进算法(A-BAQ算法)，该算法相比于BAQ算法压缩性能提升比较显著，故将本文算法与A-BAQ算法也进行比较。
表1、表2、表3分别是3种算法在不同压缩比下的数据域与图像域压缩性能指标[13-14]对比结果。
SNR=10×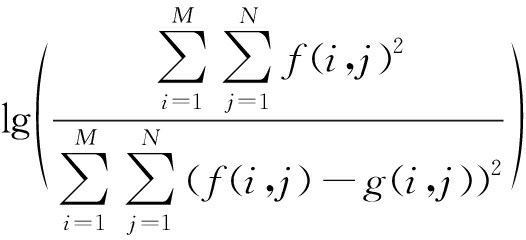
(9)
PSNR=10×
NMSE为归一化均方误差，SNR为量化信噪比，PSNR为峰值量化信噪比，定义分别如式(8)、式(9)和式(10)所示。其中，f(i,j)表示原始数据在(i,j)处的数值，g(i,j)表示f(i,j)的重构数据，对于16 bit有符号位存储的数据fmax(i,j)取值为32 768。
表1压缩比16∶2的3种算法压缩性能比较
表2压缩比16∶3的3种算法压缩性能比较
表3压缩比16∶4的3种算法压缩性能比较
表1、表2、表3的实验结果表明，无论在数据域或图像域，相同压缩比条件下，本文算法的各压缩性能指标均优于A-BAQ算法和BAQ算法。在16∶2，16∶3，16∶4压缩比下，本文算法数据域量化信噪比较A-BAQ算法分别提升3.06，3.47和2.87 dB，较BAQ算法分别提升4.94,5.79和5.37 dB；本文算法图像域量化信噪比较A-BAQ算法分别提升4.33,3.98和3.29 dB，较BAQ算法分别提升6.85,6.60和6.39 dB。这说明使用本文算法压缩次表层探测雷达数据时，算法压缩性能提升显著。
图3中4幅图分别是未经压缩的原始数据和16∶3压缩比下本文算法、A-BAQ算法以及BAQ算法重构数据的成像结果。4幅图像的对比结果表明，本文算法压缩数据成像效果最好，A-BAQ算法次之，BAQ算法效果最差；A-BAQ算法和BAQ算法压缩数据成像会产生一些类似椒盐噪声的斑点，而本文算法压缩后数据成像几乎没有斑点，相比于原始数据的成像结果，直观上没有明显恶化。
(a) 原始图像
(b) 本文算法
(c) A-BAQ算法
(d) BAQ算法
图3 压缩比16∶3的3种算法压缩数据成像与
原始数据成像效果对比
尤其值得一提的是，文献[7]中所述A-BAQ算法似乎是当前BAQ改进算法中计算复杂度增加最少的一种优化改进算法。但本文算法利用次表层探测雷达帧间数据的相似性，进行帧间差分，然后对差值数据进行分块自适应量化。相比于BAQ算法，本文算法仅增加了数据差分和方差比较过程，而这两种处理过程几乎不会增加计算复杂度，故本文算法的计算复杂度远低于A-BAQ算法。并且，本文算法压缩性能较A-BAQ算法和BAQ算法提升显著。
本文针对深空次表层探测雷达数据量大需要进行压缩的问题，在分析了次表层探测雷达帧间数据相似特点的基础上，提出一种帧间差分分块自适应量化算法。这种算法将对原始数据的量化误差转化为对差值数据的量化误差，大幅减小量化误差，提高算法压缩性能。并且本文提出采用数据方差作为量化误差的衡量指标，为选择对差值数据或原始数据进行量化提供依据，保证了算法的稳定性。通过对实测高分辨次表层探测雷达数据的仿真实验发现，本文算法在几乎不增加计算复杂度的情况下，压缩性能较A-BAQ算法和BAQ算法提升显著。在工程实现时，本文算法只需在经典BAQ算法基础上增加帧间差分和方差比较模块，计算复杂度低，硬件改动较少，具有重要的工程应用价值。
参考文献：
[1] 张洪波.火星环绕器次表层探测雷达发展综述[J].探测与控制学报，2016，38(6)：57-61.
[2] 曹志国,常文革,李召阳,等.星球次表层探测中地杂波抑制技术研究[J].雷达科学与技术，2013，11(6)：650-657.
CAO Zhiguo，CHANG Wenge，LI Zhaoyang，et al.Surface Clutter Cancellation in Planet Subsurface Sounder[J].Radar Science and Technology，2013，11(6)：650-657.(in Chinese)
[3] 俞万友,杨广玉.步进频率综合宽带多目标成像处理[J].雷达科学与技术，2017，15(5)：548-552.
YU Wanyou，YANG Guangyu.Multi-Target Image Based on Stepped Frequency Sythesis Processing[J].Radar Science and Technology，2017，15(5)：548-552.(in Chinese)
[4] ZHAO S，DENG Y，WANG R.Imaging for High-Resolution Wide-Swath Spaceborne SAR Using Cubic Filtering and NUFFT Based on Circular Orbit Approximation[J].IEEE Trans on Geoscience and Remote Sensing，2017，55(2)：787-800.
[5] 金胜,朱天林.ISAR高分辨率成像方法综述[J].雷达科学与技术，2016，14(3)：251-260.
JIN Sheng，ZHU Tianlin.A Review of High-Resolution Inverse Synthetic Aperture Radar Image Methods[J].Radar Science and Technology，2016，14(3)：251-260.(in Chinese)
[6] KWOK R，JOHNSON W T K.Block Adaptive Quantization of Magellan SAR Data[J].IEEE Trans on Geoscience and Remote Sensing，1989，27(4)：375-383.
[7] 潘志刚,王小龙,李志勇.SAR原始数据压缩的自适应比特分配BAQ算法[J].中国科学院大学学报，2017，34(1)：106-111.
[8] 潘志刚,王岩飞.基于DCT的分块自适应量化算法及其用于SAR原始数据压缩[J].电子与信息学报，2007，29(8)：1784-1788.
[9] BENZ U，STRODL K，MOREIRA A.A Comparison of Several Algorithms for SAR Raw Data Compression[J].IEEE Trans on Geoscience and Remote Sensing，1995，33(5)：1266-1276.
[10] ZHOU M，DENG Y，ZHANG Z.A New Algorithm for SAR Raw Data Compression by Using Wavelet Packets[C]// 8th International Conference on Signal Processing，Beijing： IEEE，2006：16-20.
[11] MARTONE M，BRAUTIGAM B，KRIEGER G.Azimuth-Switched Quantization for SAR Systems and Performance Analysis on TanDEM-X Data[J].IEEE Geosciences and Remote Sensing Letters，2014，11(1)：181-185.
[12] BUCKLEW J A，GALLAGHER N C.A Note on Optimal Quantization (Corresp.)[J].IEEE Trans on Information Theory，1979，25(3)：365-366.
[13] 赵耀,邓云凯,王宇,等.原始数据压缩对方位向多通道SAR系统影响研究[J].雷达学报，2017，6(4)：397-407.
[14] MARTONE M，BRAUTIGAM B，KRIEGER G.Quantization Effects in TanDEM-X Data[J].IEEE Trans on Geoscience and Remote Sensing，2015，53(2)：583-597.
LI Peng1,2,3，LIU Xiaojun1,2，FANG Guangyou1,2,3
( 1.KeyLaboratoryofElectromagneticRadiationandSensingTechnology，ChineseAcademyofSciences，Beijing100190，China; 2.InstituteofElectronics，ChineseAcademyofSciences，Beijing100190，China; 3.UniversityofChineseAcademyofSciences，Beijing100049，China)
Abstract：In this study，an algorithm (frame difference block adaptive quantization，FD-BAQ) based on the similarity of deep space subsurface sounding radar adjacent frame data is proposed to quantify the difference data adaptively.The algorithm firstly blocks the raw data，secondly makes a frame difference for the adjacent frame data，then uses the Lloyd-Max quantizer to quantify the difference data，and reconstructs the raw data utilizing the quantified data at last.Before determining whether to quantify the difference data or the raw data，the algorithm utilizes variance as an index measuring the quantization error.When the variance of the difference data is less than that of the raw data，the algorithm quantifies the difference data instead of the raw data，otherwise，the raw data can be quantized directly，which greatly reduces the quantization error.The experimental results indicate that the proposed FD-BAQ algorithm can get better performance in both the data domain and image domain compared with the existing improved BAQ algorithms.
Keywords：subsurface sounding radar； frame difference； block adaptive quantization； quantization error
DOI：10.3969/j.issn.1672-2337.2018.05.002
基金项目：国家自然科学基金(No.U1531141)
修回日期：2018-01-17
收稿日期：2017-12-16；
文章编号：1672-2337(2018)05-0471-06
文献标志码：A
中图分类号：TN957.52
作者简介：
李 朋 男，1992年生，山东临沂人，硕士研究生，主要研究方向为雷达信号处理、雷达数据压缩与探地雷达系统。
E-mail： lp0741@163.com
刘小军 男，1972年生，山东烟台人，博士，研究员，主要研究方向为超宽带雷达技术、信号与信息处理。
E-mail： lxjdr@mail.ie.ac.cn
方广有 男，1963年生，河南人，博士，研究员、博士生导师，主要研究方向为超宽带雷达成像理论与技术、探地雷达技术、地球物理电磁勘探技术、月球/火星探测雷达技术。