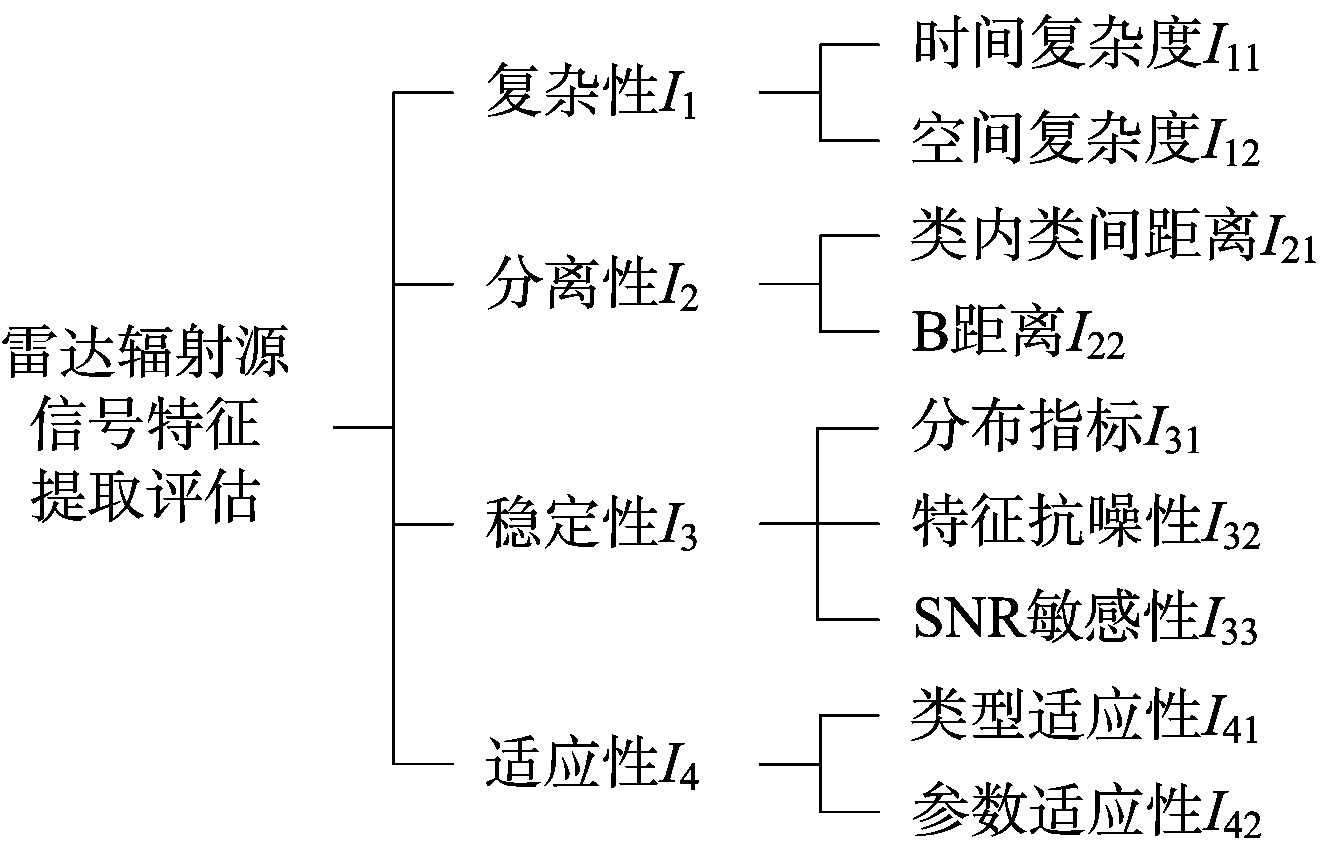
图1 雷达辐射源信号特征提取评估指标体系
韦旭，潘谊春，程柏林，韩俊，何缓
(空军预警学院, 湖北武汉 430019)
摘要：针对当前雷达辐射源信号特征提取评估的研究不够深入，存在评估方法单一和缺乏科学性等问题，提出一种新的评估方法。首先构建雷达辐射源信号特征提取评估指标体系，然后基于最小叉熵进行权重融合，并计算不同方案间的优势度，建立优势度矩阵，得到用于方案排序的统一向量形式，最后基于不同用户需求完成方案的优劣选择。仿真实验表明，该评估方法可用来选出最符合用户需求的方案，有效性检验说明了所提出方法的有效性和可行性，在雷达辐射源信号特征提取评估中具有较好的适用性。
关键词：雷达辐射源信号； 特征提取； 评估； 最小叉熵； 优势度
雷达辐射源信号分选与识别技术是信息化战争中的关键环节，也是获取雷达对抗侦察情报的主要手段，标志着先进电子对抗系统的发展与成熟。随着对雷达辐射源信号特征的深入研究，目前出现了许多提取方法，如何科学地对其进行评估成为了重要课题。
传统的评估方法[1-3]主要有基于满意、粗集理论和主成分分析的特征选择法，但它们都是基于某个指标进行的评估，缺乏合理性。近年来，多指标评估[4-5]受到不少学者的青睐，形成了一些科学合理的评估方法，如采用SPA-AHP方法对弹道目标识别特征效能进行评估，采用TOPSIS方法对雷达信号识别效能进行评估等[6-7]。但雷达辐射源信号特征提取评估的研究还不够深入，存在评估方法单一和缺乏科学性等问题，为此本文提出了一种新的评估方法。在构建的雷达辐射源信号特征提取评估指标体系的基础上，首先基于最小叉熵对两种客观权重和主客观权重分别进行融合，使所得权重既能充分考虑用户需求，又能具有一定的客观性，然后计算不同方案间的优势度，建立优势度矩阵，得到用于方案排序的统一向量形式，最后基于不同用户需求完成优劣选择。
评估指标体系的科学构建是进行雷达辐射源信号特征提取评估的前提，但由于当前雷达辐射源信号密集、复杂和多变的特点，使得构建的评估指标体系很难面面俱到。为此，在遵循目的性、科学性和系统性等评估原则的前提下，鉴于当前雷达辐射源信号的特点，本文选择复杂性、分离性、稳定性和适应性四个方面作为特征提取的评估准则。而后，科学选择每个准则所对应的指标，即从时间和空间两个方面来表征特征提取的复杂性，综合特征的空间分布和分类错误率的上界来衡量特征提取的分离性，考虑特征的分布情况、抗噪性和对SNR的敏感性来度量特征提取的稳定性，从信号类型和参数两个方面来研究特征提取的适应性。由此，得到包括目标、准则和指标三层结构的雷达辐射源信号特征提取评估指标体系，如图1所示。
图1 雷达辐射源信号特征提取评估指标体系
为了便于后文描述，记方案数M={1,2,…,m}，指标数N={1,2,…,n}；评估方案集记为X={xi|i∈M}，图1的指标层记为指标集C={cj|j∈N}，评估的原始决策矩阵记为Y=(yij)m×n，其中yij表示方案xi在指标cj下的值，评估的规范化决策矩阵记为Z=(zij)m×n，zij与yij的关系如下：
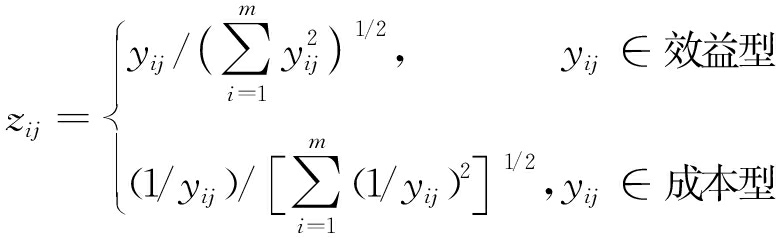
(1)
在雷达辐射源信号特征提取的评估中，科学地确定指标权重是评估的关键。根据战场环境和用户需求，本文设计以下3种情况：1)要求实时处理；2)要求高准确率；3)兼顾处理速度和准确率。在不同情况下，采用层次分析法确定主观权重，采用熵权法和CRITIC法得到两种客观权重，最后基于最小叉熵对两种客观权重以及主客观权重进行融合。权重确定方法如图2所示。
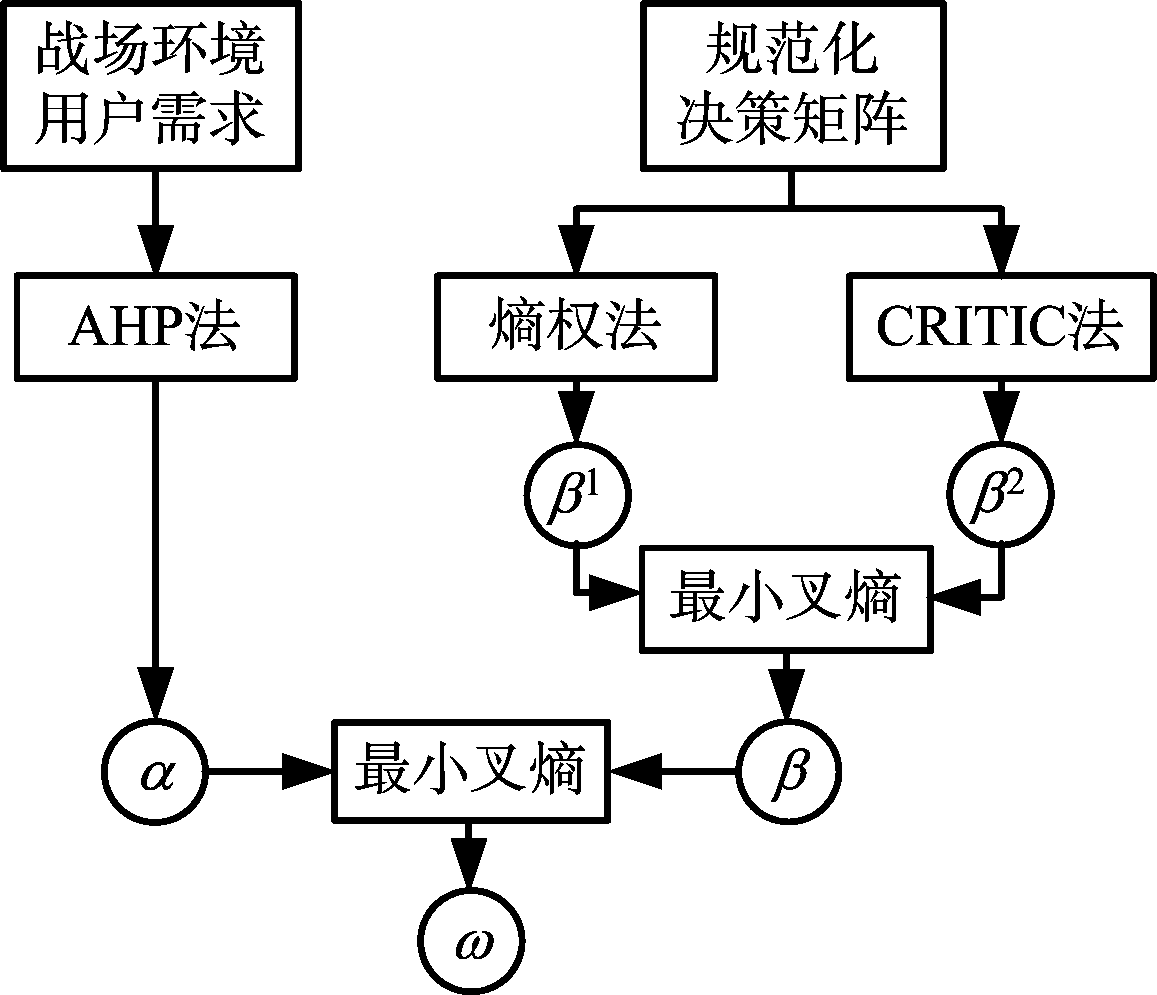
图2 权重确定方法
主观权重是决策者主观意愿的体现，不以指标的实际数据为依据，只考虑决策者的经验和需求。在众多的主观赋权法中，层次分析法(AHP)具有将复杂问题层次化且定性与定量分析相结合的优点，即按照因素间的隶属关系，将复杂的评估问题分解为多层次结构模型，使问题归结为最低层相对于最高层的相对重要权值的确定问题，可以对雷达辐射源信号特征提取的指标进行科学主观赋权。AHP法确定主观权重的流程[7]如图3所示。由图3可知，基于AHP法所得的主观权重即为α=(α1,α2,…,αn)。
图3 层次分析法流程示意图
客观权重的确定取决于实际数据间的差异，不受决策者的影响。为了对数据进行全面刻画，本文采用熵权法来体现数据的离散型，用CRITIC法来体现数据的对比强度和冲突性[8]。
根据规范化决策矩阵Z=(zij)m×n，利用熵权法计算第j个指标的熵值为
式中，pij=zij/
，且规定pij=0时，Ej=0。计算第j个指标的权重为
则基于熵权法所得的指标权重即为
,
,…,
利用CRITIC法计算第j个指标的权重为
式中，σj为指标j的标准差，rij为指标i与j的相关系数，其表达式为
则基于CRITIC法所得的指标权重即为
,
,…,
叉熵也称为Kullback-Leibler散度或距离，它能够反映不同概率分布间的“距离”，可以作为两者间差异性的度量[9]。其定义为：若p=(p1,p2,…,pn)和q=(q1,q2,…,qn)为两个不同的概率分布，则两者间的叉熵即为
D(p,q)
可见，叉熵越小，两者间的差异性越小。
为了使客观权重能充分体现数据的离散型、对比强度和冲突性，将基于最小叉熵对熵权法和CRITIC法进行权重融合，则建立如下的优化模型：
Model1:
式中，γ为熵权法和CRITIC法的分配比。
为了求解Model1，构造如下的Lagrange函数：
L(βj,λ)=γ
γ
λ
βj-1)
(8)
式中，λ为Lagrange乘子。然后分别对βj(j∈N)和λ求偏导并化简，得到如下方程组：
求解式(9)可得Model1的最优解为
则熵权法和CRITIC法的融合权重即为β=(β1,β2,…,βn)。
为了综合主客观权重，再次采用最小叉熵建立优化模型，假设主客观权重的分配比为η:
Model2:
采用求解Model1的方法可求得Model2的最优解为
则主客观融合权重即为ω=(ω1,ω2,…,ωn)。
为了对雷达辐射源信号特征提取进行科学评估，本文借鉴文献[10]中方案比较的思想，构建基于优势度的评估模型，首先对两两方案进行指标值比较、优劣距离度量以及绝对优劣幅度的计算，然后确定不同方案间的优势度，建立优势度矩阵，最终得到用于方案排序的统一向量形式，评估结果较为严谨可靠。
Step 1 确定优势、劣势和等势指标集。在雷达辐射源信号特征提取的评估中，根据所得的规范化矩阵Z=(zij)m×n，选出两两方案间的优劣指标。即
式中，
(i=1,2,3)分别表示方案p对方案q的优势、劣势和等势指标集,
∪
∪
Step 2 计算优势和劣势距离。以不同方案的规范化值之差作为优势和劣势距离的度量，且以优势指标集计算优势距离，以劣势和等势指标集计算劣势距离，即为
式中，
,
分别表示方案p对方案q在指标cj处的优势和劣势距离，0≤,≤1。
Step 3 计算优势量和劣势量。为了反映不同方案间的绝对优劣幅度，结合每个指标对应的权重和优劣势距离，得到如下定义的优势量和劣势量：
式中，ω
,ω
分别表示方案p对方案q优势量和劣势量，0≤ω,ω≤1。
Step 4 计算优势度。不同方案间的优势度定义为方案间比较时的相对优劣幅度，即为
式中:若κpq=0.5，则方案p和方案q具有相同的优势；若0.5<κpq<1，则方案p比方案q具有更大的优势，且该值越大，优势越明显；若0<κpq<0.5，则方案p比方案q具有更大的劣势，且该值越大，劣势越明显。
由文献[10]可知，不同方案的优势度构成的优势度矩阵Κ=(κpq)m×m是一致性的互补判断矩阵，因此只需选择一种方案作为基准即可完成排序。在优势度矩阵中，以方案i为基准，方案i对所有方案比较所得的优势度向量定义为高点优势向量，记为
κi1,κi2,…,κim)；所有方案对方案i比较所得的优势度向量定义为低点优势向量，记为
高点优势向量中的优势度越小，方案越优；低点优势向量中的优势度越大，方案越优。
当选择不同的基准方案时，虽然排序结果相同，但没有统一的向量形式来体现方案间的差异。因此，为了求得统一的向量形式，对优势度矩阵作如下处理：
Step 1 根据互补判断矩阵的性质[11]：κpq+κqp=1，将高点优势向量
转化为低点优势向量
Step 2 令
κji，
，对低点优势向量
作平移变换，得到统一的向量形式：
,
,…,
Τ=
(κ1i+εi,κ2i+εi,…,κmi+εi)Τ
(17)
Step 3 对统一的向量形式作如下归一化：
则最终用于方案排序的统一向量形式即为
,
,…,
统一向量中
越大，方案p越优。
为了对本文评估方法的实现过程进行分析，本文选取以下几种特征提取方法作为方案集进行评估，如表1所示。
表1评估方案
Step 1 根据图1所示的雷达辐射源信号特征提取评估指标体系，通过仿真实验得到原始决策矩阵，如表2所示。
Step 2 在上述指标中，c3，c4，c7为效益型指标，其他为成本型指标，按式(1)对原始决策矩阵进行规范化处理，得到规范化决策矩阵，如表3所示。
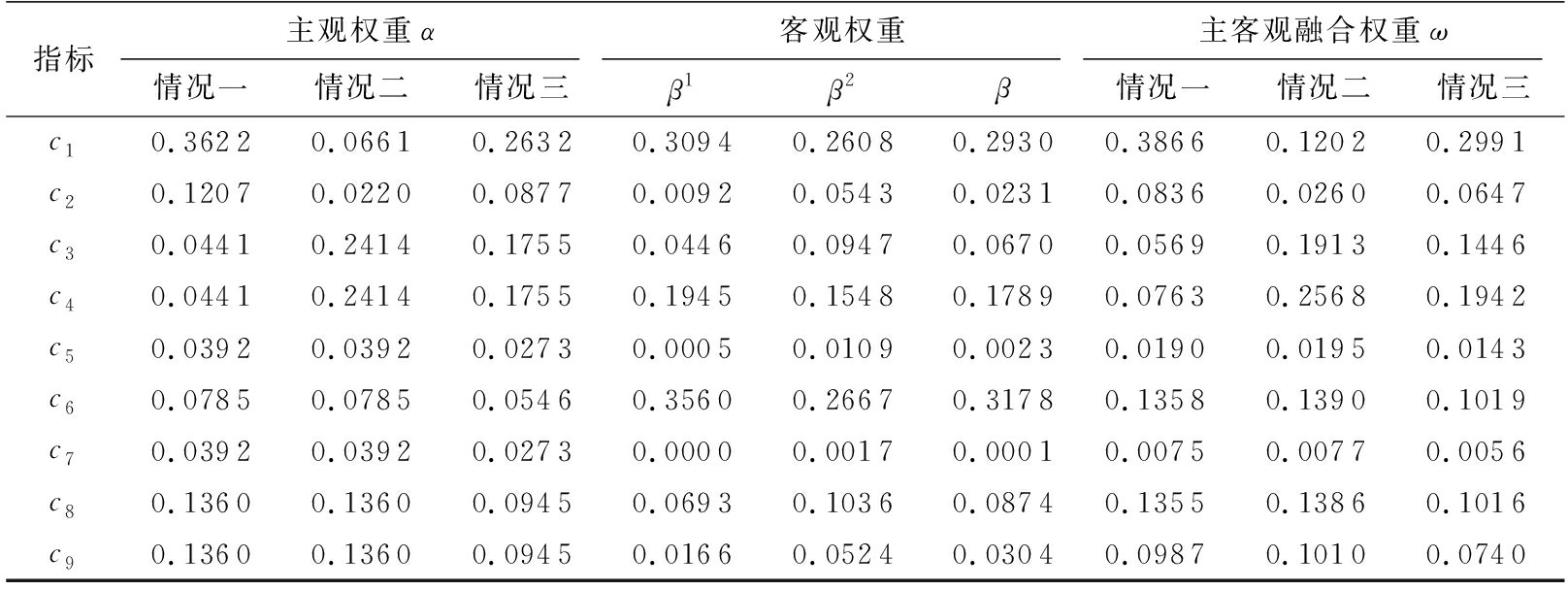
Step 3 为了不同情况下的权重既能充分考虑用户需求，又能具有一定的客观性，采用AHP法得到3种情况的主观权重；采用熵权法和CRITIC法得到两种客观权重；基于最小叉熵进行权重融合，分配比γ=0.5,η=0.7，得到各指标权重如表4所示。
表2原始决策矩阵
表3规范化决策矩阵
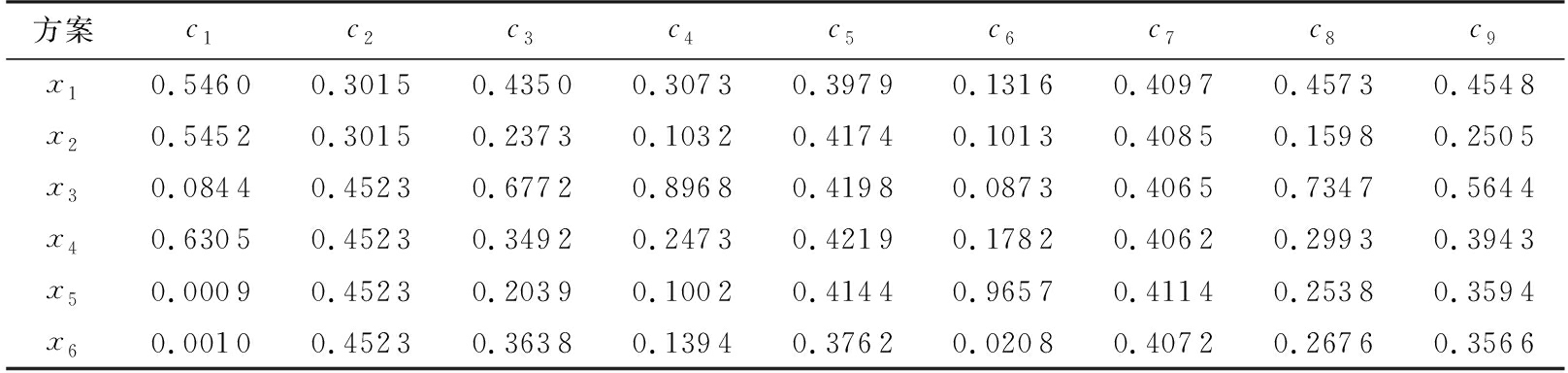
表4不同情况下的各指标权重
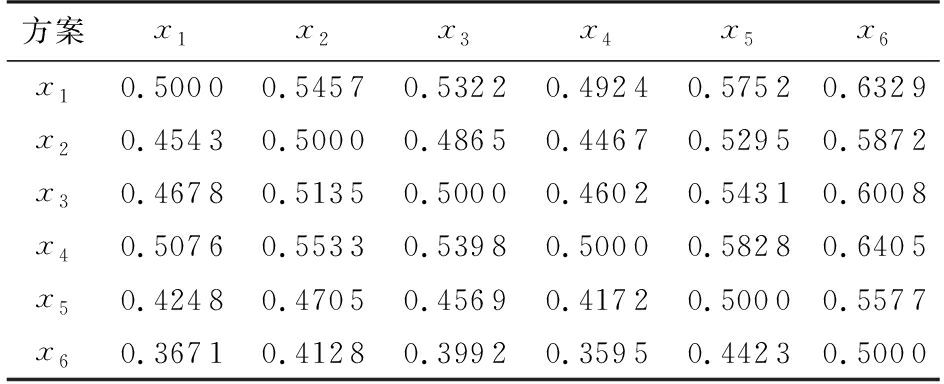
Step 4 以情况一为例，根据3.1节优势度的计算方法，得到优势度矩阵Κ1，如表5所示。可根据每一行进行排序，优势度越小方案越优，也可根据每一列进行排序，优势度越大方案越优。
Step 5 为了便于对方案进行排序和体现方
表5优势度矩阵
案间的差异，按照3.2节优势度矩阵的处理方式，结合表5可以得到情况一时用于方案排序的统一向量形式，同理可得情况二和情况三的统一向量形式，如表6所示。
表6不同情况下的统一向量形式
Step 6 根据统一向量形式对方案进行排序。在要求实时处理的情况下，方案排序为x4>x1>x3>x2>x5>x6，方案x4最优；在要求高准确的情况下，方案排序为x3>x1>x4>x5>x2>x6，方案x3最优；在兼顾处理速度和准确率的情况下，方案排序为x3>x1>x4>x2>x5>x6，方案x3最优。因此，本文的评估方法可用来选出最符合用户需求的方案。
为了检验本文评估方法的有效性，以情况一为例，基于文献[12]提出的3个标准来说明。
1) 标准1的检验
标准1：在不改变各指标相对重要性的前提下，用一个更差的方案代替原非最优方案，不改变原最优方案的选择，则说明该评估方法有效。为了说明本文的评估方法满足标准1，将方案x1用更差的方案
代替，其中方案各指标值假设为(0.002,3,1.5,40,0.8,0.12,0.08,0.05,0.1)。采用本文的评估方法进行排序，可得新的方案排序为
，可得最优方案仍为x4，满足标准1。
2) 标准2的检验
标准2：将原评估问题分解为几个较小的问题，运用相同的评估方法，得到较小问题的方案排序，该排序结果与原评估问题中的顺序一致，则说明该评估方法有效。为了说明本文的评估方法满足标准2，将本文的评估问题分解为对方案(x1,x2,x3,x4)，(x2,x3,x4,x5)和(x3,x4,x5,x6)这3个小问题的评估。采用本文的评估方法进行排序，得到这3个小问题的方案排序分别为x4>x1>x3>x2，x4>x3>x2>x5和x4>x3>x5>x6，与原评估问题中的方案排序一致，即满足标准2。
3) 标准3的检验
标准3：将原评估问题分解为几个较小的问题，如果综合考虑较小问题的方案排序即可得原评估问题的排序，则说明该评估方法具有传递性。为了说明本文的评估方法满足标准3，采用检验标准2的例子，由3个小问题的方案排序即可得原评估问题的排序为x4>x1>x3>x2>x5>x6，说明本文的评估方法具有传递性，即满足标准3。
针对当前雷达辐射源信号特征提取评估的研究不够深入，存在评估方法单一和缺乏科学性等问题，本文提出一种基于优势度的评估方法。在构建的评估指标体系下，该方法首先基于最小叉熵对两种客观权重和主客观权重分别进行融合，使所得权重既能充分考虑用户需求，又能具有一定的客观性；然后计算不同方案间的优势度，建立优势度矩阵，得到不同用户需求下的统一向量形式完成方案排序。仿真实验表明，该评估方法可用来选出最符合用户需求的方案，且通过3个标准的检验说明本文方法的有效性和可行性，具有一定的参考价值。
参考文献：
[1] ZHANG Gexiang，JIN Weidong，HU Laizhao.A Novel Feature Selection Approach and Its Application[C]∥ First International Conference on Computational and Informa-tion Science，Shanghai：Springer，2004:665-671.
[2] 安利平,陈增强.基于粗集的多准则决策分析[J].控制与决策，2013，28(1):1-11.
[3] 陈韬伟,金炜东.基于主成分分析的雷达辐射源信号数量估计[J].西南交通大学学报，2009，44(4):501-506.
[4] HAN Jun，HE Minghao，TANG Zhikai，et al.Estimating In-Pulse Characteristics of Radar Signal Based on Multi-Index[J]. Chinese Journal of Electronics，2011，20(1):187-191.
[5] 陈昌孝,何明浩,冯明月,等.基于CSS体系的雷达辐射源信号特征参数评估[J].现代防御技术，2015，43(5):33-38.
[6] 李陆军,李飞,丁建江,等.基于SPA-AHP弹道目标识别特征效能评估[J].空军预警学院学报，2017，31(4):257-260.
[7] 徐璟,何明浩,陈昌孝,等.基于理想排序的雷达信号识别效能评估方法[J].电波科学学报，2015，30(3):554-559.
[8] 宋冬梅,刘春晓,沈晨,等.基于主客观赋权法的多目标多属性决策方法[J].山东大学学报(工学版)，2015，45(4):1-9.
[9] 何大义,陈小玲,许加强.多属性群决策问题中基于最小叉熵的权重集成方法[J].控制与决策，2017，32(2):378-384.
[10] 孙金辉,林志明,李东.改进的优势度决策法及其排序方法[J].控制与决策，2017，32(4)：763-768.
[11] TANINO T.Fuzzy Preference Orderings in Group Decision Making[J].Fuzzy Sets and Systems，1984，12(2):117-131.
[12] WANG X，TRIANTAPHYLLOU E.Ranking Irregularities when Evaluating Alternatives by Using Some ELECTRE Methods[J].Omega，2008，36(1):45-63.
WEI Xu，PAN Yichun，CHENG Bolin，HAN Jun，HE Huan
(AirForceEarlyWarningAcademy，Wuhan430019，China)
Abstract：The current research on evaluation of radar emitter signal feature extraction is insufficient and the evaluation method is simple and lack of science.To solve these problems，a novel evaluation method is proposed.Firstly，the evaluation index system of radar emitter signal feature extraction is built.Then，the weight fusion based on minimum cross-entropy is carried out.The dominance degrees of different schemes are calculated，and dominance matrix is built to get the uniform vector form for scheme sorting.At last，the scheme choice based on different user requirements is completed.According to simulation experiments，this evaluation method can select the most suitable scheme meeting user requirements.The validity test shows the effectiveness and feasibility of the proposed method.It has good applicability in the evaluation of radar emitter signal feature extraction.
Keywords：radar emitter signal； feature extraction； evaluation； minimum cross-entropy； dominance degree
DOI：10.3969/j.issn.1672-2337.2018.05.007
基金项目：湖北省自然科学基金(No.2016CFB288)；国家自然科学基金(No.41406049)
修回日期：2018-01-10
收稿日期：2017-12-13；
文章编号：1672-2337(2018)05-0505-06
文献标志码：A
中图分类号：TN971；TP391.9
作者简介：
韦 旭 男，1994年生，江苏宜兴人，硕士研究生，主要研究方向为电子对抗信息处理。
E-mail：weixu_1003@163.com
潘谊春女，1962年生，湖南长沙人，教授，主要研究方向为雷达与电子对抗。
程柏林男，1972年生，安徽桐城人，讲师，主要研究方向为雷达对抗、电子对抗作战指挥。
韩俊男，1983年生，安徽合肥人，博士，讲师，主要研究方向为雷达对抗、信息处理。
何缓女，1979年生，湖南岳阳人，博士，讲师，主要研究方向为雷达对抗、电磁散射研究。