
图1 机载雷达阵列天线几何模型
机载雷达利用阵列天线实现空域采样,假设雷达天线是由N个阵元组成的均匀线阵,一个相干处理间隔(CPI)内的脉冲数为K。阵列天线的采样数据,即STAP系统的输入数据可以看作是一个N×K×L的三维立方体数据块,如图2所示,其中L表示距离单元的个数。STAP技术就是分别对每个距离单元的空时采样数据进行匹配滤波,每个距离单元的空时采样数据可用式(1)来表示:
李骥阳,毛睿达,汤建龙
(西安电子科技大学电子信息攻防对抗与仿真技术教育部重点实验室, 陕西西安 710071)
摘要:空时二维自适应处理(STAP)技术具有卓越的抑制杂波和抗干扰性能,常规的干扰手段难以对其产生理想的干扰效果。研究了机载雷达STAP系统的信号模型,提出了一种基于收发分时体制的卷积调制干扰方法。该方法首先对截获到的雷达信号进行间歇采样并进行存储,然后将读出的信号与存储的噪声进行卷积调制,最后将得到的干扰信号延时叠加转发。理论分析表明该干扰方法能产生幅度随机起伏且间隔随机分布的假目标群,破坏了训练样本独立同分布的条件,造成STAP系统性能下降。计算机仿真结果验证了该干扰方法的有效性。
关键词:空时自适应处理(STAP);收发分时; 间歇采样; 卷积调制干扰
空时二维自适应(STAP)技术具有优秀的抑制杂波和干扰的特性[1-2],是新一代高性能雷达的关键技术之一[1,3],近年来还应用到了导航、通信以及声呐等领域[3-6]。STAP技术的发展给雷达对抗一方也提出了严峻的挑战,但目前国内外公开的文献资料对STAP干扰方法的研究却十分有限。文献[7]提出了一种针对STAP技术的密集干扰的方法,用多部干扰机占用系统自由度,使STAP系统因缺乏足够的系统自由度而性能下降,但当阵元和脉冲个数较大时,所需干扰机的数量也比较庞大。文献[8]提出了一种自卫式相干散射欺骗干扰方法,虽然能有效掩护受保护目标,但未考虑到收发分时体制下干扰机如何快速响应的问题。文献[9]提出了一种利用阶梯波移频法构造距离假目标的干扰方法,虽然能形成非均匀环境,使STAP系统性能下降,但其形成的假目标数量较少,并且呈现一定的规律性。
针对现有干扰方法在收发分时体制下无法快速响应和假目标数量较少且呈现一定规律性等问题,本文研究了机载雷达STAP系统的信号模型,提出了一种基于间歇采样的卷积调制叠加转发干扰方法。这种干扰方法将间歇采样、卷积调制和延时叠加三种方法相结合,提高了收发分时体制下干扰机的响应速率,产生了大量的幅度随机起伏、间隔随机分布的假目标信号。
图1为机载相控阵雷达的几何模型图。假设雷达载机的飞行高度为H,以恒定的速度v作匀速直线飞行,雷达天线采用均匀线阵,各阵元的间距d=λ/2,λ为雷达发射电磁波的波长,θ和φ分别为天线波束指向的方位角和俯仰角,ψ为杂波散射体相对阵列天线的入射锥角,并满足cosψ=cosθcosφ的数量关系,α为阵列天线的载机航行方向的夹角。

图1 机载雷达阵列天线几何模型
机载雷达利用阵列天线实现空域采样,假设雷达天线是由N个阵元组成的均匀线阵,一个相干处理间隔(CPI)内的脉冲数为K。阵列天线的采样数据,即STAP系统的输入数据可以看作是一个N×K×L的三维立方体数据块,如图2所示,其中L表示距离单元的个数。STAP技术就是分别对每个距离单元的空时采样数据进行匹配滤波,每个距离单元的空时采样数据可用式(1)来表示:

(1)
式中,xn,k,n=1,2,…,N,k=1,2,…,K表示第n个天线阵元接收到的第k个时刻的空时二维的采样数据。在后续处理中,为了方便理解与表示,将每个距离单元的数据写成(NK×1)维的向量形式。
雷达回波数据为X,其通常由目标信号回波St、杂波信号C、噪声n和干扰信号J组成,即
X=St+C+n+J
(2)
设STAP系统的自适应权矢量为W,即
W=[w11,…,w1K,w21,…,w2K,…,
wN1,…,wNK]T
(3)
滤波处理后输出为Y,则STAP系统的输出为
Y=WHX
(4)
自适应最优权矢量Wopt为
(5)
式中,R=EXHX为NK×NK维杂波、干扰、噪声协方差矩阵,S为NK×1维目标信号空时二维导向矢量。在R确知的情况下,STAP技术有良好的杂波抑制和抗干扰性能,但实际中通常选择一定数量的训练样本来得到R的估计值![]() ,如图2所示。
,如图2所示。
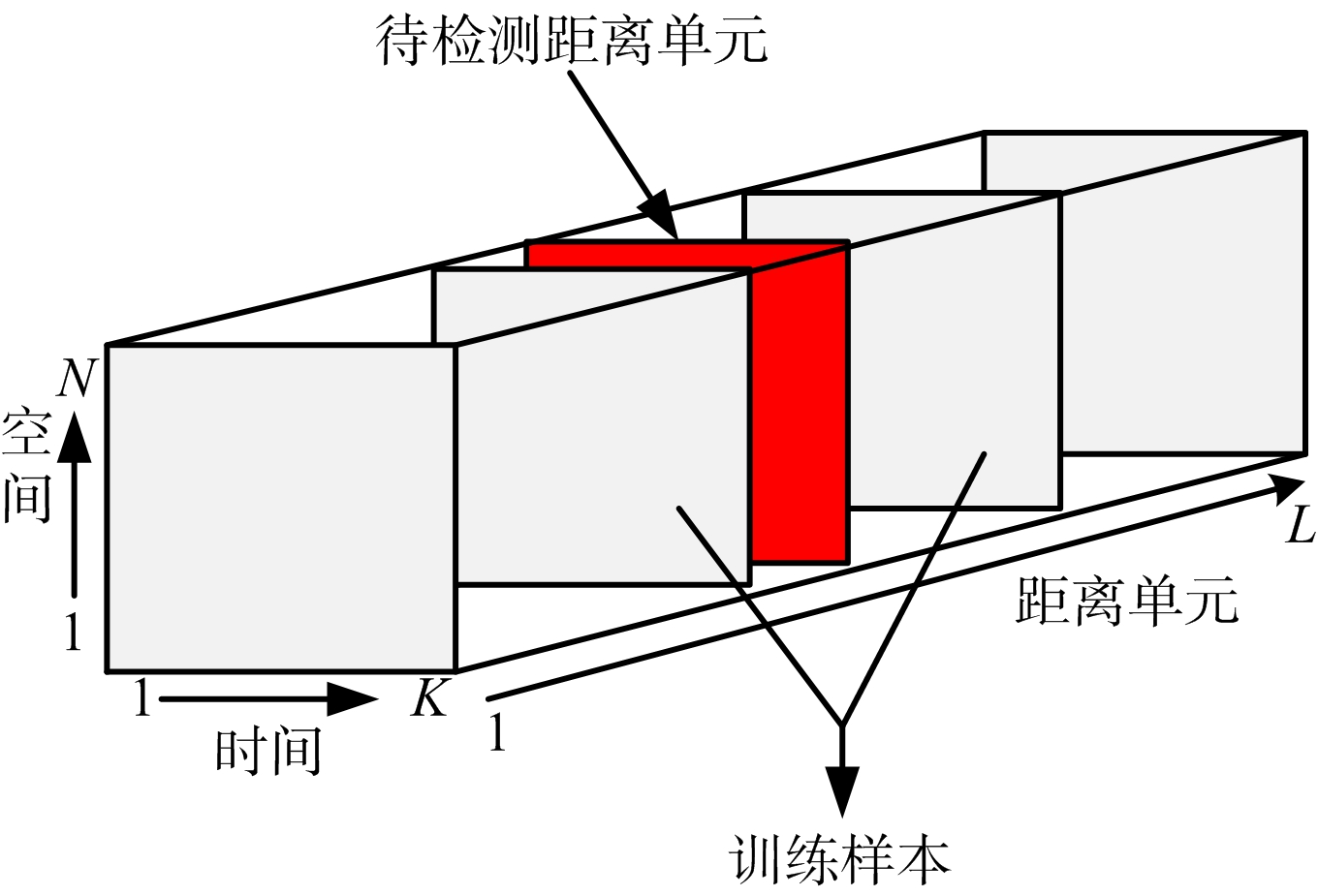
图2 输入数据模型
利用训练样本估计出的协方差矩阵![]() 代替真实的杂波干扰协方差矩阵R,将使得STAP系统的输出信杂噪比下降。为了保证STAP系统的性能,参与训练的样本数据必须满足独立同分布,且训练样本的数量要大于系统自由度的两倍。
代替真实的杂波干扰协方差矩阵R,将使得STAP系统的输出信杂噪比下降。为了保证STAP系统的性能,参与训练的样本数据必须满足独立同分布,且训练样本的数量要大于系统自由度的两倍。
受机载平台应用的限制,干扰机收发隔离度难以保证,机载平台干扰机通常采用收发分时体制。为了使干扰机快速响应,通常对截获到的雷达信号进行间歇采样。如图3所示,在侦收窗内(WR为高电平期间,其中Δt为系统延时),干扰机对截获信号进行检测。当检测信号DET为高电平,启动DRFM对信号进行存储,当信号脉冲宽度大于系统设定的间歇时间τ,即信号存储τ长度后,干扰发射选通信号JT变为高电平,并同时将存储的信号读出;数据读出完毕后,JT再次降为低电平,存储τ时间长度信号数据后,JT再次变为高电平,将新存储的数据读出;该过程持续直至DET转低,即雷达脉冲结束。图中Tj为干扰窗长度。
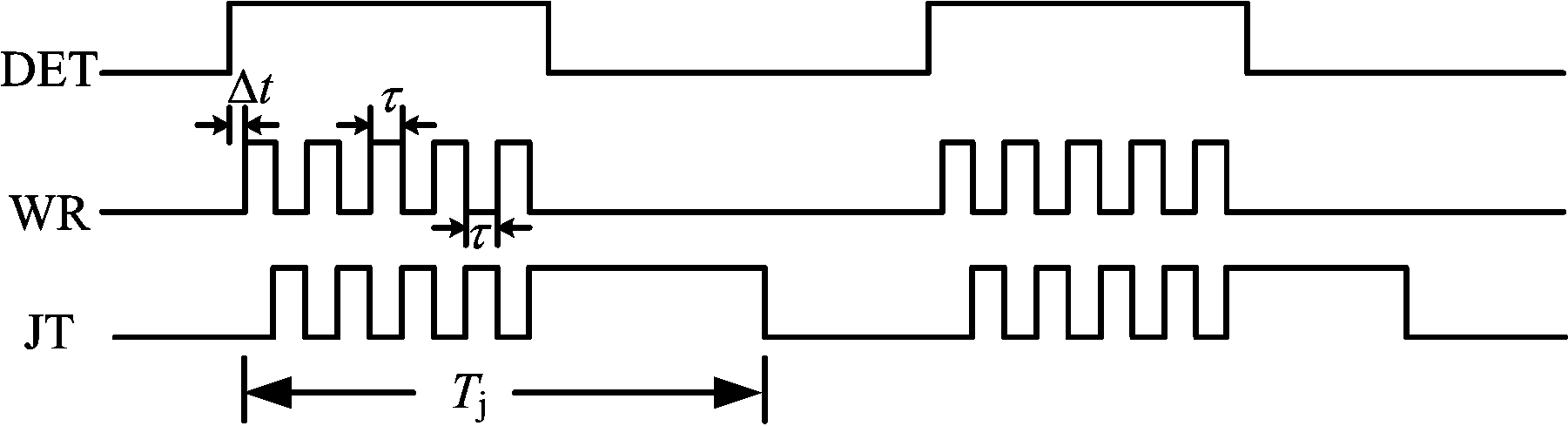
图3 间歇采样原理
设间歇采样信号是一个脉冲宽度为τ,脉冲重复周期为Ts的矩形包络脉冲串。间歇采样脉冲串信号c(t)和频谱C(f)为
![]() δt-nTs
δt-nTs
(6)
![]() τfsSanπfsτδf-nfs
τfsSanπfsτδf-nfs
(7)
雷达发射线性调频信号为x(t),时宽为T,带宽为B。使用间歇采样脉冲串信号对雷达发射信号进行采样,即可得到间歇采样转发干扰信号xs(t),其频谱为Xs(f):
xs(t)=c(t)x(t)
(8)
Xs(f)=C(f)*X(f)=
![]() τfsSanπfsτXf-nfs
τfsSanπfsτXf-nfs
(9)
由式(9)可得,当n对应取不同值时,干扰信号频谱与雷达频谱形状相似,只是在中心频率处发生了±nfs的频移,并在幅度上有一定衰减。设匹配滤波器为h(t),则目标回波和干扰信号经过匹配滤波器的响应分别为y(t),ys(t):
ys(t)=xs(t)*h(t)=
![]() ·
·![]() ·y(t)
·y(t)
(10)
分析式(10)可得,经匹配滤波后干扰信号会形成一组由主假目标和分布在其两侧的次假目标群。雷达回波信号的匹配滤波输出和间歇采样转发干扰信号的匹配滤波输出的仿真结果分别如图4(a)和图4(b)所示(T=10 μs,B=2.5 MHz,τ=1 μs,Ts=2 μs)。假目标的幅度由间歇采样脉冲信号的脉宽和重复周期决定,并且任意相邻两个假目标的间隔为
Δ![]()
(11)
为了保证假目标群的产生且任意两相邻假目标不发生混叠,间歇采样周期Ts必须满足:
(12)

(a) 雷达信号匹配滤波输出
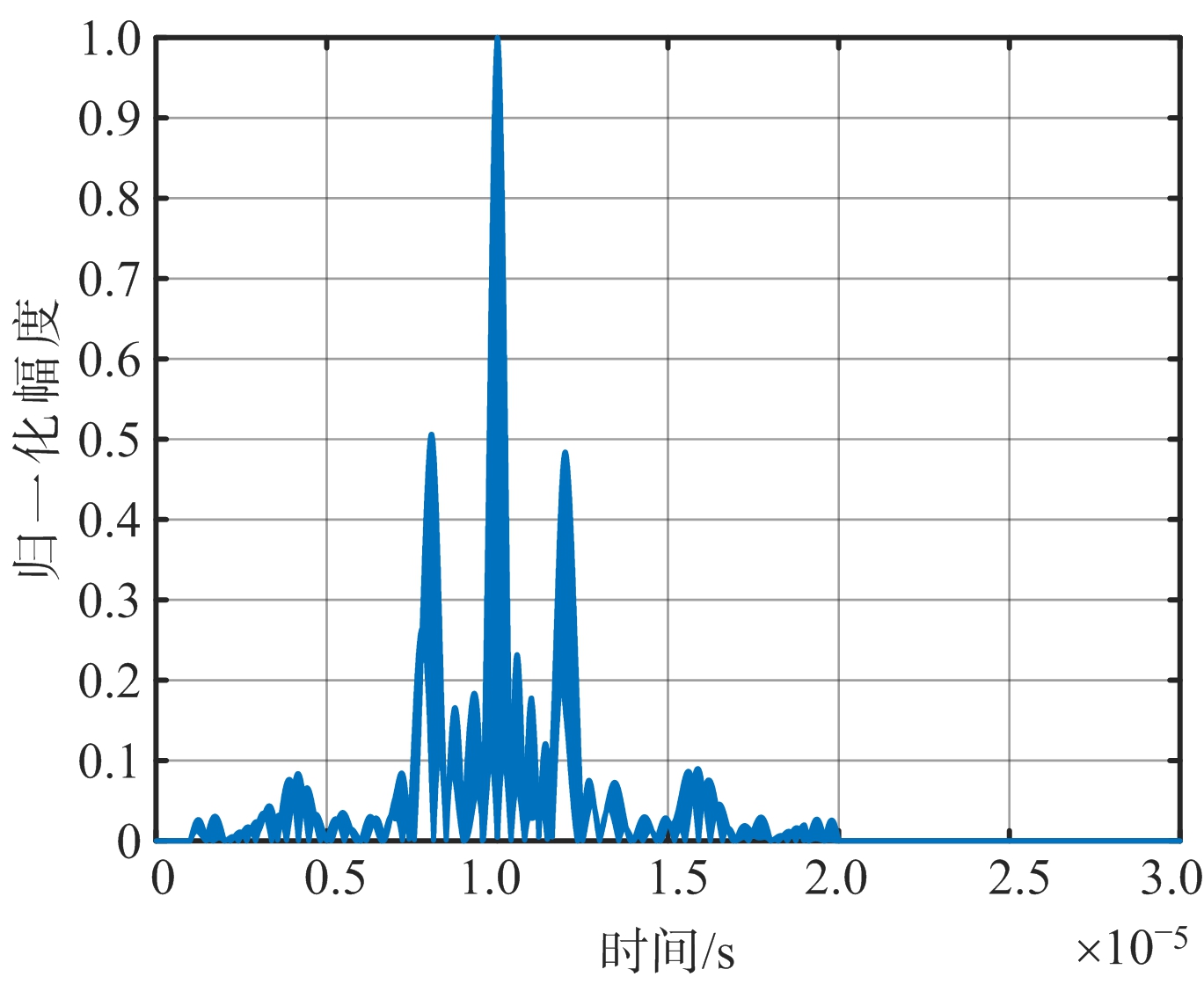
(b) 间歇采样转发干扰信号匹配滤波输出
图4 间歇采样干扰转发信号
由上述分析和仿真可知,对雷达信号进行间歇采样会造成干扰信号经过匹配滤波形成的假目标的间隔保持固定(Δt=2 μs),并且假目标的幅度会呈现一定规律性的衰减。但这样产生的假目标数量较少,且假目标呈现出一定的规律性,无法产生较好的干扰效果。为了改善直接间歇采样转发干扰的不足,将间歇采样后的信号与噪声作卷积运算,并将得到的干扰信号延时叠加转发。其原理如图5所示,其中xst-τi,i=1,2,…,N是对xs(t)的延时(由于干扰机收发分时的机制,这里必须保证延时转发量τi是间歇采样宽度τ的整数倍),n(t)为干扰机存储的视频噪声信号,j(t)为最终生成的干扰信号。

图5 基于间歇采样的噪声卷积延迟叠加转发干扰原理
经过间歇采样的雷达信号xs(t)与视频噪声n(t)进行卷积运算后产生的干扰回波信号j(t)及其频谱J(f)为
![]() *ni(t)
*ni(t)
(13)
J(f)=![]() ·e-j2πfτi·Ni(f)=
·e-j2πfτi·Ni(f)=
![]() ·X(f)·e-j2πfτi·Ni(f)=
·X(f)·e-j2πfτi·Ni(f)=
![]() τfs·
τfs·![]() ·
·
Xf-mfs·e-j2πfτi·Ni(f)
(14)
由式(14)可知,由于有Ni(f)的存在,使得干扰信号的频谱在幅度上产生随机起伏的现象。干扰信号j(t)经过匹配滤波器h(t)的输出为jpc(t),则
jpc(t)=j(t)*h(t)=
![]() *h(t)*ni(t)=
*h(t)*ni(t)=
![]() *ni(t)=
*ni(t)=
![]() ·ys-τi+
·ys-τi+
![]() ·
·![]() ·y(s-τi)
·y(s-τi)
(15)
噪声卷积后的干扰信号经过匹配滤波后会产生很多的假目标,式(15)中第一项为主假目标,并且幅度![]() 随机变化,第二项为副假目标串,其幅度
随机变化,第二项为副假目标串,其幅度![]() ·ni·
·ni·![]() 也随机起伏,并且由于主假目标间的副假目标串随机起伏,相互叠加,因此会在真实目标附近形成幅度随机起伏、间隔随机变化的密集假目标群,图6(a)和图6(b)对比了直接延时叠加转发和本文所提的干扰信号的时域波形,可以发现本文所提采用干扰信号的波形的幅度随机起伏,并且在各个发射时间段也随机分布。图6(c)和图6(d)对比了直接延时叠加转发干扰和本文采用的间歇采样噪声卷积叠加转发干扰的信号经过匹配滤波后的结果,可以看出相对于直接延时叠加转发干扰本文方法所产生的干扰信号有更好的干扰效果。
也随机起伏,并且由于主假目标间的副假目标串随机起伏,相互叠加,因此会在真实目标附近形成幅度随机起伏、间隔随机变化的密集假目标群,图6(a)和图6(b)对比了直接延时叠加转发和本文所提的干扰信号的时域波形,可以发现本文所提采用干扰信号的波形的幅度随机起伏,并且在各个发射时间段也随机分布。图6(c)和图6(d)对比了直接延时叠加转发干扰和本文采用的间歇采样噪声卷积叠加转发干扰的信号经过匹配滤波后的结果,可以看出相对于直接延时叠加转发干扰本文方法所产生的干扰信号有更好的干扰效果。
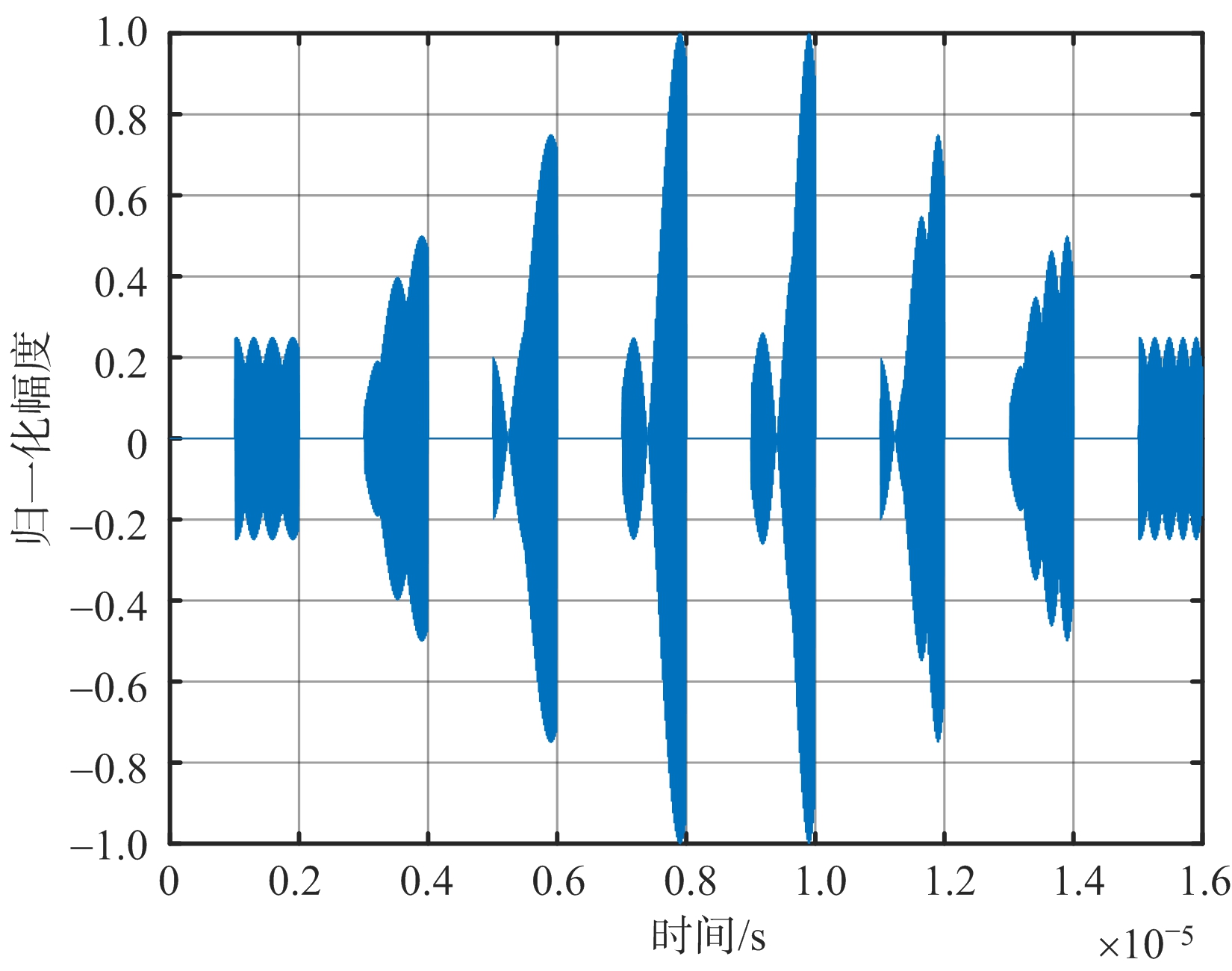
(a) 直接延时叠加转发干扰信号

(b) 本文方法产生的干扰信号

(c) 直接延时叠加转发干扰信号匹配滤波输出

(d) 本文干扰信号匹配滤波输出
图6 干扰信号对比
上述密集假目标群的引入将会破坏训练样本的独立同分布的条件,造成STAP系统得不到足够的独立同分布的训练样本,从而使获得的协方差矩阵估计误差变大,输出信杂噪比下降,滤波器凹口展宽。这样就造成了STAP系统对干扰和杂波的抑制效果急剧下降。
仿真参数:机载雷达工作频率f0=450 MHz,脉冲重复频率PRF=300 Hz,天线采用均匀线阵,阵列天线与载机航向的夹角α=0°,阵元个数N=16,脉冲积累数M=16,杂噪比CNR=40 dB,信噪比SNR=0 dB,干噪比JNR=28 dB,用30 dB切比雪夫加权。 载机速度vp=150 m/s,载机高度H=9 000 m,目标的方位角ψt=0°,速度vt=75 m/s,干扰机的方位角ψj=30°,速度vj=30 m/s,采用512个训练样本。仿真结果如图7~图11所示。

图7 无干扰环境下杂波空时功率谱

图8 杂波+干扰空时功率谱

图9 杂波环境下STAP对目标的检测
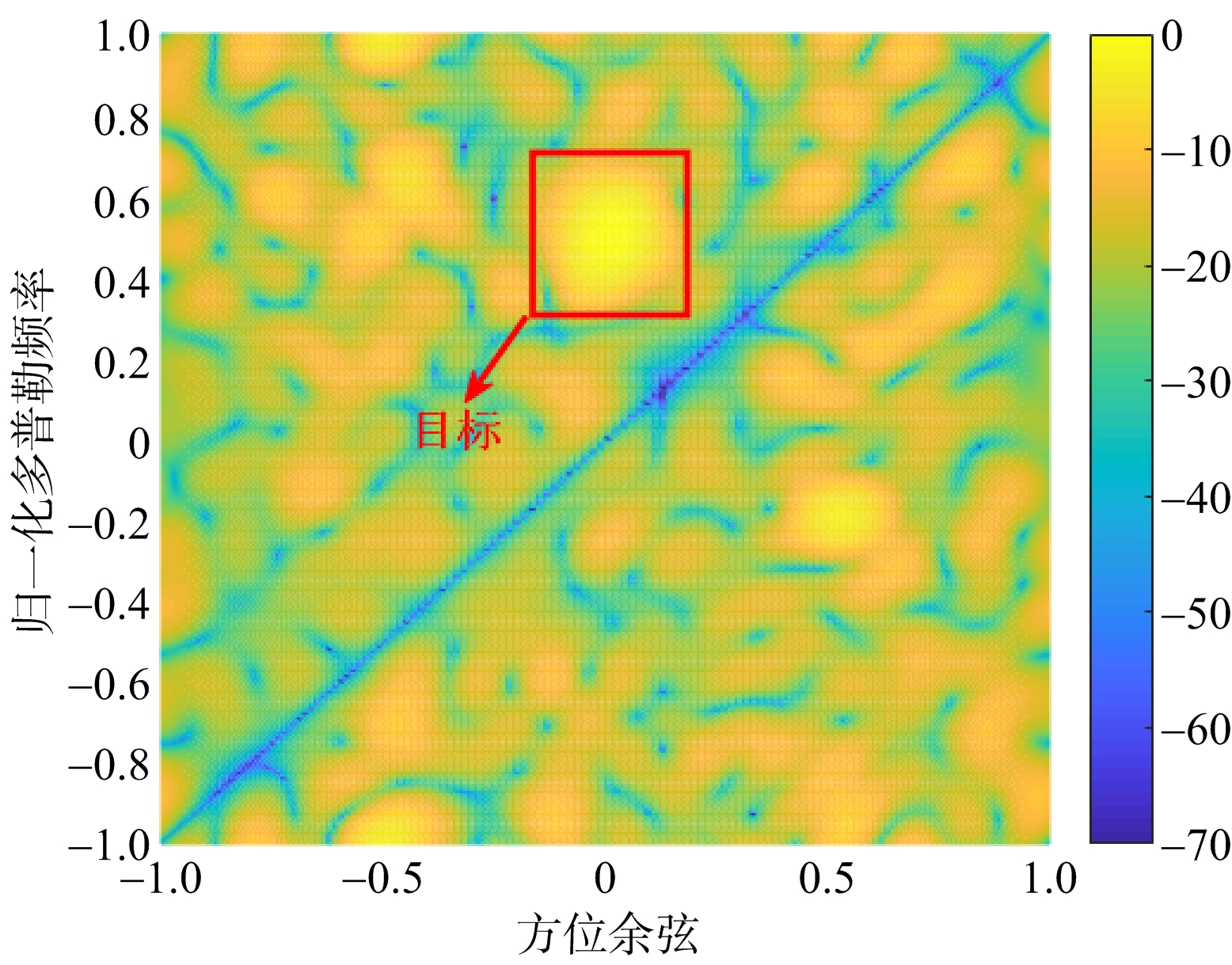
图10 杂波+干扰环境下STAP对目标的检测

图11 改善因子对比
图7和图8分别是杂波环境下和杂波加干扰环境下的空时二维功率谱,图中对角线处为杂波。与图7对比,图8的仿真结果可以看出,在干扰加杂波环境下的空时二维功率谱的部分地方产生了随机起伏的现象,这是由于干扰的加入使得训练样本在距离-多普勒域不再满足独立同分布的条件。图9和图10分别是杂波环境和杂波加干扰环境下STAP系统对目标的检测效果,对角线处为杂波抑制凹口,从仿真结果对比可以看出,在干扰加杂波环境下STAP系统对目标的检测效果受到较大的影响,这是因为STAP系统无法获得足够的独立同分布的训练样本导致![]() 与真实值R偏差较大。图11对比了杂波环境和杂波加干扰环境下STAP系统的改善因子,可以看出在干扰条件下STAP系统的改善因子下降了约30 dB,并且用于抑制杂波的凹口也有一定的展宽,这说明STAP系统的性能急剧下降。上述仿真结果有效地验证了本文干扰方法对空时自适应技术的干扰效果。
与真实值R偏差较大。图11对比了杂波环境和杂波加干扰环境下STAP系统的改善因子,可以看出在干扰条件下STAP系统的改善因子下降了约30 dB,并且用于抑制杂波的凹口也有一定的展宽,这说明STAP系统的性能急剧下降。上述仿真结果有效地验证了本文干扰方法对空时自适应技术的干扰效果。
本文研究并分析了机载雷达STAP系统的信号模型,将间歇采样、卷积调制、延时叠加转发等方法相结合,提高了收发分时体制下干扰机的响应速率,并且针对STAP系统产生了大量的不满足独立同分布的干扰训练样本,造成STAP系统无法准确估计用于抑制杂波和干扰的协方差矩阵,大大降低了STAP系统的性能。仿真结果验证了该干扰方法降低了STAP系统的输出信杂噪比并展宽了滤波器凹口,造成STAP系统的性能下降。
参考文献:
[1] 张良,祝欢,杨予昊,等. 机载预警雷达技术及信号处理方法综述[J]. 电子与信息学报, 2016,38(12):3298-3306.
[2] JEON H, CHUNG Y, CHUNG W, et al. Clutter Covariance Matrix Estimation Using Weight Vectors in Knowledge-Aided STAP[J]. Electronics Letters, 2017, 53(8):560-562.
[3] 刘春生,张正言,唐孝国. 对机载雷达STAP系统的调频干扰研究[J]. 现代防御技术, 2016,44(3):141-147.
[4] MARCOS E P, KONOVALTSEV A, CUNTZ M, et al. STAP as a Solution for Imperfections in Multi-Antenna GNSS Receivers[C]∥ NAVITEC, Noordwijk, Netherlands: IEEE, 2016:14-16.
[5] 洪玺,王文杰,殷勤业. 基于多级维纳滤波器的空时自适应信号处理及其在无线通信系统中的应用[J]. 信号处理, 2017, 33(3):430-436.
[6] 李玉伟,周敏佳. 主动声纳空时自适应处理算法研究[J]. 舰船电子工程, 2017, 37(5):127-130.
[7] 张昀,盛骥松,刘禹. 基于密集干扰的机载雷达STAP技术的干扰研究[J]. 舰船电子对抗, 2013,36(6):6-8.
[8] 唐孝国,张剑云,王珽. 对空时自适应处理技术的欺骗干扰研究[J]. 航天电子对抗, 2012, 28(5):61-64.
[9] 薛冰心,张友益. 基于频移假目标对机载雷达STAP技术干扰效果的研究[J]. 舰船电子对抗, 2012, 35(1):11-13,59.
LI Jiyang, MAO Ruida, TANG Jianlong
(KeyLaboratoryofElectronicInformationCountermeasureandSimulationTechnology,MinistryofEducation,XidianUniversity,Xi’an710071,China)
Abstract:Space-time adaptive processing (STAP) technology brings forward severe challenge to electronic countermeasure for its excellent performance of clutter-suppression and anti-jamming. This paper firstly studies the signal model of airborne radar STAP system, and then proposes a convolution modulation jamming algorithm based on transmit/receive time-sharing. In this algorithm, the jammer starts intermittent sampling when it receives radar signal, then gains the convolution result from the noise and the output radar signal as convolution factors, finally postpones and transmits the jamming signal. The analysis shows that this jamming algorithm can generate false targets with random amplitude and interval, break the IID conditions of training samples and decrease STAP system’s performance. The simulation results show the effectiveness of this jamming algorithm.
Keywords:space-time adaptive processing(STAP); transmit/receive time-sharing; intermittent sampling; convolution modulation jamming
DOI:10.3969/j.issn.1672-2337.2018.05.008
基金项目:中央高校基本科研业务费专项资金资助课题(No.JB160220)
修回日期:2017-12-11
收稿日期:2017-11-17;
文章编号:1672-2337(2018)05-0511-06
文献标志码:A
中图分类号:TN972
作者简介:

李骥阳 男,1991年生于河南灵宝,硕士研究生,主要研究方向为雷达干扰技术。
E-mail:lijiyang1991@163.com