蒋留兵1,2,刘永吉3,车俐1,2
( 1.广西无线宽带通信与信号处理重点实验室, 广西桂林 541004; 2.桂林电子科技大学计算机与信息安全学院, 广西桂林 541004; 3.桂林电子科技大学信息与通信学院, 广西桂林 541004)
摘要:相位解缠是干涉合成孔径雷达信号处理的关键步骤之一,而噪声和数据欠采样等因素的存在使得这一过程非常困难。网络流算法有效抑制了噪声对高相干区域的影响并且能够克服“孤岛现象”,能够把误差传递限制在一个很小的范围内,但是由于噪声的影响,解缠结果还是会有明显的“尖峰毛刺”现象。针对网络流的特点,结合残差点的思想和曲面拟合法提出了一种新的相位解缠算法。新的算法根据相关度从初步解缠结果中找出噪声点,然后运用最小曲面拟合法重构值代替噪声点的数值,最后沿着已保存的积分路径更正所有包含此误差点的路径的结果。重复迭代直至将所有的噪声点全部消除,最终的解缠结果是由多个最小曲面多次构成。仿真实验和实测数据实验都证明新算法可以有效改善解缠结果中的“尖峰毛刺”现象的同时,可以进一步抑制解缠误差的传递,提高解缠精度。
关键词:干涉测量; 相位解缠; 网络流法; 最小曲面拟合
相位解缠是干涉合成孔径雷达(Interference Synthetic Aperture Radar,InSAR)干涉测量的关键流程[1-3],它的准确程度直接影响到InSAR生成的数字高程模型的精确性[3]。干涉图的相位展开方法有多种,主要分为4类:第一类是路径跟踪法[4-5],第二类是最小范数法[6-7],第三类是网络流法[8],第四类是其他方法。
路径跟踪法最常用的是枝切法。利用枝切法进行相位解缠是Goldstein等首先提出的[4]。枝切法在相干性差、残差点较多的区域难以选择准确的枝切线,容易形成一个个被枝切线包围的孤立区间,即“解缠孤岛”,积分路径都无法到达从而无法解缠。“解缠孤岛”由于没有明显的联系,单独解缠时会造成很大误差。最小范数法最典型的就是最小二乘法,它是一种全局算法。解缠结果中不存在不能进行相位展开的区域,但由于此算法穿过而非绕过残差点,很容易使相位误差传递到整个区域。这就造成了整体上结果为连续的,但实际上没有一点相位的值是准确的[9]。网络流法是通过全局范围搜索最优路径和最短枝切线来求得最小化问题的最优解。在网络流成熟的条件下网络流算法可大大提高运算的效率[10],与此同时保证一定的精度,在误差的限制方面有着良好的效果,可以防止误差传递到整个区域内,对于噪声较为严重的干涉图也可以进行解缠并取得较为精确的结果[11-13]。但是在噪声较大的环境下网络流法的解缠结果会将噪声不可避免地沿着积分路径传递,造成解缠结果的严重“尖峰毛刺”现象,使得解缠结果不理想。
结合残差点的思想、曲面拟合法以及网络流法提出了一种新的相位解缠算法。新算法根据相关度找出解缠结果的噪声点,然后运用最小曲面拟合法重构值代替噪声点的数值,最后沿着积分路径更正有误差传递的结果。逐一处理所有噪声点,最终的解缠结果可以看作是由多个最小曲面多次贴合的结果。本文首先介绍相关理论,然后介绍新算法的具体步骤和推导,最后通过实验验证可行性。
网络流算法最早见于Costantini等提出的基于网络流的相位解缠方法[8],从根本上来讲此种方法仍属于路径跟踪法。这种方法是将相位解缠问题转化为最小化问题,通过在全局范围内搜索路径和最短枝切线来求得最小化问题的最优解。在一个M×N大小的方格网内,设φ和φ分别表示解缠和未解缠的相位,则有
φ(i,j) =φ(i,j) + 2πn
(1)
式中,n为整数,φ(i,j)∈[-π,π],相位解缠就是从φ(i,j)到φ(i,j)的过程。根据二维行为解缠原理,定义相邻像素点间的差分估计[14]:
Δφ1(i,j)=φ(i+1,j)-φ(i,j)+2πn1
(2)
Δφ2(i,j)=φ(i,j+1)-φ(i,j)+2πn2
(3)
式中,n1(i,j),n2(i,j) 为基于先验知识选取,使Δφl(i,j)∈[-π,π)(l=1,2) 成立的整数值。由于积分路径的不同,Δφl(i,j)∈[-π,π)(l=1,2) 并不能和相邻点的差分保持一致,因而定义以下差分残差:
由于k1(i,j),k2(i,j)都是非常小的数,可以用如下的最小化问题来估计残差:

如图1所示,根据网络流理论,式(5)这个最小化问题可以转化为最小费用流来解决。最小费用流问题的输入为各个节点的度,即各个残差的值和每条流的费用,式中c1(i,j),c2(i,j)可以根据像素点的相关度得出,而该问题的输出为各条流的流量。式(5)的最小化问题可转化为如下公式:
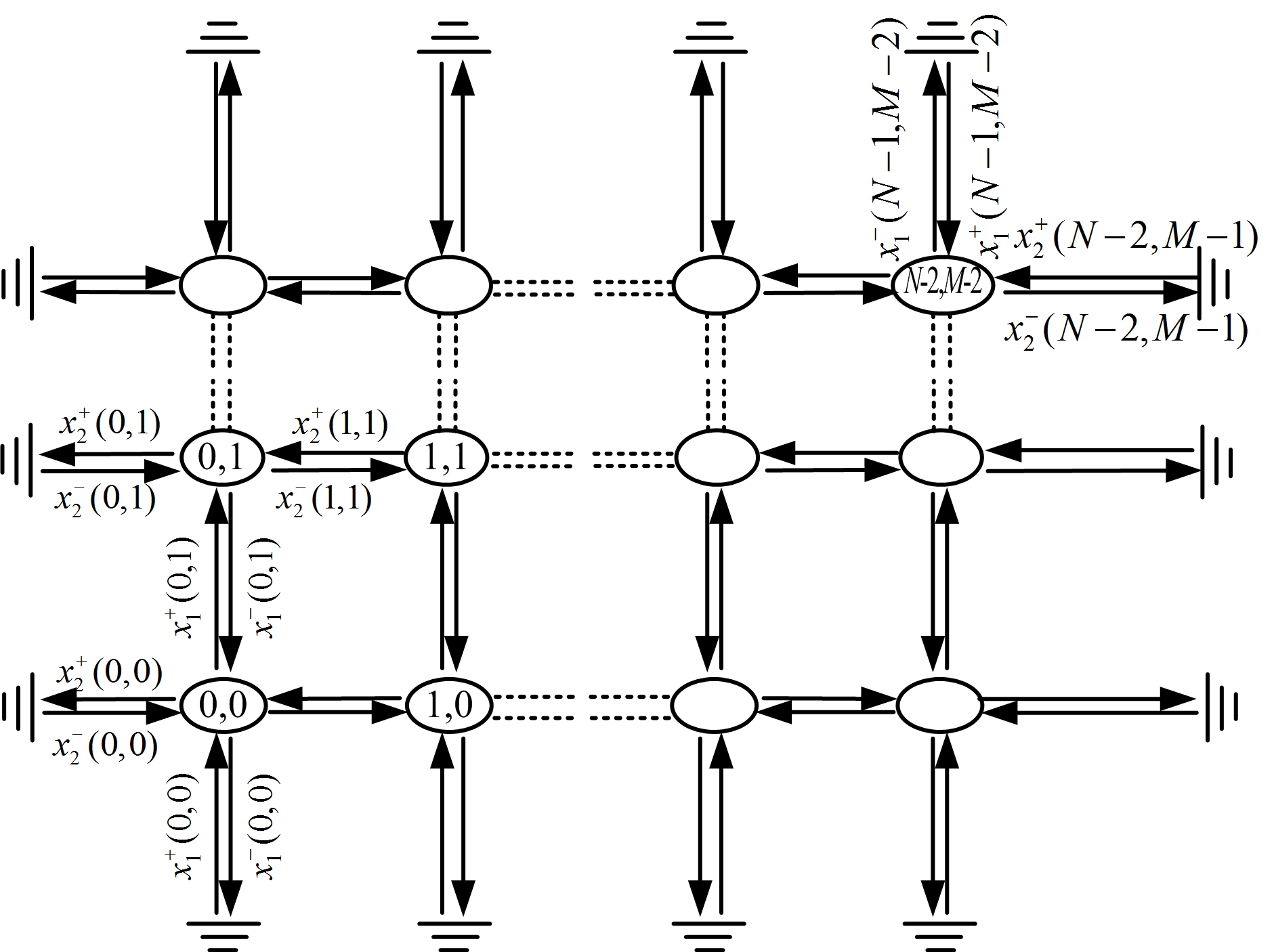
图1 网络图
![]() (i,j)\5
(i,j)\5
![]() ,
,![]()
(6)
![]() (i,j)=max(0,k1(i,j)),
(i,j)=max(0,k1(i,j)),![]() (i,j)=
(i,j)=
min(0,k1(i,j))
(7)
![]() (i,j)=max(0,k2(i,j)),
(i,j)=max(0,k2(i,j)),![]() (i,j)=
(i,j)=
min(0,k2(i,j))
(8)
在计算出k1(i,j)和k2(i,j)之后,再计算相位梯度,最终有
φ(i,j)=φ(0,0)![]()
(9)
由后面的实验结果可以看出,通过网络流方法的解缠结果和枝切法、最小二乘法相比有很大的优势,没有“解缠孤岛”的现象,并且解缠精度要比其他两种方法高。但是在噪声较大的环境下网络流法的解缠结果会将噪声不可避免地沿着积分路径传递,造成解缠结果的严重“尖峰毛刺”现象,造成解缠结果的失真。很明显这些随机出现的“毛刺”点是由于噪声的干扰引起的。可以设计方法识别出这些有误差的点,然后根据这个点与周围其余点的联系重新构造出更准确的值。通过误差点识别方法找出这些由于噪声出现的“毛刺”点的集合,假设这些点(i,j)∈S1(i=0,1,…,n-1,j=0,1,…,m-1),设集合S1的残差值k1(i,j),k2(i,j):
i=0,1,…,n-1,j=0,1,…,m-1
(10)
然后通过设计最小曲面拟合的方法来实现对集合S1的数据重构,设重构后的集合为![]() ,而重构后集合的每一个点的残差值
,而重构后集合的每一个点的残差值![]() (i,j),
(i,j),![]() (i,j):
(i,j):
![]()
![]()
i=0,1,…,n-1,j=0,1,…,m-1
(11)
误差点的重构值是根据其与周围点相关程度和曲面趋势进行的重构,经过重构后的相位值在一定程度上降低了噪声的干扰,减少了噪声的叠加,所以可以得出
从而得出经过重构后的网络图的目标函数:
![]()
![]() ,
,![]() (i,j)|+
(i,j)|+
![]() ,
,![]()
结合式(5)、式(12) 和式(13)可以得出
目标函数最小化是相位解缠的本质,以上的推导可以证明通过对网络流算法解缠结果中的噪声点进行精准识别、定位与重构后,可以有效改善“毛刺”现象,并且能够进一步最小化目标函数,从而提高解缠结果的准确度。考虑到解缠算法的时间成本以及内存要求,对于误差点的识别和利用曲面拟合重构数值分别设计了以下方法实现。
受到枝切法中识别“残差点”思想的启发,按照如下方法对误差点进行识别并处理。根据二维解缠原理连续相位的假设,首先设置π为阈值,再依次检验所有解缠后的像素点。在像素点周围3×3的区域内进行检测,如果像素点与其所有周围的8个点的差值的绝对值都大于阈值,那么识别此像素点为误差点。如图2(a)所示,3×3区域的像素点中心点明显比其周围的8个像素点的值大很多。因为经过网络流处理后的数据在大概率上可以代替真实相位值,那么基于连续相位的解缠假设,如果出现上述的像素点就可以认定此点由于噪声的干扰造成了数据的严重失真,可以将此点识别记录,认定为误差点,称之为E1误差点。
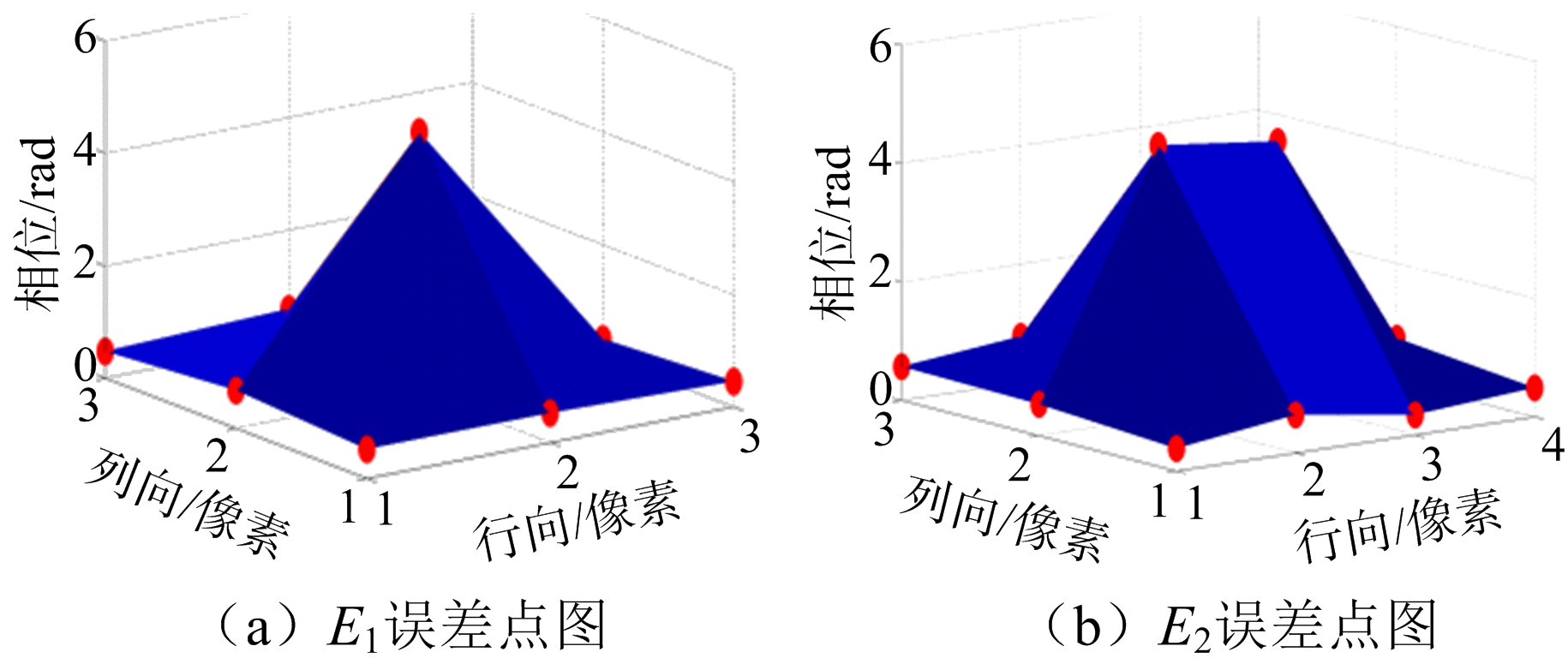
图2 E1,E2误差点三维示意图
经过第一轮的筛选后,可以标记出所有单个的误差点。但是,误差点中还会出现两个连在一起的误差点。可以运用相同的规则,将范围扩大为3×4和4×3的区域识别中心两个点,如果区域中心的两个像素点的值的差比阈值小,且两个点中较小的值与其周围的10个像素点的差值大于阈值,那么这两个点认定为误差点,将3×4和4×3区域内识别出的这两种类型的点统称为E2误差点,如图2(b)所示。
经过两轮筛选后,考虑到时间花销仍用像素点周围3×3的区域内进行检测。如果像素点与其周围的大于4、小于8个点的差值的绝对值都大于阈值,那么定义此像素点为E3误差点。对于剩余的情况,即像素点与其周围的最多4个点(大于0个点)的差值的绝对值都大于阈值,那么暂且定义此点为E4误差点。
由于每一个误差严重点的积分路径有迹可循,可以利用其周围的点与此噪声点的联系来重构此误差点的值。由于考虑到算法的效率和时间的消耗,尽可能多地利用误差点周围直接包裹它的有效点的信息增加重建值可靠度,进行最快速的曲面趋势模拟,最终重构误差点的值,该方法称之为最小曲面拟合。对于E1和E2两种误差点的最小曲面拟合分别用以下方法操作。
如图3(a)所示的9个像点,其中点N5为3×3区域识别的E1误差点,而其余的8个点均是认定的可靠数据。用图3(a)中8个像素点的值,分别乘以像素点中(1,2),(1,4),(4,7),(2,3),(3,6),(6,9),(7,8),(8,9)这8对点的相关系数,进行加权平均。即

式中,DI是像素点的相位值,而CI是根据像素点的相关度得出的权值。最终得到的D5就是利用最小曲面拟合构造的新像素点的值。
如图3(b)所示的12个像点,其中N5和N8为3×4区域识别的误差点,而其余的10个点均是认定的可靠数据。在这种情况下,将这个区域分割成两个3×3的区域,如图4所示。
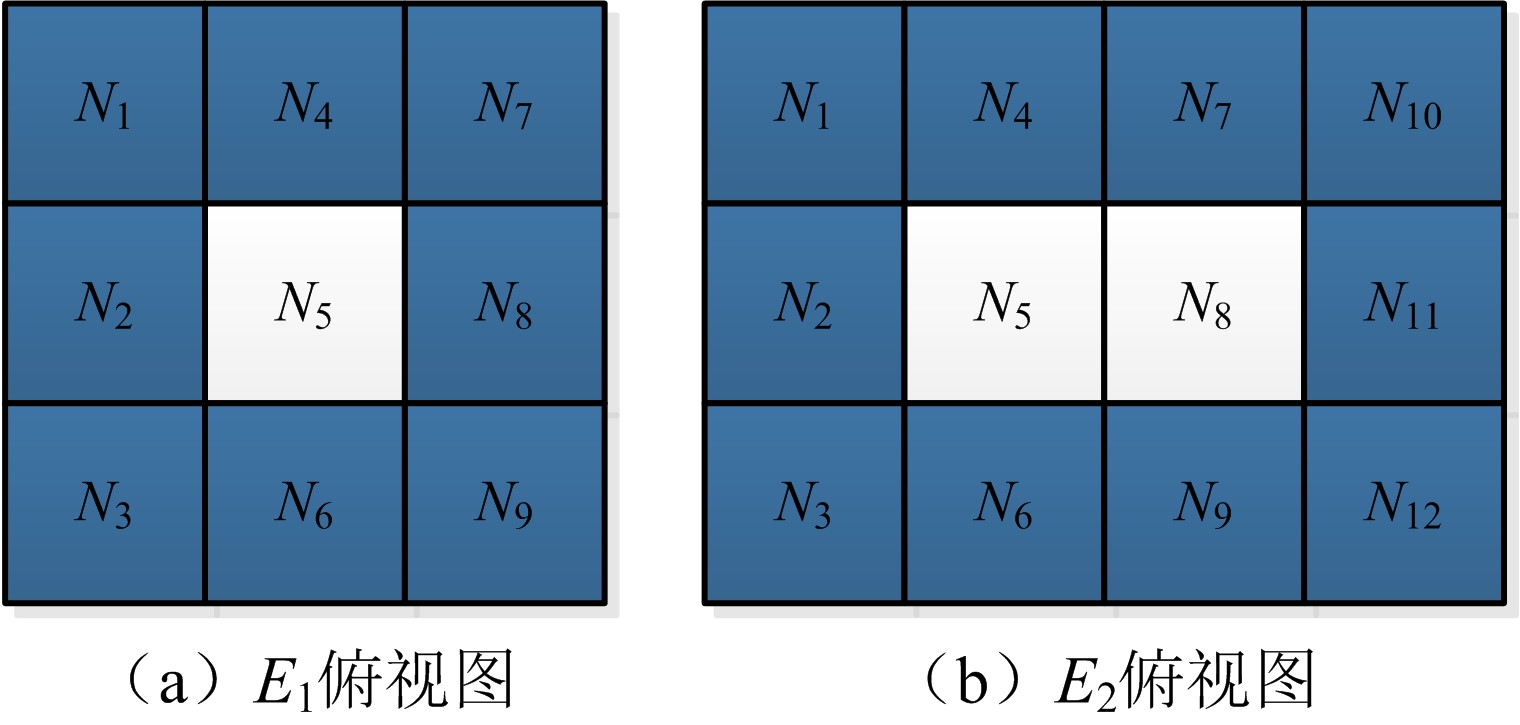
图3 E1,E2误差点二维示意图
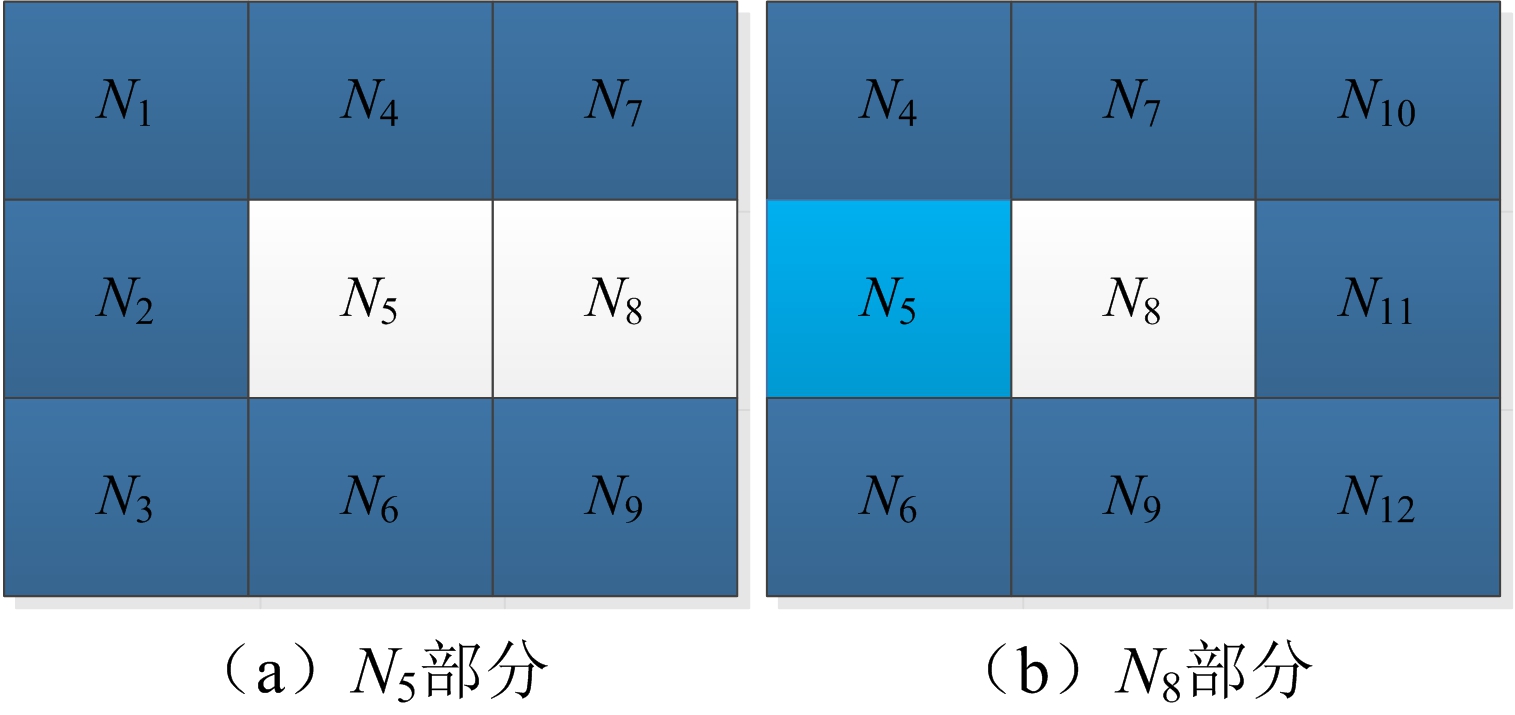
图4 E2误差点分割示意图
图4中N5周围的8个点中N8是不可靠点,其他7个点是可靠点。这种情况下,要舍弃N8点的作用,可以用(1,2),(1,4),(4,7),(2,3),(3,6),(6,9)这6对点的相关系数进行加权,得到N5的构造值![]() ,即
,即
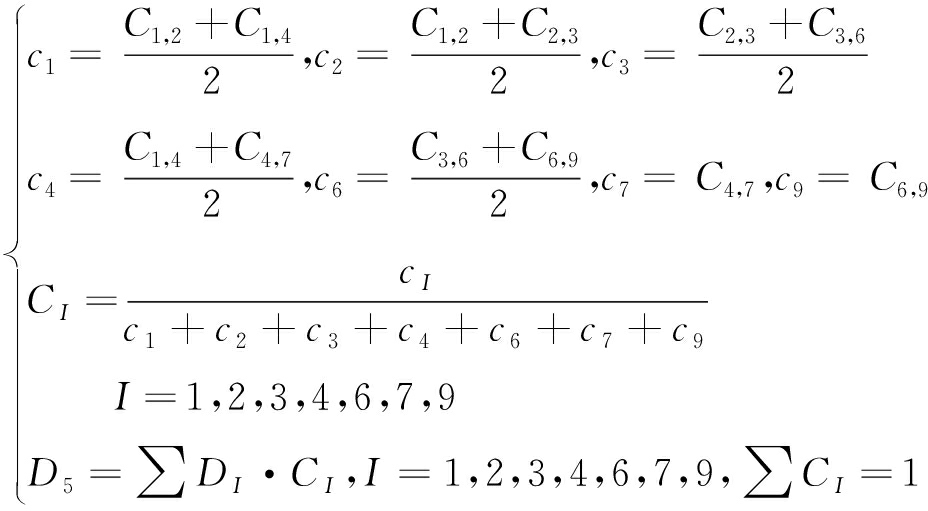
(16)
根据式(16),得到重构N5的值![]() ,然后可以利用
,然后可以利用![]() 的值。如图4(b)所示,在得到
的值。如图4(b)所示,在得到![]() 后,可以按照E1误差点的重构方式重构N8的值。
后,可以按照E1误差点的重构方式重构N8的值。

图5 E3误差点俯视图
对于E3误差点的处理,扫描误差点3×3的区域,可能出现的所有情况如图5所示。为了尽量缩短处理时间,此处不再对以上所有情况区分对待,误差点周围所有可靠点的算术平均值代替重构值。通过至少3轮识别和重构能够将有E4误差点转化为E3误差点并进行合理重构。整个重构过程其实是一个个小的曲面叠加贴合的过程。
根据以上描述的方法,实现的算法步骤如下:
步骤1:根据缠绕相位信息计算出像素点间相位的相关系数,利用原始相位信息以及各个像素点相关系数等信息,结合图论中图的概念构造网络图;
步骤2:对初步构造的图,以图论的最大流最小割定理(max flow/min cut theory)为基础的增广路径算法求得最小费用路径;
步骤3:根据求得的路径对相位进行积分求得初步的解缠结果,并保存积分路径;
步骤4:对初步解缠结果进行第1轮误差点识别,识别出所有E1点,使用最小曲面拟合方法进行数据重构,并利用重构值沿着步骤3的积分路径修正积分路径的值;
步骤5:进行第2轮误差点识别,识别出所有E2点,使用最小曲面拟合方法进行数据重构,并利用重构值沿着步骤3的积分路径修正积分路径的值;
步骤6:进行第3轮误差点识别,识别出所有E3点,使用最小曲面拟合方法进行数据重构,并利用重构值沿着步骤3的积分路径修正积分路径的值;
步骤7:重复步骤6至少两次,识别出由E4点转而来的E3点,使用最小曲面拟合方法进行数据重构,并利用重构值沿着步骤3的积分路径修正积分路径的值。
为了验证算法的有效性和正确性,分别用枝切法、等权最小二乘法、网络流法以及改进算法进行实验,并将结果进行对比。实验分为仿真数据实验和实测数据实验。模拟数据中加入不同程度的随机噪声和椒盐噪声,构成两组不同程度的信噪比进行仿真实验,用以验证不同信噪比情况下方法的正确性和精确度[15]。评定的参数用运行时间和均方根误差(REMS)两个参数来衡量,均方根误差计算公式如式(17)所示。实验环境为Matlab R2004a,计算机运算条件为Intel(R) Xeon(R) CPU E3-1241 v3+Windows 7专业版64 bit+8 G内存。

如图6所示,模拟数据是Matlab软件中peaks函数产生模拟相位曲面,大小为512像素×512像素。对模拟曲面加入随机噪声和椒盐噪声实现信噪比(SNR)为6.11 dB和-0.51 dB的模拟数据。图7(a)是信噪比为6.11 dB仿真相位的曲面图,图7(b)是缠绕相位的俯视图。将数据进行缠绕后分别运用枝切法、等权最小二乘法、网络流法和新方法进行解缠仿真。解缠结果如图8所示,运行结果如表1所示。
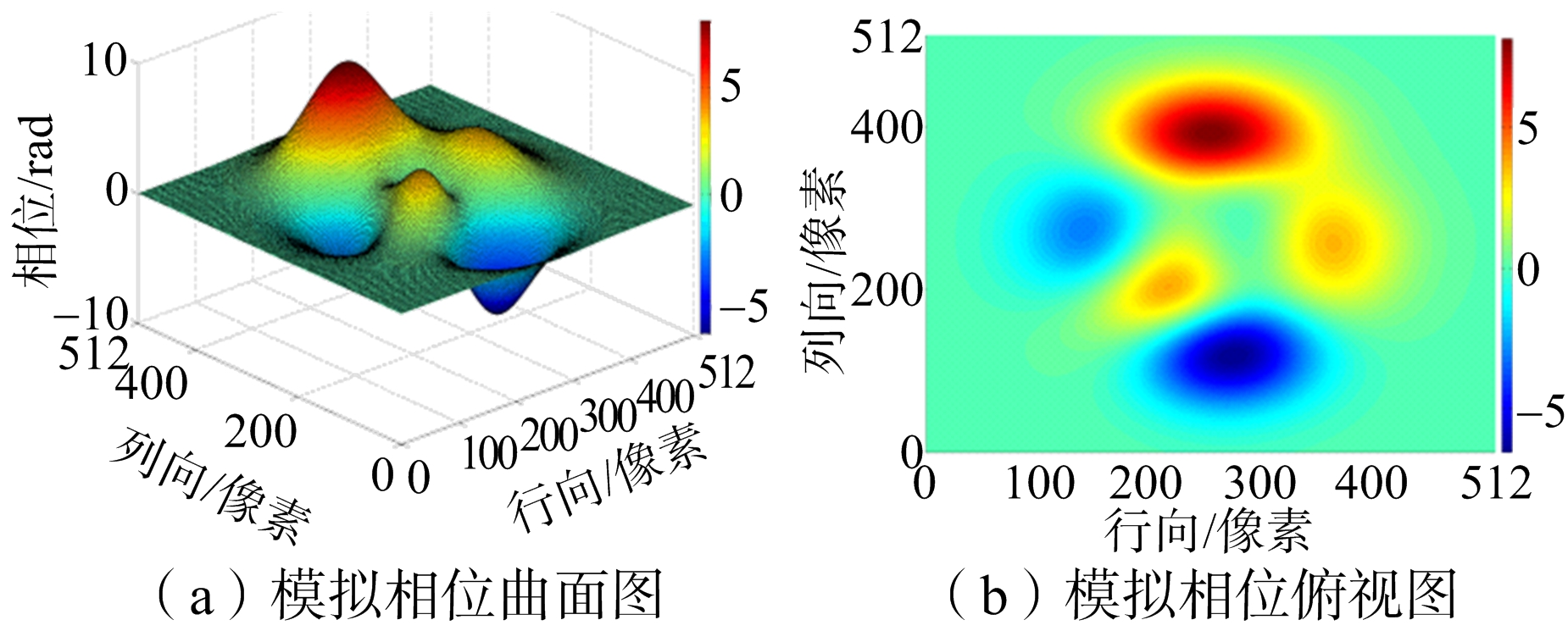
图6 模拟数据示意图
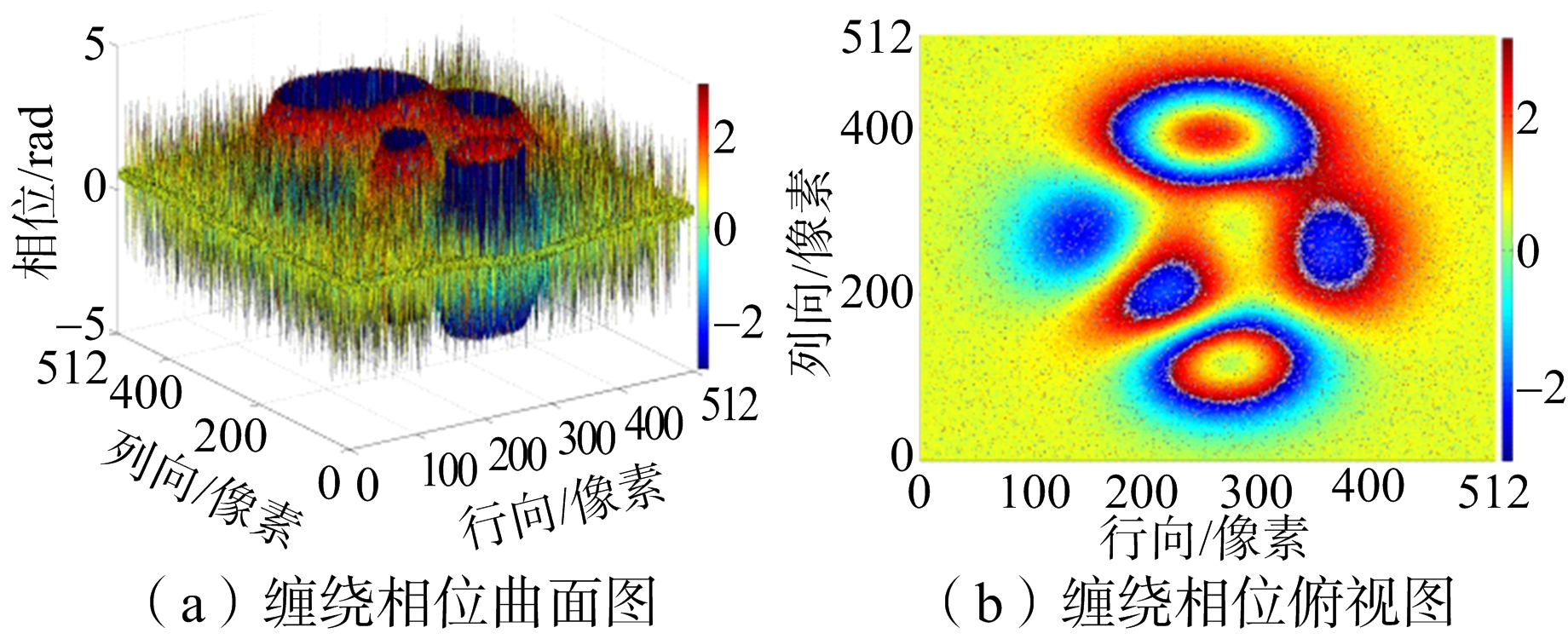
图7 SNR=6.11 dB缠绕相位图
表1SNR=6.11dB结果汇总表
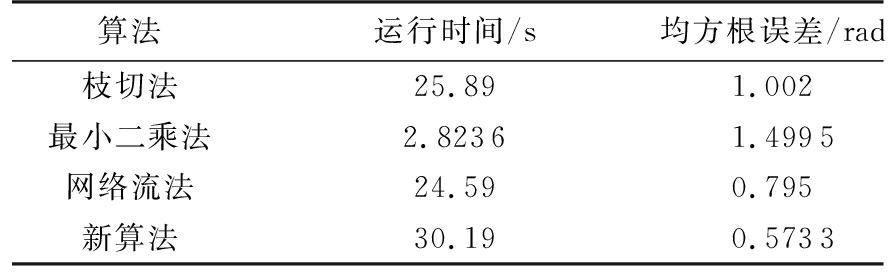
图9(a)是信噪比为-0.51 dB模拟数据的缠绕图,图9(b)是图9(a)的俯视图。将数据分别运用枝切法、最小二乘法、网络流法和新算法进行解缠仿真。解缠结果如图10所示,仿真运行结果汇总如表2所示。
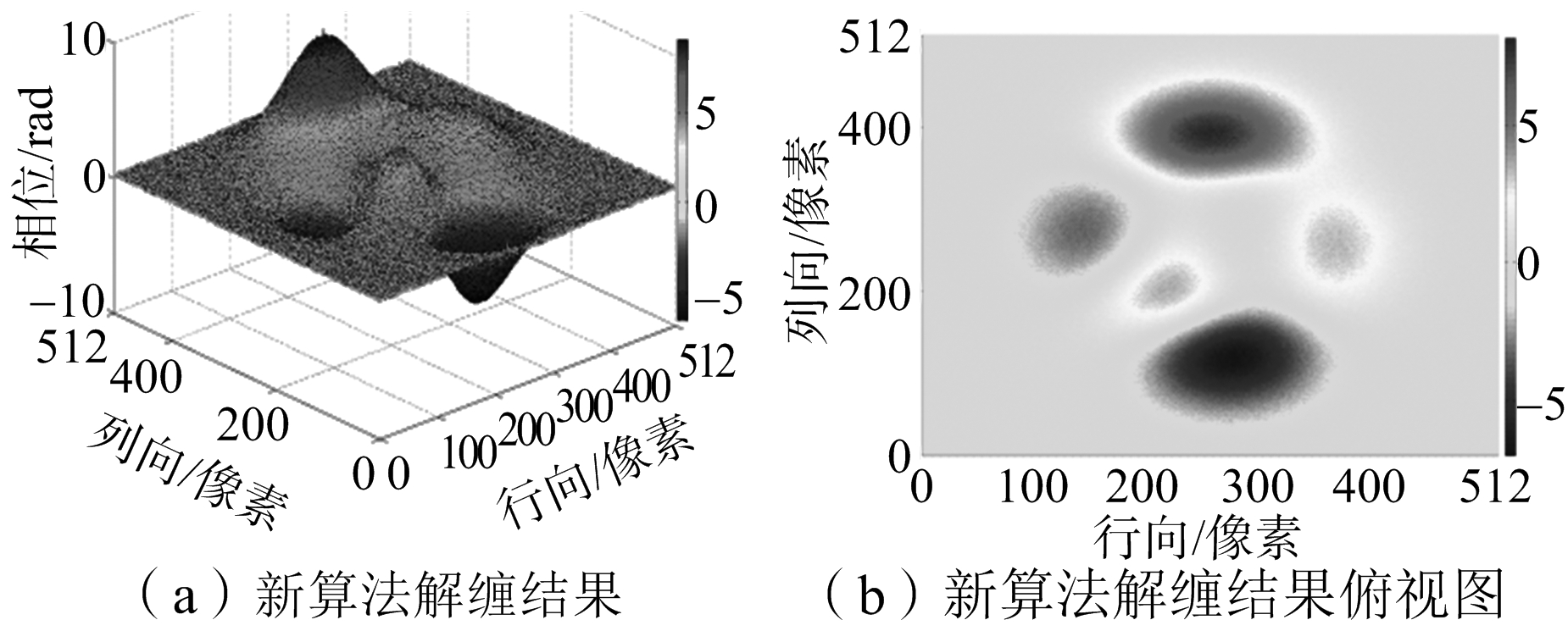
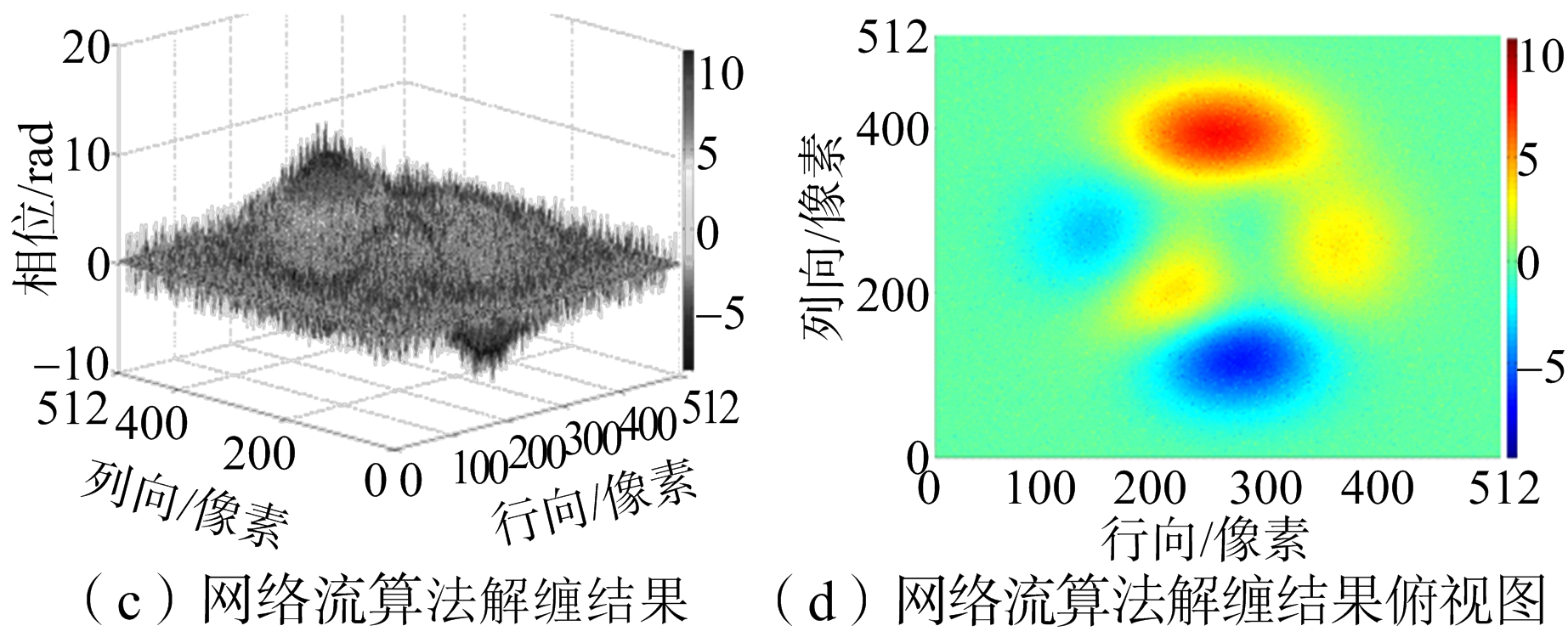
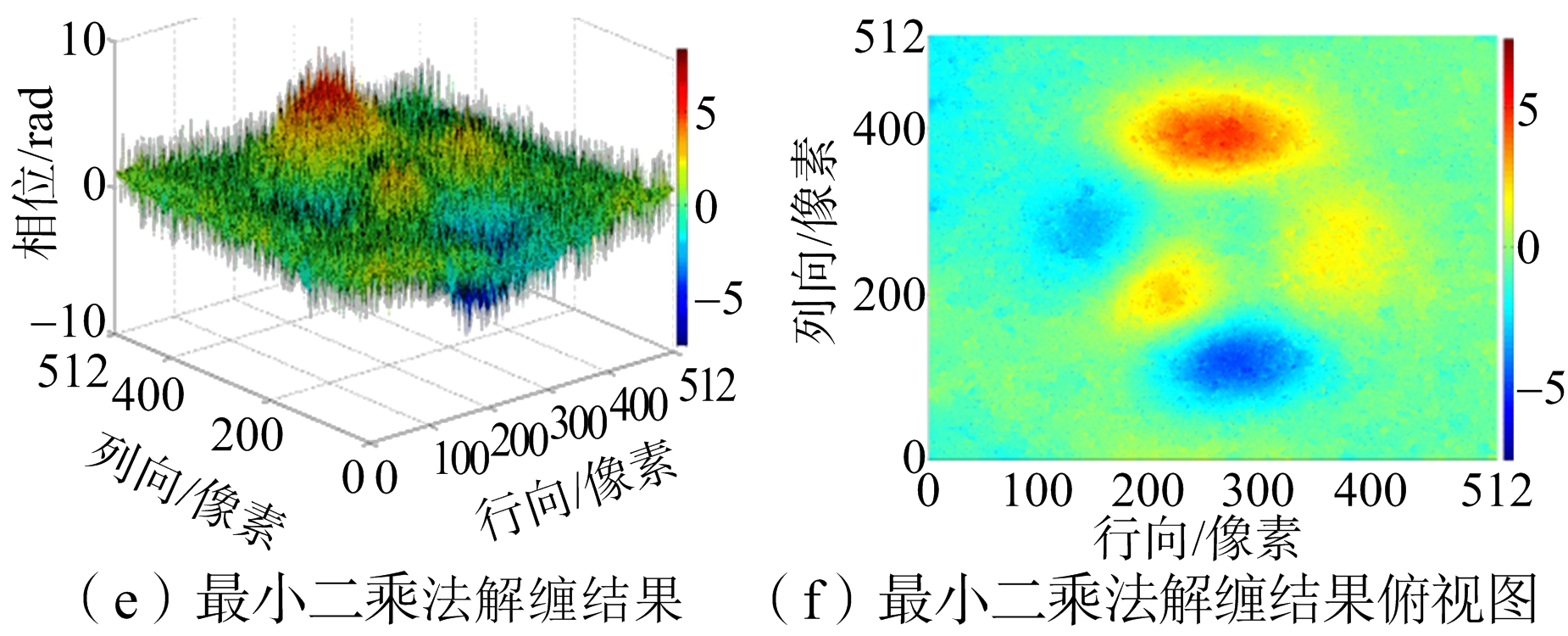
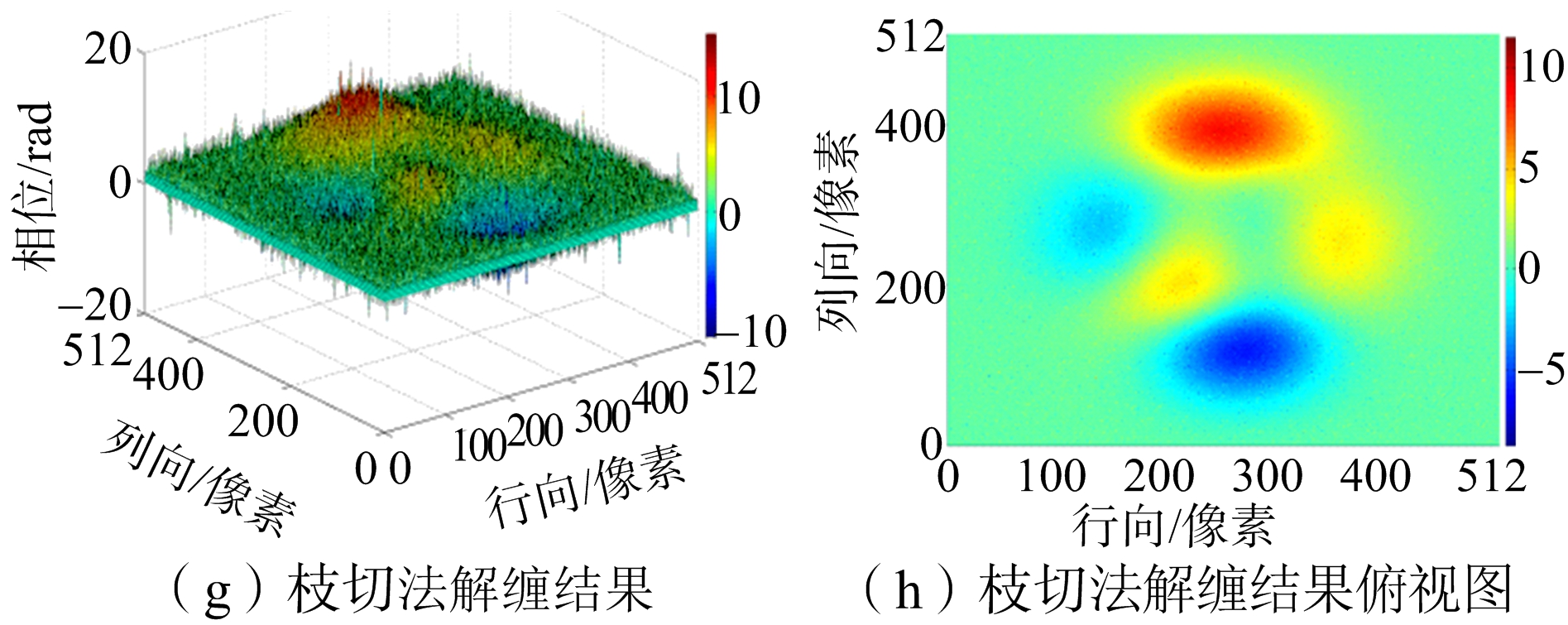
图8 SNR=6.11 dB模拟数据实验结果
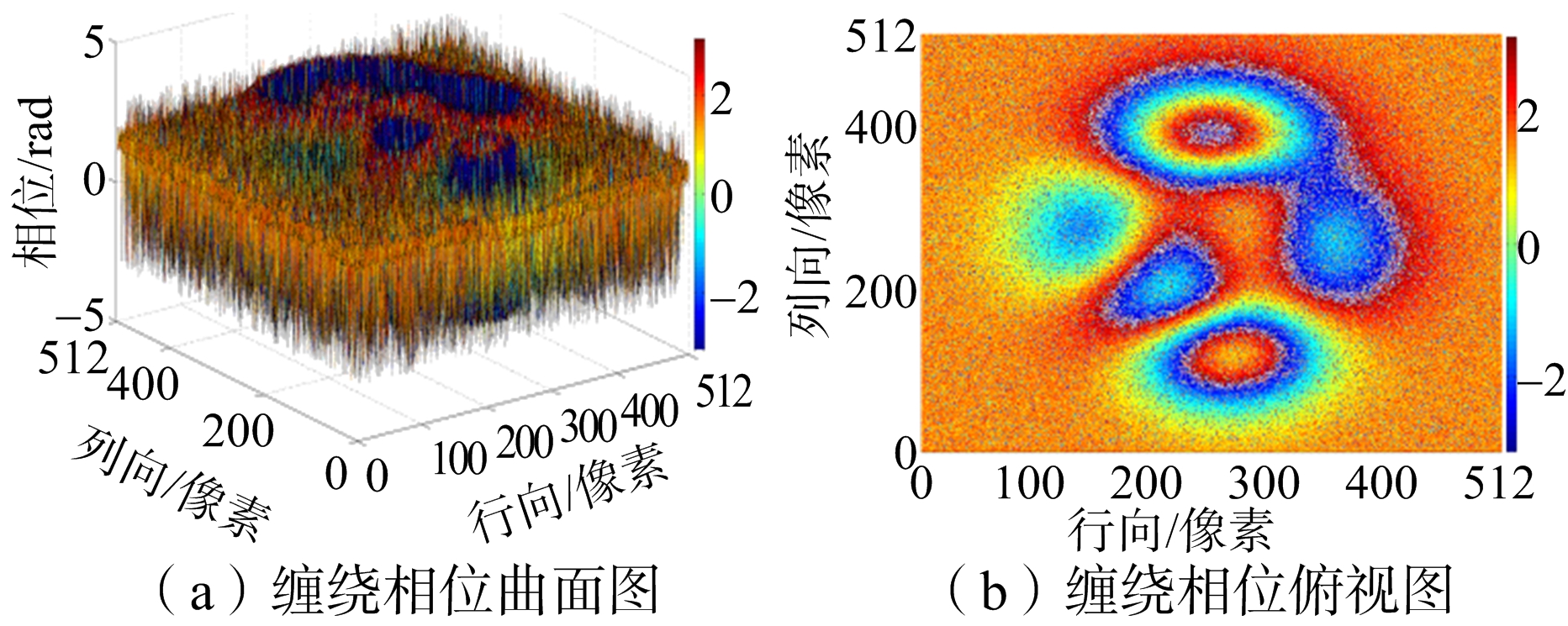
图9 SNR=-0.51 dB缠绕相位图
表2SNR=-0.51dB结果汇总表
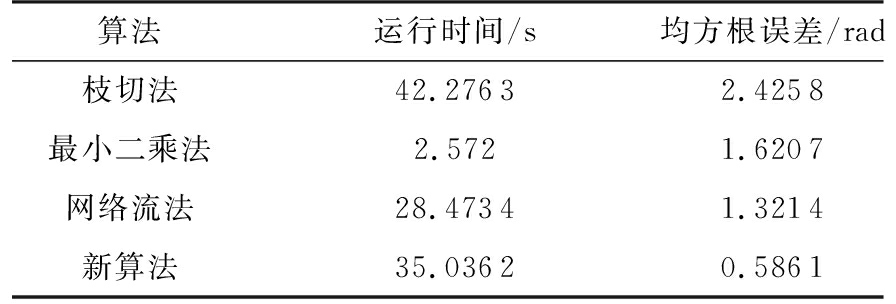
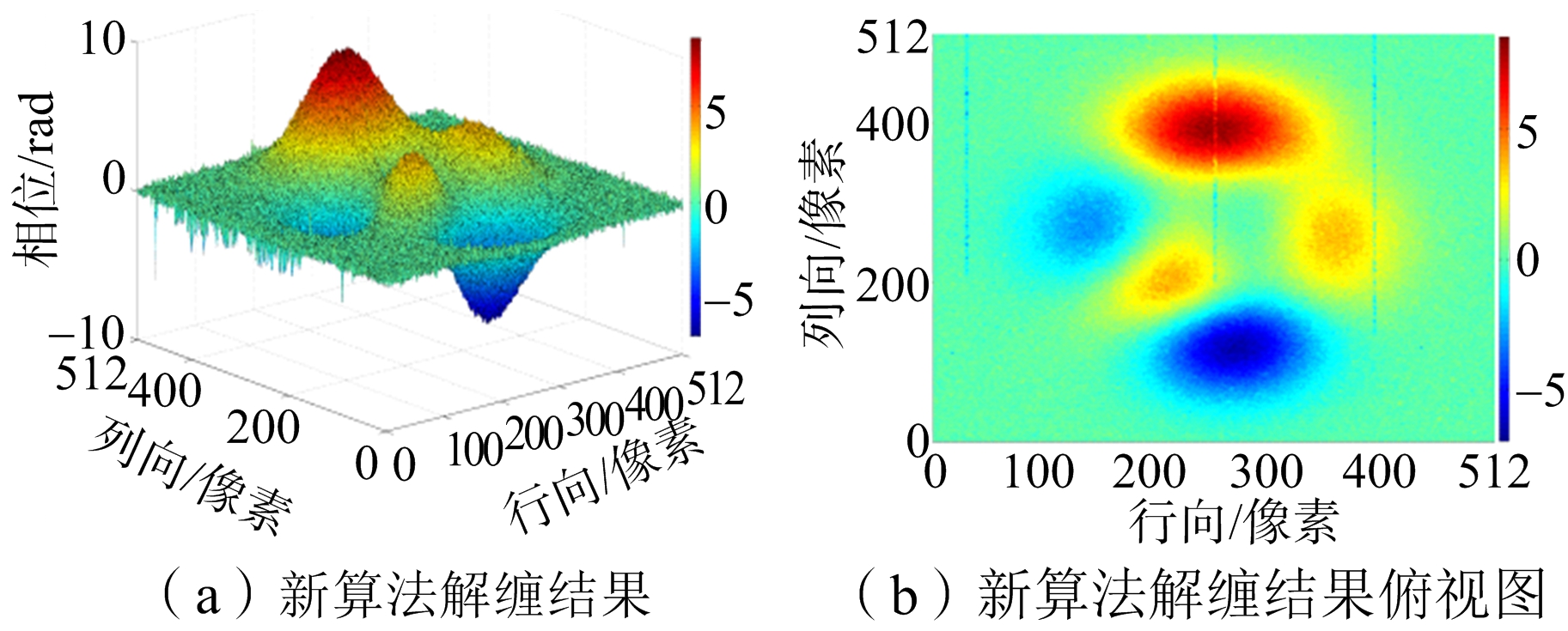
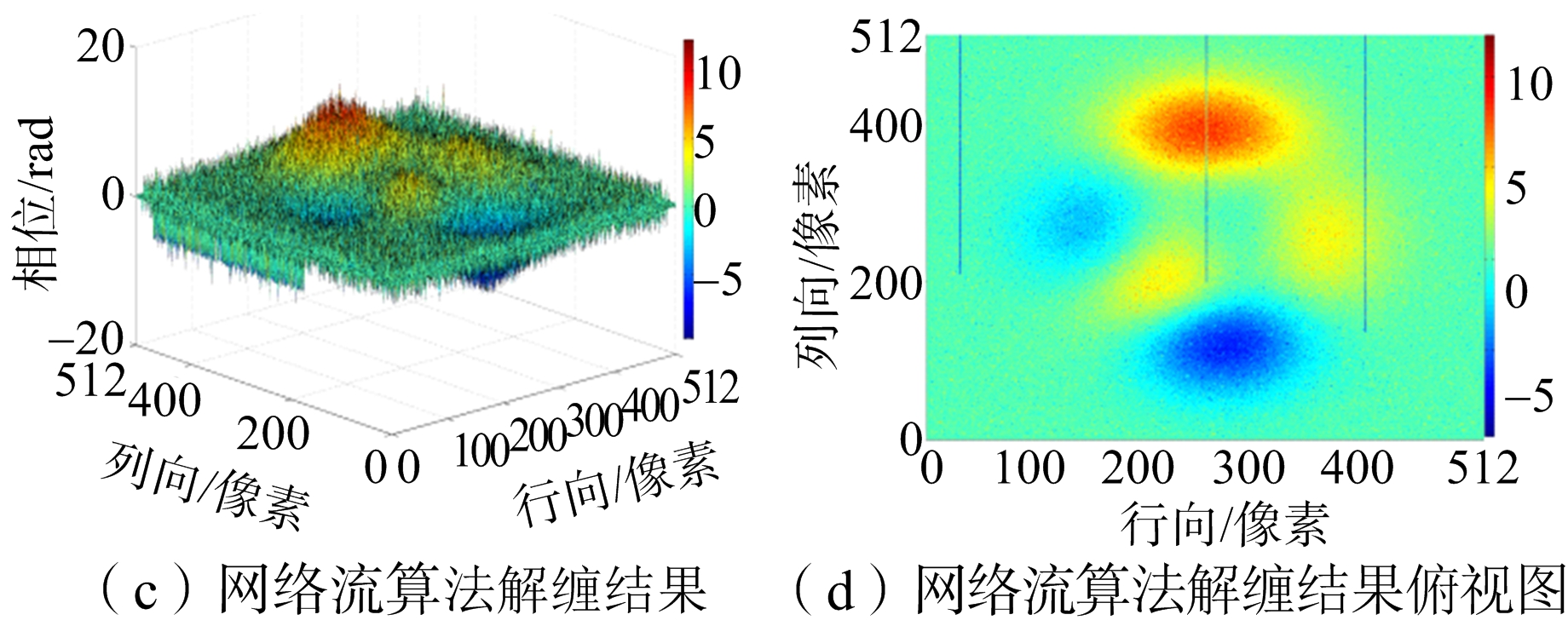
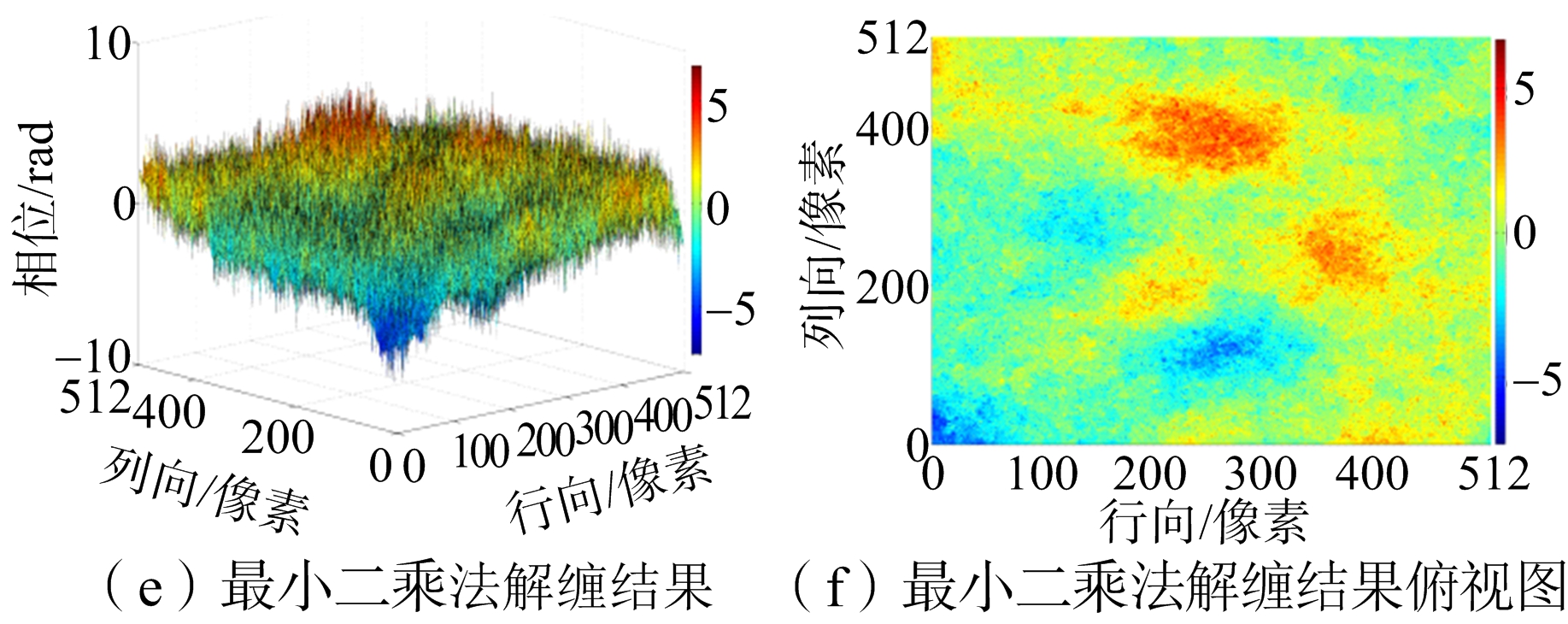
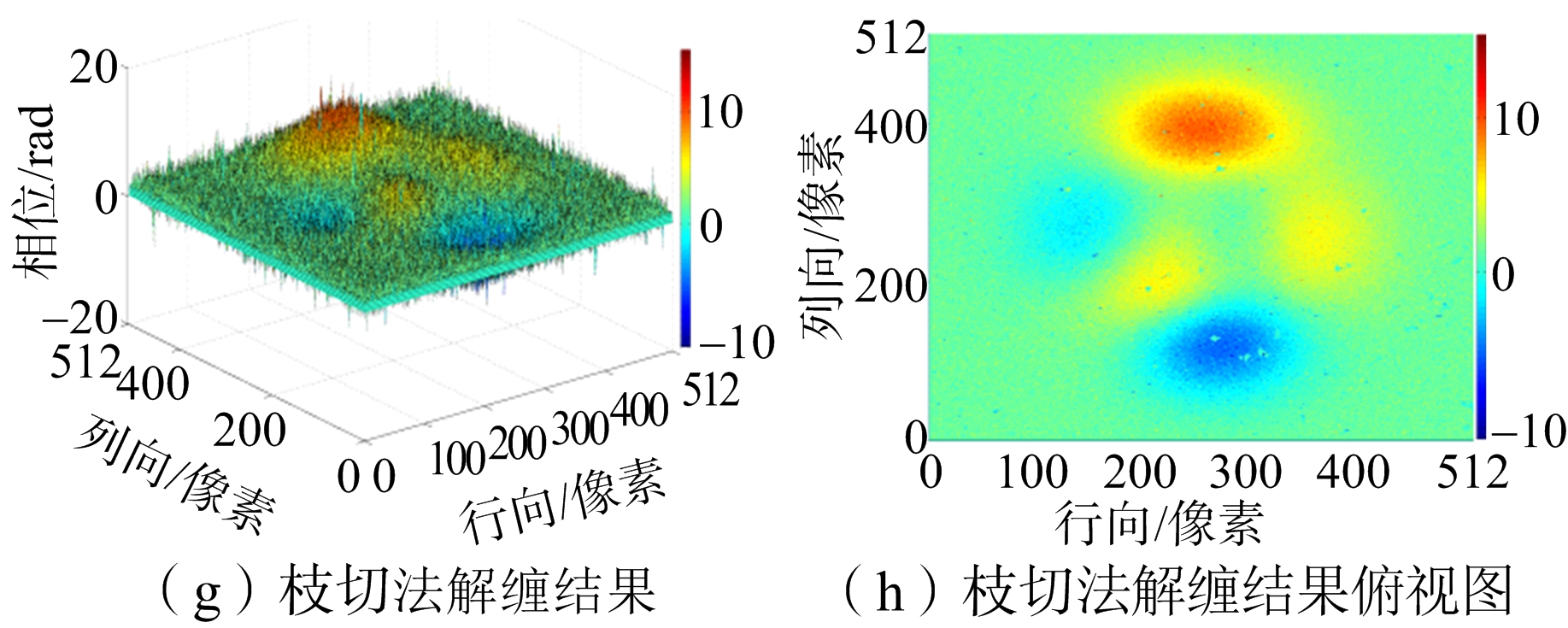
图10 SNR=-0.51 dB模拟数据实验结果
第二组数据是真实孔径雷达数据实验,来自欧洲航天局(European Space Agency)官方网站提供的2009年4月6日意大利奎拉地震ASAR数据。取2009年3月11日轨道号为36 756和2009年4月15日轨道号为37 257的地震前后两次ASAR数据进行配准、干涉处理等操作得到的真实相位干涉数据,原始实验数据实际的地理位置如图11(a)所示,数据截取如图11(b)所示的512像素×512像素大小的图像。对截取的数据分别运用4种解缠方法进行解缠实验,实验结果同样取运行时间作为评价标准。由于真实实验缺乏原始的连续相位信息,很难直接用均方根误差定量比较解缠结果的好坏,所以这对于实测数据用反缠绕均方差作为评价标准。反缠绕相位均方根误差是将相位进行反缠绕[10],把求得反缠绕相位和原始缠绕相位的均方根误差σ作为解缠精度评价的指标之一,其计算公式如式(18)所示,其中![]() 表示反缠绕相位。该指标实质是评价解缠前后的主相位值的保持性。解缠结果如图12和表3所示。
表示反缠绕相位。该指标实质是评价解缠前后的主相位值的保持性。解缠结果如图12和表3所示。
σ
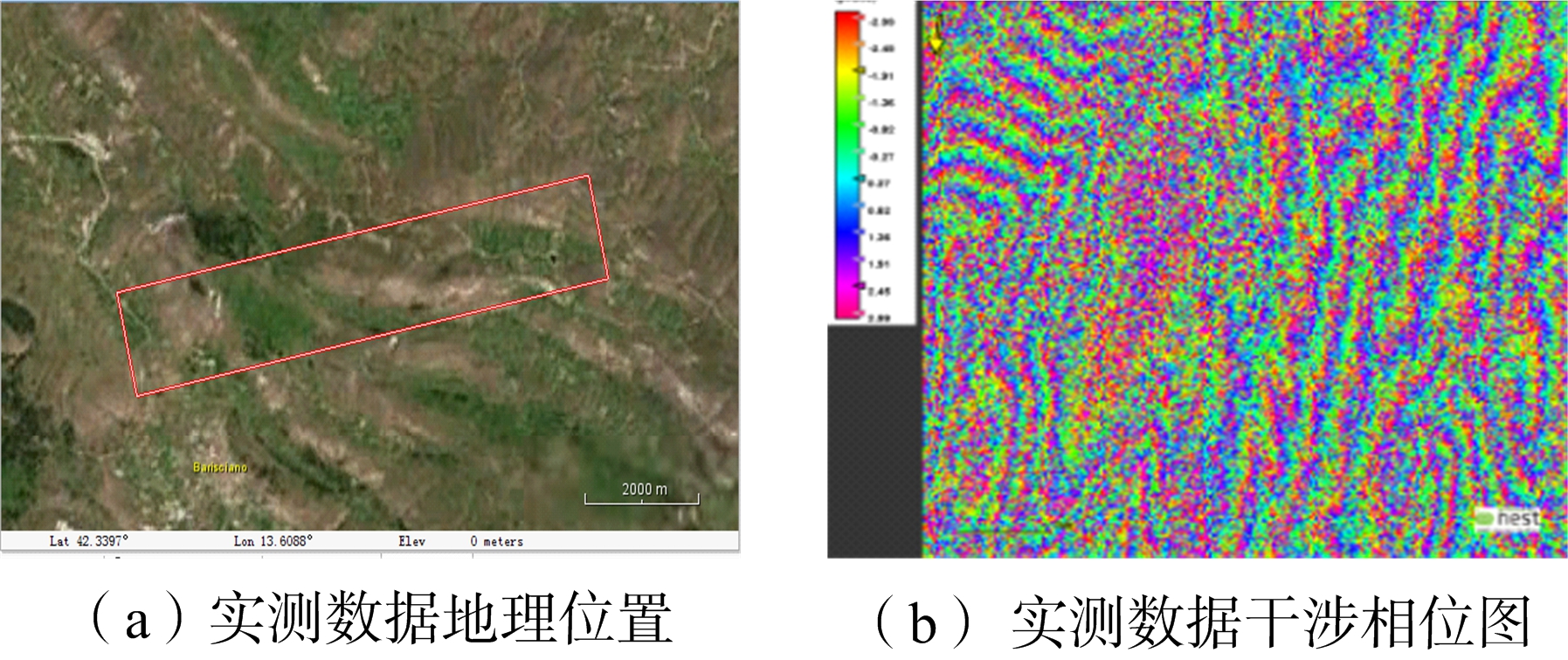
图11 实测数据
表3实测数据结果汇总表
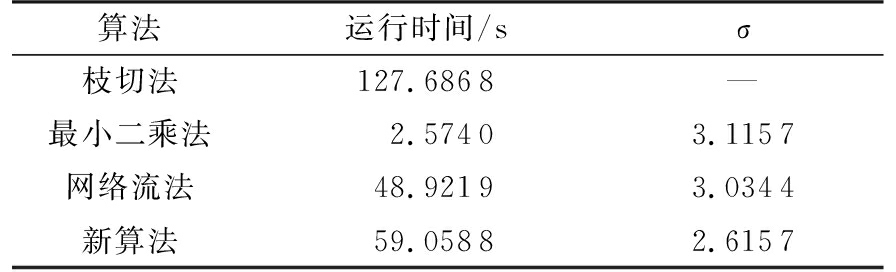
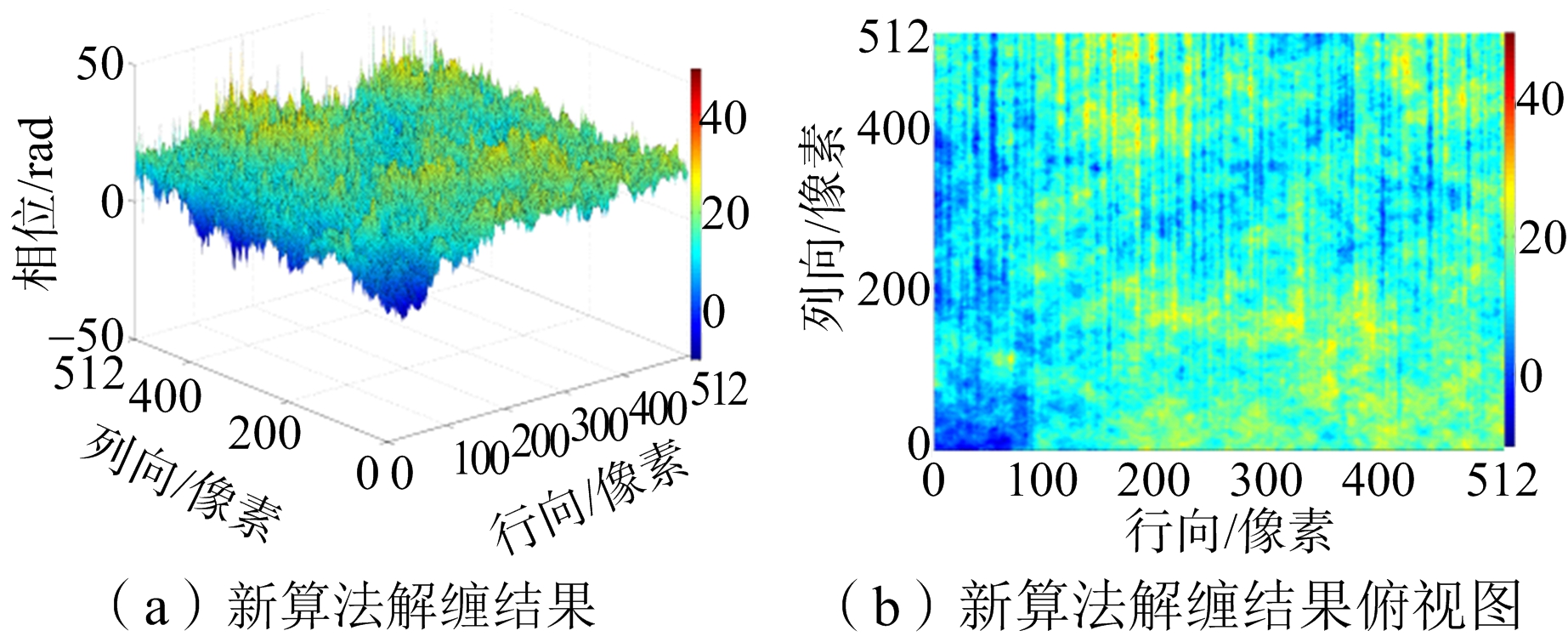
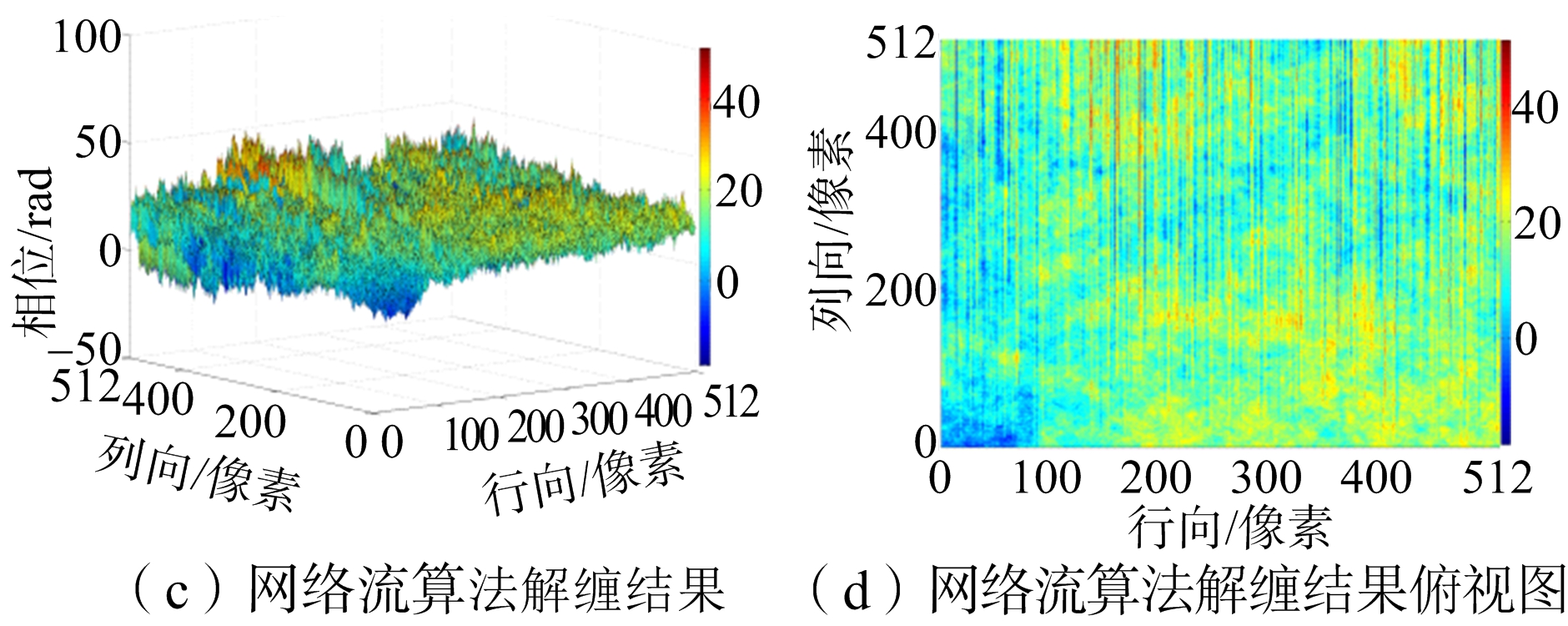
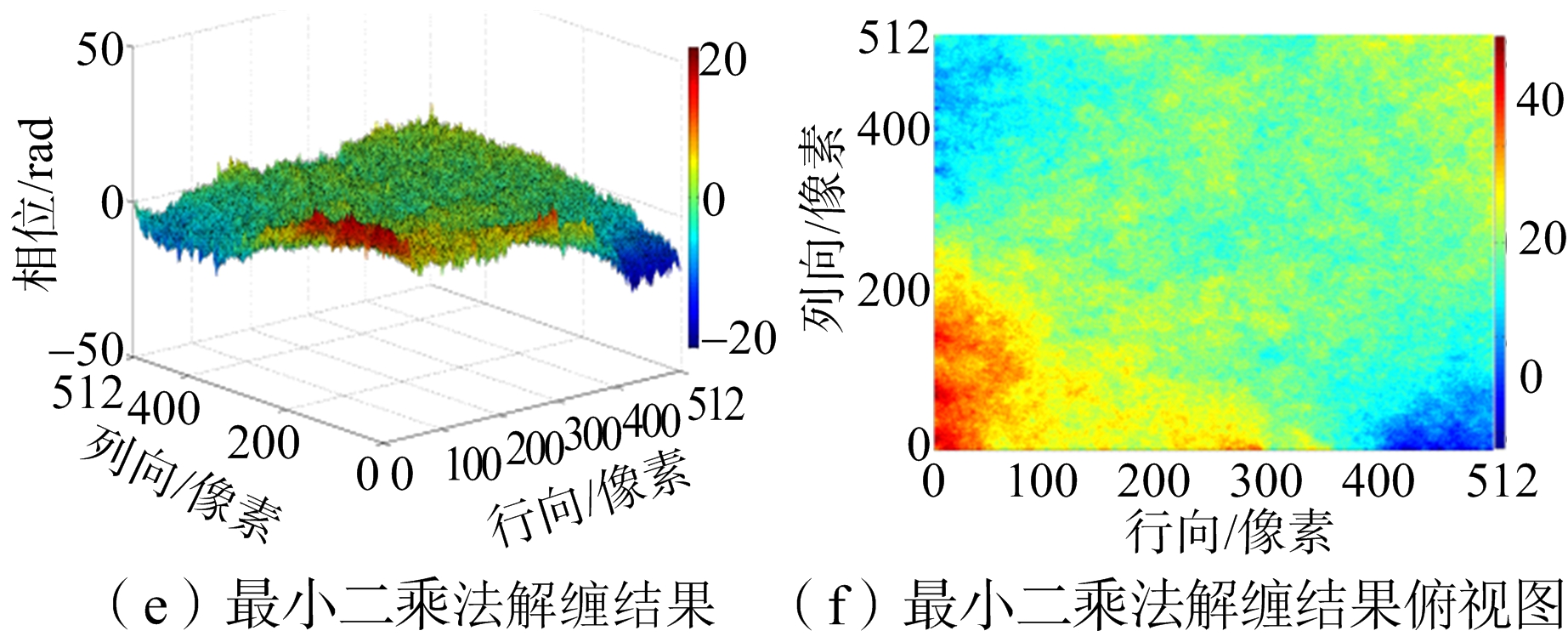

图12 实测数据实验结果
从实验结果图8、图10和图12可以看出,枝切法的解缠结果中容易出现“解缠孤岛”。因为实测数据残差点过多,枝切法解缠结果图12(g)明显是错误的。从解缠结果的俯视图可以明显看出,最小二乘法的解缠结果精度不高。网络流算法有效避免了“解缠孤岛”的出现,而且对相位曲面有较好的还原,但是存在大量的“尖峰毛刺”现象,影响了结果的精度。新算法的结果对相位曲面的还原效果是最好的,而且有效改善了网络流结果尖峰毛刺现象。从表1、表2和表3结果汇总可以看出,最小二乘法的运行速度最快但是误差最大。枝切法的运行时间比最小二乘法要长很多,解缠结果精确度要比网络流的低,而且有解缠失败和“解缠孤岛”的现象发生。网络流算法速度和枝切法的速度相当,精确度较高。新算法运行时间比其他方法稍长,但解缠精度最高,模拟数据实验和实测数据实验的结果都要比网络流解缠结果的误差提高至少10%以上。
本文的方法借鉴枝切法思想,采用网络流法和曲面拟合的方法,对网络流算法增加了最小曲面拟合的步骤。以最小的时间代价,利用网络流解缠算法过程中的中间参数和初步解缠结果,对噪声引起的错误进行了可靠重构,并沿着解缠积分路径更正了积分过程中误差的传递。无论从模拟数据实验还是真实数据实验来看,新方法都大大地增加了相位解缠精度,并证明了方法的可靠性,相比其他方法具有一定的优越性。
参考文献:
[1] XING S,GUO H.Temporal Phase Unwrapping for Fringe Projection Profilometry Aided by Recursion of Chebyshev Polynomials[J].Applied Optics,2017,56(6):1591-1602.
[2] SHEVKUNOV I. A New Phase Unwrapping Method[J].2016,737(1)[012065]:1-5.
[3] YU Hanwen,LAN Yang.Robust Two-Dimensional Phase Unwrapping for Multibaseline SAR Interferograms: A Two-Stage Programming Approach[J].IEEE Trans on Geoscience and Remote Sensing,2016,54(9):5217-5225.
[4] GOLDSTEIN R M,ZEBKER H A,WERNER C L.Satellite Radar Interferometry: Two-Dimensional Phase Unwrapping[J].Radio Science,2016,23(4):713-720.
[5] BIOUCAS-DIAS J M,VALADAO G.Phase Unwrapping via Graph Cuts[J].IEEE Trans on Image Processing,2007,16(3):698-709.
[6] FOMARO G,SANSOSTI E.Two Dimensional Region Growing Least Squares Phase Unwrapping Algorithm for Interferometric SAR[J].IEEE Trans on Geoscience and Remote Sensing,1999,37(5):2215-2226.
[7] ZEBKER H A,LU Y.Phase Unwrapping Algorithms for Radar Interferometry: Residue-Cut,Least-Squares and Synthesis Algorithms[J].Journal of the Optical Society of America A: Optics,Image Science and Vision,1998,15(3):586-598.
[8] COSTANTINI M. A Novel Phase Unwrapping Method Based on Network Programming[J].IEEE Trans on Geoscience and Remote Sensing,1998,36(3):813-821.
[9] XIE Xianming.Enhanced Multi-Baseline Unscented Kalman Filtering Phase Unwrapping Algorithm[J]. Journal of Systems Engineering and Electronics,2016,27(2):343-351.
[10] RIVERA M,HERNANDEZ-LOPEZ F J,GONZALEZ A.Phase Unwrapping by Accumulation of Residual Maps[J].Optics and Lasers in Engineering,2015,64:51-58.
[11] GHIGLIA D C,ROMERO L A.Robust Two-Dimensional Weighted and Unweighted Phase Unwrapping that Uses Fast Transforms and Iterative Methods[J].Journal of the Optical Society of America A: Optics,Image Science and Vision,1994,11(1):107-117.
[12] 刘志敏,张景发,罗毅,等.InSAR相位解缠算法的实验对比研究[J].遥感信息,2012(2):71-76.
[13] WANG Chisheng,DING Xiaoli,LI Qingquan,et al. Using an Integer Least Squares Estimator to Connect Isolated InSAR Fringes in Earthquake Slip Inversion[J].IEEE Trans on Geoscience and Remote Sensing,2016,54(5):2899-2910.
[14] DE SOUZA J C,OLIVEIRA M E,DOS SANTOS P A M. Branch-Cut Algorithm for Optical Phase Unwrapping[J].Optics Letters,2015,40(15):3456-3459.
[15] XIE Xianming.Iterated Unscented Kalman Filter for Phase Unwrapping of Interferometric Fringes[J].Optics Express,2016,24(17):18872-18897.
JIANG Liubing1,2, LIU Yongji3, CHE Li1,2
(1.GuangxiKeyLaboratoryofWirelessWidebandCommunicationandSignalProcessing,Guilin541004,China; 2.SchoolofComputerandInformationSecurity,GuilinUniversityofElectronicTechnology,Guilin541004,China; 3.SchoolofInformationandCommunication,GuilinUniversityofElectronicTechnology,Guilin541004,China)
Abstract:Phase unwrapping is a key step of signal processing in interferometric synthetic aperture radar.The unwrapped results can be strongly influenced by noise and under-sampling.The network flow algorithm can effectively suppress noise in high coherence region,overcome the side effect of ‘island’ phenomenon,and confine the error transfer to a very small range.However,spikes and glitches still exist in the results.Combining with the concept of residues,the surface fitting method and the network flow algorithm,this paper proposes a new phase unwrapping algorithm.The new algorithm locates the noise points based on the correlation degree of neighborhood pixels,reconstructs the noise value using minimum surface fitting,and finally corrects the integral results along the integration path.Repeat the iteration until all the noise points are eliminated and many minimum surfaces are fitted repeatedly to form the final unwrapping result.Results obtained from the simulated data and the measured data show that the proposed method not only achieves better solution with an acceptable time consumption,but also weakens the spikes and glitches as well as restrains the error transfer of the unwrapping process, increasing the precision of phase unwrapping.
Keywords:interferometry; phase unwrapping; network flow; minimum surface fitting
DOI:10.3969/j.issn.1672-2337.2018.05.012
基金项目:国家自然科学基金(No.61561010);广西自然科学基金(No.2017GXNSFAA198089);广西科学研究与技术开发计划项目;广西教育厅科研立项项目(No.KY2015LX096)
修回日期:2018-01-18
收稿日期:2017-11-22;
文章编号:1672-2337(2018)05-0539-08
文献标志码:A
中图分类号:TN958
作者简介:

蒋留兵 男,1973年生,江苏泰兴人,1997年于电子科技大学获得学士学位,2006年于南京理工大学获得硕士学位,桂林电子科技大学研究员,硕士生导师,主要研究方向为雷达信号处理。