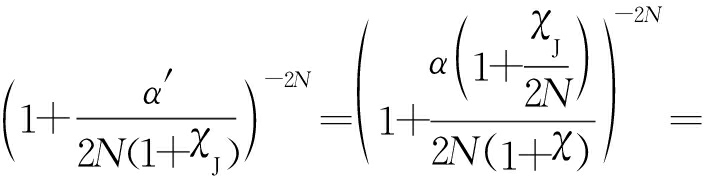一种CFAR检测雷达的可控干扰新方法
贵彦乔,吴彦鸿
(航天工程大学, 北京 101416)
摘要:针对目前常见恒虚警(CFAR)检测雷达干扰方法所产生干扰效果单一的问题,提出一种基于多相位分段调制的干扰方法。对该方法的基本原理进行说明,推导干扰信号的脉压输出结果,基于单元平均恒虚警检测方法,分析了该方法对CFAR检测雷达的干扰效果。最后进行仿真与分析,说明该干扰不仅可以形成压制干扰,还能够形成假目标欺骗干扰,并且通过对分路数、调制相位数以及调制相位值三个参数的变化,可以实现对假目标数与假目标幅值的控制,是一种灵活可控的干扰方法。
关键词:恒虚警检测雷达; 多相位分段调制干扰; 压制干扰; 假目标欺骗干扰
0 引言
恒虚警(Constant False Alarm Rate,CFAR)检测是雷达信号处理中一个重要的处理环节[1],该处理可以避免由于干扰环境的改变而引起的雷达虚警率恶化,大大提高了雷达对杂波和噪声压制干扰等非相干干扰的抑制性能[2]。如何对CFAR检测雷达进行有效干扰已成为学者研究的热点。
目前,对CFAR检测雷达的干扰方法以相干干扰为主,主要包括移频干扰和间歇采样转发干扰[3-4]。移频干扰不需要较大干信比就可以产生假目标欺骗干扰效果,然而该方法需要对接收到的雷达脉冲进行存储后再移频转发,导致假目标滞后于真目标时间较长,容易被敌方识别[5-6]。间歇采样直接转发干扰[7]能够解决移频干扰所形成假目标滞后时间过长的问题,该干扰可以产生多个强度不同的假目标,但是由于假目标间隔均匀且数量较少,可以被有效鉴别,间歇采样重复转发干扰[8]的提出改善了间歇采样直接转发干扰形成假目标数较少的缺陷,然而这是通过牺牲干扰信号相干性实现的,使得该干扰对干扰机功率提出了更高的要求。另外,不论间歇采样直接转发干扰还是间歇采样重复转发干扰,由于形成的假目标间隔均匀,均只能实现对CFAR检测雷达的压制干扰[9-10],无法形成假目标欺骗干扰。
针对以上对CFAR检测雷达干扰中存在的问题,本文提出了一种对CFAR检测雷达的多相位分段调制干扰方法,该方法不仅可以形成压制干扰,还能够形成假目标欺骗干扰,并且通过对雷达信号进行分路相位调制,可以实现对假目标数与假目标幅值的控制,是一种具有多样性和可控性的干扰样式,能够形成更可靠的干扰效果。
1 多相位分段调制干扰1.1 干扰原理
对CFAR检测雷达的多相位分段调制干扰主要分为信号分路、相位调制、信号采样、信号合成四个步骤[11],如图1所示。
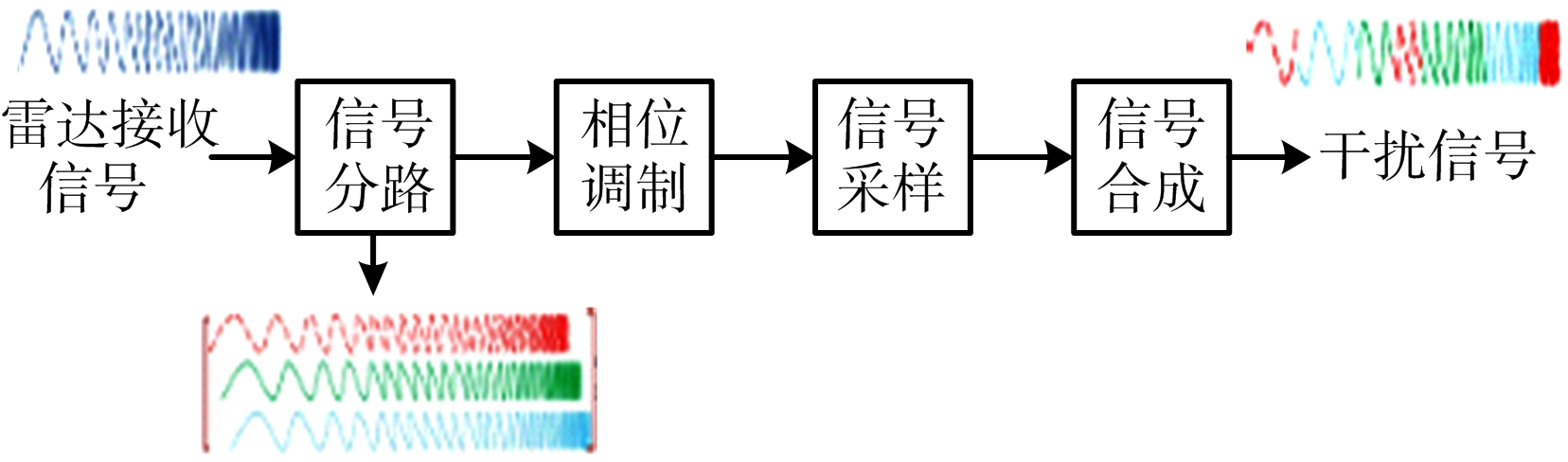
图1 多相位分段调制干扰原理图
具体步骤如下:
1) 信号分路
干扰机接收到雷达发射信号后,通过一等间距或非等间距的矩形脉冲串对存储的雷达信号进行采样,随后平移脉冲串将信号划分为NN≥2个不同分路。
2) 相位调制
在不同信号分路上按照一定的规律进行相位调制,即改变雷达发射信号波形的相位。相位调制是多相位分段调制干扰的核心环节,其具体规则如下:
① 相位调制后生成信号的总时长与雷达回波信号相等,和雷达信号的波形体制无关;
② 各分路相位调制采用的相位值可以在0,2π上随机取值,相位取值个数不少于2,并且为有限个;
③ 各分路信号的时长可以取小于雷达信号时长的任意值,并且各分路信号的时长取值可以是等分或非等分。
3) 信号采样
相位调制处理后,根据存储的子信号相位,能够对信号采样时间进行选择。对所选子信号进行实时采样,就得到了与雷达信号波形完全相同的相位调制子脉冲串。
4) 信号合成
将信号采样后、已按规律排列的各分路信号合路输出,可以在干扰时段内生成与雷达信号脉冲长度相同的干扰信号。
设CFAR检测雷达回波信号为s(t),信号分路后的各分段长度为等长τ,各分路上的相位调制值分别为φ1,φ2,φ3,…,φp,相位调制过程中,相位调制值为φ1的信号分路数为n1,所有信号分路起止时刻分别为t1si和t1ei,其余信号分段的起止时刻同理可得。
以上述参数设置为基础,用阶跃函数ε(t)表示信号各分路之间的相位调制值跳变,则多相位分段调制干扰信号等价于雷达信号与一复合函数的乘积:
sJ(t)=s(t)·p(t)
(1)
式中,
p(t)=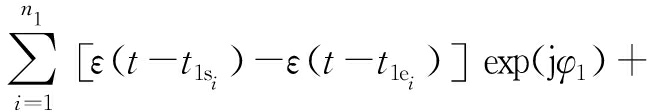 …+
…+
 σ
σ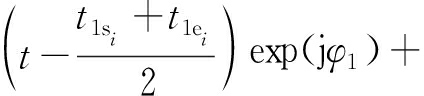 …+
…+
 σ
σ
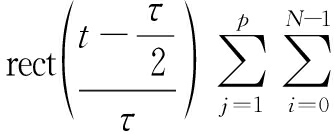 σt-iτexpjφj
σt-iτexpjφj
(2)
干扰信号总分路数N=n1+n2+n3+…+np,雷达信号脉冲时宽Tp=Nτ。
1.2 对干扰信号的脉压输出分析
设脉压过程中的环境噪声是功率谱密度为N0/2 W/Hz的高斯白噪声,输出端噪声的功率谱密度为N0/2·H0jω2W/Hz。假设脉压输出信号在t=td时刻得到峰值,则多相位分段调制干扰信号经过匹配滤波器后的输出信号表达式为
FJ(t)=
 ·
·
 \5
\5
F*jωe-jωtdejωtddω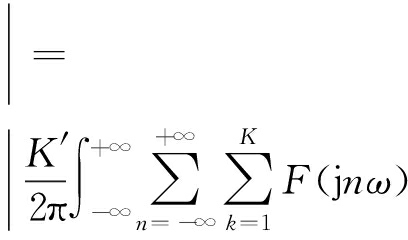 ·
·
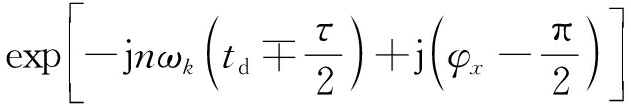 ·
·
F*jωdω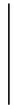
(3)
设回波信号脉宽Tp为有限值,则其在频域可以视为连续信号,那么干扰信号的匹配滤波输出信号可以进一步等效为
FJ(t)= ·
·
FJ1(t)+FJ2(t)+…+FJK(t)
(4)
设相位调制值φ1所在信号分路的带宽B1=ωH1-ωL1,由频谱偏移产生的时延量为Δt,则该分路干扰信号的脉冲压缩输出表达式为
FJ1(t)=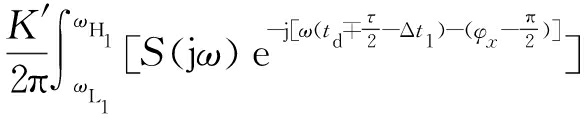 ·
·
S*jωdω=
 ·
·
 \5
\5
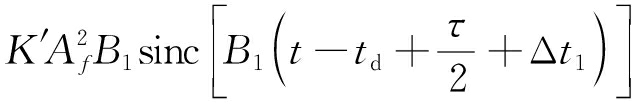 ·
·
(5)
令
(6)
-π Φ1
Φ1
(7)
则式(5)可以等价为
FJ1(t)=A1ejΦ1
(8)
将上式推广至整段干扰信号,则多相位分段调制干扰信号的脉压输出结果为

(9)
由上式可知,干扰信号的脉压输出结果可以等效为若干个信号矢量的叠加,各信号矢量的幅值与幅角与干扰信号分路数、调制相位数以及调制相位值三个参数有关。进一步分析可知,脉冲压缩后的干扰信号主瓣宽度与干扰信号分路长度成反比关系,另外,sinc函数的中心在一定范围内偏移,且偏移量与干扰信号的参数有关。
结合以上分析可得,多相位分段调制干扰可以在真实目标周围形成一定范围的局部遮盖效果,且通过对干扰信号分路数、调制相位数以及调制相位值三个参数的控制可以实现灵活多样的干扰效果。
2 对CFAR检测雷达的干扰分析
CFAR检测根据参考单元内的背景噪声、杂波以及干扰的大小来计算检测门限,从而使虚警概率处于恒定状态。典型的CFAR检测方法[12]主要包括单元平均恒虚警检测(Cell Averaging Constant False Alarm Rate,CA-CFAR)、单元平均选大恒虚警检测(Greatest of Constant False Alarm Rate,GO-CFAR)、单元平均选小恒虚警检测(Smallest of Constant False Alarm Rate,SO-CFAR)以及有序统计量恒虚警检测(Order Statistics Constant False Alarm Rate,OS-CFAR)等,在不同的背景噪声、杂波以及干扰因素下,可以通过选择不同的CFAR检测方法,以获取最优的检测效果。针对众多不同类型的CFAR检测方法,本文基于CA-CFAR检测对CFAR检测雷达的多相分段调制干扰方法进行分析。
2.1 无干扰下的CFAR检测
在CFAR检测中,各待检单元xi对应的保护单元位于其两侧,设CFAR检测器中共有2N个相邻的参考单元,且待检测单元两侧各有N个参考单元,各单元内的噪声独立同分布。CFAR检测的参考单元分布如图2所示。

图2 CFAR检测参考单元示意图
无干扰下,CFAR检测器的输入由雷达回波信号和噪声组成,设噪声为服从指数分布[13],且独立同分布的高斯白噪声,则经过平方律检波后,某待检单元中样本数据xi的概率密度函数为
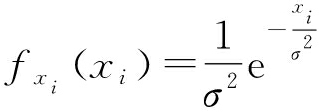
(10)
式中,σ为噪声的标准差。
推广至2N个参考单元,则由xi组成的样本矢量xx1,x2,…,x2N的联合概率密度函数为
(11)
式中,σ2的最大似然估计值[14]为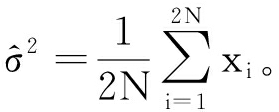
因此,无干扰下的CA-CFAR检测要求的检测门限为
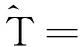 α
α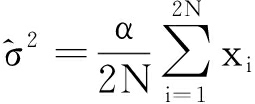
(12)
对于给定的检测门限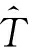 ,待检单元的检测概率PD的均值[15]为
,待检单元的检测概率PD的均值[15]为
(13)
式中,α为门限乘积因子, 为平均虚警概率,二者满足关系α
为平均虚警概率,二者满足关系α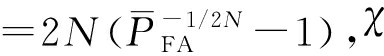 为雷达回波信号的信噪比。
为雷达回波信号的信噪比。
2.2 多相位分段调制干扰下的CFAR检测
对雷达实施多相位分段调制干扰时,CFAR检测器的输入为雷达回波信号、干扰信号以及噪声的叠加,设多相位分段调制干扰信号的干扰功率为γJ,则根据式(12)可知,多相位分段调制干扰下的CA-CFAR检测门限为
(14)
式中,αJ=α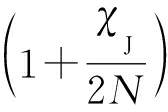 为多相位分段调制干扰下的门限乘积因子,
为多相位分段调制干扰下的门限乘积因子, J=γJ/σ2为多相位分段调制干扰信号的干噪比。
J=γJ/σ2为多相位分段调制干扰信号的干噪比。
将式(13)、式(14)结合可知,多相位分段调制干扰下的CA-CFAR检测概率 为
为
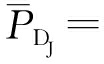
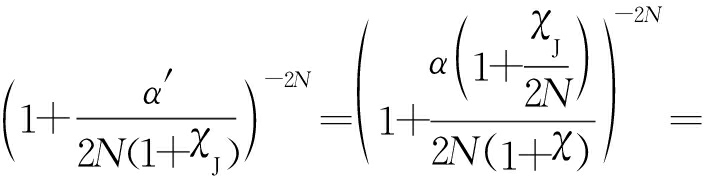
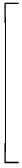 1+
1+
 -2N
-2N
(15)
对式(15)进一步分析可知,当虚警概率 和参考单元数2N一定时,多相位分段调制干扰下的CA-CFAR检测概率主要受干噪
和参考单元数2N一定时,多相位分段调制干扰下的CA-CFAR检测概率主要受干噪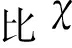 J的影响,即增大干信比(JSR)的取值,将抬升CA-CFAR检测门限,从而降低雷达对真目标的检测概率。
J的影响,即增大干信比(JSR)的取值,将抬升CA-CFAR检测门限,从而降低雷达对真目标的检测概率。
值得一提的是,由于多相位分段调制干扰功率远大于噪声功率,只要CA-CFAR检测器的参考单元中出现假目标,其检测门限就可以被抬升。在干信比(JSR)一定时,通过对多相位分段调制干扰的信号分路数、调制相位数以及调制相位值三个参数的控制,使参考单元内的假目标数增多,导致检测门限被抬升得越高,从而使雷达对真目标的检测性能恶化越严重。
3 仿真分析
3.1 实验一:干噪 J对雷达CFAR检测的影响
J对雷达CFAR检测的影响
设CA-CFAR的参考单元数目2N=36,虚警概率PFA=10-6,信噪比取值范围为0~35 dB,将无干扰下的CFAR雷达检测概率与多相位分段调制干扰信号的干噪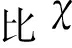 J分别取10,20和30 dB下的CFAR雷达检测概率进行仿真对比,仿真结果如图3所示。
J分别取10,20和30 dB下的CFAR雷达检测概率进行仿真对比,仿真结果如图3所示。

图3 检测概率随SNR的变化图
观察上图可知,若使雷达对目标的检测概率达到PD=0.5,无干扰下CFAR检测雷达回波的信噪比需达到13.7 dB,多相位分段调制干扰信号的干噪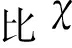 J分别取10,20和30 dB下,CFAR检测雷达回波的信噪比分别需要达14.8,19.6和28.5 dB。因此,当参考单元中存在多相位分段调制干扰时,雷达检测概率将随着干噪
J分别取10,20和30 dB下,CFAR检测雷达回波的信噪比分别需要达14.8,19.6和28.5 dB。因此,当参考单元中存在多相位分段调制干扰时,雷达检测概率将随着干噪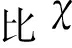 J的增大而降低,即CFAR检测雷达对真目标的检测性能逐步恶化。
J的增大而降低,即CFAR检测雷达对真目标的检测性能逐步恶化。
3.2 实验二:多相位分段调制干扰与间歇采样重复转发干扰的CFAR检测结果对比
在表1所示仿真参数设置下,干信比取30 dB,采用CA-CFAR检测器,对比多相位分段调制干扰与间歇采样重复转发干扰的CFAR检测结果,虚警概率PFA=10-6,多相位分段调制干扰采用四相位等分调制,分路数分别取20和30,各干扰信号分路的相位取值从0,π/4,2π/4,3π/4中随机选取,间歇采样重复转发干扰的采样周期Ts=2 μs、采样间隔τ=0.5 μs,仿真结果如图4所示。
表1仿真参数设置

参数名称取值参数名称取值雷达载频/GHz3FFT点数128信号带宽/MHz5信噪比/dB-3脉冲宽度/μs51信杂比/dB-8脉冲重复频率/Hz800采样率/MHz100脉冲个数100目标距离/km164.477
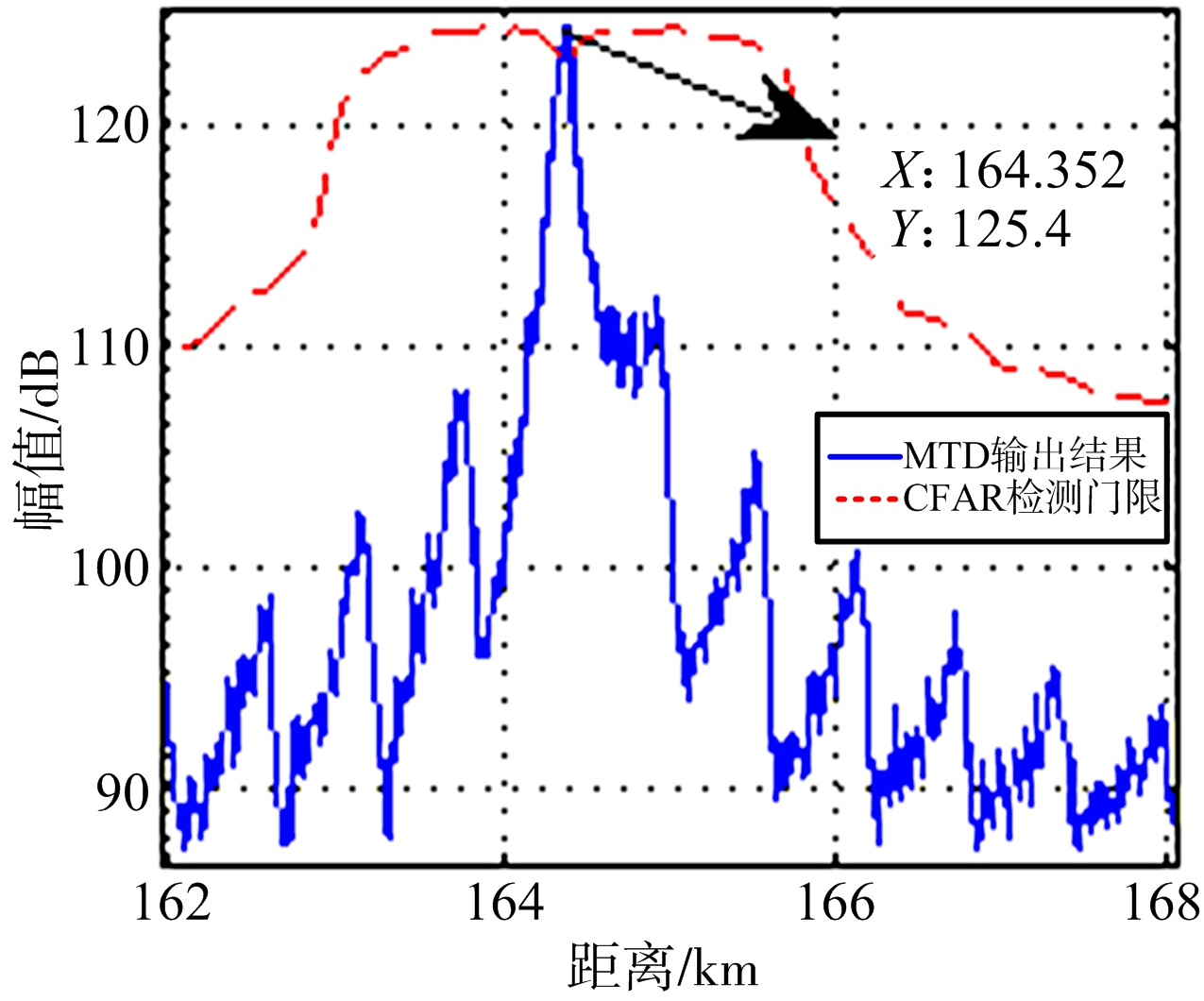
(a) 多相位分段调制干扰(20路)
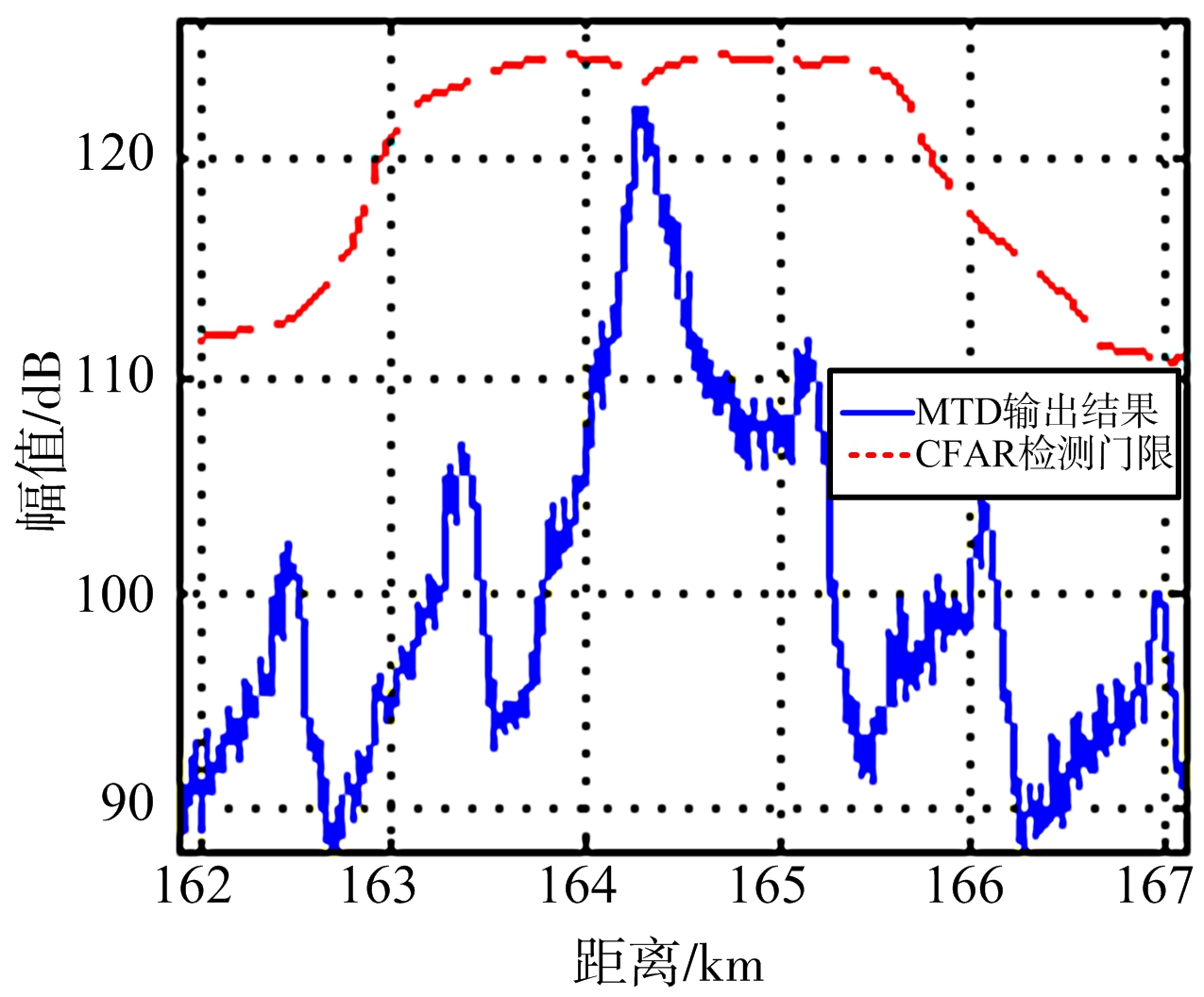
(b) 多相位分段调制干扰(30路)
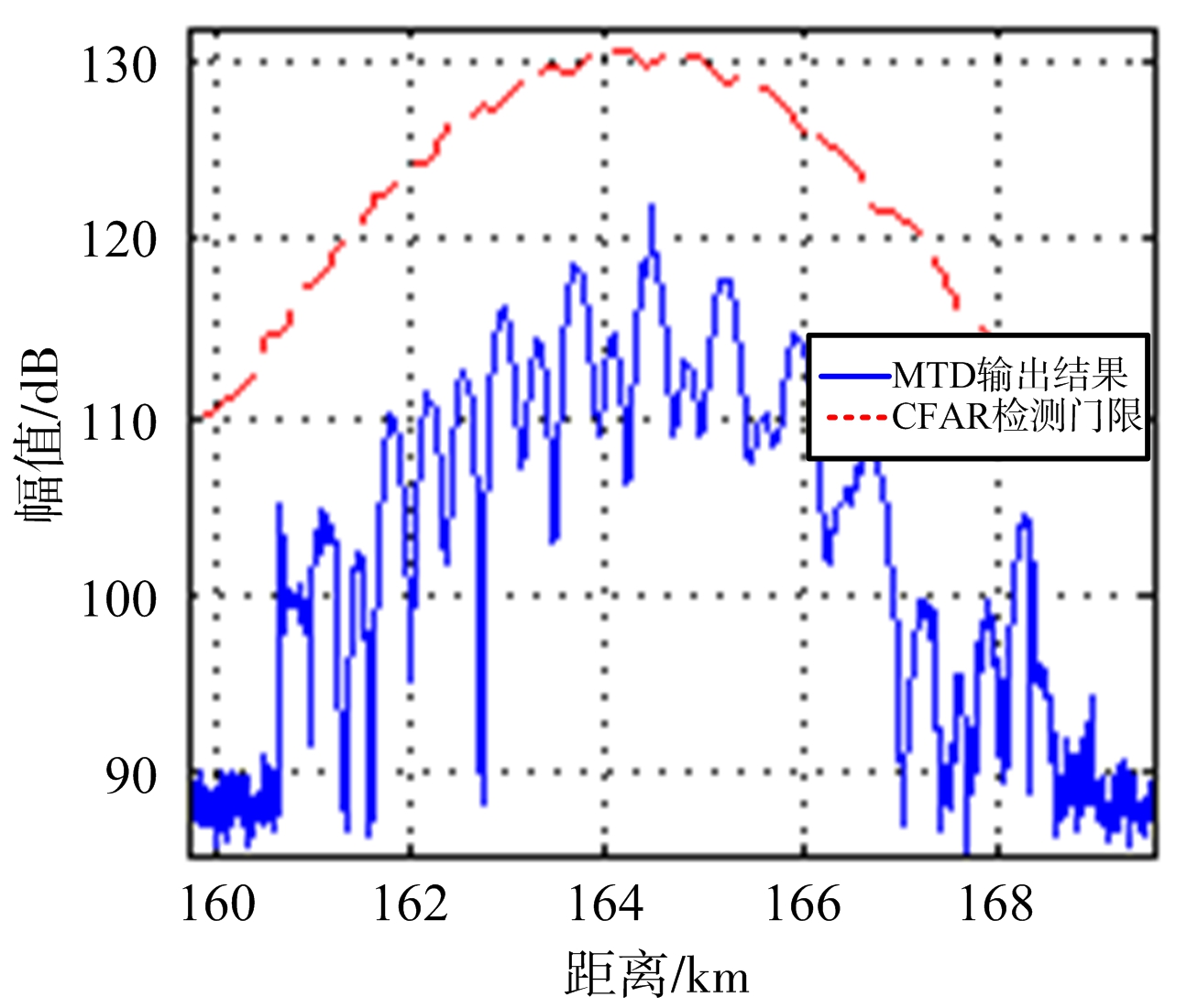
(c) 间歇采样重复转发干扰
图4 实验二仿真结果对比
观察上图可知,图4(c)中间歇采样重复转发干扰形成了数量众多的假目标,假目标分布在参考单元中使CFAR检测门限被抬升,导致雷达无法检测目标,但是由于假目标分布均匀只是形成了压制干扰效果,无法实现假目标欺骗干扰;图4(a)、图4(b)中多相位分段调制干扰破坏了雷达信号的相干性,使目标峰分裂为数量众多的子峰,子峰分布于参考单元中使检测门限升高,导致雷达无法检测到真目标,其中,分路数取30时与间歇采样重复转发干扰相似,形成了压制干扰效果,不同的是,分路数取20时雷达检测到一距离为164.352 km的目标,与真目标距离误差为-125 m,即形成了假目标欺骗干扰效果。因此,多相位分段调制干扰不仅可以对CFAR检测雷达形成压制干扰,还可以实现假目标欺骗干扰,具有多样化的干扰样式,改善了间歇采样干扰无法对CFAR检测雷达形成假目标欺骗干扰的缺陷。
3.3 实验三:不同调制参数下的多相位分段调制干扰效果变化
仿真参数设置与实验二相同,干信比取10 dB,采用CA-CFAR检测器,虚警概率PFA=10-6,由于假目标数和假目标幅度是衡量对CFAR检测雷达干扰效果的两个重要指标[16],本文在分路数、调制相位数以及调制相位值三个参数调制变化的情况下,对CFAR检测雷达的多相位分段调制干扰所形成假目标的数量和最大幅值的变化进行如下仿真,仿真结果如图5和图6所示。
1) 采用两相位等分随机调制,两个相位调制值中一个取0,在另一个相位变化的情况下,对信号分路数分别取30,50,60时,CFAR检测结果中假目标数量和最大幅值的变化曲线进行仿真;
2) 采用多相位等分随机调制,设定等间隔调制相位,在信号分路数分别取30,50,60的情况下,对调制相位数在[2,10]区间内以1为间隔取值时,CFAR检测结果中假目标数量和最大幅值的变化曲线进行仿真;
3) 采用三相位等分随机调制,信号分路数取30,本文中各调制相位值用“-”连接,3个相位调制值采用三类组合方式,分别为前两个相位值取0-π/3,0-π/4,0-π/5,第三个调制相位值以π的倍数变化。在此条件下,对CFAR检测结果中假目标数量和最大幅值的变化曲线进行仿真。

(a) 分路数变化

(b) 调制相位数变化

(c) 调制相位值变化
图5 不同调制参数变化下假目标数量的变化曲线

(a) 分路数变化

(b) 调制相位数变化
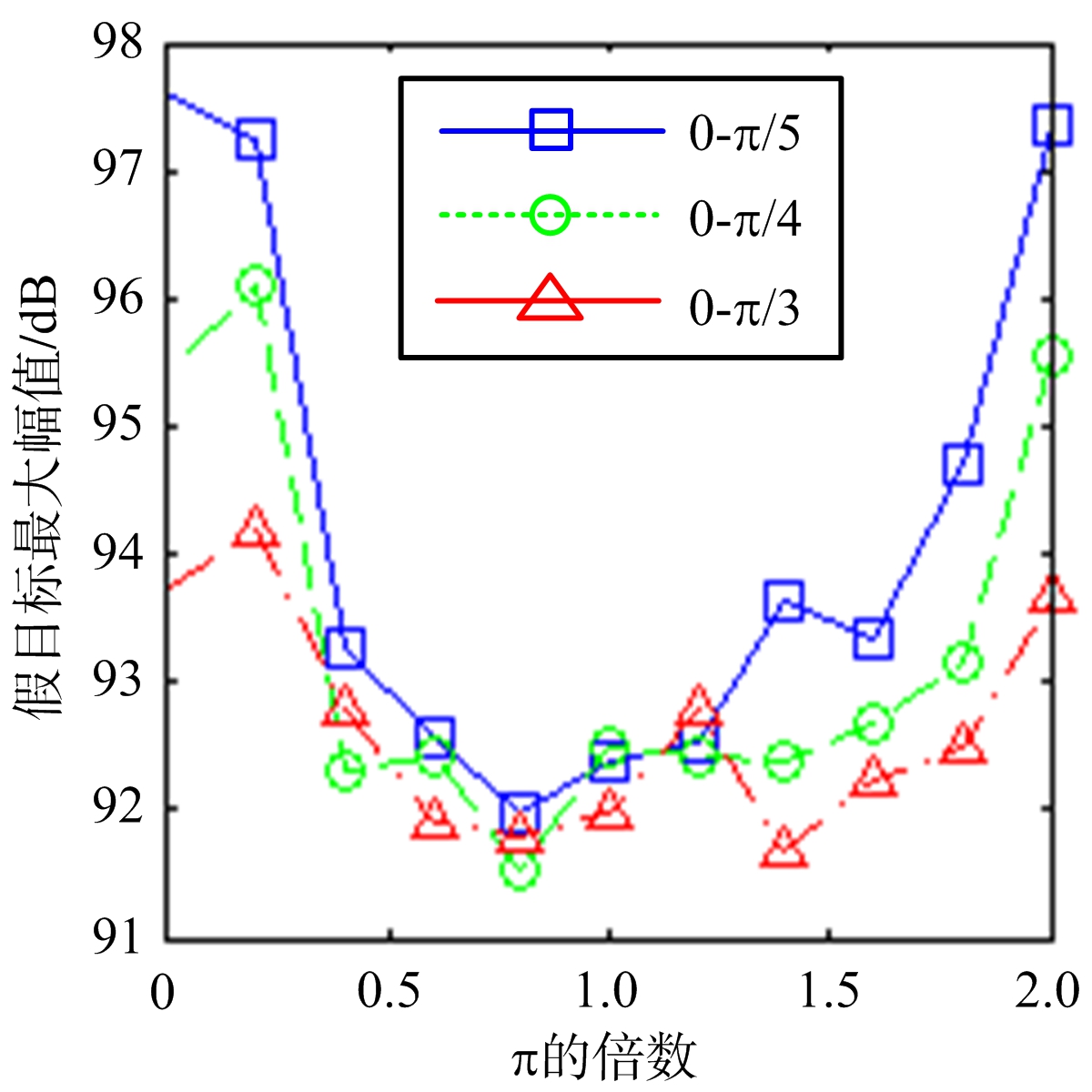
(c) 调制相位值变化
图6 不同调制参数变化下假目标最大幅值的变化曲线
对图5、图6所示仿真结果进行分析可得如下结论:
1) 不同分路数下,假目标数和假目标最大幅值的变化曲线以π为中心在[0,2π]内对称分布,[0,π/2]内假目标数与分路数成正比关系,由于假目标数越多,干扰能量分散程度越大,假目标最大幅值则与分路数成反比,[π/2,π]内假目数与分路数成反比,由于调制相位值接近π时,相位值对各分段能量分配的影响变小,该区间内假目标最大功率曲线趋于平稳。
2) 调制相位数取2~4时,假目标数与调制相位数成正比关系,假目标最大幅值与调制相位数成反比,当调制相位数超过4时,假目标数和假目标最大幅值与调制相位数的关系则反之。值得一提的是,调制相位数取2~4时,假目标最大幅值明显高于其他取值,这对于提高干扰能量利用率具有重要意义,加之调制相位数取3和4时的假目标数较多,因此调制相位数通常取3或4。
3) 不同调制相位值下,假目标数和假目标最大幅值的变化曲线以π为中心在[0,2π]内对称分布,第二个调制相位值越大,假目标数越多,相应的假目标最大幅值则越小,这是由于调制相位值越大,原始信号的相干性被破坏越严重,导致目标峰分裂出的子峰数越多,折中考虑假目标数与假目标最大幅值两个指标,实际中调制相位值可以选择0-π/4-2π/4的组合。
结合以上仿真与分析可知,多相位分段调制干扰可以实现压制干扰和假目标欺骗干扰两种干扰效果,并且通过对分路数、调制相位数以及调制相位值三个参数的变化,可以实现对假目标数与假目标幅值的控制,即对CFAR检测雷达的多相位分段调制干扰是一种具有多样性和可控性的干扰样式。
4 结束语
本文提出了一种基于多相位分段调制的CFAR检测雷达干扰方法,首先在其干扰原理的基础上,对干扰信号的脉压输出进行了推导与分析;其次以CFAR检测原理为基础,基于CA-CFAR检测方法对CFAR检测雷达的多相位分段调制干扰效果进行分析,分析表明,该干扰的脉压输出是多个信号的矢量叠加,可以有效抬升CFAR检测门限,从而降低雷达对真目标的检测概率。通过仿真分析可知,多相位分段调制干扰不仅可以形成压制干扰,还能够形成假目标欺骗干扰,并且通过对分路数、调制相位数以及调制相位值三个参数的变化,可以实现对假目标数与假目标幅值的控制,是一种具有多样性和可控性的干扰样式。如何对多相位分段调制干扰的压制范围进行控制是下一步需要重点研究和解决的问题。
参考文献:
[1] 丁鹭飞,耿富录. 雷达原理[M].3版. 西安: 西安电子科技大学出版社, 2014:128-131.
[2] PACE P E. Detecting and Classifying Low Probability of Intercept Radar[M]. 2nd ed. Boston: Artech House, 2009:81-122.
[3] 王杰贵,张鹏程. 对线性调频脉冲压缩雷达的多载波调制转发干扰[J]. 电子与信息学报, 2015, 37(11):2727-2734.
[4] 吕亚昆,杨承志,李建伟,等. 对LFM雷达的间歇采样累加干扰研究[J]. 现代防御技术, 2015, 43(1):100-107.
[5] 陈蓉,汪一鸣. 基于FRFT的LFM脉压雷达移频干扰辨识[J]. 雷达科学与技术, 2013, 11(2):192-196.
CHEN Rong, WANG Yiming. Detection of Frequency-Shifting Jamming to LFM Pulse-Compression Radar Based on FRFT[J]. Radar Science and Technology, 2013,11(2):192-196.(in Chinese)
[6] 孟超普,程林,王秀锦. 对线性调频脉压雷达的改进移频干扰研究[J]. 舰船电子对抗, 2016, 39(3):1-6.
[7] 冯德军,王伟,徐乐涛. 对V-调频信号的间歇采样转发干扰研究[J]. 雷达科学与技术, 2013, 11(2):209-213.
FENG Dejun, WANG Wei, XU Letao. Jamming V-FM Signal Using Interrupted-Sampling Repeater[J]. Radar Science and Technology, 2013, 11(2):209-213. (in Chinese)
[8] 张杨瑞,李云杰,李曼玲,等. 间歇采样非均匀重复转发实现多假目标干扰[J]. 电子学报, 2016, 44(1):46-53.
[9] 张翔,李彦志,鲁建华,等. 基于LFM雷达的时延-移频耦合性的间歇采样转发改进方法[J]. 电光与控制, 2017(3):98-101.
[10] 柳向,李东生,刘庆林. 基于OS-CFAR的LFM脉压雷达多假目标干扰分析[J]. 系统工程与电子技术, 2017, 39(7):1486-1492.
[11] YU D, WANG H, WU Y. Research on Cross-Eye Jamming Technique Based on Phase Diversity Processing[C]∥International Conference on Frontiers of Sensors Technologies, Hong Kong:[s.n.], 2016:59-64.
[12] 李志淮,谭贤四,王红,等. S-CFAR的改进型SOS-CFAR[J]. 雷达科学与技术, 2009, 7(2):135-138.
LI Zhihuai, TAN Xiansi, WANG Hong, et al. SOS-CFAR—A Modification of S-CFAR[J]. Radar Science and Technology, 2009, 7(2):135-138. (in Chinese)
[13] 吉淑娇,雷艳敏. 随机信号分析[M]. 北京: 清华大学出版社, 2014:11-12.
[14] SCHONHOFF T A, GIORDANO A A. Detection and Estimation Theory and Its Application[M]. Englewood Cliffs, NJ: Prentice Hall, 2006:175-178.
[15] RICHARDS M A. Fundamentals of Radar Signal Processing[M]. 2nd ed. New York: McGraw-Hill Education, 2014:349-352.
[16] 张克舟,李青山,陆静,等. LFM脉冲压缩雷达密集假目标干扰时序设计与分析[J]. 现代防御技术, 2015, 43(4):132-137.
ANewControllableJammingMethodforCFARDetectionRadar
GUI Yanqiao, WU Yanhong
(SpaceEngineeringUniversity,Beijing101416,China)
Abstract:Aiming at the problem that the current common jamming methods can only achieve single jamming effect on the constant false alarm rate(CFAR) detection radar, a new method based on multiple phase sectionalized modulation is proposed. Its basic principle is illustrated, and the pulse compression result of jamming signal is derived. The jamming effect of the proposed method on the CFAR detection radar is analyzed based on cell averaging constant false alarm rate (CA-CFAR) detection method. Finally, through simulation and analysis, it is obvious that this method is flexible and controllable. It can realize not only blanket jamming, but also false target deception jamming. Through the change of signal number, modulation phase number, and phase modulation value, the false target number and amplitude value can be controlled.
Keywords:constant false alarm rate(CFAR) detection radar; multiple phase sectionalized modulation jamming; blanket jamming; false target deception
DOI:10.3969/j.issn.1672-2337.2018.05.013
修回日期:2017-12-23
收稿日期:2017-10-31;
文章编号:1672-2337(2018)05-0547-07
文献标志码:A
中图分类号:TN972
作者简介:

贵彦乔 男,1993年生于甘肃白银,硕士研究生,主要研究方向为雷达信号处理。
E-mail:derrickjoe@sina.cn
吴彦鸿男,1971年生于甘肃靖远,教授、博士生导师,主要研究方向为空间信息对抗理论与技术。

 ·
·