陈泽铭
(成都中电锦江信息产业有限公司, 四川成都 610051)
摘要:海尖峰是一种离散、高幅值、极化特性强、类似小目标的海杂波,对高分辨率雷达探测海面小目标会造成严重影响。围绕海尖峰的判别介绍Posner判别准则,讨论幅度阈值、最小间隔时间、最小持续时间这3个参数的不同取值方法以及优缺点,找出Posner判别准则存在的问题并进行分析;然后在海尖峰Posner判别准则的基础上,提出采用滑窗脉冲积累的方法改进该判别准则;最后对改进前后的两种Posner判别准则的处理结果进行对比,验证了改进后的海尖峰判别准则使得海尖峰判别更加准确,减少了“毛刺”的出现,提高了海尖峰的判别精度。
关键词:海尖峰; Posner判别准则; 脉冲积累; 幅度阈值
海杂波是影响海用雷达目标探测性能的主要制约因素[1]。在部分均匀海杂波环境下,海杂波的瞬时功率波动仍然有较大起伏,导致海面目标检测的性能受到影响[2]。而海尖峰是一种离散、高幅值、极化特性强、类似小目标的海杂波。为了更好地检测海面上的小目标,高分辨率雷达越来越多地用于对海小目标检测。而对于距离高分辨对海雷达,尤其以低擦地角对海面进行照射时,海杂波时间序列幅度的概率密度函数(PDF)曲线会显示出较长“拖尾”,即高幅值海杂波序列出现的概率较大,并且具有这种特征的海杂波在空间上是离散的,在时间上不稳定且持续时间很短[3]。这是引起上述现象的原因之一,与目标的回波特性类似,导致虚警概率上升,使雷达不能准确有效地检测到目标[4]。
海尖峰的研究最初是从其表象开始的,随后才逐渐深入探索海尖峰的物理特性和统计模型[5]。Jessup等[6]通过Ku波段散射计测量海杂波,利用海杂波的多普勒谱及带宽研究海尖峰与破碎波的关系,发现80%的海尖峰与破碎波有关系。Liu等[7]通过X波段散射计测量海杂波。Melief等[8]采用阈值区分海尖峰。Walker[9]采用低通滤波器来分离海尖峰。综上研究,国内外研究人员对海尖峰从现象到判别做了大量的研究工作,但在海尖峰的量化分析方面稍有欠缺。
Posner等[10]用三准则进行海尖峰判断:幅度阈值、最小持续时间及最小时间间隔。本文基于Posner海尖峰判别准则,找出其存在的问题,然后采用脉冲积累的方法对该判别准则改进,比较两种判别准则的最终结果,发现改进后的海尖峰判别准则使得海尖峰判别更加准确,减少了“毛刺”的出现。
Posner等采用门限阈值、最小间隔时间和最小持续时间来判别海杂波中的海尖峰,具体要求为:1) 海杂波时间序列的幅值须大于门限阈值;2) 海杂波时间序列超过门限阈值的序列之间的持续时间应该大于最小给定的持续时间;3) 超过门限阈值且满足海杂波时间序列大于门限的要求后,划分小范围的海尖峰序列,尖峰间隔大于最小海尖峰间隔。
Posner等给出的判别准则中,关于幅度阈值、最小间隔时间、最小持续时间的具体取值并没有给出较为明确的标准,下面根据已有的方法讨论这3个参数的不同取值方法以及优缺点。
1.1.1 幅度阈值取值方法
关于幅度阈值的取值方法,大致有以下几种方法:
1) Greco等[11]在设置幅度阈值时,考虑单距离门时间序列间的相关性和相邻距离单元间的相关性,采用式(1)的取值方法:
(1)
式中,n为门限变量,N1为相邻参考单元的距离门数目,N2为参考距离门单元内的时间序列长度。Greco等分析IPIX数据时,取门限变量n=5,N1=1,这两个变量取值是根据实测数据特征来取,具体采用的取值准则,现在还没有具体的方法。
2) Melief等用幅值p>μ+nσ进行海尖峰判断,p为所要判断的时间序列值,μ为该参考单元里时间序列均值,σ为该参考单元里时间序列方差,n为门限变量,n的取值也是根据实测数据具体情况而定,没有具体的标准。
3) Dong等[12]将时间序列按幅值进行排序,然后取前0.1%,第0.1%对应的幅度值就是幅度阈值。
4) 利用虚警概率确定幅度阈值,这种方法应用的前提是,假设虚警目标是由海尖峰引起的。下面利用实例介绍这种阈值门限设置过程。
设雷达的归一化检测门限为Y,则基于K分布的雷达检测虚警概率Pfa(Y)为
Pfa(Y)=1-F(Y)
(2)
式中,F(·)为杂波幅度累积密度分布函数(CDF),如果杂波模型为K分布,由式(2),得到K分布的CDF表达式如下:
Fk(z)=![]() fK(t)dt=
fK(t)dt=
![]()
(3)
式中,fK(·)为K分布的概率密度函数(PDF)表达式,Kv-1为第二类Bessel函数。将式(3)代入式(2)得到K分布检测门限为Y的雷达检测虚警概率为
(4)
依据上面的虚警概率计算公式,通过IPIX实测数据进行拟合,找出1993年第54#服从K分布,如图1所示,画出K分布参数为v=1.5,b=1.72的虚警概率与门限值的关系曲线,由图2可以看出,为了达到Pfa=10-4,则采用的门限值必须高于时间序列均值的3.2倍以上。

图1 符合K分布的实测数据

图2 虚警概率与门限的关系
以上4种门限设置侧重点各有不同,第一种门限设置主要关注时间序列的均值,并且考虑相邻距离门间的相关性,门限阈值的高低取决于门限变量n;第二种门限设置主要关注的是时间序列的起伏程度的强弱,门限变量n将时间序列方差调节至适应海尖峰检测的合理取值;第三种门限设置是单纯地从最高幅值中取值,而高幅值并不代表海尖峰,所以这种方法不可取;第四种门限设置方式主要是在假定条件下,利用虚警概率与门限值的对应关系,求取的门限阈值。
1.1.2 最小持续时间和间隔取值
Posner等对最小持续时间和最小间隔时间的具体确定并没有明确的说明,Greco等分析IPIX数据中的海尖峰,根据实测数据的实际情况,假定最小持续时间为0.1 s,最小间隔时间为0.5 s。
利用上述Posner判别准则,判别IPIX雷达在1993年所测数据中的第17#数据的海尖峰。该组数据的海情:浪高为2.1 m/s,风速为9 m/s,浪向为顺浪向,擦地角为0.67°。因为该距离门内的海杂波序列服从K分布,由图2可知,取门限阈值为海杂波序列幅度均值的3倍,可使得虚警概率为10-4。取最小间隔时间为0.5 s,最小持续时间为0.1 s。
在图3中,利用门限阈值对海杂波序列进行海尖峰的初次判别,初次判别出的海尖峰序列用红色线表示,图4是对图3某一小段序列的放大图。图4中说明单脉冲通过门限阈值存在的问题:椭圆所标记的杂波序列的左右两边都超过门限阈值,而该点处幅度小于门限阈值,却被判为非海尖峰序列;而在图3中,一段海杂波序列中,出现一个幅值高于周围的海杂波序列,只有此序列高于门限而周围大部分序列却没有高于门限,利用单脉冲检测,则会以“毛刺”的形式存在。上述两种现象在单脉冲通过门限的检测中是不可避免的,因此干扰海尖峰判别。
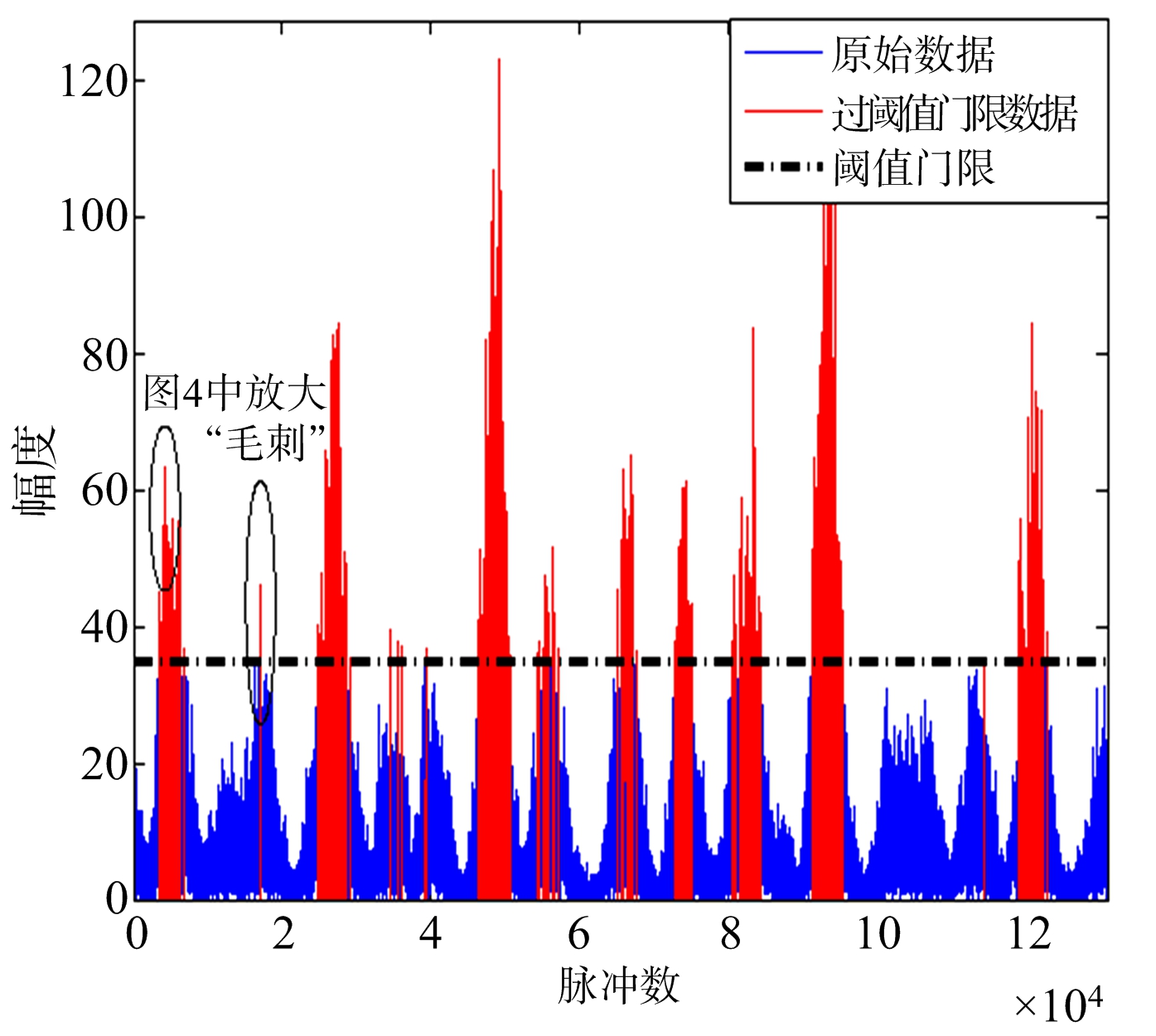
图3 取绝对值后阈值门限检测
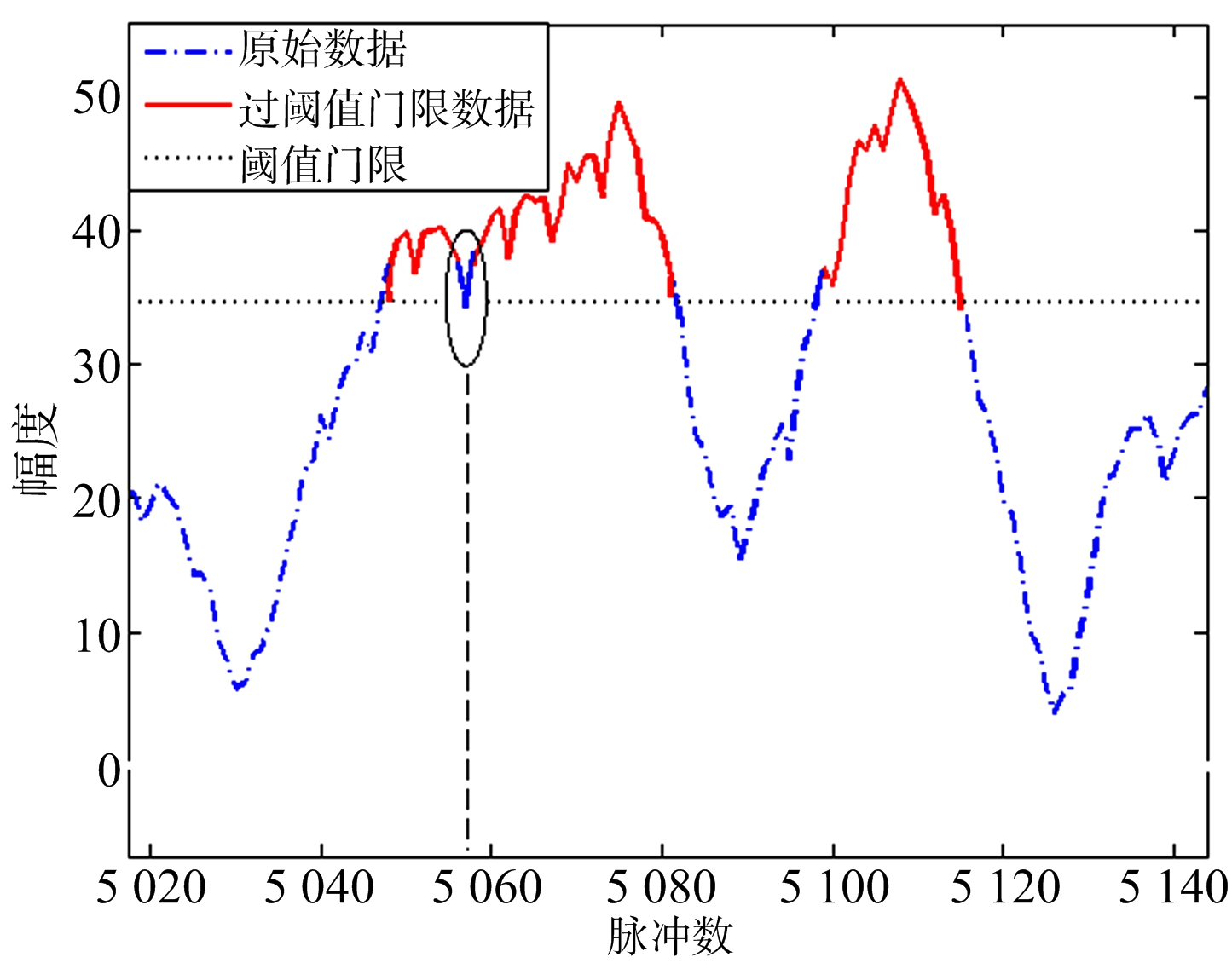
图4 图3部分区域放大图
由上述Posner检测结果中发现,检测出的海尖峰中有“毛刺”,并且使得海尖峰序列不连续,为此进行改进。
为了减小上述检测方法对海尖峰判别的影响,借鉴目标检测中采用的脉冲积累方法进行改进。具体方法为:将时间序列以一定的时间窗滑动叠加,门限阈值是原来门限值乘以该时间窗长度,然后比较滑动叠加后的时间序列幅值与门限阈值,高于门限阈值的,判定为海尖峰序列。该时间窗长度根据海杂波的散斑相关时间来确定,海杂波的散斑相关时间为10 ms左右,而IPIX雷达的脉冲重复频率(PRF)为1 000 Hz[13],所以采用长度为10个脉冲数进行滑动积累,如图5所示。相对应地,将图5中的部分序列进行放大,得到图6,椭圆处标记序列在这种检测算法下被判定为海尖峰,而且图3中判定为海尖峰的“毛刺”在图5中没有被判别为海尖峰。比较图4和图6,改进后可以得到两个明显效果:第一,经过脉冲积累的滑动计算,使得最终的时间序列较原始数据平滑;第二,在经过幅度阈值检测时,避免了一些小“毛刺”的出现,而且利用多个脉冲积累后,使得检测到的时间序列有小范围的连续性。

图5 多脉冲积累后阈值门限检测

图6 图5部分区域放大图
上述改进的Posner判别准则中,采用的脉冲积累数是10,下面讨论脉冲积累数(滑窗长度)对检测出的海尖峰序列占总脉冲数比例的影响。
脉冲积累时间的长短决定了累加后的海杂波序列幅值大小和海尖峰判别门限阈值大小,而海杂波序列幅值与门限阈值之间的差值决定了最终海尖峰脉冲所占的比例,所以,研究积累时间对海尖峰检测的影响就体现在积累脉冲数对检测的海尖峰脉冲比例的影响。图7中选取的脉冲数目范围为1~30个,海尖峰脉冲所占比例呈先增加后递减的变化趋势。
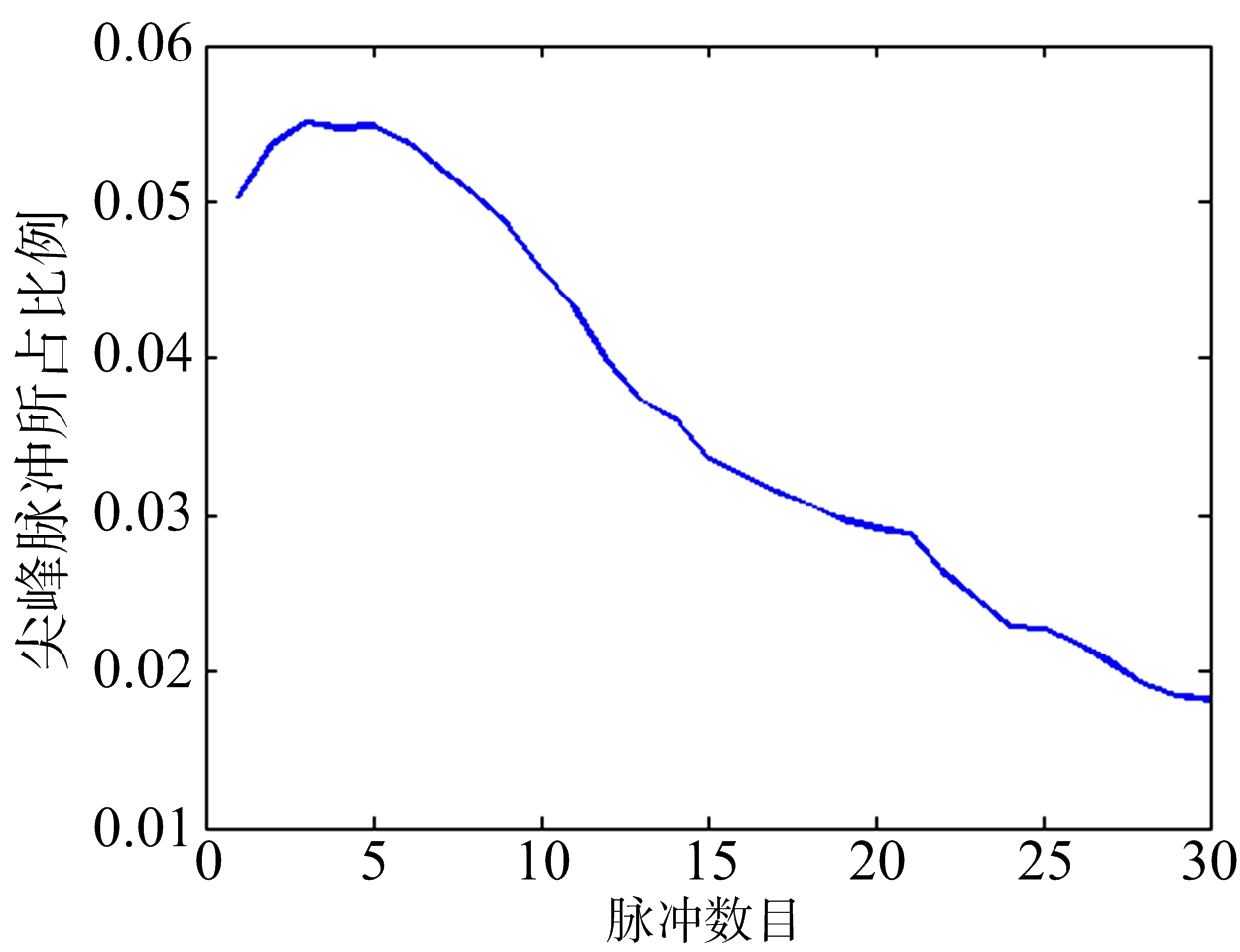
图7 积累脉冲数目影响
首先说明脉冲数的取值范围的依据:在判别海尖峰中,对海杂波脉冲积累时,一般选取的脉冲积累长度与散斑相关时间长度接近,而散斑相关时间为10 ms左右,所以选取的脉冲数目在1~30个(所选的数据PRF为1 000 Hz)。然后分析图7中曲线呈现先增加后减小趋势的原因。在积累 1~5个脉冲时,脉冲序列积累产生的序列幅值增长速度要高于门限增长的速度,所以在积累5个脉冲之前,海尖峰脉冲所占比例在不断升高,而随着脉冲积累数目大于5,检测到的海尖峰所占的比例越来越小,出现这一现象的根本原因是随着脉冲数目的增加,海杂波之间的相关性逐渐减弱,海杂波相加后抵消比较大,导致累加效果不明显。综上讨论,选择合理的积累脉冲数目,才能取得较好的海尖峰检测效果。
在进行海尖峰判别之前,首先确定门限阈值。文中采用的是第4种阈值取法。然后确定最小间隔时间和最小持续时间。具体的算法步骤如下:
1) 采用滑动窗叠加的方式对单个距离门内的时间序列进行脉冲叠加,滑窗长度为M,z(i)=z(i-1)+y(i)-y(i-M),其中z(i)是第i个脉冲处前M个脉冲之和,y(i)和y(i-M)分别是当前第i个脉冲和第i-M个脉冲的输入。
2) 计算门限阈值,设单个距离门内的时间序列长度为N,对N个数据取绝对值,并对此取均值,记为![]() ,最终的门限阈值为T=M·
,最终的门限阈值为T=M·![]() ,比较脉冲积累值与门限阈值,若z(i)>T,记下坐标数P(j)=l,杂波序列幅度大于阈值门限的下标集为{P(j)|j=1,…,X};图8对应通过初次检测后得到的海杂波序列。
,比较脉冲积累值与门限阈值,若z(i)>T,记下坐标数P(j)=l,杂波序列幅度大于阈值门限的下标集为{P(j)|j=1,…,X};图8对应通过初次检测后得到的海杂波序列。

图8 初次检测得到的海尖峰
3) 设Wmin为海尖峰的最小持续时间,Imin为海尖峰间隔时间的最小值。对幅度大于门限的指标进行处理,若P(j+1)-P(j)>Imin(j=n1,n1+1,…),记录满足条件的指标为P(n2)=P(j),在图9中表示利用时间间隔处理的时候,为了突出经过时间间隔选择的步骤,将满足大于间隔时间的海杂波序列尺度变大。
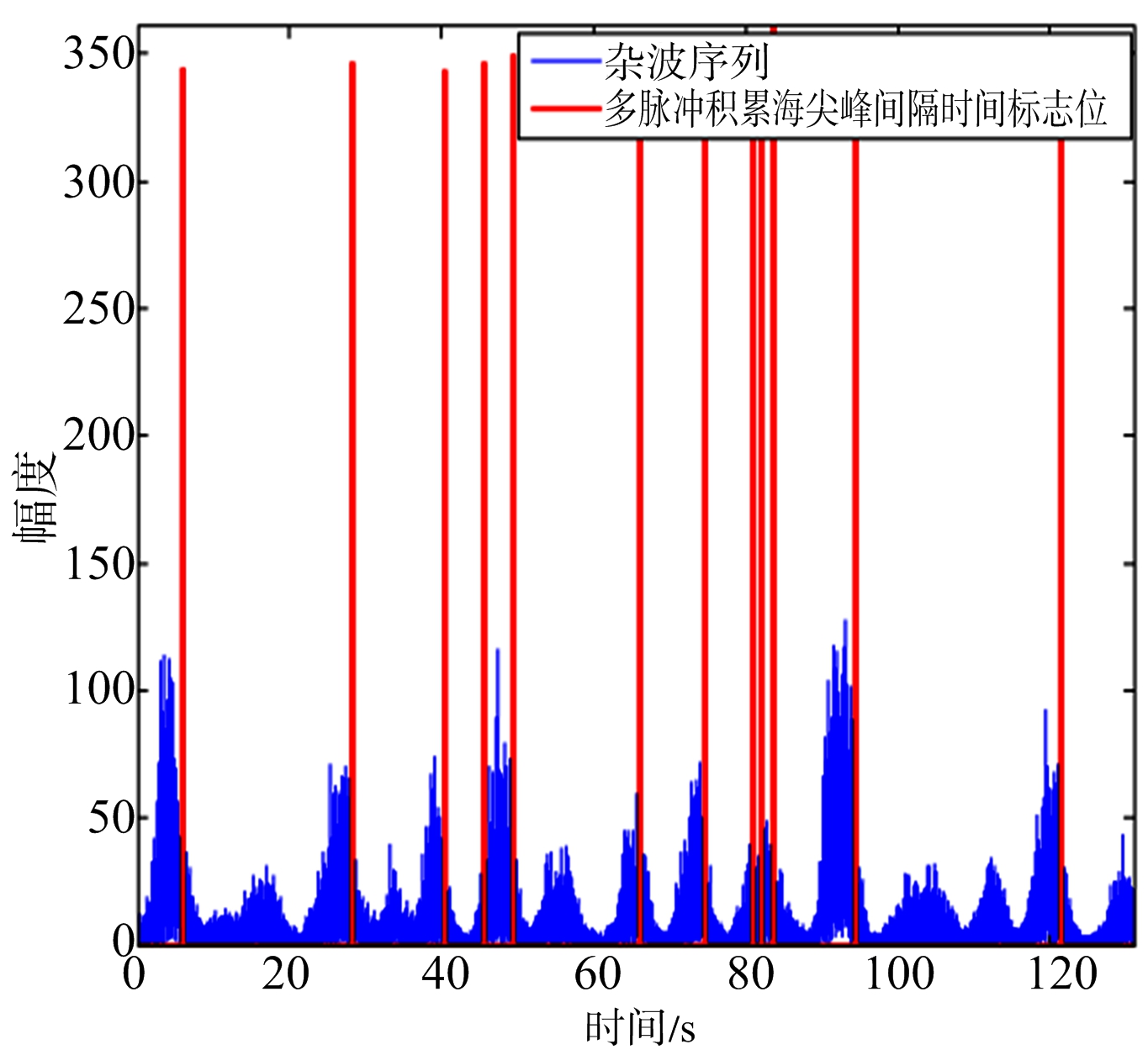
图9 第二步处理后得到的海尖峰
4) 若间隔时间内高于门限阈值的序列持续时间大于最小持续时间,则判断这些序列为海尖峰,即P(n2)-P(n1+1)>Wmin,记录海尖峰对应信号的指标集合为{l|l∈[P(n1+1),P(n2)]},如图10所示。

图10 最终处理得到的海尖峰
比较Posner判别准则改进后改进前的结果,如图10和图11所示。未改进准则下的海尖峰脉冲数占全部序列的比例是2.1%,而改进之后所占比例为1.2%,比较可得,利用脉冲积累的方法避免了一些非海尖峰序列,减少“毛刺”出现概率,使得检测的海尖峰更加准确。

图11 未改进判别准则下的海尖峰
通过对Posner判别准则的改进,利用多脉冲滑动积累的方式,对原始海尖峰回波数据进行平滑,在此基础上经过幅度阈值检测,避免了一些小“毛刺”的出现,而且利用多个脉冲积累后,使得检测到的时间序列有小范围的连续性。改进的Posner判别准则能够较准确地判别海尖峰,减少了“毛刺”的出现概率,提高了海尖峰的判别精度,为海杂波背景下小目标的检测提供了依据。
参考文献:
[1] 丁昊,董云龙,刘宁波,等. 海杂波特性认知研究进展与展望[J]. 雷达学报, 2016, 5(5):499-516.
[2] 时艳玲,林毓峰,宛汀. 部分均匀海杂波中雷达目标的平滑自适应检测[J]. 系统工程与电子技术, 2016, 38(12):2745-2751.
[3] 李重威,杨勇,李永祯,等. 基于实测数据的分时全极化雷达海杂波分布研究[J]. 电波科学学报, 2017, 32(3):253-260.
[4] 张乐杰,曾威,赵志坚. 导航雷达目标恒虚警检测方法初探[J]. 科技展望, 2016(28):129-130.
[5] 刘明,水鹏朗. 海杂波背景下的组合自适应GLRT-LTD[J]. 电子与信息学报, 2015, 37(12):2984-2990.
[6] JESSUP A T, MELVILLE W K, KELLER W C. Breaking Waves Affecting Microwave Backscatter: 1. Detection and Verification[J]. Journal of Geophysical Research: Oceans, 1991, 96(C11):20547-20559.
[7] LIU Y, FRASIER S J, MCINTOSH R E. Measurement and Classification of Low Grazing Angle Radar Sea Spikes[J]. IEEE Trans on Antennas and Propagation, 1998, 46(1):27-40.
[8] MELIEF H W, GREIDANUS H, VAN GENDEREN P, et al. Analysis of Sea-Spikes in Radar Sea Clutter Data[J]. IEEE Trans on Geoscience and Remote Sensing, 2006, 44(4):985-993.
[9] WALKER D. Model and Characterisation of Radar Sea Clutter[D]. London: University College London, 2001:101-103.
[10] POSNER F, GERLACH K. Sea Spike Demographics at High Range Resolutions and Very Low Grazing Angles[C]∥ IEEE Radar Conference, Huntsville, AL: IEEE, 2003:38-45.
[11] GRECO M, STINCO P, GINI F. Identification and Analysis of Sea Radar Clutter Spikes[J]. IET Radar, Sonar and Navigation, 2010, 4(2):239-250.
[12] DONG Y, CRISP D J. The Euler Decomposition and Its Application to Sea Clutter Analysis[C]∥ International Conference on Radar, Adelaide, SA: IEEE, 2008:133-138.
[13] 王鹏. 激化IPIX雷达回波数据处理与分析[D]. 哈尔滨: 哈尔滨工业大学, 2016:1-15.
CHEN Zeming
(CECJinjiangInfoIndustrialCorporation,Ltd,Chengdu610051,China)
Abstract:Sea spike is such a kind of sea clutter that is characterized by discrete distribution, high amplitude, strong polarization feature, and similarity to small target. It has severe influences on the sea small target detection of high resolution radar. Based on the introduction to the Posner identification criterion for sea spikes, the different value methods of amplitude threshold, minimum interval time, and minimum duration and their advantages and disadvantages are discussed. The problems of the Posner identification criterion are found out and analyzed. Then, the slide window impulse integration method is used to improve the identification criterion. Finally, a comparison between the new Posner identification criterion and the old Posner identification criterion is made. The result shows that the improved sea spikes identification criterion has higher identification accuracy and reduces the appearance of burrs.
Keywords:sea spike; Posner identification criterion; pulse integration; amplitude threshold
DOI:10.3969/j.issn.1672-2337.2018.05.014
修回日期:2018-03-22
收稿日期:2017-12-01;
文章编号:1672-2337(2018)05-0554-05
文献标志码:A
中图分类号:TN957.51
作者简介:

陈泽铭 男,1962年11月生于四川成都,高级工程师,主要研究方向为雷达系统设计,目前从事情报及气象雷达产品总体设计工作。
E-mail:czm784@vip.163.com