魏立兴,孙合敏,吴卫华,罗沐阳,吴晓彪
(空军预警学院, 湖北武汉 430019)
摘要:在机载多普勒雷达多目标跟踪(MTT)过程中,多普勒盲区(DBZ)的存在易造成连续漏检,严重地影响目标跟踪性能。针对这一问题,提出了DBZ下基于高斯混合势平衡多目标多伯努利(GM-CBMeMBer)的多目标跟踪算法。首先将带最小可检测速度(MDV)的检测概率模型代入CBMeMBer更新公式中,然后推导了带MDV和多普勒信息的GM-CBMeMBer更新公式。仿真结果表明,相比未并入多普勒和MDV信息的GM-CBMeMBer,所提算法能有效改善DBZ条件下的多目标跟踪性能。
关键词:多目标跟踪(MTT);高斯混合势平衡多目标多伯努利(GM-CBMeMBer);多普勒盲区(DBZ);最小可检测速度(MDV)
在机载多普勒雷达多目标跟踪(Multi-Target Tracking, MTT)过程中,多普勒盲区(Doppler Blind Zone, DBZ)的存在是不可回避的现实问题[1-3]。DBZ问题由传感器物理限制产生,当目标的径向速度小于最小可检测速度(Minimum Detectable Velocity, MDV)时,目标无法被传感器检测,这将导致目标漏检和航迹中断,严重影响跟踪性能[4]。
文献[5]提出了基于高斯混合(Gaussian Mixture, GM)的跟踪算法,它通过引入伪造量测来代表漏检,通过构造合适的状态依赖的检测概率,使其在DBZ里的检测概率值较低。然而,由此得到的高斯混合近似可能有负的权重,造成数值不稳定。文献[6]提出了“两伪造点”分配方法,其中,一个伪造量测代表对应检测概率小于1造成的漏检,另外一个额外的伪造量测代表由于DBZ引起的漏检。文献[7]基于二维分配方法,通过对来自同一目标的不同时间段航迹进行关联,提出了航迹段关联(Track Segment Association, TSA)方法。
然而,上述算法的实现涉及复杂的数据关联问题,实用性有待提高。作为一种可替代传统基于数据关联算法的方法,基于随机有限集(Random Finite Set, RFS)的多目标跟踪算法在解决DBZ问题中有着显著优势。其中,文献[8-9]分别将概率假设密度(Probability Hypothesis Density, PHD)和势化概率假设密度(Cardinalized PHD, CPHD)应用于DBZ条件下的地面动目标指示(Ground Moving Target Indicator, GMTI)跟踪。不同于PHD传递一阶矩、CPHD传递二阶矩和势分布,文献[10]提出的势平衡多目标多伯努利(Cardinality Balanced Multi-Target Multi-Bernoulli,CBMeMBer)滤波器通过传递多伯努利RFS来递推估计后验多目标概率密度。
CBMeMBer滤波器提供的“假设航迹”机制更有利于解决DBZ条件下的多目标跟踪问题,不过在CMeMBer框架下的相关研究还鲜有报道,所以本文在CBMeMBer滤波器中引入MDV和多普勒信息,并给出了其高斯混合执行,记为GM-CBMeMBer-D-MDV。仿真结果表明,所提滤波器能有效地改善DBZ下多目标跟踪性能。
根据RFS理论,单个目标状态可以表示为伯努利RFSr,p,其中,r表示目标存在概率,p表示目标状态概率密度。因此,多目标状态集合可以表示M个独立的伯努利RFS的并集,即多伯努利RFSπ![]() 滤波器通过传递多伯努利RFS来递推估计多目标状态的后验概率密度,主要分为预测和更新两步。
滤波器通过传递多伯努利RFS来递推估计多目标状态的后验概率密度,主要分为预测和更新两步。
假设给定k-1时刻的多伯努利RFSπk-1=![]() i=1,则预测的多伯努利RFS为
i=1,则预测的多伯努利RFS为
πk|k-1=![]() i=1∪
i=1∪
(1)
![]() =
=![]() 〈
〈![]() ,pS,k〉
,pS,k〉
(2)
![]()
(3)
式中:![]() 为存活目标多伯努利RFS;
为存活目标多伯努利RFS;![]() 为出生目标多伯努利RFS;〈·,·〉为内积运算;fk|k-1x·为状态转移概率密度函数;目标存活概率pS,k与目标状态无关。
为出生目标多伯努利RFS;〈·,·〉为内积运算;fk|k-1x·为状态转移概率密度函数;目标存活概率pS,k与目标状态无关。
假设k时刻预测的多伯努利RFSπk|k-1=![]() ,则更新后的多伯努利RFS由遗留航迹部分
,则更新后的多伯努利RFS由遗留航迹部分![]() 和量测更新航迹部分
和量测更新航迹部分![]() 组成:
组成:
πk≈![]() ∪
∪
(4)
Mk|k-1=Mk-1+MΓ,k
(5)
(6)
(7)
![]() ;z)=
;z)=
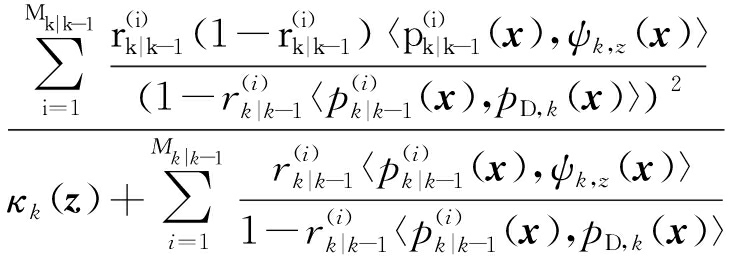
(8)
![]() ;z)=
;z)=

(9)
ψk,z(x)=gkz|xpD,k(x)
(10)
式中:pD,k(x)为目标检测概率;Zk为k时刻量测集合;κkz为杂波强度;gkz|x为目标量测似然函数。
由于考虑DBZ,所以目标检测概率不再是与状态无关,本节将其建模为关于目标状态的函数。在xyz三维坐标系下,假设k时刻目标状态![]() ,其中,xk,yk,zkT为位置分量,
,其中,xk,yk,zkT为位置分量,![]() 为速度分量。类似地,令k时刻传感器状态
为速度分量。类似地,令k时刻传感器状态![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则目标多普勒
,则目标多普勒![]() 和xk所在位置对应的背景杂波多普勒
和xk所在位置对应的背景杂波多普勒![]() 分别为
分别为
![]() hd,k(xk)=
hd,k(xk)=
(11)
(12)
![]() 与
与![]() 之差称为杂波凹口函数nc[11],定义为
之差称为杂波凹口函数nc[11],定义为
nc=![]()
![]()
(13)
目标检测概率pD,kxk是关于目标状态的函数,并且受DBZ强烈影响。具体而言,当nc<MDV时,pD,kxk非常小,甚至趋于0;当nc≫MDV时,pD,kxk趋于饱和值pD。因此,检测概率模型[11]可以建模为
pD,kxk≈pD1-exp-nc(xk)/MDV2·ln2
(14)
式中,pD为目标远离DBZ的检测概率值。
为了进一步得到检测概率模型的高斯形式,便于GM-CBMeMBer-D-MDV公式的推导,将ncxk在预测值![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 处进行一阶泰勒展开:
处进行一阶泰勒展开:
nc(xk)≈![]() ·
·
![]() ·
·
![]() ·xk=
·xk=
![]() ·xk
·xk
(15)
式中,伪量测函数yf和伪量测矩阵Hf分别为
(16)
![]()
![]()
n1,n2,n3,n4,n5,n6T
(17)
式中,![]() /
/![]() ,
,![]() /
/![]() ,
,![]() /
/![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()

![]() ,
,![]()

![]() ,
,![]()

![]() /
/![]() ,
,![]()
![]() ,atan2为四象限反正切函数,
,atan2为四象限反正切函数,![]() 和
和![]() 分别为方位角和俯仰角的估计值。
分别为方位角和俯仰角的估计值。
将式(15)代入式(14),进一步化简得到检测概率的高斯形式:
![]() ;
;![]() ·x,Rf)]
·x,Rf)]
(18)
式中,归一化因子![]() ,伪量测在多普勒域的方差Rf=MDV2/2ln2。
,伪量测在多普勒域的方差Rf=MDV2/2ln2。
由式(2)和式(3)可知,式(18)的检测概率模型不影响CBMeMBer的预测步骤,所以GM-CBMeMBer-D-MDV和GM-CBMeMBer具有相同的预测公式。假设k时刻预测的多伯努利RFSπk|k-1=(![]() ,
,![]() )
)![]() ,其中,
,其中,![]() 概率密度为高斯混合形式:
概率密度为高斯混合形式:
![]()
(19)
式中,![]() ,
,![]() 和
和![]() 分别表示第i个单伯努利RFS中第j个高斯分量的权重、均值和协方差。
分别表示第i个单伯努利RFS中第j个高斯分量的权重、均值和协方差。
出生多伯努利RFS为![]() ,其中,
,其中,![]() 也为高斯混合形式:
也为高斯混合形式:
![]()
(20)
式中,![]() ,
,![]() 和
和![]() 分别表示k时刻第i个出生单伯努利RFS中第j个高斯分量的权重、均值和协方差。
分别表示k时刻第i个出生单伯努利RFS中第j个高斯分量的权重、均值和协方差。
在推导GM-CBMeMBer-D-MDV的更新公式的过程中,利用了下述两个引理[12]:
引理1:给定适当维度的H,R,m和P,且R和P是正定的,则有
Nz;Hx,RNx;m,P=
Nz;Hm,SN(x;m+G(z-Hm),P-GSGT)
(21)
式中,S=HPHT+R,G=PHTS-1。
引理2:给定适当维度的F,Q,m和P,且Q和P是正定的,则有
![]() ;Fx,Q)N(x;m,P)dx=
;Fx,Q)N(x;m,P)dx=
N(z;Fm,Q+FPFT)
(22)
假设目标xk-1在k时刻存活,则xk-1转移到xk的概率转移密度函数为
fk|k-1(xk|xk-1)=N(xk;Fk-1xk-1,Qk-1)
(23)
式中,Fk-1为状态转移矩阵,Qk-1为过程噪声协方差。
对于多普勒体制雷达,式(10)中的量测似然函数gk(z|x)可以建模为
gk(z|x)=N(yc;Hc,kx,Rc,k)N(yd;hd,k(x),![]()
(24)
式中,z为k时刻的常规量测,包括位置量测yc和多普勒量测yd,且两者不相关,Hc,k为线性位置观测矩阵,Rc,k为位置观测噪声协方差,σd为多普勒观测噪声标准差,hd,k(x)为式(11)的非线性多普勒观测函数。
假设给定k时刻预测的多目标概率密度πk|k-1=![]() ,且
,且![]() 为高斯混合形式:
为高斯混合形式:
![]() (x)=
(x)=![]() \5
\5
N(x;![]() ,
,![]()
(25)
式中,对于第i个单伯努利RFS,![]() ,
,![]() 和
和![]() 分别为第j个高斯分量的权重、均值和协方差。
分别为第j个高斯分量的权重、均值和协方差。
将式(18)的检测概率模型和式(24)的似然函数代入式(4)中,连续使用两个引理得到GM-CBMeMBer-D-MDV的更新公式:
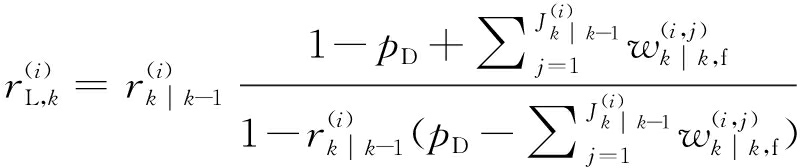
(26)
![]() (x)=
(x)=
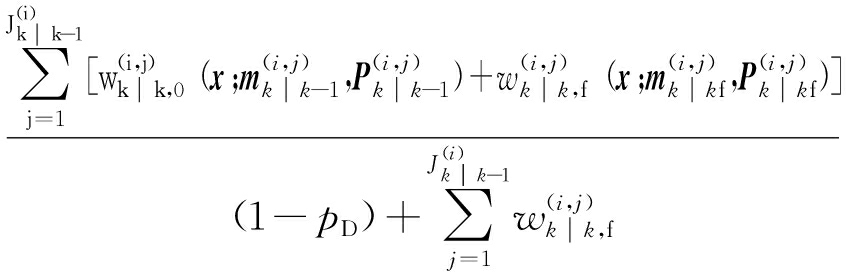
(27)
![]() ;z)=
;z)=
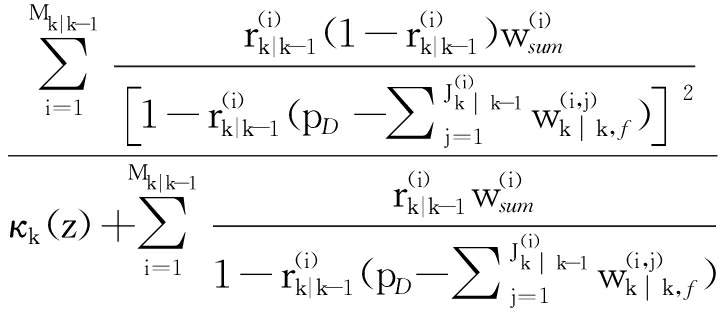
(28)
![]() ;z)=
;z)=


(29)
分量{![]() ,
,![]() ,
,![]() 由常规丢失量测更新得到:
由常规丢失量测更新得到:
![]() =(1-pD)
=(1-pD)![]()
(30)
(31)
(32)
分量{![]() ,
,![]() ,
,![]() 由伪量测
由伪量测![]() 更新得到:
更新得到:
![]() =
=![]() ;
;
![]() ,
,![]() )
)![]()
(33)
![]()
![]()
![]() ·
·![]()
(34)
![]()
(35)
式中,伪量测增益和伪量测新息协方差分别为
![]()
(36)
![]()
(37)
分量{![]() (z),
(z),![]() ,
,![]() 通过位置量测yc和多普勒量测yd序贯更新得到:
通过位置量测yc和多普勒量测yd序贯更新得到:
![]()
(38)
![]()
![]()
![]()
(39)
![]()
![]() \5
\5
![]()
(40)
类似地,![]() 和
和![]() 分别表示由位置量测yc更新得到的均值和协方差,即
分别表示由位置量测yc更新得到的均值和协方差,即
![]() [
[![]() ,
,![]() ,x
,x![]() ,
,![]() ]T=
]T=
(41)
![]()
(42)
式中,位置量测增益和位置量测新息协方差分别为
![]()
(43)
![]()
(44)
多普勒量测增益和多普勒量测新息协方差分别为
![]()
![]() ·
·
![]()
(45)
![]() (yc)=
(yc)=![]() ·
·
![]()
(46)
式(40)、式(45)和式(46)中,![]() 为hd,k(xk)在
为hd,k(xk)在![]() 处的雅克比矩阵:
处的雅克比矩阵:
![]()
![]()
[![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ]
]
(47)
式中,![]() /r
/r![]() ,
,![]() /r
/r![]() ,
,![]() /r
/r![]() ,
,![]() =cosa
=cosa![]() cose
cose![]() ,
,![]() =sina
=sina![]() cose
cose![]() ,
,![]() =sine
=sine![]() ,
,![]() ,
,![]() ,
,![]() ,e
,e![]() =
=![]() /
/![]()
基于分量{![]() (z),
(z),![]() ,
,![]() ,分量{
,分量{![]() (zf),
(zf),![]() ,
,![]() 通过伪量测
通过伪量测![]() 进一步更新得到:
进一步更新得到:
![]() (zf)=
(zf)=![]() ;
;
![]() ,
,![]() (z))
(z))![]() (z)
(z)
(48)
(49)
![]()
![]() \5
\5
![]()
(50)
![]() ·
·![]()
(51)
式中,伪量测增益和伪量测新息协方差分别为
![]()
![]() \5
\5
[![]() (z)]-1
(z)]-1
(52)
![]() (z)=
(z)=![]() ·
·
(53)
式(28)中,杂波强度κk(z)和![]() 的表达式分别为
的表达式分别为
κk(z)=κc,k(yc)κd,k(yd)
(54)
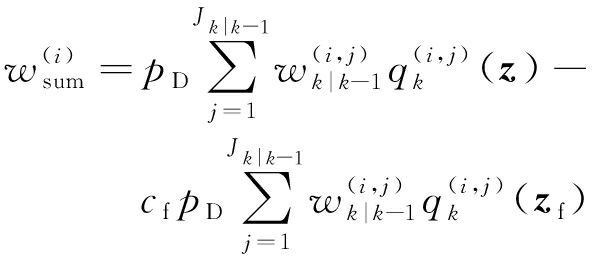
(55)
![]() (z)=N(yc;
(z)=N(yc;![]() ,
,![]() ·
·
N(yd;![]() ,
,![]() (yc))
(yc))
(56)
![]() (zf)=
(zf)=![]() (z)N(yf(
(z)N(yf(![]() (z));
(z));
![]() ,
,![]() (z))
(z))
(57)
式中,κc,k(yc)为位置分量杂波强度,κd,k(yd)为多普勒杂波强度。
此外,伯努利RFS和高斯分量随着时间迭代不断增加,如果不对其进行有效的管理,将严重影响滤波器运行效率,所以在完成更新步骤后,还需要进行“剪枝合并”操作[10]。
下面有3点值得注意:
1) 当MDV=0且cf=0时,GM-CBMeMBer-D-MDV变为带多普勒量测的GM-CBMeMBer,简记为GM-CBMeMBer-D。
2) 与GM-CBMeMBer和GM-CBMeMBer-D相同,GM-CBMeMBer-D-MDV更新步骤结束后、剪枝合并前的多伯努利RFS为{(![]() ,
,![]() )
)![]() (Mk=Mk|k-1+Zk),其中,Mk|k-1和Zk分别为k时刻遗留航迹和量测更新航迹的数量。由于式(18)的检测概率由两部分组成,所以GM-CBMeMBer-D-MDV更新步骤结束后,每个假设航迹(
(Mk=Mk|k-1+Zk),其中,Mk|k-1和Zk分别为k时刻遗留航迹和量测更新航迹的数量。由于式(18)的检测概率由两部分组成,所以GM-CBMeMBer-D-MDV更新步骤结束后,每个假设航迹(![]() ,
,![]() )中的每个高斯分量将分裂为两个。每个遗留航迹由
)中的每个高斯分量将分裂为两个。每个遗留航迹由![]() 个{
个{![]() ,
,![]() ,
,![]() 和
和![]() 个{
个{![]() ,
,![]() ,
,![]() 组成,每个量测更新航迹由
组成,每个量测更新航迹由![]() 个{
个{![]() (z),
(z),![]() ,
,![]() 和
和![]() 个{
个{![]() (zf),
(zf),![]() (zf),
(zf),![]() 组成。特别地,根据式(26)和式(33),MDV越大,遗留航迹的存在概率
组成。特别地,根据式(26)和式(33),MDV越大,遗留航迹的存在概率![]() 和权重
和权重![]() 越大,避免对应的多伯努利RFS在剪枝合并过程中被删除,有效地保存了处于DBZ中的目标状态。
越大,避免对应的多伯努利RFS在剪枝合并过程中被删除,有效地保存了处于DBZ中的目标状态。
3) 为了减少目标进出DBZ时的虚假航迹数量,仅当目标状态落入杂波凹口时,对应的高斯分量才进行分裂,即满足![]() ≤
≤![]() 条件的分量{
条件的分量{![]() ,
,![]() ,
,![]() 才进行分裂,其中,新息协方差
才进行分裂,其中,新息协方差![]() ·
·![]()
为了验证所提滤波器的有效性,在相同参数下比较GM-CBMeMBer,GM-CBMeMBer-D和GM-CBMeMBer-D-MDV三种滤波器的跟踪性能。
假设目标状态xk=[xk,yk,zk,![]() ,
,![]() ,
,![]() ,目标的存活概率pS,k(xk)=0.99,状态转移矩阵
,目标的存活概率pS,k(xk)=0.99,状态转移矩阵![]() ⊗diag([1,1,0]),过程噪声协方差
⊗diag([1,1,0]),过程噪声协方差![]() ⊗diag([σx,σy,σz])2,其中,⊗表示Kronecker乘积,采样间隔Δ=1 s,各方向上的过程噪声标准差σx=σy=2 m/s2,σz=0 m/s2。被检测概率饱和值pD=0.98,位置观测矩阵Hc,k=[I3,03],位置观测噪声协方差Rc,k= diag([σc,x,σc,y,σc,z])2,位置观测噪声标准差σc,x=σc,y=10 m,σc,z=0.1 m,多普勒观测噪声标准差σd=0.5 m/s。杂波在传感器监视区域[0,1 000]m×[-1 000,1 000]m×[-0.5,0.5]m内均匀分布,且其数量服从均值λc=50的泊松分布,杂波多普勒在[-35 m/s,35 m/s]上服从均匀分布。更新步骤结束后的“剪枝合并”参数设置:对于伯努利RFS,存在概率门限P=10-5,允许的最大数量Nmax=100;对于高斯分量,权重门限T=10-5,合并距离U=4 m,允许的最大数量Mmax=100。
⊗diag([σx,σy,σz])2,其中,⊗表示Kronecker乘积,采样间隔Δ=1 s,各方向上的过程噪声标准差σx=σy=2 m/s2,σz=0 m/s2。被检测概率饱和值pD=0.98,位置观测矩阵Hc,k=[I3,03],位置观测噪声协方差Rc,k= diag([σc,x,σc,y,σc,z])2,位置观测噪声标准差σc,x=σc,y=10 m,σc,z=0.1 m,多普勒观测噪声标准差σd=0.5 m/s。杂波在传感器监视区域[0,1 000]m×[-1 000,1 000]m×[-0.5,0.5]m内均匀分布,且其数量服从均值λc=50的泊松分布,杂波多普勒在[-35 m/s,35 m/s]上服从均匀分布。更新步骤结束后的“剪枝合并”参数设置:对于伯努利RFS,存在概率门限P=10-5,允许的最大数量Nmax=100;对于高斯分量,权重门限T=10-5,合并距离U=4 m,允许的最大数量Mmax=100。
假设在z=100 m的平面上,有一个作匀速圆周运动的传感器监视三维空间中的两个匀速直线运动的目标,监视时间为100 s,传感器角速度ωs=π/50 rad/s,目标和传感器的初始位置分别为x0,1=[0 m,0 m,0 m,5m/s,5 m/s,0 m/s]T,x0,2=[0 m,0 m,0 m,5 m/s,-5 m/s,0 m/s]T和![]() [600 m,-150 m,100 m,10 m/s,0 m/s,0 m/s]T。因此,出生多伯努利RFSπΓ,k={(rΓ,k,
[600 m,-150 m,100 m,10 m/s,0 m/s,0 m/s]T。因此,出生多伯努利RFSπΓ,k={(rΓ,k,![]() ,其中,出生目标存在概率rΓ,k=0.1,
,其中,出生目标存在概率rΓ,k=0.1,![]() (x)= N(x;
(x)= N(x;![]() ,PΓ,k),
,PΓ,k),![]() ,0 m,0 m,0 m/s, 0 m/s,0 m/s]T,PΓ,k=diag([10 m,10 m,1 m, 5 m/s,5 m/s,0.1 m/s])2。
,0 m,0 m,0 m/s, 0 m/s,0 m/s]T,PΓ,k=diag([10 m,10 m,1 m, 5 m/s,5 m/s,0.1 m/s])2。
基于上述参数设置,图1给出了传感器和目标的真实航迹,图2给出了MDV=1 m/s条件下各时刻目标多普勒速度与DBZ的关系。由图2可知,因为目标多普勒速度值小于MDV,所以目标2和目标1分别在43~52 s和59~63 s处于DBZ。图3给出了MDV=1 m/s条件下3种滤波器单次跟踪结果比较,通过比较可知,当目标离开DBZ,仅GM-CBMeMBer-D-MDV能够再次跟踪目标。
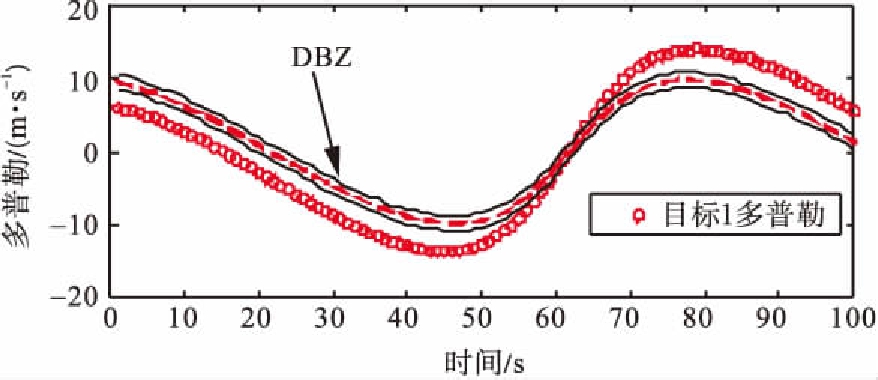
(a) 目标1

(b) 目标2
图2 各时刻目标多普勒与DBZ的关系

图3 单次跟踪结果比较

图1 传感器和目标的真实航迹
利用圆位置误差概率(Circular Position Error Probability, CPEP)[13]和最优子模式分配(Optimal Sub-Pattern Assignment, OSPA)[14]比较3种滤波器的跟踪性能。其中,CPEP可以反映滤波器对目标的“漏跟”概率,定义为
![]() ρk(x,r)
ρk(x,r)
(58)
式中,ρk(x,![]() ∀
∀![]() ∈
∈![]() ,位置误差半径r,
,位置误差半径r,![]() 表示2范数。CPEP越接近0,滤波器跟踪性能越好;CPEP越接近1,滤波器跟踪性能越差。
表示2范数。CPEP越接近0,滤波器跟踪性能越好;CPEP越接近1,滤波器跟踪性能越差。
令位置误差半径r=20 m,OSPA的阶参数p=2,截止参数c=20 m。在MDV=1 m/s条件下进行1 000次蒙特卡洛仿真,图4和图5给出了3种滤波器的CPEP和OSPA总误差统计结果。由图4可知,在43~52 s阶段,目标2处于DBZ内,而目标1处于DBZ之外,所以3种滤波器均无法跟踪目标2,但都能跟踪目标1。因此,3种滤波器在这段时间的CPEP均保持在0.5左右,而图5中3种滤波器的OSPA总误差都处于较高的值,约为15 m。当目标2在第53 s离开DBZ后,GM-CBMeMBer-D-MDV能够再次跟踪目标2,对应的CPEP和OPSA总误差回到目标2进入DBZ前的水平。但是GM-CBMeMBer和GM-CBMeMBer-D无法有效保存处于DBZ内的目标状态,当目标2处于DBZ内,传感器无法获得目标量测,所以更新步骤结束后,多伯努利RFS的存在概率逐渐减小直至低于门限P,最后在“剪枝合并”过程中被删除。目标2离开DBZ后,GM-CBMeMBer和GM-CBMeMBer-D无法再次跟踪目标2,所以它们的CPEP和OPSA总误差分别继续保持在0.5和15 m左右。类似地,在59~63 s阶段,目标1处于DBZ内,此时GM-CBMeMBer和GM-CBMeMBer-D均无法跟踪两个目标。因此,它们的CPEP和OSPA总误差进一步升高到1和20 m左右。当目标1在第64 s离开DBZ后,GM-CBMeMBer和GM-CBMeMBer-D的CPEP和OSPA总误差继续维持在1和20 m左右,说明它们均无法再次跟踪目标1。而GM-CBMeMBer-D-MDV的CPEP和OPSA总误差减小到目标1进入DBZ前的水平,说明其能够再次跟踪目标1。

图4 3种滤波器的CPEP比较
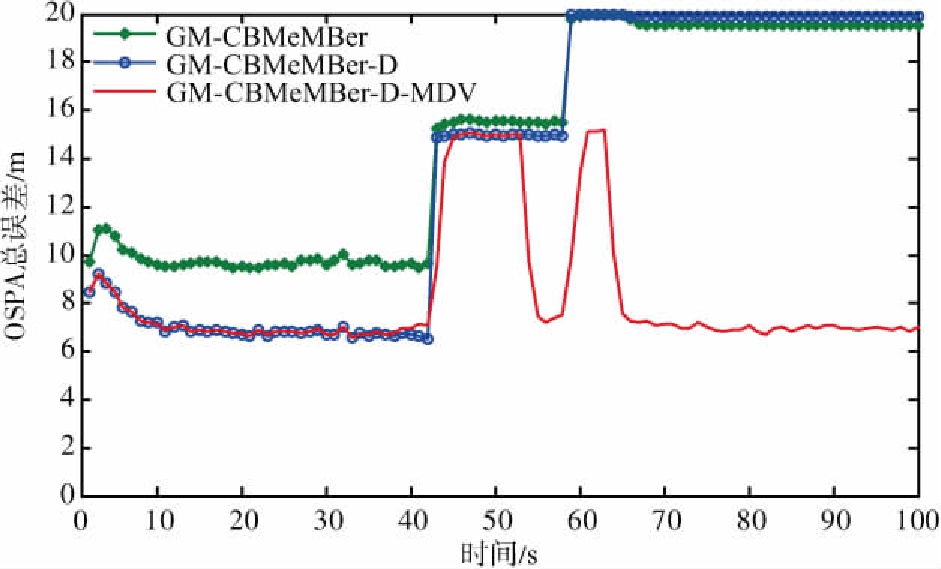
图5 3种滤波器的OSPA总误差比较
针对DBZ条件下机载多普勒雷达对目标航迹跟踪不连续的问题,提出了带最小可检测速度和多普勒信息的GM-CBMeMBer滤波器(GM-CBMeMBer-D-MDV)。该滤波器首先将带MDV的检测概率模型代入CBMeMBer中,然后给出其详细的预测和更新步骤。蒙特卡洛仿真实验结果表明,相对于未并入MDV信息的GM-CBMeMBer和GM-CBMeMBer-D,GM-CBMeMBer-D-MDV能够有效处理DBZ条件下的多目标跟踪问题,提高DBZ下机载多普勒雷达多目标跟踪性能。
参考文献:
[1]WU Weihua, LIU Weijian, JIANG Jing, et al. GM-PHD Filter-Based Multi-Target Tracking in the Presence of Doppler Blind Zone[J]. Digital Signal Processing, 2016, 52:1-12.
[2] 付莹,汤子跃,孙永健. 多普勒盲区条件下空地预警雷达多目标协同跟踪方法[J]. 红外与激光工程, 2014, 43(7):2379-2386.
[3] MERTENS M, KOCH W, KIRUBARAJAN T. Exploiting Doppler Blind Zone Information for Ground Moving Target Tracking with Bistatic Airborne Radar[J]. IEEE Trans on Aerospace and Electronic Systems, 2014, 50(1):130-148.
[4] KOCH W, KLEMM R. Ground Target Tracking with STAP Radar[J]. IEE Proceedings: Radar, Sonar and Navigation, 2001, 148 (3):173-185.
[5] CLARK J M C, KOUNTOURIOTIS P A, VINTER R B. A Methodology for Incorporating the Doppler Blind Zone in Target Tracking Algorithms[C]∥ 11th International Conference on Information Fusion, Cologne, Germany: IEEE, 2008:1-8.
[6] LIN L, BAR-SHALOM Y, KIRUBARAJAN T. New Assignment-Based Data Association for Tracking Move-Stop-Move Targets[C]∥ IEEE Trans on Aerospace and Electronic Systems, 2004, 40(2):714-725.
[7] YEOM S W, KIRUBARAJAN T, BAR-SHALOM Y. Track Segment Association, Fine-Step IMM and Initialization with Doppler for Improved Track Performance[J]. IEEE Trans on Aerospace and Electronic Systems, 2004, 40(1):293-309.
[8] KOHLLEPPEL R. Ground Moving Target Tracking of PAMIR Detections with a Gaussian Mixture-PHD Filter[C]∥ International Radar Symposium, Leipzig,Germany: IEEE, 2011:193-198.
[9] ULMKE M, ERDINC O, WILLETT P. GMTI Tracking via the Gaussian Mixture Cardinalized Probability Hypothesis Density Filter[J]. IEEE Trans on Aerospace and Electronic Systems,2010,46(4):1821-1833.
[10] VO B T, VO B N, CANTONI A. The Cardinality Balanced Multi-Target Multi-Bernoulli Filter and Its Implementations[J]. IEEE Trans on Signal Processing, 2009, 57(2):409-423.
[11] ULMKE M, ERDINC O, WILLETT P. GMTI Tracking via the Gaussian Mixture Cardinalized Probability Hypothesis Density Filter[J]. IEEE Trans on Aerospace and Electronic Systems, 2010, 46(4):1821-1833.
[12] VO B N, MA W K. The Gaussian Mixture Probability Hypothesis Density Filter[J]. IEEE Trans on Signal Processing, 2006, 54(11):4091-4104.
[13] KOHLLEPPEL R. Ground Target Tracking with Signal Adaptive Measurement Error Covariance Matrix[C]∥ 15th International Conference on Information Fusion, Singapore: IEEE, 2012:550-557.
[14] SCHUHMACHER D, VO B T, VO B N. A Consistent Metric for Performance Evaluation of Multi-Object Filters[J]. IEEE Trans on Signal Processing, 2008, 56(8):3447-3457.
WEI Lixing, SUN Hemin, WU Weihua, LUO Muyang, WU Xiaobiao
(AirForceEarlyWarningAcademy,Wuhan430019,China)
Abstract:In multi-target tracking (MTT) for the airborne Doppler radar, the existence of Doppler blind zone (DBZ) results in a series of missed detections, which strongly deteriorates tracking performance. To overcome this problem, a MTT algorithm based on Gaussian mixture cardinality balanced multi-target multi-Bernoulli (GM-CBMeMBer) is proposed in the presence of DBZ. First, we incorporate the detection probability model with minimum detectable velocity (MDV) into CBMeMBer, and then derive the update formulas of a novel GM-CBMeMBer where the MDV and Doppler information are fully exploited. The results of simulation show that the proposed algorithm outperforms the GM-CBMeMBer which doesn’t incorporate the Doppler and MDV information in the presence of DBZ.
Keywords:multi-target tracking(MTT); Gaussian mixture cardinality balanced multi-target multi-Bernoulli(GM-CBMeMBer); Doppler blind zone(DBZ); minimum detectable velocity(MDV)
DOI:10.3969/j.issn.1672-2337.2018.05.015
基金项目:国家自然科学基金(No.61601510)
修回日期:2017-12-11
收稿日期:2017-11-14;
文章编号:1672-2337(2018)05-0559-08
文献标志码:A
中图分类号:TN953
作者简介:

魏立兴 男,1992年生,硕士研究生,主要研究方向为随机有限集目标跟踪、多传感器数据融合。
E-mail:weilixing92@163.com