毫米波频率步进雷达是一种高分辨宽带雷达，具有瞬时带宽小、抗干扰能力强等特点[1]。然而，频率步进雷达存在着严重的距离-多普勒耦合问题，即运动目标的距离像将呈现出发散、移位等现象，因此如何进行运动补偿成为利用频率步进信号处理运动目标的关键[1]。
目前，常用运动补偿算法主要分为3类：1) 利用多帧回波数据估计速度，包括距离微分法、时频域相关法等，此类方法速度测量范围较大，但测量精度较低；2) 速度搜索算法，根据某一最优准则利用搜索方法进行速度估计，包括最小脉组误差法、最大脉组乘积求和法等，此类方法测量精度较高，但运算量巨大，进行全局搜索易导致系统过载[2]；3) 利用多体制进行速度测量，此类方法要进行不同体制的切换，对雷达系统的兼容性要求较高[3]。文献[4]提出了一种新的变换——离散Chirp-Fourier变换，该变换是对传统傅里叶变换理论的推广，通过引入二维参数对Chirp信号进行匹配，可用于频率步进信号的速度补偿。然而当目标速度较大时，该变换因需要进行二维参数搜索，导致运算量巨大。
在以上研究基础上，本文提出了一种基于二次速度估计的高分辨距离像补偿算法。首先，利用互相关FFT法对目标参数进行粗估计，并结合速度和距离的先验知识设置合理的搜索区间。然后基于最小波形熵准则，采用MDCFT进行精确估计，实现距离像的运动补偿。
根据频率步进雷达理论，回波信号混频后输出为
x(t)=
exp[-j2π(f0+iΔf)τ(t)]
(1)
式中，Ai为脉组中第i个脉冲回波输出幅值，T为脉冲宽度，fi=f0+iΔf，τ(t)=(2R0-2vt)/c，f0为信号载频，Δf为频率步进量，Tr为脉冲重复周期，N为频率步进数。假设目标匀速运动，R0为初始距离，v为运动速度。令采样时刻ti=iTr+2R0/c+T/2，则N个连续回波采样序列为
x(i)=Aiexp[-j2πfiτ(t)]=
i=0,1，…，N-1
(2)
目标相对静止时，对x(i)作IFFT和归一化处理后的输出取模：
|X(l)|=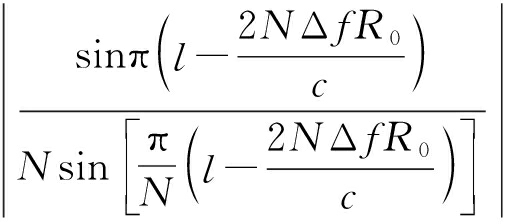
l=0,1,…，N-1
(3)
式中，l=2NΔfR0/c+kN,k∈Z时，|X(l)|取得最大值，则目标距离R0=c(l-kN)/2NΔf，不模糊距离为c/2Δf，距离分辨率为c/2NΔf。随着k取值不同，IDFT结果以N个距离单元为周期进行延拓，使距离像距离测量值模糊，这遵循了IDFT变换的周期性质。距离像模糊问题可通过文献[5]提出的解模糊算法解决。式(2)中回波序列相位可分解为
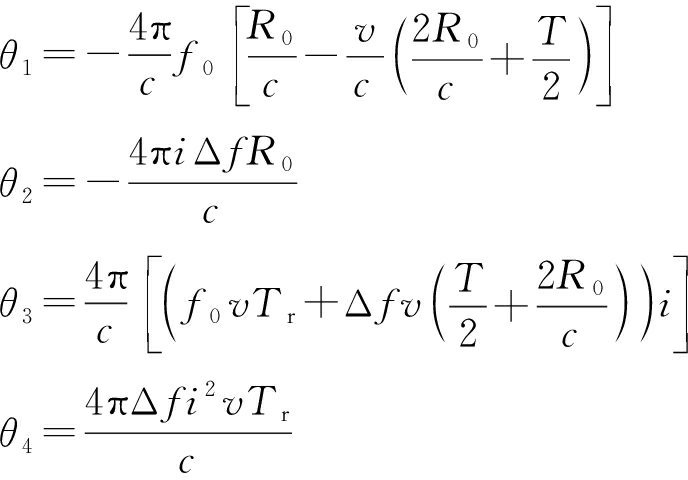
(4)
式中：θ1为载频相位项；θ2为距离相位项，包含目标距离信息；θ3为目标速度引起的线性相位项，不影响距离像的形状，但会导致移位现象，当进行运动补偿时，要求距离像峰值偏移不超过半个高分辨距离单元，即速度估计误差Δv1≤c/4f0NTr；θ4为目标速度引起的非线性相位项，会导致距离像展宽、失真和峰值降低。为使补偿后非线性相位项变化不超过π/2，速度估计误差应满足Δv2≤c/8N2ΔfTr。设本文频率步进雷达参数如表1所示。通过计算可得出线性相位的速度补偿误差Δv1≤0.17 m/s，非线性相位的速度补偿误差Δv2≤4.58 m/s。可见在工程应用中，相比二次补偿误差，一次补偿误差更难满足，对补偿算法提出了非常高的精度要求。
表1 频率步进雷达参数
参数参数值载频f0/GHz35步进频率Δf/MHz5脉冲步进数N128脉冲重复周期Tr/μs100脉冲宽度T/μs1
相邻两帧步进频信号回波的归一化表达式分别为
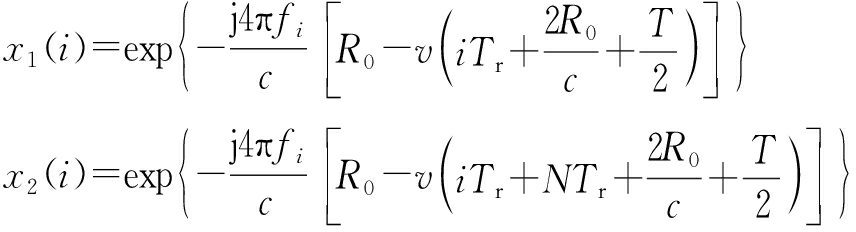
(5)
则互相关函数为
s(i)=x1(i)*x2(i)=
(6)
式中，M为FFT点数，l=Round(2NMvΔfTr/c)，继续对s(i)作FFT后归一化取模，可得
(7)
式中，当k取得l时，|S(k)|取得最大值，因此，得到速度估计值为vr=cl/2NMΔfTr，速度无模糊范围为(-c/4NΔfTr,c/4NΔfTr)，速度分辨率为Δv=c/2NMΔfTr。当M取值512，根据表1雷达参数计算可得，速度无模糊范围为(-1 171.9 m/s,1 171.9 m/s)，速度分辨率为4.58 m/s。可见，互相关FFT法测速范围很大，但是其精度很低，远不能满足线性相位速度补偿误差的要求。因此，为实现距离像的精确补偿，仍需进一步高精度测量。
另外，根据式(7)得到的速度估计值vr对目标回波进行粗补偿，即构造式(8)并进行IDFT操作即可得到目标距离的粗估计值R0r：
(8)
离散Chirp-Fourier变换是一种有效的Chirp信号检测方法，参数匹配不存在交叉项，但有两个约束条件：信号长度必须为质数；离散Chirp信号参数必须为整数。针对该限制，文献[6]提出一种修正离散Chirp-Fourier变换，其定义为
(9)
式中，k为频率维参数，l为调频维参数，
为Chirp信号初始频率，l0为调频率，N为采样点数，WN=exp(-j2π/N)。该MDCFT算法对采样点数无质数限制，且信号参数不要求为整数，极大扩展了其应用范围。
式(4)中，θ0为常数项，在进行MDCFT变换时，该相位对应乘积项绝对值为1，故对参数估计没有影响，
的值很小，均可忽略。脉组中第i个混频后回波信号可近似表示为
xi=
(10)
式中，
可见频率步进雷达脉冲组回波信号混频、采样后可视为一组离散Chirp信号。因此，目标高分辨距离像的运动补偿问题可以转化为Chirp信号参数估计问题。对式(10)结果进行MDCFT处理，得
Xc(f,u)=
(11)
式中，f为频率域参数，u为调频率域参数。当f=fc，u=uc时，积分信号相干积累，能量发生聚集，参数域相应位置上Xc(f,u)取得最大值
反之，积分信号互相抵消，Xc(f,u)幅值较小。通过二维谱峰搜索可以得到fc,uc的估计值fs,us，最终计算出目标距离与速度的精确估计值，该过程可表示为
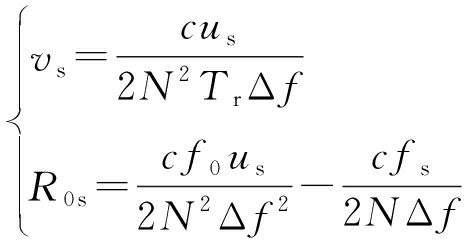
(12)
分析式(11)，可得出MDCFT的周期性质：
(13)
式(13)说明，MDCFT结果呈二维周期性，调频率维周期为N，频率维周期为N2，参数估计将会出现模糊，将会影响目标的运动补偿效果。假设有调频斜率u1，u2且Δu=u1-u2，当Δu=N2时MDCFT的参数估计结果将出现模糊，由式(13)可计算出足够引起参数估计产生模糊的最低速度为1 500 000 m/s，该值远远超过实际目标的速度，因此频率步进雷达参数估计模糊问题不予考虑。
低信噪比情况下，为避免幅值最大准则下参数估计性能恶化，采用最小波形熵准则对MDCFT变换得到的K×L矩阵Xc(f,u)进行参数估计[7]。根据最小波形熵准则，当信号能量集中于少数采样点时，包络锐化度较高，信号熵值较小；相反，若信号能量沿参数域均匀分布，信号熵值较大。同时，最小波形熵准则将MDCFT的二维参数搜索转换为一维搜索，能够减少参数搜索时间。设某个脉冲组回波信号对应于调频参数u的MDCFT谱包络矩阵为 |Xc(f,u)|=|Xc(f,u1),Xc(f,u2),…,Xc(f,uL)|，归一化包络为
定义|Xc(f,u)|的熵为
(14)
则调频率的精确估计值为
(15)
本文所提二次速度估计算法流程如下：
1) 对相邻回波互相关函数进行FFT变换得到式(7)，最大值谱线处对应的速度值为vm，假设左右次谱线处对应的速度值分别为v1，v2，则真实速度v∈(v1,v2)；
2) 将v1，v2代入式(8)完成速度粗补偿，并作IDFT处理得到距离粗估计值R01，R02，则真实距离R0∈(R01,R02)；
3) 由步骤2)得到的速度、距离粗估计值计算出MDCFT的目标参数二维搜索区间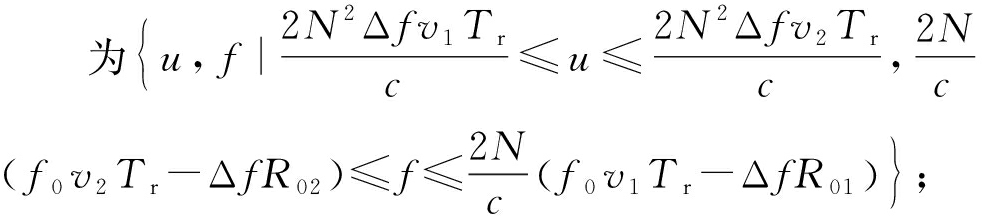
4) 参考式(11)、式(12)、式(14)、式(15)，对步骤3)得到的参数区间进行MDCFT处理，并利用最小波形熵法得到速度精确估计值vs，最后进行速度补偿后通过IDFT变换得到高分辨距离像。
假设一目标径向速度为80 m/s，距离为100 m，无参数先验知识时，直接对回波信号进行MDCFT处理的速度搜索区间为(0 m/s,80 m/s)，距离搜索区间为(0 m,100 m)，设速度、距离搜索步进间隔分别为Δv=0.01 m/s，ΔR=0.01 m，则该算法的计算量近似为8 000×10 000×N次复数乘法。本文提出的二次速度估计算法首先利用互相关FFT法得到粗估计值为77.82 m/s，确定速度搜索区间为(73.24 m/s,82.4 m/s)，距离搜索区间为(51.56 m,117.19 m)，其次对该速度-距离区间进行MDCFT处理，算法计算量近似为916×6 563×N次复数乘法，计算量减少了13.3倍。当目标距离固定为100 m，速度取值不同时，本文提出的二次速度估计算法与MDCFT算法的计算复杂度对比如表2所示。显然，目标运动速度越大，本文所提算法优势越明显。
表2 计算复杂度对比
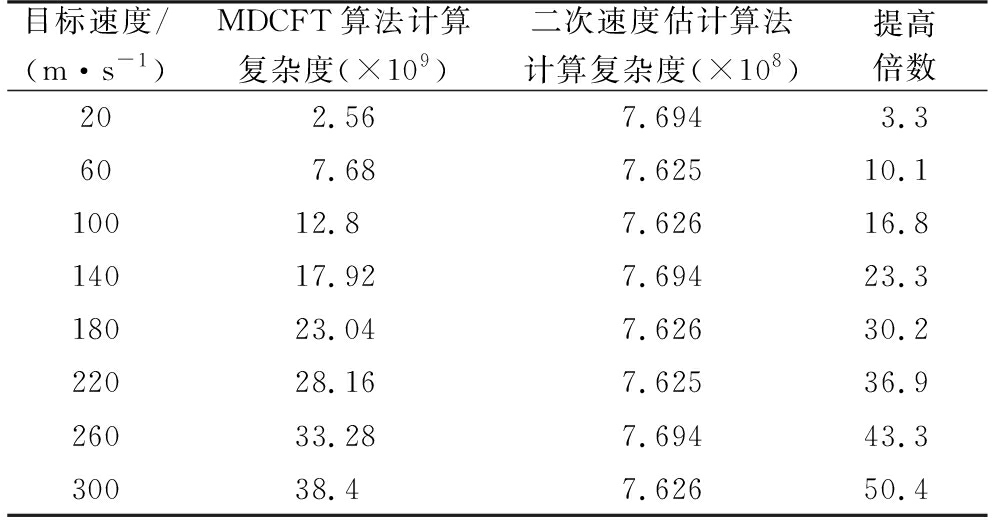
目标速度/(m·s-1)MDCFT算法计算复杂度(×109)二次速度估计算法计算复杂度(×108)提高倍数202.567.6943.3607.687.62510.110012.87.62616.814017.927.69423.318023.047.62630.222028.167.62536.926033.287.69443.330038.47.62650.4
实验1 互相关FFT法速度粗估计
考虑实际噪声情况，在仿真回波数据上叠加高斯白噪声分别使其信噪比SNR=0，10 dB，目标运动速度从0 m/s线性递增至300 m/s，FFT点数为512，采用互相关FFT法进行速度粗估计，Matlab仿真结果如图1所示。信噪比为10 dB时，测速误差基本维持在3 m/s以下，仅能满足二次相位的速度补偿误差。但当信噪比降为0 dB，速度估计值出现较大不规则波动，单独使用互相关FFT法已无法满足精度要求。因此，通常仍需在所得速度粗估计基础上进行速度精确补偿。另外，速度估计误差包络大致呈三角状，主要由FFT的栅栏效应所导致，该问题可以用Rife相关算法来得到优化[8]。
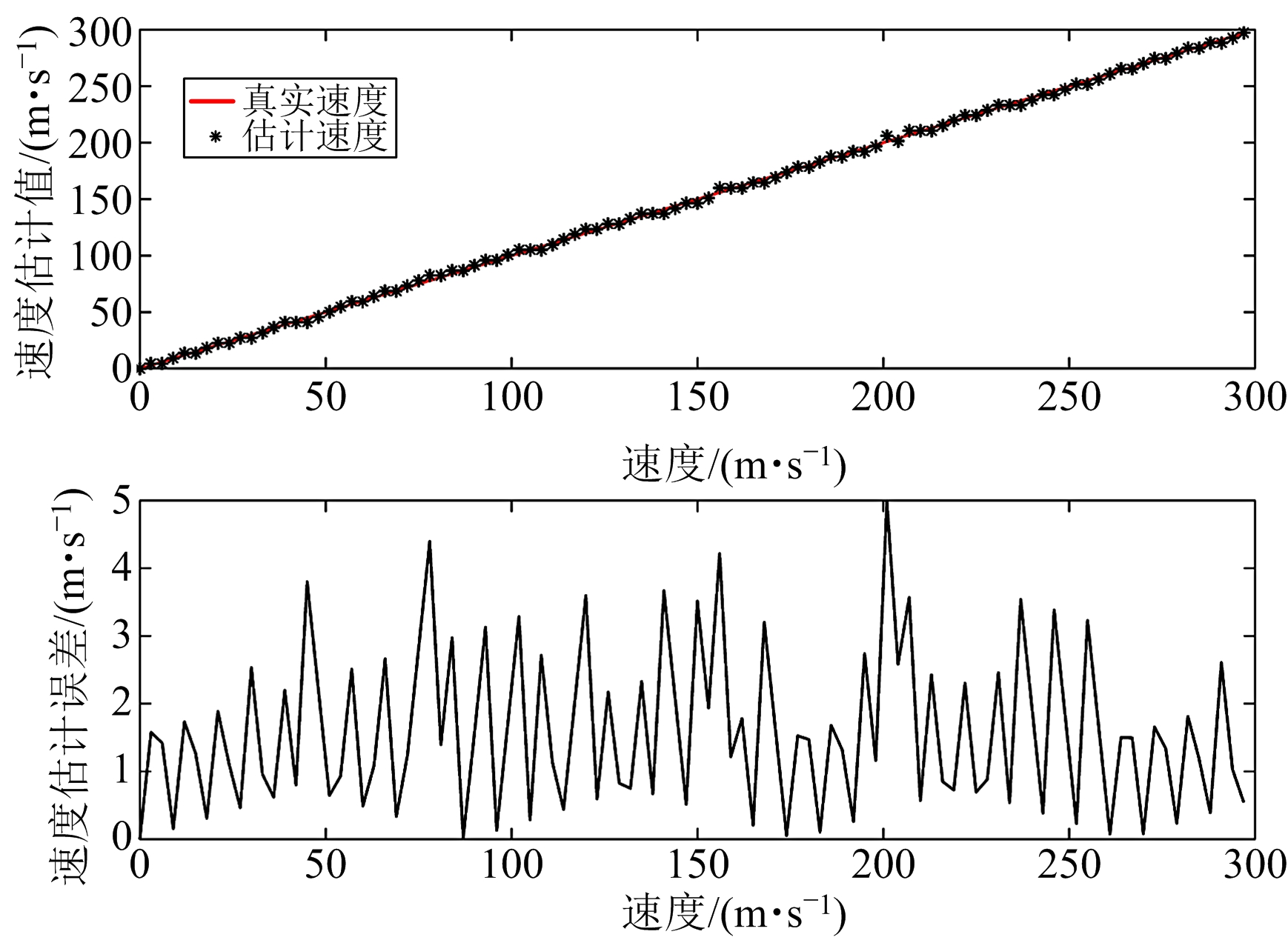
(a)SNR=0 dB
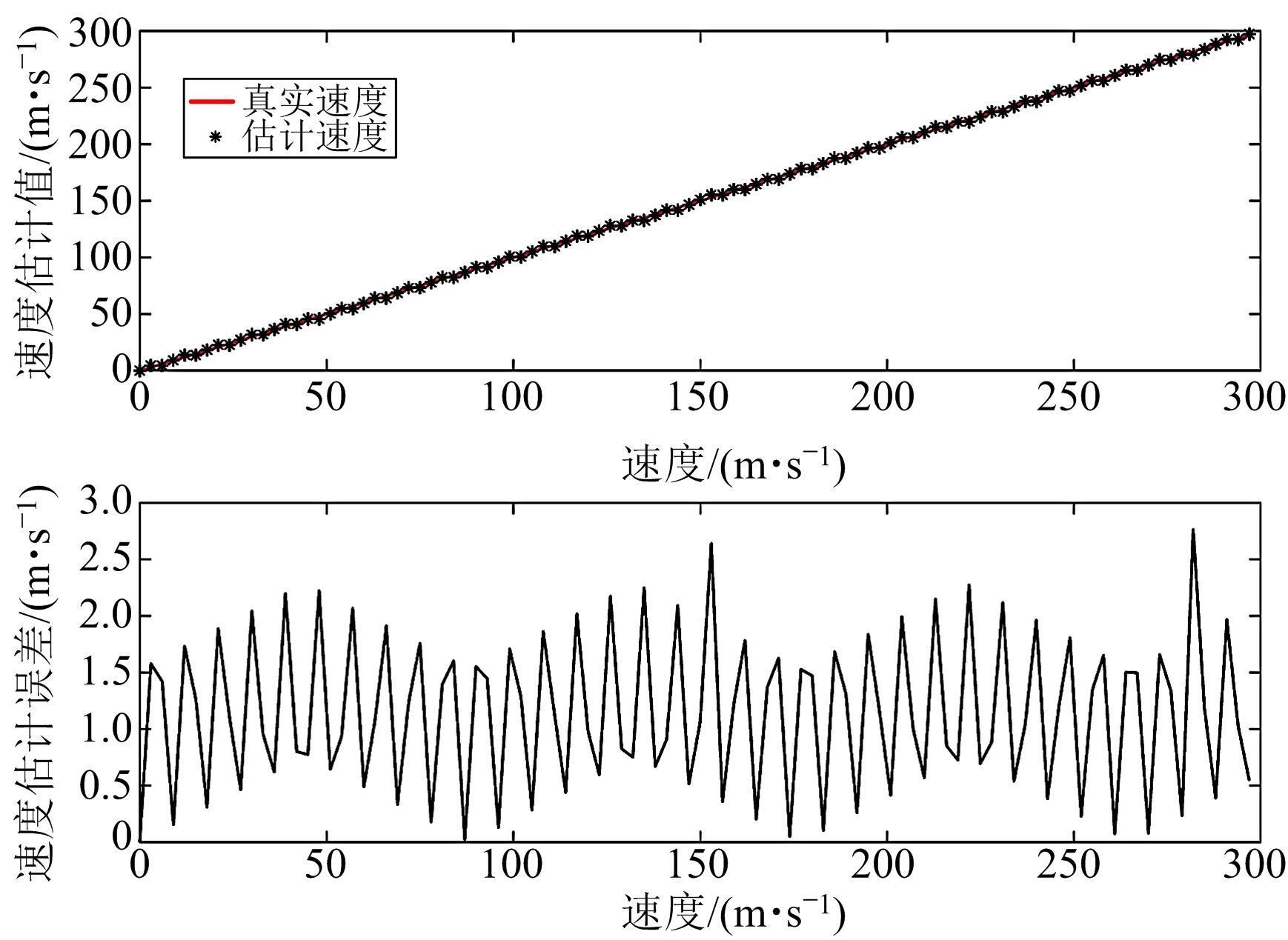
(b)SNR=10 dB
图1 速度粗估计误差
实验2 二次速度估计性能分析
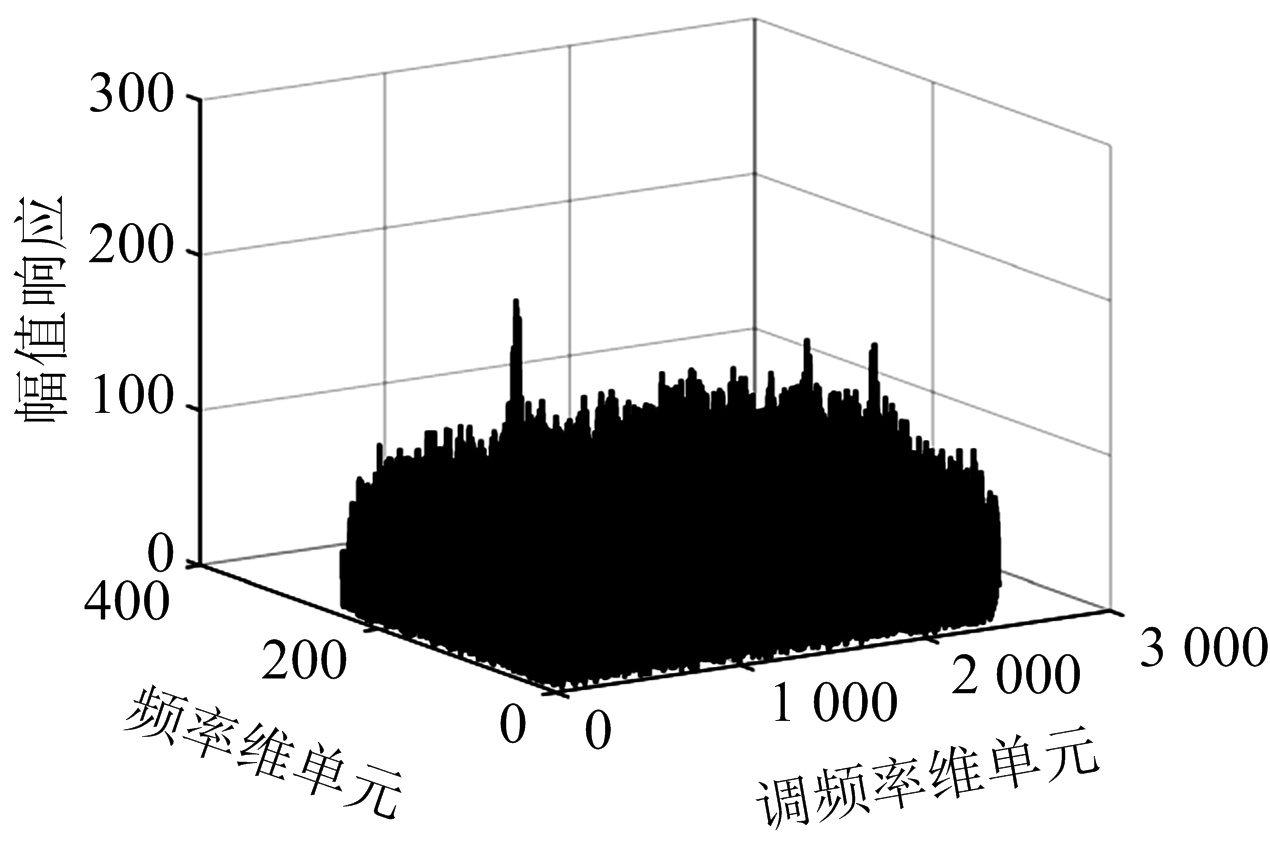
(a)SNR=-15 dB
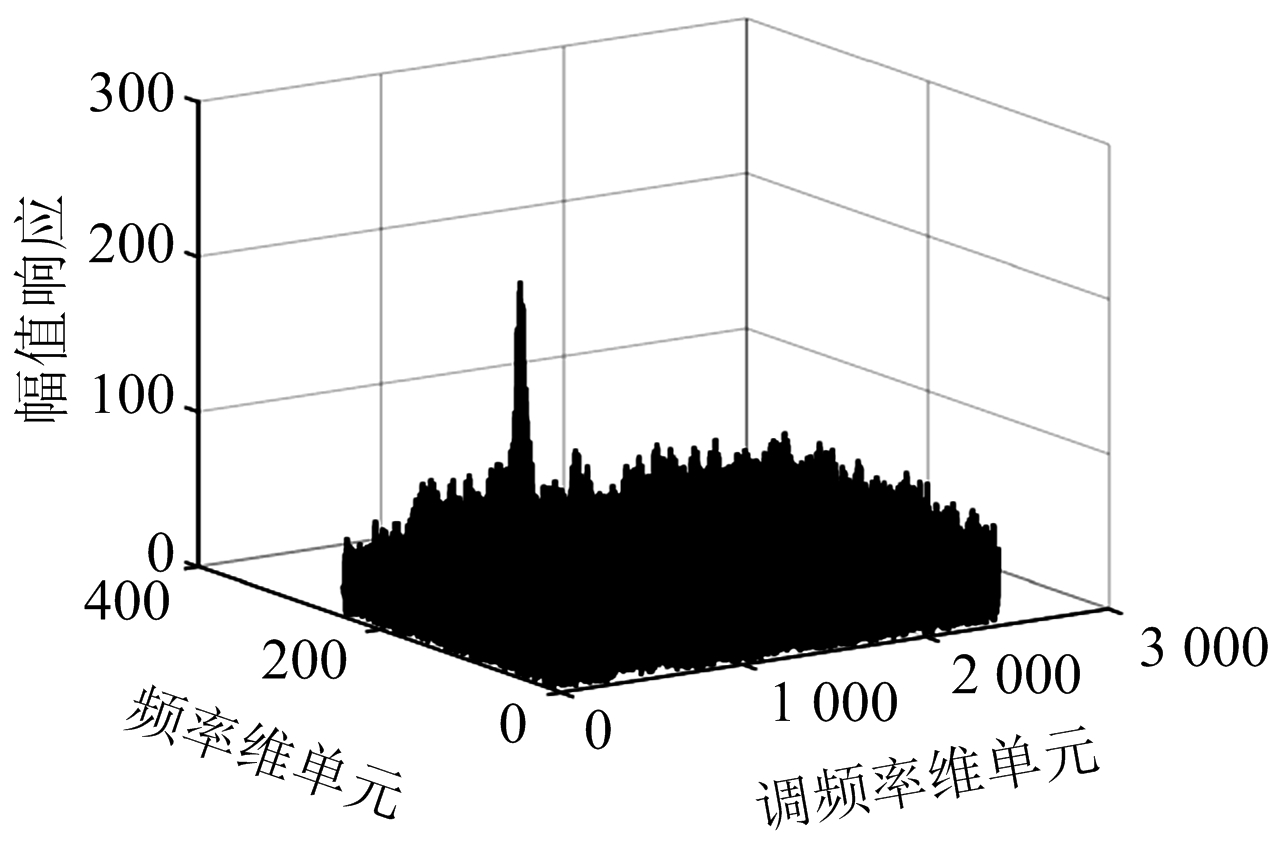
(b)SNR=-10 dB
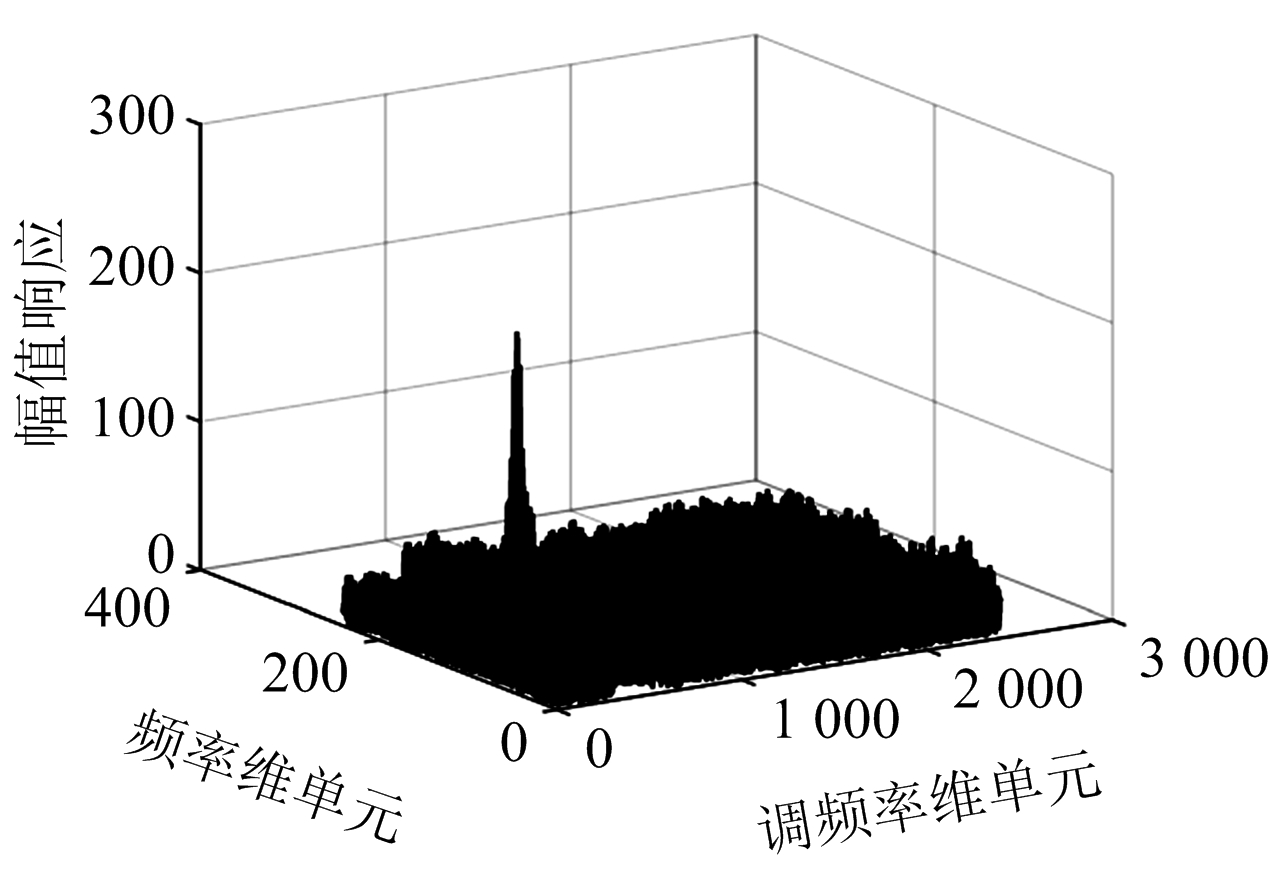
(c)SNR=-5 dB
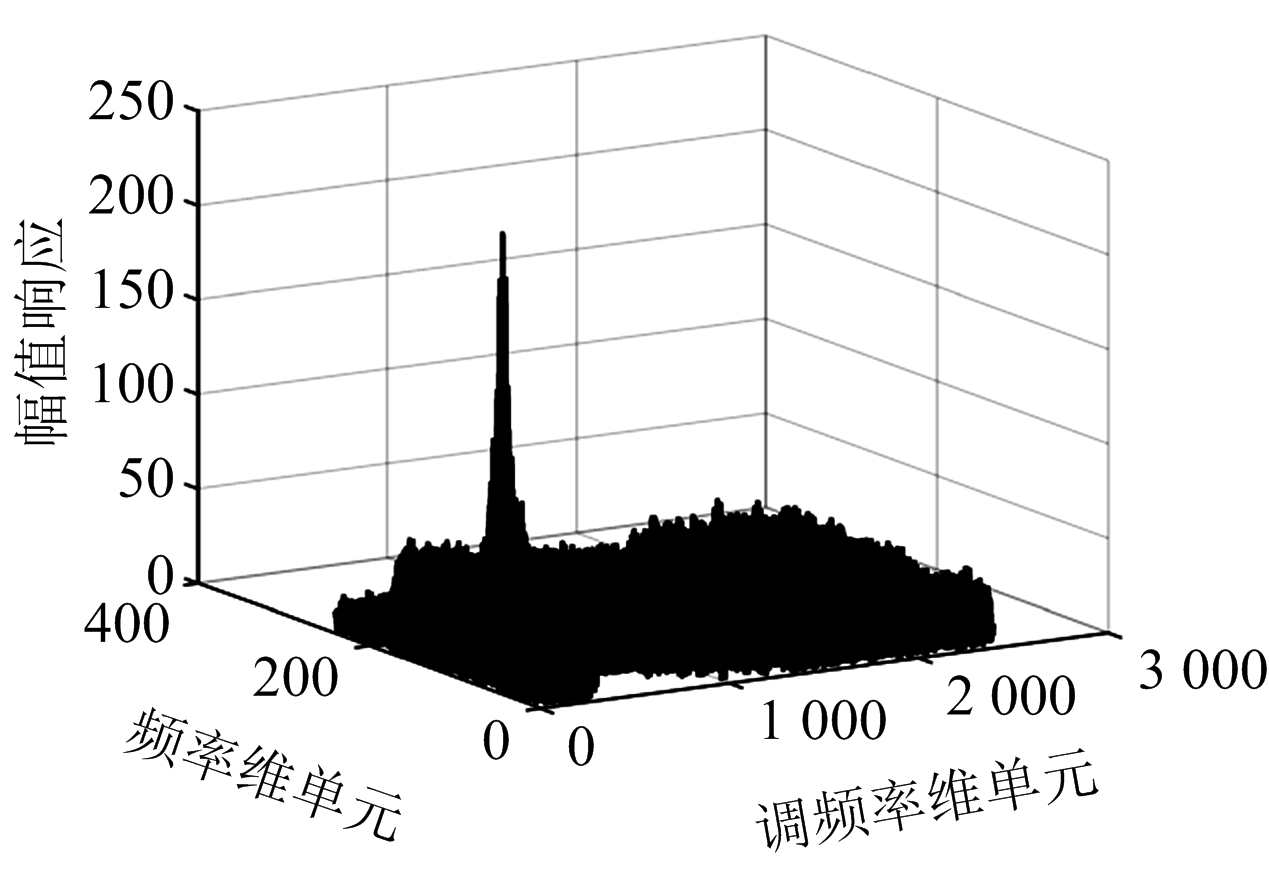
(d)SNR=0 dB
图2MDCFT信号参数估计
针对2.4节中设置目标的运动参数，其对应调频率参数uc=4.4，频率参数fc=-187.7。首先对不同信噪比条件下的MDCFT处理结果进行仿真分析如图2所示，当信噪比为-15 dB时，MDCFT依然能够准确地解析出Chirp信号参数。其次基于最小波形熵准则，分别将MDCFT处理得到的二维矩阵Xc(f,u)的每一列数据取出作为一组离散信号，并计算其熵值得到熵函数分布如图3所示。不同信噪比条件下比较发现调频单元数均为44时波形熵值最小，即对应调频参数uc=4.4，此时速度估计值最接近真实速度。另外，不同性噪比条件下，采用传统幅值最大准则与最小波形熵准则对MDCFT结果进行参数估计，得到的速度估计误差曲线如图4所示。当信噪比降至-10 dB时，最小波形熵准则的速度估计误差仍然维持在0.8 m/s以下。显然，在性噪比较低时，相比传统幅值最大准则，最小波形熵准则的估计误差有较大改善。
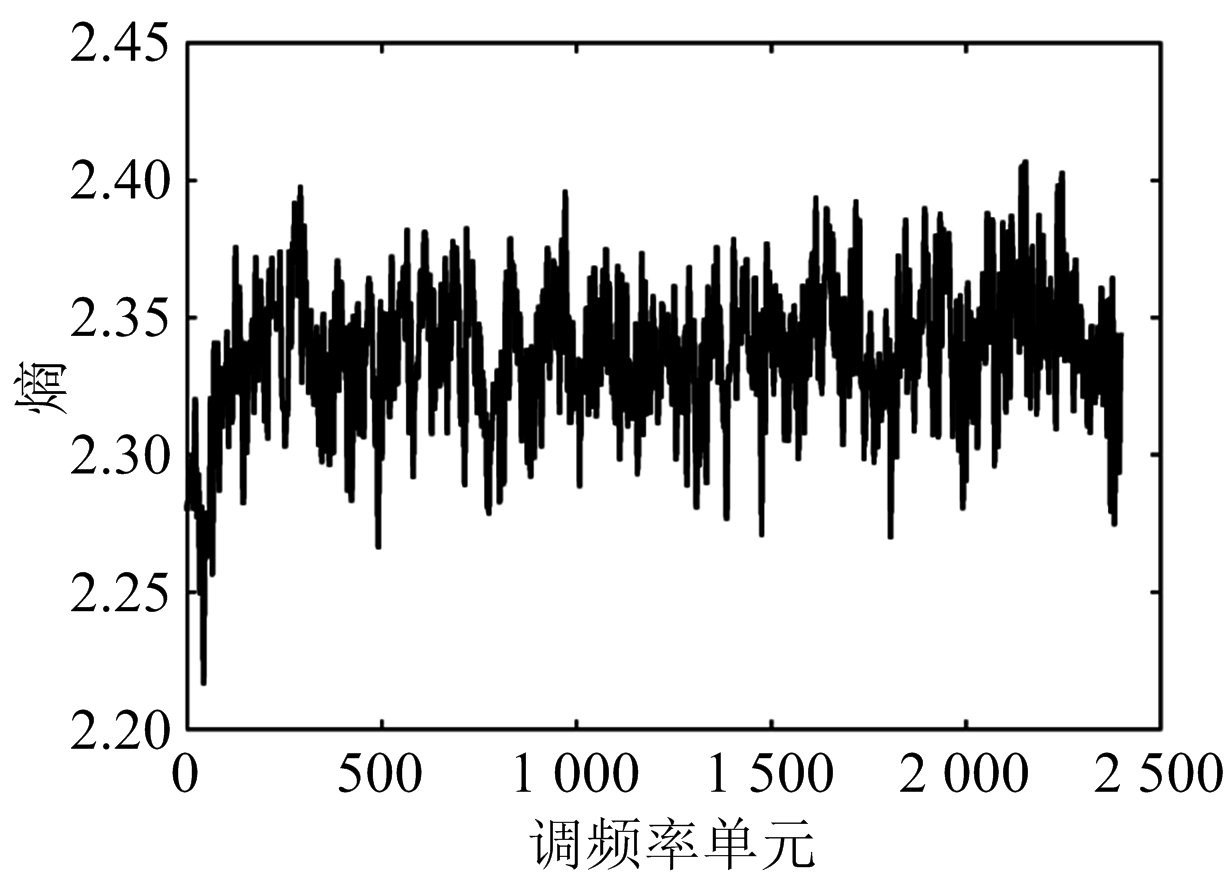
(a)SNR=-15 dB
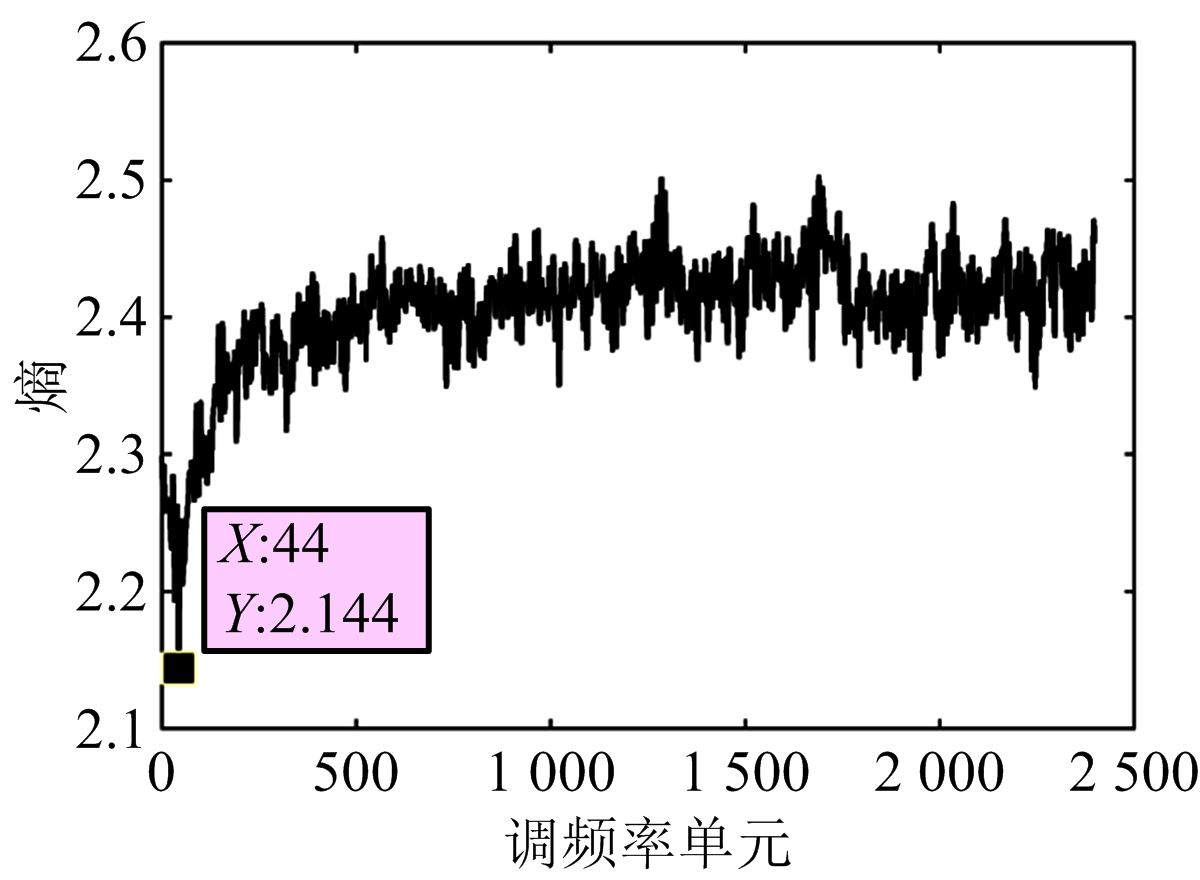
(b)SNR=-10 dB
(c)SNR=-5 dB
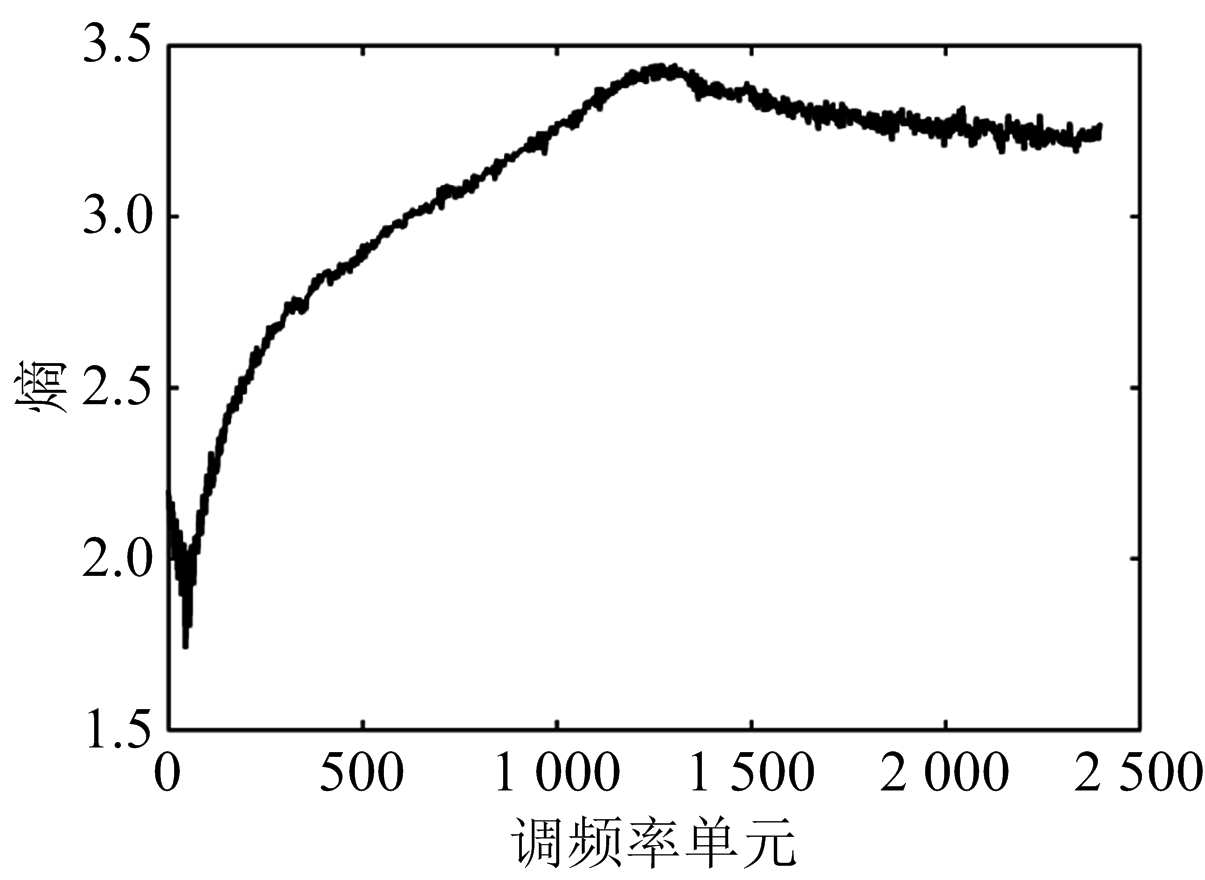
(d)SNR=0 dB
图3 熵函数分布图
图4 速度估计误差比较
实验3 高分辨距离像补偿
图5为径向速度为100 m/s的运动目标与静目标一维距离像的比较，并给出了利用二次速度估计进行运动补偿后的一维距离像。可见，补偿后的运动目标距离像的距离走动和距离扩展基本为零，和静目标的一维距离像基本吻合。
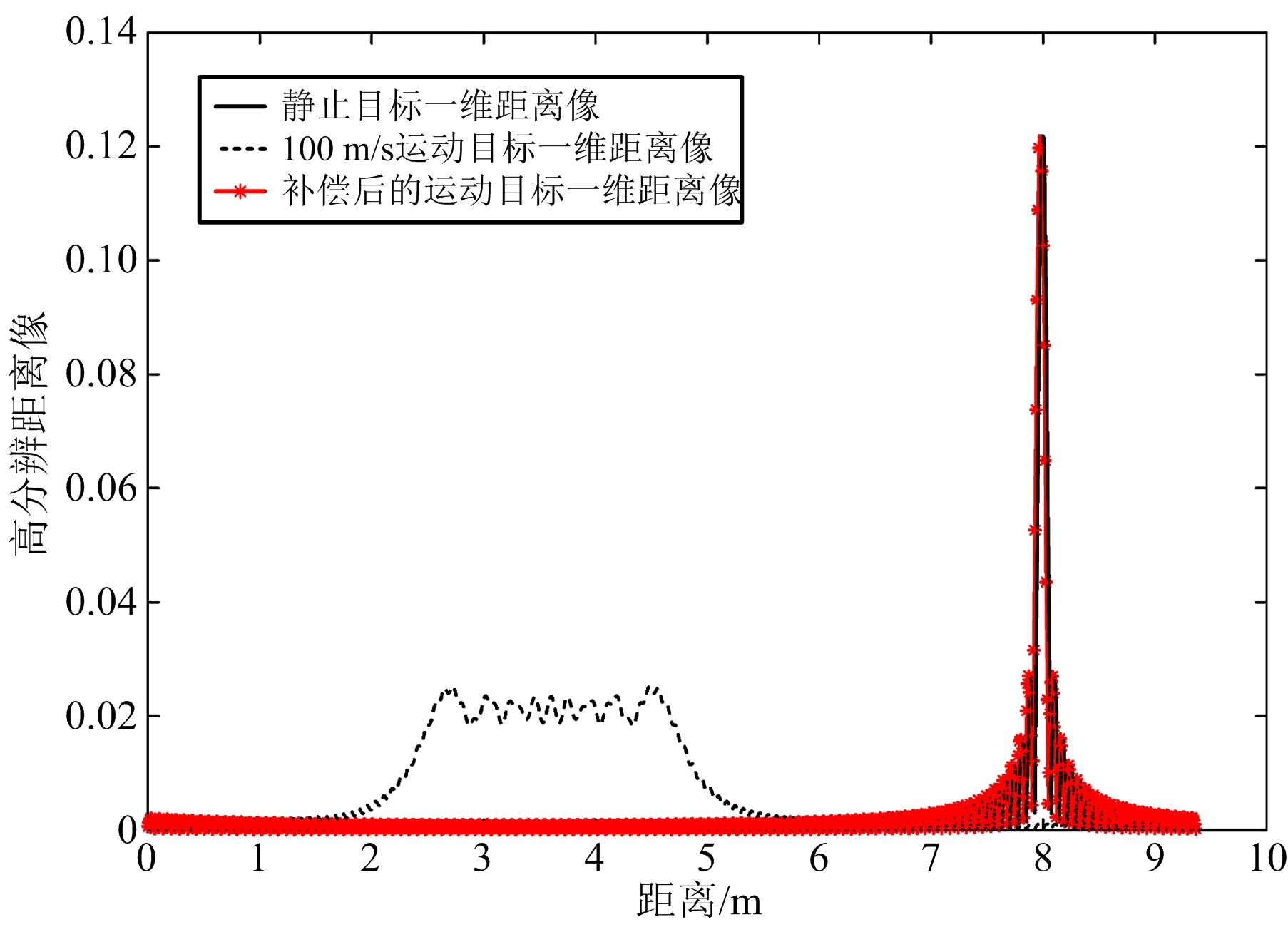
图5 距离像补偿结果
针对频率步进雷达高分辨距离像的运功补偿问题，本文提出了一种基于二次速度估计的距离像运动补偿算法。该算法首先利用互相关FFT法获得粗略估计值，然后结合基于最小波形熵的MDCFT参数估计来实现目标速度精确补偿。仿真结果证明，该联合速度补偿法具有运算效率高、抗干扰能力强、实时性好等优势，满足实际工程需要。
[1] 毛二可,龙腾,韩月秋. 频率步进雷达数字信号处理[J]. 航空学报, 2001, 22(增刊):16-17.
[2] 崔应留,罗文茂,王德纯. 基于联合调频傅里叶变换的步进频雷达目标运动的补偿[J]. 北京理工大学学报(自然科学版), 2015, 35(6):630-633.
[3] 黄文韬,周建江,路冉. 基于多核DSP的高分辨距离像运动补偿算法实现[J]. 数据采集与处理, 2014, 29(4):571-576.
[4] XIA Xianggen. Discrete Chirp-Fourier Transform and its Application to Chirp Rate Estimation[J]. IEEE Trans on Signal Processing, 2000, 48(11):3122-3133.
[5] 陈建军,王飞行,陈远征. 频率步进雷达高分辨距离像解模糊方法研究[J]. 国防科技大学学报, 2009, 31(4):94-97.
[6] 孙泓波,郭欣,顾红,等. 修正离散Chirp-Fourier变换及其在SAR运动目标检测中的应用[J]. 电子学报, 2003, 31(1):78-81.
[7] 吕明久,李少东,杨军,等. 基于全局最小熵的随机稀疏调频步进信号运动补偿方法[J]. 系统工程与电子技术, 2016, 38(8):1749-1751.
[8] 于卫东,涂亚庆,詹启东,等. 基于改进Rife算法的LFMCW雷达测距方法及实现[J]. 电子测量与仪器学报, 2015, 29(4):552-554.
