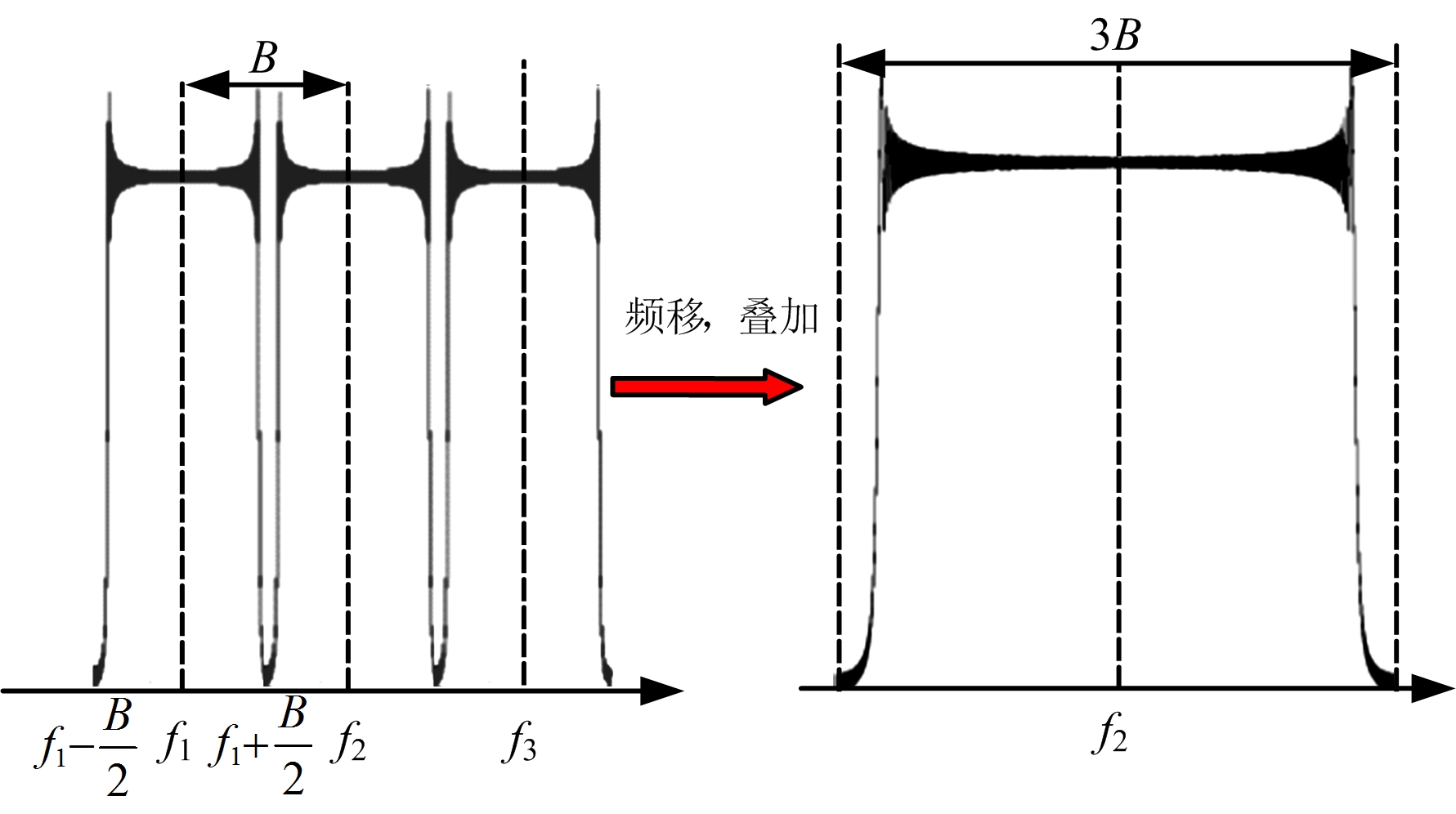
图1 频域子带合成示意图
合成孔径雷达(Synthetic Aperture Radar, SAR)是一种主动式微波遥感设备。与光学遥感设备相比，其成像能力更强，受环境因素的影响小，而且SAR工作波段多样性能够使其适用于不同的应用场景。高分辨率SAR在立体测绘、农业普查、城建勘测、减灾救灾、资源保护、海域动态监测等民用领域以及侦察、监视等军事领域有着不可替代的作用。对于分辨率越高的图像，从图像中获取的目标特征和场景信息就越丰富，其应用价值就越大[1-4]。
受到SAR图像距离向分辨率与发射信号带宽成反比的制约，增大发射信号的带宽能够有效地提高SAR的距离向分辨率，但是直接接收大带宽信号会给系统接收模块和信号采集模块的设计与硬件实现带来较大的困难。目前一些实用的高分辨率SAR系统大都采用子带合成技术来实现大带宽。法国的机载SAR系统RAMSES对5个子带进行合成，总带宽达到1.2 GHz[5]。德国FGAN公司的PAMIR机载SAR系统在2011年升级后，合成带宽由1.8 GHz增加到3.6 GHz[6-7]。国内中国科学院电子学研究所等单位也开展了相关的工作，并且实现了多子带机载SAR系统。其中中国科学院电子学研究所研制的多子带机载SAR系统，采用子带合成技术可以实现总带宽达3.6 GHz宽带信号的收发，这使得距离向分辨率最高达4.17 cm[8]。
子带信号通过系统的不同部分，不可避免地会因为系统的非理想特性引入误差，由于子带误差会降低合成后的成像质量，所以在子带合成前必须对误差进行补偿。文献[9]针对子带相位误差建立了一种两步式估计模型，仅对通道相位误差进行补偿。文献[10]提出了基于回波数据方法来补偿通道误差。文献[11]利用角反射器计算每个子带系统的相位差。文献[12]采用FIR滤波器校正系统产生的幅相误差，该方法在信号时域进行补偿。文献[13]使用一种基于空间闭环辐射测量和具有频偏误差修正的矢量网络分析技术相结合的方法进行幅相误差校正。本文针对子带合成中存在的子带内误差和子带间误差，利用地面定标数据提取出子带内相位误差曲线和幅度误差曲线，将二者补偿到每个子带数据中，由于接收的信号在时域是混叠的，只能在频域进行误差提取和补偿。针对子带间误差结合实测数据的特点，提出了基于实测数据根据对比度最大原则，采用两步式搜索方法计算子带间误差的方法，并将计算的误差补偿到原始数据中，最后在频域进行子带合成并成像。
目前实用的子带合成方案有3种：合成距离包络法[14]、时域合成法和频域合成法[15]。3种方法各有优缺点，合成距离包络法效率最高，但是存在能量溢出，导致距离向形成虚假峰，而且该方法对速度误差敏感。时域合成包含了时移、误差补偿和频谱叠加，效率最低。频域合成在完成子带内和子带间误差补偿以后，只需进行频谱的拼接，具有运算量小、实现简单、性能好等优点[16]。通过以上比较，本文采用的是频域合成法。频域合成其实就是频谱的合成，根据频率步进关系，将各子带信号进行频移，然后进行叠加即可。频域子带合成示意图如图1所示。
图1 频域子带合成示意图
实际信号处理过程中，频域子带合成的主要步骤如下：
步骤1 子带内幅度和相位误差补偿；
步骤2 子带间的延迟误差补偿；
步骤3 根据频率步进关系进行频移；
步骤4 子带信号频谱叠加并进行滤波。
子带误差补偿对于子带合成至关重要，下面将讨论子带误差提取方法。
子带内误差源于系统的非理想特性，发射机发射的信号经过接收机后，信号不再是理想的，出现了一定程度的失真，图2是单子带定标信号脉冲压缩结果。从图中可以看出信号出现了明显的畸变，旁瓣很高且不对称，必须进行补偿。
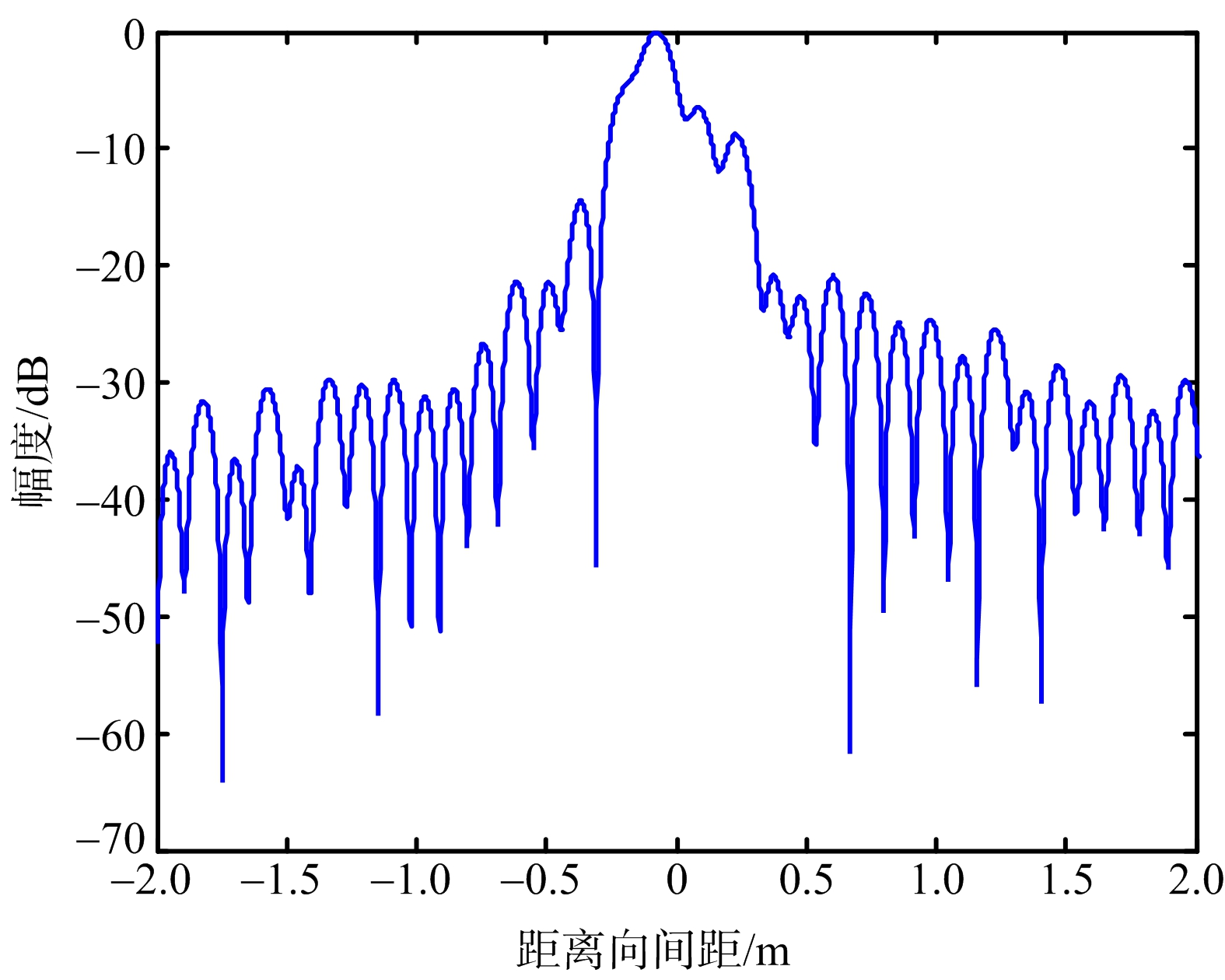
图2 单子带定标信号未补偿脉冲压缩
假设步进频率线性调频信号形式为
n=0,1,…，N-1
(1)
式中，f0为雷达起始载频，Δf为相邻子带载频差，K为距离向调频率，Tp为信号宽度。
信号经过系统后会产生幅度和相位畸变，经过解调后畸变后的定标信号可以表示为
n=0,1,2,…，N
(2)
式中，n表示第n个子带，m表示第n个子带的第m个脉冲，
表示幅度畸变，
表示相位畸变。将
和
变换到频域，表示为
和
则幅度和相位误差为
(3)
(4)
通过以上理论分析，利用定标数据，误差提取步骤如下：
步骤1 根据系统参数构造理想的线性调频信号
将定标信号
和理想信号
进行FFT。
步骤2 对
和
进行脉冲压缩，计算和脉压后峰值位置x(n)和xd(n)，相应的位置偏移量Δn=x(n)-xd(n)，并对定标信号进行补偿。
步骤3 为不失一般性，对定标信号进行每隔两个抽取一个，共抽取2 000帧信号，利用式(3)和式(4)计算该2 000帧的幅度和相位误差值，并计算幅度和相位误差的平均值
和
步骤4 对计算的幅度和相位误差平均值
和
进行平滑以滤出坏值，通过调整平滑窗的大小，使得平滑误差曲线补偿效果比较好，确定最终的误差补偿曲线。
误差提取方法的流程如图3所示。
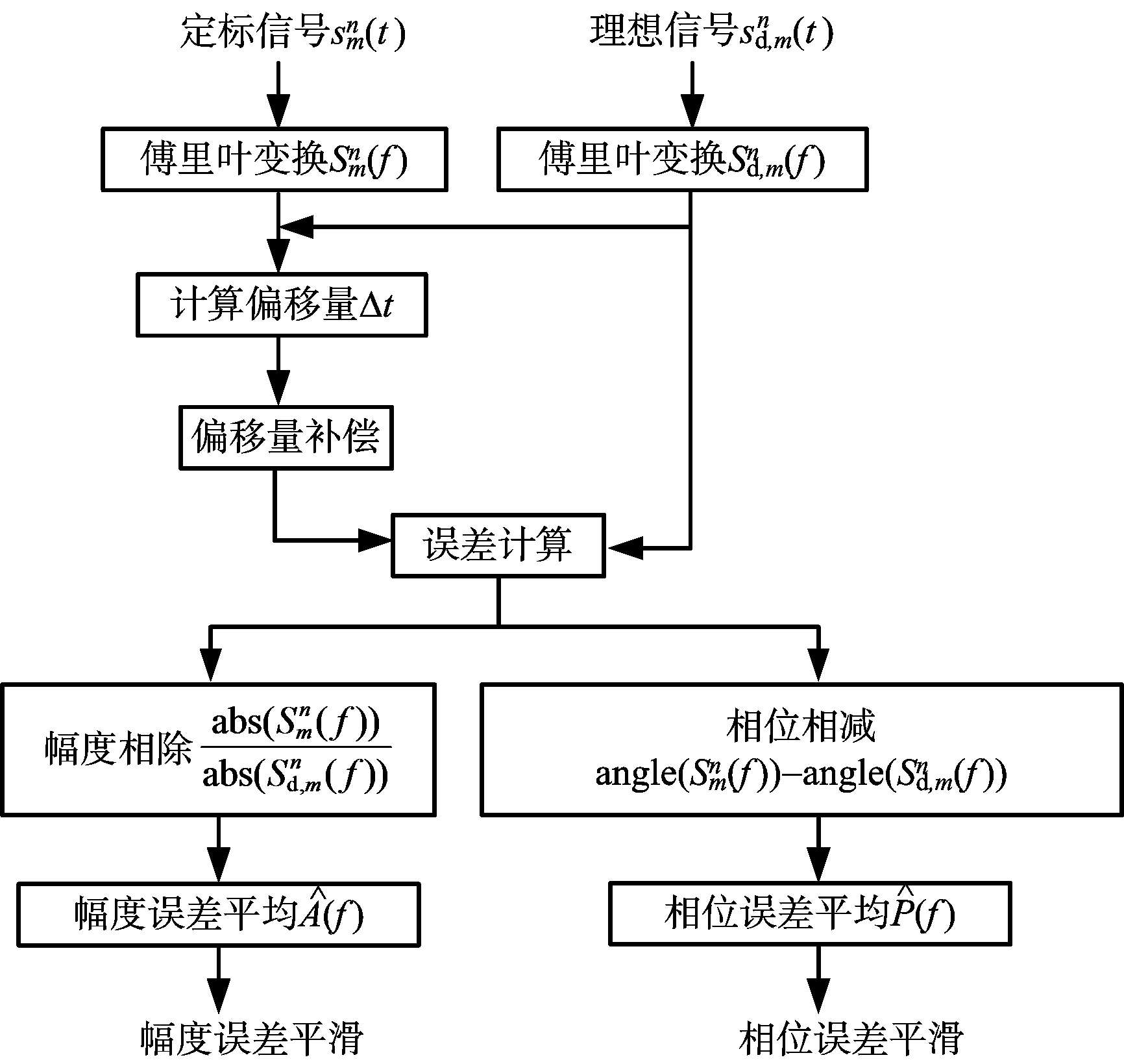
图3 子带内幅度和相位误差提取流程图
为了验证子带内误差提取的正确性，利用地面定标数据进行处理，子带内误差如图4所示，误差补偿前后脉压结果如图5所示。对误差补偿前后结果计算如表1和表2所示。
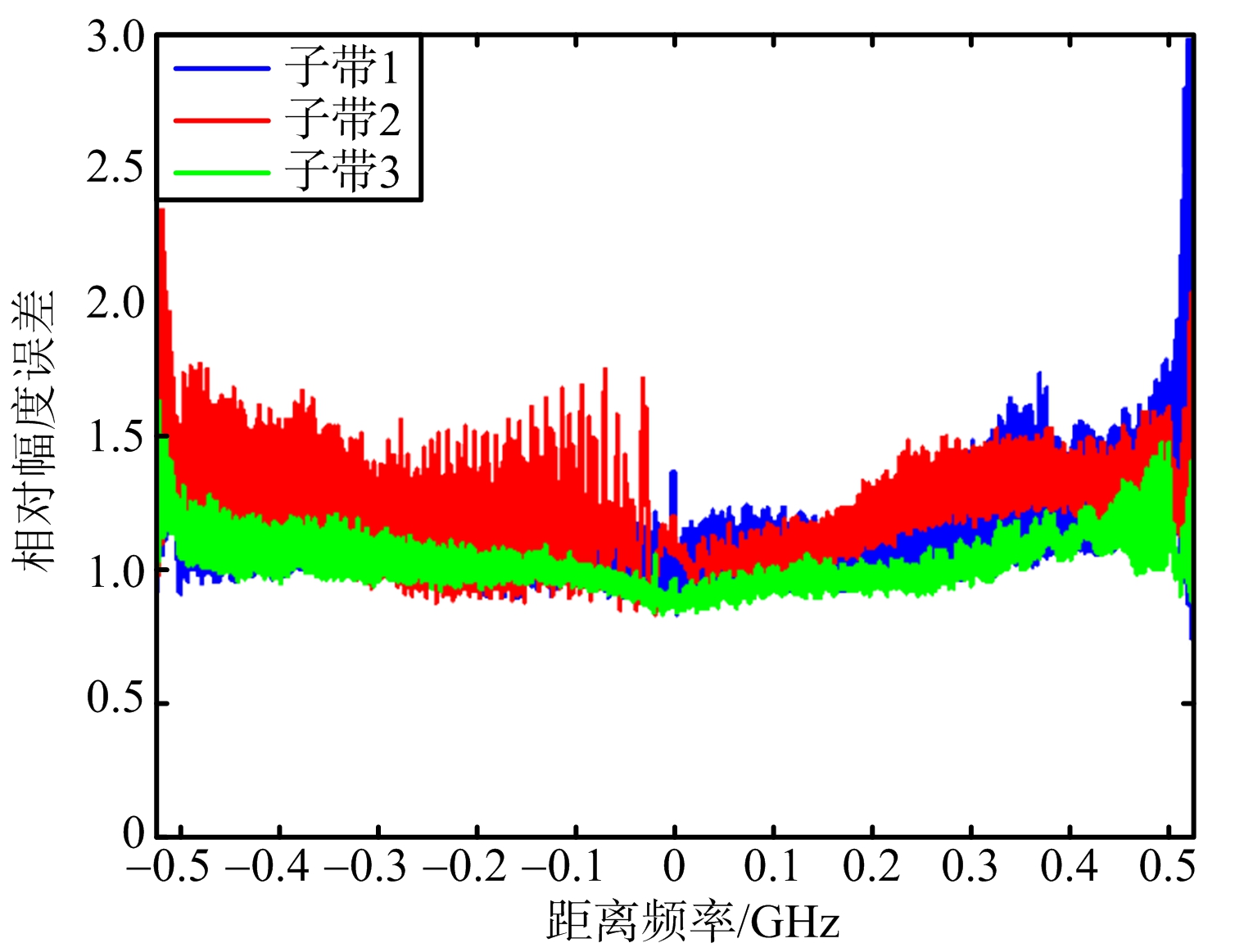
(a) 3个子带幅度误差曲线
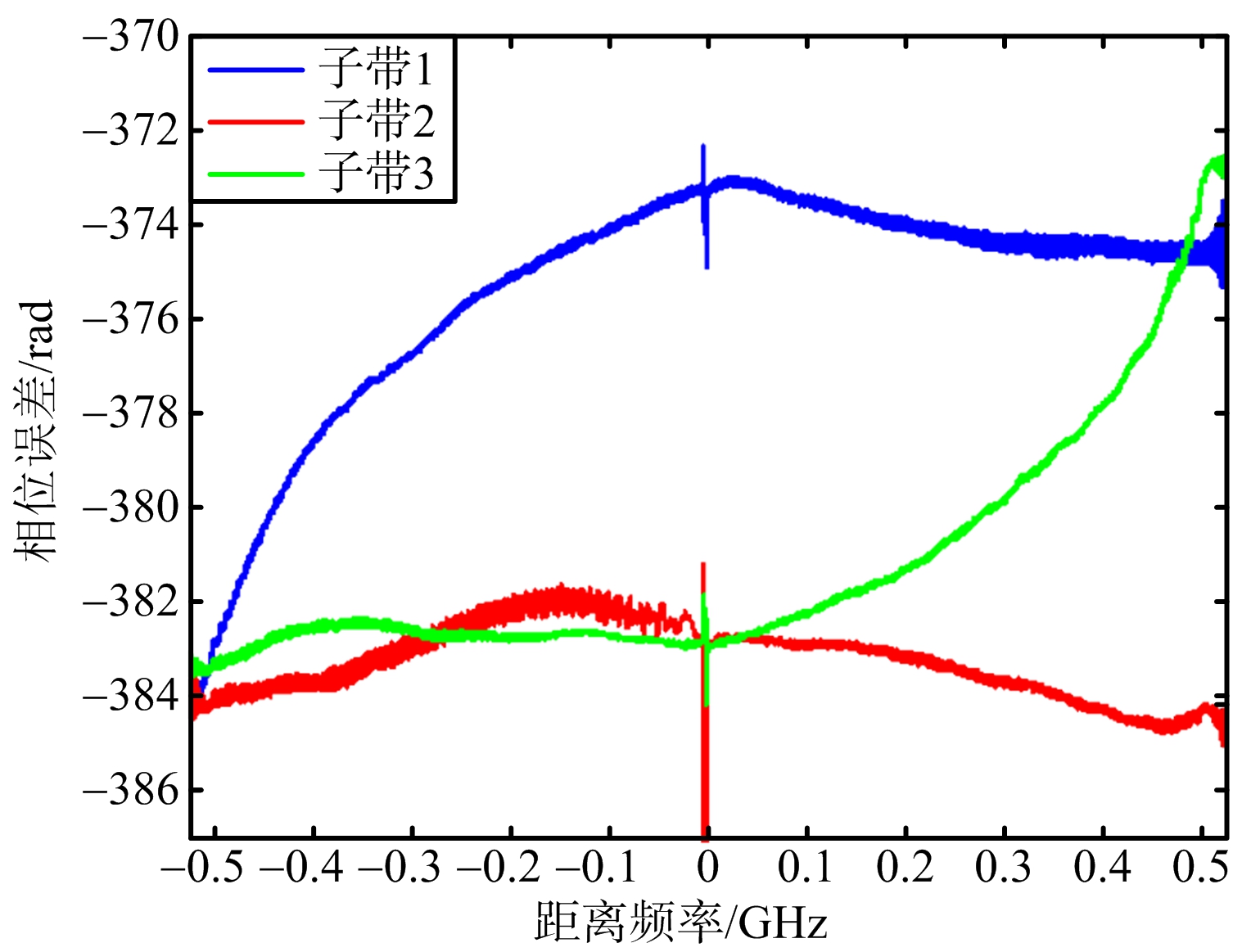
(b) 3个子带相位误差曲线
图4 3个子带幅度和相位误差曲线
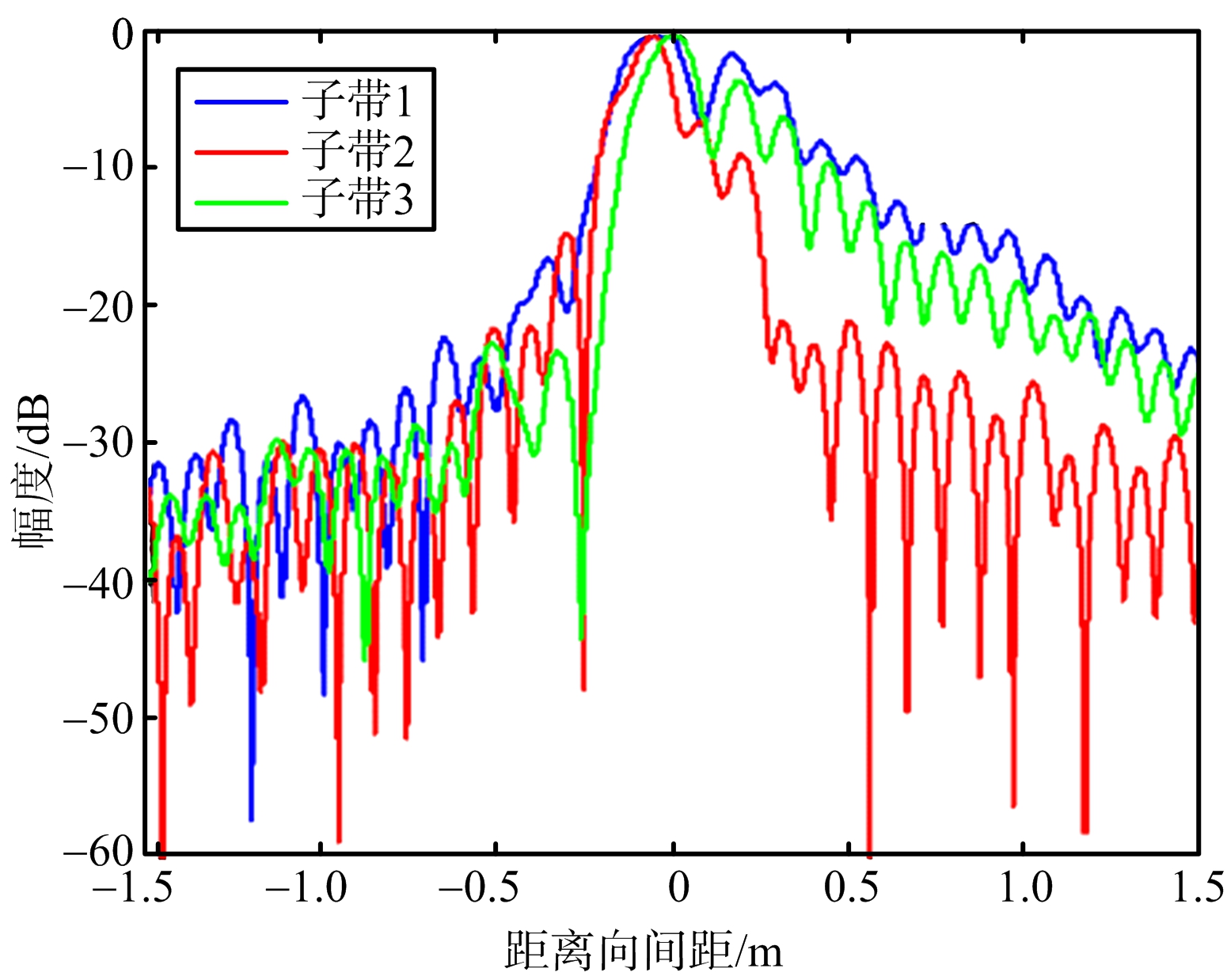
(a) 带内误差补偿前信号脉冲压缩结果
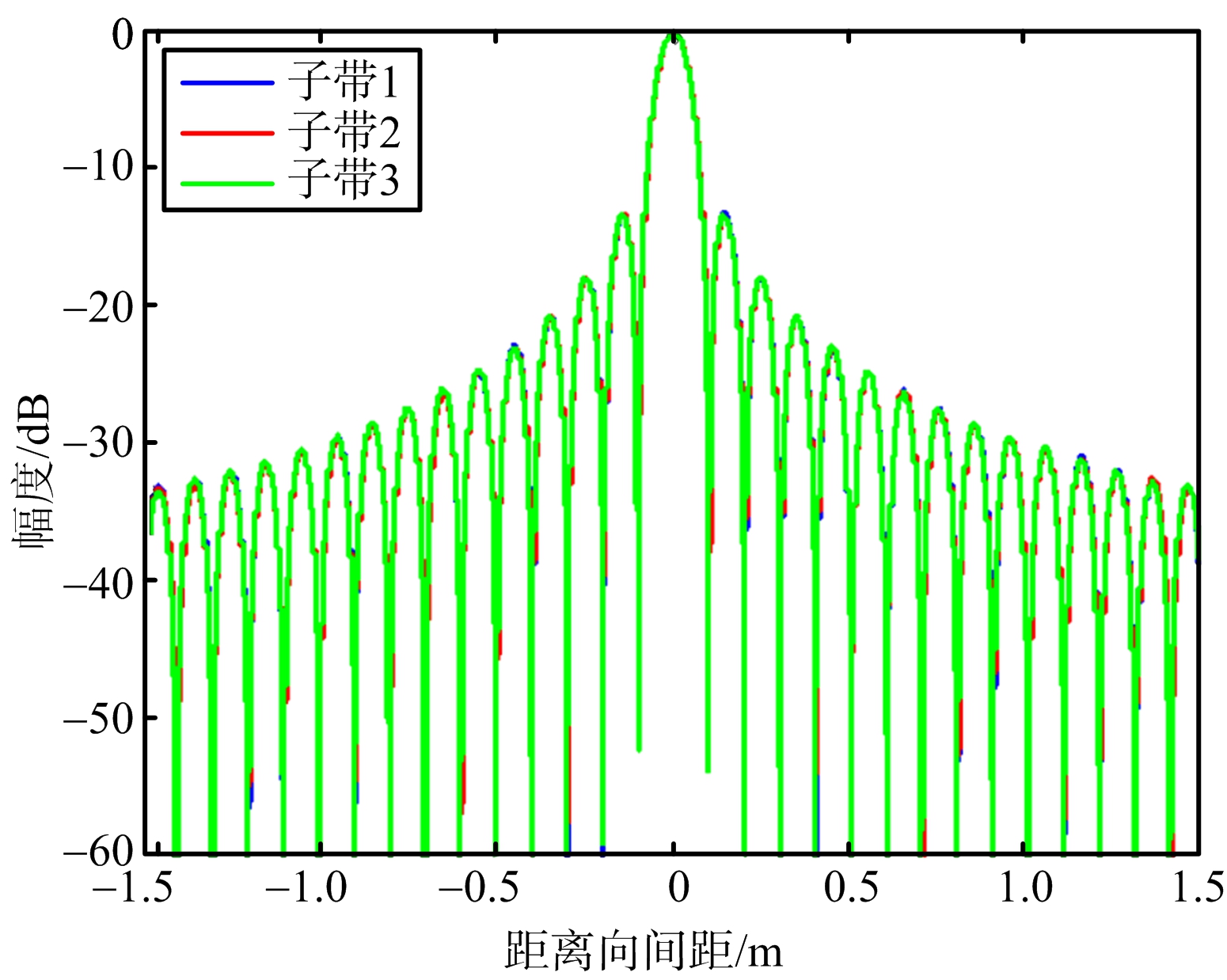
(b) 带内误差补偿后信号脉冲压缩结果
图5 带内误差补偿前后信号脉冲压缩结果
表1 子带内误差未补偿脉压指标
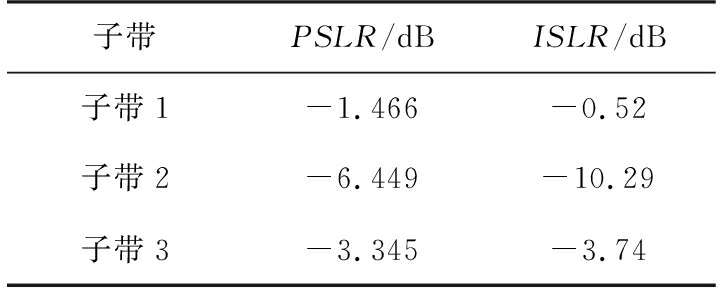
子带PSLR/dBISLR/dB子带1-1.466-0.52子带2-6.449-10.29子带3-3.345-3.74
表2 子带内误差补偿后脉压指标
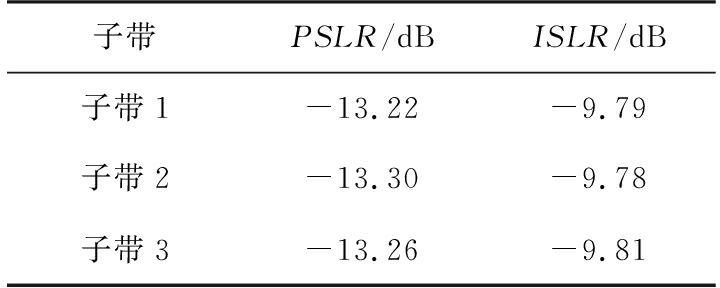
子带PSLR/dBISLR/dB子带1-13.22-9.79子带2-13.30-9.78子带3-13.26-9.81
在图4中，为了尽可能准确地提取幅度和相位误差，保留了误差曲线两端的振荡，为了便于观察比较3子带相位误差，对子带1和子带3进行了移动，数值是2π的整数倍，对结果没有影响。从图中可以看出，3个子带的幅相误差均不相同。
从图5(a)脉冲压缩的结果可以看出，单子带定标信号经过系统后出现了严重的失真，这种信号无法进行子带合成。图5(b)和3个子带指标计算结果均表明，利用本文使用的方案提取出子带内幅度和相位误差，经过误差补偿以后，单子带信号脉冲压缩结果和理想信号基本一致，为后面子带间误差计算以及最终的子带合成提供了必要条件。
由于3个子带信号经过系统的不同接收机部分，接收机之间的差异会对信号造成不同的延迟，该延迟如果不进行补偿子带合成就会失败。由于该机载SAR系统发射端使用倍频的方式直接发射的是带宽为3.6 GHz的信号，利用3个载频不同的接收机对回波信号的不同部分进行接收，所以子带间的幅度和相位误差非常小，对子带合成的影响可以忽略，主要考虑子带间的延迟，即采样点偏移量。本文提出了一种基于原始数据的相对延迟估计方法，利用对比度最大原则估计相对延迟量，并且为了提高偏移量估计的精度，采用了两级搜索方案，具体的估计步骤如下：
步骤1 对数据进行距离向脉冲压缩；
步骤2 选取子带2作为参考子带，根据系统参数对子带1和子带3进行循环移位，移位量为fs·Tp，使得3个子带基本重合；
步骤3 计算偏移量整数部分：设置搜索步长为1，对子带1和子带3分别进行循环移位，计算图像对比度，当对比度达到最大时，停止搜索，得到偏移量整数值；
步骤4 计算偏移量小数部分：在上一步的基础上，设置搜索步长0.01，对子带1和子带3进行微调，当对比度达到最大时，停止搜索，得到偏移量的小数值；
步骤5 将子带1和子带3移回到原来位置，并根据两次搜索的偏移量对子带1和子带3进行补偿。
实际操作的流程图如图6所示。
步骤2中，fs是采样率，Tp是子带信号脉冲宽度。根据以上步骤，分别对子带1和子带3相对于子带2的偏移量进行计算，并将偏移量补偿到子带1和子带3中用于后续成像。子带内和子带间误差计算完成后，接下来通过机载SAR实测数据进行验证。
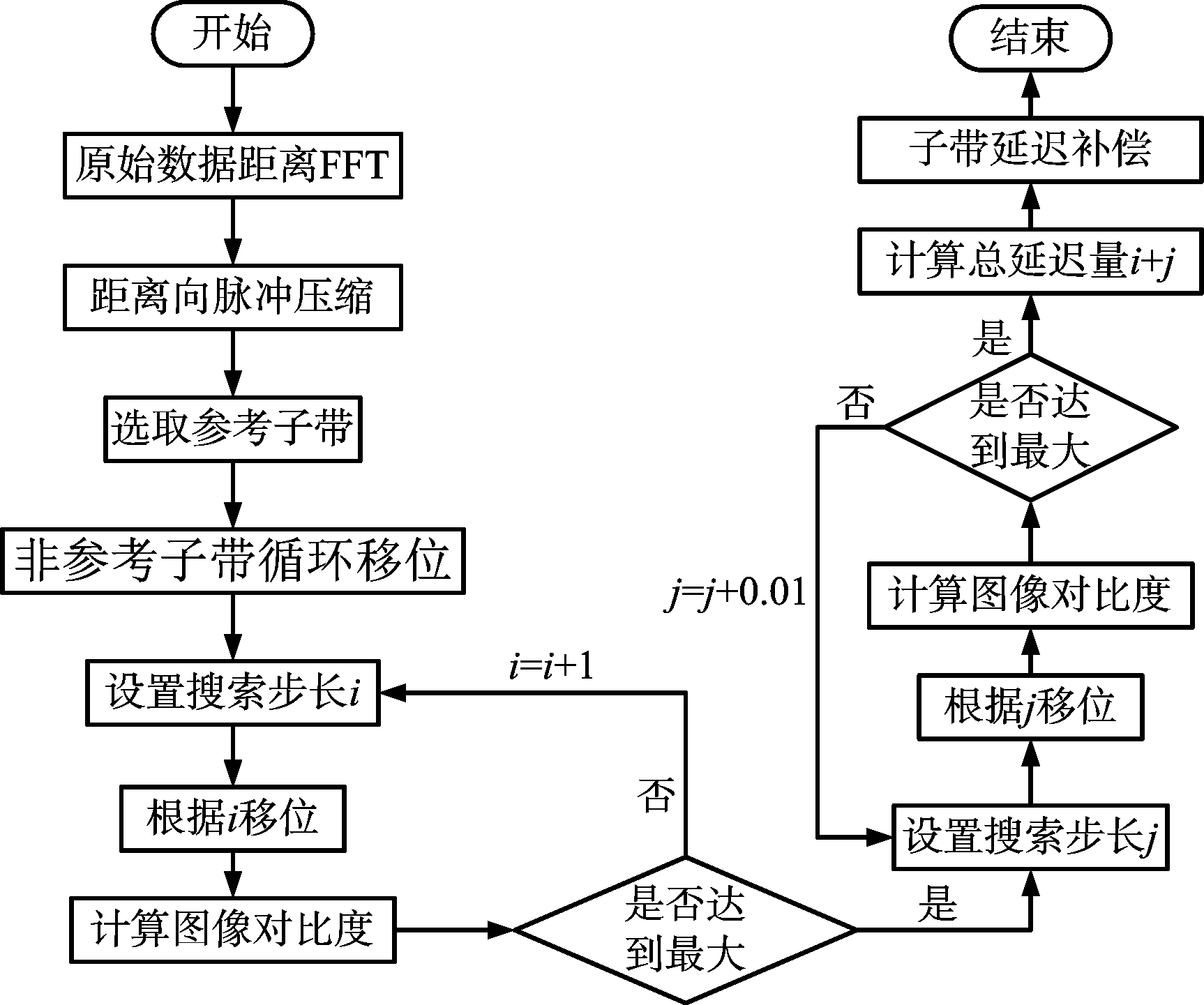
图6 子带间偏移量计算流程图
子带内和子带间误差补偿完成后，利用实际的机载数据进行成像，以验证计算结果。成像处理基本流程如图7所示。
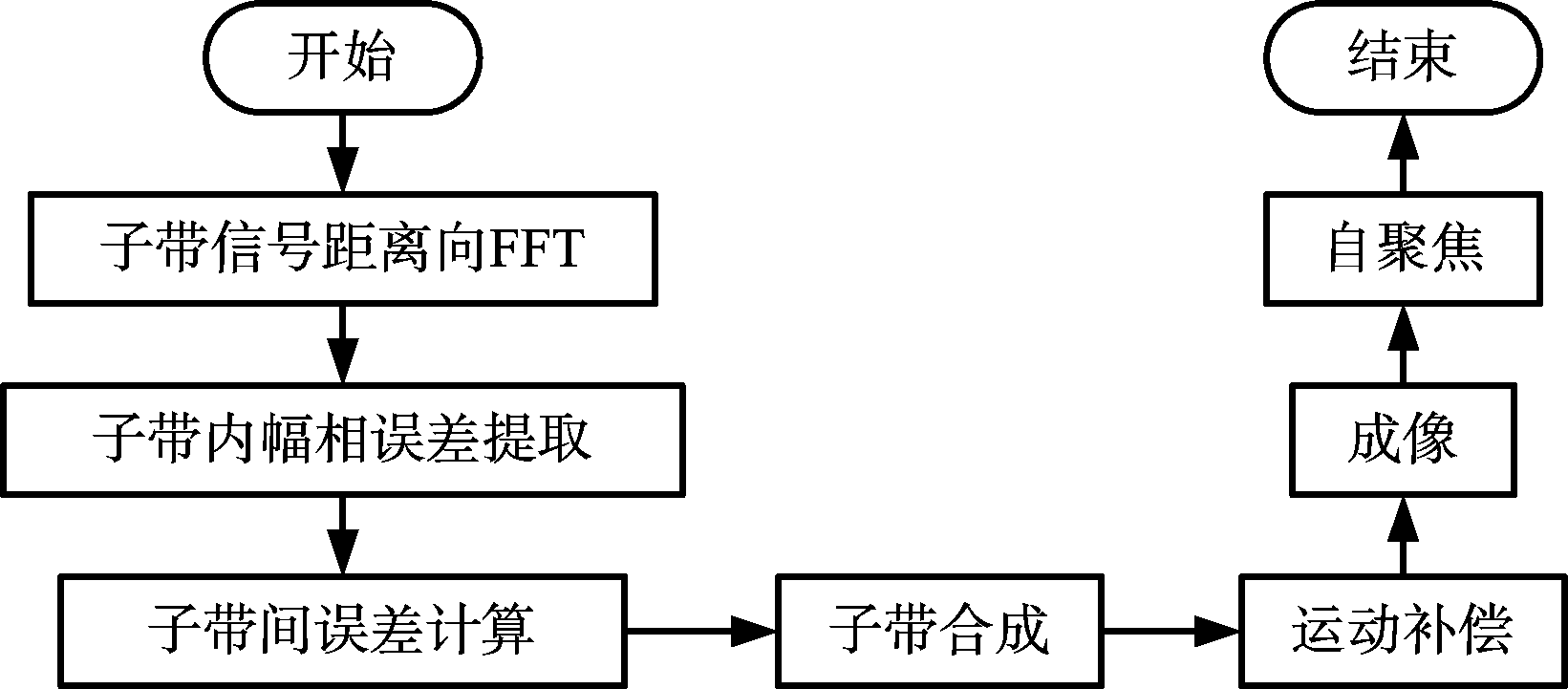
图7 多子带合成成像处理流程
实际使用的机载SAR系统的载频为9.6 GHz，3个子带信号的带宽为1.2 GHz。根据以上设计的处理流程，利用实际飞行数据进行测试，测试主要包括单子带带内误差补偿前后成像结果对比，单子带误差补偿后成像结果与3个子带误差补偿后子带合成成像结果对比。一方面验证子带内幅度与相位误差和子带间误差提取方法的正确性，另一方面可以验证通过子带合成技术能够实现大带宽信号的收发，到达高分辨率成像的目的。
在定标数据的频域提取出子带内幅度和相位误差后，先将3个子带的原始数据变换到距离频域，然后将幅度误差和相位误差与之相乘，以完成子带内误差补偿。紧接着从原始数据中提取出子带间的延迟误差，并对子带1和子带3进行补偿,然后在频域进行子带合成，利用合成后的大带宽数据进行成像，以得到高分辨率的图像。
为了验证子带内误差提取的效果，对子带2进行了成像，对比子带内误差补偿前后成像的结果，实际场景成像结果如图8所示。
(a) 子带内误差未补偿成像结果
(b) 子带内误差补偿后成像结果
图8 子带内误差补偿前后成像结果对比
从图8(a)、图8(b)可以看出，带内误差补偿前，成像场景中强目标距离向旁瓣很高，远端旁瓣数值也较高，会遮盖周围弱目标，成像效果很差。经过带内幅度和相位误差补偿后，旁瓣数值降低十分明显，远端旁瓣对周围目标的影响非常小，成像质量得到明显改善。综合以上处理结果可知，子带内幅度和相位误差得到了有效的补偿。
为了验证子带间误差提取方法的可行性和准确性，将3个子带进行合成，利用定标数据比较单子带成像与子带合成后成像的效果。经过子带内和子带间误差补偿后，3个子带信号和子带合成后信号的脉冲压缩结果如图9所示，表3给出了点目标子带合成前后性能分析。
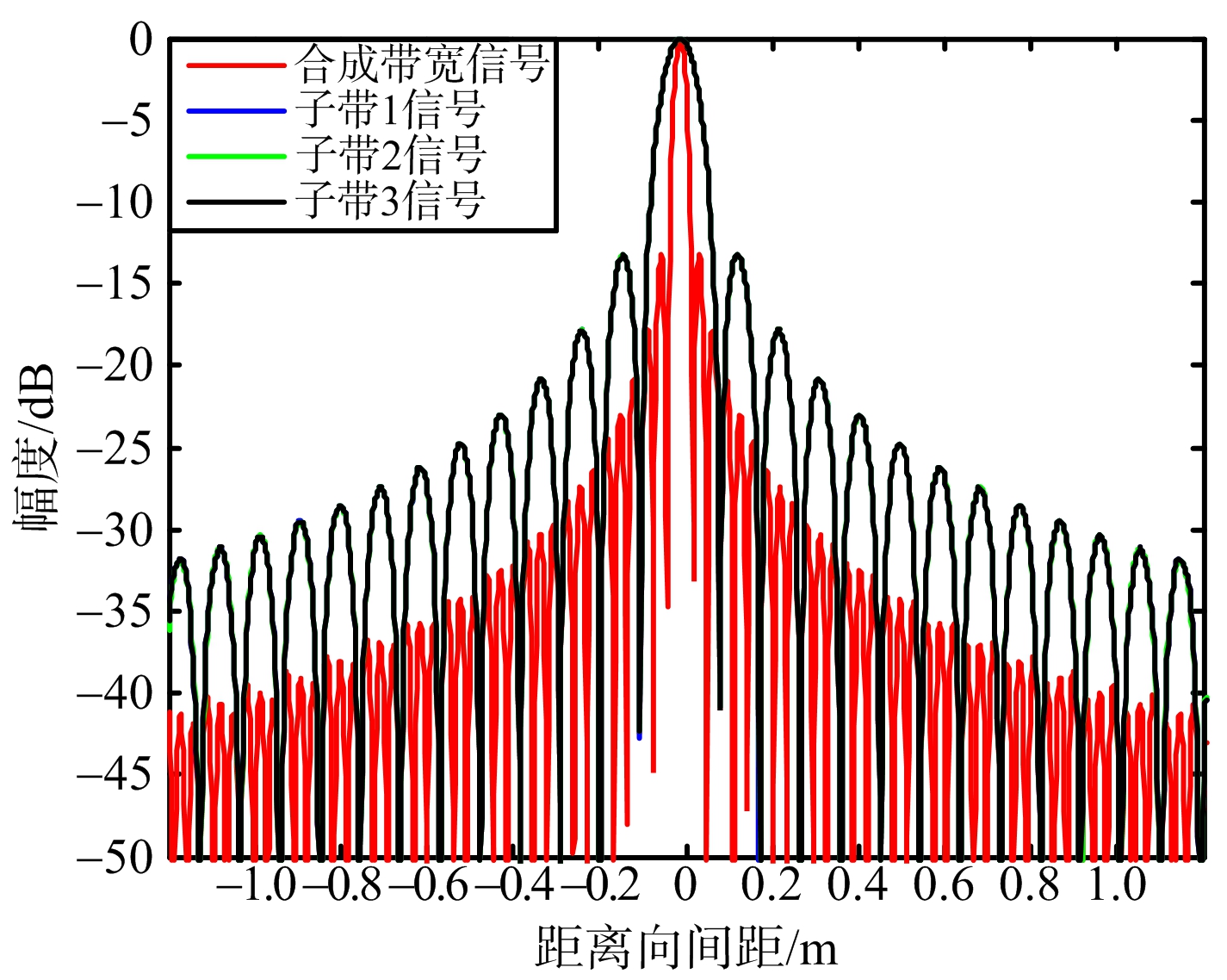
图9 带误差补偿后3个子带信号与子带合成后信号脉冲压缩结果
表3 单子带和子带合成后信号性能对比
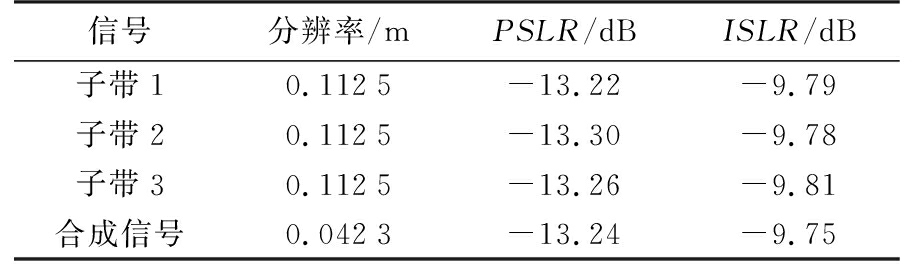
信号分辨率/mPSLR/dBISLR/dB子带10.1125-13.22-9.79子带20.1125-13.30-9.78子带30.1125-13.26-9.81合成信号0.0423-13.24-9.75
为了进一步验证结果的正确性，利用机载SAR飞行数据对实际场景进行成像，成像结果如图10所示。
(a) 子带间误差补偿前3个子带合成后成像结果
(b) 子带间误差补偿后3个子带合成后成像结果
(c) 框中单子带成像结果局部放大
(d) 子带间误差补偿前子带合成后成像结果局部放大
(e) 子带间误差补偿后子带合成后成像结果局部放大
图10 机载实测数据处理结果
按照本文提出的子带间误差计算方法，提取出误差并补偿到原始数据后，进行了3个子带合成。通过图9和表3可以看出，经过子带内误差补偿后单子带性能指标与理想值相符，而子带间误差补偿后，3个子带合成脉冲压缩结果可知，距离向分辨率与3.6 GHz带宽的理论分辨率十分接近，峰值旁瓣比和积分旁瓣比与理想值一致。实际场景成像结果如图10(b)所示，成像场景中地物信息丰富。选取一块场景进行局部放大如图10(c)所示，对比子带间误差补偿前后结果图10(d)、图10(e)可以看出，误差补偿前成像质量较差，细节很模糊，误差补偿后成像质量得到了很大的改善。对比单子带和3个带合成后成像效果，从图10(c)、图10(e)可以看出，经过子带合成后，房屋轮廓更加清晰，许多目标的辨识度更强，效果明显优于单子带成像效果，可以在实际成像处理中运用。
本文针对多子带合成技术中子带内幅度与相位误差利用定标数据进行了计算，并给出了具体的操作流程。针对子带合成技术中子带间误差提出了一种基于原始数据的计算方法，该方法根据图像对比度最大原则，采用两级计算方式，提高了子带间误差计算的精确度。最后利用定标数据和机载SAR实测数据进行成像分析，验证了本文所提出的误差计算方法的有效性。
[1] 邓云凯,赵凤军,王宇. 星载SAR技术的发展趋势及应用浅析[J]. 雷达学报, 2012, 1(1):1-10.
[2] 崔丽萍,王晓青. SAR影像建筑物震害检测方法研究综述[J]. 震灾防御技术, 2016, 11(2):239-250.
[3] 范剑超,王德毅,赵建华,等. 高分三号SAR影像在国家海域使用动态监测中的应用[J]. 雷达学报, 2017, 6(5):456-472.
[4] 王岩飞,刘畅,詹学丽,等. 无人机载合成孔径雷达系统技术与应用[J]. 雷达学报, 2016, 5(4):333-349.
[5] WANG X, WANG R, DENG Y, et al. Precise Calibration of Channel Imbalance for very High Resolution SAR with Stepped Frequency[J]. IEEE Trans on Geoscience and Remote Sensing, 2017, 55(8):4252-4261.
[6] BRENNER A R, ENDER J H G. Demonstration of Advanced Reconnaissance Techniques with the Airborne SAR/GMTI Sensor PAMIR[J]. IEE Proceedings: Radar, Sonar and Navigation, 2006, 153(2):152-162.
[7] BRENNER A R. Improved Radar Imaging by Centimeter Resolution Capabilities of the Airborne SAR Sensor PAMIR[C]∥ 14th International Radar Symposium, Dresden, Germany: IEEE, 2013:218-223.
[8] 王沛,王翔宇,李宁,等. 超高分辨率机载SAR高精度子带拼接与处理方法研究[J]. 电子与信息学报, 2017, 39(10):2325-2331.
[9] HU Jianmin, WANG Yanfei, LI Heping. Channel Phase Error Estimation and Compensation for Ultrahigh-Resolution Airborne SAR System Based on Echo Data[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(6):1069-1073.
[10] LI Jincheng, CHEN Jie, LIU Wei, et al. A Synthetic Bandwidth Method for High-Resolution SAR Based on PGA in the Range Dimension[J]. Sensors, 2015, 15(7):15339-15362.
[11] LUO X, DENG Y, WANG R, et al. Correction of Channel Imbalance for MIMO SAR Using Stepped-Frequency Chirps[J]. International Journal of Antennas and Propagation, 2014, 2014[161294]:1-8.
[12] 徐倩. 雷达波形产生系统的幅相失真校正技术研究[D]. 成都: 电子科技大学, 2015.
[13] 贾颖新,王岩飞. 一种宽带多通道合成孔径雷达系统幅相特性测量与校正方法[J]. 电子与信息学报, 2013, 35(9):2168-2174.
[14] YANG Jungang, HUANG Xiaotao, JIN Tian, et al. Synthetic Aperture Radar Imaging Using Stepped Frequency Waveform[J]. IEEE Trans on Geoscience and Remote Sensing, 2012, 50(5):2026-2036.
[15] 高梓植,李志强. 基于合成带宽提高距离分辨率的改进方法[J]. 雷达科学与技术, 2017,15(1):95-98.
GAO Zizhi, LI Zhiqiang. An Improved Method for Increasing Range Resolution Based on Synthesized Bandwidth Technique[J]. Radar Science and Technology, 2017, 15(1):95-98. (in Chinese)
[16] 丁海林,李亚超,高昭昭,等. 线性调频步进信号的三种合成方法的对比与分析[J]. 火控雷达技术, 2007, 36(4):10-16.
