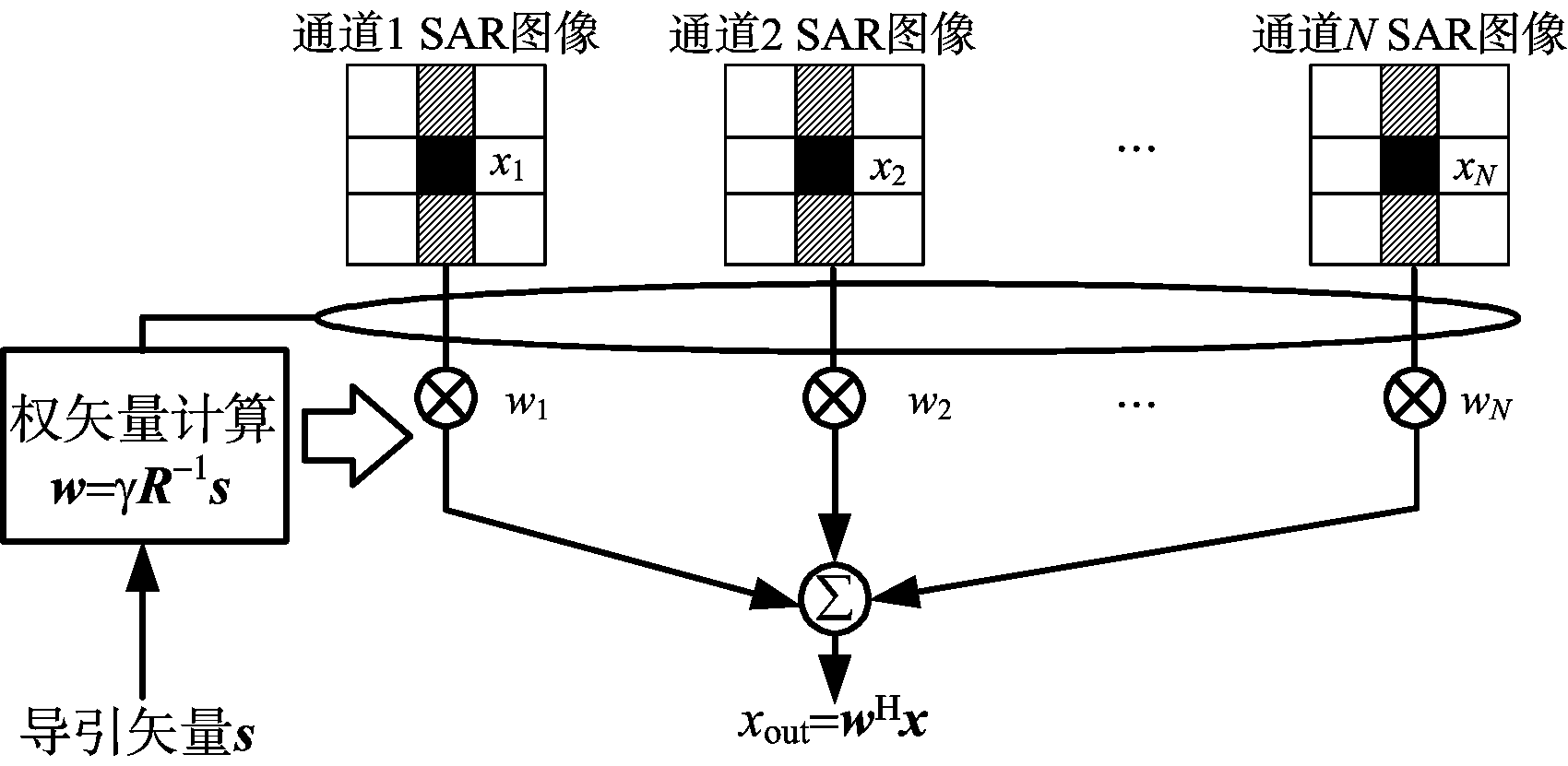
图1 图像域STAP技术原理
多通道SAR/GMTI系统能在全天时、全天候地获取高分辨SAR图像的同时,实现地面动目标检测及跟踪,已成为战略情报侦察和战场监视的重要发展趋势[1-3]。
20世纪末[4],德国的Ender首先将空时自适应处理(STAP)算法引入多通道SAR系统中,并提出了SAR-STAP概念及MSAR(Multichannel-SAR)处理算法,通过空、时两域级联处理对杂波进行抑制,进一步提高慢动目标输出信杂噪比(SCNR),能够获得更低的系统最小可检测速度(MDV)。上述优势使得此类算法获得了学者们广泛关注,经过潜心研究,已提出如特征对消算法[4]、联合像素法[5]、ACSI技术(图像域ADPCA技术)[6]等SAR-STAP处理算法。此类方案在理论提出时,均假设杂波及噪声背景为(复)高斯分布。但随着现代SAR/GMTI系统中SAR传感器分辨率的提高,分辨单元的缩小使中心极限定理不再适用,与此同时,所探测场景类别也不断增加,部分场景杂波数据统计特性不再服从(复)高斯分布。实际杂波统计特性与理论模型的冲突必将引起原有SAR-STAP算法在实际处理中的性能下降。
因此,必须寻找新的统计模型来刻画非高斯杂波,并在此基础上提出新型SAR-STAP算法。在众多非高斯杂波统计建模方案中,Alpha稳定分布[7]是满足广义中心极限定理的唯一的一类分布,其概率密度具有明显的长拖尾性质,能较好地描述雷达非高斯相关杂波[8-10]。因此,本文采用Alpha稳定分布对待检测区域杂波进行建模,并提出基于分数低阶矩的新型杂波抑制算法。与原有的SAR-STAP处理算法相比,新算法能够在非高斯杂波背景中获得良好的检测性能,且具备较强的鲁棒性。本文通过仿真及多组实测数据处理结果对算法进行了验证。
多通道SAR-STAP技术由沿航迹排列的N个通道接收信号,分别获取各接收通道的距离-多普勒图(或SAR图像)后,逐像素单元根据最小均方无畸变(MVDR)准则计算各通道加权系数,在图像间进行空域加权处理,实现杂波抑制。其原理如图1所示。

图1 图像域STAP技术原理
N通道SAR数据某一像素单元的接收信号可由N×1维列向量(空域快拍)表示为
![]()
(1)
式中,γ,s分别为动目标的幅度和导引矢量,c为杂波分量,n为噪声分量。根据MVDR准则,通过拉格朗日乘子法求解可得使输出信杂噪比(SCNR)最大的最优权矢量为
wopt=γR-1s
(2)
式中,R为杂波及噪声分量的自相关矩阵。则此滤波输出为
(3)
由于在实际处理时,杂波及噪声的统计特性未知,某一距离门的杂噪协方差矩阵往往由其极大似然估计(MLE)形式代替,即
(4)
式中,xl为与待检测单元相邻样本信号,L为样本个数。
为对算法性能进行验证,采用该算法对某型机载三通道SAR系统的一组实测数据进行了处理,表1给出了部分系统参数,处理中选取的训练样本数为32个(远大于空域自由度的2倍)。图2、图3分别给出了数据在空域处理前单通道SAR图像以及空域处理后的杂波抑制输出结果。从SAR图像中可以看出,该场景对应的区域存在建筑群,因此存在较多的强散射点杂波。而从杂波抑制结果中可以明显看出存在大量的杂波残留,实际的杂波抑制性能远远小于理论效果。
表1 三通道SAR系统参数
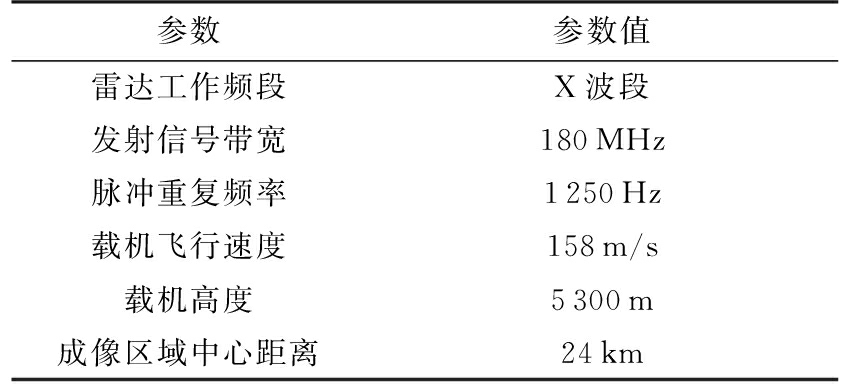
参数参数值雷达工作频段X波段发射信号带宽180MHz脉冲重复频率1250Hz载机飞行速度158m/s载机高度5300m成像区域中心距离24km

图2 单通道SAR图像

图3 三通道SAR杂波抑制结果
为寻找导致上述结果中杂波抑制性能与理论值之间的差异的原因,对该区域实测数据作进一步分析,在图4中给出了数据幅度直方图。首先采用瑞利分布对实测数据的幅度进行拟合,结果如图4所示,可以看出实测数据尾部已明显偏离瑞利分布,即该杂波背景体现出较强的非高斯性。由于上述SAR-STAP算法提出的前提即为杂波背景服从高斯分布,故采用该算法对数据进行处理必然存在性能损失。因此,寻找合适的统计模型对实际非高斯杂波进行描述,并在此基础上提出新型SAR-STAP算法,是解决上述问题的关键途径。
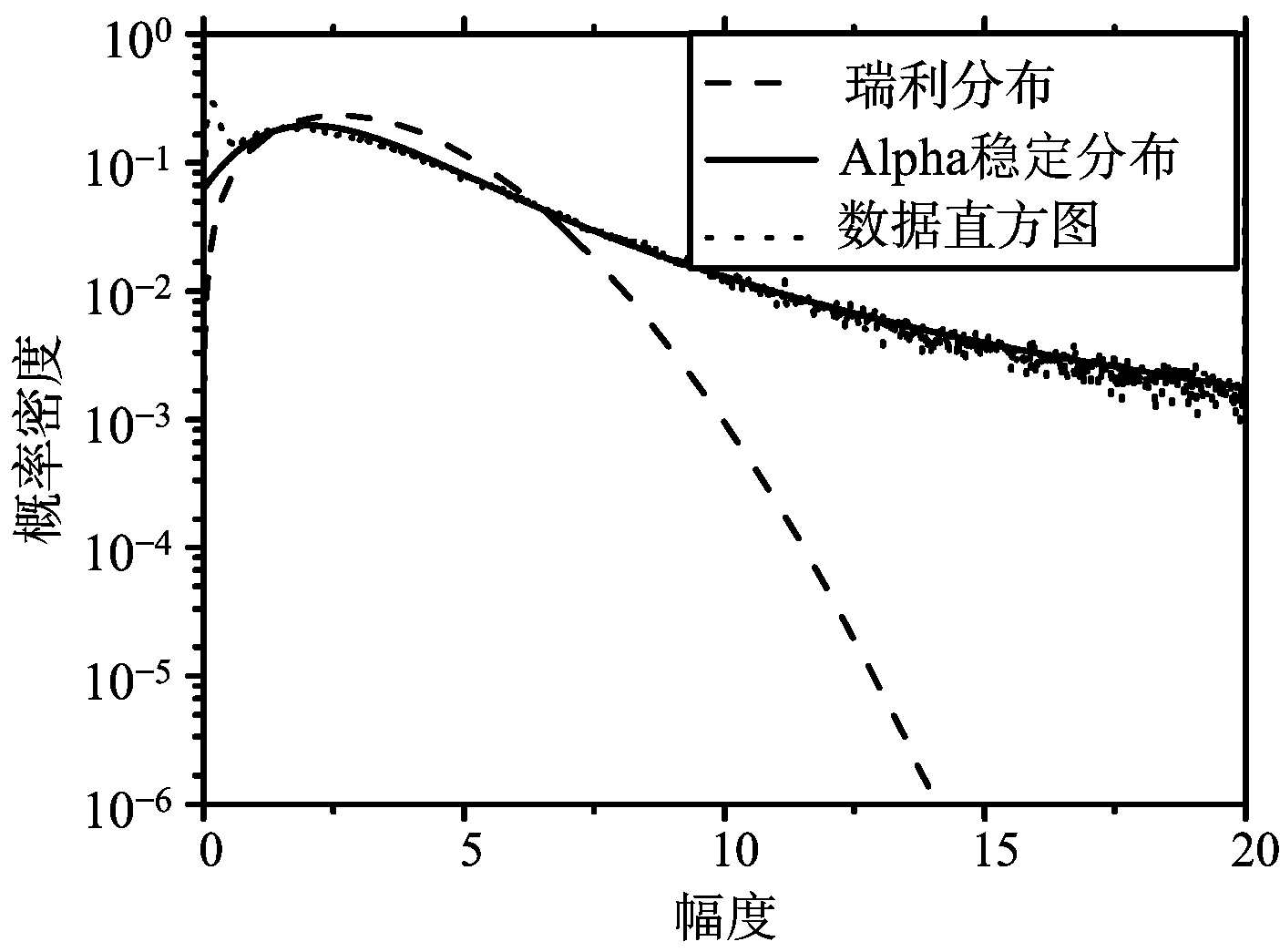
图4 概率密度函数对比图
为解决杂波理论模型与实际不符导致的杂波抑制性能下降,需寻找新的非高斯统计模型来刻画杂波。目前已经有一些针对非高斯杂波模型的研究,如韦布尔分布、K分布、广义Gamma分布、Alpha稳定分布等[11],其中Alpha稳定分布可调整参数逼近其他分布,而在采用Alpha稳定分布拟合杂波数据时发现,与高斯分布相比其统计特性与数据更为吻合。因此,若将Alpha稳定分布统计模型引入SAR-STAP算法中,导出新算法实现杂波抑制,必将提高原有SAR/GMTI系统的性能。本节将给出新算法的推导过程,并采用仿真实验对算法性能进行验证。
在实际环境中,许多杂波噪声源是非高斯的,此类信号完全可以采用具有稳定性质且同时满足广义中心极限定理的Alpha稳定分布建立统计模型[9]。
然而,由于Alpha稳定分布的概率密度函数没有闭合解,故一个服从Alpha稳定分布的随机变量X可用其特征函数描述为
E(exp(iωX))=
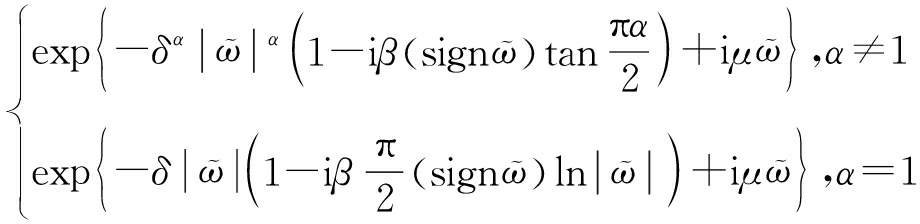
(5)
式中,0<α<2为特征指数,δ>0为离差,类似于方差,-1<β<1为对称参数,-∞<μ<∞为位置参数,sign(·)为符号函数。当β=0时,此分布被称为对称Alpha稳定(SαS)分布,当且仅当随机变量X1和X2为联合SαS分布时,复随机变量X=X1+jX2服从SαS分布。当α=2时Alpha稳定分布退化为高斯分布,但随着α的减小,分布的非高斯性变得明显,其拖尾越长。对于第2节中所给实测数据直方图,采用Alpha稳定分布进行拟合,可得α取1.3,如图4中实线所示,拟合效果明显优于瑞利分布。
由于非高斯Alpha稳定分布中不存在不小于α的高阶统计量,使得二阶统计量及高阶统计量理论不再适用。这就使得文献[12]提出的分数低阶矩理论成为研究此类非高斯相关随机变量的有力工具。一个复SαS分布随机变量X,其p阶统计量可以表示为
E(|X|p)=C1(p,α)δp/α,-1<p<α
(6)
式中,C1(p,α)为与p和α相关的常数,可表示为
C1(p,α)=2p+1Γ((p+1)/2)Γ(-p/α)/
(7)
式中,Γ(-p/2)为Gamma函数。
在Alpha(α<2)稳定杂波环境中不存在二阶统计量,只能采用基于分数低阶矩的杂波抑制算法进行处理。故可将最小方差无畸变(MVDR)准则的思想进行推广,导出分数低阶矩最小无畸变(FrMVDR)准则,并在此基础上提出基于分数低阶矩的SAR-STAP杂波抑制算法。
定义随机变量x的幂变换为
(8)
将该变换用于通道数为N的多通道SAR图像某像素单元的空域快拍x,可得
(9)
则其加权输出可表示为
(10)
式中,w=[w1,w2,…,wN]T为权矢量。式(10)称为分数低阶响应,其分数低阶输出功率可表示为
E{|y|2}=wHE{x〈p〉|x〈p〉|}w=wHR〈p〉w
(11)
式中,
(12)
可见,当p=1时,式(12)即为传统的协方差矩阵。可以证明当p<α/2时,矩阵R〈p〉是有界统计量[13]。因此FrMVDR准则可表述为
(13)
采用拉格朗日乘子法求解可得在FrMVDR意义上的最优权矢量为
(14)
在实际处理中,矩阵R〈p〉由相邻距离单元的训练样本估计所得,即
(15)
式中,L为训练样本数,参数p的设置同样需要从数据中估计所得,具体方法为:对实测数据直方图进行拟合估计α的值,选择合适的p使得p<α/2。最终处理器所采用的权矢量表示为
(16)
该算法的信号处理流程如图5所示。
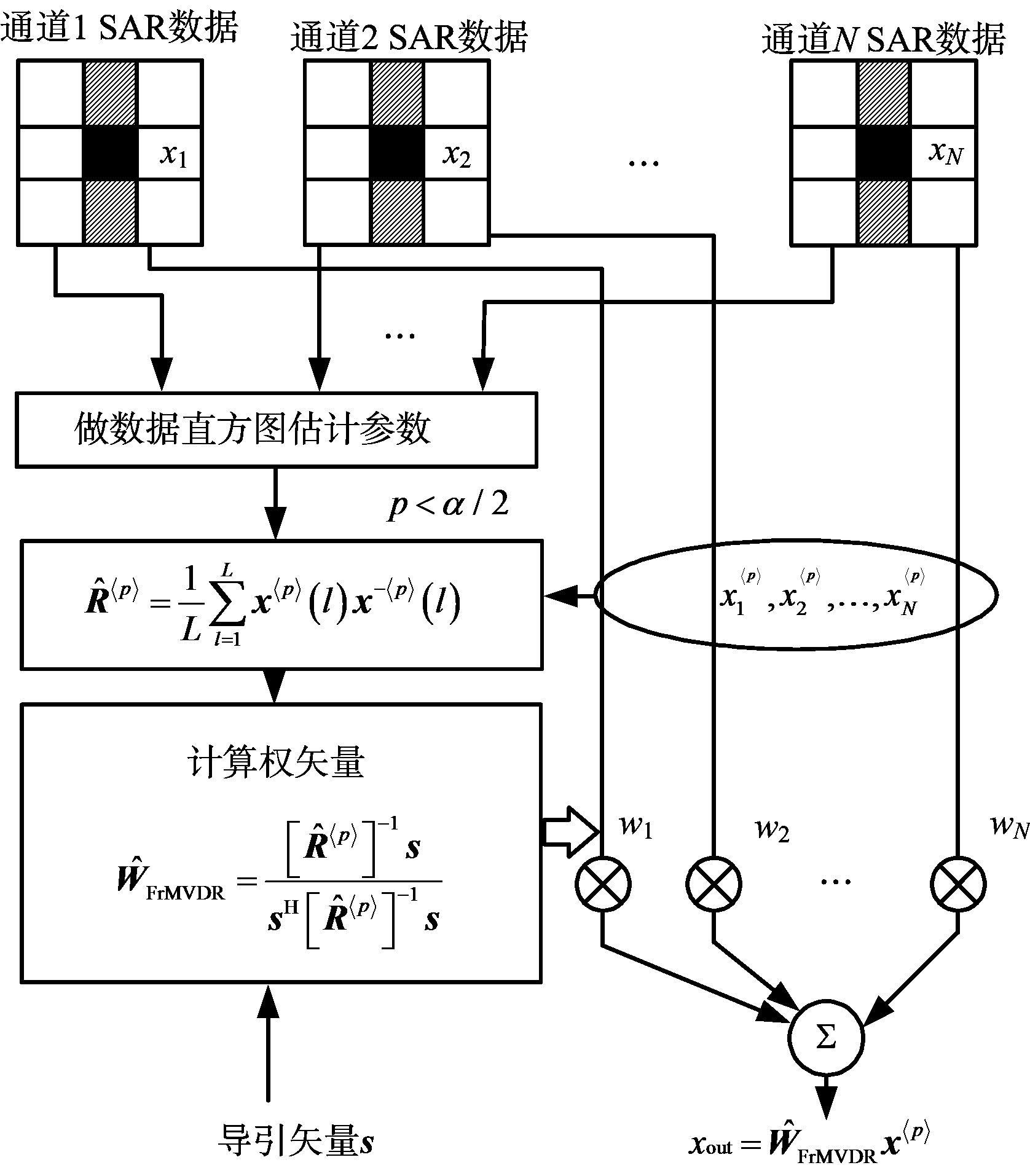
图5 基于分数低阶矩的SAR-STAP杂波抑制算法处理流程图
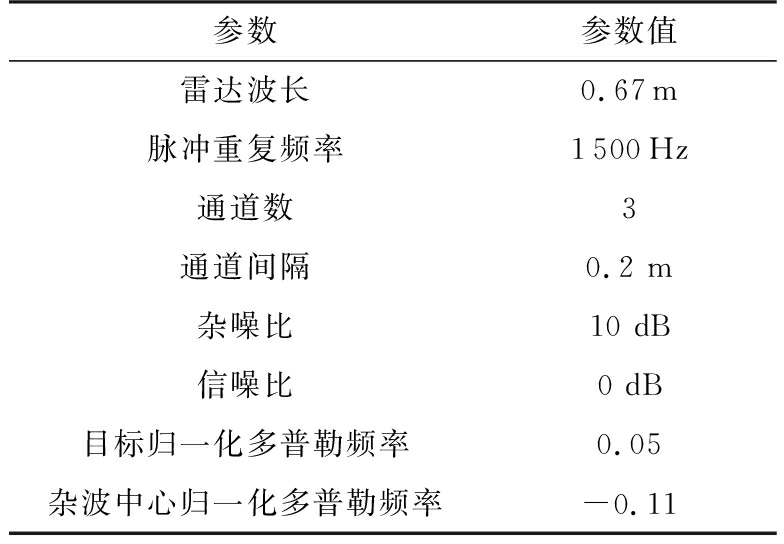
本小节将采用仿真实验对本文所提算法的杂波抑制性能进行验证,并与原有SAR-STAP算法进行比较,实验参数如表2所示。图6给出了两种算法的自适应天线方向图,图中所有曲线均为500次Monte-Carlo实验的平均结果。从图6(a)中可以看出,当α=2时(即高斯杂波背景条件下)两种算法性能基本相同,两条曲线几乎重合,都能够在目标多普勒位置形成高增益,同时在杂波多普勒中心位置形成凹口。而从图6(b)、图6(c)、图6(d)可以看出,随着α的减小,原有算法自适应方向图在杂波中心位置凹口深度明显变浅,杂波抑制性能显著下降,与之相比,无论是在杂波还是信号方向新算法都能获得较为理想的性能。
表2 仿真实验系统参数
参数参数值雷达波长0.67m脉冲重复频率1500Hz通道数3通道间隔0.2 m杂噪比10 dB信噪比0 dB目标归一化多普勒频率0.05杂波中心归一化多普勒频率-0.11
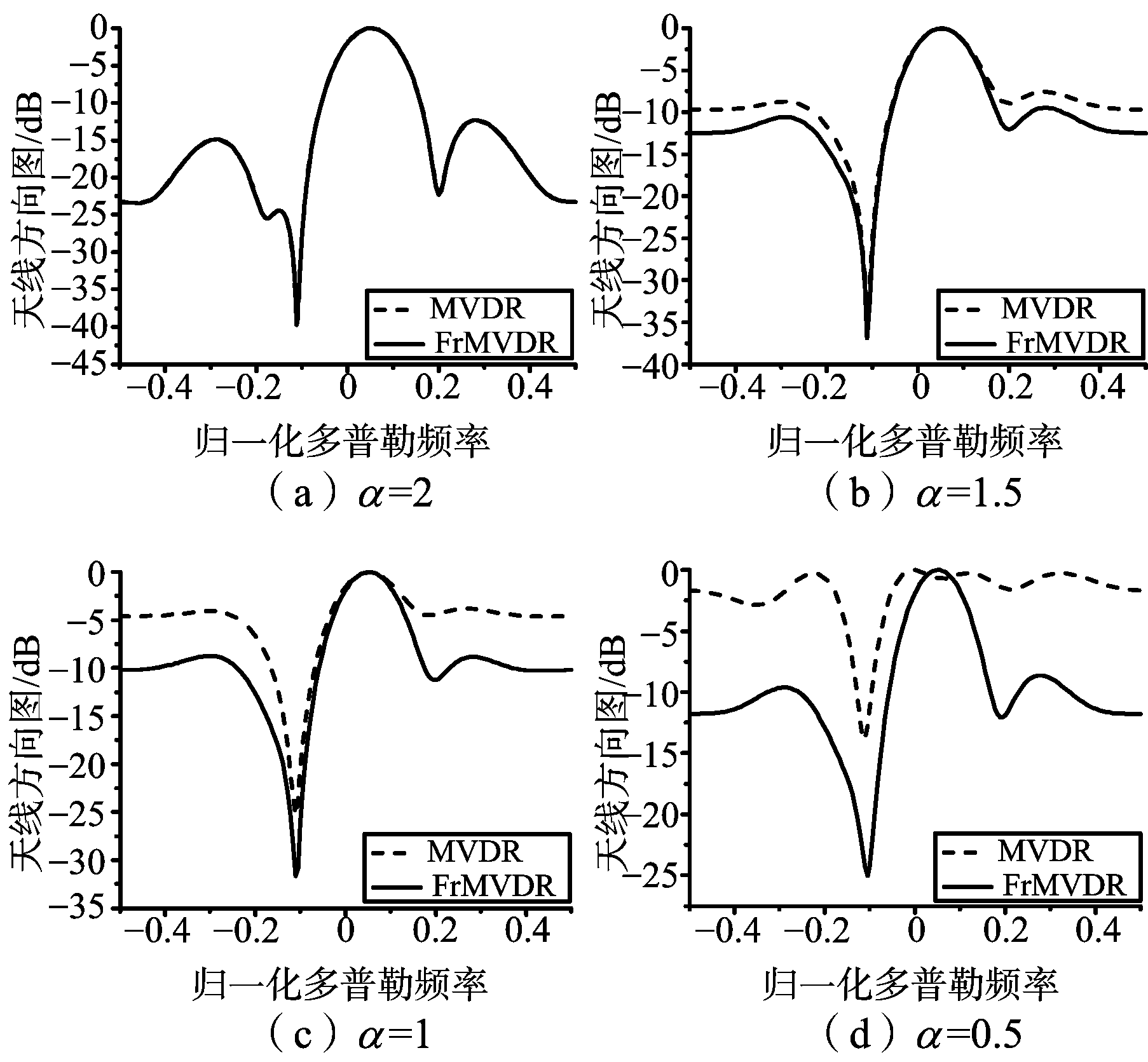
图6 原有SAR-STAP算法和基于FrMVDR的杂波抑制算法天线方向图
在上述实验基础上,通过仿真方法生成三通道SAR系统单个多普勒单元的512个距离门的杂波数据,并在其中添加3个动目标信号,分别位于第127,255,384距离门。随后,采用本文算法及原有SAR-STAP算法对数据进行处理,并在图7中给出了杂波抑制结果。此次仿真中,目标信噪比设为20 dB,其他参数同前,所有结果均为500次Monte-Carlo实验的平均值。
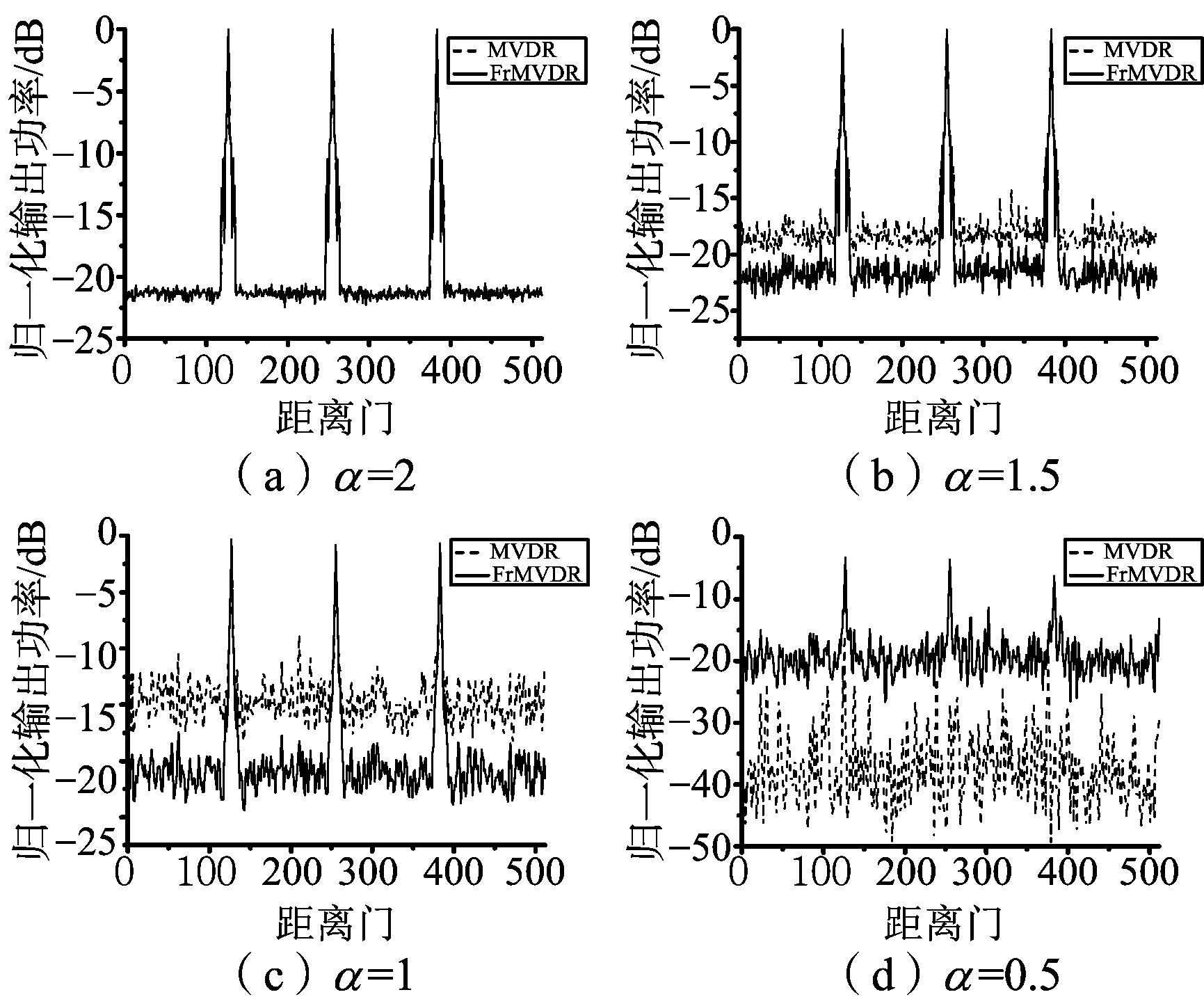
图7 原有SAR-STAP算法和新算法杂波抑制结果
可以看出,在α=2时即高斯环境下两种算法性能基本相同均能实现杂波抑制,但随着α的减小,基于传统MVDR的算法性能明显下降,在α=0.5时已经无法实现杂波抑制;而基于FrMVDR的杂波抑制算法性能虽然有所下降但仍然可以有效完成杂波抑制。
上述结果表明,在非高斯干扰明显的环境中,原有算法性能会急剧下降甚至失效,但基于Alpha稳定分布的新算法可以有效完成杂波抑制,为接下来的动目标检测奠定基础。
实际处理中,随着SAR图像的分辨率不断提高,从图像中可以看出更多的细节特征,部分成像场景中能清晰地观察到城市中的建筑群等强杂波散射点,此类SAR图像将呈现出明显的非高斯性。因此,若采用基于Alpha稳定分布的杂波抑制算法进行处理,必能提高系统的GMTI性能。
图8给出了第2节中实测数据采用新算法进行杂波抑制的处理结果,处理过程中p略小于α/2取0.6。可以看到在采用基于FrMVDR的杂波抑制算法处理后,杂波强散射点得到了有效的抑制,处理结果明显优于原有算法。对两个处理结果分别作CFAR检测,虚警概率设为10-6,结果如图9所示,图中黑点表示该像素单元为虚警点,可见新算法的虚警数明显低于传统算法。

图8 新算法处理结果
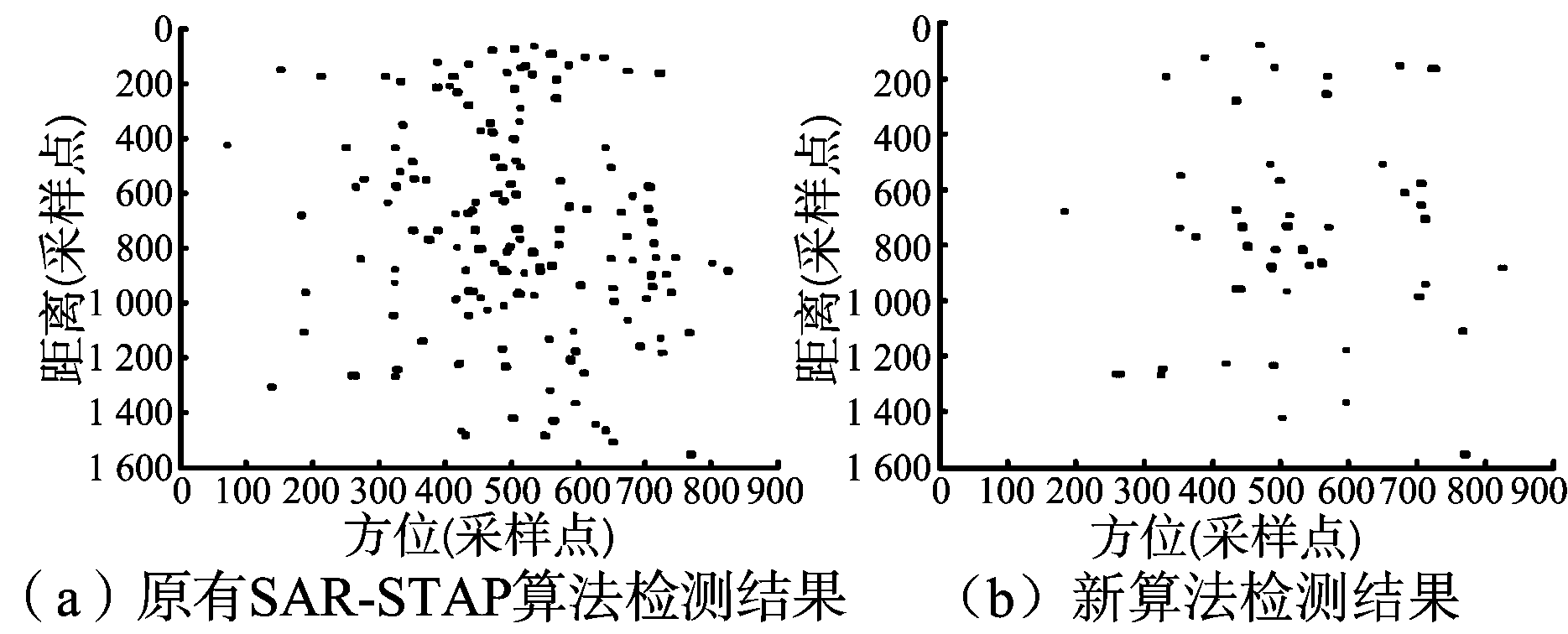
图9 CFAR检测结果
为进一步验证新算法的性能,采用此算法对另一组某型机载四通道SAR数据进行处理,表3给出了数据的部分系统参数。在处理时,首先对数据进行拟合,估计可得参数α为1.29,拟合结果如图10所示。图11为检测区域SAR图像,从图中可以看到局部区域存在大量强散射点。杂波抑制处理过程中p 略小于α/2取0.6,可见原有算法处理结果局部区域有着明显的杂波残留,如图12所示,图13给出了虚警概率为10-6的CFAR检测结果,图中黑点表示该像素单元为虚警点,可以看到该区域中虚警数严重增多。与之相比,新算法处理后这些区域可获得理想的杂波抑制效果。
表3 四通道SAR系统参数
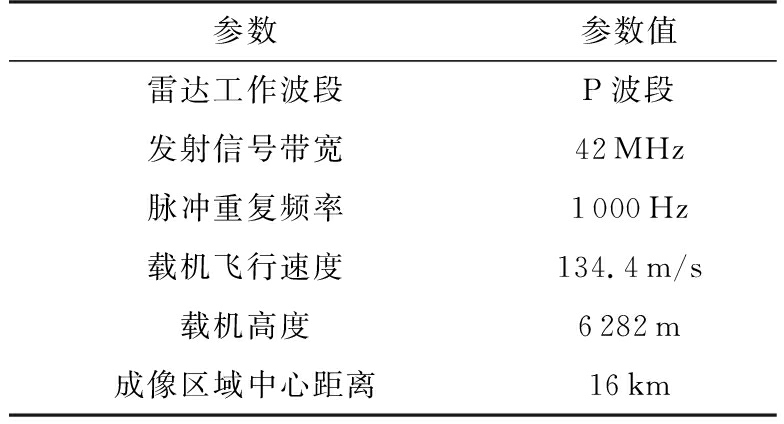
参数参数值雷达工作波段P波段发射信号带宽42MHz脉冲重复频率1000Hz载机飞行速度134.4m/s载机高度6282m成像区域中心距离16km
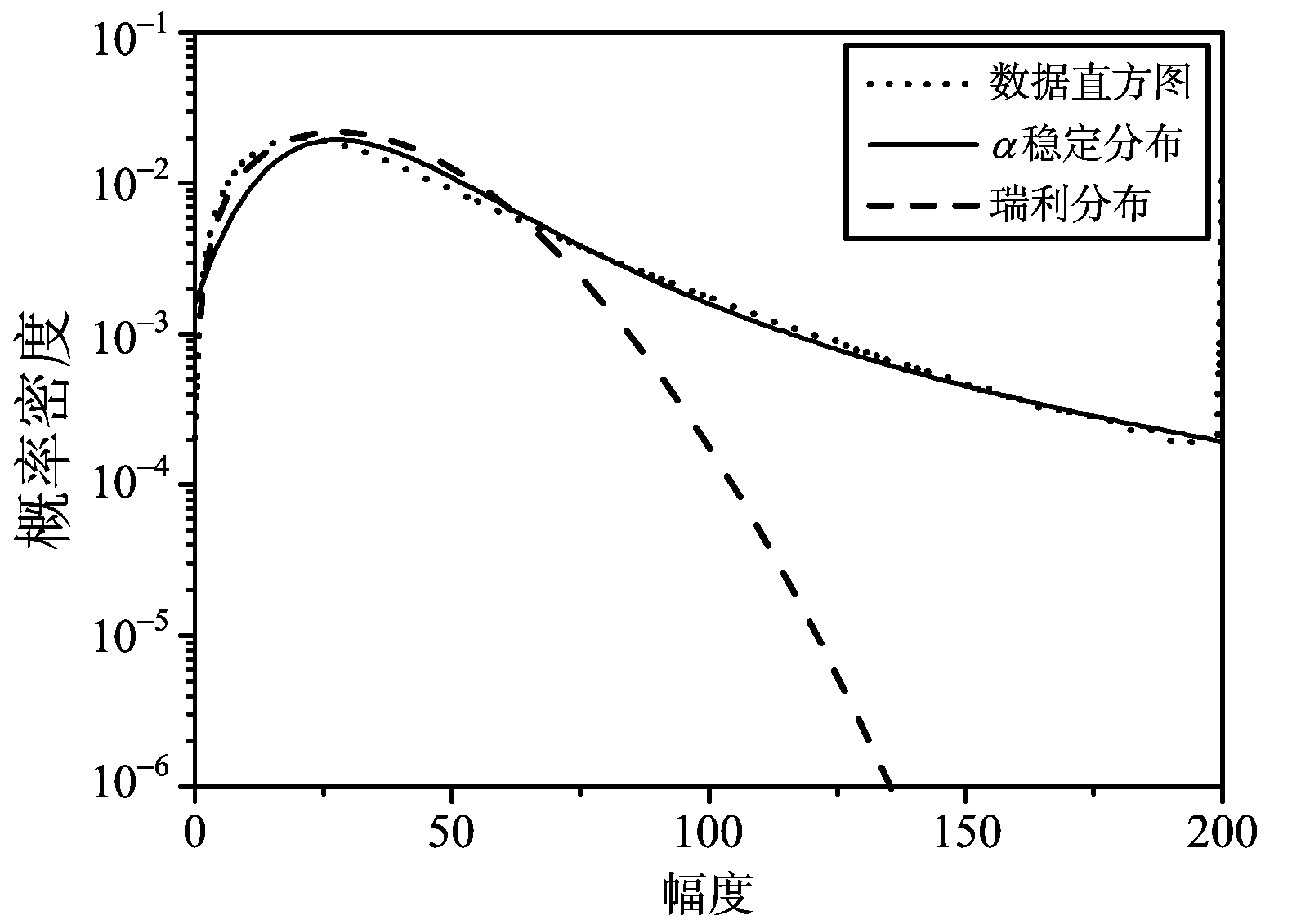
图10 概率密度函数对比图

图11 单通道SAR图像

图12 四通道SAR数据杂波抑制处理结果
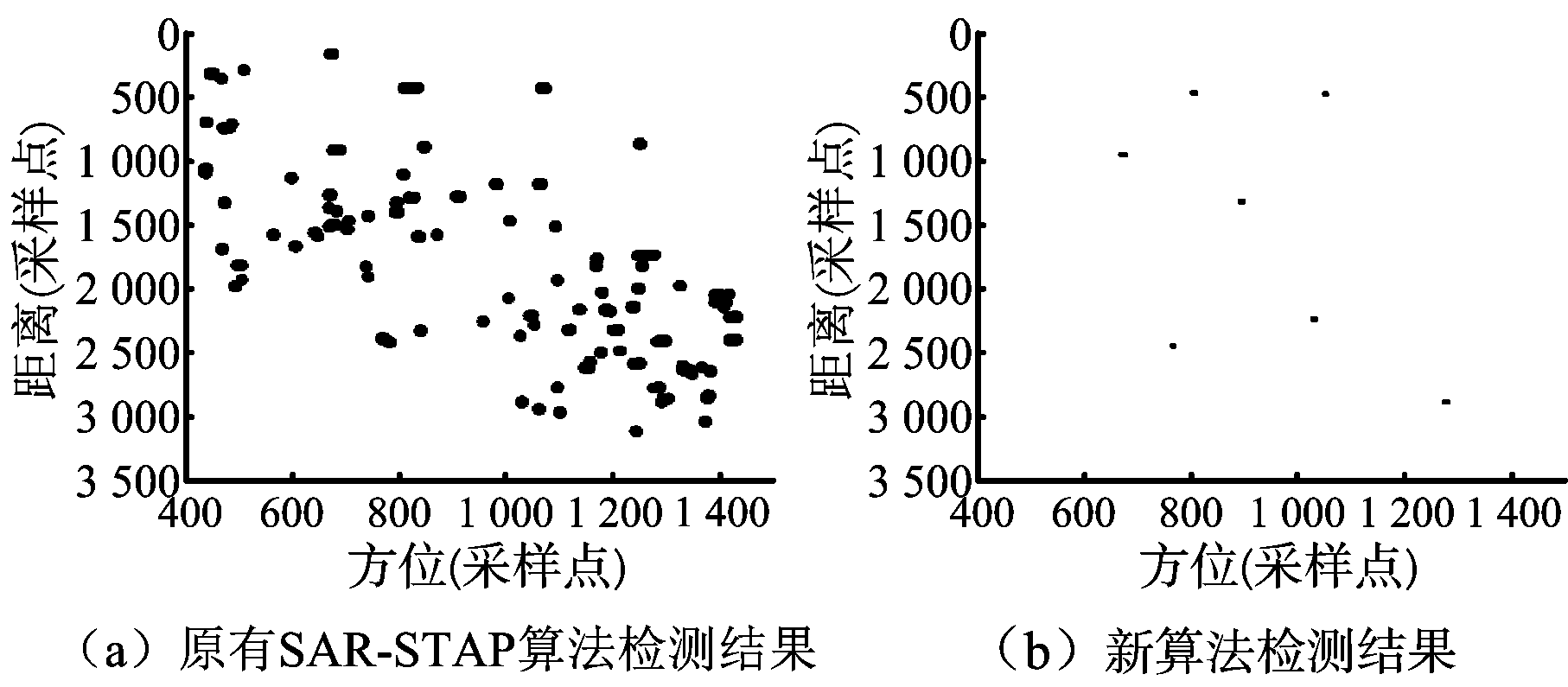
图13 四通道SAR数据动目标CFAR检测结果
为进一步对新算法进行验证,在该四通道数据中添加仿真动目标。每次试验均在此块区域内添加40个运动参数不同的仿真动目标,采用两种算法分别进行杂波抑制,在保证具有相同的目标检测数的情况下,检测结果如图14所示,图中空心点表示目标点,黑点表示虚警点。限于篇幅,仅给出其中一次检测结果图,将其余各次实验结果列于表4。从表4中可以看出,新算法可有效抑制非高斯杂波减少检测结果的虚警数,同时保证系统的检测性能。
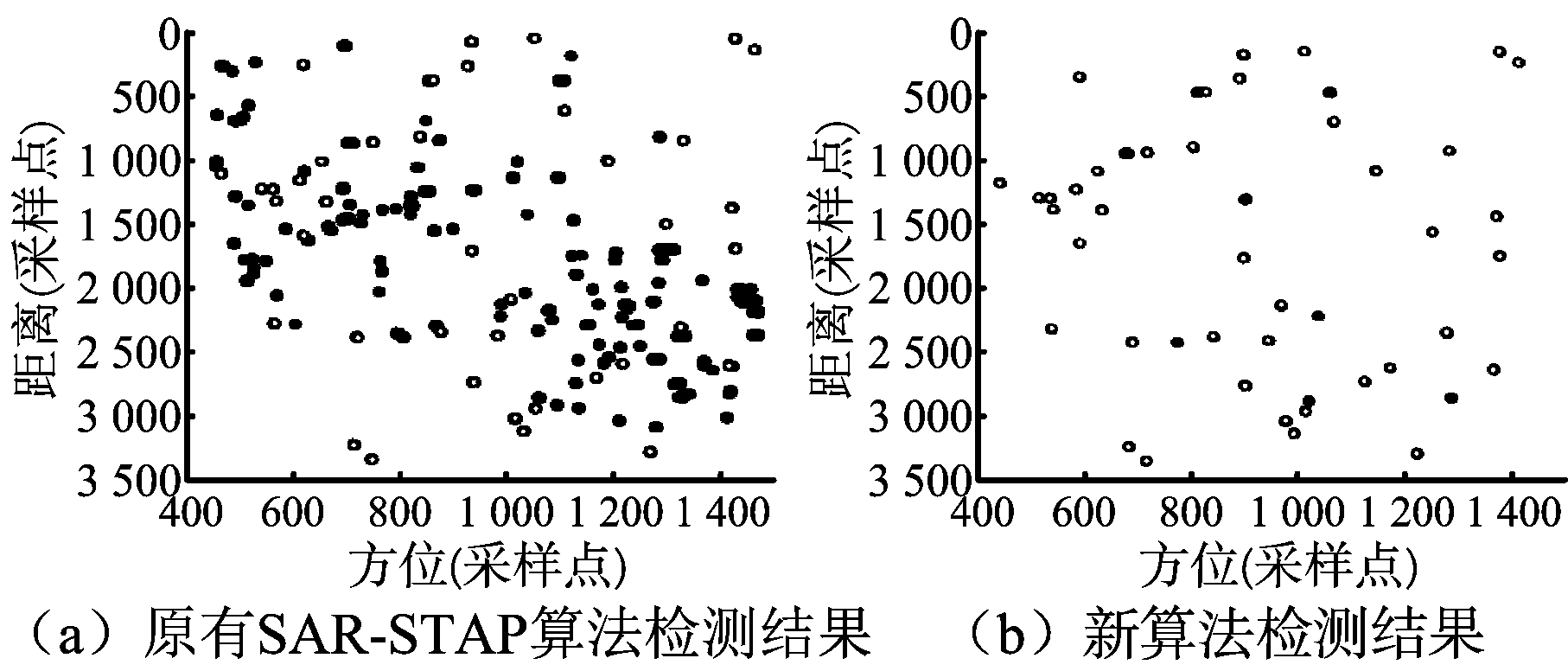
图14 四通道SAR数据仿真动目标CFAR检测结果
表4 仿真目标检测结果
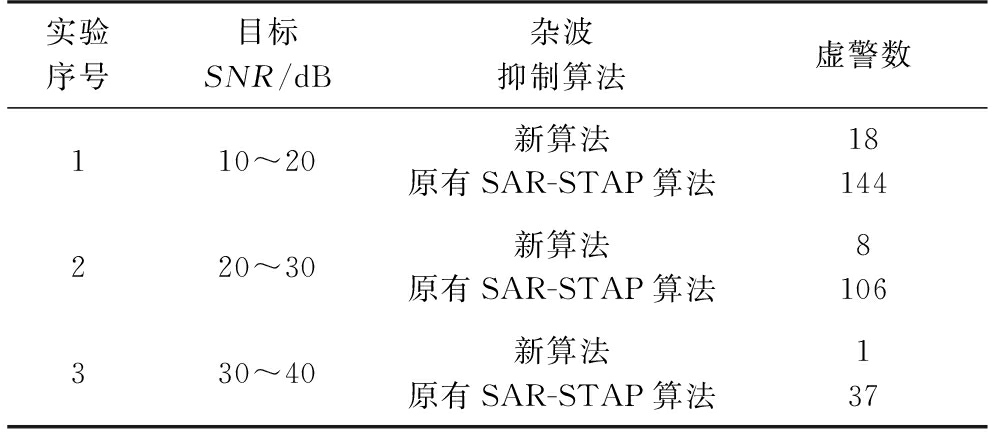
实验序号目标SNR/dB杂波抑制算法虚警数110~20新算法原有SAR-STAP算法18144220~30新算法原有SAR-STAP算法8106330~40新算法原有SAR-STAP算法137
本文针对复杂探测场景中杂波分布偏离高斯分布的情况,采用Alpha稳定分布建立杂波模型,并在此基础上提出了基于分数低阶矩的SAR-STAP杂波抑制算法。文中通过对仿真实验及多组多通道SAR实测数据处理对算法性能进行了验证,结果表明,该算法在非高斯环境中性能明显优于原有算法,并表现出良好的鲁棒性,是一种实用且有效的多通道SAR杂波抑制算法。
[1] RINCON R,FATOYINBO T,OSMANOGLU B,et al.Development of Next Generation Digital Beamforming Synthetic Aperture Radar Architectures[C]∥ IEEE International Geoscience and Remote Sensing Symposium,Beijing: IEEE,2016:2109-2111.
[2] YANG Dong,YANG Xi,LIAO Guisheng,et al.Strong Clutter Suppression via RPCA in Multichannel SAR/GMTI System[J].IEEE Geoscience and Remote Sensing Letters,2015,12(11):2237-2241.
[3] 邢孟道,孙光才,李学仕.用于高分辨率宽测绘带SAR系统的SAR/GMTI处理方法研究[J].雷达学报,2015,4(4):375-385.
[4] ENDER J H G.Space-Time Processing for Multichannel Synthetic Aperture Radar[J].Electronics & Communication Engineering Journal,1999,11(1):29-38.
[5] LIU Xiangyang,MENG Jin,LIN Hong,et al.A Comparison to Joint Pixel Vector Methods for Clutter Suppression in SAR-GMTI System[C]∥ 12th International Conference on Signal Processing,Hangzhou: IEEE,2014:2039-2043.
[6] 吴迪,朱岱寅,朱兆达.一种非均匀环境中双端口干涉SAR/GMTI杂波抑制算法[J].电子学报,2010,38(9):2179-2183.
[7] PARK J,SHEVLYAKOV G,KIM K.Maximin Distributed Detection in the Presence of Impulsive Alpha-Stable Noise[J].IEEE Trans on Wireless Communications,2011,10(6):1687-1691.
[8] ZHONG X,PREMKUMAR A B,MADHUKUMAR A S.Particle Filtering for Acoustic Source Tracking in Impulsive Noise with Alpha-Stable Process[J].IEEE Sensors Journal,2013,13(2):589-600.
[9] 陈沛,赵拥军,刘成城,等.一种分数低阶时频分解的盲波束形成算法[J].西安电子科技大学学报(自然科学版),2017,44(5):134-139.
[10] 冯子昂,胡国平,周豪,等.基于对称Alpha稳定分布的低空杂波建模仿真[J].计算机仿真,2016,33(10):62-65.
[11] 刘根旺,张杰,张晰,等.不同分辨率合成孔径雷达舰船检测中杂波模型适用性分析[J].中国海洋大学学报(自然科学版),2017,47(2):70-78.
[12]MA X,NIKIAS C L.Joint Estimation of Time Delay and Frequency Delay in Impulsive Noise Using Fractional Lower Order Statistics[J].IEEE Trans on
Signal Processing,1996,44(11):2669-2687.
[13] 何劲.α稳定分布噪声背景下阵列信号处理方法研究[D].南京: 南京理工大学,2007.


