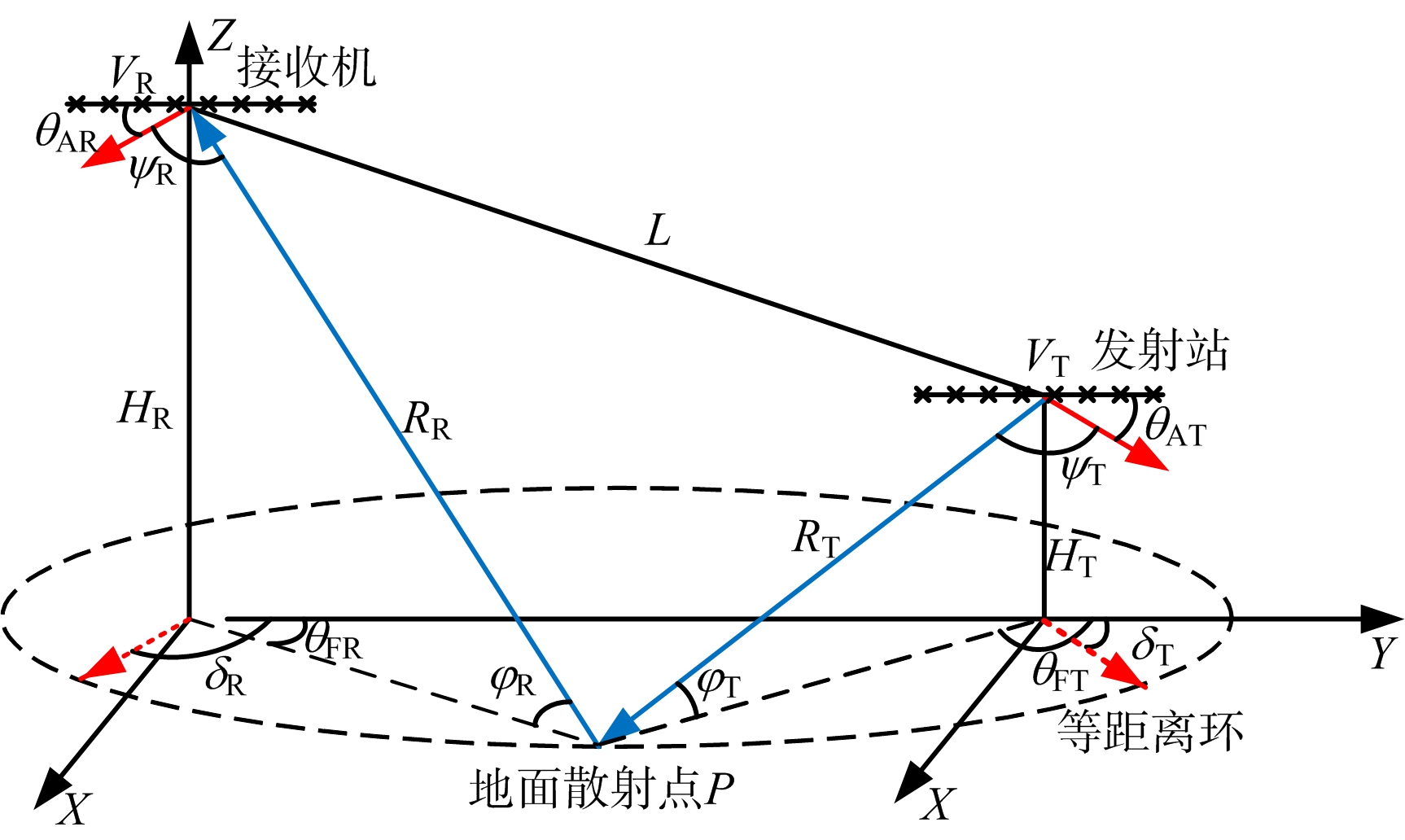
图1 双基雷达几何模型
机载双基地雷达不仅具有机载雷达监视范围宽广、机动性良好、规避地物遮挡能力强的特点,还具有双基雷达“四抗”和反隐身的优点,在提高雷达自身的生存能力和目标检测方面具有其独特的优势[1-2]。但不同于机载单基雷达杂波,机载双基雷达杂波空时分布受双基构型影响大,且呈现严重的距离依赖性。杂波距离依赖性会导致不同距离单元杂波分布离散,杂波谱中心的多普勒频率和空间频率的严重扩展,目标会淹没在分布范围很广的杂波中,导致雷达检测性能急剧退化。
为避免在不同的双基配置构型下使用不恰当的方法检测目标,研究不同双基构型的杂波特性和相应的处理方法具有重要价值。雷达杂波分类[3]的主要目的是针对不同双基构型更有效地抑制杂波。 Klemm[4]首先根据收发平台的飞行航向将双基构型归纳为4种类型,即航向一致、平行、正交和交叉,同时仿真分析了较为特殊的航向一致、平行和正交三种构型下杂波特性,没有对较一般的交叉构型进行进一步杂波特性仿真分析;文献[2,5]也从发射或接收机静止的双基构型到发射机、接收机都运动的情形进行了机载双基雷达的建模仿真,并仿真分析了典型几何配置下的杂波特性,但没有给出一般化的杂波分类及其特性分析和处理方法分析。
空时自适应信号处理(Space-Time Adaptive Processing,STAP)技术已成为机载雷达杂波抑制的一种关键技术[6]。现有STAP方法包括以多普勒翘曲[7](Doppler Warping,DW)、角度-多普勒补偿[8-10](Angle Doppler Compensation,ADC)和导数更新法[11](Derivative Based Updating,DBU)为代表的非平稳补偿类算法,以及以辅助通道法[12](Auxiliary Channel Receiver,ACR)和局域空时联合处理[13](Joint-Domain Localized,JDL)算法为代表的降维类算法,对机载双基雷达杂波抑制性能不够理想,无任何补偿措施的杂波样本协方差估计更会导致杂波抑制的凹口展宽,对地面低速运动目标的检测性能降低[14]。补偿类算法面临复杂度高、运算量大和样本支持条件难以满足的问题[15-16],很难在工程上实现。以JDL算法为典型代表的降维类方法可显著改善运算量大和样本支持条件难以满足的问题,但对误差敏感、在存在误差的情况下性能下降。
本文针对已有机载双基杂波分类方法的不足,对较一般的双基双动情形建模仿真,根据双基构型和对应的杂波分布将机载双基雷达杂波分为3类,并分析了不同类型杂波的特性。在杂波分类分析的基础上,抑制算法仿真结果表明现有的STAP方法并不能很好地适用于机载双基雷达杂波。根据机载双基雷达杂波具有严重距离依赖性的特点,提出了用训练单元协方差矩阵的加权平均作为目标单元杂波协方差矩阵的方法。通过算法仿真验证,改进的方法在3类构型下杂波抑制效果均有明显的提高。
机载双基雷达构型难以枚举,图1给出了任意几何构型下机载双基雷达的几何模型[2,17-18]。为简化问题,假设发射、接收载机平台在与地面平行的平面运动,且发射、接收天线均为正侧面放置(从杂波抑制的角度讲,侧视线阵是一种较优的天线配置方式[2]),在实际情况中这些条件是容易满足的。

图1 双基雷达几何模型
其中,L为双基基线长度,RS为双基距离和,RT,RR分别为发射机、接收机与目标之间的距离,HT,HR分别为发射机、接收机的飞行高度,VT,VR分别为发射机、接收机的平台运动速度,φT,φR分别为地面目标散射点相对于发射、接收平台天线轴向的俯仰角,ψT,ψR分别为发射、接收平台波束指向的空间角,δT,δR分别为发射、接收平台载机飞行方向相对于基线方向的方位角,θFT,θFR分别为发射、接收雷达天线波束指向相对于基线方向的方位角,θAT,θAR分别为发射、接收雷达天线相对于载机飞行方向的夹角。
根据图1中的几何关系,可以得到
(1)
已知双基距离RS为RT,RR之和,结合式(1)可以解出RR。RR是关于基线L和θFR的函数。俯仰角φT,φR的余弦以及方位角θFT的余弦可以表示为RR和θFR的函数:
(2)
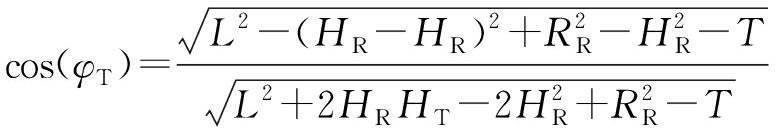
(3)
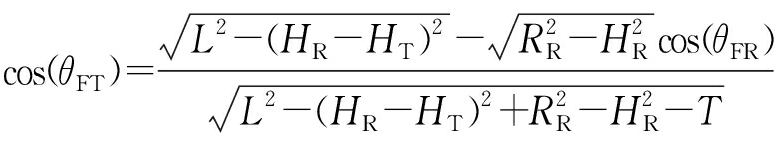
(4)
式中,
(5)
接收回波的多普勒频率可表示为
(6)
式中,
![]()
(7)
接收锥角和发射锥角的余弦可表示为
![]()
(8)
由于机载双基雷达体制的特殊性无法直接给出空间频率和多普勒频率显性的关系表达式,将RR代入各关系式后进行数值仿真,可以得到任意几何构型、载机平台任意高度、运动速度、运动方向下机载双基雷达的杂波在空间-多普勒二维平面的分布图。
在第1节中机载双基雷达模型和相关公式推导的基础上,设置参数进行任意构型下机载双基雷达杂波仿真。为不失一般性,文中主要考虑双基双动的情形。所有仿真采用统一参数,具体的仿真参数如表1所示。同时仿真中对接收波束进行40 dB的切比雪夫加权,双基距离和取远、中、近距的3个值以对比不同距离下杂波距离依赖性。仿真发现,影响杂波几何分布的最主要因素是载机平台的运动方向与基线的夹角(平台运动方向是否平行于基线)。因此,可以在平面对载机平台的运动方向与基线的夹角进行遍历,根据杂波空时分布的几何形状对杂波进行分类。
表1 系统仿真参数
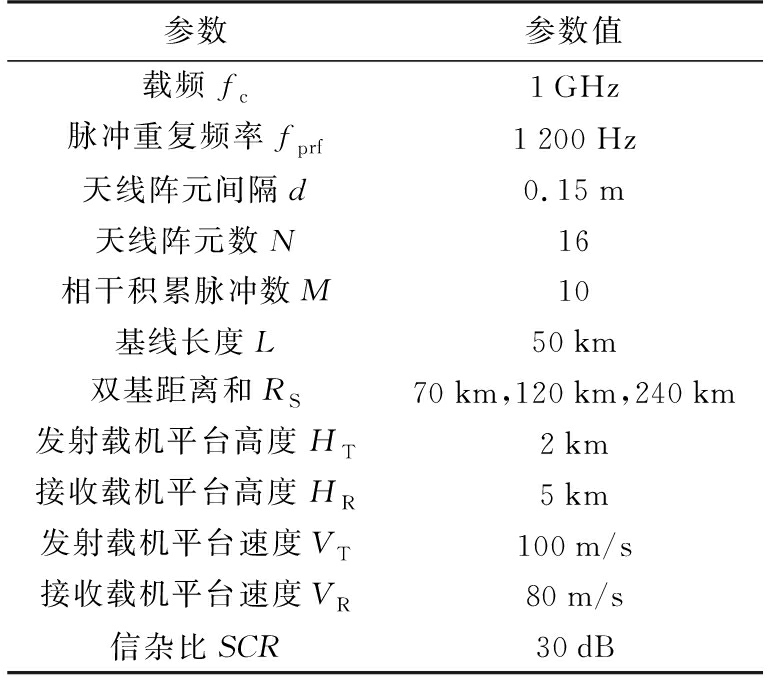
参数参数值载频fc1GHz脉冲重复频率fprf1200Hz天线阵元间隔d0.15m天线阵元数N16相干积累脉冲数M10基线长度L50km双基距离和RS70km,120km,240km发射载机平台高度HT2km接收载机平台高度HR5km发射载机平台速度VT100m/s接收载机平台速度VR80m/s信杂比SCR30dB
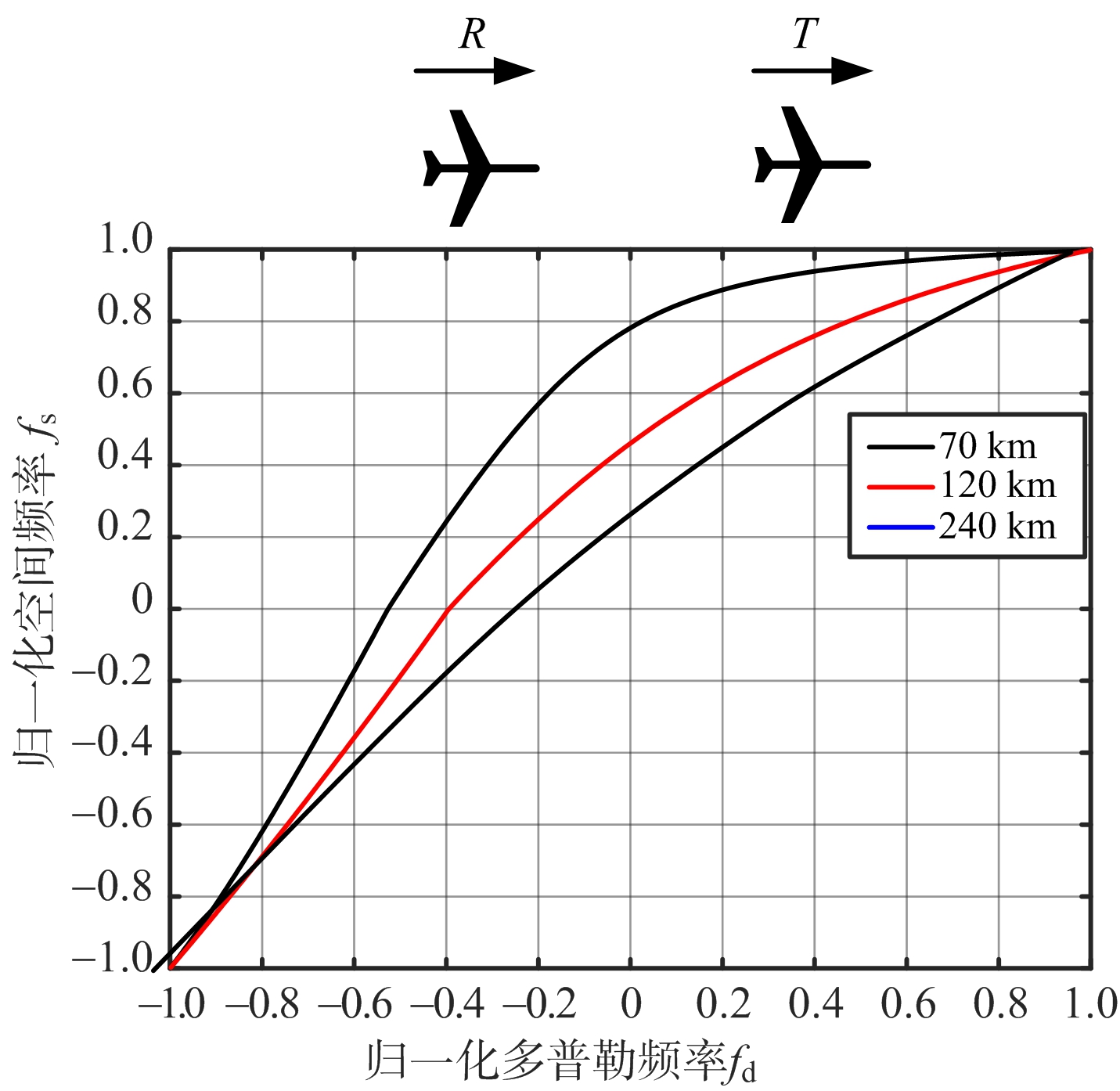
(a) T=0°杂波分布
(b) T=90°杂波分布
(c) T=135°杂波分布
图2 构型一(R=0°)不同双基配置杂波空时分布
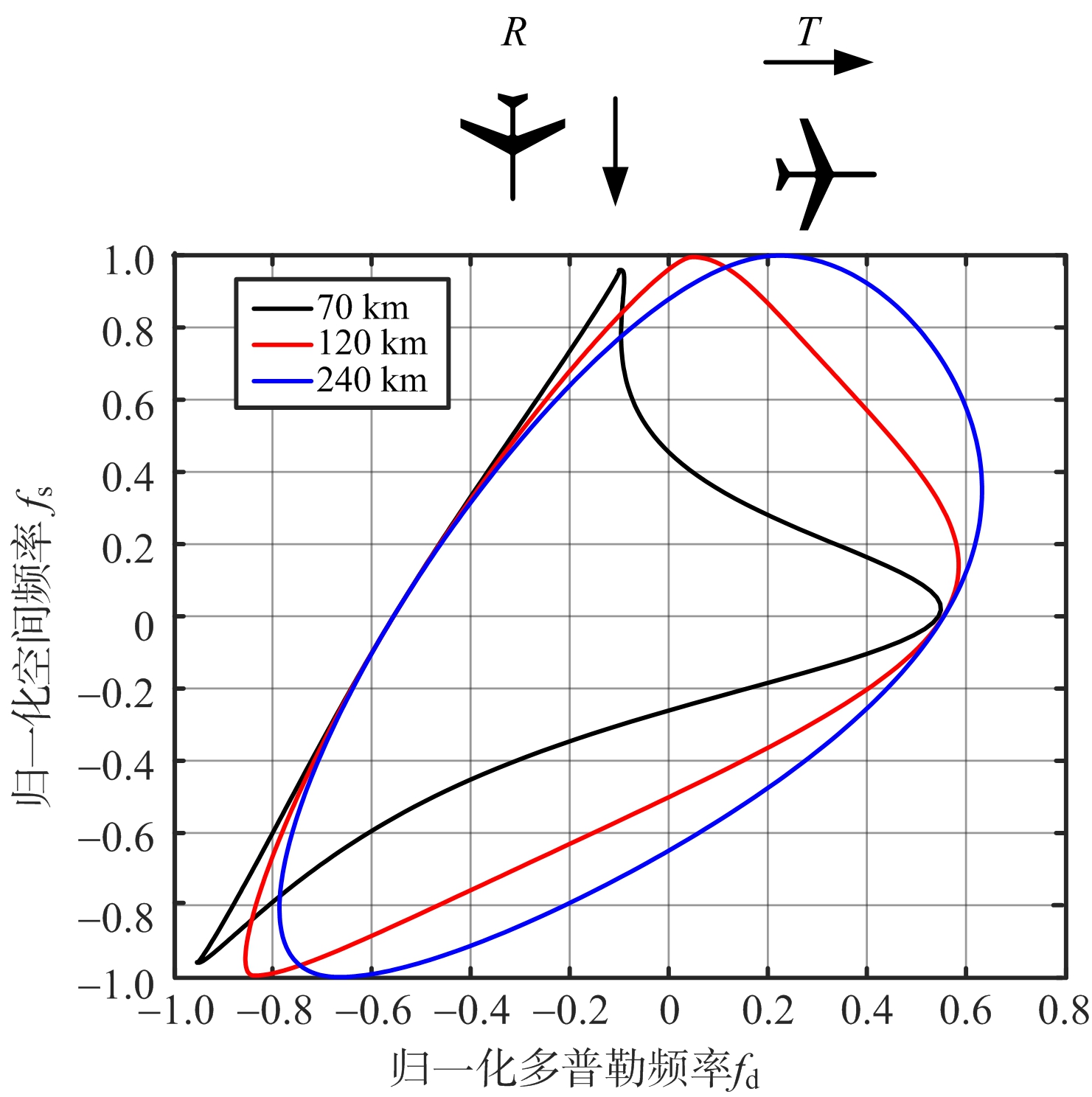
在这种双基构型下,接收机运动方向跟基线平行,发射机运动方向与基线的夹角为任意角度。图2是该种构型下,发射机角度在0°~360°变化时杂波典型的空时二维分布图。图中,R代表接收载机平台运动方向与基线的夹角,T代表发射载机平台运动方向与基线的夹角。从图中可以看出,此种构型下,杂波的空时分布是一条曲线(不闭合),在较远的双基距离和处杂波的二维分布近似于线性分布。从图2(a)~图2(c)的仿真不难发现,机载双基杂波的分布与双基构型有关,杂波二维分布不再是一条斜直线,而是与双基距离和有关的曲线。不同双基距离和下,杂波分布也不同,出现了杂波谱的拓宽。另外,在此种构型下,仿真还发现,发射机运动方向相对于基线方向夹角为δT0和运动方向相对于基线方向夹角为360°-δT0时,杂波空时分布曲线恰好相连接构成了一个封闭的曲线环。换言之,此构型下每个夹角(发射机运动方向相对于基线方向)的杂波分布是一个曲线环的一半。
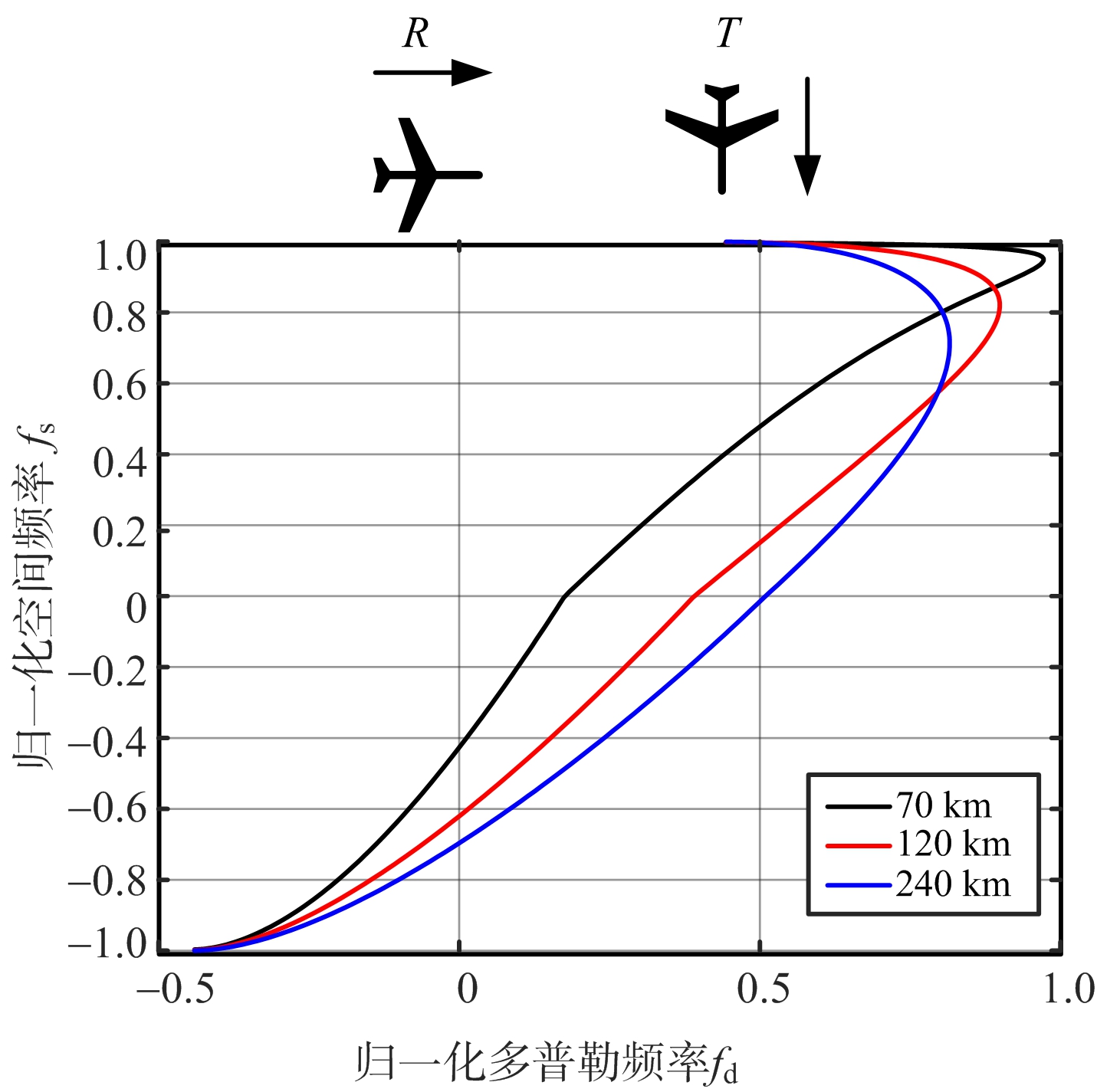
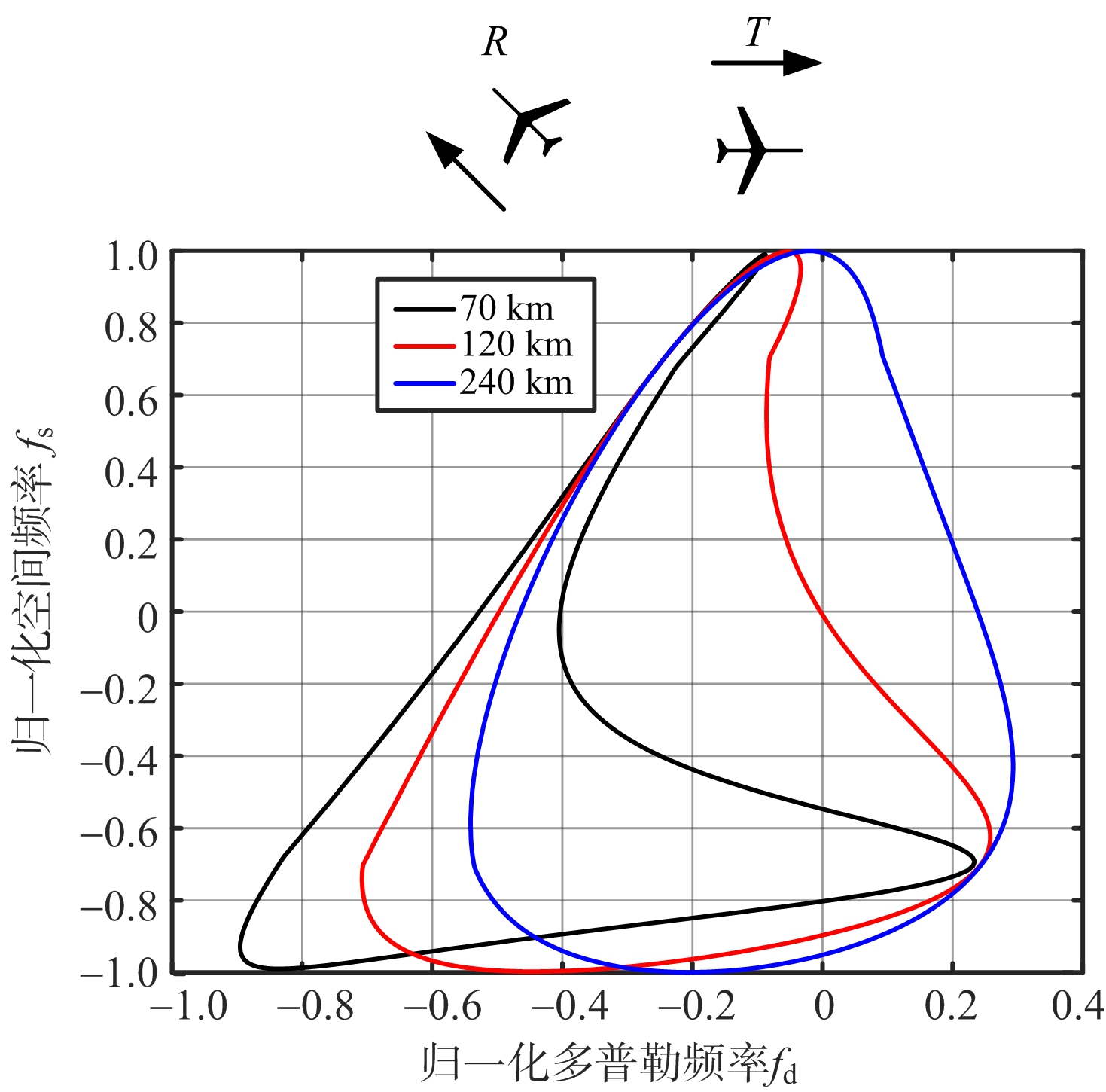
在这种双基构型下,发射机运动方向与基线平行,接收机运动方向与基线的夹角为任意角度(但不平行于基线)。图3是该种构型下,接收机角度在0°~360°变化时杂波典型的二维分布图。从图中可以看出,此种构型下,杂波的空时分布是一条闭合的环型曲线。从图3(a)~图3(c)可以看出,相同距离单元下,构型二中杂波谱的拓宽比构型一要严重。同时,结合构型一中夹角和为360°的两种情形构成封闭环的结论,可以近似认为构型一杂波分布仅仅是构型二中杂波分布的一部分;相比于构型一,构型二中杂波具有更强的距离依赖性。
(a)R=45°杂波分布
(b)R=90°杂波分布
(c)R=135°杂波分布
图3 构型二(T=0°)不同双基配置杂波空时分布
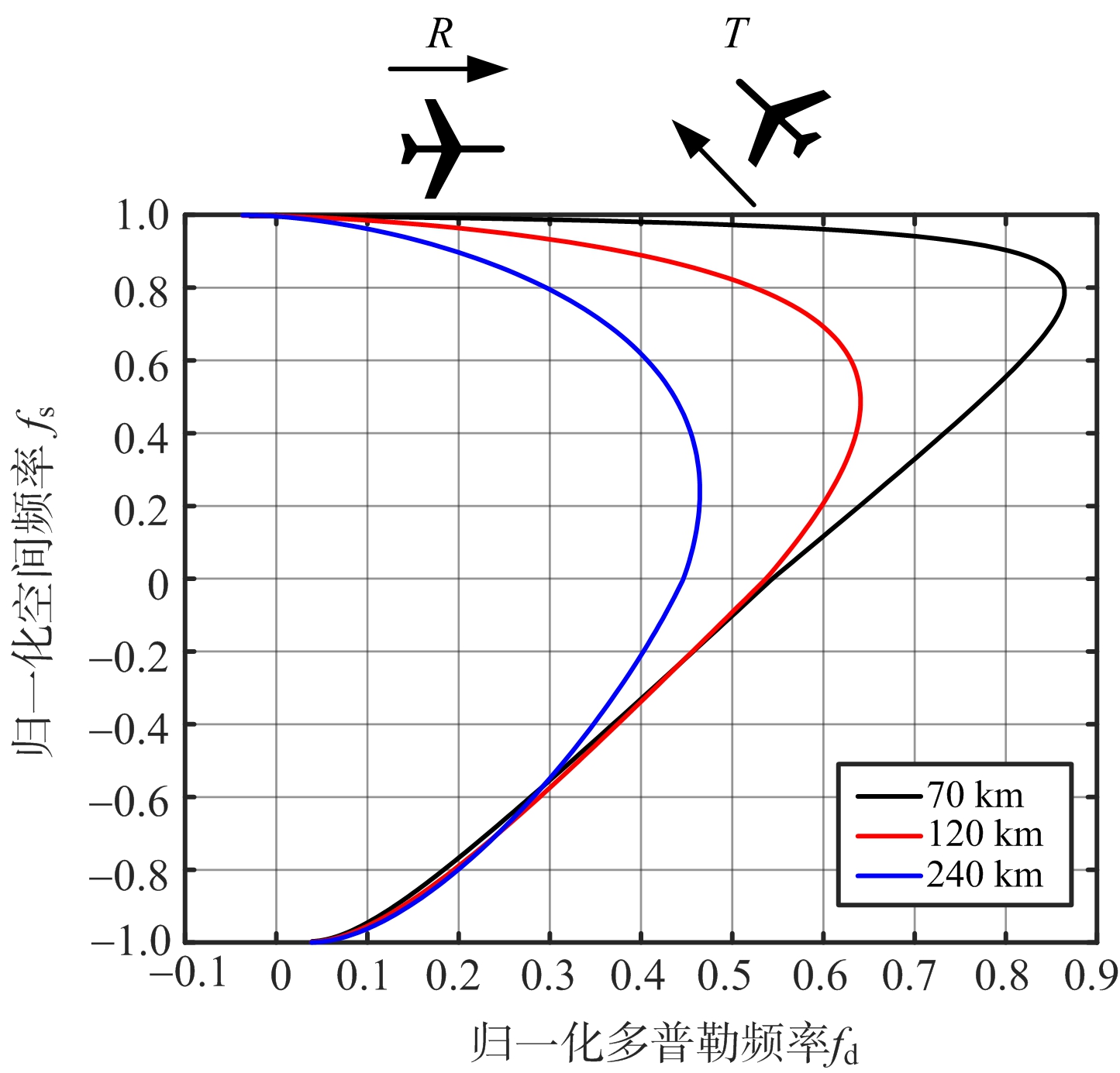
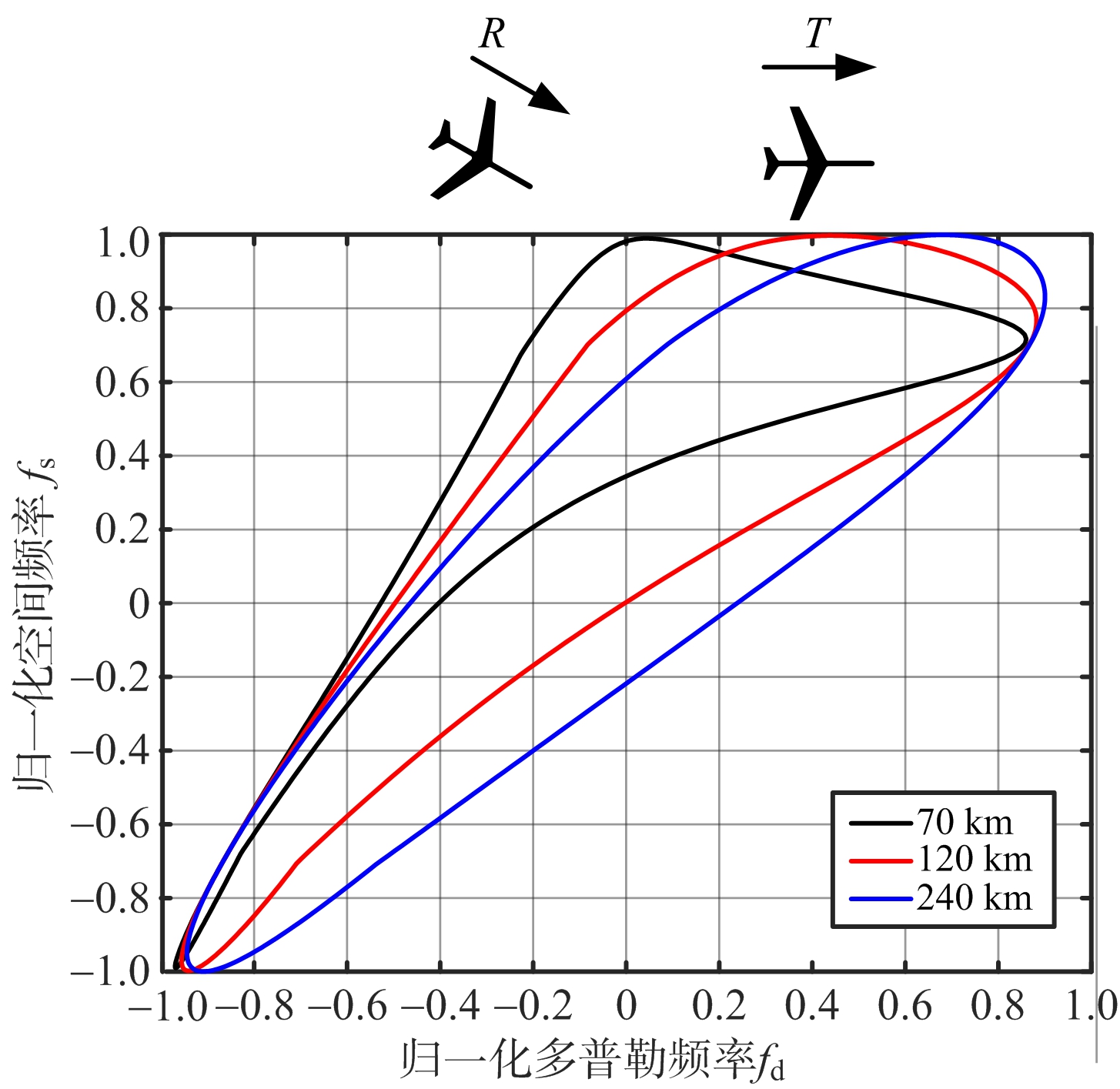
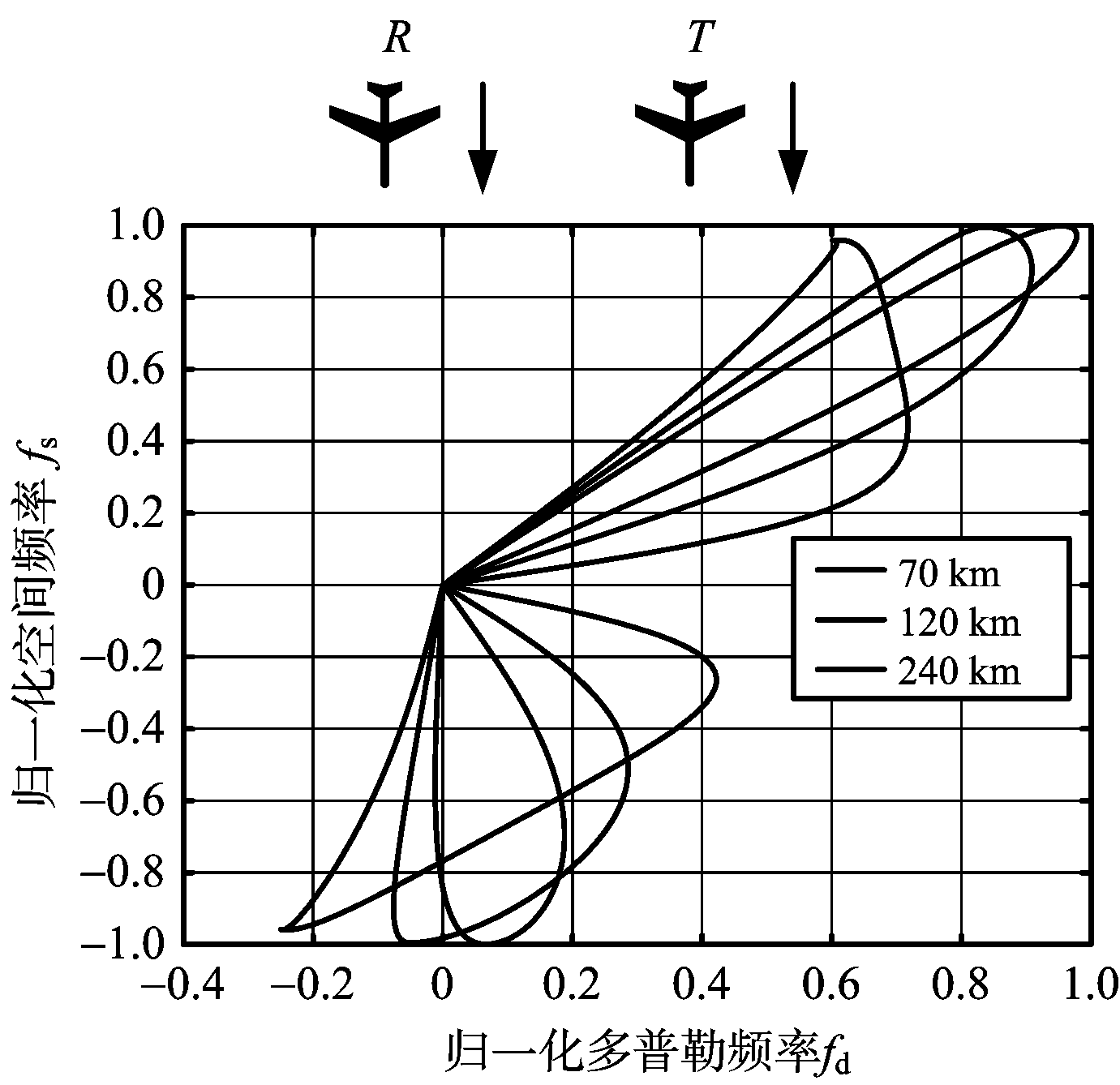
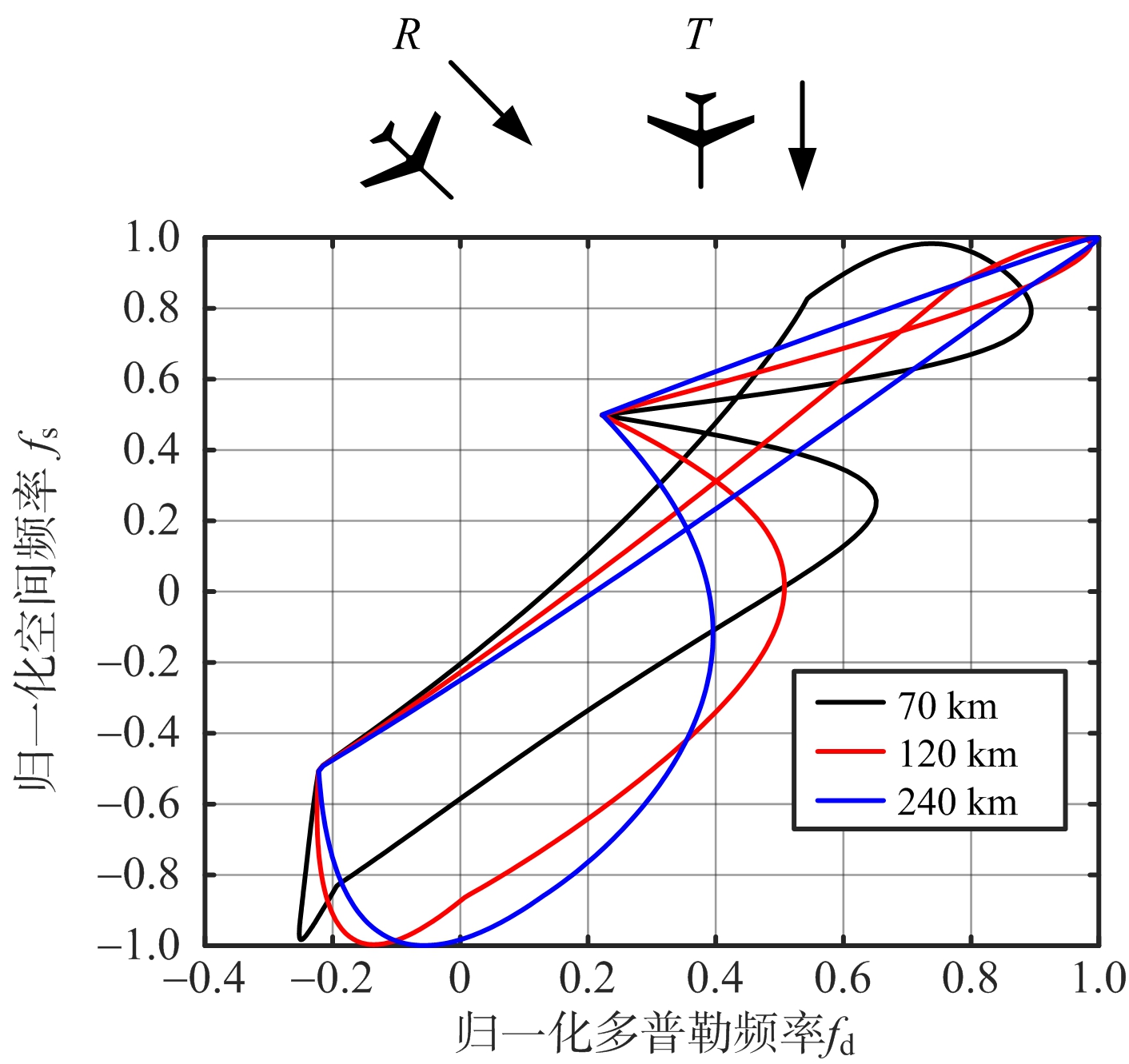
在这种双基构型下,发射机运动方向、接收机运动方向均与基线方向存在夹角(但不平行于基线)。该构型在实际情况下更为常见,杂波的空时分布开始出现曲线相交的现象,呈纽线状,仿真中也存在很少数构型下杂波分布曲线不相交的情形。同样,从图4(a)~图4(c)看出,在该构型下杂波二维分布曲线比较复杂,不同距离单元下,杂波谱存在拓宽,但相比于构型二,杂波谱拓宽较弱。
本节对机载双基雷达杂波进行仿真,给出了较为一般化的杂波分类,将机载双基雷达杂波分为3类。仿真发现,影响杂波分布的主要因素是载机平台运动方向跟基线的夹角(构型)和双基距离和(距离)。通过图2、图3、图4可以清晰地看出,机载双基雷达杂波受双基构型影响严重,且杂波在不同的距离单元分布不同,存在严重的杂波距离依赖性。基线长度、双基距离和不会从本质上改变杂波空时分布曲线的形状,只是一定程度上影响杂波分布的距离依赖性的强弱,也即不同距离单元杂波分布几何曲线的拓展程度,尤其是基线长度、双基距离和相差较大时杂波距离依赖性会有所减弱。
(a)T=90°,R=90°杂波分布
(b)T=90°,R=45°杂波分布

(c)T=135°,R=45°杂波分布
图4 构型三不同双基配置杂波空时分布
上一节对载机平台运动方向与基线的夹角在平面内遍历,根据双基构型和对应的杂波将机载双基雷达杂波分为了3类,并分析了不同类型杂波的特性。机载双基雷达杂波分布不仅与构型相关,而且具有严重的距离依赖性。相同配置参数的双基构型,远距比近距杂波距离依赖性弱。传统的STAP方法的对杂波训练单元有两个约束条件:1)各个距离单元的杂波满足独立同分布(IID)[19];2)训练单元的个数不少于两倍的系统自由度(RMB准则)[20]。机载双基雷达杂波不满足上述两个条件,利用较典型降维类(JDL)算法进行杂波抑制仿真,仿真结果表明,传统的空时自适应处理方法对机载双基雷达杂波抑制性能明显下降。分析原因在于:机载单基雷达正侧视情形下杂波不具有距离依赖性,不同距离单元的杂波均分布在角度-多普勒平面的对角线;而机载双基雷达杂波具有严重的距离依赖性,不同距离单元杂波分布不同,杂波谱扩展严重。根据机载双基雷达杂波的距离依赖特性,距离目标单元较远的训练单元与目标单元的杂波不再满足IID条件,因此对目标单元的杂波估计贡献应该越小,基于这一点,本文提出用训练单元协方差矩阵加权平均的方法代替传统的求和取平均的方法去估计目标单元杂波协方差矩阵。
在传统的STAP方法中,认为所有训练单元对于目标单元杂波的估计贡献是一致的,将训练单元的协方差矩阵求和取平均作为目标单元杂波协方差矩阵的近似,如式(9)所示:
(9)
而机载双基雷达杂波具有严重距离依赖性,不同距离的训练单元对目标单元的影响不同。距离目标单元越远的训练单元杂波对目标单元杂波的估计贡献应该越小。因此,可以用训练单元的协方差矩阵的加权平均作为目标单元杂波协方差矩阵的近似,如式(10)所示,式中λ=[λ1λ2…λL]是权系数矢量:
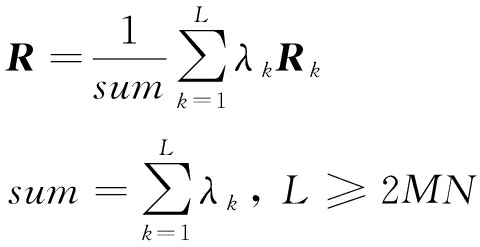
(10)
机载双基雷达构型不同,其杂波的距离依赖性的强弱不同。加权系数在不同构型下应该能灵活调整,使得在较强距离依赖性的构型下,加权系数随训练单元与目标单元距离的增大而快速减小,也即较强距离依赖性的构型下,加权的高斯曲线的方差较小。考虑到高斯函数的普遍适用性以及高斯函数可以通过方差参数方便地控制对称轴两侧曲线的下降速度,仿真中加权系数选取了高斯函数对称轴两侧的点,如图5所示。
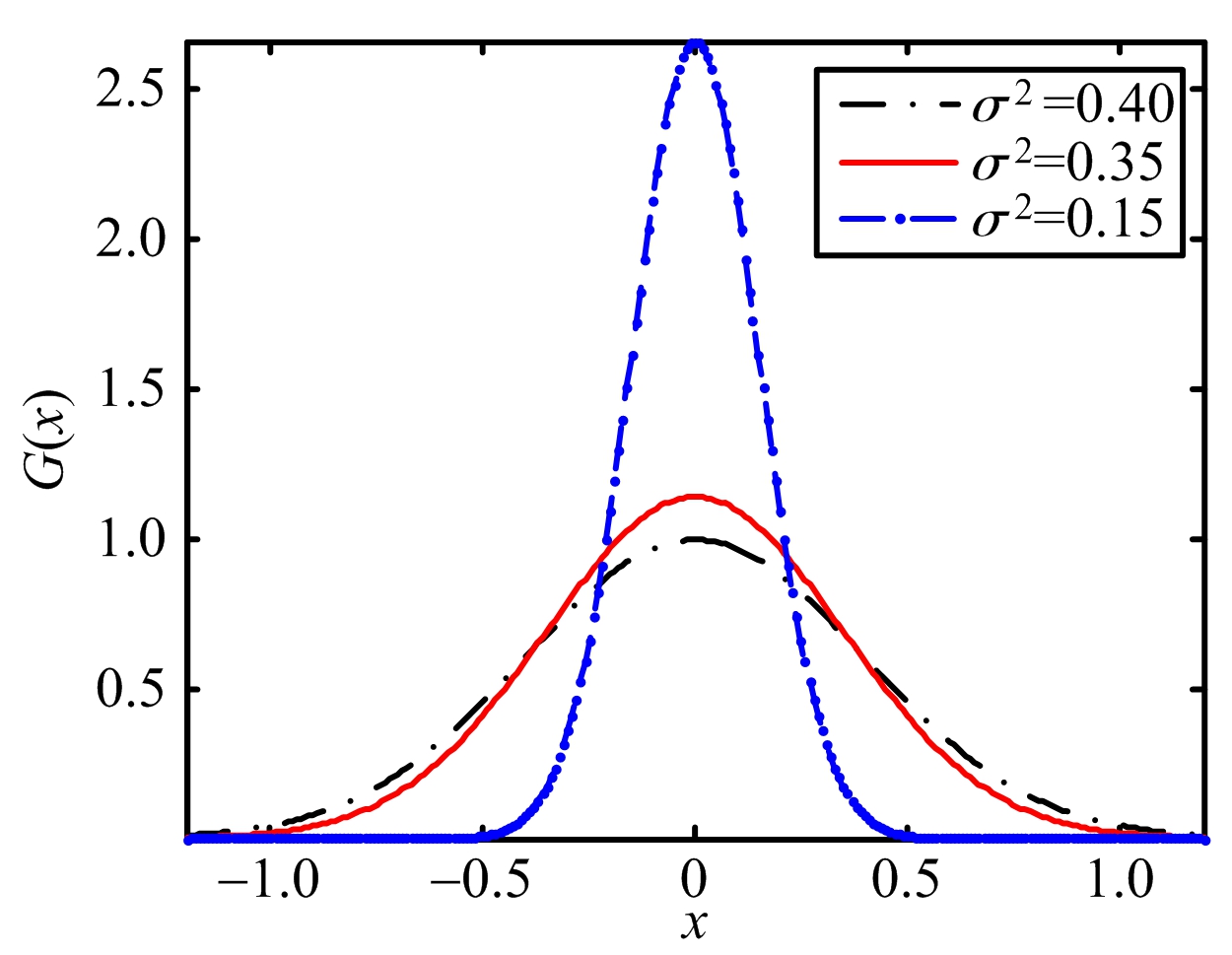
图5 不同方差时的高斯曲线
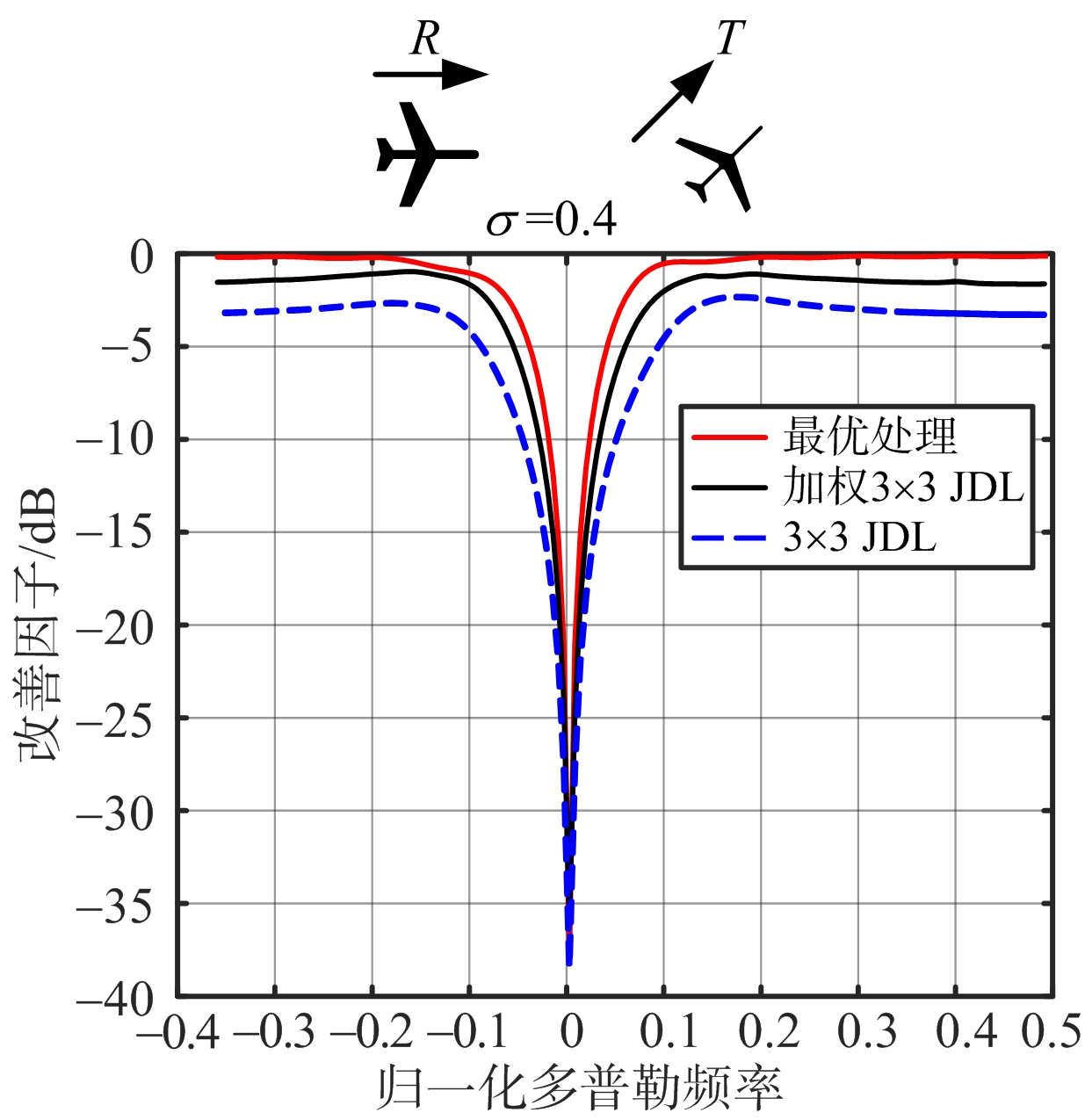
(a) 构型一改善因子曲线
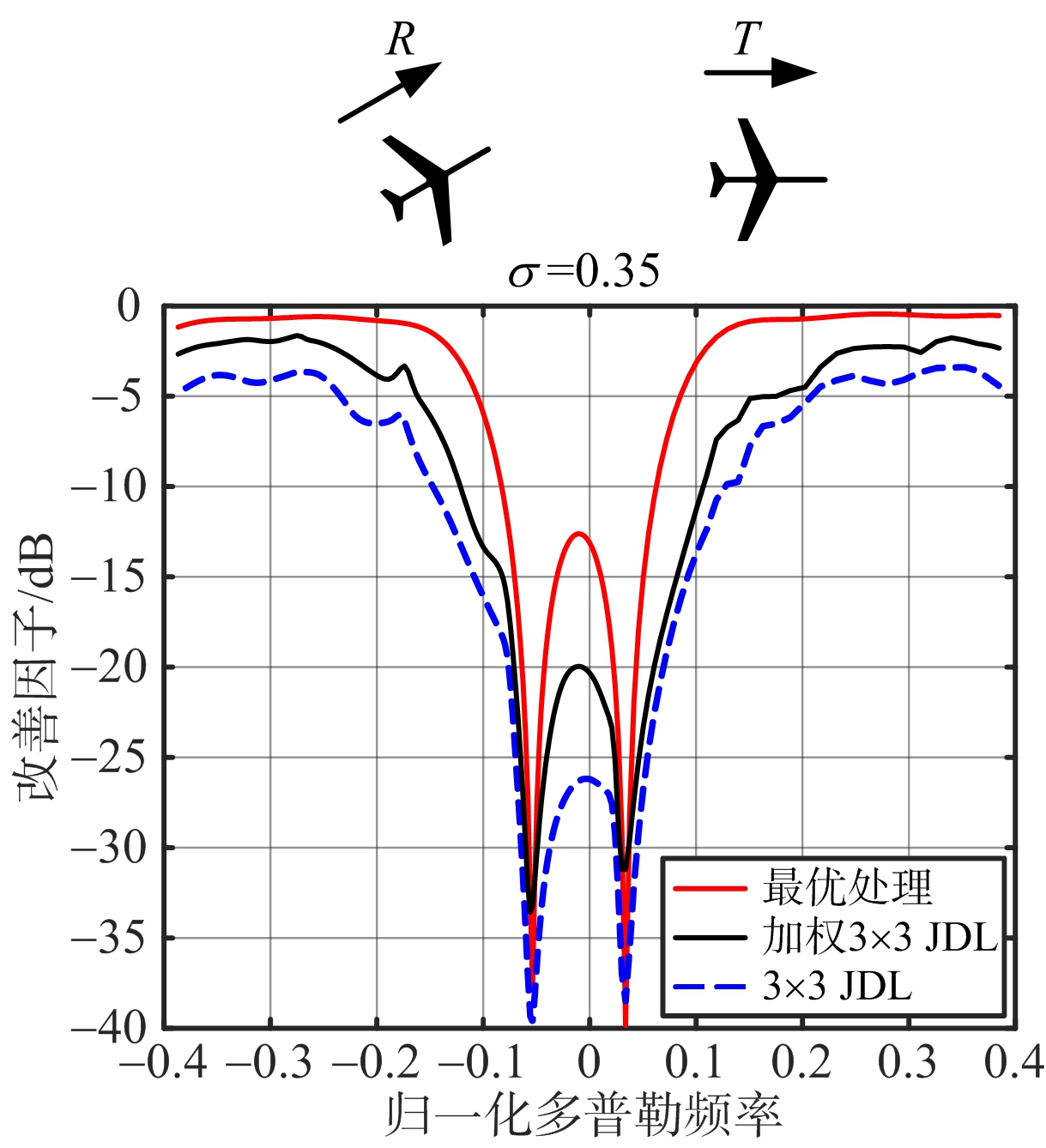
(b) 构型二改善因子曲线
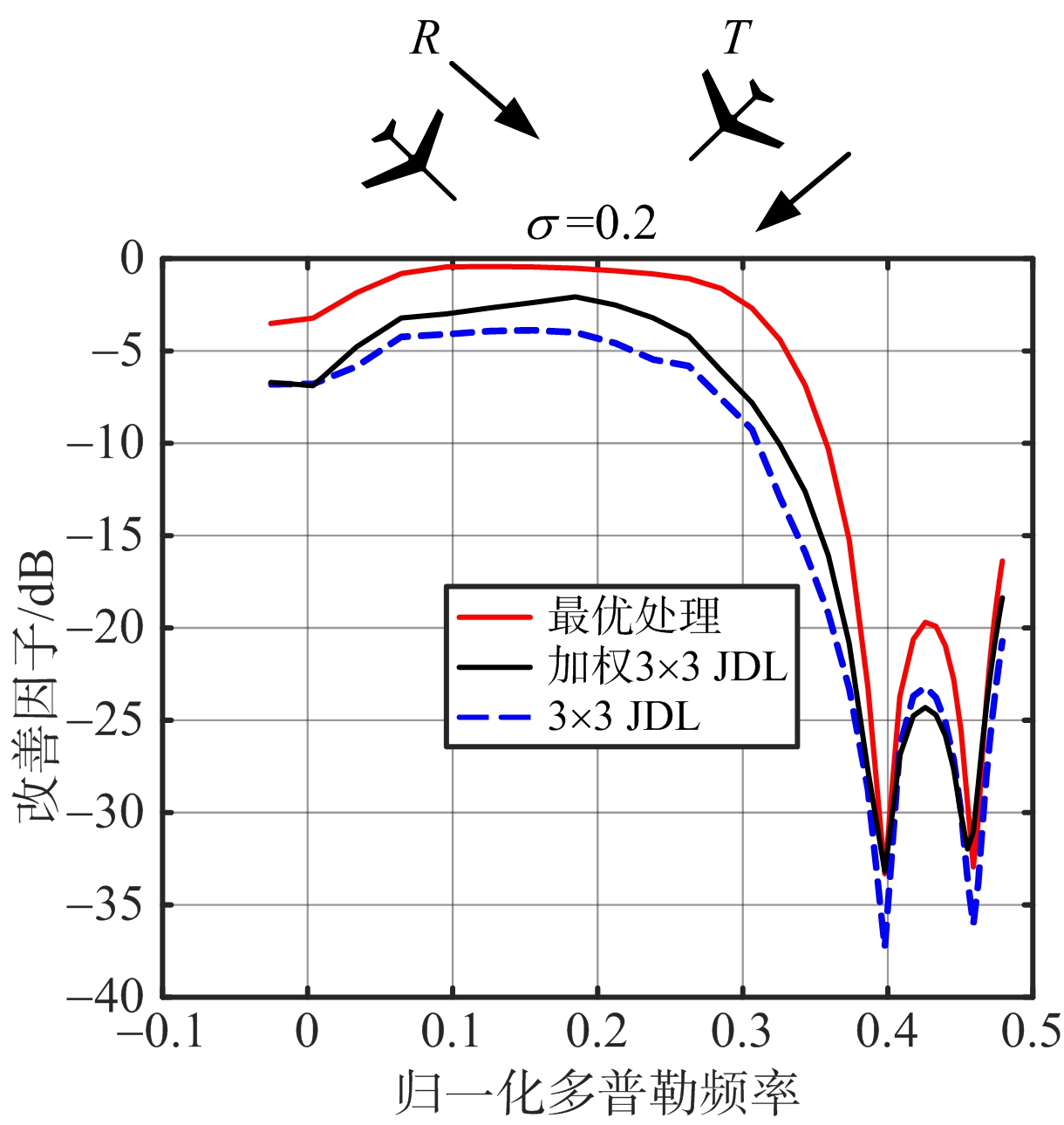
(c) 构型三改善因子曲线
图6 各算法3种不同构型下对杂波的抑制效果
图6是不同方法对3种构型下的杂波进行杂波抑制仿真的结果。其中JDL算法局部处理区域的大小选为3×3,同时加入最优STAP作为对比。仿真中训练距离单元在目标距离单元两侧选取,其数量为2倍的系统自由度,在3×3的JDL算法中训练距离单元数为2×3×3=18,训练距离单元的宽度为40 m。
从图6可以看出,在3类构型下,加权JDL方法在主波束和旁瓣区域对杂波的抑制性能相比于传统JDL方法均有明显的提高。该方法对杂波抑制性能平均有1~2 dB的提高,在第二类和第三类构型下杂波的主波束区域性能改善甚至超过5 dB。仿真实验中,基于训练单元协方差矩阵加权平均的角度多普勒补偿算法(加权ADC)相比于传统ADC算法杂波抑制性能也有明显的提升,因此该方法对于杂波抑制的补偿类和降维类方法均有较强的适用性。而且该方法易于实现,也没有明显提高算法的运算量。图中3种构型下,加权抑制算法与最优处理的性能在旁瓣区域还存在一定差距,增加空域波束数目,当JDL算法局部处理区域为3×5时,主波束两侧杂波抑制性能有所提升,在第一种类型下甚至接近最优STAP。因此,加权JDL算法可以在不显著增加运算量的情况下通过适当增加空域波束数目[21]来提高主波束和旁瓣区域杂波的抑制能力,改善算法对系统误差的敏感度,获得较好的杂波抑制效果。
本文先建立较为一般的机载双基双动雷达几何模型,然后进行杂波仿真,对载机平台运动方向与基线的夹角在平面内遍历,根据双基构型和对应的杂波分布对机载双基雷达杂波作出了较为一般化的分类并分析了对应的杂波特性,以方便在不同的双基配置构型下使用恰当的方法检测目标,为机载双基雷达杂波的进一步研究提供了重要理论基础。在杂波分类的基础上,根据杂波分布具有距离依赖性的特点,提出了训练单元协方差矩阵加权平均的方法。算法仿真表明,该方法在补偿类和降维类方法下对机载双基雷达3种构型的杂波抑制性能均有明显提升。尤其是加权JDL算法,相比于补偿类算法运算量有大幅的降低,同时使用加权方法可以在不明显增加算法复杂度的情况下,使杂波抑制性能在主波束和旁瓣区域均有明显的提高,为双基雷达杂波抑制的理论研究和工程实现提供了新的方法。
[1] WILLIS N J, GRIFFITHS H D. Advances in Bistatic Radar[J]. IEEE Aerospace and Electronic Systems Magazine, 2008, 23(7):46.
[2] 段锐. 机载双基地雷达杂波仿真与抑制技术研究[D]. 成都: 电子科技大学, 2009.
[3] 刘霞飞. 雷达杂波分类与抑制技术研究[D]. 西安: 西安电子科技大学, 2015.
[4] KLEMM R. Comparison Between Monostatic and Bistatic Antenna Configurations for STAP[J]. IEEE Trans on Aerospace and Electronic Systems, 2000, 36(2):596-608.
[5] 彭晓瑞,谢文冲,王永良. 双基地机载雷达杂波建模及仿真分析[J]. 系统仿真学报, 2011, 23(2):257-261.
[6] 谢文冲,段克清,王永良. 机载雷达空时自适应处理技术研究综述[J]. 雷达学报, 2017, 6(6):575-586.
[7] 赵军,沈明威,朱岱寅,等. 一种改进的机载双基雷达多普勒频移算法[J]. 郑州大学学报(工学版), 2015, 36(2):75-79.
[8] SHEN Mingwei, YU Jia, WU Di, et al. An Efficient Adaptive Angle-Doppler Compensation Approach for Non-Sidelooking Airborne Radar STAP[J]. Sensors, 2015, 15(6):13121-13131.
[9] 冯为可,张永顺,张丹. 一种新的角度多普勒补偿方法[J]. 西安电子科技大学学报(自然科学版), 2015, 42(6):158-163.
[10] 赵军,田斌,朱岱寅. 基于PAST处理的机载双基雷达自适应角度-多普勒补偿算法[J]. 雷达学报, 2017, 6(6):594-601.
[11] HAYWARD S D. Adaptive Beamforming for Rapidly Moving Arrays[C]∥International Radar Conference, Beijing: IEEE, 1996:480-483.
[12] KLEMM R. Adaptive Airborne MTI: An Auxiliary Channel Approach[J]. IEE Proceedings F: Communications, Radar and Signal Processing, 1987, 134(3):269-276.
[13] WANG Hong, CAI Lujing. On Adaptive Spatial-Temporal Processing for Airborne Surveillance Radar Systems[J]. IEEE Trans on Aerospace and Electronic Systems, 1994, 30(3):660-670.
[14] 同亚龙,王彤,文才,等. 一种稳健的机载非正侧视阵雷达杂波抑制方法[J]. 电子与信息学报, 2015, 37(5):1044-1050.
[15] 刘红亮. 机载雷达非均匀检测和杂波抑制方法研究[D]. 西安: 西安电子科技大学, 2016.
[16] BRENNAN L E, REED I S. Theory of Adaptive Radar[J]. IEEE Trans on Aerospace and Electronic Systems, 1973, AES-9(2):237-252.
[17] 高惠雯. 机载非协作雷达杂波建模与STAP研究[D]. 成都: 电子科技大学, 2017.
[18] 袁俊泉,袁博资,王力宝,等. 天空双基雷达回波空时二维建模与分析[J]. 系统工程与电子技术, 2016, 38(1):64-69.
[19] KLEMM R. Space-Time Adaptive Processing: Principles and Applications[J]. Electronics and Communications Engineering Journal, 1999, 11(4):172.
[20] REED I S, MALLETT J D, BRENNAN L E. Rapid Convergence Rate in Adaptive Arrays[J]. IEEE Trans on Aerospace and Electronic Systems, 2007, AES-10(6):853-863.
[21] 任娅. 机载雷达非自适应杂波抑制方法及应用研究[D]. 西安: 西安电子科技大学, 2015.

