脉压雷达所采用的宽脉冲不仅可以提高雷达的平均发射功率,还能够确保足够大的作用距离。在接收端通过脉冲压缩处理将宽脉冲转化为窄脉冲,则可实现较好的距离分辨率,因此较好地解决了雷达大作用距离和高距离分辨率之间的矛盾。此外,脉冲压缩处理大大提高了雷达对非相干干扰的抑制能力[1]。如何对脉压雷达进行有效干扰已成为电子战领域的研究热点。
线性调频(LFM)信号是脉压雷达广泛采用的信号之一,该信号存在距离和多普勒强耦合的固有缺陷[2],这使得转发式干扰对脉压雷达更容易产生干扰,间歇采样转发干扰是对抗采用LFM信号的脉压雷达的常用转发式干扰样式之一[3]。间歇采样直接转发干扰改善了由收发隔离问题所致的转发式干扰所产生假目标滞后于真目标的问题,同时兼顾了干扰信号与脉压雷达信号间的相干性[4-5]。但是间歇采样直接转发干扰形成的假目标串中,主假目标始终滞后于真目标,且次假目标幅度衰减过快,能有效形成干扰的假目标数较少[6-7]。间歇采样重复转发干扰的提出在一定程度上解决了上述问题,然而该方法无法干扰脉压雷达对目标速度信息的获取,导致所产生的假目标不满足目标运动特性,容易被敌方剔除,且对干扰机功率要求较高[8-10]。
本文提出一种基于多相位分段调制处理的脉压雷达干扰方法,该方法能够克服间歇采样重复转发干扰无法对脉压雷达获取目标速度信息产生影响的固有缺陷,通过对脉压雷达信号进行分段相位调制,部分保留和破坏脉压雷达回波信号的相干性,从而形成灵活可靠的多样化遮盖效果。
设脉压雷达采用LFM信号,则雷达脉冲信号为
(1)
式中,T为脉冲宽度,k为LFM信号的调频斜率。
间歇采样处理可等效为一矩形脉冲串p(t)对雷达信号进行采样,则单次间歇采样所得干扰信号的数学模型可表示为
xs(t)=x(t)p(t)
(2)
由上式可知,干扰信号经过脉压处理后的输出信号为
ys(t)=xs(t)*h(t)
(3)
式中,h(t)为匹配滤波器的脉冲响应函数。
设脉压雷达脉宽T是间歇采样周期Ts的整数倍,Ts是采样间隔τ的整数倍,转发信号的时长均为τ,在间歇采样周期Ts内,可转发当前采样的最高次数为M,则由式(3)可知,间歇采样重复转发干扰信号的脉压输出可表示为
ys(t)+ys(t-τ)+ys(t-2τ)+…+
(4)
式中,M=Ts/τ-1。由上式可知,间歇采样重复转发干扰实际上是对ys(t)以等间隔τ进行M次延拓。
与全样本干扰方法相比,间歇采样干扰的优势主要有:
1) 间歇采样重复转发干扰只要获得脉压雷达的最小脉宽就可实施有效干扰,因此不需要进行过多的电子战侦察工作,效率更高;
2) 间歇采样重复转发干扰的采样周期Ts取值灵活,不同取值可产生不同干扰效果,因此可适用于任何线性调频体制脉压雷达;
3) 间歇采样重复转发干扰的干扰机相比全样本干扰,体积更小,有利于工程实现。
但该干扰通常存在以下问题:
1) 假目标数较少时,不仅不能遮盖真实目标,假目标还容易成为敌方的信标,暴露真实目标位置;
2) 假目标数较多时,干扰效果类似于噪声压制干扰,敌方可能会察觉到干扰的存在,难以对敌方造成欺骗;
3) 假目标的多普勒信息与真实目标相同,利用真实目标的运动特性,可以识别假目标。
对脉压雷达的多相位分段调制干扰主要分为信号分段、相位调制、信号采样和信号合成四个步骤[11],如图1所示。
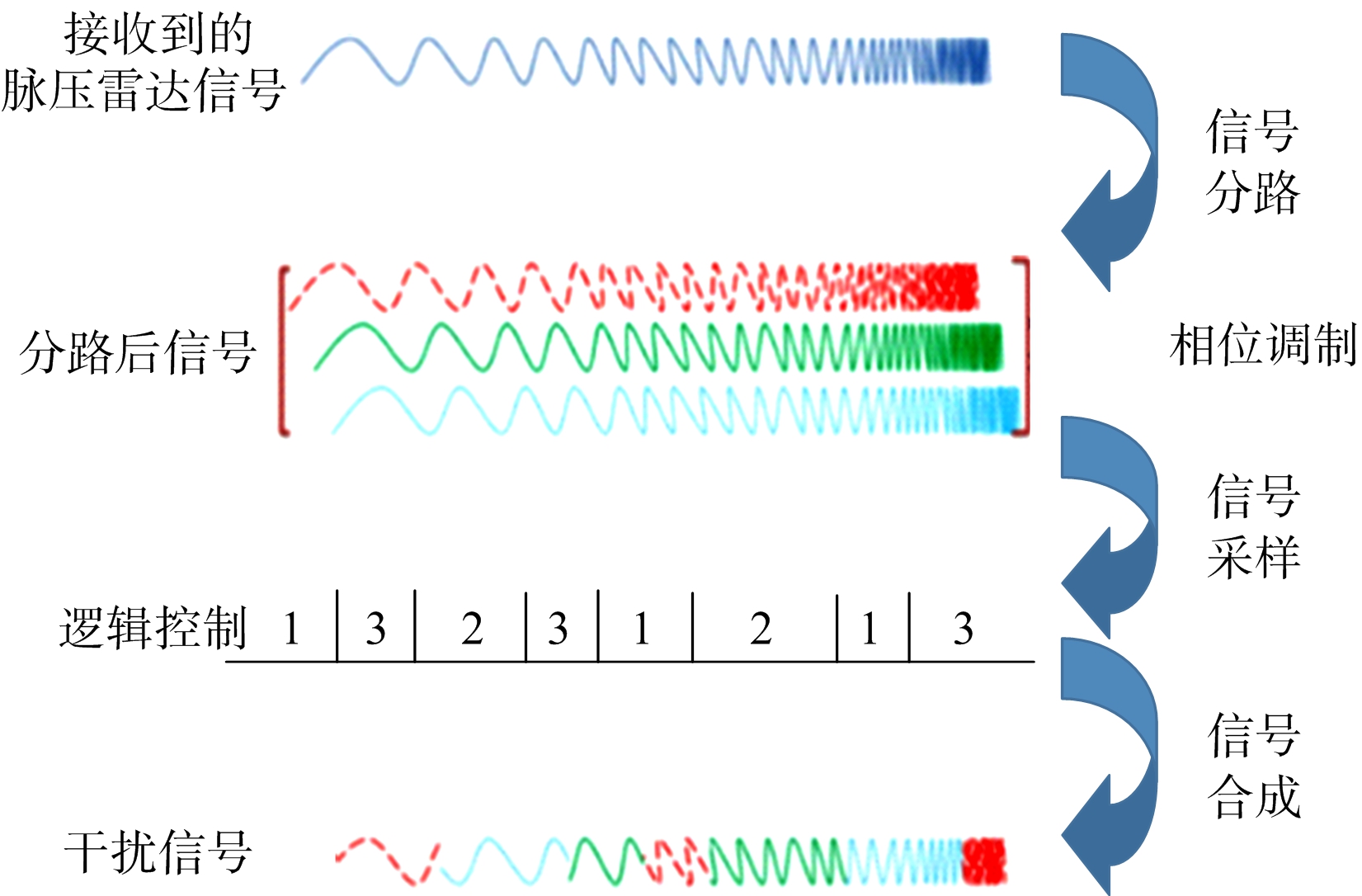
图1 多相位分段调制干扰原理图
具体步骤如下:
1) 信号分段
干扰机接收到脉压雷达发射信号后,通过一等间距或非等间距的矩形脉冲串对存储的雷达信号进行采样,随后平移脉冲串将信号划分为N(N≥2)个不同分段。
2) 相位调制
在不同信号分段上按照一定的规律进行相位调制,即改变雷达发射信号波形的相位。相位调制是多相位分段调制干扰的核心环节,其具体规则如下:
① 相位调制后生成信号的总时长与雷达回波信号相等,和雷达信号的波形体制无关;
② 各分段相位调制采用的相位值可在[0,2π]上随机取值,相位取值个数不少于2,并且为有限个;
③ 各分段信号的时长可以取小于脉压雷达信号时长的任意值,并且各分段信号的时长取值可以是等分或非等分。
3) 信号采样
相位调制处理后,根据存储的子信号相位,能够对信号采样时间进行选择。对所选子信号进行实时采样,就得到了与脉压雷达信号波形完全相同的相位调制子脉冲串。
4) 信号合成
将信号采样后已按规律排列的各分段信号合路输出,可以在干扰时段内生成与脉压雷达信号脉冲长度相同的干扰信号。
设脉压雷达回波信号为s(t),信号分段后的各分段长度为等长τ,各分段上的相位调制值分别为φ1,φ2,φ3,…,φp,相位调制过程中,相位调制值为φ1的信号分段数为n1,所有信号分段起止时刻分别为t1si和t1ei,其余信号分段的起止时刻同理可得。
以上述参数设置为基础,用阶跃函数ε(t)表示信号各分段之间的相位调制值跳变,则多相位分段调制干扰信号等价于脉压雷达信号与一复合函数的乘积:
sJ(t)=s(t)·p(t)
(5)
式中,
p(t)=![]()
(6)
干扰信号总分段数N=n1+n2+n3+…+np,脉压雷达脉冲时宽Tp=Nτ。
脉压雷达发射信号为f(t),经目标后向散射产生的雷达发射信号回波为s(t),干扰机对截获的雷达信号进行多相位分段调制处理后生成的干扰信号为sJ(t),则由接收机脉冲压缩处理后得到的输出信号为F(t)+FJ(t)。
回波信号的波形与发射信号相同,二者只是在包络幅度和产生时刻上不同,故结合式(5)可知,多相位分段调制干扰信号在时域可以表示为
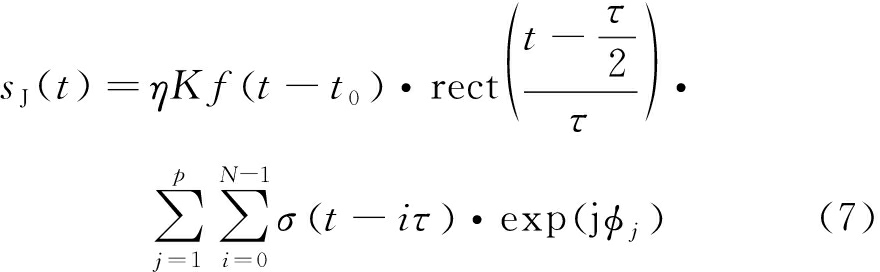
式中,K为回波信号与发射信号的包络幅度比值。
设相邻信号分路的相位调制差值均为φx,结合式(6),对式(7)作傅里叶变换可知,多相位分段调制干扰信号在频域可以表示为
SJ(jω)=ηKF(jω)e-jω t0·P(jω)=ηKF(jω)e-jω t0·
(8)
式中,K′=ηK。则多相位分段调制干扰信号的幅频特性和相频特性分别为
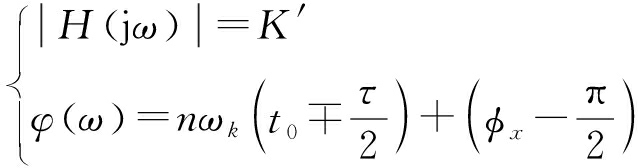
(9)
结合式(9)可知,回波信号和k=1时的多相位分段调制干扰信号的幅相特性曲线如图2所示。
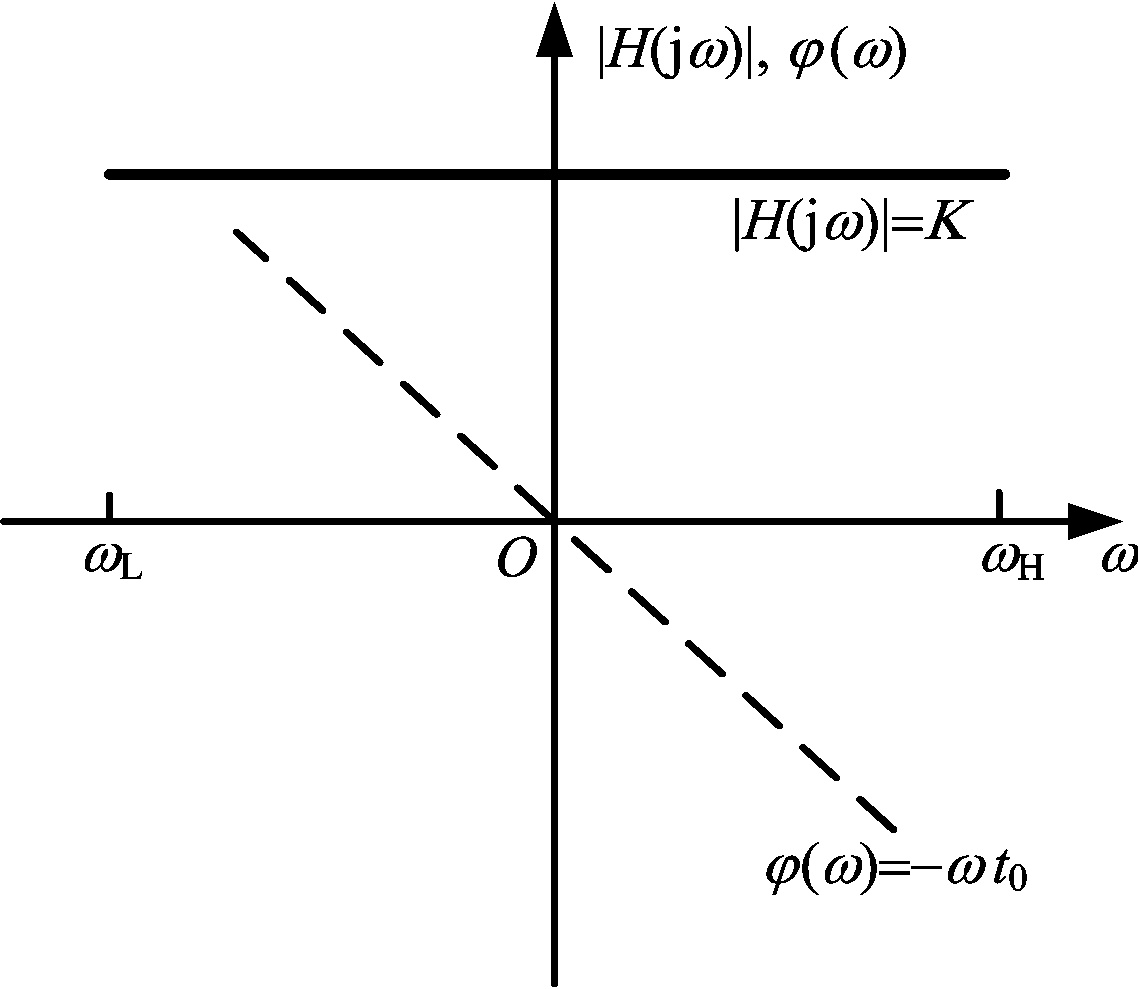
(a) 回波信号

(b) 多相位分段调制干扰信号
图2 回波信号和干扰信号的幅相特性曲线
由回波信号和多相位分段调制干扰信号的幅相特性曲线可知,干扰信号与回波信号的幅频特性在全频带内均为一常数,二者成倍数关系,干扰信号的相频特性和y轴的交点与调制相位值的大小有关,曲线斜率与分路的时间点有关。由k=1时的干扰信号幅相特性推广至k取任意值,可以看出,多相位分段调制干扰信号在单个信号分路上的相频特性依然是线性连续的,然而多个分路间的相频特性不再具有回波信号相频特性所固有的线性相位特性。
综上所述,多相位分段调制干扰是一种部分相干干扰,值得一提的是,通过各分路长度和相位调制值的不同组合,干扰方可以改变干扰信号对回波信号特征的保留程度与破坏程度,从而实现干扰效果的多样性。
设脉压过程中的环境噪声是功率谱密度为N0/2 W/Hz的高斯白噪声,输出噪声的功率谱密度为(N0/2)·|H0(jω)|2 W/Hz。假设脉压输出信号在t=td时刻得到峰值,则多相位分段调制干扰信号经过匹配滤波器后的输出信号表达式为
FJ(td)=
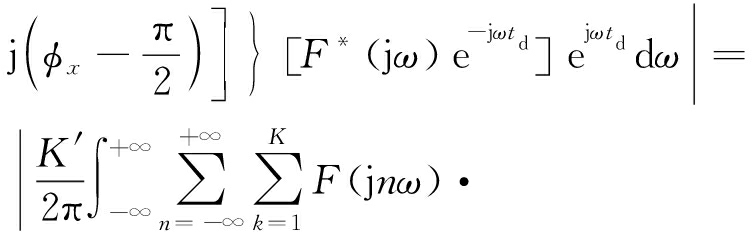
(10)
设相位调制值φ1所在信号分段的带宽B1=ωH1-ωL1,由频谱偏移产生的时延量Δt,则该分段干扰信号的脉冲压缩输出表达式为
FJ1(td)=![]()
S*![]()
(11)
令
(12)
(13)
则式(11)可以等价为
FJ1(td)=A1ejΦ1
(14)
将上式推广至整段干扰信号,则多相位分段调制干扰信号的脉压输出结果为
(15)
由上式可知,干扰信号的脉压输出结果可以等效为若干个信号矢量的叠加,各信号矢量的幅值和幅角与干扰信号分段数、调制相位数以及调制相位值三个参数有关。进一步分析可知,脉冲压缩后的干扰信号主瓣宽度与干扰信号分段长度成反比关系,另外,sinc函数的中心在一定范围内偏移,且偏移量与干扰信号的参数有关。
结合以上分析可得,多相位分段调制干扰可以在真实目标周围形成一定范围的局部遮盖效果,且通过对干扰信号分段数、调制相位数以及调制相位值三个参数的控制可以实现灵活多样的干扰效果。
在已有相关理论研究基础上,应用Matlab软件对采用LFM信号的脉压雷达MTD结果进行仿真分析,预设目标场景为一匀速运动目标,仿真参数如表1所示。
表1 仿真参数设置
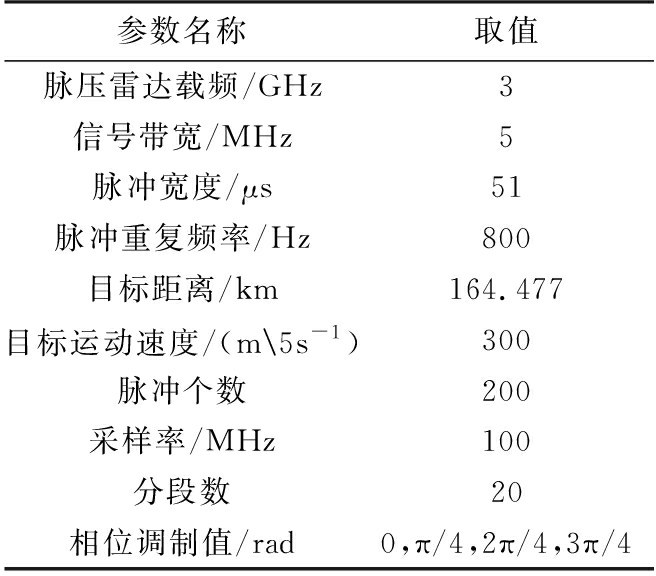
参数名称取值脉压雷达载频/GHz3信号带宽/MHz5脉冲宽度/μs51脉冲重复频率/Hz800目标距离/km164.477目标运动速度/(m\5s-1)300脉冲个数200采样率/MHz100分段数20相位调制值/rad0,π/4,2π/4,3π/4
在上述干扰场景和干扰参数下,采用四相位等分分段多相位分段调制干扰,相位值按照从小到大的顺序进行调制,与间歇采样重复转发干扰进行以下3组仿真对比实验,各实验进行100次蒙特卡洛仿真,各组MTD结果取蒙特卡洛仿真结果均值的最大值对应的距离和速度作为目标信息。
实验一:间歇采样重复转发干扰的采样周期Ts=2 μs,采样间隔τ=0.5 μs,干信比分别取20,30,40 dB,所得目标信息如表2所示,仿真结果如图3所示。
表2 实验一所得目标信息
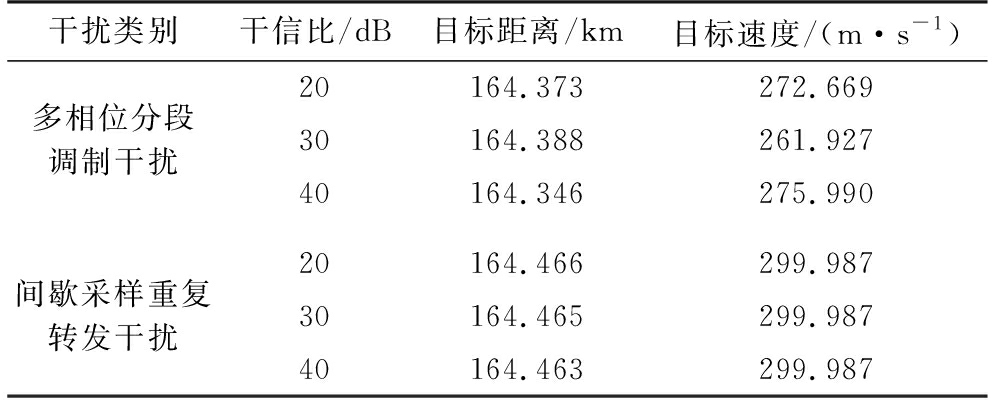
干扰类别干信比/dB目标距离/km目标速度/(m·s-1)多相位分段调制干扰20164.373272.66930164.388261.92740164.346275.990间歇采样重复转发干扰20164.466299.98730164.465299.98740164.463299.987
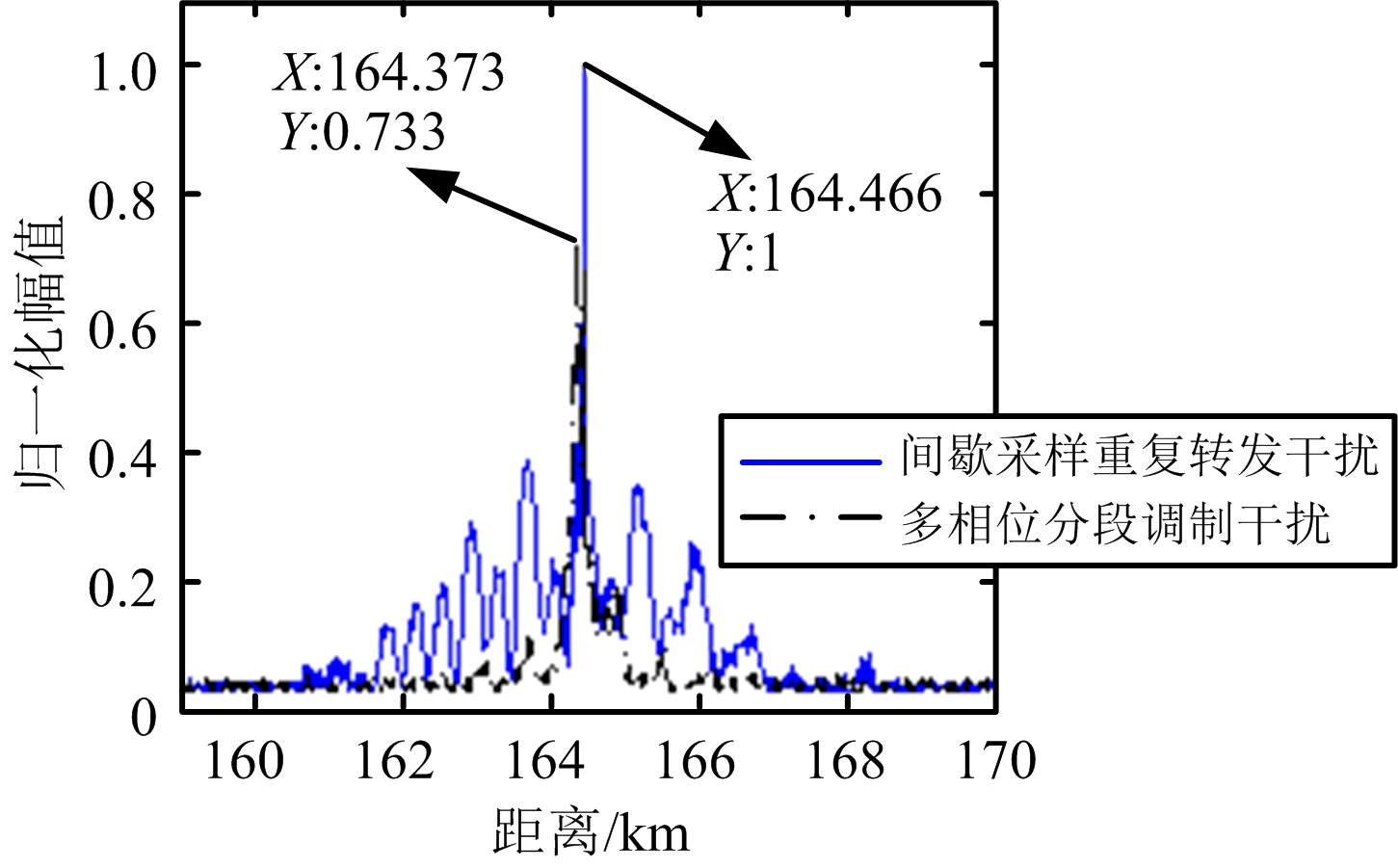
(a) 干信比20 dB
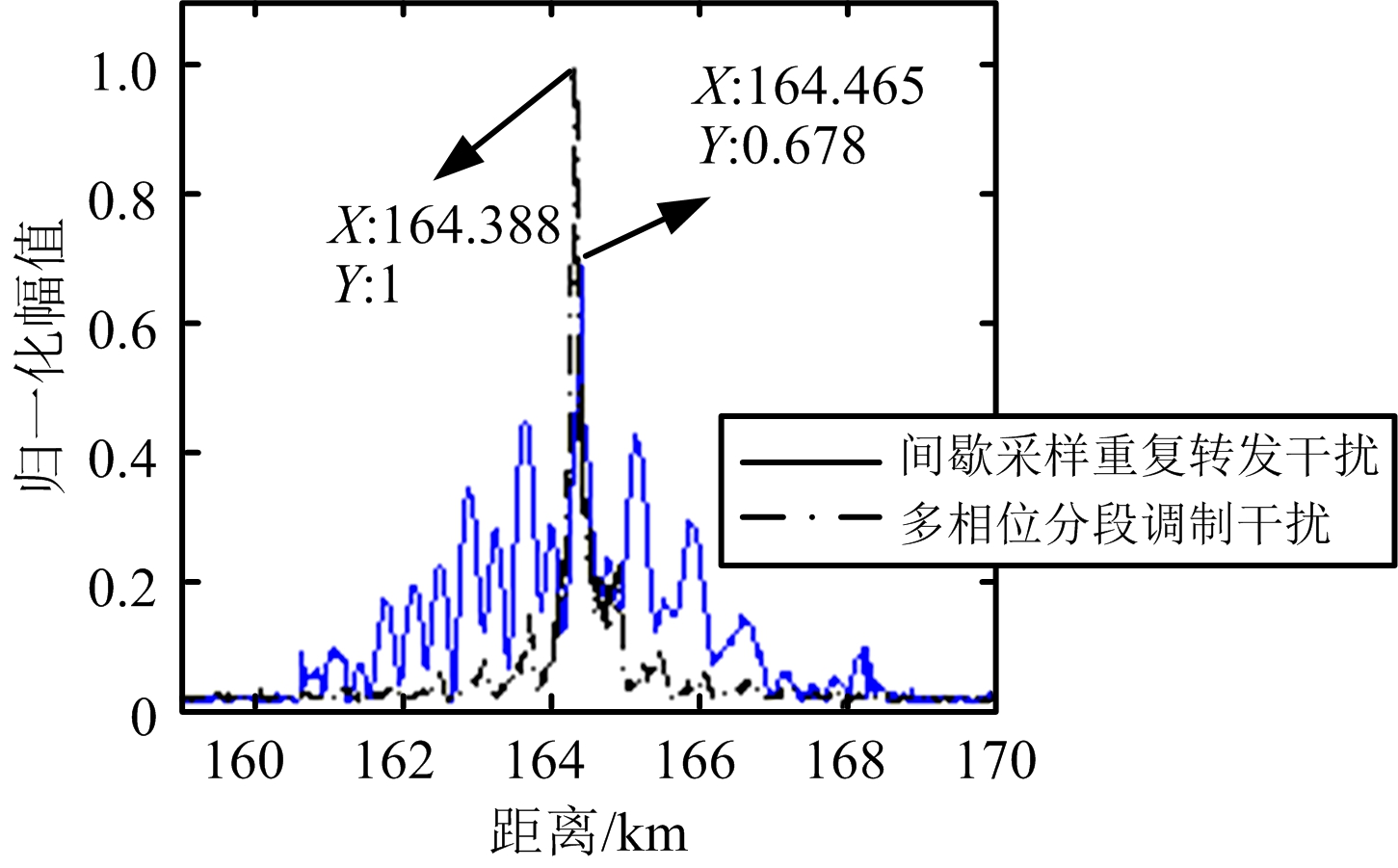
(b) 干信比30 dB
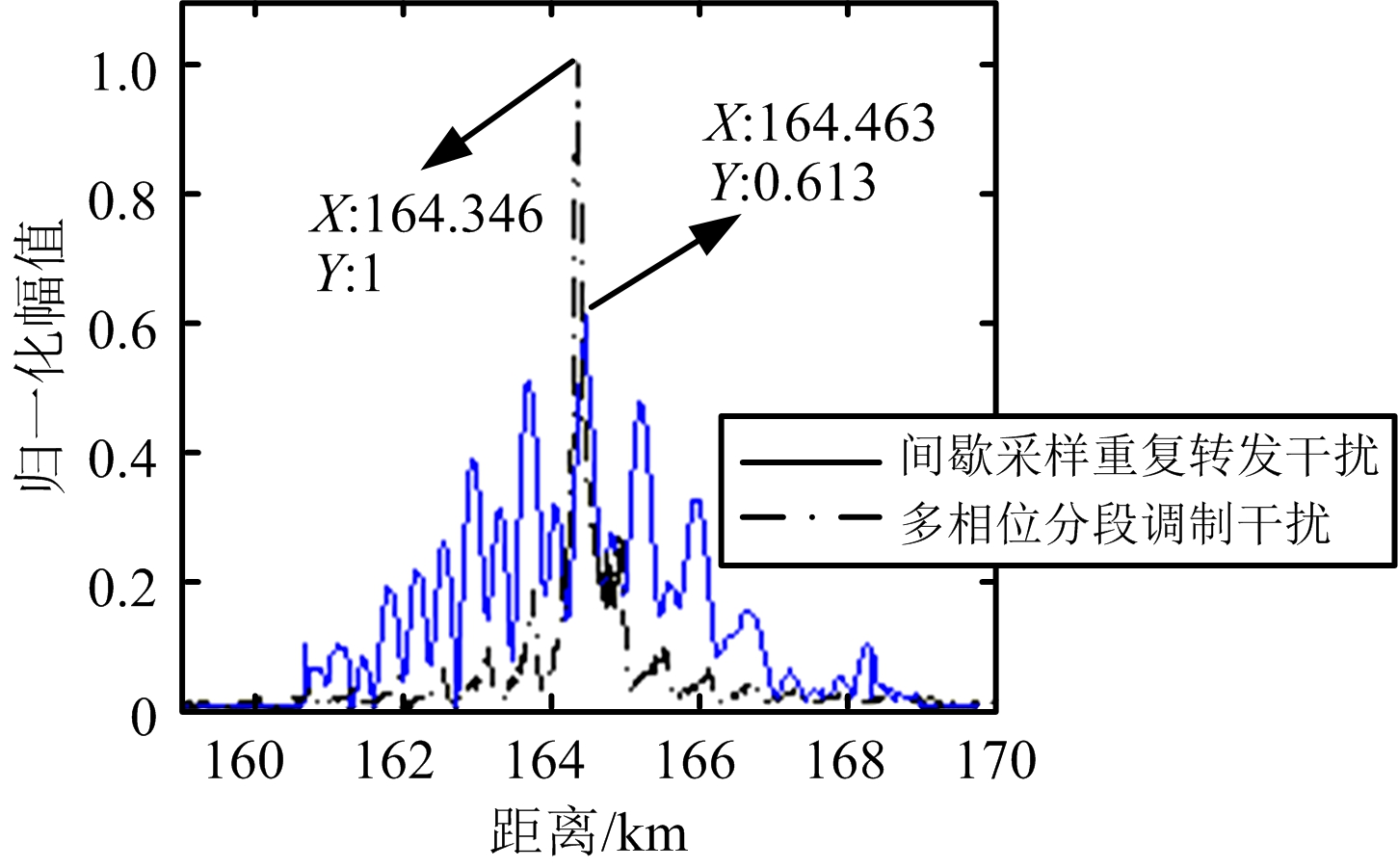
(c) 干信比40 dB
图3 实验一MTD结果对比
由图3和表2可知,3种干信比对应的间歇采样重复转发干扰下脉压雷达获取的目标距离误差分别为-11,-12,-14 m,目标速度误差均为 -0.013 m/s,距离域和速度域均未对脉压雷达形成干扰,而多相位分段调制干扰下雷达获取的目标距离信息和速度信息均与真实目标信息间存在较大误差,形成了欺骗假目标。值得一提的是,随着干信比的提高多相位分段调制干扰下的MTD峰值幅度逐步增大,在30 dB和40 dB时,明显大于间歇采样重复转发干扰,即采用大干信比时多相位分段调制干扰的干扰能量利用率高于间歇采样重复转发干扰。在实验一的基础上,后面的实验均在干信比40 dB下研究两种干扰的遮盖效果。
实验二:间歇采样重复转发干扰的采样周期Ts=3 μs,采样间隔τ=0.5 μs,干信比取40 dB,所得目标信息如表3所示,仿真结果如图4所示。
表3 实验二所得目标信息

干扰类别目标距离/km目标速度/(m\5s-1)多相位分段调制干扰164.346275.990间歇采样重复转发干扰163.991299.987
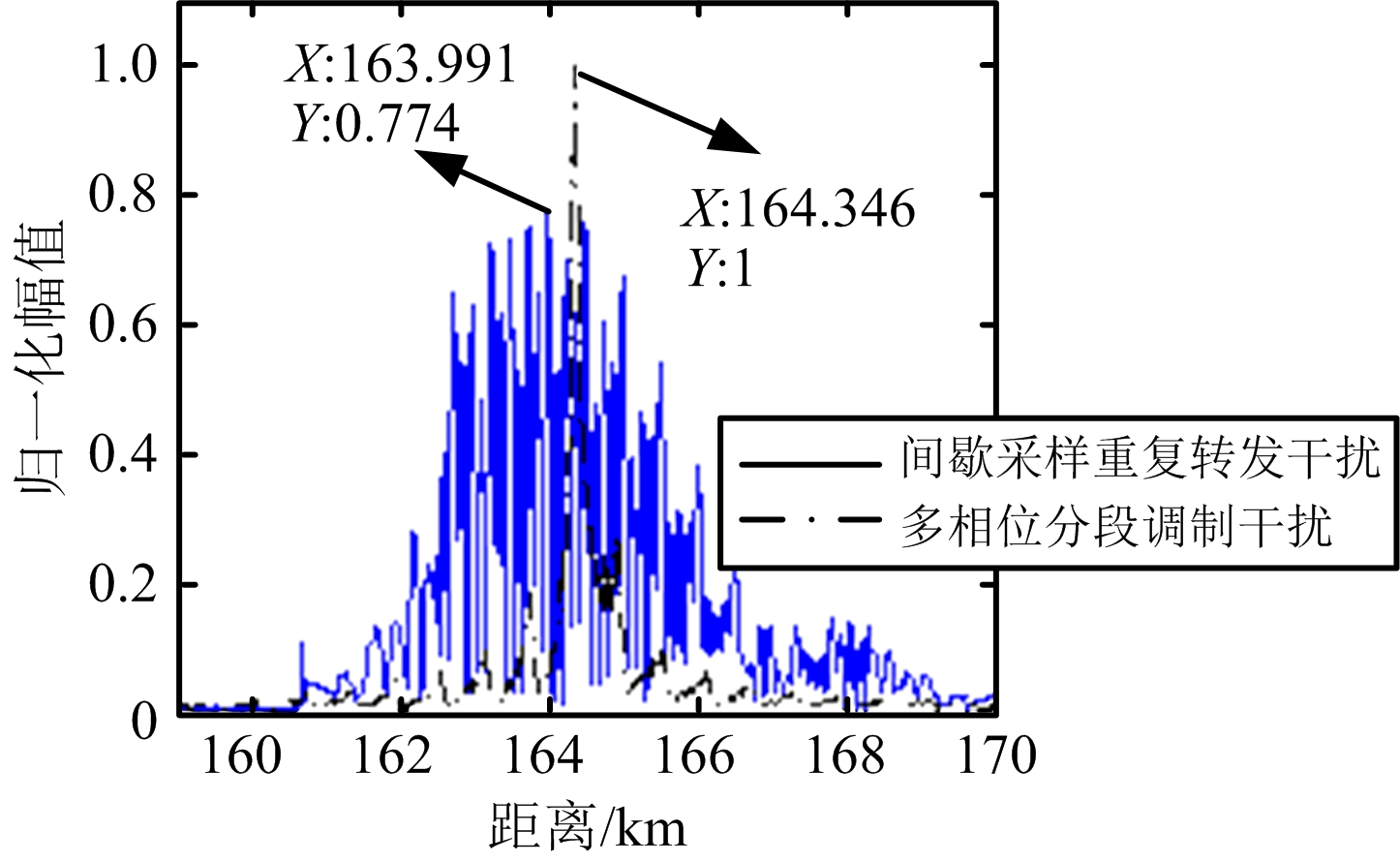
图4 实验二MTD结果对比
由图4和表3可知,增大采样周期Ts后,间歇采样重复转发干扰产生大量密集假目标,改善了对真实目标的遮盖效果。但由于间歇采样重复转发干扰并没有破坏原始信号的脉间信息,对脉压雷达获取目标速度信息无影响。与多相位分段调制干扰相比,虽然遮盖效果较好,但是没有形成欺骗干扰。
实验三:间歇采样重复转发干扰的采样周期Ts=3 μs,采样间隔τ=0.7 μs,干信比取40 dB,所得目标信息如表4所示,仿真结果如图5所示。
表4 实验三所得目标信息

干扰类别目标距离/km目标速度/(m·s-1)多相位分段调制干扰164.346275.990间歇采样重复转发干扰163.512299.987
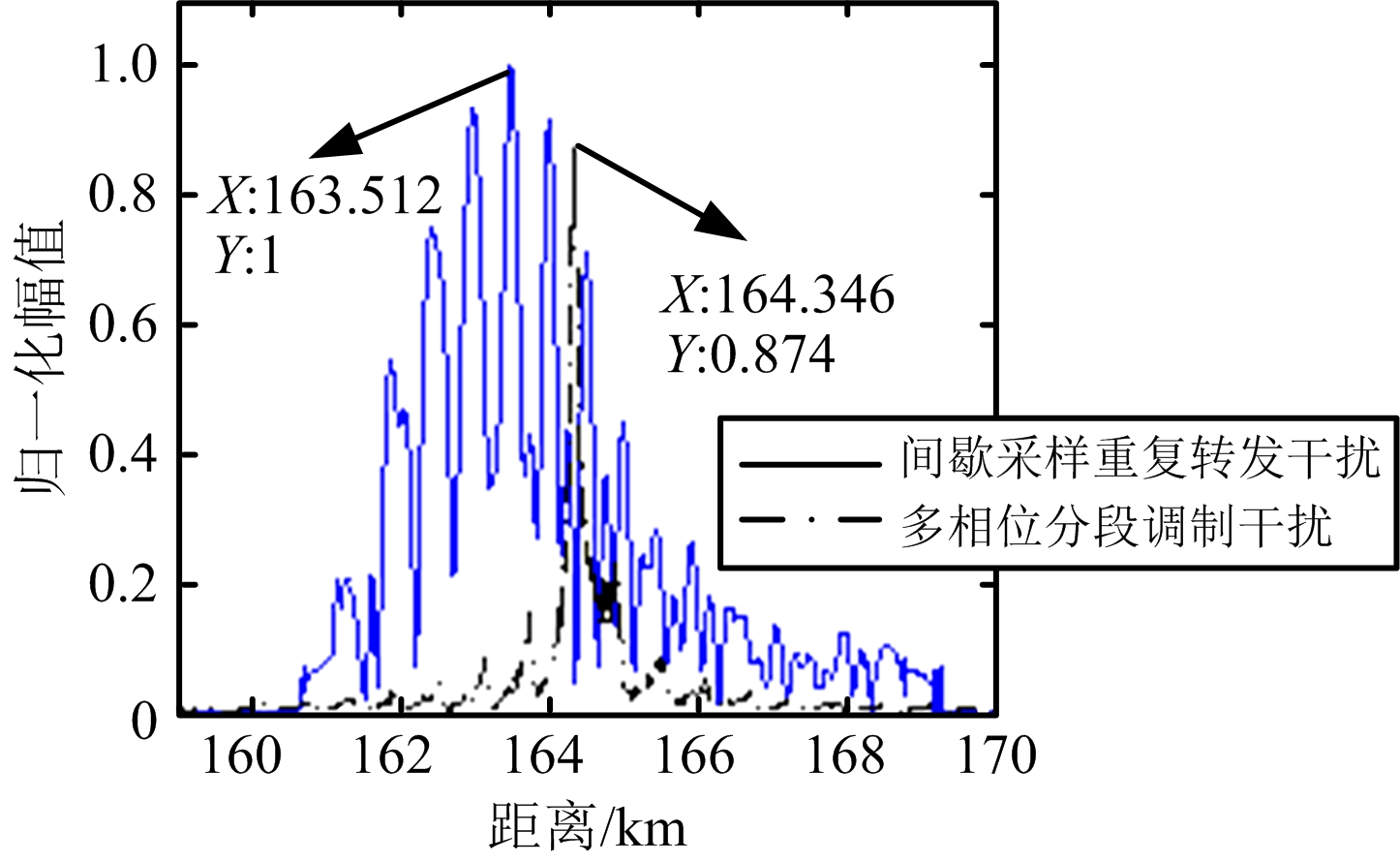
图5 实验三MTD结果对比
由图5和表4可知,增大采样间隔τ后,间歇采样重复转发干扰产生的假目标集中分布在真实目标两侧,干扰能量的分布集中至分布中心。虽然MTD所得的目标距离相比真实目标发生偏移,而速度信息仍然无偏差。与多相位分段调制干扰相比,虽然真实目标被遮盖,但没有形成欺骗效果。
本文提出了一种基于多相位分段调制处理的脉压雷达干扰方法,在其基本原理的基础上,以采用LFM信号的脉压雷达为平台,推导了干扰信号的表达式,并对干扰信号的幅相特性和脉冲压缩输出进行分析,结果表明,信号分路数、调制相位数量以及相位调制值的变化组合可以产生灵活多样的干扰效果。通过实验仿真对比了多相位分段调制干扰与间歇采样重复转发干扰的干扰效果,结果表明,该干扰克服了间歇采样重复转发干扰对目标速度无法产生欺骗且易被敌方识别的缺陷,干扰能量利用率较高,对真目标形成了相对可靠的遮盖效果。下一步将重点研究如何对多相位分段调制干扰的遮盖范围及干扰功率进行控制。
[1] 王健,王宝,万华. 脉冲多普勒雷达同频干扰研究[J]. 雷达科学与技术, 2014, 12(4):441-445.
WANG Jian, WANG Bao, WAN Hua. Study on Co-Frequency Interference between Pulse Doppler Radars [J]. Radar Science and Technology, 2014, 12(4):441-445.(in Chinese)
[2] 丁鹭飞,耿富录. 雷达原理[M]. 3版. 西安: 西安电子科技大学出版社, 2014.
[3] 杨少奇,田波. LFM脉压雷达间歇采样调相干扰研究[J]. 计算机仿真, 2016, 33(10):9-13.
[4] 王杰贵,张鹏程. 对线性调频脉压雷达的多载波调制转发干扰[J]. 电子与信息学报, 2015, 37(11):2727-2734.
[5] 冯德军,王伟,徐乐涛. 对V-调频信号的间歇采样转发干扰研究[J]. 雷达科学与技术, 2013, 11(2):209-213.
FENG Dejun, WANG Wei, XU Letao. Jamming V-FM Signal Using Interrupted-Sampling Repeater [J]. Radar Science and Technology, 2013, 11(2):209-213. (in Chinese)
[6] 张杨瑞,李云杰,李曼玲,等. 间歇采样非均匀重复转发实现多假目标压制干扰[J]. 电子学报, 2016, 44(1):46-53.
[7] 刘忠,王雪松,刘建成,等. 基于数字射频存储器的间歇采样重复转发干扰[J]. 兵工学报, 2008, 29(4):405-410.
[8] 张翔,李彦志,鲁建华,等. 基于LFM雷达时延-频移耦合性的间歇采样转发改进方法[J]. 电光与控制, 2017, 24(3):98-101.
[9] 朱宇,罗景青. 基于卷积调制的间歇采样干扰技术研究[J]. 电子信息对抗技术, 2013, 28(3):41-45.
[10] 周超,刘泉华,曾涛. DRFM间歇采样转发式干扰辨识算法研究[J]. 信号处理, 2017, 33(7):911-917.
[11] YU Daobin, WANG Hongyan, WU Yanhong. Research on Cross-Eye Jamming Technique Based on Phase Diversity Processing[C]∥ International Conference on Frontiers of Sensors Technologies, Hong Kong: IEEE, 2016:59-64.
