和占空比
两个参量，运用图像标记技术提取上述参量。当目标回波间隔距离小于或等于多帧积累时间内慢小目标的运动距离且目标回波长宽比和占空比所确定信息值相近时，把满足该条件目标回波信息值进行累加，并把累加结果作为该区域目标回波SHNN-CAD异常程度计算权值，最终通过控制异常程度值检测出可能的慢小目标，仿真结果验证了该算法的有效性。摘 要： 因杂波干扰强度大、目标回波微弱等原因，导致雷达操纵员将慢小目标误当成杂波点。把连续多帧雷达图像进行长时间积累，针对多帧雷达图像积累中目标回波不连通的情况，提出了一种目标回波不连通的慢小目标检测方法。引入目标回波最小外接矩形的长宽比和占空比两个参量，运用图像标记技术提取上述参量。当目标回波间隔距离小于或等于多帧积累时间内慢小目标的运动距离且目标回波长宽比和占空比所确定信息值相近时，把满足该条件目标回波信息值进行累加，并把累加结果作为该区域目标回波SHNN-CAD异常程度计算权值，最终通过控制异常程度值检测出可能的慢小目标，仿真结果验证了该算法的有效性。
本文讨论的探测对象是飞行速度慢、RCS小的目标，简称“慢小目标”(Slow and Small Target，SST)。随着各类满足SST特征飞行器的快速发展和我国低空开放的迫切需求[1]，SST对现代防空预警系统威胁程度越来越大。由于缺乏专用于SST的探测装备，使得目前对SST的发现概率很低。即使常规雷达信号处理能够部分检测到SST，也往往会因为杂波干扰强度大和目标回波微弱等原因[2-3]，导致雷达操纵员将其误当成杂波点[4-5]。
目标航迹检测是雷达识别的重要组成部分，目标只有完成有效航迹分析才能最终被雷达识别。SST的独特运动特性和目标特性使得SST与正常目标之间存在很大差别，在航迹处理时通常把它作为异常目标进行分析。目前国内外异常航迹分析的方法有很多，文献[6]提出了一种基于子轨迹异常检测方法，通过改变Hausdorff距离的计算方式，极大缩短异常航迹检测的时间。文献[7]提出一种基于航迹聚类的异常事件检测方法，提取出保存的轨迹聚集层级聚类并建立相关描述模型，通过对所提取聚类的模型进行比较区分出正常或异常事件。文献[8]提出一种基于多维航迹特征的异常行为检测方法，通过定义多因素定向的欧拉距离和构造多维度局部异常因子，实现对多维度航迹数据的异常检测。以上文献所提及的异常目标检测方法，针对常规目标而言具有很好效果，但对SST并没有太好的效果。对此本文立足现有雷达装备(文中若不作特殊说明，均是指现有地面情报雷达装备)的探测能力，提出一种目标回波不连通的慢小目标检测方法。
现有雷达的信号处理很难完全滤除杂波，因此，在送往雷达显示终端的0/1检测信号中，依然会存在大量的杂波剩余。其中，慢动杂波具有与SST相近的运动速度，在多帧雷达图像积累中，慢动杂波也会聚集于同一位置或同一区域。但是，由于SST和慢动杂波在运动方向和运动规律上存在较大不同，因此多帧雷达图像积累后，SST和慢动杂波的目标回波就会存在较大差异。主要表现在：
1) 慢动杂波往往是无规则运动的，多帧积累后，其回波会呈现无规则的形状，且大多无确定的方向，如图1(a)所示；
2) SST的运动是有方向的，多帧积累后，其回波会呈现具有一定长宽比的、较规则的“线状”或“航迹状”形状，如图1(b)所示。
本文讨论的算法就是基于SST和杂波多帧积累后，目标回波间存在的这种积累特性差异而设计的。
图1是慢动杂波和SST回波不连通的多帧积累示意图，当然，在实际工作中也经常会遇到SST在杂波环境中运动的情况，这时的多帧积累回波情况就会比上述目标与杂波分离的情况复杂得多。本文处理的雷达图像是一种二值图像[9-11]，其中“1”表示存在目标，“0”表示不存在目标。如果目标回波出现叠加将难以对所检测目标类型进行区分，因此本文处理的前提是假设目标回波相互间不存在叠加现象。
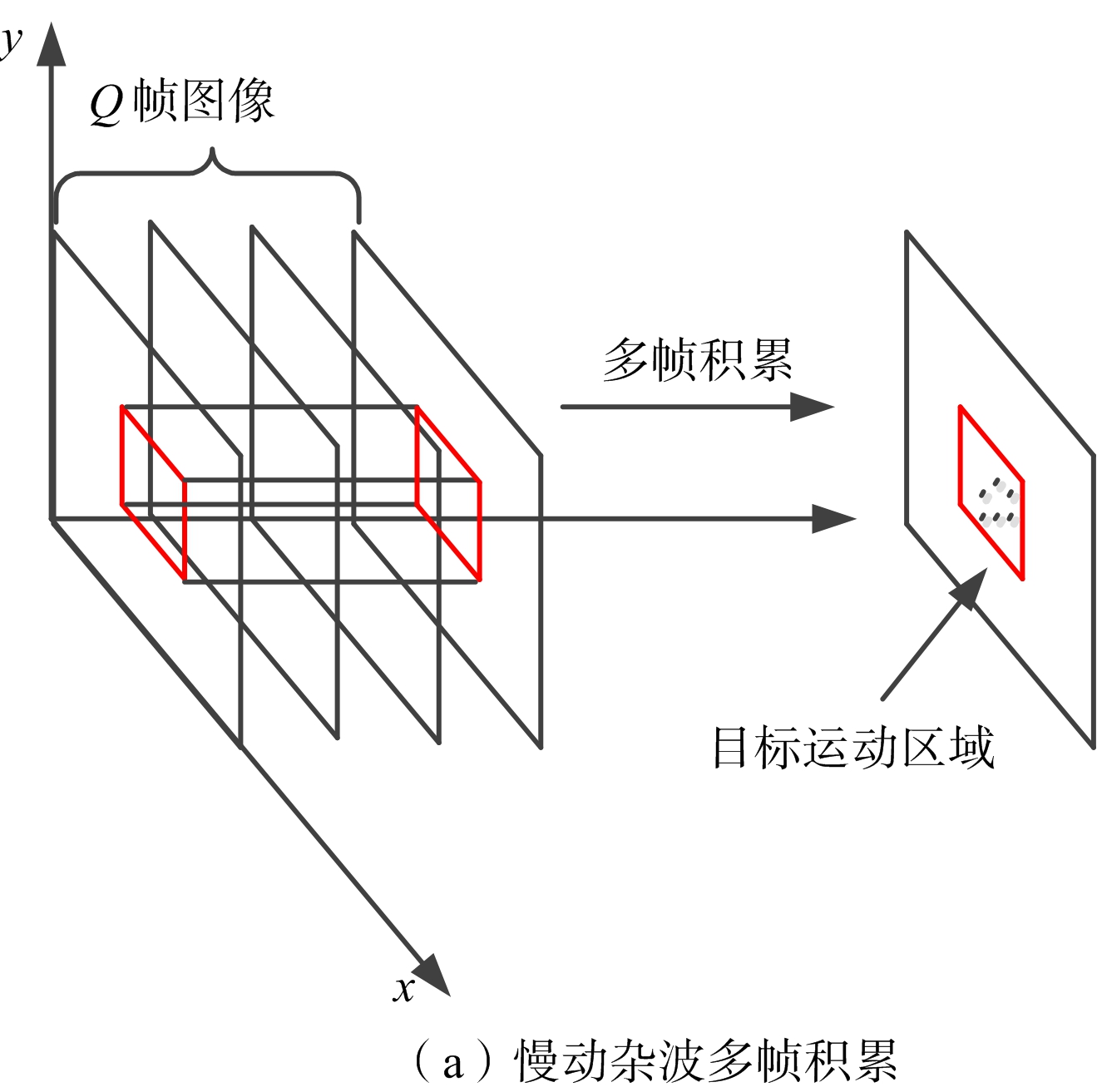
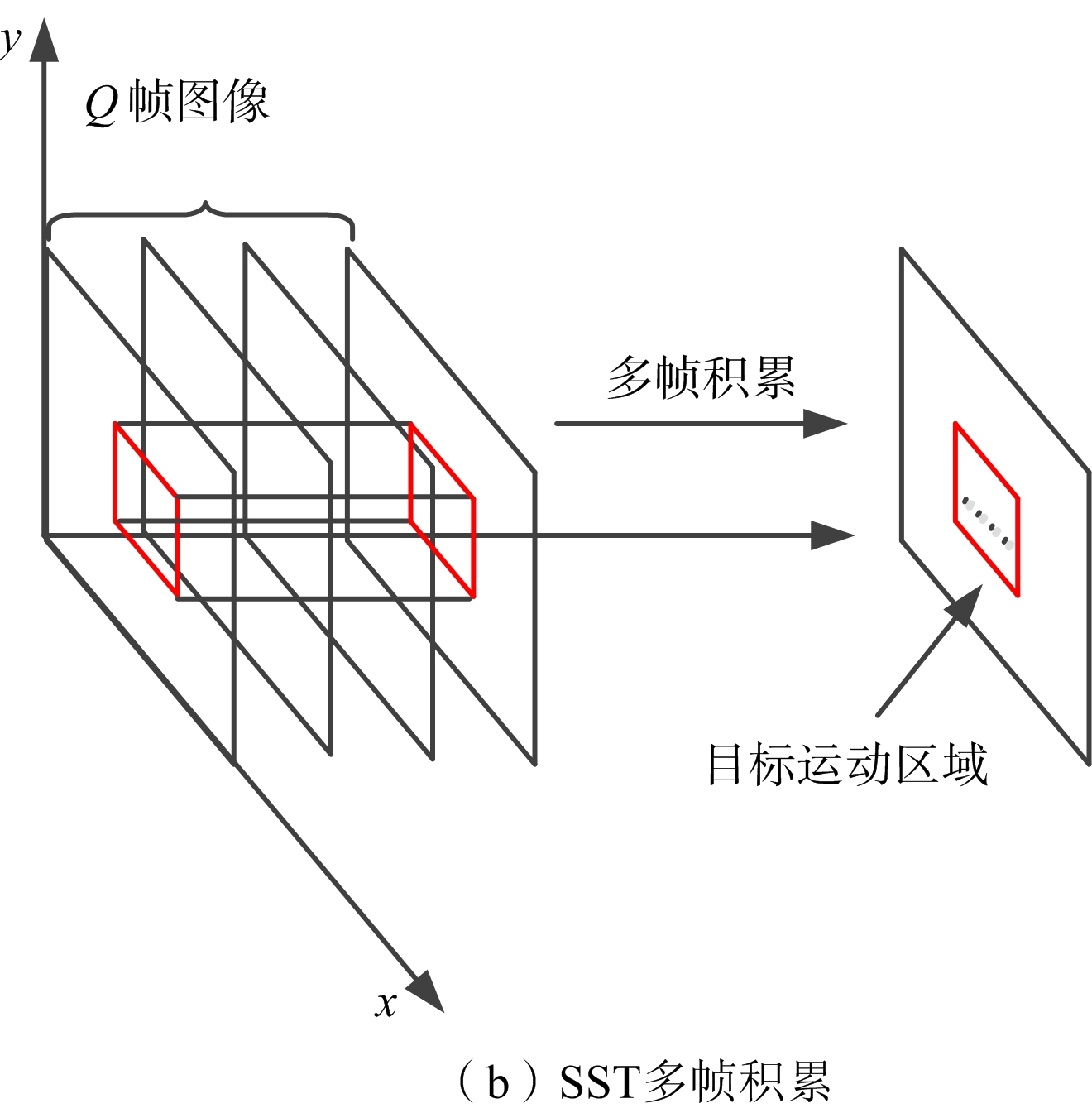
图1 慢动杂波和SST多帧积累
在慢动杂波和SST积累情况如图1所示，且目标回波相互间不存在叠加时，利用占空比和长宽比确定目标回波信息值。当目标回波间隔距离小于或等于多帧积累时间内慢小目标的运动距离且目标回波信息值相近时，把满足条件目标回波信息值进行累加，并把累加结果作为该区域目标回波SHNN-CAD的异常程度计算权值，提高SST回波的检测概率。
运用图像标记技术[12-13]对多帧雷达图像中目标回波进行标记，提取N个目标回波面积
占空比
和长宽比
目标回波的像素个数，占空比和长宽比
的定义如下所示：
(1)
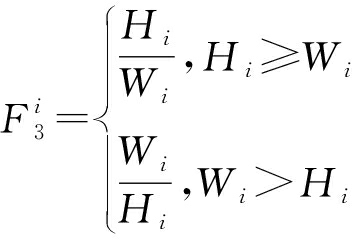
(2)
式中：Si为目标回波最小外接矩形的面积；Hi，Wi分别为目标回波最小外接矩形的长和宽。在目标回波像素值一定时，占空比越接近1，长宽比越大，则该目标回波是SST可能性就越大。
目标回波占空比和长宽比是目标回波的描述向量，同一目标相邻帧目标回波占空比和长宽比将会很相近。使用信息值[14]对目标回波占空比和长宽比进行一个整体描述， 在K×M的Q帧SST多帧积累图像中，目标回波信息值表达式为
(3)
式中，i=1,2,…,N，H(Ai)为目标回波信息值，k=1,2,…,K，m=1,2,…,M。
对于一个SST而言，SST回波间隔距离会小于或等于多帧积累时间内的SST运动距离，根据多帧积累时间和SST运动速度得到SST运动的距离门限，通过距离门限检测出可能的SST。
在多帧雷达图像中，目标回波距离值门限表达式为
(4)
式中，α为多帧积累时间内的SST运动的距离，V为SST运动速度，Tr为雷达扫描一帧的时间，R为地面雷达威力范围。
在多帧积累图像中，
为目标回波i中心坐标，
为目标回波中心坐标x轴信息，
为目标回波中心坐标y轴信息。根据欧拉公式得到目标回波间隔距离表达式为
(5)
式中:dIJ为目标回波的间隔距离;i,j=1,2,…,N;I=1,2,…,N;J=1,2,…,N。在目标回波中，若dIJ≤α，|H(Ai)-H(Aj)|<ε的条件成立，则会有H(Ai)=H(Aj)+H(Ai)，H(Ai)=H(Aj)，其中ε无限接近于0，i≠j。
根据2.2节中所得到的目标回波信息值对SHNN-CAD异常程度计算权值进行改进。目标回波间隔距离小于或等于α且信息值越相近，该目标回波是SST的概率也就越大。相反，则目标回波是杂波的概率也就越大。为了提高对这类目标回波的检测能力，把目标回波间隔距离小于或等于α且信息值相近的目标回波信息值进行累加并把累加结果作为该区域目标回波SHNN-CAD异常程度计算权值。
所以，可以得到SHNN-CAD权值表达式为
wi=H(Ai)
(6)
式中，H(Ai)为目标回波i的信息值，wi为目标回波i异常程度权值。
在K×M的Q帧积累雷达图像中，目标回波可表示为
Tr=
i=2,…,N}
(7)
式中，Tr为所提取的目标回波，
为目标回波i描述向量，ti为目标回波i提取时间，xkm为目标回波x轴坐标，ykm为目标回波y轴坐标。
假设一组训练样本集z1,z2,…,zL，zi=(
i,bi)表示目标回波i，bi={0,1}为该目标回波是否异常的标记，1表示异常，0表示正常，L为训练样本集个数。
对于每个目标回波zi，利用式(8)计算该目标回波与训练样本的不一致值αi：
αi=A(Bi,zi)
(8)
式中，Bi表示训练样本，A(·)的定义如式(9)所示：
(9)
式中，NN(zi,{z1,z2,…,zL}\zi,j)表示zi与第j训练样本最近邻，
表示集合C和D之间的Hausdorff距离，定义如式(10)所示：
(10)
式中，dist(c,d)表示两点的欧拉距离。由式(8)、式(9)可以得到每个目标回波的NCM值α1，α2，…，αN，目标回波zi的异常程度值pi计算如下：
(11)
SHNN-CAD回波检测方法主要步骤如下：
步骤1 读入Q帧K×M积累雷达图像，用图像标记技术计算出N个目标回波的像素值占空比和长宽比
步骤2 通过式(3)求出目标回波信息值H(Ai)，若dIJ≤α，|H(Ai)-H(Aj)|<ε的条件成立时，通过H(Ai)=H(Aj)+H(Ai)，H(Ai)=H(Aj)对满足该条件的目标回波信息值进行积累，并把积累结果作为该区域目标回波异常程度计算权值wi；
步骤3 建立目标回波训练样本集z1,z2,…,zL，对目标回波构造描述向量i，wi=1为标准SHNN-CAD，wi≠1为加权SHNN-CAD，根据式(8)、式(11)可得加权SHNN-CAD的NCM值αi和异常程度值pi，同理可得标准SHNN-CAD的NCM值为βi和异常程度值为pbi；
步骤4 以加权SHNN-CAD为例，若pi>ε1，则将该目标回波判定为SST，其中ε1为异常程度值门限，i=i+1；
步骤5 若pi<ε2，则该目标回波判定为正常目标，其中ε2为异常程度值门限；
步骤6 若目标回波为正常目标，则将其加入训练样本，实现样本库的在线更新，i=i+1。
为了验证所提出算法的有效性，截取部分送往雷达终端显示的280 s共28帧雷达图像，经过多帧积累得到如图2所示的目标回波积累图像。
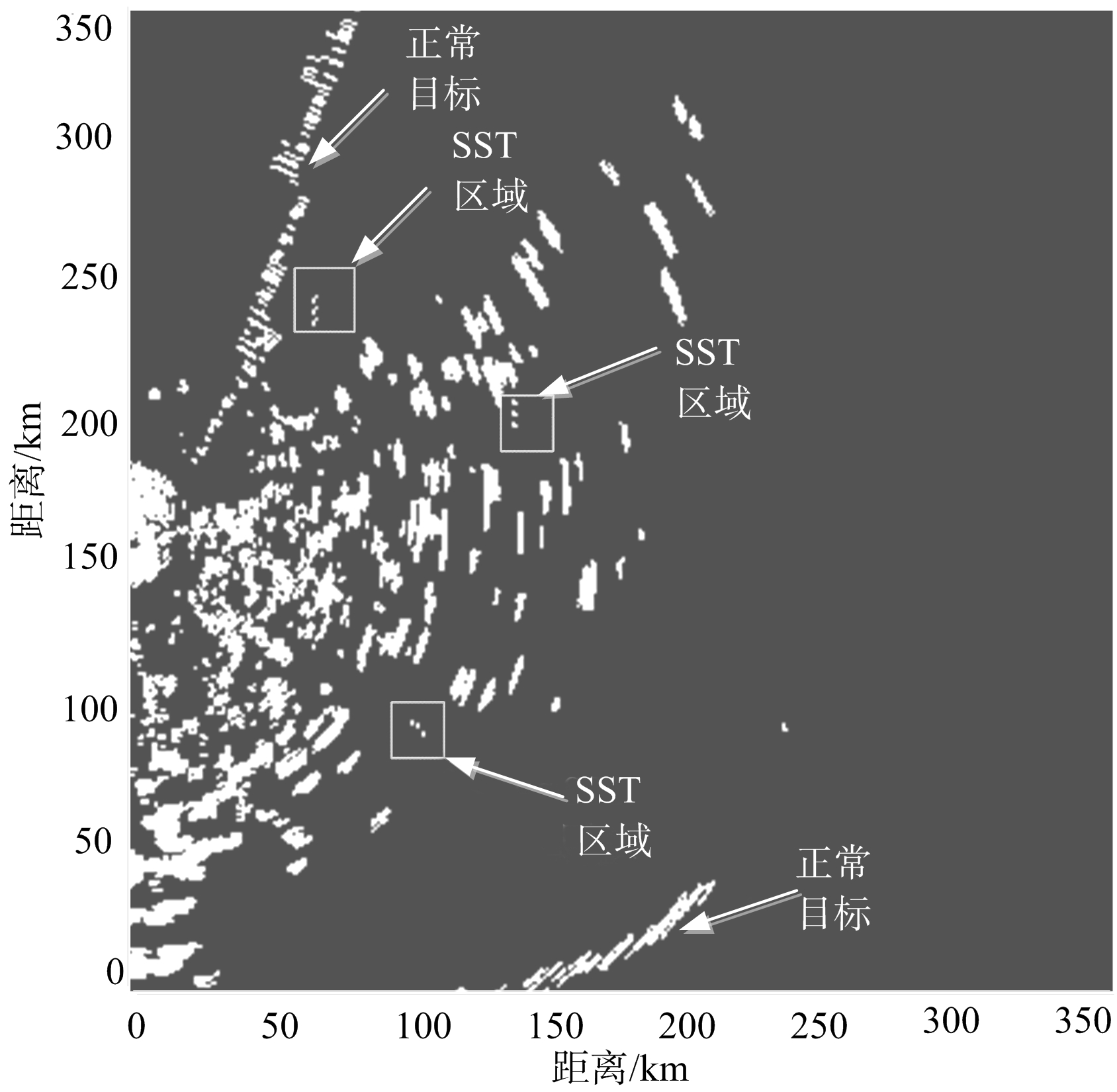
图2 目标回波积累图像
由图2可知，通过多帧积累，目标回波不连通的“SST区域”形成了一条较为明显的目标航迹，极大提高了对这类SST的检测能力。把正常目标形成的目标航迹设定为训练样本。为了简化运算量，选择“正常目标”部分目标回波作为训练样本，其他目标回波通过滤波处理和Hough变换得到如图3所示的滤波效果图。
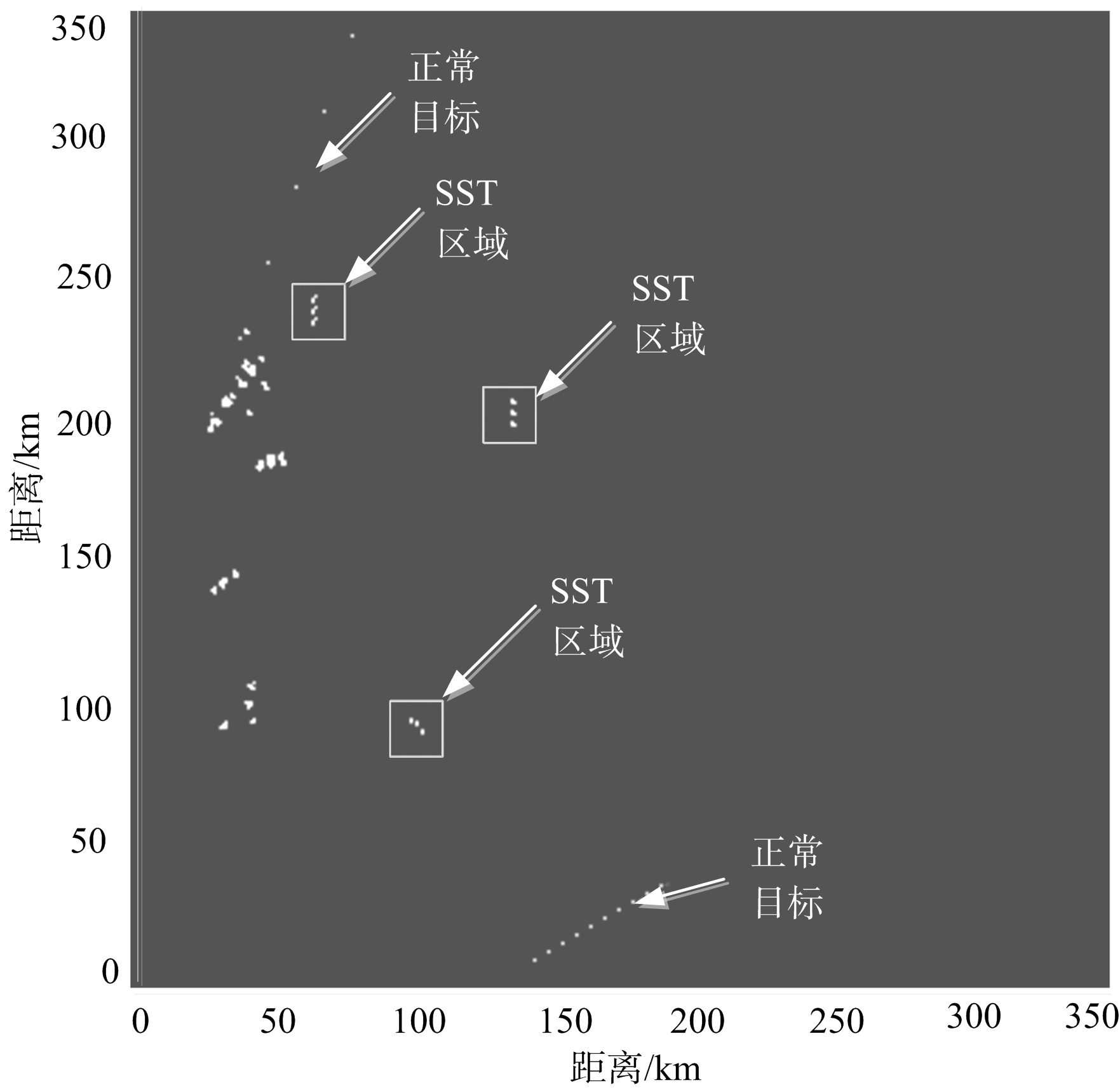
图3 滤波效果图
由图3可知，“正常目标”和“SST区域”是经过滤波处理和Hough变换的部分正常目标和SST。使用标准SHNN-CAD和加权SHNN-CAD进行回波检测，其中ε1=x·p，p为本次异常程度计算最大值，利用正确目标回波检测个数(P1)、错误目标回波检测个数(P2)、正确目标回波检测率(P1d)、错误目标回波检测率(P2d)等指标来衡量目标回波检测的优劣性，P1d和P2d的定义如式(12)、式(13)所示。当x∈(0,1)，Δx=0.1时，通过60次蒙特卡罗仿真试验可以得到两种目标回波检测方法的检测效果如表1所示。
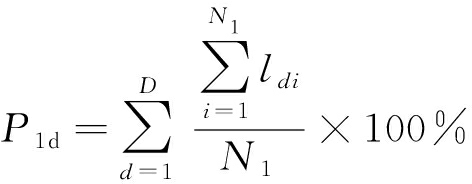
(12)
P2d=1-P1d
(13)
式中，ldi为第d次仿真试验中目标回波i是SST，D为蒙特卡罗试验次数，N1为第d次仿真分析得到的目标回波个数。
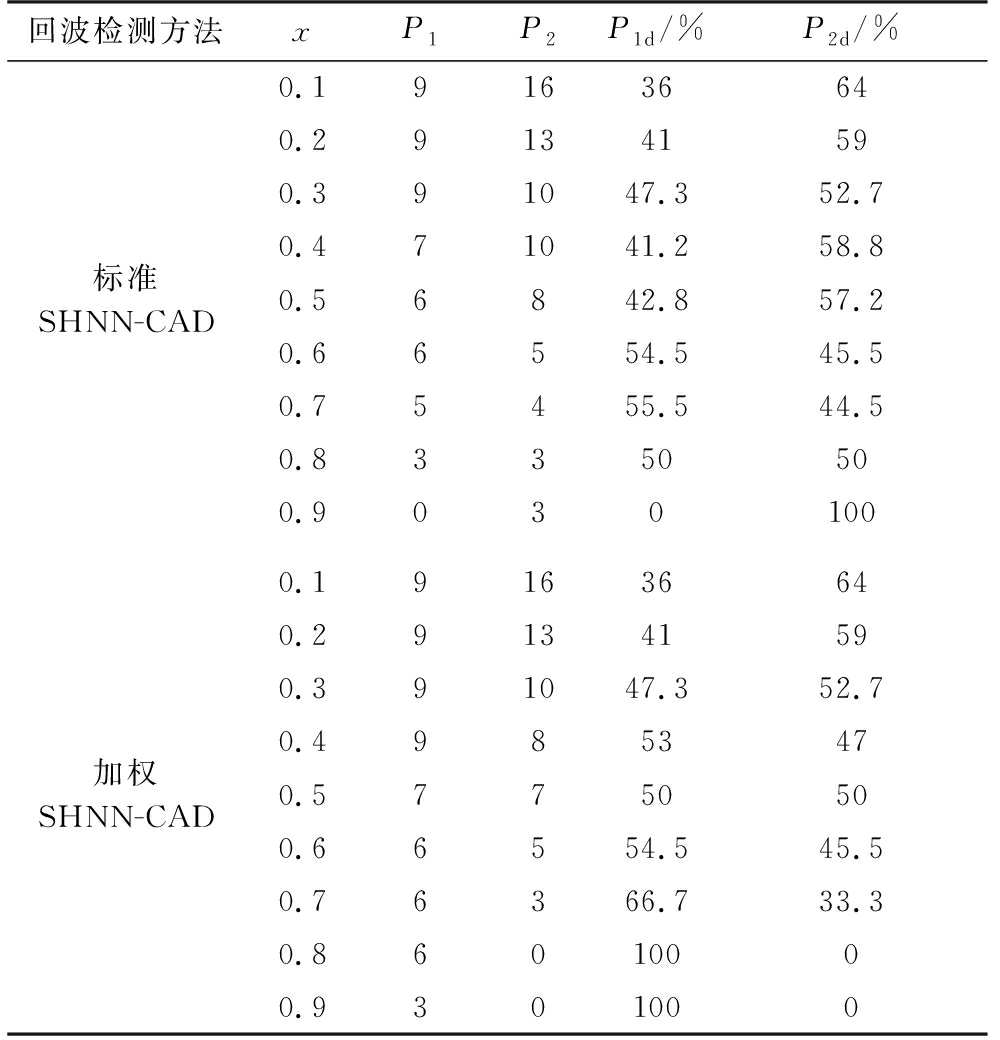
表1 积累回波分析效果
回波检测方法xP1P2P1d/%P2d/%标准SHNN-CAD0.191636640.2913 41590.3910 47.3 52.70.4710 41.2 58.80.568 42.8 57.20.665 54.5 45.50.754 55.5 44.50.83350500.9030100加权SHNN-CAD0.191636640.291341590.391047.352.70.49853470.57750500.66554.545.50.76366.733.30.86010000.9301000
由表1可知：
1)当x变大时，标准SHNN-CAD对P1d改善程度很小，加权SHNN-CAD对P1d改善程度很大，两种方法都会出现SST丢失的现象，而且加权SHNN-CAD对SST正确检测概率高于标准SHNN-CAD；
2)当x=0.4时，加权SHNN-CAD分析出全部SST，而标准SHNN-CAD分析出7个SST回波，因此加权SHNN-CAD对SST具有更好的回波检测效果，成功解决了标准SHNN-CAD对SST回波检测率低的问题。
当x=0.4时，得到如图4所示的目标回波检测效果图。
由图4可知，标准SHNN-CAD检测出17个目标回波，其中有7个属于SST，正确回波检测率为0.412；加权SHNN-CAD检测出17个目标回波，其中有9个属于SST，正确回波检测率为0.53。因此同标准SHNN-CAD相比加权SHNN-CAD对目标回波不连通SST具有更好的检测效果。
由图3和图4比较可知，通过SHNN-CAD回波检测方法目标回波个数由30减少为17，部分的慢动杂波被成功滤除，有效缩小了SST出现范围，提高了对SST的探测能力。
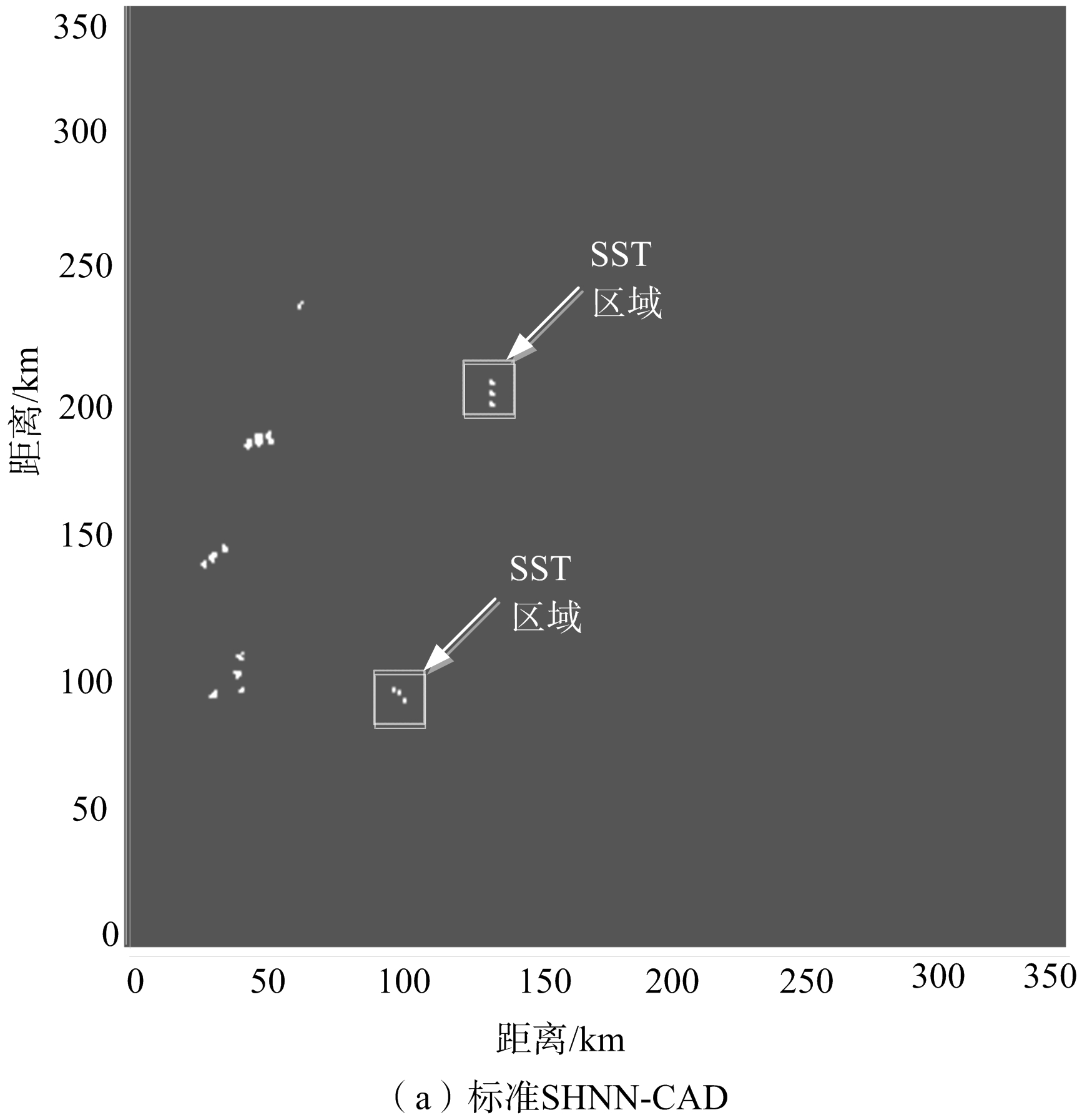
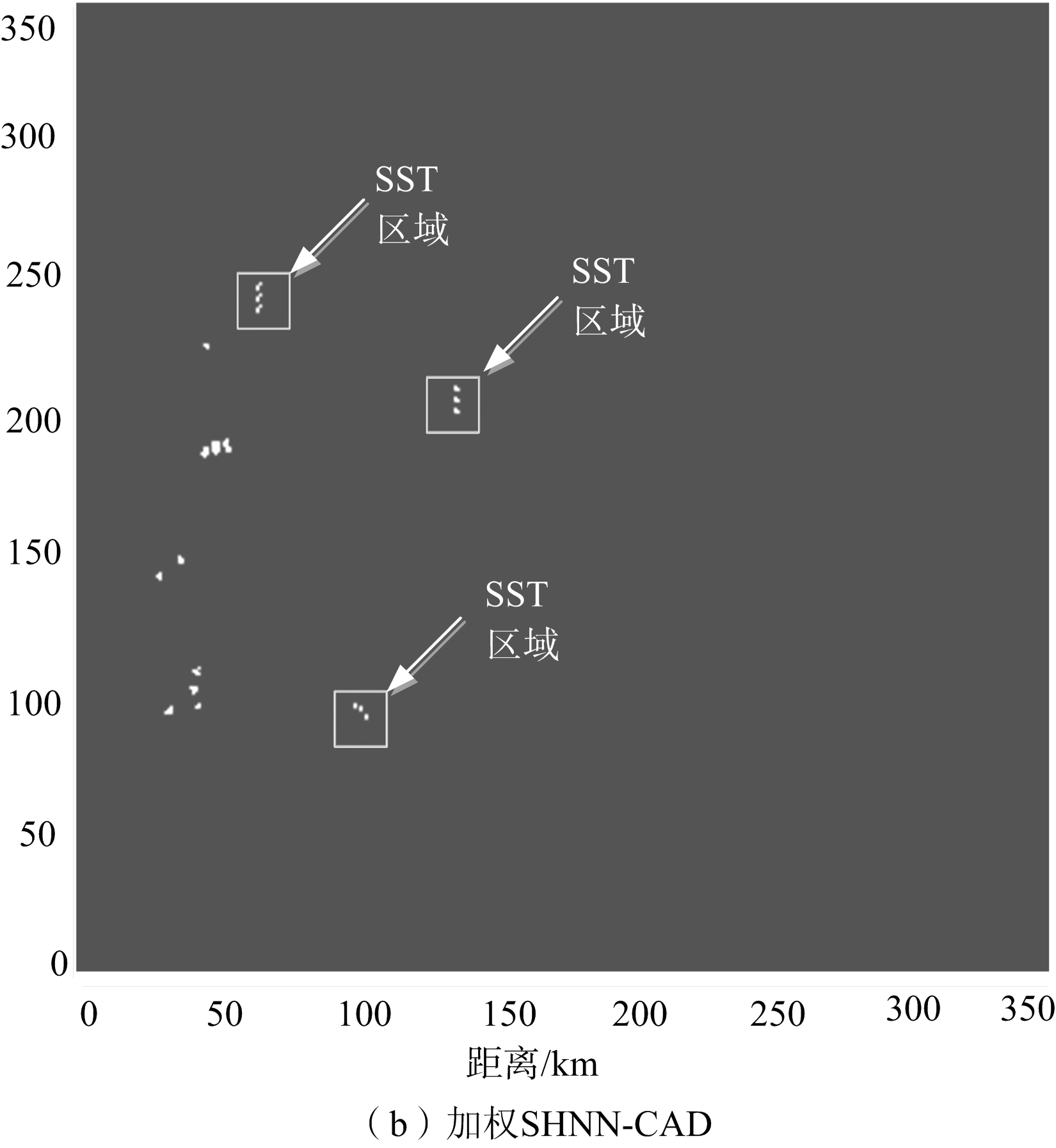
图4 目标回波检测效果图
多帧雷达图像积累会出现目标回波连通与不连通两种积累情况，本文针对目标回波不连通情况，提出了一种目标回波不连通的慢小目标检测方法。该方法运用图像标记提取目标回波长宽比和占空比作为目标回波描述向量，当目标回波间隔距离小于或等于α且目标回波信息值无限接近时，把满足条件目标回波信息值进行累加，并把累加结果作为该区域目标回波SHNN-CAD异常程度计算权值，最终通过控制异常程度值检测出可能的慢小目标。由仿真结果可知，加权SHNN-CAD同标准SHNN-CAD相比对SST具有更好的回波检测能力。
[1] SHERIDAN T B，PARK I，MEYER J，et al.Conflict Monitoring in Air Traffic Control[J].IFAC Proceedings Volumes，2001，34(16):543-548.
[2] 问翔,刘宏伟,包敏.距离扩展目标回波序列的慢时间谱积累检测器[J].西安交通大学学报，2013，47(10):18-24.
[3] 韩晓飞,蒙文,李云霞,等.激光防御低慢小目标的关键技术分析[J].激光应用技术，2013，43(8):867-871.
[4] AOUCHICHE L，FERRO-FAMIL L，ADNET C. An Adaptive Solution for the Detection of Small and Slowly Moving Targets in Highly Ambiguous Radar Context[C]∥ European Radar Conference，London: IEEE，2016:101-104.
[5] 任清安,吕春燕.雷达光电智能协同探测技术研究[J].雷达科学与技术，2016，14(2):173-177.
[6] NGO D V，DO N T，NGUYEN L A T.Anomaly Detection in Video Surveillance: A Novel Approach Based on Sud-Trajectory[C]∥ International Conference on Electronics，Information and Communications，Da Nang，Vietnam:IEEE，2016:1-4.
[7] GHRAB N B，FENDRI E，HAMMAMI M.Abnormal Events Detection Based on Trajectory Clustering[C]∥ 13th International Conference on Computer Graphics，Imaging and Visualization，Beni Mellal，Morocco: IEEE，2016:301-306.
[8] 潘新龙,王海鹏,何友,等.基于多维航迹特征的异常行为检测方法[J].航空学报，2017，38(4)[320442]:1-10.
[9] WIJAYA A P，GROESEN E V.Determination of the Significant Wave Height from Shadowing in Synthetic Image[J].Ocean Engineering，2016，114:204-215.
[10] SANDERS T，GELB A，PLATTE R B.Composite SAR Imaging Using Sequential Joint Sparsity[J].Journal of Computational Physics，2017，338:357-370.
[11] XIA Yang，SONG Zhiyong，LU Zaiqi，et al.A Novel Range-Doppler Imaging Algorithm with OFDM Radar[J].Chinese Journal of Aeronautics，2016，29(2):492-501.
[12] 陈彦军,张学典.基于MATLAB图像处理的角度测量误差分析的研究[J].计算机科学，2015，42(6A):203-208.
[13] WANG Jinli，ZHU Juan，ZHANG Shuyan.Based on Image Processing Technology of Video Precision Measurement System[J].Applied Mechanics and Materials，2013，241/242/243/244:269-271.
[14] 徐颖.基于特征的SAR图像配准算法研究[D].武汉: 空军预警学院，2014:52-60.
Abstract：The radar operators often mistake the slow and small target (SST) as a clutter point because of high clutter interference intensity and weak target echo.Accumulating the continuous multi-frame radar images for a long time and aiming at the problem that the target echoes are not connected in the multi-frame radar image accumulation，a detection method for SST based on target echo disconnection is proposed.Two parameters of the minimum circumscribed
and
introduced and these parameters are extracted from the target echoes by image marking technique.When the target echo interval is less than or equal to the moving distance of the SST within the multi-frame accumulation time and the information values determined by
and
of the target echoes are similar，the target echo information values meeting this condition are accumulated.The accumulation result is taken as the weight to compute the SHNN-CAD exception level of the target echoes in the region.Finally，the possible SST can be detected by controlling the exception level value.The simulation results verity the effectiveness of the proposed algorithm.
