目标跟踪是利用传感器获得关于目标的不精确的观测信息，对目标状态持续进行准确的估计和预测目标的真实信息。目标运动的不确定性、目标机动能力日益增强都使得准确估计目标的运动状态日益困难。在这种情况下，交互多模型混合估计方法被认为是一种最有效的混合估计方案。
交互多模型算法(IMM)是由Blom和Bar-Shalom提出的一种软切换算法，应用很广泛。近年来IMM研究的主要内容第一层是变结构交互多模及模型集自适应、转移概率自适应，而第二层是目标运动模型、非线性滤波器及其参数自适应。虽然IMM的机理从理论上仍然无法论证清晰，但交互多模型混合估计方法仍然成为机动目标跟踪领域主流的混合估计方案。
Markov转移概率是IMM算法的重要参数之一，影响子模型之间的交互与模型切换速度，一般是先验给定的。这必然会与目标的实际运动状态不匹配，引起滤波跟踪精度下降。因此，转移概率的实时自适应一直是国内外学者探讨的重要内容[1-4]。
在目标跟踪系统中，解决非线性滤波最常用的方法是EKF方法及其相关改进算法。CKF算法是近年来新出现的一种非线性滤波算法，该算法利用了三阶球面-径向容积积分准则进行了严密的数学推导，在理论上对该算法具有严格的保证[5-6]，估计精度和数值稳定性都比较高。在对CKF算法深入研究的基础上，有学者提出了降维CKF算法[6-7]，并将降维CKF成功应用于工程实践[7-8]。
本文针对机动目标跟踪，基于降维CKF，线性简化CKF [9]，采用时变Markov转移概率IMM算法，设计了交互式多模型降维容积卡尔曼滤波算法( IMM-RDCKF)，提高了算法的鲁棒性和估计精度。仿真表明，计算量约为IMM-CKF的一半，仅比IMM-EKF增加约30%，目标跟踪精度提升，便于工程应用。尤其是匀速运动速度估计精度提升约27%。这对于预警探测、火力控制、指挥控制等军事应用领域具有非常重要的意义。
常规气动目标的机动可以假设为目标在不同时间段依据不同的运动模型，因而机动目标的运动模型可以假设为具有加性高斯噪声的混合系统，是典型的非线性系统，其数学描述如下：
(1)
式中：Xk是k时刻系统状态变量；Zk是k时刻的系统量测变量；Fk是系统状态转移矩阵；Wk是过程噪声Wk～N(Wk；0,Qk)；hk(Xk)是非线性测量函数；Vk是观测噪声为Vk～N(Vk；0,Rk)。Wk与Vk相互统计独立。
本文中，系统状态向量三维空间中的9维向量：
雷达量测点迹在以雷达天线原点为中心的三维球坐标系下获得的距离r，方位角α，俯仰角β，量测向量为
设
为以雷达天线原点为中心的东北天坐标系下的坐标，量测方程为
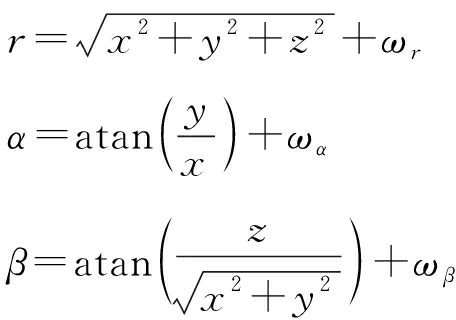
(2)
式中，ωr，ωα，ωβ分别为距离、方位和俯仰角的量测噪声。
考虑目标加速及转弯影响，目标运动模型选择三维协同转弯模型(3DCSCT)、扩维匀速直线运动模型(CV)，3DCSCT相应的过程噪声Q(ω)参见文献[10]。
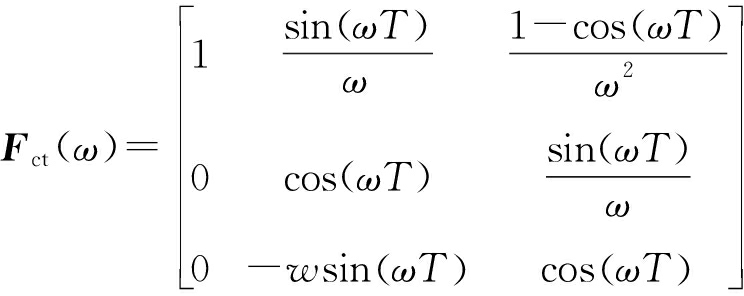
(3)
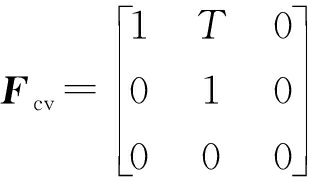
(4)
CKF是基于高斯假设的贝叶斯滤波估计的基本框架，通过容积准则能将非线性滤波问题转化成为高斯概率密度函数加权的多维几何体的容积计算。
设离散非线性系统为
(5)
式中：f(·)和h(·)为已知任意函数，系统噪声为Wk～N(Wk；0,Qk)；观测噪声为Vk～N(Vk；0,Rk)。
根据三阶球面-径向容积积分准则，CKF算法[5]的实现步骤为：
1) 一步预测：假设已知k-1时刻的状态xk-1的统计特性为
先对Pk-1作平方根分解，得Sk-1，令i=1,2,…，2n，选择容积点为
权重
计算状态预测：
xi,k|k-1=f(xi,k-1)
(6)
(7)
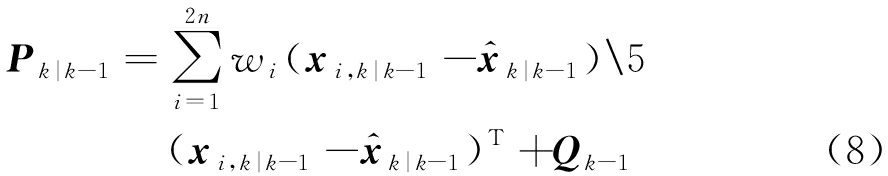
2) 量测更新：对Pk|k-1作平方根分解，得Sk|k-1，令i=1,2,…，2n，选择容积点为
权重
计算量测预测：
zi,k|k-1=h(xi,k|k-1)
(9)
(10)
计算协方差和互协方差：
Pzz,k|k-1=
(11)
Pxz,k|k-1=
(12)
状态更新：
(13)
(14)
(15)
在实际的工程应用中，状态方程、量测方程并非都是非线性的。例如导航领域中，量测方程是线性的；目标跟踪应用领域中，其状态方程是线性的。此时，针对线性的模型方程，常规线性Kalman滤波算法理论上是最小均方准则最优的，因此可以直接用线性Kalman滤波进行运算[9]。
针对式(1)描述的目标跟踪应用场景，一步预测步骤可以简化为
(16)
(17)
即为KF算法的一步预测过程，其滤波精度与式(6)～式(8)相当。
常规CKF算法采样点均是系统状态向量维数的2倍。对于导航、目标跟踪等特殊非线性模型，可以发现，影响系统非线性的只是其状态向量的部分元素，引起线性Kalman滤波算法无法使用，而只能使用非线性滤波算法。例如针对式(1)的EKF算法中，其量测矩阵H中，只有1，4，7列针对位置的偏导数不为零，而2，3，5，6，8，9列针对速度、加速度的偏导数均为零。因此在增益计算中：
Kk=Pk|k-1HT(HPk|k-1HT+R)-1
实际只有Pk|k-1的1，4，7行、列中的位置协方差对增益有贡献。据此，可以对EKF算法作一定程度的精简。
对于目标跟踪应用系统采用CKF滤波过程中，同样存在类似情况。其系统由式(1)描述，状态方程是线性的，量测方程的非线性仅与直角坐标下目标的位置x,y,z有关。对线性变量和非线性变量进行区别处理，减少采样的容积点，有利于降低计算复杂度，减少计算量[6-9]。由于降维CKF依然采用三阶球面-径向容积积分准则，理论估计精度为三阶多项式精度，因此滤波精度与常规CKF相当，针对目标跟踪的CKF算法量测更新过程可以进一步简化。
首先，对系统状态向量调整顺序，变为
对协方差Pk同步进行调整，把位置x,y,z有关的矩阵元素调整到前t行前t列，即矩阵的左上角。针对目标跟踪应用场景，t=3。
再令
表示
的前t个元素，
表示Pk|k-1前t行前t列元素组成的矩阵，
为Pk|k-1的Cholesky分解Sk|k-1的前t行前t列元素组成的下三角矩阵。
量测更新过程为：对Pk|k-1作Cholesky分解，得到Sk|k-1，进而得到
令i=1,2,…，2t，选择容积点为
权重
计算量测预测：
zi,k|k-1=h(ζi,k|k-1)
(18)
(19)
计算协方差和互协方差：
Pzz,k|k-1=
(20)
Pxz,k|k-1=
(21)
式中，
表示Sk|k-1的n行前t列元素组成的矩阵。最后，在Xk，Pk输出时，再次反向调整矩阵中元素的顺序。
至此，式(13)～式(21)构成完整的线性简化降维CKF(RDCKF)算法，将此算法与交互多模型算法结合，即可构成IMM-RDCKF算法。
IMM算法的输出是各个子模型输出结果以模型概率加权作为最终的滤波估计，各子模型依据马尔科夫链以一定的转移概率进行切换。因此，模型概率表征了子模型对目标运动的匹配度。本文采用了文献[2]的方法，实时修正模型概率。
对于IMM算法的r个子模型，k时刻子模型j的概率μj(k)，Markov矩阵中子模型i到子模型j的转移概率为pij(k)。则
pij(k)′=κj(k)pij(k-1),i,j=1,…,r
(22)
式中，κj(k)=e(μj(k)-μj(k-1))。
进一步归一化处理：
pij(k)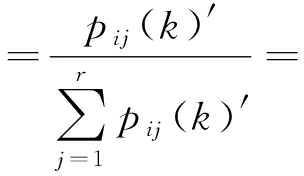
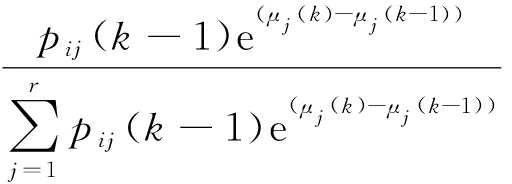
(23)
该算法通过子模型后验概率自适应地递推估计模型转移概率，提高匹配模型的概率，抑制非匹配模型的概率，因而可以提高滤波过程中的模型切换速度，从而提高跟踪精度和收敛速度。
在仿真实现过程中，发现由于数值计算误差的累积，经常出现协方差矩阵非正定导致Cholesky分解无法进行，递推中断。因此，对代码实现进行了优化：
(24)
采用式(24)替换式(15)，消除了误差累积，极大地提高了算法的鲁棒性。
同时，EKF算法在递推过程中，同样存在数值计算误差、一阶泰勒展开截断误差的累积导致协方差矩阵不可逆。因此EKF算法仅仅由于运算简单而广泛使用，但同时要忍受其精度较差、鲁棒性差的缺点。
平方根算法的优点在于递推中直接传递协方差矩阵的平方根而避免了Cholesky分解、奇异值分解等各种平方根分解步骤，因而鲁棒性较好。但是对于各种改进算法，如过程噪声自适应、量测噪声动态估计等，增加了Q，R的平方根分解，算法步骤过于复杂，计算效率不高。此时，本文算法的一系列改进既能保证精度，又能保证鲁棒性，还能进一步叠加过程噪声自适应、量测噪声动态估计等其他改进方法，其工程价值较高。
目标在三维空间的初始状态为[120 000； -426；0；2 000；0；0；2 000；0；0]，采用周期T为1 s，雷达量测误差距离标准差100 m，方位、俯仰角度标准差1°，初始协方差为P0=diag([100，10，1，100，10，1，100，10，1])，过程噪声方差阵为Q=diag([80，10，10，80，10，10，80，10，10])。仿真时长200 s，目标发生机动时刻及加速度大小如表1所示，其余时间作匀速运动，进行100次蒙特卡罗仿真。本文的算法在仿真时采用扩维CV，3DCSCT模型，作为对比，常规三模型IMM子模型选择CV，CS，3DCSCT。仿真平台是Intel Core i5-3470，主频3.2 GHz CPU，4 G内存的PC机，软件环境是Matlab 2013a。
算法性能评价指标为均方根误差：
RMSE=
(25)
IMM-RDCKF初始转移概率矩阵：
三模型IMM转移概率矩阵为
表1 目标机动运动情况表
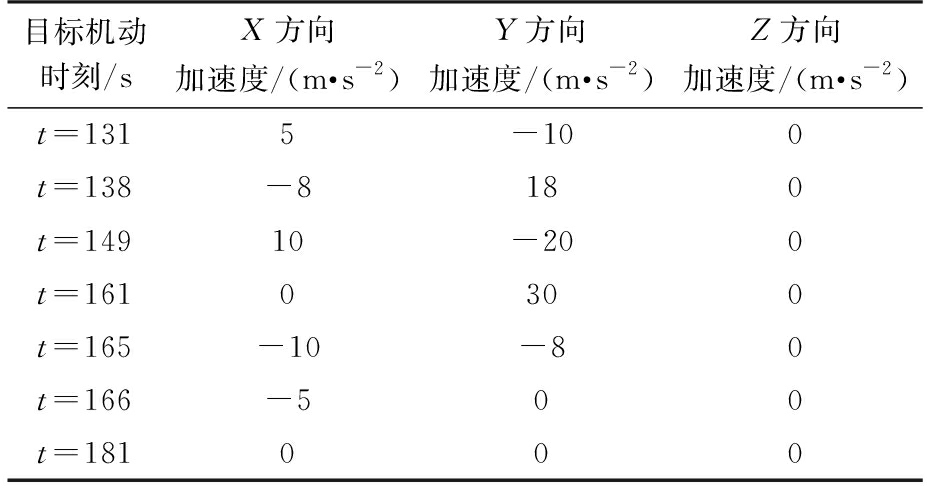
目标机动时刻/sX方向加速度/(m·s-2)Y方向加速度/(m·s-2)Z方向加速度/(m·s-2)t=1315-100t=138-8180t=14910-200t=1610300t=165-10-80t=166-500t=181000
仿真结果表明，本文算法和IMM-CKF算法都可以对目标运动进行有效跟踪。经过分析表明，IMM-RDCKF与常规IMM-EKF、IMM-CKF算法相比较，优点在于以下几点：
1) 跟踪精度提高。本文算法通过实时修正模型转移概率，使与目标运动匹配的模型概率增大，加快模型切换速度，最终提高了精度，如图1所示。从表2可以看出，在全航路，距离精度提高8.2%，速度精度提高12.9%；尤其是在匀速段，速度精度提升26.9%。另一方面，在图2中，细实线表示IMM3-EKF算法，由于IMM3中存在模型竞争，实际滤波效果比本文算法还差。
2) 算法效率提升。采用线性简化状态方程、对量测方程降维处理。与IMM2-EKF相比，时间增加了35%；与IMM3-EKF相比，时间减少了21%；与IMM2-CKF相比，时间减少了53%。
3) 算法稳定性提高。本文算法在实现时，优化了实现步骤，避免了CKF算法实现时数值计算误差积累造成的平方根分解错误，因而不必采用平方根算法即可保证算法的稳定性，同时也比EKF稳定性强。
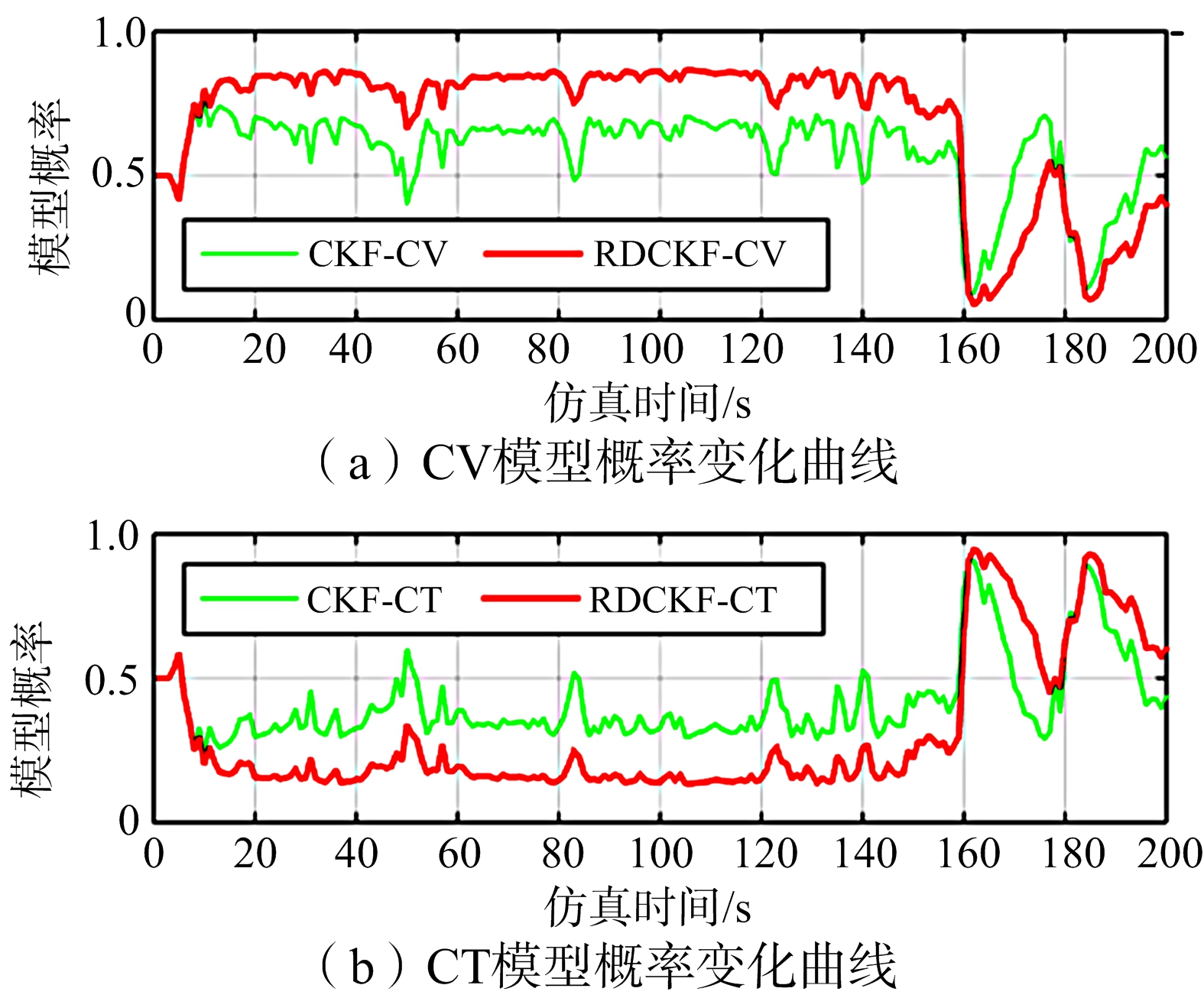
图1 模型概率变化曲线
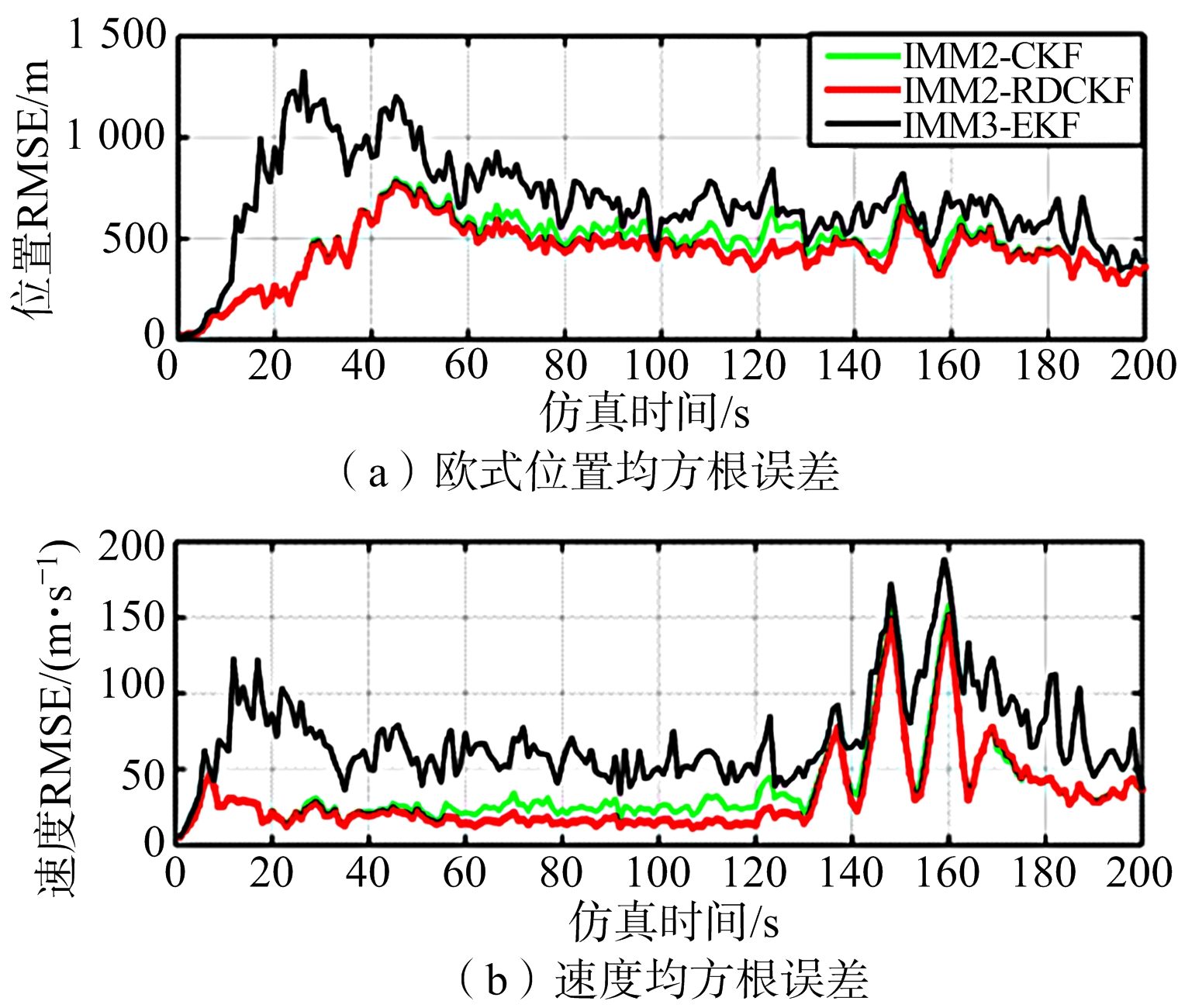
图2 位置和速度均方根误差
表2 算法性能对比
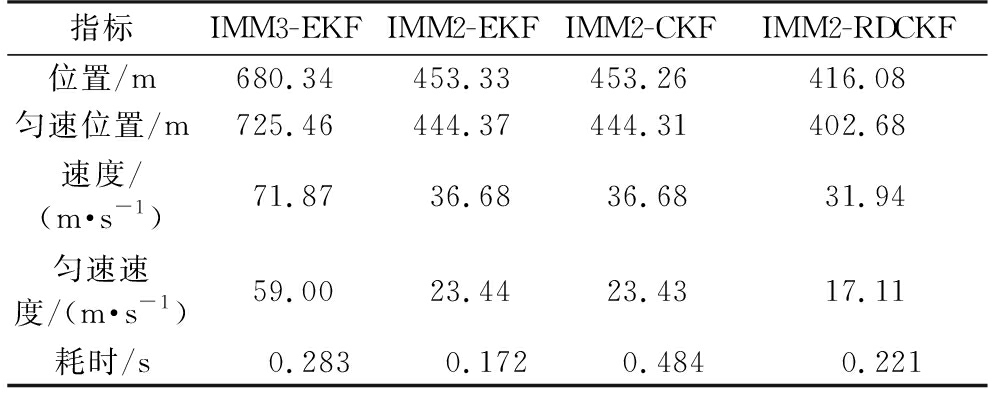
指标IMM3-EKFIMM2-EKFIMM2-CKFIMM2-RDCKF位置/m680.34453.33453.26416.08匀速位置/m725.46444.37444.31402.68速度/(m·s-1)71.8736.6836.6831.94匀速速度/(m·s-1)59.0023.4423.4317.11耗时/s0.2830.1720.4840.221
本文提出的时变转移概率IMM-RDCKF算法，充分利用了量测方程中只有部分状态变量是非线性的特点，只对非线性状态变量采样，不仅减小了计算量，而且继承了CKF算法滤波精度高的优点，有效克服了常规IMM-CKF算法计算量大的缺点；同时通过优化代码，消除了计算过程的数值计算误差积累，保障协方差矩阵在滤波过程中始终保持对称和正定，提高了算法稳定性；通过实时修正模型转移概率，使与目标运动匹配的模型概率增大，加快模型切换速度，最终提高了精度。因此，本文提出的时变转移概率IMM-RDCKF算法在计算效率、跟踪精度、鲁棒性方面都比常规交互多模算法强，是一种工程应用价值比较高的机动目标跟踪算法。
[1] 孙晓舟.机动目标时变转移概率IMM跟踪算法[J]. 电子世界, 2017(15):34-35.
[2] 郭志,董春云,蔡远利,等.时变转移概率IMM-SRCKF机动目标跟踪算法[J]. 系统工程与电子技术, 2015,37(1):24-30.
[3] 赵斌,胡建旺,吉兵,等.修正马尔可夫矩阵的IMM-GMPHD算法研究[J]. 军械工程学院学报, 2016,28(1):40-45.
[4] 汪云,胡国平,刘进忙,等.群目标跟踪自适应IMM算法[J]. 哈尔滨工业大学学报, 2016,48(10):103-109.
[5] 王世元,黄锦旺,谢智刚,等.非线性卡尔曼滤波器原理及应用[M]. 北京: 电子工业出版社, 2015.
[6] 葛磊. 容积卡尔曼滤波算法研究及其在导航中的应用[D]. 哈尔滨: 哈尔滨工程大学, 2013.
[7] 黄湘远,汤霞清,武萌.基于降维CKF和平滑的SINS/OD动基座对准[J]. 系统工程与电子技术, 2016, 38(9):2135-2141.
[8] 宋嘉钰,杨黎明,李东杰.降维CKF算法在大失准角传递对准中的应用[J]. 太赫兹科学与电子信息学报, 2017,15(5):740-744.
[9] 蔡宗平,牛创,戴定成.基于简化CKF的IMM算法[J].现代防御技术, 2015,43(6):99-103.
[10] LI X R, JILKOV V P. Survey of Maneuvering Target Tracking: Part Ⅰ Dynamic Models [J]. IEEE Trans on Aerospace and Electronic Systems, 2003,39(4):1333-1364.
